Abstract
The predictions of a theory for the anomalous mole fraction effect (AMFE) are tested experimentally with synthetic nanopores in plastic. The negatively charged synthetic nanopores under consideration are highly cation selective and 50 Å in diameter at their smallest point. These pores exhibit an AMFE in mixtures of Ca2+ and monovalent cations. An AMFE occurs when the conductance through a pore is lower in a mixture of salts than in the pure salts at the same concentration. For ion channels, the textbook interpretation of the AMFE is that multiple ions move through the pore in coordinated, single-file motion. However, because the synthetic nanopores are so wide, their AMFE shows that single filing is not necessary for the AMFE. It is shown that the AMFE in the synthetic nanopores is explained by a theory of preferential ion selectivity. The unique properties of the synthetic nanopores allow us to experimentally confirm several predictions of this theory. These same properties make synthetic nanopores an interesting new platform to test theories of ion channel permeation and selectivity in general.
INTRODUCTION
Ion channels, at their most fundamental level, are pores that conduct and select ions according to physical laws. Therefore, any ion channel theory of permeation and selectivity should be transferable to other nanopores, even synthetic ones. If the “important” characteristics of a channel are also present in the nanopore, both systems should exhibit similar conductance and selectivity properties. What these “important” characteristics are can be determined by experiments (mutations, for example) or inferred from theories. Because any inferences from theories must be tested, synthetic nanopores can serve as an important test case for these predictions. In this article, we use synthetic nanopores in plastic to probe which channel characteristics are necessary to produce an anomalous mole fraction effect (AMFE).
The AMFE occurs in some ion channels when mixtures of two ion species produce a lower conductance than the same concentration of either species by itself; when the total concentration of ions is constant, the conductance versus mole fraction (concentration proportion) curve has a minimum. According to the classical theory in ion channels, the AMFE is produced by the momentum-correlated movement of ions in a single file through a narrow channel, modeled by ions hopping over energy barriers between energy wells that are independent of the presence or absence of neighboring ions (1). This theory is still taught in textbooks (2) and similar theories are still used to model ion transport (3). Ion channel experiments are also routinely interpreted in terms of this model (4–15). However, the assumption that both the energy barriers/wells and the ions themselves are unaffected by the electrostatic potential of nearby ions contradicts the findings of recent ion channel simulations, both on the atomistic timescale (16,17) and at steady state (18).
In work by Nonner, Chen, and Eisenberg (19), a completely different theory without single filing is used to explain the AMFE in ion channels. Rather than indicating multiple ion occupancy, Nonner, Chen, and Eisenberg (19) assert that the AMFE indicates a relatively high affinity of the channel for one ion species over the other. It is this preferential binding of one ion species over another that causes the resistance of the selectivity filter to change differently with mole fraction than the resistances at the channel entrances. The AMFE occurs because these parts of the channel are in series with each other (19). Here, we use synthetic nanopores to experimentally study some predictions and new aspects of this AMFE theory.
The synthetic nanopores we use have many properties in common with ion channels (20,21), but also offer several advantages over direct channel measurements. For example, these nanopores have a large negative surface charge made of COO− groups. The protonation state of these groups can be titrated (by changing pH) to make the pore cation selective or completely nonselective. We use these characteristics to test several aspects of the new AMFE theory: 1), single filing of ions through a narrow pore is not necessary for the AMFE; and 2), the AMFE reflects the preferential selectivity of the pore for one cation species over the other. We also propose that to observe an AMFE in experiments, the conductance of the pore at mole fractions 0 and 1 must be approximately equal. We confirm these predictions with experiments and also show that a theory of variable resistances within the pore reproduces the AMFE observed in the synthetic nanopores.
THEORY AND METHODS
Experiments: the synthetic nanopores
The single double-conical (hourglass) nanopores were prepared in 12-μm-thick polyethylene terephthalate (PET) (Hostaphan, RN12, Kalle, Niederlassung der Hoechst AG, Wiesbaden, Germany) membrane by the track-etching technique (22). Briefly, this technique consists of irradiating a PET membrane with a single, accelerated, heavy ion (UNILAC, Gesellschaft für Schwerionenforschung, Darmstadt, Germany) and subsequent chemical etching of the damage tracks left by the heavy ions. Etching one side of an irradiated PET membrane in a highly concentrated base (9 M NaOH) produces a conical pore (23,24). Therefore etching from both sides produces a double-conical shape. This is shown in Fig. 1 with an electromicrograph of a freeze-fractured PET membrane (25).
FIGURE 1.
Scanning-electron micrograph of a cross section of a PET membrane that was irradiated with 107 ions per cm2, which after etching resulted in 107 pores/cm2. The membrane was etched in the same way as the single-ion irradiated foils used in this study. A special technique was used to render the polymer brittle and avoid residual strain in the freeze-fractured specimens, but this technique does not alter the pore structure (25). The middle of the double-conical pore is beyond the resolution of the microscope. (A and B) Two membranes where the cleavage plane exposes the double-conical nanopores. (C and D) Close-up images of the two nanopores indicated in panels A and B. The double-conical geometry is clearly visible. To make the pores more visible in all panels, brightness and contrast were increased. The scale bar in each panel represents 1 μm.
Etching PET membranes with NaOH naturally forms carboxyl (COOH) groups on the surface of the membrane and on the pore walls at a uniform density of approximately one group per nm2. When fully deprotonated (for example, at pH > 7), these form a surface charge of one negative charge per nm2 or −0.16 C/m2 (26). The diameter of the small opening can be calculated by the electrochemical method as previously described (23).
To measure ionic current, a membrane with a single double-conical nanopore was inserted between two chambers of a conductivity cell filled with a given electrolyte. The baths were buffered to pH values between 7 and 8 with <2 mM Tris buffer and to pH 5.5 with <2 mM MES buffer; for pH 3, they were adjusted with 0.1 M HCl. Buffers were chosen so that the ion/buffer complexes were highly soluble to avoid their precipitation within the pore (27,28). Currents were recorded with a 6487 Keithley Instruments (Cleveland, OH) picoammeter/voltage source connected to Ag/AgCl electrodes containing a saturated KCl solution. The voltage was changed in 2 mV steps, which were applied for 3 s. Conductance was determined by fitting the current/voltage curve between −100 mV and +100 mV with a line.
Theory: computing conductance
To compute the conductance g through the nanopores, we use the one-dimensional integrated Nernst-Planck equation. We outline the derivation briefly by starting with the three-dimensional Nernst-Planck equation
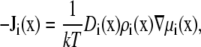 |
(1) |
where 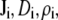 and
and 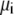 are the local flux density, diffusion coefficient, density, and chemical potential, respectively, of ion species i, k is the Boltzmann constant, and T is the temperature. By averaging these equations over equiconcentration/potential surfaces with area A (29,30), Eq. 1 can be reduced to a one-dimensional approximation (29,30),
are the local flux density, diffusion coefficient, density, and chemical potential, respectively, of ion species i, k is the Boltzmann constant, and T is the temperature. By averaging these equations over equiconcentration/potential surfaces with area A (29,30), Eq. 1 can be reduced to a one-dimensional approximation (29,30),
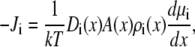 |
(2) |
where Ji is now the flux of species i, not the flux density, and is a constant. Equation 2 can be integrated from bath to bath across the pore to give the conductance
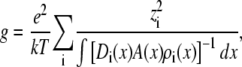 |
(3) |
where 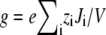 and where we have assumed that both baths are identical (which they will be in this article). Because the synthetic nanopores are highly cation-selective (see below), we only consider the contribution of the cations to the conductance.
and where we have assumed that both baths are identical (which they will be in this article). Because the synthetic nanopores are highly cation-selective (see below), we only consider the contribution of the cations to the conductance.
The nanopores we use are double cones (Fig. 1) with a cone angle θ of ∼1.5° above the pore axis (Table 1). Because the cone angle is very small, near any location x along the pore axis, the pore is effectively a straight cylinder of radius 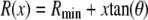 where
where 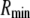 is the radius at the center of the pore. Therefore, to reduce the three-dimensional problem (Eq. 1) to one-dimensional (Eq. 2), we average over the radial direction and
is the radius at the center of the pore. Therefore, to reduce the three-dimensional problem (Eq. 1) to one-dimensional (Eq. 2), we average over the radial direction and 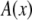 is the cross-sectional area
is the cross-sectional area 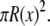 The small cone angle also allows one to estimate the resistance of species i in a small subregion of the pore (several angstroms long, for example) by
The small cone angle also allows one to estimate the resistance of species i in a small subregion of the pore (several angstroms long, for example) by
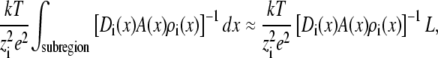 |
(4) |
where L is the length of the subregion; the diffusion coefficient, area, and concentration are locally constant because the pore geometry does not change appreciably over a few angstroms.
TABLE 1.
Parameters of the synthetic nanopores
| Pore | Small diameter | Large diameter | Cone angle | DK (m2/s) 100 mM | DCa (m2/s) 100 mM | DK (m2/s) 20 mM | DCa (m2/s) 20 mM |
|---|---|---|---|---|---|---|---|
| 1 | 54 Å | 1580 Å | 0.73° | 1.37 × 10−9 | 0.388 × 10−9 | — | — |
| 2 | 52 Å | 3982 Å | 1.88° | 1.29 × 10−9 | 0.336 × 10−9 | — | — |
| 3 | 46 Å | 1850 Å | 0.86° | — | — | 1.03 × 10−9 | 0.173 × 10−9 |
| 4 | 46 Å | 2560 Å | 1.20° | 1.20 × 10−9 | 0.323 × 10−9 | 1.06 × 10−9 | 0.181 × 10−9 |
Geometric parameters and effective diffusion coefficients for the four nanopores we used. All the nanopores have the double-cone geometry shown in Fig. 1 and are 12 μm long. The “small diameter” is the diameter at the center of the pore and the “large diameter” is the diameter at the mouths of the pore. These diameters were estimated as previously described (23). “Cone angle” is the angle of the pore wall above the long pore axis. DK and DCa are the effective diffusion coefficients needed to reproduce the data (when experimental data was available to determine them). The cation concentration (100 mM or 20 mM) is indicated for each column. For comparison, the infinite-dilution, bulk values are 1.96 × 10−9 and 0.79 × 10−9 m2/s for K+ and Ca2+, respectively.
We assume that the (radially averaged) diffusion coefficients 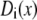 are constants that do not change with location. We do this for several reasons. First, it simplifies the theory, but the result still reproduces the experimental data (see below). Second, it is not known how diffusion coefficients change radially in a confining tube or how a radially averaged diffusion coefficient changes with pore diameter. Although work has been done on uncharged tubes, even these give different answers depending on the method used and the amount of simulation time (31–35). Little work has been done on diffusion coefficients in charged pores. Third, a diffusion coefficient computed from molecular dynamics simulations is unlikely to be transferable to our primitive model of electrolytes where water is just a background dielectric (see below). Explicitly including water molecules qualitatively changes the local structure of the double layers near the pore walls (36,37), and therefore one would not expect to compute the same conductance in both implicit and explicit water with the same diffusion coefficient in Eq. 3. In this first application of the theory, we avoid these unknowns by using an effective diffusion coefficient instead. As shown in Table 1, the computed diffusion coefficients depend on the bath concentration, but are consistent across the pores for each bath concentration.
are constants that do not change with location. We do this for several reasons. First, it simplifies the theory, but the result still reproduces the experimental data (see below). Second, it is not known how diffusion coefficients change radially in a confining tube or how a radially averaged diffusion coefficient changes with pore diameter. Although work has been done on uncharged tubes, even these give different answers depending on the method used and the amount of simulation time (31–35). Little work has been done on diffusion coefficients in charged pores. Third, a diffusion coefficient computed from molecular dynamics simulations is unlikely to be transferable to our primitive model of electrolytes where water is just a background dielectric (see below). Explicitly including water molecules qualitatively changes the local structure of the double layers near the pore walls (36,37), and therefore one would not expect to compute the same conductance in both implicit and explicit water with the same diffusion coefficient in Eq. 3. In this first application of the theory, we avoid these unknowns by using an effective diffusion coefficient instead. As shown in Table 1, the computed diffusion coefficients depend on the bath concentration, but are consistent across the pores for each bath concentration.
This leaves the concentration profile 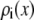 along the pore axis to be determined. For this we use equilibrium three-dimensional Monte Carlo (MC) simulations. We use these concentration profiles in the conductance equation (Eq. 3), an approach we call NP+MC for Nernst-Planck plus Monte Carlo. The one-dimensional Nernst-Planck (Eq. 2) does not implicitly assume single-filing of ions. Specifically, the Nernst-Planck equation is a statement of the conservation of mass, and it does not include the momentum conservation that would be required to model momentum-correlated, single-filing ions (38,39). Rather, it approximates the current as coming from a cross-sectional average of the three-dimensional concentration profile provided by the MC simulations (29,30).
along the pore axis to be determined. For this we use equilibrium three-dimensional Monte Carlo (MC) simulations. We use these concentration profiles in the conductance equation (Eq. 3), an approach we call NP+MC for Nernst-Planck plus Monte Carlo. The one-dimensional Nernst-Planck (Eq. 2) does not implicitly assume single-filing of ions. Specifically, the Nernst-Planck equation is a statement of the conservation of mass, and it does not include the momentum conservation that would be required to model momentum-correlated, single-filing ions (38,39). Rather, it approximates the current as coming from a cross-sectional average of the three-dimensional concentration profile provided by the MC simulations (29,30).
The synthetic nanopores are 12 μm long, so it is computationally impossible to include the entire pore in one simulation. We therefore use multiple simulations at different x along the pore with radius 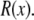 For each pore radius
For each pore radius 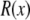 and each Ca2+ mole fraction η, we performed one MC simulation (as described below) to compute average ion concentrations
and each Ca2+ mole fraction η, we performed one MC simulation (as described below) to compute average ion concentrations 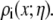 Specifically, we used
Specifically, we used 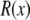 of 25.5, 39.8, and 58.9 Å because these allow an exact placement of one charge per nm2 to give a surface charge of −0.16 C/m2.
of 25.5, 39.8, and 58.9 Å because these allow an exact placement of one charge per nm2 to give a surface charge of −0.16 C/m2.
To “stitch” these different subregions of the pore together, for each Ca2+ mole fraction η, we interpolated the bath concentrations at  and the radially-averaged concentration at
and the radially-averaged concentration at  with the equation
with the equation
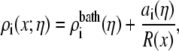 |
(5) |
where for species i the mole fraction-dependent ai is the fitting parameter. This ensured that the concentrations in the baths and in the center of the pore were correct. As a check, we ensured that concentrations at the intermediate two-pore radii (39.8 and 58.9 Å) were close to the interpolated value; the deviation was usually <10%.
For each Ca2+ mole fraction η we used (0%, 0.5%, 1%, 5%, 10%, 20%, 50%, 80%, and 100%), Eq. 5 gives 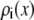 for all x. To compute
for all x. To compute 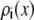 for any mole fraction η, ai was interpolated with the following formulas:
for any mole fraction η, ai was interpolated with the following formulas:
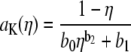 |
(6) |
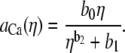 |
(7) |
These interpolated the results to within a few percent.
Substituting Eq. 5 into Eq. 3 and integrating from 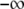 to
to 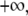 we get
we get
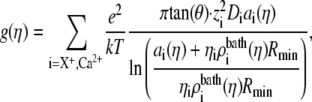 |
(8) |
where ηi is η for Ca2+ and 1 − η for the monovalent cation X+ = Li+, Na+, K+, or Cs+. We assume that the cones were infinitely long, which for these 12-μm-long pores is reasonable. With the interpolation for ai (Eqs. 6 and 7), Eq. 8 gives the conductance for all η from a small number of MC simulations. Because the pore—in both experiments and theory—cannot distinguish among different monovalent cations (see below), we only simulated K+ and used those concentration profiles for the other monovalent cations. The diffusion coefficients of these other cations X+ were the diffusion coefficient for K+ scaled by the ratio of the bulk (infinite-dilute) diffusion coefficient of X+ and K+. Therefore, the only parameters to be determined are the K+ and Ca2+ diffusion coefficients.
Several theoretical studies of PET nanopores have been done (40–45). These generally used a one-dimensional Poisson-Nernst-Planck model with point ions. In the one-dimensional approximation, the surface charge becomes a volume charge that is present throughout the pore lumen instead of just on the surface. We tried to apply this approach, but found that the volume charge did not reproduce either the cation versus anion selectivity or the divalent versus monovalent cation selectivity found in experiments. The three-dimensional MC simulations that explicitly included the surface charge and pore lumen reproduced both of these (as well as having a more realistic representation of the ions as charged, hard spheres). The previous studies (40–45) only modeled permeation of KCl and did not consider the cation versus cation selectivity in a way studied here.
Theory: Monte Carlo simulations
The three-dimensional MC simulations use a standard Metropolis grand canonical algorithm as previously described (46). Chemical potentials of the prescribed salt concentrations are calculated using the iteration method of Malasics et al. (47). The temperature is 300 K. The electrolyte is modeled with the primitive model, meaning that the ions are charged, hard spheres and water are a background dielectric, and the dielectric constant is 80 throughout the system. This model of electrolytes does not include the excluded-volume effects of water, but it uses significantly less computer time while still qualitatively reproducing the properties of ions in confined geometries ((48) and references therein). In the simulations, the ions had the following diameters: Li+ 1.20; K+ 2.66; Cs+ 3.40; Ca2+ 1.98 Å; and Cl− 3.62 Å.
Because the nanopores are 12 μm long, we simulate several subregions of the pore with different radii, as described above. The shallow cone angle of the pores allows us to approximate each subregion as an infinitely long cylinder with a hard wall in the radial direction. The infinite cylinder, produced with periodic replicas of a 200-Å-long unit cell, eliminates any edge effects of finite cylinders that is not present in the nanopore. This cylinder is simulated to be in equilibrium with a bath of given ionic concentrations. Each simulation took 2–3 h on one 2.5 GHz processor. The output is the radial distribution of ions within the cylinder. To compute the average ion concentrations 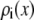 used in Eq. 5, the average number of each ion species within a 200-Å-long unit cell is computed and divided by the volume of the unit cylinder.
used in Eq. 5, the average number of each ion species within a 200-Å-long unit cell is computed and divided by the volume of the unit cylinder.
The surface charge of the nanopore is modeled by a point charge at the center of a 10 Å×10 Å tile on the surface of the cylinder. We only simulated cylinders with radii that allowed an integer number of such tiles on the cylinder surface. These charges model the discrete COO− groups on the nanopore walls at the experimental surface charge density. We only simulated fully charged nanopores (that is, pH 8).
RESULTS
Selectivity properties of the nanopores
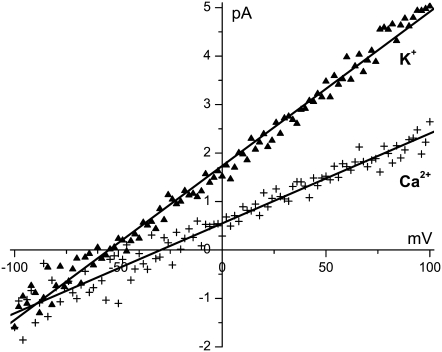
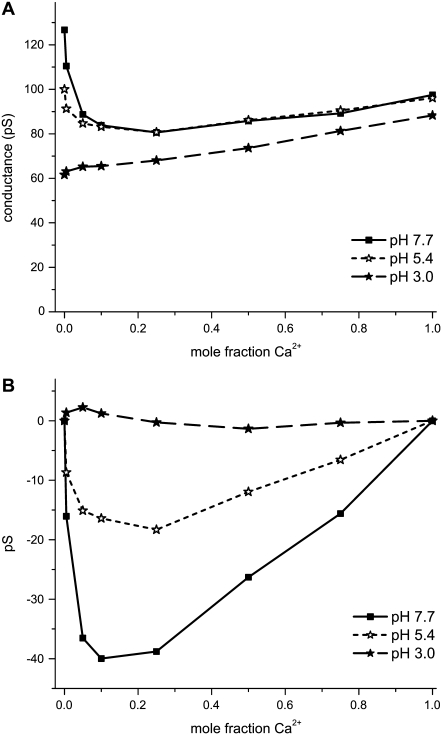
At a pH of 7.7, the COO− groups lining the synthetic nanopores create a surface charge of ∼1 negative charge per nm2 (−0.16 C/m2) (26). This is sufficient for an ∼50 Å-wide pore (pore No. 1, Table 1) to be highly cation selective: in a concentration gradient of 10 mM KCl in the cis bath and 1 mM KCl in the trans bath, the reversal potential is −54.6 mV (Fig. 2). With the same concentrations of CaCl2, the reversal potential is −29.6 mV (Fig. 2). Both of these are very close to the cations' respective Nernst potentials and give large cation versus Cl− Goldman-Hodgkin-Katz permeability ratios: 50 for KCl and >100 for CaCl2. (It is not possible to determine an exact value for the Ca2+ permeability ratio because the Cl− permeability is so close to 0.) We show later that at pH 3.0—when the COO− are fully protonated—the same nanopore is completely nonselective (see Fig. 8).
FIGURE 2.
Cation over anion selectivity of the synthetic nanopores. The current/voltage curve of pore No. 1 (Table 1) is measured with 10 mM KCl in the cis bath and 1 mM KCl in the trans bath (▴ symbols) or with the same concentration gradient of CaCl2 (+ symbols). The lines are linear least-squares fits of the data from which the reversal potential was determined. The trans bath was electrically grounded.
FIGURE 8.
Effect of decreasing pore surface charge by decreasing pH. The total cation concentration was 100 mM for the mixtures of Ca2+ and K+ with pore No. 1 (Table 1). (A) The mole fraction experiment is done at pH 7.7 (▪), 5.4 (⋆), and 3.0 (★). The pH 3.0 result is a line (p < 0.0001). (B) The same data in panel A, but with the line connecting the mole fraction 0 and 1 data point subtracted off.
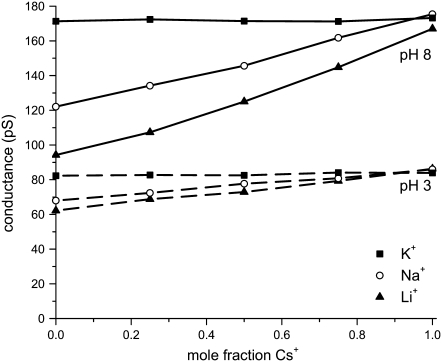
The conductances in pure monovalent-Cl (mole fraction 0) also support the high cation over anion selectivity: the ratio of the conductances (in pure KCl and LiCl, for instance) is equal to the ratio of the bulk diffusion coefficients of the cations. For example, the ratio of KCl to LiCl conductance in Fig. 3 is 1.82 at pH 8.0 whereas the ratio of the K+ and Li+ diffusion coefficients is 1.90. When the pore surface charge is zero (at pH 3.0), the KCl/ LiCl conductance ratio is only 1.32 (Fig. 3). Similar results were found in all the pores we studied with all combinations of monovalent cations (Figs. 4 A and 5), indicating that the cations carry the vast majority of the current.
FIGURE 3.
Mole fraction experiments with mixtures of Cs+ with Li+, Na+, or K+ in pH 8.0 (solid lines) and pH 3.0 (dashed lines) in pore No. 4 (Table 1). At pH 8.0, the COO− groups that make the pore surface charge are fully deprotonated. At pH 3.0, they are fully protonated and the pore has no surface charge. The total cation concentration is 100 mM.
FIGURE 4.
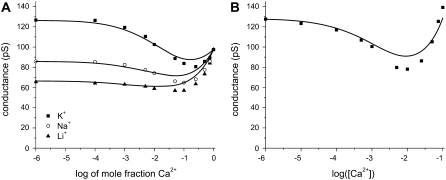
(A) Mole fraction experiment with mixtures of Ca2+ with Li+, Na+, or K+ in pore No. 1 (Table 1). The total cation concentration is 100 mM. (B) [K+] = 100 mM and CaCl2 is added to the baths (pore No. 1). In both panels, the symbols are the experiments and the lines are theory. The diffusion coefficients for K+ and Ca2+ from panel A were used to compute the line in panel B.
FIGURE 5.
Mole fraction experiment with mixtures of Ca2+ with Li+, Na+, K+, or Cs+. (A) Experiments are performed with pore No. 2 (Table 1) and a total cation concentration of 100 mM. (B) Experiments are performed with pore No. 3 (Table 1) and a total cation concentration of 20 mM. In both panels, the symbols are the experiments and the lines are theory. The dashed line corresponds to Cs+, which has a slightly larger diffusion coefficient than K+ (2.06 × 10−9 m2/s for Cs+ and 1.96 × 10−9 m2/s for K+).
When different cations compete for the pore, divalent cations are preferred: 1 mM Ca2+ added to 100 mM K+ has a measurable effect on the current, reducing it by 20% (Fig. 4 B). The synthetic nanopores cannot, however, distinguish among different monovalent cations. This is shown in Fig. 3 (solid lines) where Li+, Na+, or K+ compete for the pore with Cs+ in a mole fraction experiment. Each conductance versus mole fraction curve is very close to linear, indicating that each monovalent's contribution to the conductance is proportional to its mole fraction in the bath; that is, the pore does not preferentially conduct one monovalent cation over the other. When the pH is lowered to 3.0, these conductance versus mole fraction curves are still linear (Fig. 3, dashed lines).
AMFEs in the nanopores
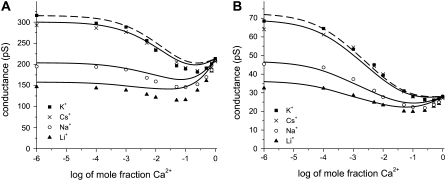
Even though the four nanopores we consider are >45 Å in diameter, they exhibit AMFEs in all the mixtures of Ca2+ and monovalent cations we tested (Li+, Na+, K+, and Cs+). In pore No. 1 (Table 1), we found an AMFE if [X+] + [Ca2+] (X+ = Li+, Na+, and K+) was held constant at 100 mM (Fig. 4 A, symbols). We also found an AMFE if [K+] is kept fixed at 100 mM and Ca2+ was added symmetrically to both baths (Fig. 4 B, symbols). This produces a 40% block of K+ current, which is similar to the 50–60% block of monovalent current found in the ryanodine receptor (RyR) calcium channel (49), but significantly less than the 90% block of Na+ current found in the L-type calcium channel (50). (We did not test Li+, Na+, or Cs+ with this added-salt protocol.)
We also found AMFEs in the other nanopores we prepared. Like pore No. 1, pore No. 2 (Table 1) also exhibited an AMFE when [X+] + [Ca2+] = 100 mM (X+ = Li+, Na+, K+, and Cs+). This is shown in Fig. 5 A. Pore No. 2 had approximately the same diameter at the pore center as pore No. 1, but 2.5 times the cone angle (3.74° vs. 1.46°). In pore No. 3 (Table 1), which had a geometry similar to pore No. 1, we tested a different total concentration (20 mM). This, too, produced an AMFE (Fig. 5 B).
The experiments shown in Figs. 4 and 5 (symbols) then demonstrate that single filing of ions in a pore is not necessary to produce an AMFE. Whereas the textbook, single-filing theory of the AMFE cannot explain our data, the theory of Nonner, Chen, and Eisenberg (19) can. According to this theory, the AMFE is the result of the electrical resistances in different regions of the pore and that they change differently with mole fraction because of the preferential binding of one ion species over another. The same thing happens in the synthetic nanopores. In any region of a pore, the local diffusion coefficient, cross-sectional area, and concentration are approximately constant. The resistance of ion species i in a subregion of the pore near x (Eq. 4) is then proportional to 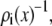 the reciprocal of the concentration.
the reciprocal of the concentration.
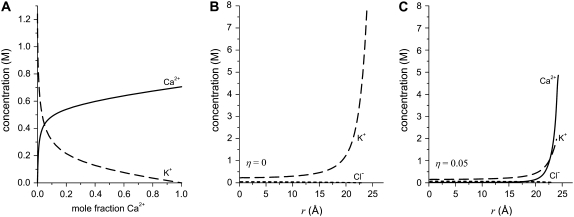
How the resistance in any region of the pore changes with mole fraction then depends on how the local concentration changes with mole fraction. Near the mouths of the pore that are almost 1500 Å wide, the concentration is very similar to the bath concentrations; the concentration changes linearly with mole fraction. The story is different in the middle of the pore where the diameter is only ∼50 Å, as shown in Fig. 6 A. There, the Ca2+ concentration is always greater than linear whereas the K+ concentration is less than linear; that is, Ca2+ is present in higher proportion than in the bath whereas K+ is present in lower proportion. This is what is meant by “preferential selectivity”, in this case of Ca2+ over K+. This displacement of K+ from the pore is also shown in Fig. 6, B and C, with radial concentration profiles for two Ca2+ mole fractions η. This preferential binding of Ca2+ causes the resistance in the middle of the pore to change differently from that in the outer regions. This produces an AMFE when the conductance of the entire pore is computed (Eq. (8)).
FIGURE 6.
Ion concentrations determined from MC simulations in a 51 Å-wide pore. The total cation concentration was 100 mM. (A) Average concentration of Ca2+ (solid line) and K+ (dashed line) as the mole fraction of Ca2+ is changed. (B and C) Concentration profiles of Ca2+ (solid line), K+ (dashed line), and Cl− (dotted line) in the radial direction (r) of the pore. An electrical double layer that is many ions wide is formed near the charged wall. In panel B, the Ca2+ mole fraction η is 0. In panel C, η = 0.05. The average concentration shown in panel A is determined by averaging the radial concentration profiles like those shown in panels B and C.
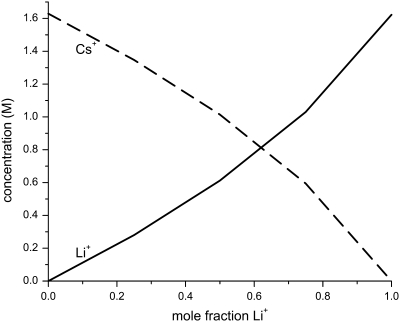
On the other hand, mole fraction experiments with two monovalent cations do not produce an AMFE (Fig. 3). Our simulations show why: the cation concentrations at the center of the pore are approximately linear functions of mole fraction; neither cation is preferentially bound in the pore (Fig. 7). Therefore, the resistance in the middle of the pore changes in the same way with mole fraction as the resistance in the mouth regions.
FIGURE 7.
Average concentration of Li+ (solid line) and Cs+ (dashed line) as the mole fraction of Li+ is changed. The ion concentrations were determined from MC simulations in a 51 Å-wide pore. The total cation concentration was 100 mM.
AMFE and pore cation affinity
This theory of the AMFE then suggests an experiment: reducing the affinity of the pore for Ca2+ over K+ should reduce the size of the AMFE. The synthetic nanopore offers an easy way to explore this change in affinity by changing pH to change the (average) protonation state of the COO− groups on the pore surface. Reducing the negative surface charge will reduce the affinity of the pore for Ca2+ by reducing the Ca2+ to K+ ratio in the pore; in the limit of zero surface charge, the Ca2+ to K+ ratio should be the ratio in the baths (which is very different from the ratio in the fully charged pore shown in Fig. 6 A). The idea of preferential binding would predict that the conductance versus mole fraction curve should become more linear as surface charge is reduced.
This is what we find when pH is changed from 7.7 (large negative pore surface charge) to 3.0 (zero surface charge). Fig. 8 A shows the results of a mole fraction experiment where [K+] + [Ca2+] = 100 mM. The pH = 7.7 curve (squares) is the K+ versus Ca2+ mole fraction curve shown in Fig. 4 A. When pH = 5.4 (open stars), the conductance in pure KCl (zero Ca2+ mole fraction) has changed. To see if the curve is more linear, we subtract the line connecting the endpoints at mole fraction 0 and 1. This is shown in Fig. 8 B. If a conductance versus mole fraction curve in Fig. 8 A were linear, that curve would be zero at all mole fractions in Fig. 8 B. The pH = 5.4 curve is significantly closer to zero than the pH = 7.7 curve. At pH = 3.0, the pore is completely nonselective, as indicated by the linear conductance versus mole fraction curve (Fig. 8, solid stars).
This result makes sense intuitively. Our wide pore should become a nonselective pipe (with a linear conductance versus mole fraction curve) when all the surface charge is removed. As the surface charge is systematically lowered, the curve must become more and more linear as the nonlinear, fully charged curve (Fig. 8 A, squares) is transformed into the linear, uncharged curve (Fig. 8 A, solid stars). However, if the cause of the AMFE is not due to the selectivity properties of the pore (for example, if the shape of the pore makes correlated ion motion, like in the textbook theory) then alternative theories must explain why the AMFE in a wide pore appears as the surface charge is increased and disappears as the surface charge is decreased. Moreover, alternative theories must explain why there is an AMFE for Ca2+/monovalent mixtures, but not for monovalent/monovalent mixtures. The theory of preferential binding explains both of these experiments.
AMFE and the endpoint conductances
One aspect of the AMFE that was not explored by Nonner, Chen, and Eisenberg (19) is the role of the “endpoint” conductances (that is, the conductances at mole fractions 0 and 1). They noted that different ion diffusion coefficients (which produced different endpoint conductances) gave “a variety of shapes for the AMFE curves.” Here, we propose that to observe an AMFE, it is necessary that the endpoint conductances are approximately equal; the farther the endpoint conductances are apart, the more the conductance needs to be depressed to have a minimum. The synthetic nanopores allow us to test this.
Fig. 3 shows that the synthetic pores are nonselective among different monovalent cations; the conductance versus mole fraction curves are linear. This implies that using Li+ (for example) instead of K+ does not change the monovalent versus Ca2+ affinity of the pore. What does change is the pure monovalent endpoint conductance (at zero Ca2+ mole fraction). Therefore, by using different monovalent cations, we can directly test the prediction that changing one endpoint conductance will affect the depth of the AMFE. Specifically we will show that the closer the two endpoint conductances g(0) and g(1) are (that is, the smaller g(0)–g(1) is), the deeper the AMFE. Also, we will show that the converse: the farther the two endpoint conductances g(0) and g(1) are apart (that is, the greater g(0)–g(1) is), the more shallow the AMFE (if it exists at all).
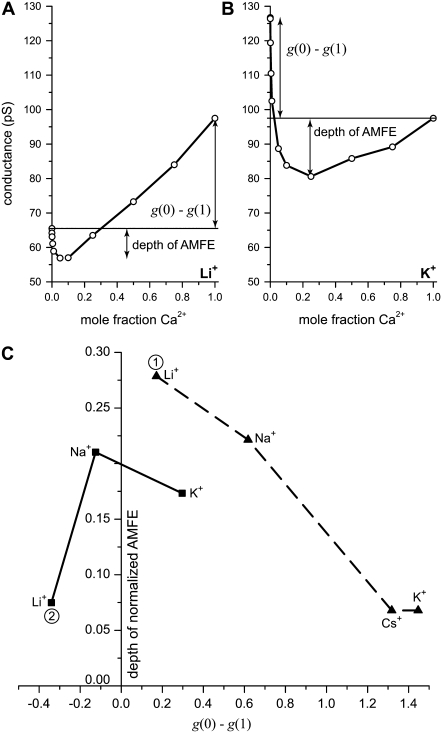
We measure the depth of the AMFE by computing how far the minimum conductance is below the smallest endpoint conductance. This is shown in Fig. 9 where panels A and B show some of the experimental results for pore No. 1 shown in Fig. 4 A. Fig. 9 C shows how the depth of the AMFE varies with g(0)–g(1) for both pores No. 1 and No. 3. The results for pore No. 2 are very similar to pore No. 1 (data not shown).
FIGURE 9.
Correlation of the depth of the AMFE and how far the endpoint conductances g(0) and g(1) are apart. (A and B) The mole fraction curves for mixtures of Ca2+ and Li+ (A) and K+ (B) in pore No. 1. These curves are shown with a logarithmic x axis in Fig. 4 A. The depth of the AMFE is defined as the conductance difference between the minimum and the smallest endpoint conductance. (C) Summarizing the dependence of AMFE depth and g(0)–g(1) in pores No. 1 and No. 3 (Table 1). The results for pore No. 2 were similar to pore No. 1. The AMFE is deepest when the endpoints are approximately equal and shallowest when the endpoints are far apart. For each pore, the conductance was normalized with the pure Ca2+ conductance.
We confirm that the deepest AMFE in both experiments occurs when the endpoint conductances are nearly equal (Fig. 9 C). Conversely, the farther the endpoint conductances are apart, the more shallow the AMFE (Fig. 9 C). Although these conclusions hold for all the monovalents in general, the story is different when individual monovalents are compared between the two experiments. For Li+, for example, when [Li+] + [Ca2+] = 20 mM, Li+ has the deepest AMFE (point 1 in Fig. 9 C), but when [Li+] + [Ca2+] = 100 mM, Li+ has the most shallow AMFE (point 2 in Fig. 9 C). This is the result of the conductance properties of each monovalent (relative to Ca2+) changing when the total concentration is raised from 20 mM to 100 mM. At 20 mM, the conductance of each monovalent (g(0)) is greater than the conductance of Ca2+ (g(1)), whereas at 100 mM, only K+ has a higher conductance than Ca2+ (compare Fig. 5 B and Fig. 4 A).
By using different monovalent cations, we changed one endpoint conductance without changing the binding affinity of the pore. Fig. 9 C then confirms that the depth of the AMFE is not a good measure of the strength of the binding affinity because it depends strongly on the conductance (diffusion) properties of the ions.
DISCUSSION
The usual theory of the AMFE taught in ion channel textbooks requires a narrow pore where the ions' single filing produces momentum-correlated motion and the AMFE (1,2). This interpretation remains a popular way to interpret experimental results (4–15) because it seems to give useful information about a channel: an AMFE implies that a channel is occupied by multiple ions moving through the pore in a single file.
Here we extended work by Nonner, Chen, and Eisenberg (19) to show that this interpretation is not true. Specifically, we used synthetic nanopores in plastic to test some predictions of this theory:
An AMFE can occur in a wide pore without single filing of ions (19). Single filing is an integral component of the textbook theory of the AMFE taught in ion channel textbooks (2). Here, we showed that negatively charged synthetic nanopores exhibit an AMFE even though they are >45 Å in diameter. Moreover, our results are robust; the AMFEs in these nanopores occur in all the mixtures of monovalent cations and Ca2+ we tested (Figs. 4, 5, and 8 A), except when the surface charge was completely neutralized (Fig. 8, solid stars).
The AMFE is produced by the series resistances of regions of the pore that change differently with mole fraction. The simplified theory that uses this principle reproduces the experimental data (Figs. 4 and 5, lines). Consistent with this theory, we found an AMFE whenever the cation concentrations in the center of the pore changed nonlinearly with mole fraction (Figs. 4, 5, and 6 A). Conversely, we did not find an AMFE when these concentrations were approximately linear (Figs. 3, 7, and 8).
The AMFE reflects the preferential selectivity of the pore for one ion species over the other. Consistent with this theory, we found an AMFE when the Ca2+ was present in the center of pore in proportions greater than in bulk and the monovalent cation was present in lower proportions (Figs. 4, 5, and 6 A). Conversely, no AMFE was found when such preferential cation binding was not present (Figs. 3, 7, and 8).
To see an AMFE in experiments, the conductance of the pore at mole fractions 0 and 1 must be approximately equal. This was a new prediction. We found that the closer together the endpoint conductances g(0) and g(1) are, the deeper the AMFE (Fig. 9 C). Conversely, the farther apart the endpoint conductances are, the more shallow the AMFE (Fig. 9 C).
The synthetic nanopores we used here are a unique platform to test our AMFE theory—and, we would argue, a unique platform to test many ion channel theories. Any theory of permeation or selectivity in channels is based on physical principles and must therefore be transferable to systems where those principles apply, even a hole in plastic.
Whereas at 12 μm long the synthetic nanopores are macroscopic compared to channels, 80% of the resistance falls over only ∼200 Å (51); the pores are effectively 200 Å long. Most importantly, they are narrow-like channels; their pores can easily be made down to 20 Å in diameter (52). By adding bulky groups to the wall, they may be made even smaller in the future. Here, we used wider pores to prove a point about the AMFE. But, these wide pores already exhibit several of the properties associated with calcium channels: charge selectivity (Fig. 2), an affinity for Ca2+ of ∼1 mM (Fig. 4 B), and Ca2+ block of monovalent current of ∼40% (Fig. 4 B). Both of these are similar to what is found in the RyR calcium channel (49). This is why we believe that these nanopores can be interesting test beds for calcium channels at the very least.
The synthetic nanopores are, of course, not the same as ion channels. However, because of the negative surface charge of COO− groups, the charge selectivity and the screening of ions inside the synthetic nanopores must be present in ion channels, too. But, because the synthetic nanopores do not share all the physics present in ion channels, they cannot reproduce all the properties of ion channels. This is a strength of our approach. To test any physical theory, it is useful to apply it to a completely different system that shares many of the necessary properties. If the theory is correct, it should predict which channel properties will be reproduced in the nanopore and which will not. For example, our three-dimensional MC simulations confirmed that the nanopores cannot distinguish between monovalent cations the way that the L-type or RyR calcium channels do. On the other hand, MC simulations in similar pores have demonstrated the micromolar Ca2+ affinity of the L-type channel. However, such high Ca2+ affinity was not expected for the synthetic nanopores because the micromolar Ca2+ affinity occurs only in very narrow channels with a diameter of ∼7 Å and when the dielectric properties of the protein are considered (53).
Although testing theories in a similar system is important, the synthetic nanopores also offer several advantages over working with ion channel directly:
pH can change the pore surface charge continuously. Many ion channels can only be studied in a limited range of pH (7.5 ± 1). The synthetic nanopores can, however, be studied down to pH 3.0 to titrate the protonation state of the surface charge (Figs. 3 and 8). Changing the surface charge down to zero in the synthetic nanopores is a unique opportunity for theorists that cannot be done in an ion channel. Changing the charge inside the selectivity filter of an ion channel is only possible with mutations. Even if the mutations do not change the local structure of the pore, creating and expressing the mutants involves significant time and effort.
The surface charge profile can be changed in the synthetic nanopores. In this article, we used COO− groups to form the uniform surface charge for the nanopores we used. But, these are not the only charged groups that can be used. For example, diamines can be used to create a positive surface charge (54,55). Moreover, positive and negative groups can be placed on the surface in different patterns (55,56); a uniform surface charge is only one of many options. Mutations are the only way to achieve this in ion channels. However, introducing a positively charged amino acid (for example) where there was none before is likely to produce a large change in the local protein structure. The charged groups that line the synthetic nanopores do not change the shape of the pore.
A range of pore diameters can be studied with synthetic nanopores. Because of the techniques used to create them, no two synthetic nanopores are the same. The general shape is the same, but the cone angle and the minimum diameter will vary. This is a strength of the nanopore approach because then the effect of different pore diameters can be explored, which is impossible in ion channels. This is generally not a weakness of the nanopore approach because it is straightforward to create pores of approximately the same diameter (Table 1). Even though each pore is different, …
… each synthetic nanopore is viable for weeks. A battery of experiments can be performed with the same pore, days, or even weeks apart.
Different pore geometries can be studied with synthetic nanopores. In this article, we used double-conical nanopores (Fig. 1), but this is not the only shape possible. Single-conical nanopores, with a narrow diameter at one end of the membrane and a large diameter at the other, are also easily produced. These nanopores have different current/voltage characteristics from the double-conical nanopores we use; they can rectify the current (24,51,52,57). This opens the opportunity to study whether some ion channels rectify current simply with geometry.
The synthetic nanopores do not gate or inactivate. An ion channel's open probability (Po) is affected by many things, such as mutations and pH. Po can also be affected by the ion species in the baths. For example, in both the L-type and RyR calcium channels, millimolar Ca2+ in the cytosolic bath significantly reduces Po, making many interesting experiments impractical. Moreover, L-type calcium channels are difficult to study with single-channel recordings because they inactivate within minutes of being patch clamped. Being made of plastic, this is generally not a problem for the synthetic nanopores, especially pores in polyimide (rather than the rougher-walled PET (20)).
The synthetic nanopores can be incorporated into a standard bilayer setup. This opens the possibility that currents through these nanopores can be measured by many electrophysiologists.
Our testing of the AMFE theory shows how useful these synthetic nanopores can be. Moreover, the theory of conductance we have developed provides a relatively fast and accurate method for computing the conductance and the selectivity of the nanopores.
Acknowledgments
The authors are grateful to Bob Eisenberg for useful comments on the manuscript.
D.G. and D.B. were supported through National Institutes of Health grant GM076013 (Robert Eisenberg, principal investigator). D.G. was also supported by National Institutes of Health grant AR054098 (Michael Fill, principal investigator). D.B. was also supported by the Hungarian National Research Fund (OTKA K63322). Z.S.S. acknowledges the financial support from the Pacific Southwest Regional Center for Excellence and the Institute for Complex Adaptive Matter. Z.S.S. is an Alfred P. Sloan Research Fellow.
Editor: Ron Elber.
References
- 1.Hille, B., and W. Schwarz. 1978. Potassium channels as multi-ion single-file pores. J. Gen. Physiol. 72:409–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hille, B. 2001. Ion Channels of Excitable Membranes. Sinauer Associates, Sunderland, MA.
- 3.Zilman, A., S. Di Talia, B. T. Chait, M. P. Rout, and M. O. Magnasco. 2007. Efficiency, selectivity, and robustness of nucleocytoplasmic transport. PLoS Computational Biology. 3:e125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yue, D. T., and E. Marban. 1990. Permeation in the dihydropyridine-sensitive calcium channel. Multi-ion occupancy but no anomalous mole-fraction effect between Ba2+ and Ca2+. J. Gen. Physiol. 95:911–939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mironov, S. L. 1992. Conformational model for ion permeation in membrane channels: a comparison with multi-ion models and applications to calcium channel permeability. Biophys. J. 63:485–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ravindran, A., H. Kwiecinski, O. Alvarez, G. Eisenman, and E. Moczydlowski. 1992. Modeling ion permeation through batrachotoxin-modified Na+ channels from rat skeletal muscle with a multi-ion pore. Biophys. J. 61:494–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tabcharani, J. A., J. M. Rommens, Y. X. Hou, X. B. Chang, L. C. Tsui, J. R. Riordan, and J. W. Hanrahan. 1993. Multi-ion pore behaviour in the CFTR chloride channel. Nature. 366:79–82. [DOI] [PubMed] [Google Scholar]
- 8.Sabovcik, R., J. Li, P. Kucera, and B. Prod'hom. 1995. Permeation properties of a Ca2+-blockable monovalent cation channel in the ectoderm of the chick embryo: pore size and multioccupancy probed with organic cations and Ca2+. J. Gen. Physiol. 106:149–174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ismailov, I. I., V. G. Shlyonsky, O. Alvarez, and D. J. Benos. 1997. Cation permeability of a cloned rat epithelial amiloride-sensitive Na+ channel. J. Physiol. 504:287–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Linsdell, P., J. A. Tabcharani, and J. W. Hanrahan. 1997. Multi-ion mechanism for ion permeation and block in the cystic fibrosis transmembrane conductance regulator chloride channel. J. Gen. Physiol. 110:365–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Qu, Z., and H. C. Hartzell. 2000. Anion permeation in Ca2+-activated Cl− channels. J. Gen. Physiol. 116:825–844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Winters, C. J., and T. E. Andreoli. 2002. Cl channels in basolateral TAL membranes. XVII. Kinetic properties of mcClC-Ka, a basolateral CTAL Cl− channel. J. Membr. Biol. 186:159–164. [DOI] [PubMed] [Google Scholar]
- 13.Lindsay, A. R., S. D. Manning, and A. J. Williams. 1991. Monovalent cation conductance in the ryanodine receptor-channel of sheep cardiac muscle sarcoplasmic reticulum. J. Physiol. 439:463–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tinker, A., and A. J. Williams. 1992. Divalent cation conduction in the ryanodine receptor channel of sheep cardiac muscle sarcoplasmic reticulum. J. Gen. Physiol. 100:479–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sather, W. A., and E. W. McCleskey. 2003. Permeation and selectivity in calcium channels. Annu. Rev. Physiol. 65:133–159. [DOI] [PubMed] [Google Scholar]
- 16.Chung, S.-H., T. W. Allen, M. Hoyles, and S. Kuyucak. 1999. Permeation of ions across the potassium channel: Brownian dynamics studies. Biophys. J. 77:2517–2533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Corry, B., T. W. Allen, S. Kuyucak, and S.-H. Chung. 2001. Mechanisms of permeation and selectivity in calcium channels. Biophys. J. 80:195–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Boda, D., W. Nonner, M. Valisko, D. Henderson, B. Eisenberg, and D. Gillespie. 2007. Steric selectivity in Na channels arising from protein polarization and mobile side chains. Biophys. J. 93:1960–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nonner, W., D. P. Chen, and B. Eisenberg. 1998. Anomalous mole fraction effect, electrostatics, and binding in ionic channels. Biophys. J. 74:2327–2334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lev, A. A., Y. E. Korchev, T. K. Rostovtseva, C. L. Bashford, D. T. Edmonds, and C. A. Pasternak. 1993. Rapid switching of ion current in narrow pores: implications for biological ion channels. Proc. R. Soc. Lond. B. Biol. Sci. 252:187–192. [DOI] [PubMed] [Google Scholar]
- 21.Bashford, C. L., G. M. Alder, and C. A. Pasternak. 2002. Fluctuation of surface charge in membrane pores. Biophys. J. 82:2032–2040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fleischer, R. L. 1975. Nuclear Tracks in Solids: Principles and Applications. University of California Press, Berkeley, CA.
- 23.Apel, P. Y., Y. E. Korchev, Z. Siwy, R. Spohr, and M. Yoshida. 2001. Diode-like single-ion track membrane prepared by electro-stopping. Nucl. Instrum. Methods Phys. Res. Sect. B. 184:337–346. [Google Scholar]
- 24.Siwy, Z. S. 2006. Ion-current rectification in nanopores and nanotubes with broken symmetry. Adv. Funct. Mater. 16:735–746. [Google Scholar]
- 25.Orelovitch, O. L., P. Y. Apel, and B. Sartowska. 2003. Preparation of porous polymer samples for SEM: combination of photo oxidation degradation with a freeze fracture technique. Mater. Chem. Phys. 81:349–351. [Google Scholar]
- 26.Wolf-Reber, A. 2002. Building of an ion scanning conductance microscope: fluctuations of ion current in nanopores. PhD thesis. Johann Wolfgang Goethe Universität, Frankfurt am Maim, Germany.
- 27.Siwy, Z. S., M. R. Powell, A. Petrov, E. Kalman, C. Trautmann, and R. S. Eisenberg. 2006. Calcium-induced voltage gating in single conical nanopores. Nano Lett. 6:1729–1734. [DOI] [PubMed] [Google Scholar]
- 28.Powell, M. R., M. Sullivan, I. Vlassiouk, D. Constantin, O. Sudre, C. C. Martens, R. S. Eisenberg, and Z. S. Siwy. 2008. Nanoprecipitation-assisted ion current oscillations. Nature Nanotechnology. 3:51–57. [DOI] [PubMed] [Google Scholar]
- 29.Nonner, W., and B. Eisenberg. 1998. Ion permeation and glutamate residues linked by Poisson-Nernst-Planck theory in L-Type calcium channels. Biophys. J. 75:1287–1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gillespie, D. 1999. A Singular Perturbation Analysis of the Poisson-Nernst-Planck System: Applications to Ionic Channels. Rush University, Chicago, Illinois. [DOI] [PMC free article] [PubMed]
- 31.Mamonov, A. B., M. G. Kurnikova, and R. D. Coalson. 2006. Diffusion constant of K+ inside gramicidin A: a comparative study of four computational methods. Biophys. Chem. 124:268–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tang, Y. W., I. Szalai, and K. Y. Chan. 2001. Diffusivity and conductivity of a primitive model electrolyte in a nanopore. Mol. Phys. 99:309–314. [Google Scholar]
- 33.Tang, Y. W., I. Szalai, and K. Y. Chan. 2001. Diffusivity and conductivity of a solvent primitive model electrolyte in a nanopore by equilibrium and nonequilibrium molecular dynamics simulations. J. Phys. Chem. A. 105:9616–9623. [Google Scholar]
- 34.Tang, Y. W., K. Y. Chan, and I. Szalai. 2004. Structural and transport properties of an SPC/E electrolyte in a nanopore. J. Phys. Chem. B. 108:18204–18213. [Google Scholar]
- 35.Lynden-Bell, R., and J. C. Rasaiah. 1996. Mobility and solvation of ions in channels. J. Chem. Phys. 105:9266–9280. [Google Scholar]
- 36.Tang, Z., L. E. Scriven, and H. T. Davis. 1992. A three-component model of the electrical double layer. J. Chem. Phys. 97:494–503. [Google Scholar]
- 37.Peter, C., and G. Hummer. 2005. Ion transport through membrane-spanning nanopores studied by molecular dynamics simulations and continuum electrostatics calculations. Biophys. J. 89:2222–2234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lundstrom, M. 2000. Fundamentals of Carrier Transport. Cambridge University Press, New York.
- 39.Chen, D. P., R. S. Eisenberg, J. W. Jerome, and C. W. Shu. 1995. Hydrodynamic model of temperature change in open ionic channels. Biophys. J. 69:2304–2322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cervera, J., B. Schiedt, P. Ramirez. 2005. A Poisson/Nernst-Planck model for ionic transport through synthetic conical nanopores. Europhys. Lett. 71:35–41. [Google Scholar]
- 41.Cervera, J., B. Schiedt, R. Neumann, S. Mafe, and P. Ramirez. 2006. Ionic conduction, rectification, and selectivity in single conical nanopores. J. Chem. Phys. 124:104706. [DOI] [PubMed] [Google Scholar]
- 42.Cervera, J., A. Alcaraz, B. Schiedt, R. Neumann, and P. Ramirez. 2007. Asymmetric selectivity of synthetic conical nanopores probed by reversal potential measurements. J. Phys. Chem. C. 111:12265–12273. [Google Scholar]
- 43.Siwy, Z., and A. Fulinski. 2004. A nanodevice for rectification and pumping ions. Am. J. Phys. 72:567–574. [Google Scholar]
- 44.Fulinski, A., I. Kosinska, and Z. Siwy. 2005. Transport properties of nanopores in electrolyte solutions: the diffusional model and surface currents. N. J. Phys. 7:132. [Google Scholar]
- 45.Constantin, D., and Z. S. Siwy. 2007. Poisson-Nernst-Planck model of ion current rectification through a nanofluidic diode. Phys. Rev. E. 76:041202. [DOI] [PubMed] [Google Scholar]
- 46.Boda, D., M. Valiskó, B. Eisenberg, W. Nonner, D. J. Henderson, and D. Gillespie. 2006. The effect of protein dielectric coefficient on the ionic selectivity of a calcium channel. J. Chem. Phys. 125:034901. [DOI] [PubMed] [Google Scholar]
- 47.Malasics, A., D. Gillespie, and D. Boda. 2008. Simulating prescribed particle densities in the grand canonical ensemble using iterative algorithms. J. Chem. Phys. In press. [DOI] [PubMed]
- 48.Valiskó, M., D. Boda, and D. Gillespie. 2007. Selective adsorption of ions with different diameter and valence at highly-charged interfaces. J. Phys. Chem. C. 111:15575–15585. [Google Scholar]
- 49.Gillespie, D. 2008. Energetics of divalent selectivity in a calcium channel: the ryanodine receptor case study. Biophys. J. 94:1169–1184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Almers, W., and E. W. McCleskey. 1984. Non-selective conductance in calcium channels of frog muscle: calcium selectivity in a single-file pore. J. Physiol. 353:585–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Heins, E. A., Z. S. Siwy, L. A. Baker, and C. R. Martin. 2005. Detecting single porphyrin molecules in a conically shaped synthetic nanopore. Nano Lett. 5:1824–1829. [DOI] [PubMed] [Google Scholar]
- 52.Siwy, Z., and A. Fulinski. 2002. Fabrication of a synthetic nanopore ion pump. Phys. Rev. Lett. 89:198103. [DOI] [PubMed] [Google Scholar]
- 53.Boda, D., M. Valiskó, B. Eisenberg, W. Nonner, D. J. Henderson, and D. Gillespie. 2007. Combined effect of pore radius and protein dielectric coefficient on the selectivity of a calcium channel. Phys. Rev. Lett. 98:168102. [DOI] [PubMed] [Google Scholar]
- 54.Siwy, Z., E. Heins, C. C. Harrell, P. Kohli, and C. R. Martin. 2004. Conical-nanotube ion-current rectifiers: the role of surface charge. J. Am. Chem. Soc. 126:10850–10851. [DOI] [PubMed] [Google Scholar]
- 55.Vlassiouk, I., and Z. S. Siwy. 2007. Nanofluidic diode. Nano Lett. 7:552–556. [DOI] [PubMed] [Google Scholar]
- 56.Kalman, E. B., I. Vlassiouk, and Z. S. Siwy. 2008. Nanofluidic bipolar transistor. Adv. Mater. (Weinheim, Fed. Repub. Ger.). 20:293–397. [Google Scholar]
- 57.Apel, P. Y., I. V. Blonskaya, S. N. Dmitriev, O. L. Orelovitch, A. Presz, and B. A. Sartowska. 2007. Fabrication of nanopores in polymer foils with surfactant-controlled longitudinal profiles. Nanotechnology. 18:305302. [Google Scholar]