Salt Dependence of Nucleic Acid Hairpin Stability

Abstract

Single-stranded junctions/loops are frequently occurring structural motifs in nucleic acid structures. Due to the polyanionic nature of the nucleic acid backbone, metal ions play a crucial role in the loop stability. Here we use the tightly bound ion theory, which can account for the possible ion correlation and ensemble (fluctuation) effects, to predict the ion-dependence of loop and stem-loop (hairpin) free energies. The predicted loop free energy is a function of the loop length, the loop end-to-end distance, and the ion (Na⁺ and Mg²⁺ in this study) concentrations. Based on the statistical mechanical calculations, we derive a set of empirical formulas for the loop thermodynamic parameters as functions of Na⁺ and Mg²⁺ concentrations. For three specific types of loops, namely, hairpin, bulge, and internal loops, the predicted free energies agree with the experimental data. Further applications of these empirical formulas to RNA and DNA hairpin stability lead to good agreements with the available experimental data. Our results indicate that the ion-dependent loop stability makes significant contribution to the overall ion-dependence of the hairpin stability.

INTRODUCTION

Nucleic acids (RNAs and DNAs) are highly charged polyanionic molecules. The metal ions in the solution, such as Na⁺ and Mg²⁺ ions, play an essential role in stabilizing the folded structure through electrostatic screening (1–23). Single-stranded junctions and loops between helices are important structural and functional components of nucleic acids (24–42). Thermodynamic properties of loops and junctions, such as the ion-dependence of loop stability, play an important role in the overall stability of the nucleic acid structures. This study addresses the ion-dependent loop stability and its effect on the ion-dependence of hairpin-folding stability.

The thermodynamic parameters for different types of (hairpin, bulge, and internal) RNA and DNA loops have been measured at standard 1 M NaCl condition (24–42). These parameters form the basis for predicting nucleic-acid folding stability (24–42). However, different ionic conditions can lead to different thermodynamic behaviors of the molecules (43–58), especially in the presence of multivalent ions, such as Mg²⁺ (59–68). For DNA and RNA helices, salt-dependent extensions of the thermodynamic parameters have been derived from experimental data (30,36,56–58) and from statistical mechanical modeling (67,68). However, no such relationship is available for loops. In this article, we develop a statistical mechanical model for the ion-dependent loop stability.

For treating the ion-nucleic acid interactions, there have been mainly two types of classic polyelectrolyte theories: the counterion condensation (CC) theory (69,70) and the Poisson-Boltzmann (PB) theory (71–77). Both (CC and PB) theories are successful in predicting thermodynamics for a broad range of systems with nucleic acids in ionic solutions (69–77). The CC theory is based on the simplified nucleic acid structural model and is a double-limit law, i.e., it is developed for dilute salt solution and nucleic acids of infinite length. The PB theory is a mean-field theory and ignores ion correlation and fluctuation effects which can be important for multivalent ions (e.g., Mg²⁺) solutions (78–82). Recently, we developed a statistical mechanical theory, namely, tightly-bound ion (TBI) theory, to account for correlations and fluctuations for strongly correlated ions (79–82). The theory has been validated through extensive comparisons with experiments on the stability of DNA and RNA helices in pure/mixed Na⁺/Mg²⁺ solutions (67,68) and on the ion-mediated DNA helix assembly and bending (80–82).

Here we will use the TBI theory to investigate the folding thermodynamics of loops and RNA hairpins in Na⁺ and Mg²⁺ solutions. Specifically, we will use the virtual-bond polymer model (Vfold model; (83–85)) to produce loop conformational ensembles, and for each conformation, we use the TBI theory to treat ion-chain interactions. The ensemble average over all the possible conformations gives the ion-dependent loop free energy. We will calculate the loop thermodynamics for different chain length, end-to-end distance, and Na⁺ and Mg²⁺ concentrations. Furthermore, based on the computed loop free energies, we will derive a set of simple empirical formulas for the ion-dependent loop thermodynamic parameters. We will also present extensive experimental tests for these empirical formulas and apply the theory to predict the ion-dependent nucleic acid hairpin folding stabilities.

METHODS

Chain conformational ensemble

For a given length of polynucleotide chain, we apply the Vfold model (83–85) to generate the conformational ensemble of loop conformations. The basic idea is to represent a nucleotide by two virtual bonds: C₄-P and P-C₄ (83–87), where P and C₄ stand for the phosphate and carbon (C₄) atoms, respectively; see Fig. 1 A. The conformation of an N-nt chain is described by the three-dimensional configuration of the 2N virtual bonds. The conformational ensemble of the loop can be generated through self-avoiding walks of the 2N virtual bonds in the three-dimensional space. A survey for the virtual bond configurations in the known RNA structures suggests that diamond lattice bonds can well describe the virtual bonds in realistic structures (88). Therefore, we can generate the loop conformational ensemble through an exhaustive self-avoiding walk of the virtual bonds in a diamond lattice.

FIGURE 1.

Illustrations of the structural model for single-stranded nucleotide chain used in the work. (A) The virtual-bond model for nucleotide chain (83–85). (B) The coarse-grained chain model where P atoms are represented by a series of spheres with charge −e (electronic charge) at the centers (79,89). (C) A three-dimensional chain conformation for the coarse-grained chain model where coordinates of P atoms are produced from the virtual bond model on diamond lattice (83–85). (D) The RNA and DNA hairpin sequences used in our calculations. The thermodynamic parameters at 1 M NaCl, and experimental references for these hairpins are listed in Table 2. The values i and j are the numbers of nucleotides of U's and T's in RH6 and DH1 loops, respectively.

To model the electrostatic properties of the chain, we represent each phosphate group, which carries one electronic charge (−e), by a sphere of radius 2.1 Å (79,89) and place a point charge −e at the center of the sphere (see Fig. 1, B and C). The radius of the sphere is equal to 2.1 Å, which is adopted from the groove-primitive model (79,89). For each chain conformation, we use the TBI theory (79–82) to calculate the electrostatic free energy.

Tightly-bound ion theory

The TBI theory has been described in detail in the literature (67,68,79–82). Here, we only give a brief overview of the theory.

Tightly-bound ions and tightly-bound region

In the TBI theory (67,68,79–82), the monovalent ions are treated as the ionic background as described by the mean-field Poisson-Boltzmann equation (PB) (68,82). For multivalent ions, to account for the possible ion-ion correlation effect, we classify them into two types (79–82) according to the correlation strength: the (strongly correlated) tightly bound ions; and the (weakly correlated) diffusive ions. Correspondingly, the regions where the two types of ions are distributed are denoted as the tightly-bound region and the diffusive region, respectively. For the diffusive ions, we use PB, and for the tightly-bound ions, we use a separate treatment by considering the ion-ion correlations and fluctuations (ensemble) of ion distributions.

Electrostatic free energy

For a single-stranded RNA (or DNA) chain with N phosphate spheres, we divide the whole tightly-bound region into N cells, each around a phosphate. We define a mode of the tightly-bound ion distribution by a set of numbers m₁, m₂, …, m_N, where m_i is the number of the tightly-bound ions in the i^th cell. For z-valent (z ≥ 2) multivalent ions, a cell with m_i = 1 multivalent cation would become positively charged, which makes further addition of ions less likely. Therefore, in practice, we assume that m_i = 0 or 1.

The total electrostatic partition function Z for a given polynucleotide chain conformation is given by the summation over all the possible binding modes M for z-valent ions,

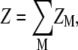(1)

where Z_M is the partition function for a given ion-binding mode M,

(2)

where Z^(id) is the partition function for the uniform ion solution (without the polyelectrolyte). N_z/V is the bulk concentration of the z-valent ion for a 1:z ionic solution (N_z is the total number of the z-valent ions and V is the volume). N_b is the total number of the tightly-bound ions for mode M. 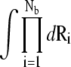is the volume integral for the tightly-bound ions. ΔG_b in Eq. 2 is the mean Coulombic interaction energy between all the charge-charge pairs (including the phosphate groups and the tightly-bound ions) in the tightly-bound region; ΔG_d in Eq. 2 includes the free energy for the electrostatic interactions between the diffusive ions and between the diffusive ions and the charges in the tightly-bound region, as well as the entropic free energy of the diffusive ions. 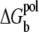is the (Born) polarization energy for the charges in the tightly-bound region (82). The calculations of ΔG_b, ΔG_d, and 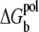have been described in detail in the literature (67,68,79–82).

From Eqs. 1 and 2, the electrostatic free energy G_E for a polynucleotide chain conformation is equal to

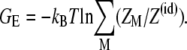(3)

Parameter sets and numerical details in TBI calculations

In this study, the ions are assumed to be hydrated, and the radii of hydrated Na⁺ and Mg²⁺ ions are taken as 3.5 Å and 4.5 Å (67,68,79–82,90), respectively. The dielectric constant ε of molecular interior is set to be 20 (82), and ε of solvent is set as the value of bulk water (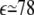 at 25°C). A thin layer of thickness equal to one cation radius is added to the molecular surface to account for the excluded volume layer of the cations (9,79–82). Moreover, we use the three-step focusing process to obtain the detailed ion distribution near the molecules (71,79–82). For each run, the electrostatic potentials are iterated to a convergence of <10⁻⁴ k_BT/e. The grid size of the first run depends on the salt concentration used. Generally, we keep it larger than four times of the Debye length, and the resolution of the first run varies with the grid size to make the iterative process computationally feasible (67,68,79–82). The grid size (L_x, L_y, L_z) for the second and the third runs are kept at (204 Å, 204 Å, 204 Å) and (102 Å, 102 Å, 102 Å), respectively, and the resolutions are kept at 1.36 Å per grid and 0.68 Å per grid, respectively. Correspondingly, the number of the grid points is 151 × 151 × 151 in the second and the third runs. Our results are tested against different grid sizes, and the results are stable.

Loop free energy

As we discussed above, we use exhaustive enumeration of the self-avoiding walk trajectories (on diamond lattice) (83–85) to generate the ensemble of the loop conformations. We use the end-to-end distance x to describe the conformation of the loop, where x is the distance between the phosphates at the 5′ end and the phosphate at the 3′ end of the loop. In general, there are a large number of chain conformations for a given x. We use Ω(N, x) to denote the number of conformations for an N-nt chain with end-to-end distance x.

Loop conformations in the context of RNA structures are often described by the coordinates/configurations of the (two) terminal nucleotides. A given end-to-end distance x, which is defined through the positions of the phosphates, can correspond to multiple possible configurations of the terminal nucleotides of the loop. The average number of loop conformations for given set of configurations of the terminal nucleotides is given by 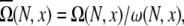where ω (N, x) is the number of different configurations of the terminal nucleotides for a given x. The number of coil conformations is given by the summation over all possible x values: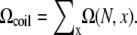

A rigorous treatment for the electrostatic contribution to the loop and coil free energies requires the computation of the electrostatic free energy for each conformational state. However, the number of chain conformations is huge. For instance, for a 13-nt chain, the number of coil conformations is ∼15 × 10¹⁰. Therefore, it is practically impossible to calculate the electrostatic free energy for every chain conformation. In our computational procedure, we randomly select Ω₀(N, x) conformations from the conformational ensemble. During the enumeration of chain conformations, we select conformations through a pseudo random number generator, and simultaneously store the coordinates of P atoms for each selected conformation. In our practice, we choose see Table 1. For each selected conformation, we calculate the electrostatic free energy G_E (through Eq. 3). The average over all loop conformations gives the free energy ΔG(N, x) for an N-nt chain with end-to-end distance x,

(4)

where z(N, x) is the (electrostatic) partition function averaged over loop conformations,

(5)

Here is the electrostatic free energy of the i^th loop conformation. is the electrostatic free energy of the reference state, which is chosen as the fully stretched conformation: x = Nd with equal to the distance between adjacent nucleotides. If ignoring the electrostatic interactions, then 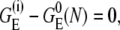and Eq. 4 is reduced to the following form:

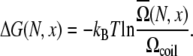(6)

TABLE 1.

The number of randomly selected loop conformations Ω₀ used in calculations

	x/d
N (−nt)*	1	2	3	4	5	6	7	8	9	10	11	12	13
13	232	237	232	239	257	225	236	233	216	180	150	99	1
11	178	194	192	188	176	170	175	175	153	93	1	−	−
9	115	144	139	175	158	144	102	73	1	−	−	−	−
7	89	111	117	112	112	76	1	−	−	−	−	−	−
5	71	85	60	58	1	−	−	−	−	−	−	−	−
3†	12	26	1	−	−	−	−	−	−	−	−	−	−
2†	2	1	−	−	−	−	−	−	−	−	−	−	−

In the calculations, we use these number of single-stranded chain conformations for calculating electrostatic free energy, and the partition function for the whole conformation ensemble can be calculated through a mean-field approach; see Eqs. 4 and 5.

^*N is the chain length and the loop size is N – 2.

^†For these N values, we make calculations for more values of x/d than listed here.

RESULTS AND DISCUSSIONS

In the following, by considering the electrostatic interactions, we calculate the loop free energies for different chain length, end-to-end distance x, and a broad range of Na⁺ and Mg²⁺ concentrations: [Na⁺] ∈ [0.001 M,1 M], [Mg²⁺] ∈ [0.0001 M,0.1 M]. Based on the calculations, we will derive empirical formulas for the loop free energy for three specific types of loops, namely, hairpin, bulge, and internal loops. The derived empirical relations will be validated through experimental comparisons for the salt-dependent RNA and DNA hairpin stability in Na⁺ and Mg²⁺ solutions.

Conformational ensemble

Fig. 2, A–D, show the values of Ω(N, x), ω(N, x), 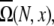and 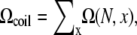respectively. From Ω(N, x), ω(N, x), we calculate the loop free energy in the absence of the electrostatic interactions (Eq. 6) by assuming the chain backbone is electrically neutral. Fig. 3 shows the chain free energy as a function of end-to-end distance. The predicted loop free energy ΔG(N, x) (Eq. 6) is positive because the loop formation is entropically unfavorable. As compared with experimental data for DNA hairpin loop free energy, the predicted electrostatics-free ΔG(N, x) from Eq. 6 overestimates the loop stability (N = 13 nt and for the phosphate-phosphate distance for a basepair in an B-form DNA helix, and d = 6.4 Å is the phosphate-phosphate distance for the adjacent nucleotides along the sequence). The discrepancy between the electrostatics-free predictions and the experimental data may be partially attributed to the neglect of electrostatic interactions. Nucleotide chain is negatively charged and the Coulombic repulsion between monomers on backbone would make loop formation more unfavorable than an electrically neutral chain. In the following, we investigate how the electrostatic interactions (in addition to the conformational entropy) determine the loop stability.

FIGURE 2.

The chain conformational ensemble produced from the virtual bond model on diamond lattice (83–85). (A) The number Ω(N, x) of all conformations with end-to-end distance x; (B) the number ω(N, x) of lattice nodes visited by the flexible chain end with end-to-end distance x; (C) the number of chain conformations with x averaged to one direction 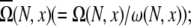and (D) the number Ω_coil of chain coil states, which includes all the conformations produced by the self-avoiding walk on a diamond lattice.

FIGURE 3.

The calculated loop formation free energy ΔG as functions of end-to-end distance x for different chain-lengths N for the electrostatics-free case (calculated through Eq. 6), i.e., by assuming chain backbone is neutral. The dotted line denotes the DNA hairpin loop free energy at 1 M NaCl for a 13-nt chain (loop size = 11-nt) (36).

Ion-dependent loop free energy

First, we calculate the electrostatic partition function z(N, x) (Eq. 5) for each given end-to-end distance x and chain-length N. The predicted z(N, x) (Fig. 4) decreases with the decrease of end-to-end distance x, and such effect is more pronounced for lower salt concentration and longer chain. This means that the small-x states are electrostatically unfavorable. Physically, this is because the electrostatic repulsion between the nucleotides is stronger for more compact chain conformations (smaller x). Therefore, z(N, x) decreases for smaller x.

FIGURE 4.

The partition function z(N, x) averaged for one chain conformation as a function of end-to-end distance x for different Na⁺ (A–C) and Mg²⁺ (D–F) concentrations. The chain lengths are 5-nt (A and D), 9-nt (B and E), and 13-nt (C and F). The averaging is over Ω₀ (lines) and Ω₀/2 (symbols) randomly selected chain conformations except for the fully stretched conformation. The agreement between lines and symbols show that the calculations are rather stable for different (large) numbers of conformations sampled. The Ω₀ values used for calculations are listed in Table 1. For the comparisons, we also show z(N, x) calculated from the PB theory (dotted lines).

Due to ion-polynucleotide electrostatic interaction, counterions in solution tend to be distributed around the polynucleotide chain (often termed diffusive-binding) to partially neutralize the backbone charge. At a lower ion concentration, such ion binding would accompany a large decrease in the ion's translational entropy and thus lead to a weak ion binding. As a result, fewer ions become bound for low ion concentration, causing weaker screening/neutralization and stronger polynucleotide charge-charge repulsion effect. Thus, the decrease of z(N, x) with x is more pronounced at low ion concentration.

For a longer loop (larger N), the electrostatic repulsion would be stronger, and the compaction of longer chain with small x would cause more massive charge repulsion, thus z(N, x) decreases with decreasing x more strongly for longer chain than for shorter chain.

In addition, Fig. 4 shows that Mg²⁺ gives much more effective neutralization than Na⁺ even at the same ionic strength. For example, z(N, x) at 0.1 M [Mg²⁺] is larger than that at 1 M [Na⁺]. This is due to the higher valency of Mg²⁺ than Na⁺ and hence stronger ion-polynucleotide interaction. Also shown in Fig. 4 are the z(N, x) results calculated with the PB theory. It is obvious that the PB theory underestimates the ability of Mg²⁺ in neutralizing the polyanionic nucleotide chain, i.e., z(N, x) from the PB decreases more sharply than that from the TBI. Physically, due to the higher charge of Mg²⁺, the interion correlations can be strong, while the PB theory ignores such interion correlation with the mean-field approximation. One of the effects of ion correlation is that the bound Mg²⁺ ions can self-organize to form low-energy state beyond the mean-field state, causing stronger Mg²⁺ ion effect. Ignoring this effect would cause underestimation for the effect of Mg²⁺ ion binding (79,91). Our TBI model takes into account the interion correlation and ion-binding ensemble (fluctuation) effects and gives improved predictions on Mg²⁺-binding and electrostatic free energy (79–82).

From the partition function z(N, x), we compute the loop stability ΔG(N, x) through Eq. 4 (shown in Fig. 5). The loop free energy is more positive, and the loop is less stable for longer loops and low salt concentration. In RNA and DNA folding, the unfavorable loop formation is often compensated by the favorable formation of helices and other noncanonical basepairing and base stacking. In this model, two factors determine the loop stability: the conformational entropy of the nucleotide chain and the electrostatic interactions. Both factors oppose the loop formation due to the decreased chain entropy and the increased charge-charge repulsion, respectively. For example, for longer loop, the random coil state has many more conformations, thus the loop formation would bring a larger decrease in chain entropy. The contribution of intrachain Coulombic repulsion can be modulated by the ions in solutions, which will be discussed in the following.

FIGURE 5.

The three-dimensional loop free-energy landscapes ΔG/k_BT as functions of end-to-end distance x for different chain lengths N and different [Na⁺] (A–D) and [Mg²⁺] (E–H). For the comparisons, we also show the loop free energy for different [Mg²⁺] computed from PB theory (I–L). The three-dimensional plots are produced from the empirical formulas for Na⁺ (Eq. 9), Mg²⁺ (Eq. 12), and for Mg²⁺ with the PB treatment (Data S1, Eq. S1). The red and blue colors represent the low and high loop free energies, respectively. In Data S1, Figs. S11–S13, we shows the comparisons between the calculated results and the respective empirical formulas.

In Na⁺ solutions

For loops with small/moderate end-to-end distance x (x/d ≲ N/2) (d is the distance between two adjacent nucleotides and Nd is the length of the fully stretched chain), the loop formation is less unfavorable for higher [Na⁺] (see Fig. 5, A–D; also shown in Supplementary Material, Data S1, Fig. S11). Such [Na⁺]-dependence of the loop stability is stronger for larger loops. This is because closing a loop with small/moderate end-to-end distance is opposed by the repulsion between the closely approached backbone negative charges. A higher [Na⁺] would reduce such repulsive force due to stronger charge neutralization/screening and thus improve the loop stability. For larger loops, more charges are involved and the charge repulsion effect is more significant. Therefore, the [Na⁺]-induced loop stability change is more pronounced.

In Mg²⁺ solutions

The ion concentration-dependence of the loop free energy in a Mg²⁺ solution (see Fig. 5, E–H; also see Data S1, Fig. S11) shows qualitatively similar behavior as in a Na⁺ solution. The loop stability increases with the increase of [Mg²⁺] due to the stronger Mg²⁺ binding. Compared with Na⁺ (Fig. 5, A–D), 1), Mg²⁺ is more effective in neutralizing the negative backbone charges, thus the loop formation in Mg²⁺ is apparently less unfavorable than in Na⁺ (even at the same ionic strength); and 2), the dependence of loop stability on [Mg²⁺] is obviously weaker than on [Na⁺]. Such difference between Mg²⁺ and Na⁺ comes from the higher ionic charge of Mg²⁺. Due to the stronger Mg²⁺-phosphate attraction, Mg²⁺-binding is more enthalpically favorable and (effectively) less entropically unfavorable (than Na⁺). As a result, the polynucleotide chain reaches stronger charge neutralization (screening) in Mg²⁺ (than Na⁺) solution. Therefore, Mg²⁺ is much more efficient in charge neutralization than Na⁺ and the loop formation free energy in Mg²⁺ solution exhibits the weaker dependence on [Mg²⁺].

For comparison, we use the PB theory to calculate the free energy of loop formation in Mg²⁺ solutions; see Fig. 5, I–L (also see Data S1, Fig. S12). Fig. 5, E–L, shows that the PB theory underestimates the role of Mg²⁺ in stabilizing loop, especially for large loop at high [Mg²⁺]. This may arise from the ignored interion correlations in the PB theory and the consequent underestimation of Mg²⁺ ion binding (79,91). Our results indicate that the PB theory underestimates the loop stability in Mg²⁺, especially for larger loop and higher [Mg²⁺], which may involve stronger ion-ion correlations. By contrast, the TBI model, which accounts for the ion correlation and ion-binding ensemble effects, gives improved free energy predictions (67,68,79–82).

Na⁺ versus Mg²⁺

To quantitatively compare the loop free energies in Na⁺ and Mg²⁺ solutions, we choose two typical ionic conditions: 1 M [Na⁺] and 0.01 M [Mg²⁺]. 1 M [Na⁺] and 0.01 M [Mg²⁺] have been previously shown to be approximately equivalent in stabilizing short DNA (and RNA) helices (60,67,68). For the two cases, Fig. 6 shows that the loops approximately have the same free energies, suggesting that 1 M [Na⁺] and 0.01 M [Mg²⁺] are approximately equivalent in stabilizing loops. Such TBI-predicted equivalence is in accordance with the experiment (60) and is beyond the mean-field description (e.g., ionic strength effect) due to the effects of ion correlation and ion-binding ensemble (fluctuation) for Mg²⁺ ions.

FIGURE 6.

The comparisons between the calculated loop free energy ΔG for two typical ionic conditions: 0.01 M MgCl₂ and 1 M NaCl. The chain lengths are N = 13, 9, and 5 nucleotides, respectively.

In mixed Na⁺/Mg²⁺ solutions

Since the mixed ion solution is of biological significance, we also make the calculations for mixed Na⁺/Mg²⁺ solutions. As shown in Data S1, Fig. S13, the free energy for loop formation depends on the competition between [Na⁺] and [Mg²⁺]. In analogy to the DNA and RNA helix stability in mixed [Na⁺]/[Mg²⁺] solutions (68), there are three regimes: for high [Mg²⁺] (relatively to [Na⁺]), the system is dominated by Mg²⁺, and the loop free energy is close to that in pure Mg²⁺ solution; for high [Na⁺] (relatively to [Mg²⁺]), Na⁺ ion effect dominates the system, and the loop free energy is close to the values in pure Na⁺ solution; for the intermediate regime, loop free energy is determined by the competition between [Mg²⁺] and [Na⁺]. When [Mg²⁺] is high (relative to [Na⁺]), Mg²⁺-binding is dominating due to strong Mg²⁺-phosphate attraction and low ion-binding entropy penalty, and Na⁺-binding is fully suppressed. Thus, Mg²⁺ dominates the loop stability. With the addition of Na⁺, Mg²⁺ ion-binding would be suppressed and hence the efficient roles of Mg²⁺ in stabilizing loop conformation is weakened. When [Na⁺] becomes very high, Mg²⁺ would be completely pushed away from the molecular surface, and the (high-concentration) Na⁺ ions dominate the loop stability.

Thermodynamic parameters for ion-dependent loop free energy

In this section, following the previous works (30,36,67,68), we will fit empirical formulas for loop free energies as functions of chain length N, end-to-end distance x, and Na⁺ and Mg²⁺ concentrations. Such empirical formulas for loop thermodynamic parameters are potentially useful for predicting secondary structure stability in an arbitrary Na⁺/Mg²⁺ solution.

In Na⁺ solutions

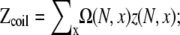Based on our calculations, we obtain the following empirical relations for the partition functions of loop ( see Eq. 4) and coil ( see Eq. 4) in pure Na⁺ solutions:

(7)

The coefficients a₁, b₁, c₁, and d₁ are given by

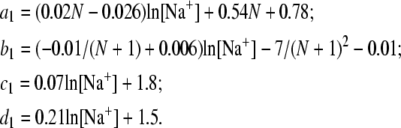(8)

Here, Z_loop(N, x) and Z_coil are the partition functions for the loop and the coil, respectively. Then the free energy for a loop formation in a Na⁺ solution is given by Eq. 4:

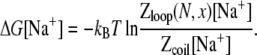(9)

As shown in Data S1, Fig. S11, A–D, the above empirical relations fit the TBI calculations very well for loop formation free energy in Na⁺ solutions.

In Mg²⁺ solutions

In analogy to Na⁺ solutions, for Mg²⁺ solutions, we obtain the following similar empirical relations:

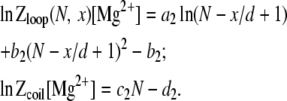(10)

The coefficients a₂, b₂, c₂, and d₂ are given by

(11)

Then the free energy for a loop formation in Mg²⁺ solution is calculated by

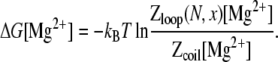(12)

As shown in Data S1, Fig. S11, E–H, the above empirical relations give good fit for loop formation free energy in Mg²⁺ solutions, as compared with the TBI calculations.

In mixed Na⁺/Mg²⁺ solutions

For a mixed Na⁺/Mg²⁺ solution, the free energy for a loop formation is given by

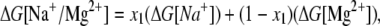(13)

where ΔG[Na⁺] and ΔG[Mg²⁺] are given by the above formulas (Eqs. 9 and 12). The expressions x₁ and 1 − x₁ describe the fractional contributions from Na⁺ and Mg²⁺, respectively, and x₁ is given by

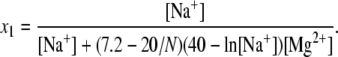(14)

As shown in Data S1, Fig. S13, the formulas give very good fits to the TBI calculations for mixed Na⁺/Mg²⁺ solutions. These formulas for mixed Na⁺/Mg²⁺ may also be used to estimate loop formation free energy in mixed K⁺/Mg²⁺ solutions, since K⁺ and Na⁺ have similar electrostatic properties (36).

For comparison, based on the calculations with the PB theory for the pure Mg²⁺ and mixed Na⁺/Mg²⁺ solutions, we also fit the empirical formulas for the loop free energies from the PB calculations (see Data S1, Fig. S12).

Ion-dependent hairpin, bulge, and internal loop free energies

After obtaining the above general empirical relations, we can conveniently calculate the ion-dependent free energies for the three types of specific loops, namely, hairpin, bulge, and internal loops.

Hairpin loop

For RNA and DNA, the end-end distance of the hairpin loop is (83,92). Using x_hairpin for x in Eqs. 9, 12, and 13 gives the free energy for an N-nt hairpin loop:

(15)

The fluctuation of x_hairpin at ∼17 Å only brings very slight fluctuation in the estimated hairpin loop free energy (see Fig. 5, and Data S1, Fig. S11).

Fig. 7, A and D, shows the hairpin loop free energies for different [Na⁺] and [Mg²⁺]. Also shown in the figures are the available experimental data (1 M NaCl). The predicted free energy ΔG_{hairpin loop} at 1 M NaCl is slightly higher than the experimental data for DNA loop (28), and slightly lower than the data for RNA loop (27). With the decrease of ion concentration, the predicted loop free energy increases and the loop becomes less stable. Such ion effect is stronger for Na⁺ and for longer loops, which is in accordance with the recent experimental measurements (93).

FIGURE 7.

The calculated loop free energies ΔG as functions of loop size (N – 2) for different [Na⁺] and [Mg²⁺]. (A and D) Hairpin loop; (B and E) bulge loop; and (C and F) internal loop. The symbols are experimental data for RNA (♦) (27) and DNA (□) (36) at 1 M NaCl, and the lines are calculated from Eqs. 15–17, respectively. From the bottom to top, ion concentrations are: (A–C) [Na⁺] = 1 M, 0.1 M, 0.01 M, and 0.001 M; (D–F) [Mg²⁺] = 0.1 M, 0.01 M, 0.001 M, and 0.0001 M, respectively.

Bulge loop

For a bulge loop, considering that the two helical arms connected by the bulge loop can fluctuate or bend, we allow the end-to-end distance x of the loop to fluctuate in a certain range. Due to the possible stacking between the two helix stems (83,85), very large end-end distance x for a bulge loop may be unfavorable. We select a fluctuation range of x ∈ [d, 2d], where d is the distance between two adjacent nucleotides. Our control test for the different fluctuation ranges of x indicates that the predicted loop free energy is not very sensitive to the choice of the fluctuation limits of x. For instance, using [d, 3d] instead of [d, 2d] causes an decrease in loop free energy by 10% at 1 M NaCl and 8% at 0.001 M NaCl. We compute the folding free energy for an N-nt bulge loop as

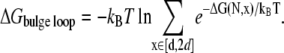(16)

Fig. 7, B and E, shows the folding free energy for bulge loops as a function of loop size for Na⁺ and Mg²⁺ solutions. Compared with experimental data at 1 M NaCl, our predicted free energy ΔG is slightly larger than that of DNA loop (36) and slightly smaller than that of RNA loop (27). As [Na⁺] or [Mg²⁺] is decreased, the loop free energy ΔG increases. Such effect is more pronounced for larger loops.

Internal loop

An internal loop contains two single-stranded chains. For a given N-nt internal loop, the two single-stranded chains can have different lengths (N₁-nt and N₂-nt, respectively). To compute the loop free energy as a function of the loop size N, we average over different N₁ and N₂ values with the constraint N₁ + N₂ = N,

(17)

where 〈…〉 denotes averaging over different N₁ and N₂ values and x_max(= min(N₁d, N₂d)) is the length of the shorter chain in the internal loop. The value x_max is the fully stretched distance of the chain and is thus the maximum end-to-end distance for the single-stranded chains for given N₁ and N₂.

Fig. 7, C and F, shows the free energy for the formation of internal loop in Na⁺ and Mg²⁺ solutions. The comparisons between the predicted free energy and the available experimental data at 1 M NaCl show the same trend (Fig. 7, A, B, D, and E). Our predictions slightly underestimate the internal loop free energy ΔG, as compared with the experimental data for RNA loop (27), and slightly overestimate ΔG, as compared with the data for DNA loop (36). The decrease of ion (Na⁺ and Mg²⁺) concentration and the increase of loop size both increase the free energy penalty for loop formation. Fig. 7, C and F, show that internal loop has a weaker ion-dependence of the free energy than hairpin and bulge loops of the same size (N). Such weaker ion-dependence is due to the shorter single-stranded chains (of lengths N₁ and N₂) in an internal loop than in a hairpin or bulge loop (of length N = N₁ + N₂).

As shown in Fig. 7, for the three types of loops, our predicted free energies for 1 M NaCl generally lie between the experimental values for RNA and DNA loops, except for very small loops. One possible reason is that our used value of d, distance between two adjacent nucleotide, is ∼6.4 Å, which lies between the values for RNA (∼6 Å) and DNA (∼6.6 Å) chains. A smaller d would result in a stronger intrachain Coulombic repulsion and consequently make the loop formation more unfavorable. Thus, with the use of the intermediate d, the predicted loop free energies are larger than the values of DNA loops and smaller than those of RNA loops. For very short loops (e.g., 1-nt bulge loop), the predictions obviously deviate from the experimental measurements, which may be due to the neglected intraloop and loop-helix interactions. In Fig. 7, we only present the predictions for pure Na⁺ and Mg²⁺ solutions. For mixed Na⁺/Mg²⁺ solutions, the loop free energy parameters can be conveniently calculated by using the general formulas for loop formation parameter (Eq. 13) and the specific formulas for the three types of loops (Eqs. 15–17).

Ion-dependent RNA and DNA hairpin stability

To validate the above empirical formulas for ion-dependent loop free energy, we compute the ion-dependent RNA and DNA hairpin stability by combining the above analytical formulas (derived from our TBI model) for loop free energy and the previously obtained analytical formulas (derived also from TBI) for RNA and DNA helix thermodynamic parameters (67,68). Based on the assumption of additive nearest-neighbor model (27,36), the enthalpy, entropy, and free energy for a hairpin can be calculated as

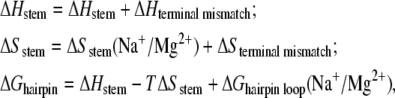(18)

where ΔH_stem, ΔH_{terminal mismatch}, and ΔS_{terminal mismatch} can be obtained from the nearest-neighbor model with the measured thermodynamic parameters (Turner rules) (27,31,36,42). In our calculations, the parameters for base stacks in helix stem are from Xia et al. (31) for RNA hairpin and from SantaLucia (30) for DNA hairpin. The RNA terminal mismatch parameters are from Serra and Turner (27). For DNA hairpin, the terminal mismatch parameters, which are not directly available (36), are approximated by the dangling end parameters (94). ΔG_{hairpin loop}(Na⁺/Mg²⁺) are calculated through the above analytical formula (Eq. 15), and ΔS_stem(Na⁺/Mg²⁺) can be calculated from the previously developed analytical formulas for ion-dependent RNA and DNA helix stability (67,68). After obtaining ΔG_hairpin, the melting temperature can also be calculated from the condition ΔG_hairpin = 0.

Based on the above formulas (Eq. 18), we investigate the salt-dependent stability for RNA and DNA hairpins which are shown in Fig. 1. The thermodynamic parameters for these hairpins are listed in Table 2, along with the experimental references (20,49,93,95–97). We calculate the free energy and melting temperature over wide ranges of [Na⁺] and [Mg²⁺], and make quantitative comparisons with the available experimental data. In the calculations, for mixed K⁺/Mg²⁺ solution, we also use our formulas for mixed Na⁺/Mg²⁺, since Na⁺ and K⁺ have similar electrostatic properties (36).

TABLE 2.

The thermodynamic parameters for nucleic acid hairpins used in the calculations

Label*	Ref.	Helix length (bp)	Loop size	−ΔH° (kcal/mol)†	−ΔS° (cal/mol K)†	ΔG°loop (kBT)‡	−ΔG°37 (kcal/mol)§
RH1	(49)	6	10	63.6	161.7	8.4	8.3
RH2	(49)	6	8	63.6	161.7	7.9	8.6
RH3	(20,95)	5	6	60.0	150.3	7.2	8.9
RH4	(96)	7	9	68.8	179.3	8.2	8.1
RH5	(97)	7	12	77.9	203.8	8.7	9.3
RH6	(93)	5	j+2	50.2	131.0	¶	¶
DH1	(93)	7	i	53‖	143‖	¶	¶

In our calculations for salt-dependent nucleic acid hairpin thermodynamics, we use the values listed in the table at 1 M NaCl.

^*The sequences of the hairpins are shown in Fig. 1.

^†The listed thermodynamic parameters are calculated for helix stem at standard salt (1 M NaCl), through the nearest-neighbor model. The parameters for base stacking are taken from Xia et al. (31), and the parameters for terminal mismatches are taken from Serra et al. (27).

^‡The loop free energy is obtained from our calculations for loops (Eq. 15), rather than the experimentally derived values.

^§Calculated for the whole RNA hairpin at standard salt (1 M NaCl).

^¶The loop and hairpin free energies depend on the loop sizes j+2 and i.

^‖The DNA hairpin terminal mismatch parameters are approximated by the dangling end parameters (94), and the parameters for helix stem are from SantaLucia (30).

In Na⁺ solutions

Fig. 8 shows the folding free energy ΔG°₃₇ and melting temperature T_m as functions of [Na⁺] for three hairpins: RH1, RH2, and RH3; see Fig. 1 and Table 2. The increase of [Na⁺] enhances the RNA hairpin folding stability (decrease in the folding free energy and increase in the melting temperature) (20,49,95,98). Our predictions agree with the available experimental data very well (20,49,95). Physically, at higher [Na⁺], the entropic cost for Na⁺-binding is lower, and consequently more Na⁺ ions bind near the phosphate groups to neutralize the negatively charged backbone. Thus, hairpins have higher stability (lower ΔG°₃₇ and higher T_m) at higher [Na⁺].

To test the importance of the ion-dependence of the loop stability, instead of using the above [Na⁺]-independent loop free energies, we use loop free energies at fixed 1 M NaCl for all other [Na⁺] values. Our test results (Fig. 8) show that ignoring the ion-dependence of the loop free energy would lead to notable inaccuracy, especially for large loop (e.g., see the curves for RH1 in Fig. 8). Therefore, the salt-dependence of loop free energy cannot be ignored, though the helix stem may contribute predominantly to the overall salt dependence of the hairpin stability due to its higher charge density.

FIGURE 8.

The RNA hairpin folding free energy ΔG°₃₇ (A) and melting temperature T_m (B) as functions of [Na⁺] for three sequences RH1, RH2, and RH3. (Symbols) Experimental data: ⋄, RH3 in Na⁺ solution (20); ▴, RH3 in Na⁺ solution (95); ♦, RH2 in Na⁺ solution (49); and □, RH1 in Na⁺ solution (49). (Solid lines) Predictions with salt-dependent loop free energy (ΔG[Na⁺]); (dotted lines) predictions with invariable loop free energy at 1 M NaCl (ΔG[1 M Na⁺]). Hairpins RH1, RH2, and RH3 are shown in Fig. 1 and Table 2.

In mixed Na⁺/Mg²⁺ solutions

Fig. 9 shows the folding free energy ΔG°₂₅ and melting temperature T_m in mixed Na⁺ (or K⁺)/Mg²⁺ solutions for three RNA hairpins: RH3, RH4, and RH5 (as shown in Fig. 1, and Table 2). Comparisons with the experimental data indicate that our model gives good predictions for RNA hairpin stability in mixed Na⁺ (or K⁺)/Mg²⁺ solutions. As shown in Fig. 9, similar to the DNA and RNA helix stability in mixed Na⁺/Mg²⁺ solutions (68), the ion-dependence of the hairpin stability can be classified into three of the aforementioned [Na⁺]/[Mg²⁺] regimes (see In Mixed Na⁺/Mg²⁺ Solutions). When Na⁺ (or K⁺) and Mg²⁺ compete with each other, adding Na⁺ (or K⁺) ions can weaken Mg²⁺ ion binding and thus destabilize the hairpin.

The predictions with invariable loop free energy at 1 M NaCl (ΔG[1 M Na⁺]) are also shown in Fig. 9. The comparisons with experimental data show that the Na⁺ (or K⁺)/Mg²⁺-dependence of loop free energy plays an important role in the overall ion-dependence of hairpin stability, especially for large loop; e.g., see the curves for RH5 in Fig. 9.

FIGURE 9.

The RNA hairpin folding free energy ΔG°₂₅ (A–C) and melting temperature T_m (D–F) as functions of [Mg²⁺] for different [Na⁺]. Three sequences used are RH3, RH4, and RH5, which are shown in Fig. 1 and Table 2. (Symbols) Experimental data: (A) ♦, RH3 in 0.054 M [Na⁺] (20); (E) ♦, RH4 in 0.1 M [K⁺] (96); (F) ♦, RH5 in 0.1 M [K⁺] (97). (Solid lines) Predictions with salt (Na⁺/Mg²⁺) dependent loop free energy ΔG[Na⁺/Mg²⁺]; (dotted lines) predictions with invariable loop free energy at 1 M NaCl (ΔG[1 M Na⁺]). In panels A–C, we calculate ΔG°₂₅ instead of ΔG°₃₇ because of the available experimental data at 25°C. In the calculations, we use the same salt empirical formula for K⁺ as that for Na⁺, since Na⁺ and K⁺ have the similar electrostatic properties (36). For the comparisons, we also show the predictions with the loop free energy from the PB empirical formulas (Data S1, Eqs. S1 and S3) (dashed lines).

Also shown in Fig. 9 are the curves from the PB calculations on loop free energy. The comparisons between the predictions of the TBI model, the PB theory, and the experimental data suggest that the PB theory underestimates the ability of Mg²⁺ in stabilizing loop, especially for large loops at high [Mg²⁺]. As discussed above, the PB theory neglects the ion-ion correlation and ion fluctuation, and consequently predicts less-bound Mg²⁺ ions (79,91), causing the overestimation of (positive) loop free energy in Mg²⁺. Our TBI model explicitly accounts for these effects (79–82) and can give improved predictions for hairpin stability in Mg²⁺ solutions.

Loop-size dependence of hairpin stability

Fig. 10 shows the melting temperatures T_m for RH6 and DH1 (Fig. 1) as a function of the loop size. In general, the theoretical results agree well with the experimental data (93) except for 33 mM [Mg²⁺] in Fig. 10 B, where the theory slightly overestimates the T_m. This theory-experiment difference may come from neglecting loop-stem interactions, which can cause overestimation on the number of loop conformations and hence the loop stability. As shown in Fig. 10, larger loop gives lower hairpin stability. Such effect is more pronounced for lower ion concentration and for monovalent ion solution due to weaker charge neutralization and thus stronger charge repulsion upon loop closure.

FIGURE 10.

The melting temperatures T_m of DNA (DH1, A and B) and RNA (RH6, C) hairpins as a function of loop size for different ionic conditions: 0.1 M Na⁺ (A), 2.5 mM and 33 mM Mg²⁺ (B), and 2.5 mM Mg²⁺ (C). (Lines) Predictions from our theory; (symbols) experimental data (93).

CONCLUSIONS AND DISCUSSIONS

In this article, the tightly-bound ion (TBI) theory (67,68,79–82) and the Vfold model (83–85) are combined together to quantify the ionic dependence of nucleic acid loop thermodynamics. Based on the TBI calculations, we obtain fitted analytical formulas for loop free energies as functions of end-to-end distance, chain length, and Na⁺/Mg²⁺ concentrations. The analytical formulas are validated by quantitative comparisons with the extensive experimental data for ion-dependent RNA and DNA hairpin stability. The following are the major conclusions:

1. Loop formation is unfavorable due to backbone charge-charge repulsion. Na⁺ and Mg²⁺ can increase the loop flexibility by neutralizing the phosphate charges, causing the loop formation to be less unfavorable. Therefore, the increase of [Na⁺] and [Mg²⁺] leads to the decrease of the free energy cost for loop formation.

2. Mg²⁺ is more effective than Na⁺ in neutralizing backbone charges, and ion concentration-dependence of loop free energy for Mg²⁺ is weaker than that for Na⁺. Specifically, 1 M [Na⁺] and 0.01 M [Mg²⁺] are approximately equivalent in stabilizing loops.

3. For the loop formation in Mg²⁺ solutions, the TBI model makes better predictions for loop free energy than the PB theory, which tends to overestimate the (unfavorable) loop free energy, especially for large loops at high Mg²⁺ concentration.

4. The ion-dependence of loop free energy plays an important role in the overall salt-dependence of hairpin stability, especially for large loops.

5. Based on the TBI calculations, we obtain a set of fitted analytical formulas for loop free energy as function of chain length, end-to-end distance, and Na⁺/Mg²⁺ concentrations. These formulas are validated through comparisons with experimental data. These formulas, combined with the previously derived analytical formulas for the ion-dependent helix stabilities, can give good predictions for RNA and DNA hairpins at arbitrary Na⁺/Mg²⁺ concentrations.

Although our calculations can give quantitative predictions that are validated by the extensive experimental data, we have made several important simplifications and approximations in our theory. First, we use a coarse-grained chain model to represent the polynucleotide chain. As a result, the model cannot treat atomic details, which can be important for more accurate and detailed description of ion-binding. Second, the theory does not treat bases and possible intraloop basepairing and stacking (92), which can be important for sequence-specific interactions that help to stabilize the triloops and tetraloops (35,36,99). Thus this theory is unable to predict the sequence-specific tetraloop stability. Third, in our calculation for the loop stability, we ignored the influence from the helices that are connected to the loop. The loop-helix interactions can affect the loop conformational distribution (83). Fourth, in the TBI theory, we use hydrated ions and the current model cannot treat ion dehydration effect and possible specific ion-binding (9,100). In addition, we ignore the contributions from the dangling tails to the overall hairpin stability. Single-strand stacking in dangling tails can contribute sequence-dependent stability. For example, at room temperature, while poly(U) forms a random coil, poly(A) is largely stacked (1). Finally, our present computation is based on a randomly sampled loop conformational ensemble because the electrostatic calculations for the complete conformational ensemble is computationally not viable. Nevertheless, the agreements with available experimental data suggest that our predictions and the obtained analytical formulas are able to provide reliable ion-dependent thermodynamic stabilities for loops and hairpins. Further development of the theory might enable us to treat RNA (DNA) secondary and even simple tertiary structures at different ionic conditions.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.