Universal physical responses to stretch in the living cell

Abstract

With every beat of the heart, inflation of the lung or peristalsis of the gut, cell types of diverse function are subjected to substantial stretch. Stretch is a potent stimulus for growth, differentiation, migration, remodelling and gene expression^1,2. Here, we report that in response to transient stretch the cytoskeleton fluidizes in such a way as to define a universal response class. This finding implicates mechanisms mediated not only by specific signalling intermediates, as is usually assumed, but also by non-specific actions of a slowly evolving network of physical forces. These results support the idea that the cell interior is at once a crowded chemical space³ and a fragile soft material in which the effects of biochemistry, molecular crowding and physical forces are complex and inseparable, yet conspire nonetheless to yield remarkably simple phenomenological laws. These laws seem to be both universal and primitive, and thus comprise a striking intersection between the worlds of cell biology and soft matter physics.

Soft materials such as tomato ketchup, shaving foam and tooth-paste tend to fluidize when subjected to shear^4–7, as do granular materials including sugar in a bowl, coffee beans in a chute⁸ and even certain geophysical strata during an earthquake⁹; each transforms from a solid-like to a fluid-like phase, stiffness falls, and the material flows. Underlying microscopic stress-bearing elements, or clusters of elements, interact with neighbours to form a network of force transmission, but how flow is initiated and the nature of energy barriers that must be overcome remain the subject of much current attention^5–9.

The response of a living cell to transient stretch would seem to be a different matter altogether. Very early literature shows that in response to application of a physical force the cell acutely softens (Supplementary Note 4), but more recent literature uniformly emphasizes stiffening (Supplementary Note 5)^1,10. Nevertheless, we demonstrate here that the living cell promptly fluidizes and then slowly re-solidifies much as do the inert systems described above. Moreover, underlying structural rearrangements on the nanometre scale promptly accelerate and then slowly relax. In addition, in experiments spanning wide differences in cellular interventions, cell type and even integrative scale, these physical events conform to universal relationships.

Shear fluidization of inert matter is usually attributed to the presence of physical interactions that possess energy barriers that are so large that thermal energies by themselves are insufficient to drive microconfigurations to thermodynamic equilibrium. The material is then unable to explore its configuration space⁵, and structural rearrangements become limited by long-lived microconfigurations in which the system becomes trapped. If these microconfigurations were metastable, then their longevity could depend upon agitation energy of some non-thermal origin. In the case of living cells, one such source of non-thermal agitation is ATP-dependent conformational changes of proteins¹¹, which release energy of about 20k_BT per event, where k_B is Boltzmann’s constant and T is temperature, whereas another is energy injected into the system by stretch.

To test this last idea, we developed a novel experimental system in which we could subject the adherent human airway smooth muscle (HASM) cell to a transient isotropic biaxial stretch–unstretch manoeuvre of 4 seconds duration with zero residual macroscale strain. We could then monitor, on the nanometre scale, cell mechanical properties, remodelling dynamics and their changes (Methods; Supplementary Fig. 1; Supplementary Note 2).

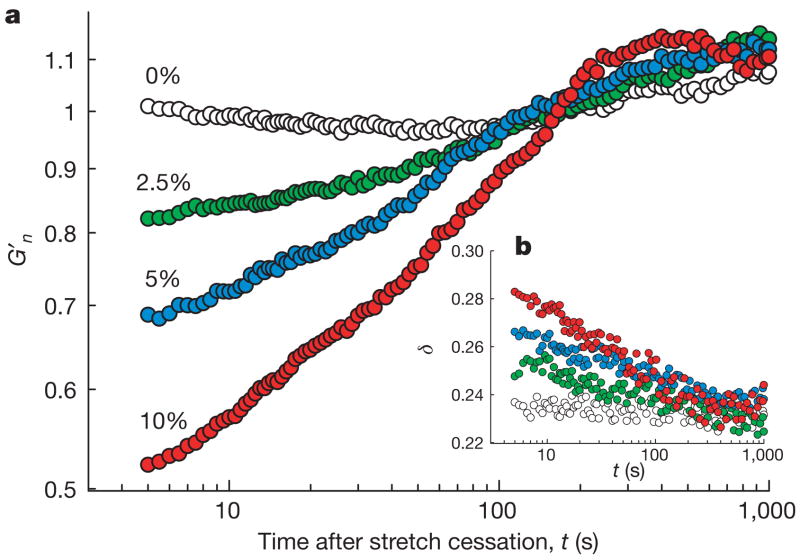
Stiffness after stretch relative to stiffness of the same cell immediately before was denoted G′_n. When no stretch was applied, this fractional stiffness did not change, but immediately after cessation of a single transient stretch G′_n promptly decreased and then slowly recovered (Fig. 1a). These responses varied systematically with the amplitude of the imposed stretch, but little with the number of imposed stretch cycles (Supplementary Fig. 2). Immediately after stretch cessation, the phase angle δ = tan⁻¹(G″/G′) promptly increased and then slowly recovered (Fig. 1b), where for a hookean solid δ = 0 and for a newtonian fluid δ = π/2. In the living cell 0.15 < δ <0.50, thus placing the living cell closer to the solid-like state, and δ is virtually invariant with changes of frequency, thus setting cytoskeleton rheology within the paradigms of structural damping and scale-free dynamics^12–17. These prompt changes establish that shear tended to fluidize the cell, and did so in a manner comparable to the effect of shear on soft materials including colloidal glasses, emulsions and pastes^4,5 (Supplementary Note 7). However, fluidization in response to transient stretch contrasts with strain-stiffening behaviour that is observed in response to sustained stretch of cells¹⁵ or reconstituted crosslinked actin gels^18,19; in Supplementary Note 6 we reconcile these seemingly contradictory behaviours.

Figure 1. A single transient stretch drives fractional stiffness G′_n down and the phase angle δ up, indicating fluidization of the cytoskeleton.

a, Evolution of G′_n of HASM cells after a single transient stretch of 0% (no stretch, open circles), 2.5% (green), 5% (blue) and 10% (red). The response of each bead was normalized to its pre-stretch value. b, Evolution of the phase angle after stretch application. Compare with Box 1 in Supplementary Note 7.

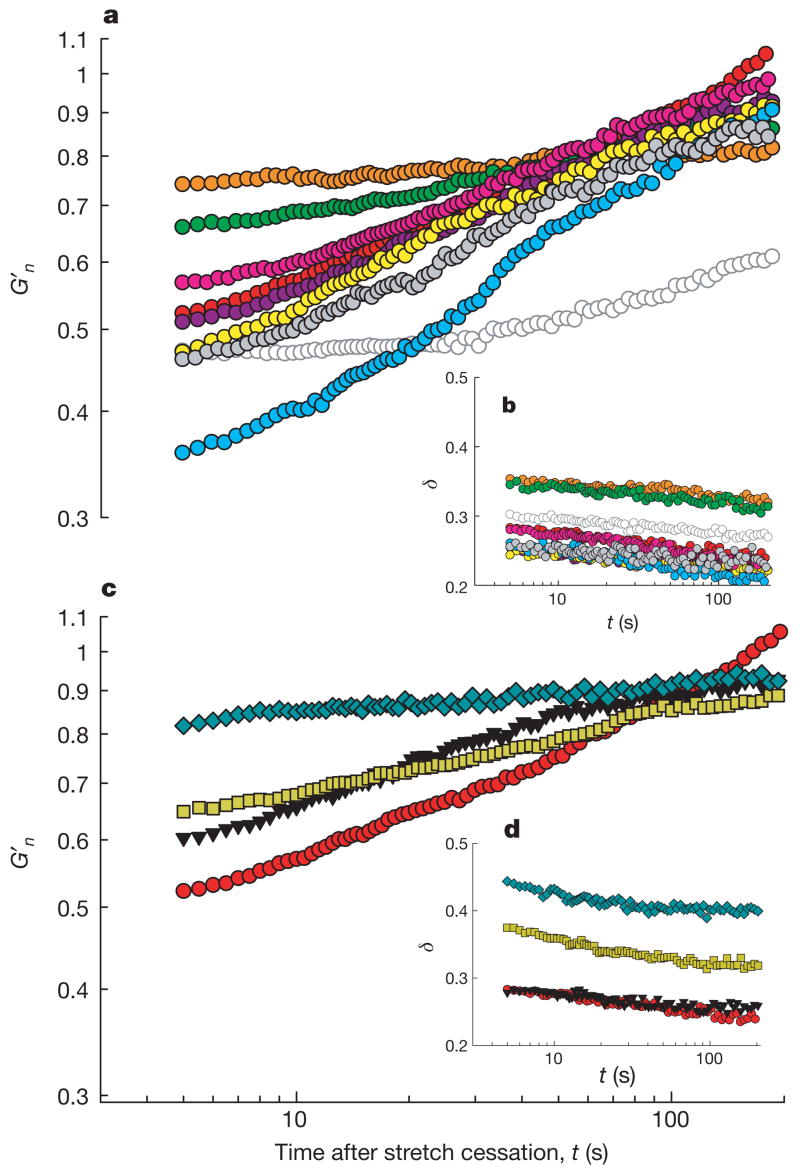
To assess the robustness of these responses, we pre-treated cells with an extensive set of mechanistically distinct drugs. These interventions caused expected changes in baseline material properties (Supplementary Table 1). Despite wide differences in baseline values, each cell could serve as its own pre-stretch control. Across the panel of interventions, fluidization–resolidification responses to stretch were similar in quality but markedly disparate in magnitude and time course (Fig. 2a). When F-actin was stabilized with jasplakinolide, stretch caused the largest fractional decrease in stiffness and displayed the fastest recovery, whereas when F-actin was depolymerized with latrunculin A, stretch caused the smallest fractional decrease of stiffness and a relatively slow recovery. Inhibition of the myosin light chain kinase with ML7 blocked contractile activation as expected (Supplementary Fig. 3), but the time course of G′_n remained almost unchanged. Similarly, when extracellular calcium was chelated with EGTA to prevent calcium influx through stretch-activated channels, the time course of G′_n remained largely unchanged. In contrast, ATP depletion caused stiffness recovery to slow dramatically. In all experimental conditions, the phase angle showed a rapid increase followed by a slow decrease (Fig. 2b).

Figure 2. A broad variety of cell systems were fluidized by a transient stretch of 10% amplitude.

a, b, G′_n (a) and δ (b) of pharmacologically treated HASM cells after application of a single transient stretch of 10% amplitude (see Methods and Supplementary Table 1 for pre-stretch baseline values and treatment details). Groups are latrunculin A (orange), DBcAMP (green), ML7 (10 min incubation, bright pink; 45 min incubation, dark pink), histamine (yellow), EGTA (grey), jasplakinolide (bright blue), ATP depletion (open symbols), and untreated cells (red). G′_n (c) and δ (d) of MDCK (blue diamonds), HBE (yellow squares), HLF (black triangles) and HASM (red circles). Compare with Box 1 in Supplementary Note 7.

To assess the generality of these results, we also evaluated human lung fibroblasts (HLF), Madin–Darby canine kidney epithelial cells (MDCK) and human bronchial epithelial cells (HBE). Again, we found responses that were similar in quality but disparate in magnitude and time course (Fig. 2c, d).

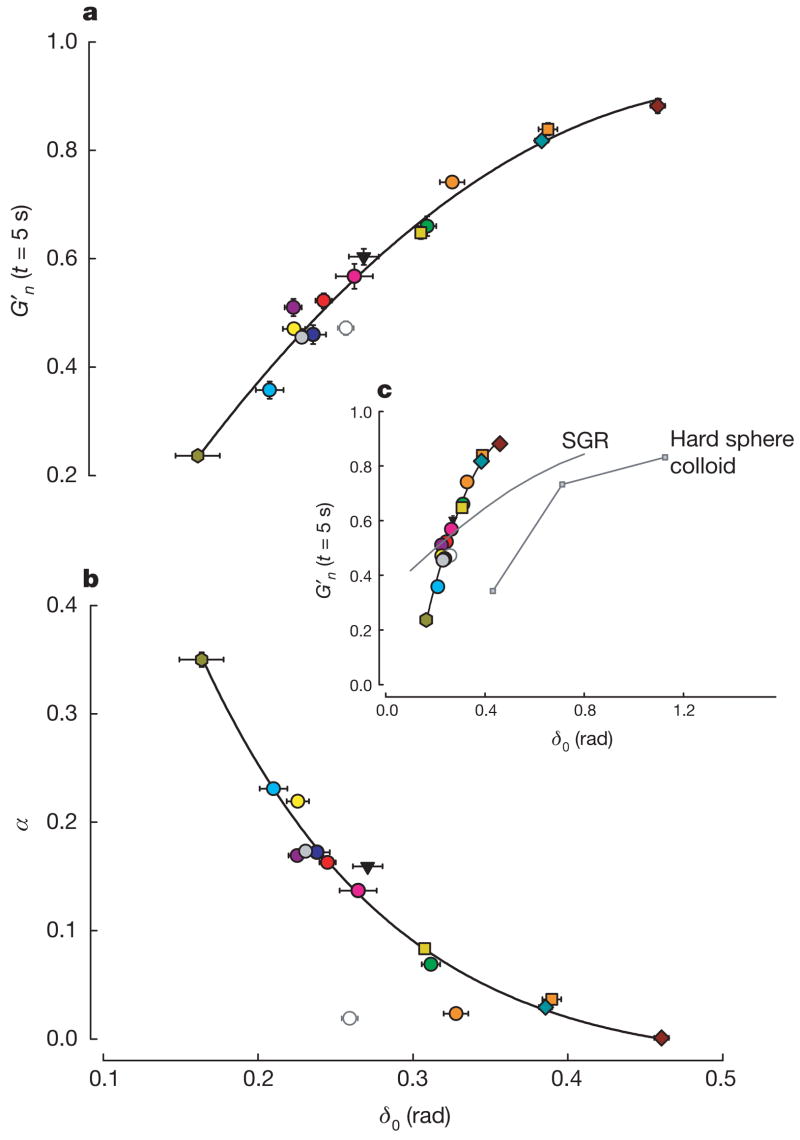
A striking unification of these diverse responses was established when we focused on the prompt stiffness reduction G′_n (assessed at the earliest measurable time point, t = 5 s) and its initial rate of recovery α (assessed from the fit of G′_n to t^α for the first 30 s of response). Despite the broad diversity of drug interventions and cellular systems, when G′_n (at t = 5 s) was plotted against the pre-stretch value of the phase angle (δ₀), all data collapsed onto a single unifying relationship (Fig. 3a). Similarly, when the rate of stiffness recovery was plotted against δ₀ another master relationship was defined, although ATP depletion fell off that relationship (Fig. 3b). Moreover, at the level of an isolated bovine airway smooth muscle tissue strip mounted in a muscle bath, maximally activated, and then stretched using a servo-controller²⁰, data fell onto the very same relationships as did single cells in culture (Fig. 3).

Figure 3. Two unifying relationships describe the response to stretch of a broad variety of cell systems.

In every case, the closer the system was to the solid-like state (δ₀ = 0) before being subjected to transient stretch, the greater was the extent of its fluidization and, except for the case of ATP depletion, the faster was its subsequent recovery. Master curves of G′_n at the earliest time point recorded after stretch (a) and of the initial rate of stiffness recovery α versus the pre-stretch phase angle δ₀ (b). α was assessed by fitting a power-law $G_n^{\prime }\propto t^{\alpha }$ to the first 30 s of response after stretch cessation. Error bars indicate standard errors. When plotted again over the full range possibilities (c), cells are seen to lie much closer to the solid-like (δ₀ = 0) than the fluid-like (δ₀ = π/2) state. In response to shear of similar magnitude, cells show a fluidization response comparable to but to the left of hard sphere colloids (data adapted from ref. 4). Soft glassy rheology theory⁵ (Supplementary Note 7) captures these trends but substantially underestimates sensitivity to changes of δ₀. n values are given in Supplementary Table 1. Colours are as in Fig. 2 with the addition of HASM PBS (dark blue), HBE Latrunculin A (orange squares), MDCK cytochalasin D (brown diamonds) and BASM tissue (green hexagons).

Although these wide ranges of cellular systems, interventions and integrative scales might have led to a quagmire of inconsistencies, they instead unveiled a pattern of consistency (Fig. 3). The closer the system was to the solid-like state before being subjected to transient stretch, the greater was the extent of its fluidization and, except in the case of ATP depletion, the faster was its subsequent resolidification (Fig. 3). Behaviour of this kind is crudely reminiscent of that observed in inert soft materials such as hard-sphere colloids and is predicted by coarse-grained trap models of soft glassy rheology (Fig. 3c; Supplementary Note 7).

To test this interpretation further, we made direct observations of molecular-scale structural rearrangements. Cells were subjected to 10% transient stretch–unstretch, but instead of measuring forced bead motions using optical magnetic twisting cytometry (OMTC), as above, we measured spontaneous nanoscale bead motions and used them as a direct index of the rate of molecular-scale structural rearrangements¹⁶. The evolution of mean square bead displacement (MSD) on the nanometre scale—both before the transient stretch and at different waiting times (t_w) after stretch cessation—showed that when no stretch was applied the MSD evolved as we have reported previously^16,21 (Fig. 4). But when a transient stretch was applied, the rate of remodelling kinetics accelerated promptly and by more than an order of magnitude; comparatively, macromolecular mobility in unstretched cells was markedly retarded. However, as t_w increased, those kinetics progressively slowed, but relaxed more slowly than any exponential process^5–7 (Fig. 4b). This constellation of out-of-equilibrium features (Figs 1–4) represents the strongest evidence yet available to suggest slow relaxation of a glassy phase (Supplementary Note 7).

Figure 4. Structural relaxation takes place on timescales that grow with the time elapsed since the application of stretch and is slower than any exponential process.

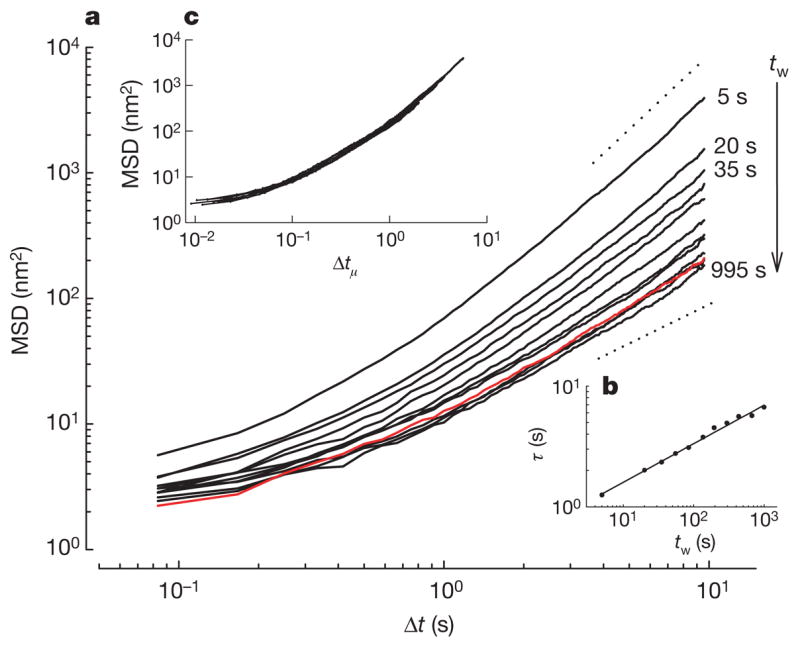
a, Spontaneous motions of beads bound to HASM cells at different t_w after stretch cessation (n = 1,062 beads). Waiting times are 5, 20, 35, 55, 85, 135, 195, 295, 435, 665 and 995 s from top to bottom. The red line is the MSD before stretch application. The dashed lines indicate diffusion exponents of 1 and 2. b, To characterize the progressive slowing of rearrangement kinetics, we defined a time τ at which MSD(τ)=d², where d was taken as an arbitrary threshold and τ thus represented the average time required for a bead to move (diffuse) a distance d. For any value of d, we found that τ increased with t_w as a power law τ ∝ t_w^μ with μ≈0.3, indicating that the decay was slower than any exponential process, and that within the experimental time window no steady state was achieved. Data are shown for d² = 100 nm² and the solid line is a fit to a power law with exponent μ = 0.32. c, After rescaling the time axis using $\mathrm{\Delta }{t}_{\mu }=\mathrm{\Delta }t/t_w^{\mu }$ with μ = 0.32, all data collapsed onto a master curve. This indicates that the kinetics at each waiting time were self-similar. In inert soft glassy materials, such slowing of rearrangement kinetics as well as the absence of a steady state is referred to as physical ageing and μ is identified as the ageing coefficient. Physical ageing can be interrupted by injection of mechanical energy through shear; shear drives inelastic structural rearrangements⁷,²³, in which case it is presumed that elements can then ‘hop’ out of the deep energy wells in which they are trapped, erase system memory, and push the system farther from thermodynamic equilibrium. In inert soft materials these events reset system evolution to some earlier time and for that reason are called physical rejuvenation⁶,⁷.

The conventional understanding of cytoskeleton dynamics has been based on the ideas that physical forces act to stiffen the network through both passive mechanical strain-stiffening^18,19 and active signalling-mediated reinforcement^1,10. The results presented here show this viewpoint to be incomplete. Rather than merely triggering biochemical signalling cascades, as is usually assumed, cell stretch is seen to set into motion ongoing physical events in cell signalling that are not limited to the initiating upstream molecular transducers: physical forces seem to be more than a trigger. The absence of molecular specificity in the early events of this process is highlighted by the fact that over wide ranges of systems and circumstances, the abilities of a cell to fluidize suddenly in response to stretch and to resolidify subsequently (Figs 3 and 4) seem to be insensitive to molecular details, and instead depend solely on the proximity of the cell to a solid-like state before the stretch (δ₀). This simple result is remarkable, but as more data accrue the cases in which this universality class is violated are likely to be most instructive.

These findings of universality and non-specificity, taken together with the striking analogy to dynamics in inert glassy systems (Fig. 3c; Supplementary Note 7), imply ongoing actions of a network of slowly evolving physical forces, but it remains unclear if these observations can be interpreted in terms of the onset of a non-equilibrium phase transition controlled by external stress that separates a jammed phase from a flowing phase^5,22. Despite the underlying variety of molecular mechanisms, all such glassy systems are thought to have one feature in common—structural rearrangements that are slow, localized and inelastic—and the applicability of such a point of view is justified by the universality of the phenomenology, including inert matter^4–7,23, proteins²⁴, cells^16,25,26 and integrated tissues²⁰. In the case of physical interactions between cytoskeletal molecules, such inelastic rearrangements might include disruption or unfolding of crosslinking proteins, resolution of steric constraints, detachment of myosin crossbridges, rupture of hydrogen bonds or cytoskeleton filaments, or actions of force-dependent capping proteins controlling filament polymerization²⁷.

While fluidization of living and inert systems clearly differ (Fig. 3c), the constellation of out-of-equilibrium features displayed by the cytoskeleton of the living cell is seen to be rich, nontrivial and unexplained, and would appear to describe a glassy matrix close to a glass transition. We now have firm phenomenological evidence, moreover, that dynamics in the cytoskeleton of the living adherent cell revolve around the master parameter δ₀ (or, equivalently, x; Supplementary Note 7), which sets the power-law rheology exponent^12,13, the rate of nanoscale structural rearrangements and their relaxation (Fig. 4)¹⁶, the extent of fluidization in response to stretch (Figs 2 and 3a) and the rate of subsequent resolidification (Fig. 3b). In turn, this master parameter δ₀ is set by cytoskeletal tension (pre-stress)²⁸. As such, two major concepts in cytoskeletal biology that are each understood in its own right to be highly unifying are now seen to be linked intimately to one another—cytoskeletal tension on the one hand and glassy dynamics on the other. Although a mechanism explaining why this might be so is unknown²⁹ (Supplementary Notes 7, 8), these phenomena, taken together, define the most primitive features of the cytoskeletal phenotype, namely, its abilities to deform, to contract and to remodel, and might have arisen as early as the cytoskeleton itself, about two billion years ago³⁰ (Supplementary Note 9).

We traditionally think about molecular interactions within the cytoskeleton as being highly specific, whereas in a crowded³ glassy phase the nature of molecular interactions and their rate of progression become highly constrained, severely regularized, and non-specific (Figs 3 and 4; Supplementary Note 8). Conventional descriptions of physical interactions based upon viscoelasticity, the fluctuation-dissipation theorem, specific signalling cascades, dilute solution chemistry, and even emerging notions of protein interaction maps, fail to account for these dynamics. Because physical interactions are now seen to play out within a glassy phase, they will have to be rethought within a rather different conceptual perspective.

METHODS SUMMARY

Cell culture

HASM, HLF, HBE and MDCK cells were grown on collagen I-coated silastic substrates (Flexcell) for 5–14 days, depending on the cell type. Cells were allowed to reach confluence before being serum-deprived for experiments.

Measurement of cell rheology

We measured cell rheology using OMTC^12,13 (Supplementary Notes 2). Ferrimagnetic beads (4.5 μm) coated with a synthetic Arg–Gly–Asp (RGD)-containing peptide are allowed to bind integrins on the cell surface and become tightly anchored to the cytoskeleton through focal contacts. The beads are permanently magnetized in the horizontal plane of the cell culture and subsequently twisted in an oscillatory magnetic field with frequency 0.75 Hz. The twisting field causes each bead to rotate towards alignment with the oscillatory field and, as result, a weak mechanical torque is applied to the cell. The complex modulus of the cells (G*) is computed from the Fourier transform of the applied mechanical torque (T) and of the resulting lateral bead displacement (D):

$$G^{\ast }=G^{\prime }+j{G}^{″}=\stackrel{\sim }{T}/\stackrel{\sim }{D}$$ (1)

where * denotes a complex number, the tilde overbar denotes the Fourier domain, and j² = −1. For each experimental condition, data are reported as medians of the bead populations (215–719 beads on a similar number of cells per experimental condition).

Spontaneous bead motions

Spontaneous bead motions were measured by tracking the position of the centroid of each bead. Data were recorded during time intervals of 10 s starting at different waiting times t_w after stretch cessation. We computed the MSD of each bead i as:

$$\text{MSD}(\mathrm{\Delta }t,t_{\text{w}})=<{(x_i(t+\mathrm{\Delta }t,t_{\text{w}})-x_i(t,t_{\text{w}}))}^2>$$ (2)

where Δt is the time lag, x is the bead coordinate, and brackets indicate an average over t. The distribution of the MSD(Δt,t_w) from bead to bead was approximately log-normal. Accordingly, data are reported as the median of the bead population.

Supplementary Material

Full Methods and any associated references are available in the online version of the paper at www.nature.com/nature.

Supplementary Information is linked to the online version of the paper at www.nature.com/nature.