Abstract
The purpose of this study is to understand why otoacoustic emission (OAE) levels are higher in normal-hearing human infants relative to adults. In a previous study, distortion product (DP) OAE input/output (I/O) functions were shown to differ at f2=6 kHz in adults compared to infants through 6 months of age. These DPOAE I/O functions were used to noninvasively assess immaturities in forward/reverse transmission through the ear canal and middle ear [Abdala, C., and Keefe, D. H., (2006). J. Acoust Soc. Am. 120, 3832–3842]. In the present study, ear-canal reflectance and DPOAEs measured in the same ears were analyzed using a scattering-matrix model of forward and reverse transmission in the ear canal, middle ear, and cochlea. Reflectance measurements were sensitive to frequency-dependent effects of ear-canal and middle-ear transmission that differed across OAE type and subject age. Results indicated that DPOAE levels were larger in infants mainly because the reverse middle-ear transmittance level varied with ear-canal area, which differed by more than a factor of 7 between term infants and adults. The forward middle-ear transmittance level was −16 dB less in infants, so that the conductive efficiency was poorer in infants than adults.
I. INTRODUCTION
This report evaluates the role of normal ear-canal and middle-ear functioning on the interpretation of otoacoustic emission (OAE) responses produced within a healthy cochlea. Based on the hypothesis that the cochlear mechanics are mature at birth and ear-canal and middle-ear mechanics are immature, Abdala and Keefe (2006) used measurements of distortion product (DP) OAE input/output (I/O) functions in infants and adults to calculate a relative forward transfer-function level ΔLF and a relative reverse transfer-function level ΔLR between the ear canal and the base of the cochlea. These levels assessed differences in acoustic ear-canal and middle-ear transmission in infants compared to adults. Each level in infants from newborn to 6 months of age was defined relative to an adult group. The ΔLF in term infants was found to be −15 dB lower than adults and ΔLR in term infants was 13 dB higher than adults for a DPOAE at 4 kHz. The higher ΔLR in infants is responsible for DPOAE levels being higher in a healthy newborn relative to an adult ear. The goal of this report is to explain this 28 dB relative difference between term infants and adults in their combined forward and reverse transmission of sound.
A one-dimensional scattering-matrix theory of the acoustical-mechanical functioning of the ear canal, middle ear and cochlea (Shera and Zweig, 1992b) is introduced and extended to include ear-canal and maturational effects as well as incorporating the energy-reflecting properties of the ear-canal probe (Secs. II A through II I). Theoretical predictions are summarized in Section II J for the reader specifically interested in the results concerning the effect of immaturities in ear-canal and middle-ear functioning on DPOAEs. Using the above-described results of Abdala and Keefe (2006), along with newly reported measurements of ear-canal reflectance that were obtained in the same groups of subjects, the theory is applied to analyze the effects of immaturities in ear-canal and middle-ear functioning on the forward and reverse transmission of DPOAEs.
II. THEORY OF DPOAE GENERATION AND TRANSMISSION
A. General model and pressure variables
The DPOAE source model is based on a one-dimensional transmission-line model of acoustical/mechanical signal flow in the external, middle and inner ears (see Fig. 1). A probe consisting of one or more sound sources and a microphone is inserted into the ear canal a distance ℓ from the tympanic membrane (TM). The pressure at a given location in the ear canal or cochlea is the sum of a forward pressure signal (each forward signal denoted by a superscript +) directed into the ear and a reverse pressure signal (each reverse signal denoted by a superscript −) directed away from the TM and towards the probe. The pressure Pe measured by the microphone is decomposed into . A reverse signal directed toward the probe leads to a reflected forward signal according to
FIG. 1.
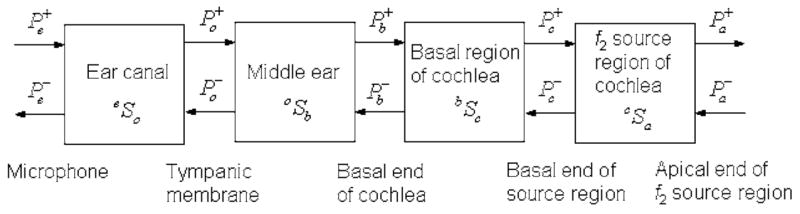
Signal flow diagram in external, middle, and inner ears. On pressure variables and S matrices, a superscript + denotes wave in forward direction, and superscript − denotes wave in reverse direction.
| (1) |
in which Rs is the source reflectance of the probe. The acoustic propagating mode in the ear canal is coupled to the middle ear by the pressure acting over the TM. The middle-ear energy is coupled into the cochlea, in which a pressure difference acts across the basal end of the cochlear partition.
In a DPOAE test, two sinusoidal tones are presented at frequencies f1 and f2 with f2/f1 ≈ 1.2, and the DPOAE is measured at frequency fDP=2f1−f2. The model of cochlear function is assumed to be one-dimensional along the cochlear partition. For a low-level, sinusoidal excitation at frequency f2, the forward traveling wave on the basilar membrane has its maximum displacement at its tonotopic place. The cochlear model is decomposed into a set of connected regions (see Fig. 1): (1) a basal region, in which the basilar-membrane displacement varies approximately linearly with the stimulus amplitude, (2) a f2-source region, in which the basilar-membrane displacement varies nonlinearly with a stimulus amplitude at f2, and (3) an apical region, which includes the tonotopic place of fDP, and more apical locations. A cochlear pressure acts at the boundary between basal and f2-place regions, while a cochlear pressure acts at the apical side of the f2-source region.
The theory of one-dimensional acoustic transmission lines to represent energy flow in the external, middle, and inner ear can be formulated using a variety of equivalent representations. One representation of one-dimensional transmission lines is the ABCD matrix approach. This has the property that spatially connected regions are represented by matrices that are concatenated together by the ordinary rules of matrix multiplication. Another representation of one-dimensional transmission lines is the scattering (S) matrix approach used in the present report. The S-matrix is advantageous for analyzing bidirectional energy flow in what can be called forward and reverse directions through a transmission line. The bidirectional model in terms of propagating signals in the forward and reverse directions is well suited to understanding effect of middle-ear transmission on the process of OAE generation, because the underlying parameters of a S matrix model, which are reflectances and transmittances, are applied in a simple manner to each of the stimulus and OAE response signals. The ABCD and S-matrix representations are equivalent representations of the same system, i.e., results obtained using a S matrix can also be obtained using an ABCD matrix.
It should be cautioned that neither the ABCD matrix nor the S-matrix representation is a detailed model of middle-ear mechanics. What each representation provides is a frame-work for relating measurements at the tympanic membrane to measurements at the oval and round windows. A more detailed model of middle-ear mechanics would have the goal of explaining the ABCD or S-matrix parameters in terms of variables related to middle-ear structures. Such a goal was outside the scope of the present study.
B. Scattering matrix properties
Figure 1 shows a set of four networks drawn as boxes, with each network represented by a S matrix that relates the acoustic pressure at locations on either side of the network. The S matrix transforms the incoming waves into outgoing waves. For example, the forward and reverse components of the ear-canal pressures Pe and Po are related by the S-matrix eSo in Fig. 1, which represents sound propagation in the ear canal. For this network, the incoming waves are from the left and from the right, and the outgoing waves are to the left and to the right. The incoming and outgoing waves are each represented by a two-element column vector, and the ear-canal S matrix is a two-by-two matrix of complex coefficients:
| (2) |
A general S-matrix 1S2 relating location 1 on the left and location 2 on the right is written
| (3) |
The r+ is the (pressure) reflectance, and t+ is the (pressure) transmittance of an incoming, or incident, forward wave in the absence of an incoming reverse wave ( ). The r− is the (pressure) reflectance, and t− is the (pressure) transmittance of an incoming reverse wave in the absence of an incoming forward wave ( ).
A cascaded network is one in which the output from one network is the input to the following network. Suppose that a S-matrix 1S3 is the cascade of scattering matrices 1S2 followed by 2S3, with 2S3 defined by
| (4) |
The 1S3 is calculated using a product operator ⊗, which is defined using Eqs. (3) and (4) by (Shera and Zweig, 1992b)
| (5) |
The off-diagonal terms are simple products of the transmittances through the individual S matrices, while the diagonal terms are complicated by the presence of reflection sites within each element. Fortunately, the present model has few such reflection sites so that the resulting products remain relatively simple in form.
A one-dimensional transmission line can be represented using a pair of variables, one of which is a generalized force and the other is a generalized velocity. For the acoustic transmission line used herein, the acoustic pressure is the generalized force and the acoustic volume velocity is the generalized velocity. This type of transmission line falls into the class of systems that satisfy reciprocity (Strutt, 1873). Middle-ear functioning is reciprocal to the extent that it is adequately described by such a system of generalized forces and velocities. Middle-ear mechanics has been assumed to satisfy reciprocity in previous studies (Shera and Zweig, 1991; Shera and Zweig, 1992a; Puria, 2003; Voss and Shera, 2004) as in this study.
Consider a general S matrix 1S2 terminated on the left by an acoustic transmission line with characteristic impedance Z1 and on the right by a line with characteristic impedance Z2. Reciprocity in a one-dimensional S-matrix model implies (Shera and Zweig, 1992b)
| (6) |
Reciprocity directly relates reverse and forward transmission with a coefficient α equal to the ratio of the characteristic impedances at the ends.
C. S-matrix formulation of ear-canal/middle-ear/cochlear model
A time dependence of ej2πft with unit imaginary number j, frequency f, and time t is used throughout (the symbol t is frequently used elsewhere to denote a transmittance, but the meaning is always clear from the context). The S-matrix between the ear-canal microphone and the basal end of the cochlea for the model in Fig. 1 is eSc=eSo ⊗oSb⊗bSc. If the cross-sectional area of the ear canal is slowly varying along its midline relative to its wavelength, then any forward or reverse incident wave travels without reflection. The resulting ear-canal S matrix over a distance ℓ is parametrized by the forward ( ) and reverse ( ) ear-canal transmittances
| (7) |
For constant ear-canal area, the transmittances satisfy
| (8) |
in which c is the acoustical phase velocity. The ear-canal length ℓ is sufficiently short that viscothermal wall loss in the ear canal can be neglected, although additional losses are likely present due to motion of the ear-canal walls in young infants (Keefe et al., 1993).
The stimulus levels are assumed sufficiently low that middle-ear muscle reflex effects are absent, so that the middle ear acts as a linear system. The middle-ear S matrix is parametrized according to the general form of Eq. (3) by
| (9) |
It follows from Eq. (6) that
| (10) |
in which the acoustical characteristic impedance in the ear canal is ζ with ear-canal cross-sectional area Aec and equilibrium density of air ρ. The characteristic impedance associated with the cochlear traveling wave at the basal end of the cochlea is ZCb. If αM is real, then Eq. (10) predicts that T+ and T− have equal phase responses. Because the phase of ZCb may differ from zero, the reverse middle-ear transmittance phase is the difference in the forward middle-ear transmittance phase and the phase of ZCb.
Because the basilar-membrane mechanics are linear in the basal end of the cochlea, the forward and reverse pressure waves travel therein without reflection, so that bSc has the form
| (11) |
Reciprocity implies that
| (12) |
in which the cochlear impedance at the cochlear vestibule ZCb and that at the basal boundary of the f2 source region (location c in Fig. 1) in the cochlea is ZCc. The long-wavelength approximation to cochlear mechanics is thought to be accurate in the basal region (Zweig, 1991).
For modeling DPOAEs, the S-matrix cSo in the f2-source region is assumed to have the same form as in Eq. (11), but in which the transmittances may vary with signal level (Shera and Zweig, 1992b). The dependence on signal level is indicated here and elsewhere, where needed for clarity, by a tilde over the variable. This S matrix is
| (13) |
The S-matrix eSc=eSo⊗oSb⊗bSc between the probe microphone and the basal boundary of the f2 source region in the cochlea is written using Eqs. (5) and (7)–(12) as
| (14) |
This is the most general S matrix needed for subsequent analyses.
D. Forward transmission
The ear-canal source generates a forward incident pressure . Its forward transmission is analyzed between the stimulus pressure Pe in the ear canal and the cochlear pressure Pc at the basal end of the f2-source region.
1. SFOAE effects on ear-canal reflectance and the forward cochlear wave
If the stimulus frequency (SF) OAE source lies in the tonotopic region of the cochlea, a reverse cochlear SFOAE source is related to the cochlear forward stimulus signal and an apical cochlear reflectance RSF by
| (15) |
The coherent reflection emission theory predicts a specific form of RSF (Zweig and Shera, 1995), but the representation in Eq. (15) applies to any source mechanism apical to node c in Fig. 1. The eSc in Eq. (14) is analyzed with Eq. (15) to solve for the reverse ear-canal pressure in terms of the ear-canal stimulus with the result
| (16) |
The term (without a tilde) is the ear-canal reflectance in the absence of any SFOAE, and is given by the first term on the right-hand side of the above
| (17) |
This is the product of round-trip travel in the ear canal and the reflectance at the eardrum. It is the commonly measured ear-canal reflectance, whose squared magnitude (called energy reflectance) is also commonly interpreted as a middle-ear response by neglecting the OAE contribution in Eq. (16).
The last term on the right-hand side of Eq. (16) represents the effect of SFOAEs on the reflectance measurement through its dependence on the apical cochlear reflectance RSF. The denominator describes the effect of multiple internal reflections of the SFOAE within the cochlea. In the experiments to be described, the ear-canal reflectance was measured using a wideband click, so that the OAE generated is a transient evoked (TE) OAE, which is spectrally decomposed here into its SFOAE component at f. TEOAEs in human ears are likely generated through the process of coherent reflection emissions. Because of basilar-membrane compression, the relative contribution of the TEOAE in Eq. (16) to the measured ear-canal reflectance decreases with increasing stimulus level (Keefe, 1997; Burns and Keefe, 1998). The effect of the TEOAE on the reflectance spectrum in the ear canal produces a ripple in the response that is otherwise dominated by the middle-ear reflectance and the ear-canal phase delay.
The P̃c is the cochlear pressure at the stimulus frequency that includes the effect of the SFOAE. The S-matrix eSc is further analyzed with Eqs. (15)–(17) to solve for P̃c in terms of the ear-canal stimulus Pe and the SFOAE (via RSF) as follows:
| (18) |
in which the cochlea pressure Pc in the absence of any SFOAE is
| (19) |
The TF(f) is the forward pressure transfer function through the middle ear and the basal region of the cochlea to the location where Pc(f) is defined.
2. Forward stimuli for DPOAEs
In a DPOAE test, the sinusoidal stimuli at primary frequencies f1 and f2 lead to cochlear pressures P̃c(f1) and P̃c(f2). If the SFOAEs at the primary frequencies are neglected, then the cochlear pressures Pc(f1) and Pc(f2) are found from Eq. (19) to be
| (20) |
When testing at stimulus levels near the DPOAE threshold, the SFOAE contributions to P̃c(f1) and P̃c(f2) in Eq. (18) may be relevant in interpreting the low-level DPOAE responses. For example, DPOAE I/O functions recorded in individual ears with f2/f1 = 1.2 are sometimes nonmonotonic even when the signal to noise ratio appears adequate (Gorga et al., 1994), even though the I/O functions averaged across ears may be monotonic. Aside from these low-level effects near threshold, it suffices in the following to interpret the DPOAE using Pc(f1) and Pc(f2) given in Eq. (20).
E. DPOAE generator source model
The resulting DPOAE source pressure was calculated by Shera and Zweig (1992b) as
| (21) |
in which each term on the right-hand side is evaluated at fDP. This equation represents a two-source model of DPOAE generation. The first source is generated within the f2-source region and travels in the reverse direction towards the ear canal. The second source is generated within the f2-source region, and travels in the forward direction to the more apical DP tonotopic place where it is reflected back. The is multiplied by the apical cochlear reflectance R̃a, measured with respect to the most apical region in Fig. 1. This reflectance is defined by The t̃− is the reverse transmittance defined in Eq. (13) across the f2-source region. The denominator of Eq. (21) includes R̃a and transmittances defined in Eq. (13) as well as , which is described below.
Equation (21) is analyzed in the limit of small internal reflections, i.e., . Each reflectance and transmittance in this inequality has a magnitude between zero and one (ignoring any spontaneous OAEs present at fDP). The inequality is typically satisfied so that Eq. (21) can be approximated using a first-order Taylor series as . The first term in parentheses on the right-hand side is the two-source term and is independent of middle- and external-ear functioning. The second term in brackets has terms representing cochlear nonlinearity and , which depends on middle-and external-ear functioning. Consider averaging over a group of subjects, in which the effect of the total internal reflections would tend to average out. The group mean of would be approximately equal to 1. It follows that the group mean of the magnitude , which is denoted by G, is a function only of the source terms as follows:
| (22) |
The DP source at fDP is created by a nonlinear function G of the cochlear overlap of the two primaries [as described by Eq. (20)], and each primary input depends on the forward transmittance and the ear-canal reflectance. The second row shows the explicit dependence of G on f1 and f2, which accounts for frequency-dependent variations in the DP source strength, and on their corresponding cochlear pressure amplitudes.
F. Reverse transmission
The DPOAE pressure at the probe microphone is calculated using Eq. (14). The DPOAE in the cochlea is specified as the driving source. The boundary condition at the probe is that of Eq. (1), so that . At frequency fDP, Eq. (14) becomes
| (23) |
Using the top row of this equation and the fact that , the resulting probe microphone pressure Pe is
| (24) |
The middle equation is that of Eq. (17) evaluated at fDP. The DPOAE pressure is proportional to TR(fDP), which is the reverse pressure transmittance at the TM. Using Eqs. (14) and (19), the reverse and forward transmittances at the TM are related by
| (25) |
The bottom row of Eq. (23) with Eq. (22) provides the traveling wave ratio , which occurred in the denominator of Eq. (21), i.e.
| (26) |
G. Predicting forward and reverse transmission
For analyzing a group set of DPOAE I/O functions, the source term is replaced by its group mean G. The magnitude of Eq. (24) is expressed as
| (27) |
The reverse transfer function HR is a product of the magnitudes of the reverse middle-ear transfer function and a reverse ear-canal transfer-function ER, which depends on the ear-canal reflectance and the source reflectance of the probe.
The forward transfer function HF is defined for use in Eq. (22) by
| (28) |
The transfer function EF varies with ear-canal reflectance. Magnitudes are converted to levels, i.e., the defined levels are L1 and L2 for stimuli, LDP for DPOAEs, LF for forward transfer function, LR for reverse transfer function, and Lα for the reciprocity factor:
| (29) |
The reference pressure is P0=0.000 02 Pa.
Using Eqs. (22), (27), and (29), LDP is expressed using a DPOAE source level g as
| (30) |
This simplifies in measurements with fixed frequency ratio f2/f1 and fixed level difference ΔL = L1−L2. Because f2/f1 = 1.2 is close to 1, the forward transmittance and ear-canal reflectance are assumed to vary sufficiently slowly that LF(f1) ≈ LF(f2). The resulting DPOAE level is the same as in the model of Abdala and Keefe (2006)
| (31) |
The explicit dependence of g on f2 may be omitted in the following because the DPOAEs of Abdala and Keefe were measured at a single f2, i.e., g(f2, L2+LF(f2)) = g(L2+LF).
H. Cochlear maturity and external/middle ear immaturity
In testing the hypothesis that cochlear functioning is mature in infants, Abdala and Keefe used a particular form of g in Eq. (31) to fit the mean adult DPOAE data in units such that the mean reverse transfer-function level in adults and the mean forward transfer-function in adults were each normalized to zero, i.e.
| (32) |
A superscript a on any variable denotes the adult group and i denotes any infant group. The infant DPOAE I/O functions were fitted with the same function g as in adults (consistent with the hypothesis of mature cochlear function), and their forward transfer-function level ΔLF and reverse transfer-function level ΔLR were calculated with respect to the adult level.
With Eqs. (19) and (28), the forward transfer function is decomposed into
| (33) |
The ratio ΔHF of the forward transfer-function magnitude in infants re: adults is
| (34) |
The hypothesis that cochlear functioning is adult-like was used in the above, so that the basal-region cochlear transmittance [see Eq. (11)] is the same in infants and adults (t+,i = t+,a). The term ΔHF is expressed as a relative level ΔLF by
| (35) |
The relative forward transfer-function level ΔLF is expressed as a sum of a relative forward ear-canal level ΔLFE and a relative forward middle-ear transmittance level ΔLFM. The measurements of ear-canal reflectance in infants and adults provide a measurement of ΔLFE via Eq. (28). Combining this measured ΔLFE with the measured ΔLF by Abdala and Keefe (2006) provides an estimate of ΔLFM, which quantifies the effects of maturation on forward middle-ear transmittance.
Concerning reverse transmission, reciprocity was expressed in Eq. (29) in terms of α=αCαM. If cochlear functioning is mature in infants, then αC in the basal cochlear region is the same in infants and adults. Thus, ΔLα in infants re: adults is given using Eq. (10) by
| (36) |
in which Aa is the cross-sectional area of the ear canal in adults, and Ai in infants. The above used the fact that ZCb is mature in infants with the hypothesis of mature cochlear function in full-term infants. The ΔLα varies with the ratio of the average ear-canal areas in adults and infants. The relative reverse transmittance ΔLR in infants compared to adults is defined based on the middle row of Eqs. (27), (35), and (36):
| (37) |
The relative level ΔLRE is calculated using the ear-canal and source reflectances [see bottom row of Eq. (27)]. The relative level ΔLR is a sum of relative levels involving the area, the ear-canal and source reflectances, and the forward middle-ear transmittance.
The reverse middle-ear transmittance T− is related by reciprocity in Eq. (10) to the forward middle-ear transmittance T+. Converting that equation to a form showing the relative level difference between infants and adults, the relative reverse middle-ear transmittance level ΔLRM is given by
| (38) |
The second row of the above is based on the assumed maturity of the characteristic impedance ZCb in infant ears that occurs in Eq. (10), the bottom equation in Eqs. (35) and (36). It follows from Eqs. (37) and (38) that ΔLR(fDP) = ΔLRE(fDP)+LRM(fDP), which is the analog for reverse transmission to the top Eq. (35) for forward transmission. Thus, ΔLRM is directly measured using
| (39) |
I. Acoustic estimate of ear-canal area
The ear-canal area needed to calculate ΔLα in Eq. (36) was acoustically estimated using the following procedure. The reflectance in the ear canal was measured according to methods described in Sec. III B, in particular, based on the area Acal of a calibration tube. Its corresponding characteristic impedance was ζcal=ρc/Acal. The ear-canal acoustic impedance at the probe tip was calculated in the kth frequency bin by
| (40) |
The click response was recorded at a sample rate fs using N samples; the kth frequency was fk = (k/N)fs (fs = 22.05 kHz, N = 1024). If the area A of a particular ear were measured, then the characteristic impedance of that ear canal would be ζ = ρc/A. Using this ζ, a new reflectance can be defined such that the acoustic impedance takes the form
| (41) |
The in variance in impedance in Eqs. (40) and (41) is possible because the plane-wave impedances on opposite sides of an area discontinuity are equal (Morse and Ingard, 1968). This expression can be rearranged into and expressed in the time domain as a recursive function of sample number n by (Sondhi and Resnick, 1983; McIntyre et al., 1983)
| (42) |
The asterisk denotes time-domain convolution and δ[n] equals 1 for n = 0, and 0 otherwise. The time-domain impedance and reflectance in Eq. (42) are defined using the N-sample inverse discrete Fourier transform (DFT) by
| (43) |
The is causal so that . It follows from Eq. (42) at n = 0 that . Combining this with the top equation of Eq. (43) at n = 0 leads to
| (44) |
The latter form of the above uses DFT symmetry properties for the case that ζ = ρc/Aec is real. Its right-hand side is expressed in terms of the real part of the impedance. The converges to ζ at high frequencies, and is approximated as ζ (an improved theory would introduce a complex ζ at frequencies <0.25 kHz), so that
| (45) |
Thus, the ear-canal area A was calculated in terms of the frequency average of the real part of the impedance by
| (46) |
Keefe et al. (1992) reported this relation with an incorrect coefficient, although this reference and Keefe et al. (1993) used the correct equation (46) to calculate the area. Huang et al. (2000) correctly reported this relation. Its practical application may be limited in that the bandwidth of the averaging of was limited to 0.25–8 kHz. Nevertheless, this finite-bandwidth approximation gave accurate area estimates for calibration tubes to within a couple of percent, so it is likely to be acceptable for area estimates in ears as well.
Any were reset to 0 but included in the average. Such negative values may have occurred due to small inaccuracies in reflectance calibration, errors related to a probe-tip placement close to the ear-canal wall, or by partial or complete blockage of the tip by cerumen. This procedure differed slightly from that of Huang et al. (2000), who omitted frequencies from the average at which . The two procedures were compared across infant ears, and the differences in area estimates were within 10% in 88 of 106 ears. The maximum procedural difference for any ear was 44%, but this case involved a measurement with significant artifact. The median difference in estimating the area was zero for infants and 1.3% for adults. Thus, the acoustic area estimate was judged sufficiently accurate for use in interpreting reverse middle-ear transmission differences across age. The within-ear area differences attributable to choice of procedure were smaller than the between-ear differences.
This area estimation procedure assumed that the ear-canal walls were rigid. However, neonatal ear canals have nonrigid walls that move in response to sound below 1 kHz (Keefe et al., 1993), which would introduce some error. The fact that the average extended over a wider frequency range (up to 8 kHz) would suggest that the contribution of nonrigid walls did not have a major effect in data from young infants, but the size of this error is unknown.
J. Summary of model predictions
For interpreting the relative forward (ΔLF) and reverse (ΔLR) transfer-function levels derived from measured DPOAE I/O functions, the main result of the model is to partition these levels in infants relative to adults into ear-canal and middle-ear components by
| (47) |
| (48) |
| (49) |
The ΔLF is determined in Eq. (47) from DPOAE measurements (Abdala and Keefe, 2006), and ΔLFE from reflectance measurements, so that the relative forward middle-ear transmittance level ΔLFM(f2) = ΔLF(f2)− ΔLFE(f2) may be calculated at f2.
The in Eq. (48) is the predicted relative reverse transmission level, which is compared with the measured ΔLR from DPOAE measurements (Abdala and Keefe, 2006). The ΔLRE(fDP) was calculated from reflectance data, and ΔLα from the ratio of the adult to the infant ear-canal cross-sectional area, as estimated acoustically. Because forward transmission was measured by Abdala and Keefe across the stimulus frequencies f1 and f2, but not at fDP, ΔLFM(fDP) in Eq. (48) was approximated using ΔLFM(f1), i.e., it was calculated based on measurements at the stimulus frequency f1 closest to fDP. This ΔLFM(f1) was calculated using a relation similar to Eq. (47) at f1, i.e., ΔLFM(f1) ≈ ΔLF(f2)−ΔLFE. The level difference e in predicted and measured relative reverse transmission levels was defined as
| (50) |
The notation ε(fDP;f1) means that the dominant difference is compared at fDP, but that the prediction of ΔLR(fDP) depends on ΔLFM(f1) at f1. The level difference in ε(fDP;f1)was judged with respect to the reported 28 dB difference in terms infants between ΔLR and ΔLF.
By analogy with the above discussion of forward transmission, the ΔLR(fDP) is determined in Eq. (49) from DPOAE measurements (Abdala and Keefe, 2006), and ΔLRE(fDP) from reflectance measurements, so that the relative reverse middle-ear transmittance level ΔLRM(fDP) = ΔLR(fDP) − ΔLRE(fDP) may be calculated at fDP.
III. METHODS
This section describes the methods used to measure ear-canal reflectance in the same set of subjects in whom DPOAE responses were collected. DPOAE methodology and results for infant and adult subjects are completely described in Abdala and Keefe (2006).
A. Subjects
Ten normal-hearing adults and 35 normal-hearing infants participated as subjects in this part of the study. The adults had a mean age of 27.5 years and audiometric thresholds < 15 dB HL for frequencies from 250 to 8000 Hz. Of the infant subjects, 21 were term born and 14 were infants born prematurely (mean age at birth=35 postconceptional weeks) but tested after they reached term-like status, i.e., 37–41 postconceptional weeks. Infants had a mean birth weight of 2920 g and mean apgar scores of 7.7 and 8.7. Other than premature birth, none of the infants had high-risk factors for hearing loss; the hearing in all infant subjects was within normal limits. Subjects included both males and females, and data were collected in one ear per subject. Each age group included both right and left test ears.
Ear-canal reflectance was analyzed in a subset of these ears. Inasmuch as some data were obtained longitudinally, data were dropped if the DPOAE in the same subject dropped by 10 dB or greater from one test session to another and parent reported the infant to be sick or congested, which indicated a possible upper respiratory infection. Data were dropped if the energy reflectance was close to zero and/or if the equivalent volume was extremely negative at low frequencies (≤1 kHz). The presence of either or both conditions indicated a likely leak of the probe in the ear canal (Keefe et al., 2000). Data were dropped if the energy reflectance at high frequencies (6–8 kHz) exceeded 1.2. In the absence of spontaneous OAEs, the energy reflectance should not exceed 1.0, but data with energy reflectances between 1.0 and 1.2 were retained in the data set, even though there was some artifact present in the measurement. We preferred to retain data with modest amounts of artifact at some frequencies rather than to discard all the subject’s data. This artifact may have been due to a partially blocked probe tip by cerumen or resulting from placement near the ear-canal wall, or reflectance calibration errors at high frequencies. The final numbers of subjects analyzed in each age group was seven term infants, eight of age 1.5 months, nine at each of ages 3, 4, and 5 months, 13 at age 6 months, and ten adults.
B. Reflectance procedures
An Etymotic ER10C probe was used with two receivers and a microphone, with a manufacturer’s modification to provide +20 dB additional gain to each receiver. This same probe was used in Abdala and Keefe (2006). DPOAE and reflectance responses were acquired, whenever possible, based on the same ear-canal insertion. Receiver 1 delivered a brief “click” approximating a band-limited impulse from 0.25 to 8 kHz. Receiver 1 was driven by the output of a digital to analog converter (DAC) of a computer sound card (CardDeluxe) using custom-written software. The microphone output was synchronously recorded using an analog to digital converter (ADC) on the sound card. The sample rate was 22.05 kHz using a DAC and ADC buffer length of 1024 samples.
The response was a time average of eight ADC buffers in each infant’s ear and 16 ADC buffers in each adult’s ear. The shorter test duration in infants provided a response when the infant was judged by the operator to be quiet. Up to six responses were stored so that the operator could acquire multiple responses and choose the “best” response afterwards.
The ear-canal reflectance was calculated based on the click response and a calibration procedure performed before the subject was tested. The calibration used click responses recorded in a long and a short cylindrical, rigid-walled tube, with each tube closed at its far end. The calibration was based on a model of viscothermal wave propagation in each tube. The two main outputs from the calibration were the incident pressure response and the source (pressure) reflectance of the probe [see Eq. (1)]. The incident pressure was the acoustic click response in the absence of reflections. The adult probe was calibrated using a pair of large-diameter tubes (of nominal lengths 292 and 8.2 cm) with a diameter (7.94 mm) close to that of the adult ear. The infant probe was calibrated using a pair of small-diameter tubes (of lengths 237 and 5.9 cm) with a diameter (4.76 mm) close to that of the infant ear canal.
Other calibration outputs, which are further described in Keefe and Simmons (2003), included the root-mean-squared error ΔR in the calibration and a final estimated value of a dimensionless parameter χ, which equaled one if the actual viscothermal loss was the same as the model wall loss, and otherwise slightly exceeded one, indicating that the measured loss exceeded the model loss. A reflectance calibration was valid for the adult probe if ΔR ≤ 0.014 and ≤ χ ≤ 1.11, and valid for the infant probe if ΔR ≤ 0.014 and 1 ≤ χ ≤ 1.09. These validity criteria were set after analyzing preliminary results. After calibration, the ear-canal reflectance was calculated based on the incident pressure, the source reflectance and the ear-canal pressure.
The procedure was similar to previous work except for the following. Keefe and Simmons erroneously stated that ear-canal reflectance was calculated [in their Eq. (13)] using an additional input, the “measured ear-canal area” based on the size of the probe tip. In fact, their ear-canal reflectance results were calculated using their Eq. (8), in which the “nominal pressure reflectance” was normalized to the area of the tube set used in calibration. This error was fortuitous, because it is inaccurate to estimate the ear-canal area by the area of the probe tip (Keefe, 2004). The present ear-canal reflectance results were calculated using Eq. (8) of Keefe and Simmons (2003). In Keefe and Simmons, the source reflectance was calculated as a weighted average of the source reflectances measured in the short and long tubes. In the present study, the source reflectance was that measured using the short tube. An iterative loop within the calibration procedure was used to improve the model fit to the data by adjusting the estimates of tube lengths and χ.
Distributions of source reflectance measurements using adult and infant probes were collected based on calibrations on different days, and are plotted in Fig. 2. The median source reflectance magnitude of the adult probe exceeded that of the infant probe at all frequencies. This may be due to the fact that the sum of the areas of the two receiver ports and of the microphone port is the same for both probes, but their summed port area relative to the ear-canal area was smaller in the adult than the infant probe. This would result in a larger reflection amplitude from the adult probe. The median source reflectance phase remained within ±35 degrees for both probes at all frequencies. The median reflectance magnitudes of both probes were relatively high across frequency except for minima near 2.6 and 5 kHz. If the probe functioned as an ideal closed-end termination, its source reflectance would have a magnitude of 1 and a phase of 0°. The Rs of the adult probe was more similar than that of the infant probe to this idealized source reflectance.
FIG. 2.
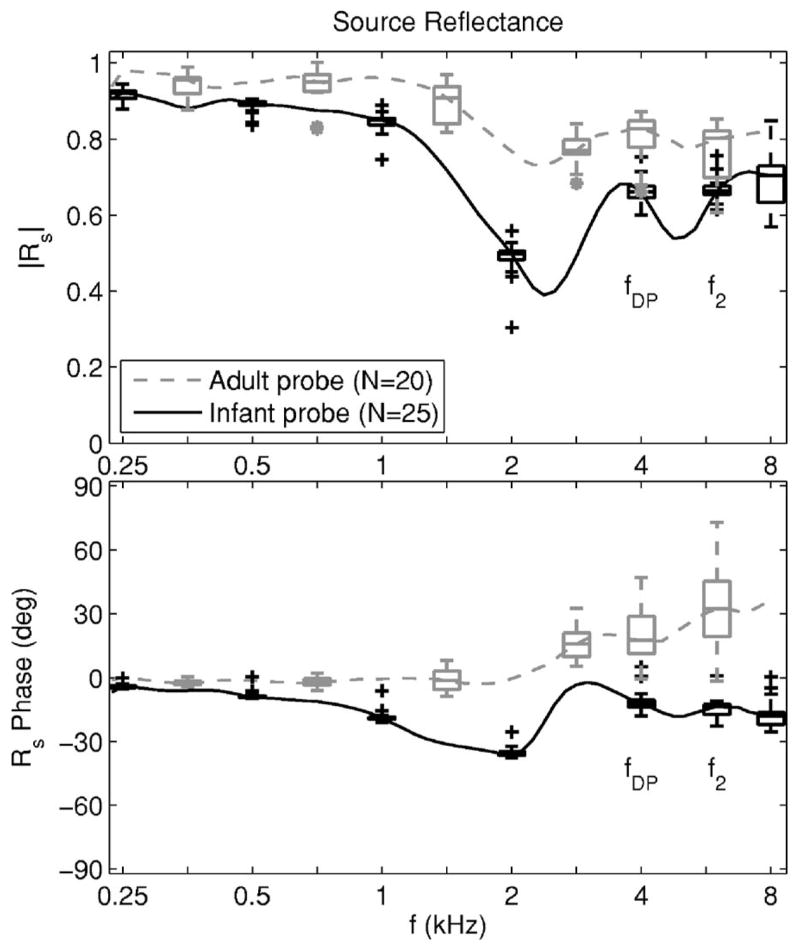
The median source reflectance is shown for the probe used in infant (black solid line) and adult measurements (gray dashed line), while the distribution of source-reflectance responses is shown by the corresponding box and whisker plots spaced an octave apart. Box and whiskers plots are also shown at each of the fDP and f2 frequencies. The magnitude of the source reflectance is shown in the top panel and the phase of the source reflectance is shown in the bottom panel. The distribution of responses was based on N=20 calibrations of the adult probe and N=25 calibrations using the infant probe, with each calibration performed on a separate day.
The source reflectance phase φs for the adult probe showed a positive slope that was repeatable (see box and whiskers plot at 6 kHz for the adult probe in Fig. 2). The φs of 35° at 8000 Hz is expressed as a phase advance τs by φs=2πfτs, with τs=12 μs. The source of the phase advance may have been an effect of higher-order evanescent modes. These modes describe the nonplane-wave coupling between source and receiver at the probe surface. Such evanescent-mode effects should be more pronounced in the adult than infant probe, because, as described earlier, there is a larger discontinuity for the adult-sized calibration tubes between the summed port area compared to the calibration-tube area. At frequencies (such as in the present study) for which the highest analysis frequency was much less than the lowest cuton frequency of any higher-order mode (Morse and Ingard, 1968), the impedance measured at the probe tip is the sum of the impedance of the plane-wave mode [as in Eq. (40)] plus an inertance that includes the effect of all the evanescent higher-order modes. The inertance impedance is parametrized as jζEka in terms of the ear or calibration-tube radius a and a dimensionless evanescent mode factor E. The E depends on the specific geometry of source and receiver, but a typical value is of order 1 or less (Keefe and Benade, 1981). This means that evanescent-mode effects on acoustic pressure (e.g., inside the ear canal) are important only within an axial distance of order Ea from the probe surface. Taking E=1 as an estimate and a≈4 mm for the adult probe, the corresponding characteristic time associated with this inertance is of order τe=Ea/c≈7 μs. This is similar in magnitude to τs=12 μs. The inertance would act as a perturbation in calculations of the incident pressure signal, the acoustic estimates of the lengths of the calibration tubes, and thus the source reflectance, but more study is needed.
Regarding the distributions of source reflectance data in Fig. 2, each box in a box and whiskers plot includes the inter-quartile range (IQR) between the 25th and 75th percentiles of responses, and each whisker above and below a box extends to the lesser of 1.5 IQR or the maximum data range. Individual outliers outside the whiskers were plotted with a black + for the infant probe and a gray * for the adult probe. The maximum number of outliers in magnitude or phase at any frequency never exceeded 3 out of a population of N =20 adult-probe and N=25 infant-probe calibrations. The variability in source reflectance was smaller for the infant than the adult probe, as assessed by the narrower IQRs. This is likely due to the compressible foam eartip used in the adult probe, which differed in compression for each calibration. Sometimes when compressed, the foam was also slightly pushed out at its ends, which may have contributed to the variability. The variability increased slightly (i.e., the IQRs were wider) with increasing frequency. The particular f2 and fDP frequencies from the DPOAE data set are indicated in Fig. 2, and the median source reflectance at fDP was used in calculating ΔLRE(fDP).
The click stimulus to measure reflectance was delivered at a fixed voltage level to the receiver in each adult ear, and at a slightly different fixed level in each infant ear. The click amplitude in each ear was assessed in terms of the peak-to-peak pressure amplitude of the response. This pressure amplitude had a mean and standard deviation (SD) of 640 ±151 mPa in adults, and a mean and SD of 588 ±264 mPa in infants. The mean amplitudes expressed as peak sound pressure levels (pSPLs) were 90.1 dB for adults and 89.4 dB for infants. These are slightly less than the 85–95 dB pSPL click level used in typical measurements of a TEOAE using the nonlinear differential stimulus method (Kemp et al., 1990). The pSPL does not adequately characterize the stimulus: the bandwidth of the click in the present study was broader (up to 8 kHz) than that used in typical TEOAE tests (up to 5–6 kHz), and the input voltage wave form was designed so that the acoustic stimulus was a band-limited impulse (Keefe and Simmons, 2003), whereas that used in typical TEOAE measurements is an electrical finite-duration impulse. The resulting click level in reflectance measurements had slightly lower spectral energy at frequencies where TEOAEs are typically measured. This emphasizes the fact that the reflectance stimulus did elicit TEOAE responses, which show up as a ripple on the individual-ear reflectance responses [see Eq. (16)].
C. Assessment of variability
Variability in measuring ΔLF and ΔLR from DPOAE I/O functions and variability in measuring the reflectance-based functions ΔLFE, ΔLRE and ΔLα produced variability in derived estimates of ΔLFM and ΔLR. The effects of these sources of variability on estimating ΔLFM and ΔLR were assessed by calculating a (bootstrap) standard error (SE) of the mean for each variable across the population of responses using the methods of Efron and Tibshirani (1986).
The bootstrap method analyzed 1000 synthetic data sets (using the MATLAB Statistics Toolbox), in which each synthetic data set was created by randomly sampling Nd observations at a time with replacement from the actual Nd observations in each data set. This involved independent sampling of the DPOAE and reflectance data sets. The DPOAE data set comprised the set of DPOAE SPLs in each ear for each age group at each L2, and the reflectance data set comprised the set of reflectances and impedances measured in each ear for each age group.
IV. RESULTS
A. Ear-canal reflectance
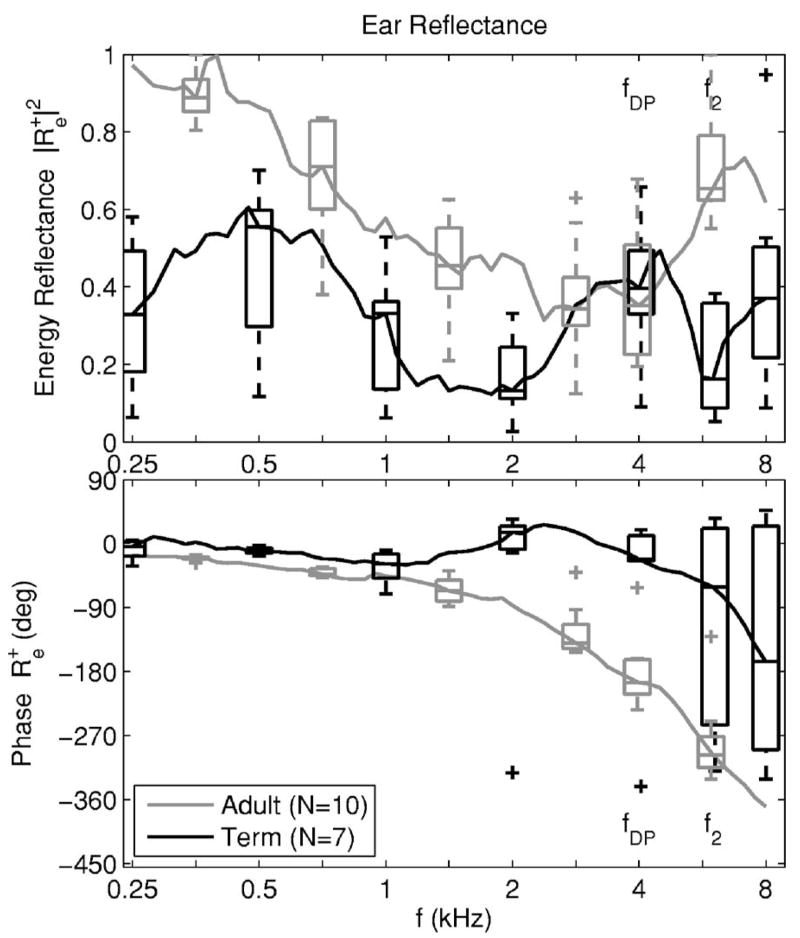
The distribution of ear-canal energy reflectance and unwrapped phase responses is plotted as 1/12th octave averages in Fig. 3 for the term-infant and adult groups. The energy reflectance was plotted rather than because it has often been reported in previous studies. The averaging partially smoothed out the ripples in that were a signature of a TEOAE response superimposed on the middle-ear reflectance, but some effects of OAE ripple remained. The 1/12th octaves were chosen because they include 4.00, 5.04 and 5.99 kHz, which are close to the DPOAE frequencies of fDP (4 kHz), f1 (5 kHz) and f2 (6 kHz), respectively. Reflectance values at some of these frequencies were used in subsequent modeling.
FIG. 3.
The median ear-canal reflectance (average in frequency over each 1/12th octave) is shown for the adult group (gray line) and the full-term infant group (black line). The distribution of ear-canal reflectance responses in each group is also shown by box and whisker plots spaced an octave apart. Box and whiskers plots are shown at each of the fDP and f2 frequencies. The ear-canal energy reflectance is shown in the top panel and its unwrapped phase is shown in the bottom panel.
The median energy reflectance was larger in adults than in term infants except at 4 kHz. The median reflectance phase delay was much larger in adults than term infants, mainly due to the larger distance between the probe tip and tympanic membrane in adults. The IQRs were more variable in the reflectance of term infants than in adults, especially in the energy reflectance at low (0.25 and 0.5 kHz) and high (6 and 8 kHz) frequencies. This increased variability in term infants was likely a result of differing maturational rates of ear-canal and middle-ear functioning. The variability in reflectance phase was small below 1 kHz in term infants and adults. At high frequencies in term infants, some reflectance phase responses required unwrapping and others did not, which increased the variability at 6 and 8 kHz. Each reflectance phase response was unwrapped in the adult group.
The median energy reflectance and unwrapped phase delay of were plotted in Fig. 4 for the adult group (gray line) and infant groups ranging in age from full term to 1.5, 3, 4, 5, and 6 months. These reflectances were plotted as 1/3 octave averages to more fully remove the TEOAE-induced ripple. Except for full-term infants, which differed from the older infant age groups, the energy reflectance increased at low frequencies with increasing age. The energy reflectance in adults and infants of 1.5 months age and older had a minimum near 2–4 kHz, but the minimum energy reflectance was approximately 0.4 in adults versus 0.1 in infants. The unwrapped phase of had increasing delay with increasing frequency from 0.25 to 1.2 kHz in all age groups, with larger age variations above 2 kHz.
FIG. 4.
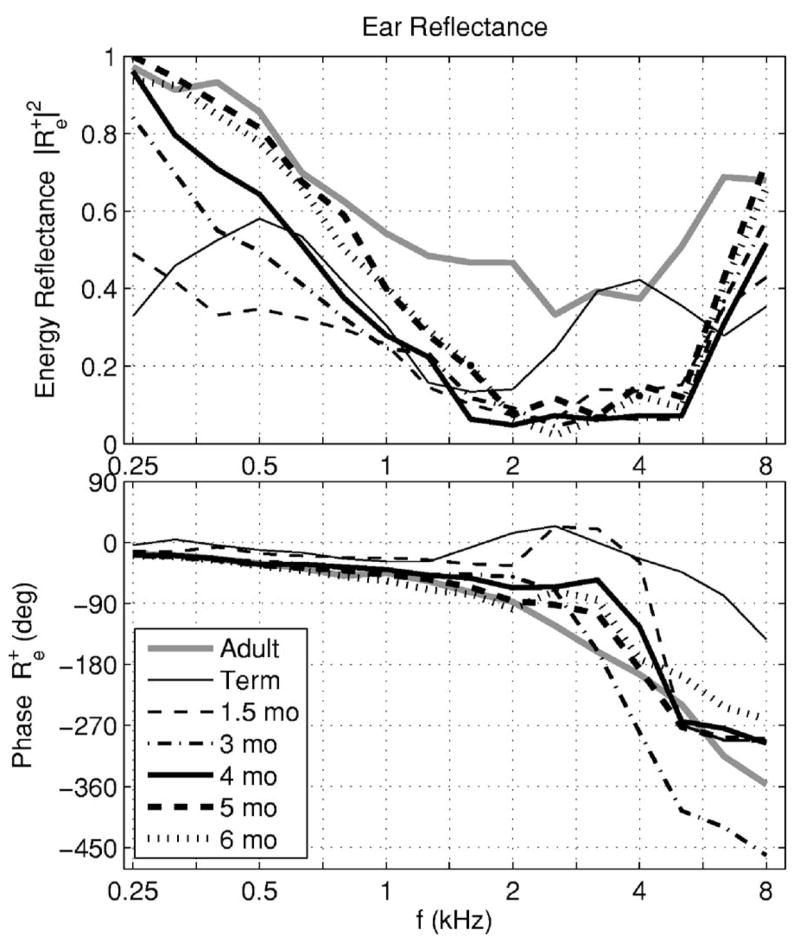
The median ear-canal reflectance (average in frequency over each 1/3 octave) is shown for the adult group (gray line) and six infant groups (black lines). The magnitude of the ear-canal reflectance is shown in the top panel and its unwrapped phase is shown in the bottom panel. The line style and line thickness for each age group is listed in the legend.
B. Ear-canal effects on forward and reverse transfer functions
The theory presented in Sec. I decomposed the forward and reverse transfer functions into ear-canal, middle-ear, and cochlear components. The measurement of ear-canal and source reflectances provided the ear-canal components of these transfer functions. Using Eqs. (28) and (33), a forward ear-canal transfer-function level LFE (in dB) is
| (51) |
Using Eq. (27), a reverse ear-canal transfer function level
| (52) |
The forward LFE is relevant to interpreting ear-canal transmission in any hearing test that uses an insert earphone to deliver sound, and is relevant to a DPOAE test at stimulus frequencies f1 and f2. The reverse LRE is relevant to interpreting an OAE test outcome at the OAE frequency. The median LFE(f) and LRE(f) are plotted in Fig. 5 for infant and adult groups.
FIG. 5.
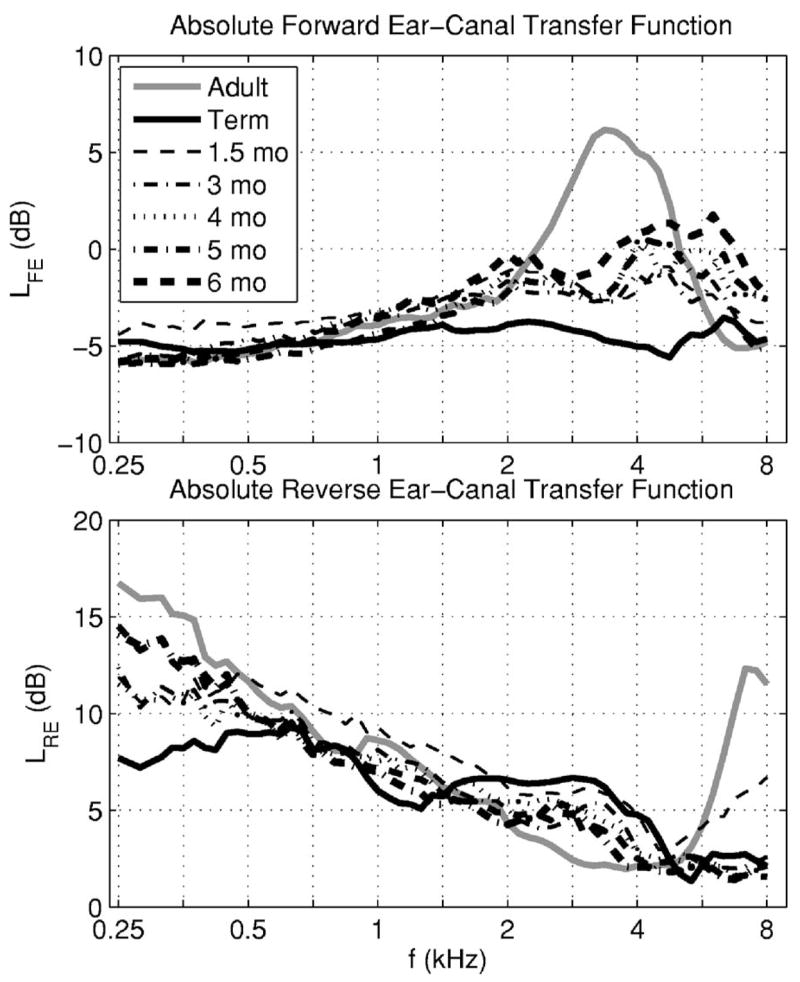
The absolute level of the median forward ear-canal transfer function is shown in the top panel for the adult group (gray line) and six infant groups (black lines). The line style and line thickness are listed in the legend for each infant age group. The corresponding absolute level of the median reverse ear-canal transfer function is shown in the bottom panel.
The forward level LFE in the adult group had a well-defined maximum at frequencies in the range from 3 to 4 kHz—e.g., LFE was 5 dB at 4 kHz, but only −2 dB at 2 kHz and −3 dB at 6 kHz. The LFE in the adult and infant groups were similar at frequencies up to approximately 1.4 kHz. The full-term infant group had a relatively constant LFE close to −5 dB at all frequencies. The infant groups at ages between 1.5 and 6 months had relatively small differences in LFE. Their LFE were between the adult and term-infant group levels between 2 and 4 kHz, and exceeded the adult and term-infant levels at and above 6 kHz.
The reverse level LRE decreased with a slope of approximately −3 dB/octave between 0.6 and 5 kHz. The LRE varied only slightly with age in this mid-frequency range, except for a 5 dB boost in term infants relative to adults near 2.8 kHz. In a common DPOAE screening procedure with f2 of 4 kHz and f2/f1 of 1.2, the corresponding fDP is 2.7 kHz. Thus, full-term infants received a boost relative to adults in the DPOAE response at this frequency due to reverse ear-canal transmission, while the adult received a larger boost relative to the full-term infant due to forward ear-canal transmission. Above 5 kHz, LRE increased rapidly with increasing frequency up to approximately 7–8 kHz in adults. It remained approximately constant in infants, except for a small increase at high frequencies in the 1.5 month group. Below 0.6 kHz, LRE varied significantly with age; the level at 0.25 kHz in the adult group was approximately 9 dB larger than that in the term-infant group. This result may be related to the presence of ear-canal wall motion at low frequencies in younger infants. This effect contributes with the presence of their higher noise levels to the difficulties of measuring DPOAEs at low frequencies in young infants. These forward and reverse ear-canal levels interact differently in a DPOAE test in contrast to a SFOAE or TEOAE test. This is because forward transmission in a DPOAE test occurs at the f2 (and f1) frequencies and the DPOAE returns at the fDP frequency.
The round-trip effect of these ear-canal transfer functions in a DPOAE test with f2/f1 = 1.2 (so that fDP=2f2/3) was represented by plotting LFE(f2)+ LRE(fDP) (see top panel of Fig. 6). The most salient feature of this plot was that the adult group round-trip level had a maximum near 3.4 kHz. In a SFOAE test or a frequency-specific comparison in a TEOAE test, forward and reverse transmission occur at the same stimulus frequency. The round-trip effect of these ear-canal transfer functions in a SFOAE test was represented by plotting LFE(f2)+ LRE(f2) at the same stimulus frequency f2 (see bottom panel of Fig. 6). The actual round-trip ear-canal level for the SFOAE test was somewhat flatter across frequency than for the DPOAE test within each age group (except for adults below 0.5 kHz, at which SFOAEs are rarely measured). It should be cautioned that the respective OAE levels are not strictly proportional to these sums of LFE and LRE, because the forward level is modified by cochlear non-linearity.
FIG. 6.
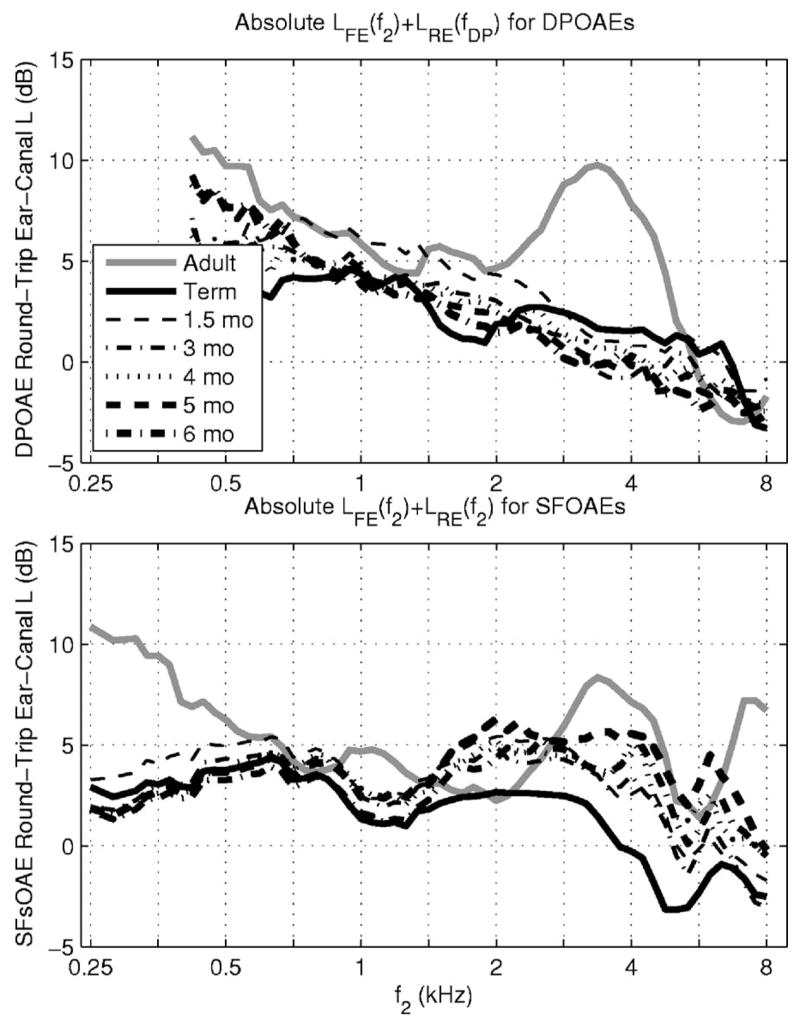
Top panel: a round-trip ear-canal transfer function for a DPOAE test with f2/f1 = 1.2 is plotted vs f2 as the sum of the medians of the forward ear-canal transfer function level LFE(f2) and the reverse ear-canal transfer function level LRE(fDP). Bottom panel: a round-trip ear-canal transfer function for a SFOAE test is plotted vs its stimulus frequency (denoted f2) as the sum of the medians of the forward ear-canal transfer-function level LFE(f2) and the reverse ear-canal transfer-function level LRE(f2). Results are shown for differing age groups with line styles as in Fig. 5.
The age differences in forward and reverse ear-canal transmission are revealed by defining the relative forward ear-canal transfer-function level ΔLFE and relative reverse ear-canal transfer-function level ΔLRE in infants compared to adults by
| (53) |
These definitions are equivalent to Eqs. (35) and (37). These relative levels in the infant groups are plotted in Fig. 7 in terms of the levels plotted in Fig. 5. The age effects in forward transmission were less than 2 dB at frequencies up to 2 kHz and above 6 kHz, but infant groups showed forward attenuation of up to 11 dB relative to adults at frequencies in the 3–4 kHz range. The relative reverse level in infants was attenuated below 0.6 kHz, boosted between 1.4 and 5 kHz, and attenuated above 5 kHz by as much as −10 dB at 8 kHz.
FIG. 7.
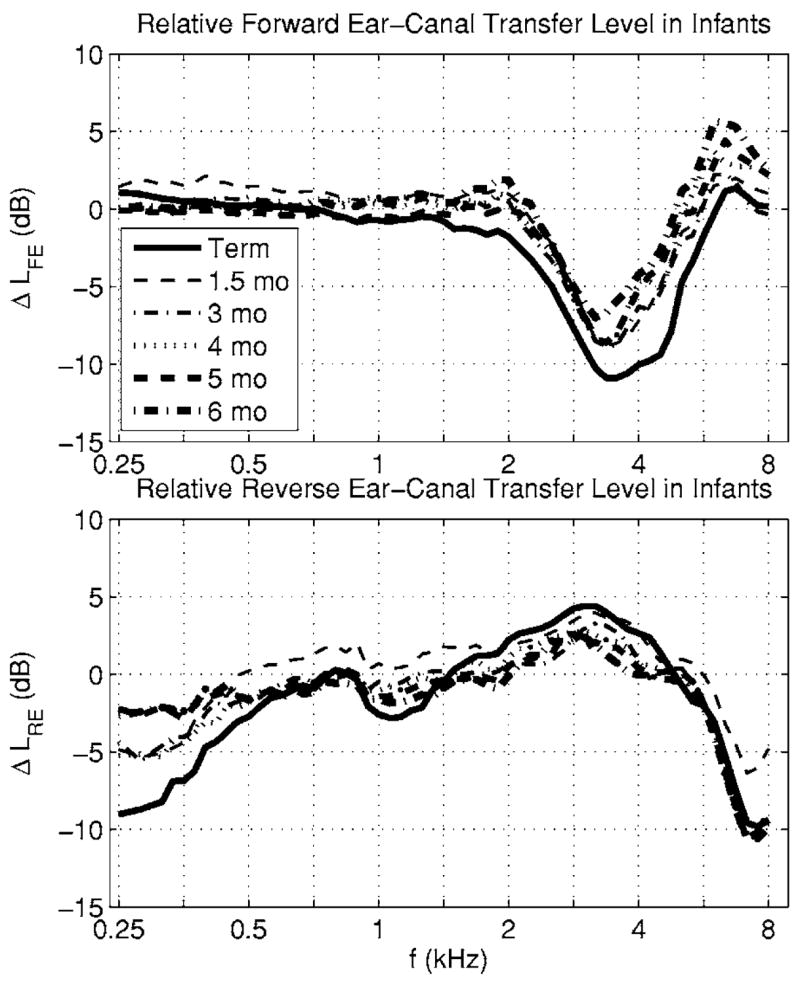
Top panel: the level of each infant group relative to the adult group of the median forward ear-canal transfer function is plotted. The line style and line thickness are listed in the legend for each infant age group. Bottom panel: The corresponding level of each infant group relative to the adult group of the median reverse ear-canal transfer function is plotted.
The theory in the Introduction identified the cross-sectional area A of the ear canal as important to reverse transmission of OAEs. The areas Aa in adults and Ai in infants were acoustically estimated using Eq. (46). The distributions of these areas were plotted in Fig. 8 using box and whiskers plots. The right vertical axis of the plot shows the approximate equivalent ear-canal diameter (equal to ) for the area A labeled on the left vertical axis at each tick mark. The median ear-canal area was only 8 mm2 in the term-infant group and increased monotonically with increasing age to 31 mm2 in 6 month olds, a value that was approximately half the median adult area of 58 mm2. The IQR in each infant group was narrower than the adult IQR, although the IQRs relative to their medians were more similar. No more than one outlier was present at any age. The acoustic estimates of ear-canal area from Keefe et al. (1993) are also shown in Fig. 8 (dashed line) at infant ages 1, 3, and 6 months, and in adults.
FIG. 8.
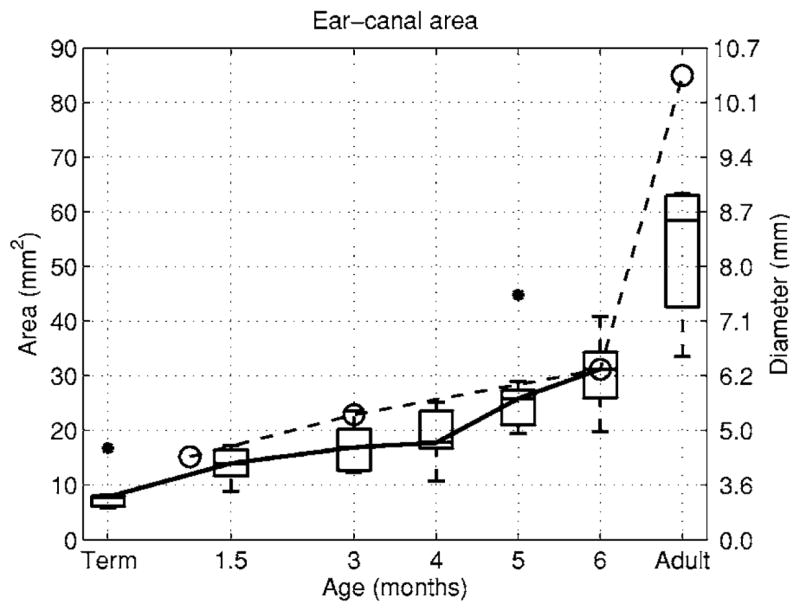
The median of the acoustic estimate of the cross-sectional area of the ear canal is plotted as a function of age for infants and adults (solid line). Box and whisker plots show the distribution of measured areas in the present study with asterisks denoting an outlier in the term-infant group and in the 5 month group. The right-hand axis expresses this area as the diameter (in mm) of the equivalent circular cross section. The acoustic estimate of the ear-canal area from Keefe et al. (1993) are shown in a dashed line with circles as markers.
The relative area level ΔLα=20 log(Aa/Ai) introduced in Eq. (36) controlled the difference in reverse transmission between infants and adults. The distributions of ΔLα in the infant groups were plotted in Fig. 9 as a set of box and whiskers plots. These box and whiskers plots were constructed for the distributions of infant ear-canal area relative to the median adult area (shown in Fig. 8). The median area level was 17 dB for term infants (corresponding to an adult area seven times larger than the infant area), and decreased with increasing age to 5 dB at 6 months.
FIG. 9.
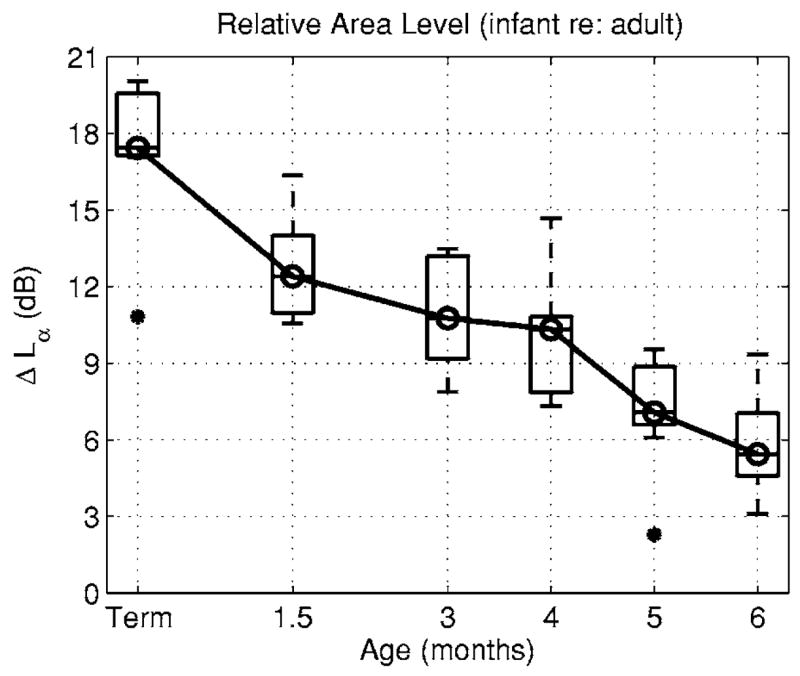
The box plots of the median and IQR of relative area level ΔLα (in dB) are plotted as a function of age based on the ratio of the median adult ear-canal area to the distribution of ear-canal areas in each infant age group.
The model-based decomposition of the relative forward level ΔLF into an ear-canal component (ΔLFE) and a middle-ear component (ΔLFM=ΔLF− ΔLFE) is shown in the top panel of Fig. 10. The mean ΔLF results are derived from Abdala and Keefe (2006), and the mean ΔLFE is evaluated at f2, (see corresponding median response in the top panel of Fig. 7). The mean ΔLFM at f2 showed an attenuation of 16 dB in term infants relative to adults; the attenuation decreased with increasing age to 7 dB in 6 month olds. The variability in each estimate was calculated as ±1 SE. The variability in ΔLFE across reflectance measurements was small compared to that in ΔLF derived from DPOAE measurements, so that the variability obtained in ΔLFM was similar to that in ΔLF. Forward middle-ear transmission was not yet adult-like at age 6 months, and, in fact, the ΔLFE was the least adult-like at the oldest age. This is evidence that the processes of ear-canal and middle-ear immaturity are far from complete at age 6 months.
FIG. 10.
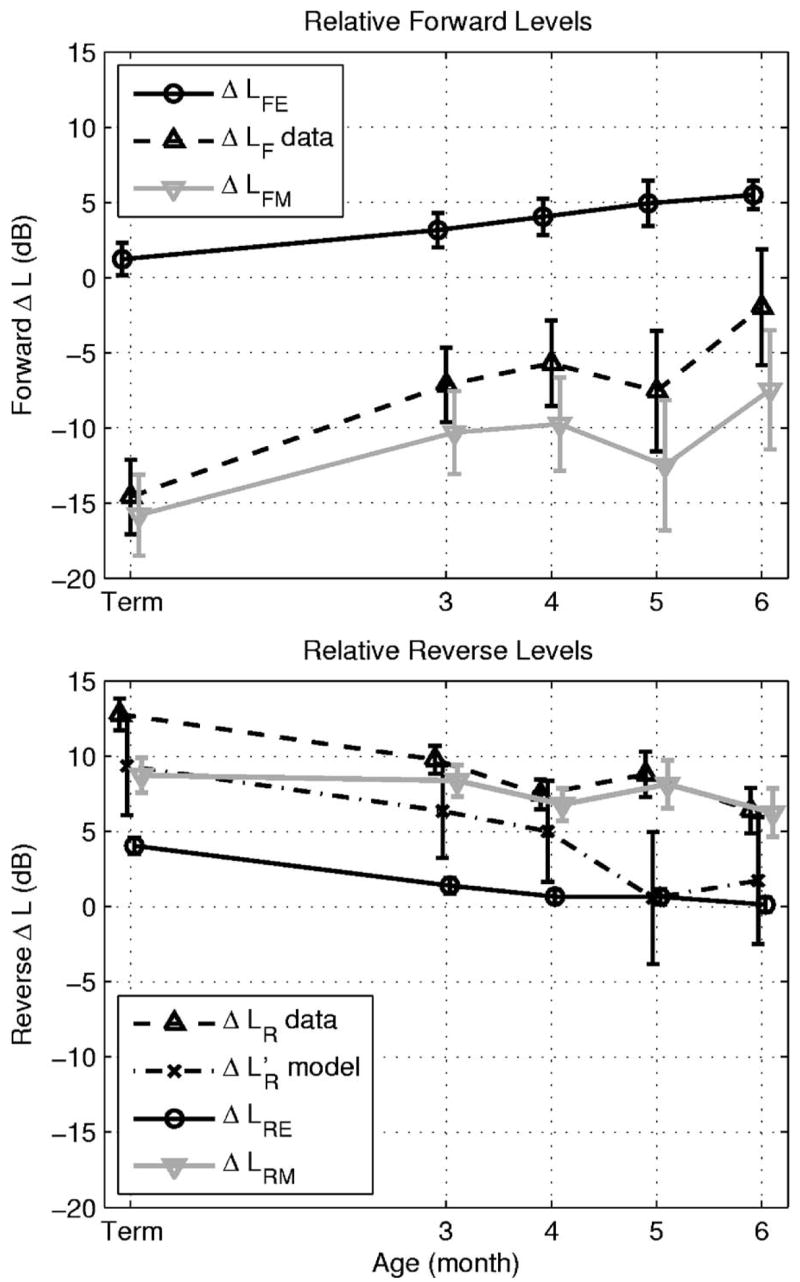
Top panel: the relative forward transfer-function level ΔLF data of Abdala and Keefe (2006) (dashed line, upwards triangle marker) and the ear-canal component ΔLFE (solid black line, circle marker) are used to estimate the relative forward middle-ear transmittance level ΔLFM (solid gray line, downwards triangle marker) at f2=6 kHz as a function of infant age. Bottom panel: the relative reverse transfer-function level ΔLR data of Abdala and Keefe (2006) (dashed line, upwards triangle marker) are plotted as a function of infant age at LDP=4 kHz, as is its ear-canal component ΔLRE (solid black line, circle marker), and its middle-ear component ΔLRE (solid gray line, downwards triangle marker). The ΔLR is compared to the model estimate plot (dashed-dotted line, × marker). The error bars in each estimate are shown as ±1 SE. Some data are slightly offset horizontally to improve clarity in viewing error bars.
The relative reverse level ΔLR was compared with its ear-canal component ΔLRE and the predicted [see Eq. (48)] in the bottom panel of Fig. 10. The ΔLRE was 4 dB in term infants and decreased to 0 dB in 6 month olds relative to adults. The variability in ΔLRE was smaller than that of ΔLR However, the variability in the mean of the model ΔL’R was larger than either, because its calculation was based in part on ΔLFM(f1), which had similar variability to that of ΔLFM(f2) shown in the top panel of Fig. 10. The dominant contributor to variability was that associated with the measurement of ΔLF in Abdala and Keefe (2006). The mean measured and predicted relative reverse levels were within measurement variability at all ages except at age 5 months. However, the trend was that the ε(f;f1)<0 at all ages [see Eq. (50)], with a mean difference of −4 dB. The relative reverse middle-ear level ΔLRM(fDP) in the bottom panel of Fig. 10 was calculated using Eq. (49), and its variability was only slightly larger than that of ΔLR and ΔLRE. The δLRM(fDP) had a gain of 9 dB in full-term infants, which decreased with increasing age to 6 dB in six month olds. Reverse middle-ear transmission was not yet adult-like at age 6 months, due mainly to immaturities in ear-canal area and in forward middle-ear transmission.
V. DISCUSSION
A. Maturational effects
A model of acoustical and mechanical transmission through the ear canal, middle ear, and cochlea was applied to interpret DPOAE and reflectance measurements in infants and adults. This allowed the estimation not only of the relative forward and reverse transmission levels in infants compared to adults, but also decomposed each of these forward and reverse levels into ear-canal and middle-ear components. The model to account for maturational differences in DPOAEs was based on the hypothesis that cochlear function and anatomy are adult-like in term infants. If this hypothesis were false, then at least some of the resulting model predictions would be expected to differ from measured data. Results from an analysis of human DPOAE I/O functions (Abdala and Keefe, 2006) suggested that cochlear function was, indeed, adult-like in newborns. The present analyses added a more refined test and further supports this hypothesis, inasmuch as the model assumed that several cochlear variables were adult-like in infant ears. These variables included: (1) the cochlear DPOAE source level g [see Eq. (30)], which was the cochlear variable that was assumed adult-like in infant cochleae by Abdala and Keefe, (2) the transmittance t+ in the basal region of the cochlea [see Eq. (34)], and (3) the characteristic impedances of the cochlea in basal and more apical regions [see Eqs. (10) and (12)]. Cochlear immaturity in any of these variables would have resulted in inaccuracies in model predictions. No gross inaccuracies were observed; the residual inaccuracies were likely due to assuming that each of ear-canal and middle-ear transmission were approximately constant over the frequency range between fDP and f2 (see below).
Regarding forward transmission near the stimulus frequencies of f1 = 5 and f2=6 kHz, there was a forward attenuation ΔLF of −15 dB of sound between a probe microphone in the ear canal and the cochlea in term infants relative to adults (Abdala and Keefe, 2006). After partitioning out the effect of ear-canal acoustics, the relative forward attenuation in middle-ear transmission in term infants compared to adults was ΔLFM of −16 dB (see top panel of Fig. 10). This 16 dB of additional attenuation in the forward middle-ear transmittance of term infants relative to adults affects not only DPOAE measurement, but any OAE measurement, and, in fact, any hearing experiment in which sound is delivered through the middle ear to the cochlea. The presence of immaturity in middle-ear forward transmission has significance for the study of hearing in young infants.
As described further in a brief review of middle-ear maturation in Abdala and Keefe (2006), the observed age dependence of ear-canal area is unrelated to the size of the tympanic membrane, which is of adult size in term infants. The plane of the tympanic membrane is more horizontal in infants than in adults (Ikui et al., 1997), which accommodates the smaller ear-canal area in infants. There were similarities and differences in the ear-canal area results reported in the present study compared to those in Keefe et al. (1993). The average area in 1 month olds in Keefe et al. was consistent with the present median estimates at term and 1.5 months. The area in 3-month-olds in Keefe et al. (1993) was slightly elevated above the IQR of the present study, and the results agreed in 6-month-olds. A large discrepancy in adult ears was identified by Keefe et al, who reported an average area (and standard deviation) of 85±33 mm2. The median adult area in the present study was 58 mm2 with an IQR from 43 to 63 mm2. The present results are in good agreement with measured cross-sectional areas in adult ear-molds at a location corresponding to a 10-mm insertion depth into the ear canal: the average earmold area was approximately 50 mm2 with a range from 30 to 70 mm2 (Stinson and Lawton, 1989). The adult area estimates of Keefe et al. (1993) were likely contaminated by either a lack of accuracy in measuring the acoustic impedance or an atypical distribution of adults with larger ear canals.
Regarding reverse transmission ΔLR at fDP=4 kHz, Abdala and Keefe (2006) reported a 13 dB increase in total DPOAE level in newborn infants compared to adults (see bottom panel, Fig. 10), and this relative DPOAE gain decreased with increasing age. The increase in reverse transmission in infants is what accounts for their large OAE levels compared to adults. The reverse ear-canal component ΔLRE accounted for 4 dB of this increase in newborns, partitioning the remaining 9 dB of ΔLR into ΔLRM. The model explained most of this difference as due to reciprocity in middle-ear mechanics, which predicts that the reverse middle-ear transmittance is equal to the product of the forward middle-ear transmittance and the ratio of the ear-canal characteristic impedance to the cochlear characteristic impedance [see Eq. (10)]. The reciprocal relation between forward and reverse middle-ear transmittance appears helpful in understanding the relationships between forward and reverse middle-ear transfer-function measurements in human-cadaver temporal bones and in nonhuman mammalian ears in vivo, but a review of this subject is outside the scope of this report. Nevertheless, maturation effects have been reported in young postnatal gerbils in the form of an attenuation of forward middle-ear transmission (Overstreet and Ruggero, 2002). Such effects are similar to those that were observed noninvasively in the present study in human infants.
The fact that ΔLR and agreed overall in Fig. 10 to within 4 dB confirmed the basic theory that maturational differences in DPOAEs are controlled by maturation in external- and middle-ear functioning. The additional discrepancy at 5 months was likely due in part to inaccuracies in estimating ΔLF and ΔLR (Abdala and Keefe, 2006), which showed the least accurate fits in the same 5-month and 6 -month age groups in which the largest magnitudes of ε(f;f1) were found. Other sources of this discrepancy might include error in the reflectance measurements or model accuracy, and any difference in the effect of immaturity on forward transfer of energy at fDP relative to that at f1 and f2. These immaturity effects might be further investigated by measurements in infants and adults over a broader frequency range.
The model accounted for approximately 24 dB of the 28 dB difference between ΔLR and ΔLF in term infants relative to adults. The immaturity in ear-canal area (see Fig. 9) accounted for 17 dB of this difference. Most of the remaining relative level was explained by reverse transmission (ΔLRE=4 dB, bottom panel, Fig. 10).
Consider the responses for newborns (i.e., the “Term” infant data in Fig. 10). The ΔLFM(f2) = −16 dB (top panel, Fig. 10) and ΔLRM(fDP) = 9 dB (bottom panel, Fig. 10) represent an attenuation in forward middle-ear transmission and a gain in reverse middle-ear transmission in the ears of newborns relative to adults. The round-trip difference was ΔLRM(fDP)− ΔLFM(f1) = 9−(−16) = 25 dB. While not plotted in Fig. 10, the difference using forward transmission at f1 was ΔLRM(fDP)− ΔLFM(f1) = 9−(−11) = 20 dB in newborns. If these were measured at the same frequency, then the model would predict [see Eqs. (37) or (48)] that ΔLRM(fDP) − ΔLFM(fDP) = ΔLα=17 dB. It appears that the difference is converging towards ΔLα as the frequency at which forward transmission is assessed moves towards fDP. Thus, immaturity in middle-ear mechanics in infants results in the attenuation of the forward-directed stimulus through the middle ear (at 5–6 kHz), while immaturity in the ear-canal area size results in an overall gain in the reverse-directed DPOAE (at 4 kHz) measured in the ear canal. These effects of immature function in infant ears are an attenuation of a sound stimulus to a lower effective level on the basilar membrane, but a boost in the resulting OAE level in the small ear canal of the infant.
The decomposition in Fig. 10 of forward and reverse transmission effects in infant ears relative to adults strictly applies to only one particular set of DPOAE frequencies. Forward transmission was assessed at f2=6 kHz and f1 = 5 kHz primaries, and reverse transmission was assessed at the 4 kHz DP frequency. The extent to which these results generalize to other frequencies is unknown. It should be noted that the restriction in this study to a single DPOAE frequency was required because a time-consuming DPOAE suppression protocol was implemented with each infant subject. Because of the length of this protocol, it was not possible to collect DPOAE I/O data at other frequencies. It would be useful to apply the procedures of the present study across a wide range of DPOAE frequencies to assess maturational differences in DPOAEs in terms of maturational differences in ear-canal and middle-ear functioning.
The results in Fig. 10 show that the 6 month old is not yet adult-like in terms of both ear-canal and middle-ear functioning. An unexpected finding from the ΔLFE results (Fig. 10) is that ΔLFE in older infants up to age six months was more different from adults than ΔLFE in younger infants. While this is only a 5 dB effect, it helps make the point that maturation of DPOAEs due to ear-canal and middle-ear development continues in infants older than 6 months. This is consistent with the reports that ear-canal and middle-ear functioning, as assessed by acoustic reflectance and impedance measurements, is not yet adult-like at age 24 months (Keefe et al. 1993), and ear-canal impedance is not yet adult-like even at age 11 years (Okabe et al. 1988). It may be that the remaining maturation after age 11 years and through puberty is related to increases in ear-canal area and the distance from the probe-tip location from the tympanic membrane (which might involve both area and ear-canal length changes), but more study in older children is needed.
B. Ear-canal transfer functions for different OAE types
Ear-canal reflectance and probe source reflectance measurements were used to calculate forward and reverse ear-canal transfer-function levels in adults and infants, and forward and reverse levels were combined to simulate the linear-systems effect of round-trip ear-canal transmission in a DPOAE measurement, and in a TEOAE or SFOAE measurement. In addition to their significance for understanding maturational effects, these ear-canal transfer function measurements have significance for interpreting differences in OAE type. The dominant effect of ear-canal acoustics occurred for adults in DPOAE measurements for f2 in the range of 3–4 kHz in the forward ear-canal transfer-function level in Fig. 5, and in the round-trip level shown in Fig. 6. This effect was not undone by the reverse ear-canal transfer-function level. This increased stimulus transmission in a DPOAE measurement near a f2 of 4 kHz in adults is shown in the frequency dependence of LFE(f2) in Fig. 5. This increase may explain why DPOAEs were better able than TEOAEs to classify a population of test ears of adult and older children (⩾3 years of age) as having normal or a sensorineural hearing loss at 4 kHz (Gorga et al. 1993). This advantage also may explain why SFOAEs in adult ears had a similar test performance to DPOAEs for predicting sensorineural hearing loss at octave frequencies from 1 to 8 kHz, except at 4 kHz where DPOAEs had better test performance (Ellison and Keefe, 2005). There is no such pronounced effect of ear-canal acoustics in newborns on DPOAEs for f2 in the range of 3–4 kHz or at other frequencies in the range from 0.5 to 8 kHz compared to TEOAEs or SFOAEs (see Figs. 5 and 6). This is consistent with the finding of no difference in test performance of DPOAEs and TEOAEs at any frequency in classifying infant ears as normal or hearing impaired (Norton et al, 2000). The longer ear-canal length in adults is one important factor in this effect. Thus, the predicted effect of differences in ear-canal and middle-ear functioning on OAE signal levels is consistent with differences observed in test performance across OAE test type in adult ears, and with the absence of an effect of OAE test type in infant ears.
VI. CONCLUSIONS
Using a one-dimensional scattering matrix model of energy transmission in the ear canal, middle ear and cochlea, the forward and reverse transfer functions describing bidirectional sound transmission between the ear canal and cochlea were decomposed into ear-canal and middle-ear components. This decomposition was based on DPOAE and ear-canal reflectance responses measured in the same infants and adults.
The reflectance was sensitive to frequency-dependent effects of ear-canal and middle-ear transmission that differed across subject age groups and between DPOAE and SFOAE test types. A notable outcome in adult ears was that the frequency dependence of forward transmission appears to account for the better performance at 4 kHz of DPOAEs compared to TEOAEs and SFOAEs in classifying ears as normal or as having a sensorineural hearing loss.
Regarding the main goal of the study, the immaturities in DPOAE I/O functions observed by Abdala and Keefe (2006) in infants ranging from newborn to 6 months of age were explained in terms of immaturities in ear-canal and middle-ear functioning. For the 2f1 − f2 DPOAE measured at f1 = 5 kHz and f2=6 kHz, the results show a relative attenuation (in infants compared to adults) of 16 dB in the forward-transmitted stimulus energy through the middle ear. The results provide evidence that DPOAEs are larger in infant than adult ears, mainly because of the effect of ear-canal area growth, which contributes a 17 dB increase in the DPOAE measured in the newborn compared to the adult ear. Neither ear-canal nor middle-ear functioning were adult-like at age 6 months.
Acknowledgments
This research was supported by the NIH (NIDCD Grant Nos. DC003784, DC003552, and DC006607), and the House Ear Institute. The authors would like to thank Dr. Ellen Ma and Sandy Oba for collection of infant data. The lead programmer in implementing the reflectance software at BTNRH was Dr. Denis F. Fitzpatrick.
Contributor Information
Douglas H. Keefe, Boys Town National Research Hospital, 555 North 30th Street, Omaha, Nebraska 68131.
Carolina Abdala, House Ear Institute, Los Angeles, California 90057.
References
- Abdala C, Keefe DH. Effects of middle-ear immaturity on distortion-product otoacoustic emission suppression tuning in infant ears. J Acoust Soc Am. 2006;120:3832–3842. doi: 10.1121/1.2359237. [DOI] [PubMed] [Google Scholar]
- Burns EM, Keefe DH. Energy reflectance can exceed unity near SOAE frequencies. J Acoust Soc Am. 1998;103:462–474. doi: 10.1121/1.421122. [DOI] [PubMed] [Google Scholar]
- Ellison JC, Keefe DH. Audiometric predictions using stimulus-frequency otoacoustic emissions and middle ear measurements. Ear Hear. 2005;26:487–503. doi: 10.1097/01.aud.0000179692.81851.3b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Tibshirani R. Bootstrap methods for standard errors, confidence intervals, and other measurements of statistical accuracy. Stat Sci. 1986;1:54–77. [Google Scholar]
- Gorga MP, Neely ST, Bergman BM, Beauchaine KL, Kaminski JR, Peters J, Schulte L, Jesteadt W. A comparison of transient-evoked and distortion product otoacoustic emissions in normal-hearing and hearing-impaired subjects. J Acoust Soc Am. 1993;94:2639–2648. doi: 10.1121/1.407348. [DOI] [PubMed] [Google Scholar]
- Gorga MP, Neely ST, Bergman BM, Beauchaine KL, Kaminski JR, Liu Z. Towards understanding the limits of distortion product otoacoustic emission measurements. J Acoust Soc Am. 1994;96:1494–1500. doi: 10.1121/1.410227. [DOI] [PubMed] [Google Scholar]
- Huang GT, Rosowski JJ, Puria S, Peake WT. A non-invasive method for estimating acoustic admittance at the tympanic membrane. J Acoust Soc Am. 2000;108:1128–1146. doi: 10.1121/1.1287024. [DOI] [PubMed] [Google Scholar]
- Ikui A, Sando I, Sudo M, Fujita S. Postnatal change in angle between the tympanic annulus and surrounding structures. Acta Otol Rhinol Laryngol. 1997;106:33–36. doi: 10.1177/000348949710600106. [DOI] [PubMed] [Google Scholar]
- Keefe DH. Otoreflectance of the cochlea and middle ear. J Acoust Soc Am. 1997;102:2849–2859. doi: 10.1121/1.420340. [DOI] [PubMed] [Google Scholar]
- Keefe DH. Using reflectance phase to estimate acoustic response at the tympanic membrane. J Acoust Soc Am. 2004;115:2499. Abstract. [Google Scholar]
- Keefe DH, Benade AH. Impedance measurement source and microphone proximity effects. J Acoust Soc Am. 1981;69:1489–1495. [Google Scholar]
- Keefe DH, Bulen JC, Hoberg Arehart K, Burns EM. Ear-canal impedance and reflection coefficient of human infants and adults. J Acoust Soc Am. 1993;94:2617–2638. doi: 10.1121/1.407347. [DOI] [PubMed] [Google Scholar]
- Keefe DH, Folsom RC, Gorga MP, Vohr BR, Bulen JC, Norton SJ. Identification of neonatal hearing impairment: Ear-canal measurements of acoustic admittance and reflectance in neonates. Ear Hear. 2000;21:443–461. doi: 10.1097/00003446-200010000-00009. [DOI] [PubMed] [Google Scholar]
- Keefe DH, Ling R, Bulen JC. Method to measure acoustic impedance and reflection coefficient. J Acoust Soc Am. 1992;91:470–485. doi: 10.1121/1.402733. [DOI] [PubMed] [Google Scholar]
- Keefe DH, Simmons JL. Energy transmittance predicts conductive hearing loss in older children and adults. J Acoust Soc Am. 2003;114:3217–3238. doi: 10.1121/1.1625931. [DOI] [PubMed] [Google Scholar]
- Kemp DT, Ryan S, Bray P. A guide to the effective use of otoacoustic emissions. Ear Hear. 1990;11:93–105. doi: 10.1097/00003446-199004000-00004. [DOI] [PubMed] [Google Scholar]
- McIntyre ME, Schumacher RT, Woodhouse J. On the oscillations of musical instruments. J Acoust Soc Am. 1983;74:1325–1345. [Google Scholar]
- Morse PM, Ingard KU. Theoretical Acoustics. McGraw–Hill; New York: 1968. [Google Scholar]
- Norton SN, Gorga MP, Widen JE, Folsom RC, Sininger Y, Cone-Wesson B, Vohr BR, Mascher K, Fletcher K. Identification of neonatal hearing impairment: Evaluation of transient evoked otoacoustic emission, distortion product otoacoustic emission, and auditory brain stem response test performance. Ear Hear. 2000;21:508–528. doi: 10.1097/00003446-200010000-00013. [DOI] [PubMed] [Google Scholar]
- Okabe K, Tanaka S, Hamada H, Miura T, Funai H. Acoustic impedance measurement on normal ears of children. J Acoust Soc Jpn (E) 1988;9:287–294. [Google Scholar]
- Overstreet EH, III, Ruggero MA. Development of wide-band middle ear transmission in the Mongolian gerbil. J Acoust Soc Am. 2002;111:261–270. doi: 10.1121/1.1420382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puria S. Measurements of human middle ear forward and reverse acoustics: Implications for otoacoustic emissions. J Acoust Soc Am. 2003;113:2773–2789. doi: 10.1121/1.1564018. [DOI] [PubMed] [Google Scholar]
- Shera CA, Zweig G. Phenomenological characterization of eardrum transduction. J Acoust Soc Am. 1991;90:253–262. doi: 10.1121/1.401295. [DOI] [PubMed] [Google Scholar]
- Shera CA, Zweig G. Middle-ear phenomenology: The view from the three windows. J Acoust Soc Am. 1992a;92:1356–1370. doi: 10.1121/1.403929. [DOI] [PubMed] [Google Scholar]
- Shera CA, Zweig G. Analyzing reverse middle-ear transmission: Noninvasive Gedankenexperiments. J Acoust Soc Am. 1992b;92:1371–1381. doi: 10.1121/1.403930. [DOI] [PubMed] [Google Scholar]
- Sondhi M, Resnick J. The inverse problem for the vocal tract: Numerical methods, acoustical experiments and speech synthesis. J Acoust Soc Am. 1983;73:985–1002. doi: 10.1121/1.389024. [DOI] [PubMed] [Google Scholar]
- Stinson MR, Lawton BW. Specification of the geometry of the human ear canal for the prediction of sound-pressure level distribution. J Acoust Soc Am. 1989;85:2492–2503. doi: 10.1121/1.397744. [DOI] [PubMed] [Google Scholar]
- Strutt JW. London Mathematical Society, IV, 357–368. Reprinted in Scientific Papers by Lord Rayleigh. Vol. 1. Dover; New York: 1873. Some general theorems relating to vibration; pp. 170–181. 1964. [Google Scholar]
- Voss SE, Shera CA. Simultaneous measurement of middle-ear input impedance and forward/reverse transmission in cat. J Acoust Soc Am. 2004;116:2187–2198. doi: 10.1121/1.1785832. [DOI] [PubMed] [Google Scholar]
- Zweig G, Shera CA. The origin of periodicity in the spectrum of evoked otoacoustic emissions. J Acoust Soc Am. 1995;98:2018–2047. doi: 10.1121/1.413320. [DOI] [PubMed] [Google Scholar]
- Zweig G. Finding the impedance of the organ of Corti. J Acoust Soc Am. 1991;89:1229–1254. doi: 10.1121/1.400653. [DOI] [PubMed] [Google Scholar]