Abstract
Grouping the 20 residues is a classic strategy to discover ordered patterns and insights about the fundamental nature of proteins, their structure, and how they fold. Usually, this categorization is based on the biophysical and/or structural properties of a residue’s side-chain group. We extend this approach to understand the effects that side-chains have upon backbone conformation and perform a knowledge-based classification of amino acids by comparing their backbone φ,ψ distributions in different types of secondary structure. At this finer, more specific resolution, the torsion angle data is often sparse and discontinuous (especially for the non-helical classes) even though a comprehensive set of protein structures is used. To insure the precision of the Ramachandran plot comparisons, we applied a rigorous Bayesian density estimation method that produces continuous estimates of the backbone φ,ψ distributions. Based on this statistical modeling, a robust, hierarchical clustering was performed using a divergence score to measure the similarity between plots. There were 7 general groups based on the clusters from the complete Ramachandran data: nonpolar/β-branched (Ile & Val), AsX (Asn & Asp), long (Met, Gln, Arg, Glu, Lys, & Leu), aromatic (Phe, Tyr, His, & Cys), small (Ala & Ser), bulky (Thr & Trp), and lastly the singletons of Gly and Pro. At the level of 4 types of secondary structure (helix, sheet, turn, and coil), these groups remain somewhat consistent, although there are a few significant variations. Besides the expected uniqueness of the Gly and Pro distributions, the nonpolar/β-branched and AsX clusters were very consistent across all types of secondary structure. Effectively, this consistency across the secondary structure classes imply that side-chain steric effects strongly influence a residue’s backbone torsion angle conformation. These results help to explain the plasticity of amino acid substitutions on protein structure, and should help in protein design and structure evaluation.
Keywords: Ramachandran Plot, Torsion Angles, Bayesian Density Estimation, Clustering, Residue Backbone Similarity
Introduction
Classification of the 20 amino acids simplifies analysis and helps uncover relationships that are important to protein structure, folding and function. Such an understanding is especially important in explaining the less-than-straightforward plasticity found between sequence and structure space. Many positions within a protein sequence can absorb a wide variety of substitutions. In this study, the amino acids are grouped based on the differences and similarities in backbone torsion angle distributions seen in Ramachandran plots1. As shown previously, Ramachandran plots provide a simple and direct evaluation of the main-chain’s conformational space2–3. In this work, we take a knowledge-based approach to amino acid classification measures the similarity that the various side-chain functional groups have upon the conformation of the main-chain polymer.
Typical classification of amino acids has naturally focused on the side chain or the portion of a residue that is different, since the main chain is a repetitive polymer. The most straightforward method has been to use the chemistry of an amino acid, like hydrophobicity4, in grouping amino acids. However, size, shape and chimeric chemistry of some side-chains complicate such chemical classification. For example, the side chain of Lys is considered a charged group, but the positive charge follows a long non-polar chain of 4 carbon atoms. On the other hand, Trp is a bulky, aromatic group with some hydrophilic tendencies, but this side-chain is often considered a large hydrophobic residue. Using these hydrophobicity based groupings to reduced the amino acid alphabet, insights into protein design have been made in structure/folding5 as well as enzyme catalysis6. Computational/knowledge-based approaches have also been used to group amino acids7–10. Such clustering of amino acids have been used to improve sequence alignments11 as well as remote homolog detection12–13.
In this work, we approach amino acid clustering from a classical structural point of view based on φ,ψ backbone distributions, which has been done previously14–17. Taking this analysis a step further, we increase the resolution of this analysis by also making classifications based on 4 secondary structure types: helix (H), sheet, (E), turn (T), and coil (C). To make accurate comparisons between different residues’ Ramachandran plots, we must first overcome the sparse and discontinuous sampling of φ,ψ space in the Protein Data Bank (PDB)18. Even though the information on known structures is the substantial19 in the PDB, it is not complete enough to adequately sample backbone torsion angle space for all residues16 and especially when the data is further divided into secondary structure types. Several approaches have been use to address this sampling problem. One of the simplest is to use a large set of PDB structures14, which oversamples certain folds and therefore regions of φ,ψ space, or use an increased bin size of 10° by 10° or larger14–17, but space as well as reduces the resolution and accuracy. Another approach is to smooth the data using basic interpolation20, a Gaussian approximation16, or an empirically derived, density-dependent mask21. When the data becomes too sparse, smoothing unknown values becomes less reliable. In this work, we consider Bayesian density estimated representations of residue’s φ,ψ distributions to deal with the sparcity of data. Such modeling allows meaningful comparisons between Ramachandran plots, and is particularly effective for analyses classified by secondary structure, where data is even sparser. A Bayesian based approach has been used previously22 on the complete backbone torsion angle space. Unlike our objective of modeling continuous densities from sparse data, the goal of their Fourier based statistical formulation was to avoid over-sampling regions of the Ramachandran plot and produce a single, well-behaved distribution for use as a statistical potential function. In this work, we model all 20 amino acids (as well as their 4 separate secondary structure classes) by taking a nonparametric Bayesian approach with a Dirichlet process mixture model that recognizes the uncertainty in the number of components and allows it to vary. This estimation in our model is simple and can be carried out via standard, computational methods. The results of this modeling allow us to investigate the backbone propensities at a finer resolution of individual secondary structure. As an example, we cluster residues based on their φ,ψ distributions and to infer constructive insights into the relationship between protein sequence and structure. In effect, by grouping on the φ,ψ torsion angle distributions, we are able to investigate the influence of the side chain on its respective backbone’s accessible conformational space.
Results/Discussion
As described in the Methods, backbone torsion angles were calculated from a set of non-redundant protein structures and classified in the following ways. First, the φ,ψ angle pairs were grouped according to amino acid, which will be further referred to as the All set for simplicity. Then, for each amino acid, the angles were separated according to 4 classes of secondary structure using DSSP. In this work, the following shorthand will be used to reference these sets: helix (H), sheet (E), coil (C), and turn (T). This approach resulted in 5 groupings of the data per amino acid. The raw φ,ψ angles are shown as grey points in the Ramachandran plots for the amino acid Ala in Figure 1. Next, the distributions of these torsion angle sets were calculated either by binning or by Bayesian nonparametric estimation. Contour representations of the density estimates for Ala are reported in Figure 1, overlaid on the raw data. These highlight the most populated areas in the plots, i.e. the modes of the distributions. For Ala, there are values in all 4 types of secondary structure, although H is dominant in the All plot. Separating the data into the 4 individual secondary structure elements allows us to see the local effect of each side chain on their respective backbones. In general, for all 20 amino acids the distributions were similar to those shown in Figure 1 except for the known differences to Gly and Pro. With only a hydrogen as a side-chain group, Gly exhibits the most flexibility in backbone conformation and very broad distribution of φ,ψ angles, whereas Pro is the most constricted in φ due to its side-chains covalent ring structure involving its main-chain nitrogen. As expected, the H class is the best defined of the 4 secondary structure classes and is followed by T. The E and C classes display similar variations, although the C class is less well populated.
Figure 1.
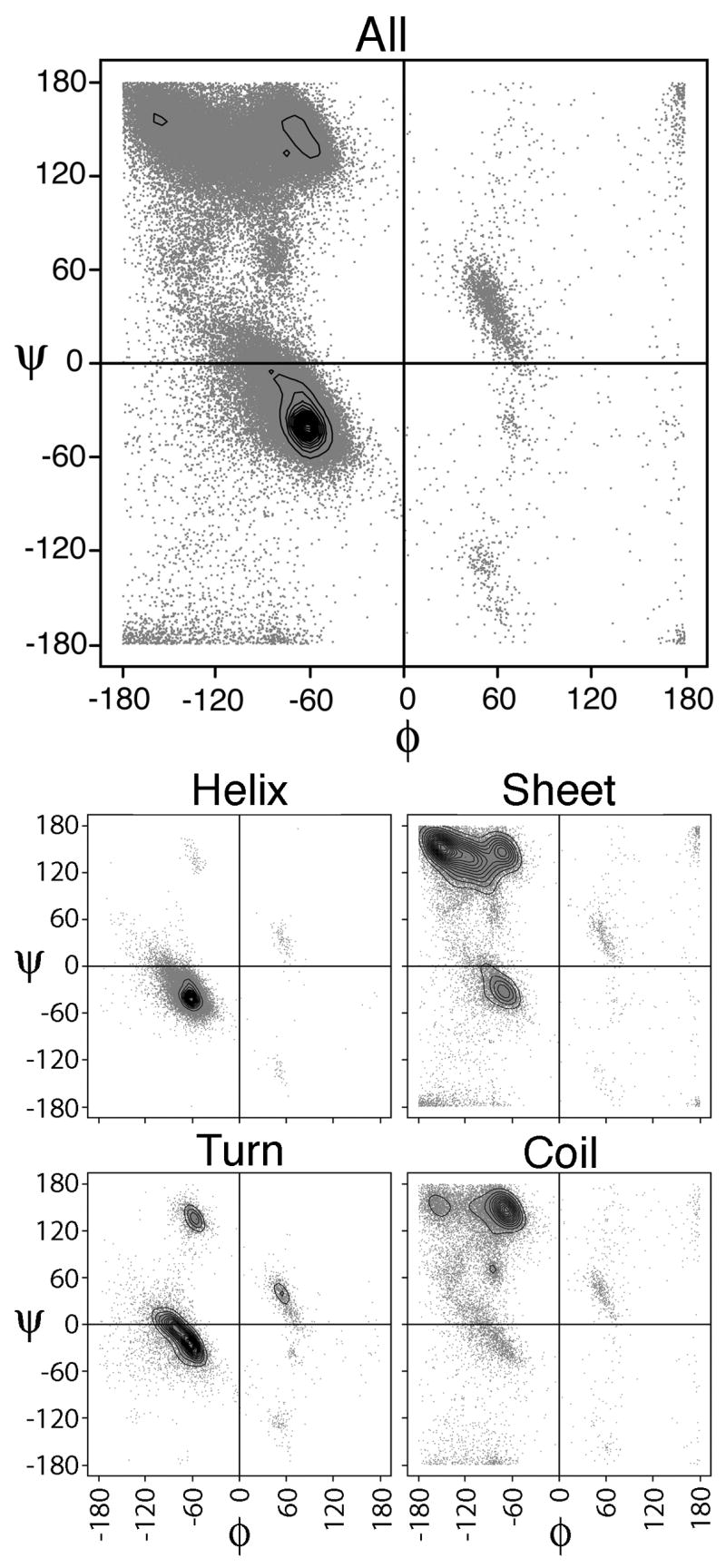
Ala Ramachandran plots of the 5 classes. Raw torsion angle data is shown by grey dots, while density estimated distributions are overlaid using contour representations of the. Distribution classes are labeled above their respective plots. Highest peak in the All and Helix (H) distributions occurs at (−65°, −40°). For Sheet (E), this peak is at (−150°,150°), for Turn (T) at (−65°,−20°) and for Coil (C) at (−70°,140°).
Binning versus Density Estimation
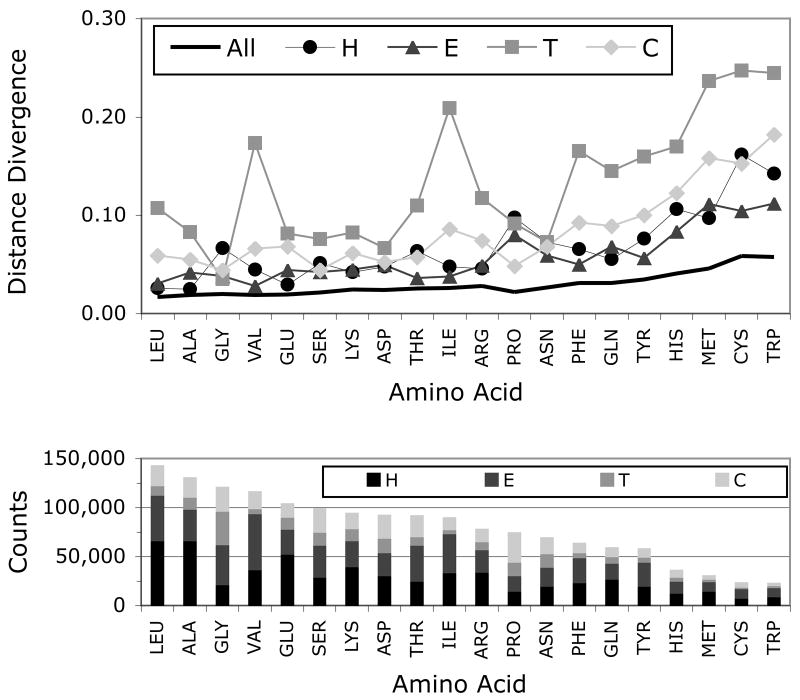
The simplest approach to estimating distributions is to bin the data. However, in many cases, the data is sparse and the binning method results in coarse estimates subject to random fluctuations. We therefore used a Bayesian nonparametric approach to generate estimates (see Methods). Because these estimates only considered the data bounded from 180° to −180°, we wanted to make sure that we were reproducing the periodic boundary at 180°/−180° correctly. As a check of our estimated distributions, the distance between the binned and density estimated φ,ψ torsion angle distributions was calculated. Divergence scores ranged from 0.017 to 0.247. The top of Figure 2A shows this comparison for each of the 5 classes described above, while bottom of Figure 2A depicts the number of φ,ψ observations for each amino acid and class. While H is the most populated overall, the amino acids branched at the Cβ atom (Val, Ile, and Thr) favor E, as expected. Coil is well populated, whereas T has the least number of members. By combining the analysis in both parts of Figure 2A, we find as expected that the number of observations correlate with distance divergence: more observations produce lower divergence scores and vice versa. Figure 2B provides examples of this relationship. The upper portion of Figure 2B contrasts the binning and density estimated distributions from the most populated class Leu All with the lowest distance divergence. In such a well-sampled case, the distributions are very similar to each other. Both show the same peak in the helical area with a slight variation in connecting the distribution over the sheet/coil region. This demonstrates that our Bayesian density estimation method closely matches the simpler binning approach when data is plentiful. The lower portion of Figure 2B shows the same comparison for the least populated case and second highest divergence distance of Trp T. The binned distribution on the left is clearly uneven and rather coarse, whereas the Bayesian density estimation produces a regular, smooth distribution that models well the diversity in the data. While the binned distribution is informative, making comparisons becomes problematic for such irregular distributions. In the Bayesian density estimation, the left and right-handed conformations are identified and the sheet-like angles are also found. In both cases, the 180°/−180° boundary is reproduced, although most of the data falls away from the periodic boundary. Overall, these results demonstrated that our Bayesian estimation method faithfully represents the distribution of data and produces smooth estimates to permit more natural comparisons.
Figure 2.
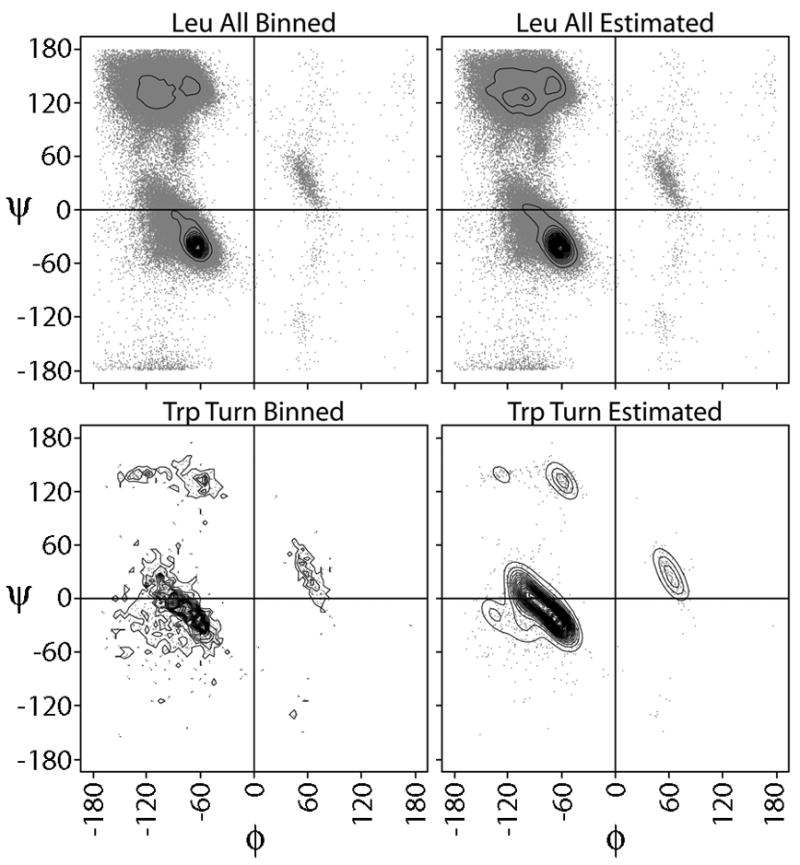
Comparison of binning versus density estimation. A) Top line graph shows the distance divergence between the binned and the Bayesian density estimation representations of the Ramachandran plots for each 20 amino acids in each of the 5 classes: All, H (Helix), E (Sheet), T (Turn) and C (Coil). Bottom stacked histogram shows the number of observations for each class, where the stacked total is the number of observations for the All class. B) Ramachandran plots are shown for the distributions with the highest number of observations (Leu All) and lowest number (Trp T). Data points are shown in grey and the calculated distributions are shown by the contour lines. Binned estimates are on the left and Bayesian density estimates on the right.
Density Estimated Distributions
While the distributions are similar, there are perceptible and significant differences. Overall, the density estimated distributions cover the expected areas of the Ramachandran plot23–24, and as expected, the disallowed regions25 are note well sampled. The peaks fall into the well known regions of the Ramachandran map21. Each secondary structure class will be discussed individually.
H Class
For the H class, it is primarily the shape of the distribution with peaks at values primarily between −60° to −65° in ψ and −40° to −45° in ψ, which is primarily in the α region. Of all the classes, this H class exhibits the most consistent distributions. The only exception is for Pro, which is restricted in φ, and produces a peak lower in φ,ψ value at −55°,−35°. For the remaining classes, peak and distribution shape are both factors to the clustering.
T Class
The T class is most similar to H (Figure 2), but has a broader distribution and additional strong peaks in the left-handed helical region. In direct comparison to the H class, the T class peaks are consistently more negative in φ and more positive in ψ, and therefore move to the left and up in the Ramachandran plot towards the 310 helical conformation. This is even so for Pro. In this class, the exception is Gly which shows a primary peak in the left-handed helical region at φ,ψ of 80°,10°. Generally, the other clusters also have secondary peaks in the left-handed helical region. For example, the Asn, Asp cluster’s second peak is at φ,ψ of 55°,40°.
E Class
In the E class, the distributions are shaped more broadly with major peaks ranging in the upper left region of the Ramachandran plot from −95° to −150° in φ and 125° to 155° in ψ. Secondary peaks are located around the polyPro region with a φ around −65° and similar ψ values as the major peak. As before, the Gly peak is in the left-handed helical region at φ,ψ of 80°,10°, but has many values in the classic upper left E region of the Ramachandran plot. Closer inspection reveals that these values are due to Gly at the ends of β-sheets. As expected, being restricted in φ, the Pro peak in the E class is centered in the polyPro region at −65°, 145°.
C Class
Although covering the same region, the C class distributions are also broad. In comparison to the E class, the C class peaks are located in the polyPro region. They are smaller and less varied in φ (−65° to −95°) but similar in ψ (135° to 155°). These peaks are moved over slightly to the right. Thr and Gly are exceptions with higher ψ values of 165° and 170°, respectively, but also have secondary peaks in the polyPro region. Once more, Pro is restricted to the φ value of −65° and centered in the polyPro region.
As a composite of the 4 secondary structure classes, the All class is more complicated and exhibits all the characteristics described above, although the highest peak is usually the right handed helical region.
Clustering within Classes
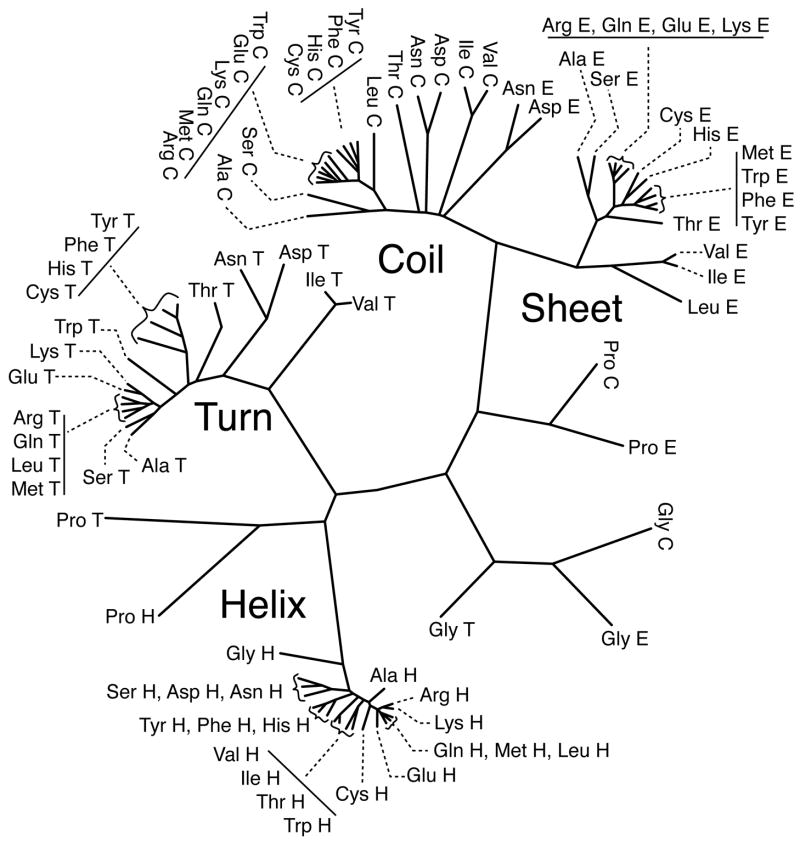
For each class (All, H, E, C, T), divergence distances were calculated and used to cluster the 20 amino acids. Table 1 summarizes the resulting clusters. As shown in Table 1, clusters were taken when one of two criteria were met: 1) all the amino acids were in clusters of at least 2 members besides Gly and Pro or 2) the clustering distance became larger than the lowest divergence distance to a distribution in another class. This was done since the Gly and Pro distributions are so different from all the others. The divergence scores for Gly and Pro clearly separate these distributions from the others, which is expected. Without a side-chain group, Gly is flexible and populates all quadrants of the map. In contrast, Pro is restricted in φ since the side chain makes a covalent bond with the backbone nitrogen. Their difference to all the other distributions, even within each class, is very evident in Figure 3, where a tree diagram shows the similarity relationship between the 4 secondary structure classes. Figure 3 clearly shows that the H class exhibits the smallest divergences between residues, which clusters at 0.021 in Table 1. T, C, and E cluster at 0.045, 0.048, and 0.051 respectively. The All class has the highest value at 0.0.64.
Table 1.
Amino Acid clusters.
| All | Helix | Turn | Sheet | Coil | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Cluster | Dist* | Cluster | Dist* | Peak | Cluster | Dist* | Peak | Cluster | Dist* | Peak | Cluster | Dist* | Peak | ||||
| φ | ψ | φ | ψ | φ | ψ | φ | ψ | |||||||||||
| 1 | Ile Val | 0.015 | Ile Val | 0.004 | −65 | −45 | Ile Val | 0.010 | −65 | −25 | Ala Ser | 0.028 | −145 | 153 | Phe Tyr His Cys | 0.020 | −70 | 140 |
| 2 | Glu Met Gln Arg Lys Leu Ala |
0.027 | Arg Lys Gln Met Leu Glu Cys |
0.009 | −65 | −40 | Met Leu Gln Arg Glu Lys Ala Ser |
0.024 | −72 | −16 | Phe Tyr Trp Met His Cys Lys Glu Gln Arg Thr |
0.028 | −127 | 142 | Ile Val | 0.020 | −75 | 130 |
| 3 | Asn Asp | 0.029 | His Phe Tyr | 0.014 | −62 | −43 | Phe Tyr His Cys |
0.029 | −96 | 6 | Asn Asp | 0.033 | −98 | 118 | Gln Lys Met Arg Glu Trp Leu |
0.021 | −73 | 144 |
| 4 | Phe Tyr Trp Cys His Ser Thr |
0.039 | Thr Trp | 0.015 | −63 | −43 | Asn Asp | 0.038 | −90 | 5 | Ile Val Leu | 0.035 | −117 | 127 | Asn Asp | 0.029 | −80 | 120 |
| 5 | Gly | - | Asn Asp Ser | 0.018 | −65 | −40 | Thr Trp | 0.047 | −70 | −20 | Gly | - | 85 | 10 | Ala Ser | 0.045 | −73 | 150 |
| 6 | Pro | - | Ala | - | −65 | −40 | Pro | - | −60 | −25 | Pro | - | −65 | 145 | Thr | - | −85 | 165 |
| 7 | Gly | - | −65 | −40 | Gly | - | 80 | 10 | Pro | - | −65 | 150 | ||||||
| 8 | Pro | - | −55 | −35 | Gly | - | −80 | 170 | ||||||||||
Average Distance Divergence of the Cluster
Figure 3.
Unrooted tree diagramming the relationship between the density estimated Ramachandran distributions of the four secondary structure classes H (Helix), E (Sheet), C (Coil), and T (Turn). The tree was drawn with the DrawTree program from the Phylip package (Felsenstein, 2005), where the lengths of the branches are an indication of the divergence distance between 2 distributions.
In general, the amino acids group in certain cases according to similar biophysical characteristics, but there are some interesting cases. Since it combines all the secondary structure types, the All class will be used as a reference point. The All class produced 6 clusters, and they will be described from the most different to the most similar (bottom up). The two singleton clusters are Gly and Pro, as expected. Next is a group combining the residues with planar delocalized rings (aromatics Phe, Trp, & Tyr with imidazole His) with the hydroxyl containing residues (Ser, Thr, & again Tyr) and Cys. For reasons made clearer in the discussion of the clusters within secondary structure classes, this cluster is named the aromatic group. Asn and Asp make up the next cluster and are similar in shape and chemistry, differing by a replacement of an oxygen in Asp by a amide in Asn. Asp is usually charged, while Asn is polar. Following known conventions, this group is termed the AsX group. For the same reason, Gln and Glu also group together, but always with other amino acids. The reason for this is that the Gln distribution is more similar to the Met while Glu is more similar to Arg. This group usually also includes Lys and sometimes Leu. This resulting group is a mix of hydrophobic (Leu, Ala, & Met), polar (Gln) and charged (Arg and Lys). Structurally, they are mostly longer side chains, except for Ala, and none are branched at their Cβ, although this also pertains to other previous clusters. So this group will be termed the long cluster. The most similar cluster consists of the hydrophobic Ile and Val, and will be termed the nonpolar/β-branched. Both are branched at their side-chain Cβ atoms, but differ in that Ile is longer by a methylene group. Surprisingly, the other Cβ-branched residue Thr is not in this group, although Thr is very different chemically with a hydroxyl group.
In comparison to previous classifications, our clusters shown in Table 1 are similar like the Gly and Pro singletons and the AsX group, but there are significant differences. For the smaller structure set and 20° by 20° binning15, Ile and Val are found grouped like ours, but His and Cys are singletons and one large cluster combines our aromatic and long clusters together. This is most likely due to the smaller sample size available at the time of the study, where certain distributions did not have enough data to show their true distribution. For the study based on a larger structure set and/or broader 10° × 10° binning14, there are similarities where our results concur on the singletons of Gly and Pro as well as the AsX group (Table 1). We differ in that our analysis does not include Thr with Ile and Val, but instead it clusters with the hydroxyl containing residues. The long cluster is similar, but ours also includes Ala, Gln, and Met. We also include all the aromatics together. These differences are due primarily to our smaller sampling bins that capture finer details. Also, we were more rigorous in our structure set, so that we could avoid oversampling especially in the helical area. As can be clearly seen, the helical region contains most of the density in the All distributions, and therefore can dominate any comparisons. For this reason, we performed the same analysis using the 4 secondary structure classes.
For the 4 secondary structure classes, Gly and Pro are always independent clusters as a result of our cutoff criteria, but this is reasonable considering their very dissimilar distributions. Although Gly can have very broad distributions, Gly can be restrained especially in the H class, where Gly is most similar to the Glu distribution at 0.042. In the T class, the Gly distribution produces its worst comparisons with Pro at 0.514 and Val at 0.465. Being restricted in φ, the Pro distributions are very different and are no more similar than 0.137 in the T class with Ala. Also, except for the C class, where it is the third worst, the Pro distributions are involved in the highest divergences for all classes, where the overall worst value is 0.517 between Ile and Pro in the E class.
Of the remaining, the most consistent clusters across the 4 secondary structure classes are the nonpolar, β-branched and the AsX clusters. The nonpolar, β-branched pair is strongly similar in H and T. In C, they are the second most similar, and in E they are interestingly joined by Leu. In the E, C, & T classes, AsX clusters as the pair, but in the H class, it is joined by Ser. The aromatic class splits in the T and C classes as Phe, Tyr, His & Cys. In the H class, the aromatic class is only His, Phe, & Tyr, and in the E class, the aromatic class joins the long class. The long class is the same in the T class, but loses Ala and Ser in the H and C classes. Interestingly, the long and aromatic clusters are joined in the E class. As for other interesting clusters, the Ala distribution’s strong helical content puts it in a singleton cluster in the H class. For E and C, Ala pairs with Ser, although these are small and only differ by addition of a single hydroxyl to Ser. In the H and T class, Thr & Trp are independent of the aromatic cluster. Since Thr is β-branched and Trp is large, these could be considered bulky. In the C class, Trp joins the long cluster and Thr is a singleton mostly because Thr has such a broad distribution with strong density around ψ values of 170°.
Overall, this clustering of amino acid Ramachandran distributions between the various secondary structure classes suggest the following general groupings. Nonpolar/β-branched (Ile &Val), AsX (Asn & Asp), long (Met, Gln, Arg, Glu, Lys, & Leu), aromatic (Phe, Tyr, His, & Cys), small (Ala & Ser), bulky (Thr & Trp), and lastly the singletons of Gly and Pro. Although most stay within their group, a number (Ala, Cys, Leu, Ser, Trp, Thr) cluster differently depending on secondary structure class.
Clustering between Classes
Using the distance divergence, the amino acid distributions from each of the 4 secondary structure classes were also clustered against each other and the results are shown by the tree diagram in Figure 3. Except for H class, Gly and Pro distributions separate themselves from the other amino acids, yet somewhat follow the secondary structure classes. The most different are the Gly distributions in C, E, & T classes that group together and away from all the other distributions. . Although also separate from the other amino acids, the Pro distributions mimic the overall class distributions in that E and C are closer together in class and H and T are closer together.
For the remaining 18 amino acids, the secondary structure classes group together. As stated before, the H class is the most similar cluster and even includes Gly. The T class is more similar to the H class than E or C. Likewise, the E and C classes are more similar to each other than to H or T. The clusters described in Table 1 can clearly be seen in this diagram. In each secondary structure class, the nonpolar/β-branched and AsX clusters clearly group together and away from the other groups. Also, the diversity in distributions based on secondary structure types can be seen. While the broadest class looks to be the T class, the E class distributions of Asn and Asp actually cluster closer to the C class, which explains why the E class is the broadest. It is interesting that there is not more overlap between secondary structure classes. This result indicates how distinct these types of protein structure are even though they sample similar regions of torsion angle conformational space.
Conclusion
As shown in Figures 1 and 2, the Bayesian nonparametric density estimation allows us to provide a reasonable approximation of a Ramachandran distribution especially when the data is sparse. This result is particularly satisfying as our density estimations were made without including periodicity. Comparisons to a periodic treatment that we are new developing show no significant differences for the data we analyze in this paper 26 (see Methods). Using a distance divergence metric, the distributions can now be consistently compared and clustered for all 20 amino acids as well as their respective secondary structure classes. The result is a higher resolution scheme to classify amino acids based on their differences in sampling backbone conformational space. Although calculation of main-chain torsion angles examines a regular polymer of repeating atoms, the similarities/differences between the plots must be attributed to the individual influences that side-chain functional groups have on their respective backbones. As with any knowledge-based clustering, the data dictates the results, which do not always follow expectations. For example, the groupings themselves do not suggest that two amino acids like Thr and Trp are similar in chemistry, but the analysis shows that they both affect the backbone in the same manner. The theme for the clusters seems to be less about their chemistry and more about their shape or sterics. It follows that the principal effect that the side-chain group has upon the backbone is steric, since the chemistry (polarity/charge) would be difficult to bring to bear on a residues own main-chain atoms. Therefore, this analysis shows that side-chains affect the backbone according to 7 types: nonpolar/β-branched (Ile &Val), AsX (Asn & Asp), long (Met, Gln, Arg, Glu, Lys, & Leu), aromatic (Phe, Tyr, His, & Cys), small (Ala & Ser), bulky (Thr & Trp), and lastly the singletons of Gly and Pro. As with any categorization of amino acids, there are caveats like the behavior of Ala, Cys, Leu, Ser, Trp, Thr in certain secondary structure classes.
These results certainly do not take the place of most common classification of protein side-chains. In particular, these results have very little bearing on the non-local tertiary environment that is effected upon amino acid change. Instead, these results can explain why point mutations in many cases have no effect on the structure or function of a protein. In other words, the results from our clustering provide the explanation that the side-chain functional groups affect their backbone conformations in a similar fashion. For example, in terms of substitution matrices like BLOSUM6227, our clustering helps to explain the somewhat surprising yet favorable substitution pairs like Glu/Lys, Ala/Ser, and His/Tyr. In fact, similar work has been used to create amino acid substitution matrices15–16, which have been useful for identifying structurally similar regions between proteins. In this work, we are focused more on the structural implications of these results and find that amino acids substitutions do not drastically perturb the allowable backbone conformational space upon mutation, excluding Gly and Pro. On the contrary, the closeness of the distributions as seen in Figure 3 imply that mutation to another residue changes the range of possible main-chain conformations at a position and allows protein structures the potential for evolution change. Such conclusions have impact not only on understanding protein evolution, but also on using amino acid substitutions in protein structure prediction (mutation and template based modeling) as well as protein design.
Materials and Methods
In biochemistry, a torsion angle or dihedral angle is defined by 4 atoms connected by three covalent bonds and describes the rotation around the central bond of the outer two bonds with respect to each other. Because the backbone of a protein structure in its most simplest form can be described as a covalent polymer made up of three repetitive atoms per residue (nitrogen N, alpha carbon Cα, and carbonyl carbon C), torsion angles must involve more than one residue. For reference, the i subscript refers to the relative position in the protein chain. There are 3 backbone torsion angles. The φ angle consists of the atoms Ci−1, Ni, Cαi and Ci. The ψ angle consists of the atoms Ni, Cαi, Ci, and Ni+1. The last angle consists of the atoms Cαi, Ci, Ni+1, and Cαi+1. The first two range over 360° but the convention is to report values between −180° and 180°. The third torsion angle ω is usually fixed at 0° (less so) and 180° (more so) due to resonance and partial double bond characteristics28. For this reason, our study will not include statistics on ω and will concentrate on the variation found in residue φ,ψ torsion angles.
Data Set
Our data set of non-homologous structures was generated from the PISCES server29 generated from the May 20th, 2003 release of the PDB, using the following criteria: percent identity <= 50%; resolution 0.0 – 2.5 Å; and R-factor < 1. Only X-Ray entries were considered. The resulting list of 6,702 separate protein chains is available upon request.
Structural Analysis
A C program was written that calculates the backbone φ,ψ torsion angles of residues in a protein chain in the following manner. To avoid complications from variations in bond angles, the actual torsion angle is calculated as the angle between the normals of two planes as done classically1. The φ angle is computed between the normal to the plane made by three atoms Ci−1, Ni, and Cαi and the normal to the plane made by the three atoms Ni, Cαi, and Ci. The ψ angle is calculated between the normals made by the Ni, Cαi, Ci plane and the Cαi, Ci, Ni+1 plane. Since no residue precedes the first residue, it lacks a φ angle. Similarly, the last residue lacks a ψ angle without a residue following it. Therefore, these residues were excluded from the calculation. The output consists of the amino acid, its φ,ψ torsion angle pair, and secondary structure as defined by the Definition of Secondary Structure for Proteins (DSSP) program30. The normal 8 classes were condensed to four: helices (H), sheets (E), coils (C), and turns (T). This output was used as the raw data from which all statistics were calculated.
Data Binning
The binning method estimates the torsion angle density as simply a bivariate step function whose value is constant in 5° by 5° squares. Its value within the square is proportional to the number of φ,ψ pairs in the dataset that fall into that square. Since each axis ranges spans 360°, there are a total of (360/5)2 = 5184 squares.
Nonparametric Bayesian Density Estimation
The backbone torsion angles φ,ψ calculated from the PDB and classified based on amino acid as well as secondary structure type (see above) can be viewed as samples from the joint distribution of the φ,ψ torsion angles. We estimated the joint distribution of the φ,ψ torsion angles using Bayesian nonparametric density estimation31–32. For a particular grouping of torsion angles based on amino acid and secondary structure, suppose we have n entries in the PDB, i.e., n pairs of angles measured in degrees ranging from −180° to 180°. We propose the following Dirichlet process mixture (DPM) model:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where DP(mC(x)) denotes the Dirichlet process33 with mass parameter m and centering distribution C(x). The distributions F, G0 and H0 are given as:
| (6) |
| (7) |
| (8) |
where N2(x|m,p) denotes the bivariate normal distribution with mean m and variance p−1 for the random vector x and Wi2(x|α,β) denotes the two-dimensional Wishart distribution with mean α/β.
Density estimation is accomplished by estimating μi, the mean vector for the ith observation, and λi, the precision matrix (i.e., the inverse of the covariance matrix) for the ith observation. We fit the model using standard methods for Bayesian inference. In particular, we used a Gibbs sampling to update the model parameters (μ‘s and λ‘s) and updated the allocation of observations using the Auxilary Gibbs sampler with one auxiliary variable34.
Parameter Settings
The model described in Section 2.4 requires choosing values for the six hyperparameters. The mass parameters η0 and τ0 were both set to 1 (implying for example that, for n=94, the μ’s and the λ’s will cluster into about 5.1 clusters each). The hyperparameter μ0 is set to (0,0) and λ0 is a diagonal matrix whose elements are 1/1802. This provides for a diffuse centering distribution G0(μ), since the most extreme angle of −180° or 180° is only one standard deviation from the mean. Finally, α0 is set to 1 and β0 is a diagonal matrix whose diagonal elements are 202. This provides for a diffuse centering distribution H0(λ).
Convergence was assessed by running two independent chains from initial states chosen from the prior. The first 5,000 iterations from each chain were discarded as burn in and output from the two chains were pooled to yield 40,000 samples.
Predictive Inference
From the Gibbs sampling output, the posterior predictive density of a new (φ,ψ) pair was obtained32. Briefly, at each iteration of the sampler, new μ and λ values were drawn from their posterior distribution and the resulting multivariate normal density was evaluated on a fixed, two-dimensional grid with steps of 5°. Averaging over the iterations yielded an estimate of the height of the joint density at that point. The conditional distribution of one of the angles given the other was obtained by linear interpolation of the two closest sets of grid values. Figure 1 shows representative images of the bivariate density generated using our density estimation model.
Although this approach does not directly account for the periodic nature of torsion angle data, we are confident in our fits as most of the data is typically far away from the boundary at 180°/−180°. At the boundary, we require two mixture components to model the data at the −180°/180° boundary. We are currently developing a newer model that will account for this periodicity26; however, initial comparisons show no strong differences for the data analyzed in this paper besides needing an extra component to represent the density at this boundary.
Distance of Divergence
The similarity of two densities P and Q was assessed using the Jensen-Shannon divergence:
| (9) |
where
| (10) |
The minimum for the Jensen-Shannon divergence is 0 for exactly matching densities. Therefore, distances closer to 0 indicate that the two densities closely match, and those farther from 0 indicate that the two densities match poorly.
Clustering
The density estimated torsion angle distributions were clustered using the above Jensen-Shannon divergence score as a distance. An agglomerative approach to clustering was used that only added a new member if its distance was lower than all others, which is in the same spirit as an average linkage clustering. This was done because the distance divergence similarity is not associative. For example, A being similar B and B being similar to C does not directly imply that A and C would also have a low divergence distance.
Acknowledgments
We would like to acknowledge J. Bradley Holmes, Jerod Parsons, and Robert Bliss for help with the torsion angle calculations, as well as Chuck Staben for assistance with substitution matrices. Tsai, Dahl, and Vannucci are supported by NIH/NIGMS grant R0GM81631. Vannucci is also supported by NIH/NHGRI grant R01HG003319 and by NSF/DMS grant number DMS-0605001.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Ramachandran GN, Ramakrishnan C, Sasisekharan V. Stereochemistry of polypeptide chain configurations. J Mol Biol. 1963;7:95–9. doi: 10.1016/s0022-2836(63)80023-6. [DOI] [PubMed] [Google Scholar]
- 2.Kleywegt GJ, Jones TA. Phi/psi-chology: Ramachandran revisited. Structure. 1996;4:1395–400. doi: 10.1016/s0969-2126(96)00147-5. [DOI] [PubMed] [Google Scholar]
- 3.Kleywegt GJ, Jones TA. Databases in protein crystallography. Acta Crystallogr D Biol Crystallogr. 1998;54:1119–31. doi: 10.1107/s0907444998007100. [DOI] [PubMed] [Google Scholar]
- 4.Cornette J, Cease KB, Margalit H, Spouge JL, Berzofsky JA, DeLisi C. Hydrophobicity Scales and Computational Techniques for Detecting Amphipathic Structures in Proteins. J Mol Biol. 1987;195:659–685. doi: 10.1016/0022-2836(87)90189-6. [DOI] [PubMed] [Google Scholar]
- 5.Riddle DS, Santiago JV, Bray-Hall ST, Doshi N, Grantcharova VP, Yi Q, Baker D. Functional rapidly folding proteins from simplified amino acid sequences. Nat Struct Biol. 1997;4:805–9. doi: 10.1038/nsb1097-805. [DOI] [PubMed] [Google Scholar]
- 6.Walter KU, Vamvaca K, Hilvert D. An active enzyme constructed from a 9-amino acid alphabet. J Biol Chem. 2005;280:37742–6. doi: 10.1074/jbc.M507210200. [DOI] [PubMed] [Google Scholar]
- 7.Chan HS. Folding alphabets. Nat Struct Biol. 1999;6:994–6. doi: 10.1038/14876. [DOI] [PubMed] [Google Scholar]
- 8.Li T, Fan K, Wang J, Wang W. Reduction of protein sequence complexity by residue grouping. Protein Eng. 2003;16:323–30. doi: 10.1093/protein/gzg044. [DOI] [PubMed] [Google Scholar]
- 9.Wang J, Wang W. A computational approach to simplifying the protein folding alphabet. Nat Struct Biol. 1999;6:1033–8. doi: 10.1038/14918. [DOI] [PubMed] [Google Scholar]
- 10.Cannata N, Toppo S, Romualdi C, Valle G. Simplifying amino acid alphabets by means of a branch and bound algorithm and substitution matrices. Bioinformatics. 2002;18:1102–8. doi: 10.1093/bioinformatics/18.8.1102. [DOI] [PubMed] [Google Scholar]
- 11.Melo F, Marti-Renom MA. Accuracy of sequence alignment and fold assessment using reduced amino acid alphabets. Proteins. 2006;63:986–95. doi: 10.1002/prot.20881. [DOI] [PubMed] [Google Scholar]
- 12.Murphy LR, Wallqvist A, Levy RM. Simplified amino acid alphabets for protein fold recognition and implications for folding. Protein Eng. 2000;13:149–52. doi: 10.1093/protein/13.3.149. [DOI] [PubMed] [Google Scholar]
- 13.Ogata K, Ohya M, Umeyama H. Amino acid similarity matrix for homology modeling derived from structural alignment and optimized by the Monte Carlo method. J Mol Graph Model. 1998;16:178–89. 254. doi: 10.1016/s1093-3263(98)80002-8. [DOI] [PubMed] [Google Scholar]
- 14.Anderson RJ, Weng Z, Campbell RK, Jiang X. Main-chain conformational tendencies of amino acids. Proteins. 2005;60:679–89. doi: 10.1002/prot.20530. [DOI] [PubMed] [Google Scholar]
- 15.Kolaskar AS, Kulkarni-Kale U. Sequence alignment approach to pick up conformationally similar protein fragments. J Mol Biol. 1992;223:1053–61. doi: 10.1016/0022-2836(92)90261-h. [DOI] [PubMed] [Google Scholar]
- 16.Niefind K, Schomburg D. Amino acid similarity coefficients for protein modeling and sequence alignment derived from main-chain folding angles. J Mol Biol. 1991;219:481–97. doi: 10.1016/0022-2836(91)90188-c. [DOI] [PubMed] [Google Scholar]
- 17.Pal D, Chakrabarti P. Conformational similarity indices between different residues in proteins and alpha-helix propensities. J Biomol Struct Dyn. 2000;18:273–80. doi: 10.1080/07391102.2000.10506665. [DOI] [PubMed] [Google Scholar]
- 18.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Research. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Levitt M. Growth of novel protein structural data. Proc Natl Acad Sci U S A. 2007;104:3183–8. doi: 10.1073/pnas.0611678104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hovmoller S, Zhou T, Ohlson T. Conformations of amino acids in proteins. Acta Crystallogr D Biol Crystallogr. 2002;58:768–76. doi: 10.1107/s0907444902003359. [DOI] [PubMed] [Google Scholar]
- 21.Lovell SC, Davis IW, Arendall WB, 3rd, de Bakker PI, Word JM, Prisant MG, Richardson JS, Richardson DC. Structure validation by Calpha geometry: phi,psi and Cbeta deviation. Proteins. 2003;50:437–50. doi: 10.1002/prot.10286. [DOI] [PubMed] [Google Scholar]
- 22.Pertsemlidis A, Zelinka J, Fondon JW, 3rd, Henderson RK, Otwinowski Z. Bayesian statistical studies of the Ramachandran distribution. Stat Appl Genet Mol Biol. 2005;4(Article35) doi: 10.2202/1544-6115.1165. [DOI] [PubMed] [Google Scholar]
- 23.Ho BK, Thomas A, Brasseur R. Revisiting the Ramachandran plot: hard-sphere repulsion, electrostatics, and H-bonding in the alpha-helix. Protein Sci. 2003;12:2508–22. doi: 10.1110/ps.03235203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ramachandran GN, Sasisekharan V. Conformation of polypeptides and proteins. Adv Protein Chem. 1968;23:283–438. doi: 10.1016/s0065-3233(08)60402-7. [DOI] [PubMed] [Google Scholar]
- 25.Gunasekaran K, Ramakrishnan C, Balaram P. Disallowed Ramachandran conformations of amino acid residues in protein structures. J Mol Biol. 1996;264:191–8. doi: 10.1006/jmbi.1996.0633. [DOI] [PubMed] [Google Scholar]
- 26.Lennox K, Dahl D, Vannucci M, Tsai J. Density Estimation for Bivariate Circular Data Using a Bayesian Nonparametric Model. 2008 in preparation. [Google Scholar]
- 27.Henikoff S, Henikoff JG. Amino acid substitution matrices from protein blocks. Proc Natl Acad Sci U S A. 1992;89:10915–9. doi: 10.1073/pnas.89.22.10915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pauling L. The shared-electron chemical bond. Proc Natl Acad Sci U S A. 1928;14:359–362. doi: 10.1073/pnas.14.4.359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang G, Dunbrack RL. PISCES: a protein sequence culling server. Bioinformatics. 2003;19:1589–1591. doi: 10.1093/bioinformatics/btg224. [DOI] [PubMed] [Google Scholar]
- 30.Kabsch W, Sander C. Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-Bonded and Geometrical Features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- 31.Escobar MD, West M. Bayesian density Estimation and inference using mixtures. J Amer Stat Assoc. 1995;90:577–588. [Google Scholar]
- 32.MacEachern M, Müller P. Efficient meme schemes for robust model extensions using encompassing dirichlet process mixgture models. In: Insua DR, Ruggeri F, editors. Robust Bayesian Analysis. Springer-Verlag Inc; 2000. pp. 295–315. [Google Scholar]
- 33.Ferguson TS. A Bayesian analysis of some nonparametric problems. The Annals of Stat. 1973;1:209–230. [Google Scholar]
- 34.Neal RM. Markov chain sampling methods fo dirichlet process mixture models. J Comp and Graph Stat. 2000;9:249–265. [Google Scholar]