Simultaneous Confidence Intervals Based on the Percentile Bootstrap Approach

Abstract

This note concerns the construction of bootstrap simultaneous confidence intervals (SCI) for m parameters. Given B bootstrap samples, we suggest an algorithm with complexity of O(mB log(B)). We apply our algorithm to construct a confidence region for time dependent probabilities of progression in multiple sclerosis and for coefficients in a logistic regression analysis. Alternative normal based simultaneous confidence intervals are presented and compared to the bootstrap intervals.

1 Introduction

In this note, we consider the problem of constructing simultaneous (1 − α)-bootstrap confidence intervals given data X. In particular, we look for a confidence region for m parameters θ = (θ₁, θ₂, …, θ_m) of the form $C^{\alpha }=C_1^{\alpha }\times C_2^{\alpha }\times \cdots \times C_m^{\alpha }$, where for each j, $C_j^{\alpha }=[a_j(\mathbf{X}),b_j(\mathbf{X})]$ is a confidence interval for θ_j with a simultaneous coverage level of 1 − α:

$$P({\cap }_{j=1}^m\{a_j(\mathbf{X})\le {\theta }_j\le b_j(\mathbf{X})\})\ge 1-\alpha .$$ (1.1)

Although such confidence regions are usually inefficient for formal testing purposes [4], they can be easily drawn in two dimensions and provide clues for model deviations, hence are very useful for graphical testing [3]. Theoretical merits of simultaneous bootstrap confidence regions are discussed in bootstrap textbooks [3, 8] along with comparison to normal based confidence regions. However, an algorithm for constructing a rectangular region such as in (1.1) does not seem to exist in the literature. Davison and Hinkley [3] do provide an algorithm to a related simpler problem of calculating the overall coverage of simultaneous confidence intervals (SCI) (see [3] Page 154). Their algorithm counts the number of bootstrap samples that fall outside the confidence region. In order to calculate SCI of a pre-specified level 1 − α, one can repeat their algorithm for several values until obtaining the target coverage. However, this trial and error method is inefficient and a direct algorithm that first assigns ranks to the bootstrap samples and then specifies the SCI according to the quantiles of the ranks is provided here. The suggested algorithm takes into account the multivariate nature of the problem and the possibility that a bootstrap sample has large ranks in several coordinates and small ranks in others.

In Section 2 we present our algorithm. As for any bootstrap method, the algorithm is computer intensive and requires some programming and computer time. For comparison purposes, we present also two normal based SCI that are computationally simpler. The first uses the maxima of a multivariate normal vector and the second is based on Efron’s multiple testing approach [5]. These SCI, however, depend on the accuracy of the normal approximation for the distribution of (θ̂₁, …, θ̂_m), the estimator of the parameters, which may be poor, especially in the tails. Section 3 describes a study of progression of multiple sclerosis and illustrates calculation of the different SCI methods. Section 4 demonstrates the use of SCI in a logistic regression analysis. Section 5 completes the paper with a discussion.

2 Construction of SCI

2.1 Bootstrap SCI

Suppose that the data X were generated by a law F and we are interested in SCI for (θ₁, …, θ_m) = (θ₁(F), …, θ_m(F)). In this section, we present an algorithm for construction of SCI for (θ₁, …, θ_m) with a simultaneous coverage of 1 − α based on B bootstrap samples. The algorithm ranks each bootstrap estimate according to the coordinate which is most discrepant from the pointwise medians and then uses these ranks to define the SCI. For pedagogical reasons, a simpler version of the algorithm that in several cases is too conservative is presented first, then later extended. The algorithm derives the upper limit of the SCI with level 1 − α (construction of the lower limit is analogous):

Algorithm 1

1. Generate B bootstrap samples from F̂, an estimate of F. For each sample, X_b, calculate the estimates ${\stackrel{\sim }{\theta }}_b=({\stackrel{\sim }{\theta }}_{b1},\dots ,{\stackrel{\sim }{\theta }}_{bm})$.

2. For each coordinate j, order the bootstrap estimates and denote them by ${\stackrel{\sim }{\theta }}_{(1j)}<{\stackrel{\sim }{\theta }}_{(2j)}<\cdots <{\stackrel{\sim }{\theta }}_{(Bj)}$. Define r(b, j) to be the rank of θ̃_bj, i.e., ${\stackrel{\sim }{\theta }}_{bj}={\stackrel{\sim }{\theta }}_{(r(b,j)j)}$.

3. Define the sample-b rank r(b) = max_j r(b, j) to be the largest rank associated with the b’th bootstrap estimate.

4. Calculate r_1−α/2, the 1 − α/2 percentile of r(b).

5. Take the upper limits of the SCI to be ${\stackrel{\sim }{\theta }}_{(r_{1-\alpha /2}1)},\dots ,{\stackrel{\sim }{\theta }}_{(r_{1-\alpha /2}m)}$.

By construction, at most α/2 of the bootstrap estimates have a coordinate with value larger than the upper limit of the SCI. Moreover, when the probability of ties is small, one can make the proportion of bootstrap estimates with a coordinate larger than the upper limit close to α/2 by increasing B. The lower limit is constructed in the same way. Letting A₁ be the event that at least one coordinate of a bootstrap sample lies below the lower limits and A₂ be the event that at least one coordinate lies above the upper limit, it follows that $P(A_1\cup A_2)\le P(A_1)+P(A_2)\le \alpha$, and the SCI have the declared coverage probability. The first inequality in the last formula signifies that a realization can be below the SCI at some coordinates and above it at others. Such a realization is counted twice in the above construction and makes the SCI too conservative. Although these realizations should occur infrequently, they can be handled by a simple modification of Algorithm 1 through use of relative ranks rather than the ranks themselves:

Algorithm 2

1. Repeat Steps 1 and 2 of Algorithm 1.

2. Define the relative ranks r*(b, j) = ∣{r(b, j)−(B+1)/2}∣ and their signs s*(b, j) = sign{r(b, j)−(B + 1)/2}. Thus, a high r*(b, j) means an extreme estimate of θ_j, either small s*(b, j) = −1 or large s*(b, j) = 1.

3. Define r*(b) = max_j r*(b, j) to be the largest relative rank of the b’th bootstrap estimate and let s*(b) be the associated sign. It is possible that the maximum is obtained at several j’s. r*(b) is well defined in such cases but the corresponding sign may not. If this is the case, choose s*(b) arbitrarily.

4. Let r(b) = (B + 1)/2 + r^*(b)s^*(b) be the original rank corresponding to the most discrepant coordinate of the b’th sample.

5. For all j and all b, replace θ̃_bj with θ̃_(r(b)j). This yields one rank for each bootstrap estimate with a possibility of ties, i.e., the new estimates are comparable with respect to the relation >.

6. Apply Algorithm 1 on the new values generated in Step 5.

In practice, instead of Step 6 one can determine the SCI directly from the percentiles of r^*(b), i.e., define the SCI by the estimate θ̃_b which corresponds to r*(b)’s that are greater than the chosen percentile.

It is straightforward to check that the coverage of the SCI calculated by the algorithm of [3] is 1 − α, which is the target level.

Algorithms 1 and 2 implicitly assume that there are no ties. In the case of ties, we recommend that the maximum rank of tied observations (instead of the mean rank) be assigned to large values (greater than the median) and the minimum rank be assigned to ties of small values. This procedure works well when the number of tied values is relatively small. A large number of ties, especially near the limits of the interval, requires an ad hoc solution such as replacing the two-sided intervals with one-sided ones or constructing the SCI for part of θ only.

2.2 Normal-based SCI

We next provide two normal based SCI that demand much less computational expense, but rely on the accuracy of the normal approximation. These intervals are compared to the bootstrap SCI in the next sections. Suppose that

$$\sqrt{n}(\widehat{\theta }-\theta )\to N(0,{\mathrm{\Delta }}^{1/2}\Upsilon {\mathrm{\Delta }}^{1/2})$$ (2.1)

where $\mathrm{\Delta }=\mathrm{diag}({\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_m^2)$, ${\sigma }_j^2=\mathrm{Var}(\sqrt{n}{\widehat{\theta }}_j)$ and ϒ is the asymptotic correlation matrix of θ̂. A typical normal based SCI region is of the form

$$C_j=[{\widehat{\theta }}_j-{\widehat{\sigma }}_{j}c(\alpha )/\sqrt{n},{\widehat{\theta }}_j+{\widehat{\sigma }}_{j}c(\alpha )/\sqrt{n}]\hspace{0.17em}(j=1,\dots ,m),$$ (2.2)

where c(α) is chosen to satisfy (1.1). The familiar pointwise and Bonferroni confidence intervals use c(α) = Φ⁻¹(1 − α/2) and c(α) = Φ⁻¹{1 − α/(2m)}, where Φ denotes the standard normal cumulative distribution function. In our context, we seek SCI that exploit (2.1), and an obvious choice is the 1 − α quantile of the maximum of a normal vector, i.e., the c that solves

$$P\left(\max \left\{\right|Z_1|,\dots ,|Z_m\left|\right\}>c\right)=\alpha ,$$ (2.3)

where (Z₁, …, Z_m) ~ N (0, ϒ). SCI that are based on (2.3) will be referred to as “normal exact” SCI. The critical value c = c(α) can be found by simulation; the Cholesky factorization of ϒ is first calculated and then used to generate the correlated normal vector.

The normal exact SCI can be calculated in almost all statistical software packages without much programming, still require some computational effort. Instead, bounds for the maximum of a correlated normal vector used by Efron [5] for the problem of simultaneous hypothesis testing can be utilized. Efron’s work is based on improved Bonferroni bounds for a union of events developed independently by Hunter [9] and Worsley [13], and is slightly more robust than (2.3) to the assumption (2.1). Let ϕ denote the density function of a standard normal variable and let L_j = arccos(∣ρ_j∣), where ρ_j = corr(θ̂_j, θ̂_j−1). Efron’s method for simultaneous testing is inverted for SCI estimation by using as c(α) the c that solves

$$\overline{\mathrm{\Phi }}(c)+\varphi (c)\mathrm{\sum }_{j=2}^m\frac{\mathrm{\Phi }(c{L}_j/2)-\frac{1}{2}}{c/2}=\alpha /2.$$ (2.4)

It can be shown that the left hand side of (2.4) decreases with c for c > 0 and hence c(α) can be found by a simple bisection search, starting from the pointwise value Φ⁻¹(1−α/2) and the Bonferroni value Φ⁻¹{1−α/(2m)}. (In certain situations, Efron’s bound is less than α/2 at the Bonferroni critical value and hence is useless, i.e., the Bonferroni method provides shorter intervals.) We point out that the intervals can be further improved by pairing the estimates in an optimal way and by calculating $P(\{\left|Z_1\right|>c\}\cup \{\left|Z_2\right|>c\})$ exactly using numerical integration (see [5] for details and references), but this involves more computational eαort and sacrifices the advantage of simplicity of this approach.

3 Illustration I - Progression of Multiple Sclerosis

3.1 Data and Model

CLIMB is a large natural history study of Multiple Sclerosis (MS) ongoing at the Partners MS Center in Boston [6]. It aims at understanding the development of the disease in the current era of available treatments. The data analyzed here were collected during the years 2000-2005 and contain semiannual evaluations of disability for 267 MS patients of type relapsing-remitting as measured on the expanded disability status scale (EDSS). The patients enrolled in the study are in the first stage of their disease most having minimal or no disability. One important aim of the study is estimation of time dependent probabilities of progression defined by having an EDSS of three or higher. This corresponds to a moderate disability in at least one of seven functional systems. The EDSS values were grouped as EDSS≤1.5, coded as 1 (no disability), EDSS of 2 or 2.5, coded as 2 (minimal disability) and EDSS of 3+, coded as 3 (moderate to severe disability). In a previous paper ([12], hereafter MGGWB), a Markov model was fitted to the sequence of EDSS values and a method to construct probability curves for time to progression and pointwise confidence intervals was presented. The pointwise confidence intervals are not satisfactory as aforementioned, and here we show how to construct SCI for such curves. Simulation studies revealed that normal based confidence intervals may perform poorly for short term prediction when certain transition probabilities are small (being either anti-conservative or too conservative; see MGGWB, Section 4.4), hence bootstrap methods seem more appropriate.

MGGWB analyzed the data using a first-order Markov model. They contrasted their model with a second-order Markov model using a goodness-of-fit test, and this favored the latter. A second-order assumption is reasonable because of the relapsing remitting nature of MS, where increase of EDSS in one visit may be related to a transient event. Here we reanalyze the data using a second-order Markov model and estimate time dependent probabilities of progression defined by reaching state (3,3), i.e., two consecutive visits with EDSS of three or more (see also [7]). The definition of the endpoint event by two consecutive visits uses the same reasoning as the choice of the second-order model. Increase of EDSS may be a transient event due to a relapse, and increase observed in two consecutive visits is regarded as sustained progression which is of much more interest. Most clinical and observational studies in MS use this reasoning (e.g., [2]).

Due to staggered entry, our 267 patients have different number of visits with a total of 1364 visits. For the second-order Markov model, triplets of consecutive visits are needed, where the first two visits are considered as the initial state or the baseline value. Forty eight visits are missing and the data comprise of 726 complete triplets and 104 triplets with a missing coordinate (to ease estimation, we dropped out seven patients after their second missed visit). Because of small numbers, the EDSS histories of (1,3) and (2,3), and (2,1) and (3,1) were combined. In terms of modelling, this means that the transition probabilities from state (1,3) are assumed equal to those from state (2,3), and similarly the transition probabilities from state (2,1) and (3,1) are assumed equal. Biologically it means that transition probabilities are determined by the current disability status and whether it has been improved or worsened from the previous visit (but the exact value then is unimportant). This is a reasonable model for relapsing remitting diseases and it is similar to the model of Albert [1] who studied experimental allergic encephalomyelitis which is an animal model of MS. Table 1 summarizes the complete transitions and the estimated transition probabilities as described below.

Table 1.

Transitions between EDSS scores. Frequency for the complete data (left) and maximum likelihood estimates using all the data (right).

	current EDSS score			current EDSS score
Previous EDSS scores	1	2	3	1	2	3
(1,1)	366	33	2	.906	.089	.005
(1,2)	29	18	3	.578	.369	.053
(1,3)+(2,3)	3	11	14	.120	.397	.484
(2,1)+(3,1)	48	18	3	.698	.261	.041
(2,2)	20	63	11	.207	.684	.109
(3,2)	2	9	10	.084	.416	.500
(3,3)	1	12	50	.017	.183	.800

3.2 Estimation

3.2.1 Estimating the transition matrix

Maximum likelihood estimation is conducted under the assumption of missing completely at random. Let Y_ji be the EDSS at visit j of subject i, (i = 1, …, N; j = 1, …, m_i), and denote by p_(k,l)r = P(Y_ji = r∣Y_(j−2)i = k, Y_(j−1)i = l) and π_(k,l) = P(Y_0i = k, Y_1i = l) the transition probabilities and the baseline probabilities, respectively, then the likelihood is

$$\prod _{i=1}^N\mathrm{\sum }_{(y_0,y_1,\dots ,y_{m_i})\in {\mathrm{\Omega }}_i}\left\{{\pi }_{(y_0,y_1)}\prod _{j=2}^{m_i}{p}_{(y_{j-2},y_{j-1})y_i}\right\},$$ (3.1)

where Ω_i is the set of possible values that subject i can take. For example, for a subject with no missing visits, Ω_i = {(y_0i, y_1i, …, y_m,i)}, where y_ji is the realization of Y_ji in the sample, for a subject whose second visit is missing,

Ω_i = {(y_0i, 1, y_2i, …, y_mi), (y_0i, 2, y_2i, …, y_mi), (y_0i, 3, y_2i, …, y_mi)}, and so forth. In our example, at most one visit is missing for each subject and estimation could be carried out by direct maximization of (3.1). Table 1 presents the maximum likelihood estimate (MLE) of the transition matrix.

3.2.2 Estimating time to event

Let P̂ be an estimator of the transition matrix P of a Markov chain having s states. In the current example s = 9 and the state space is defined by {(k, l) : k, l = 1, 2, 3}. Let Q be as P, but the last row replaced with all elements zero except the last one which is 1. Thus, Q changes the state (3, 3) to be an absorbing state. The (i, 9)’th cell in the j’th power of Q̂, the estimator of Q, contains our estimator of θ_j which is the probability of progression during j visits for a subject whose baseline EDSS is i.

Asymptotically, the estimators have a normal law [12]. To be more explicit, denote by vec(Q) the vector representation of Q that stacks the rows of Q one on the other. Then the transformation vec(Q) → vec(Q^j) has the s² × s² Jacobian matrix D_j whose (k − 1)s + l’th column is

$$\mathrm{vec}\left(\mathrm{\sum }_{r=0}^{j-1}{Q}^r{\mathrm{\Delta }}_{kl}{Q}^{j-r-1}\right),$$ (3.2)

where Δ_kl is an s × s matrix whose elements are all zeros except the (k, l) cell which is one, and Q⁰ is the identity matrix with dimension s. Thus, given that $\sqrt{n}\{\mathrm{vec}(\widehat{Q})-\mathrm{vec}(Q)\}\to N(0,\mathrm{\sum })$, then $\sqrt{n}\{\mathrm{vec}({\widehat{Q}}^j)-\mathrm{vec}(Q^j)\}\to N(0,D_j\mathrm{\sum }{D}_j^T)$ and an asymptotic pointwise confidence interval for θ_j can be constructed by plugging estimates of Q̂ in (3.2).

To construct SCI, the results of MGGWB should be extended to the law of all of the transformations Q^j (j = 1, …, m) together. The estimator of all transition probabilities in the m steps, $\widehat{\mathbf{Q}}={({\mathrm{vec}}^T({\widehat{Q}}^1),{\mathrm{vec}}^T({\widehat{Q}}^2),\dots ,{\mathrm{vec}}^T({\widehat{Q}}^m))}^T$ has an asymptotic normal distribution with covariance-variance matrix given by

$$\mathrm{\Psi }=\left(\begin{array}{c}{D}_1\\ D_2\\ ⋮\\ D_m\end{array}\right)\mathrm{\sum }(D_1^T{D}_2^T\dots D_m^T).$$

The covariance of ${\widehat{q}}_{kl}^j$ with ${\widehat{q}}_{kl}^r$ is in the (k − 1)s + l row and (k − 1)s + l column of $D_j\mathrm{\sum }{D}_r^T$ where ${\widehat{q}}_{kl}^j$ is the (k, l)’th element of Q̂^j. This matrix is used for calculation of the normal-based SCI described in Section 2.2.

3.3 Results

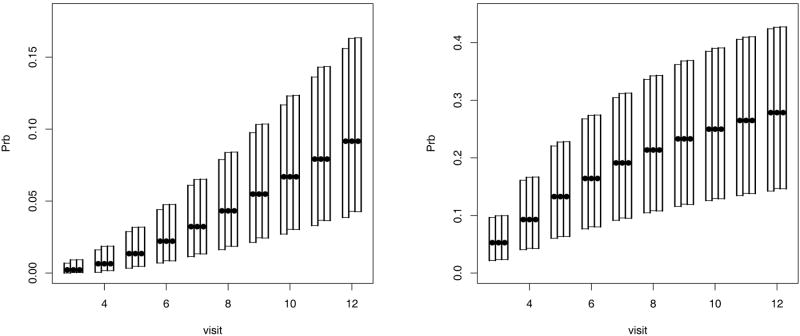
The bootstrap and the normal based SCI are displayed in Figure 1. The SCI are for the probabilities of visiting state (3,3) at or before visit j (j = 3, …, 12) starting from state (1,1) (left panel) or (2,2) (right panel). The construction of the normal based SCI deviated slightly from (2.2). The SCI defined in (2.2) are symmetric around the point estimates and may include values outside the parameter space. An alternative that is frequently used to calculate the variance of the Kaplan-Meier estimator is to apply the log(− log) transformation (e.g., [10]). A comparison of confidence intervals with and without the log(-log) transform revealed that the former performed better. Thus, the SCI’s for log(− log(θ)) were calculated, as described in Section 2, and then the inverse transformation was applied to obtain the SCI’s of Figure 1.

Figure 1.

Probabilities (bullets) and 95% SCI (bars) of two consecutive visits with moderate to severe disability given initial state is (1,1) (left panel) and (2,2) (right panel). The confidence intervals are, from left to right, bootstrap, normal exact, Efron.

Since several of the cells in Table 1 are small, the validity of the normal approximation (2.1) is questionable. As an alternative, a parametric bootstrap SCI were calculated conditionally on the number of visits of each subject and the data on the first two visits. Specifically, the parameters used were the MLEs of π_k,l and p_(k,l)r. For each subject, an initial state was generated giving his data on EDSS at the first two visits (in particular, for subjects without missing values the observed states were used), and then the remaining transitions were generated with the total number of visits and the structure of missing visits fixed at the observed values. This process was repeated B = 5, 000 times, with the remaining steps following Algorithm 2.

All calculations were performed on a PC with 1.2 GHz processor and 1 GB of RAM. We used SAS version 9.1 to generate the 5000 samples and to estimate the parameters of the Markov model (we used nlmixed procedure with the default dual quasi-Newton optimization algorithm). We used R version 1.9.1 to estimate θ̃_b = (θ̃_b1, …, θ̃_bm) from the Markov model results, and to generate the bootstrap and normal based SCI.

Several interesting features appear in Figure 1. First, the bootstrap intervals have smaller limits than the normal based intervals, but still have similar lengths. Thus, the normal approach seems to overestimate θ (this is even more pronounced when not applying the log(− log) transformation). Second, the difference is larger on the left panel which shows progression of patients with normal neurological exam (initial state (1,1)). The estimated transition probability from state (1,1) to state (1,3) is very small (only 0.05), which probably results in a less accurate normal approximation for the distribution of θ̂ in the left panel as compared to the right panel. Third, the two normal SCI are very similar even though the method due to Efron uses a bound for the exact value.

4 Illustration II - Logistic Regression

In this section we apply the method to parameters of a logistic regression. Replacing pointwise with simultaneous confidence intervals is beneficial as it deals with multivariate comparisons, but still give interpretable information on each of the parameters. Table 2 presents confidence intervals for coefficients of the logistic model of Table 5.10 of Hosmer and Lemeshow [11]. This is part of a study on the efficacy of treatment approach for drug abusers, where the dichotomous outcome is the return to drug use. There are ten covariates and 575 individuals, which is usually sufficient for normal approximation. For a detailed description of the study and covariates see [11] Sections 1.6.4 and 4.2.

Table 2.

Pointwise and simultaneous confidence intervals for the logistic regression model of Hosmer and Lemeshow’s (2000) Table 5.10

Variable	Pointwise	Bonferroni	Efron	bootstrap
Intercept	[-9.234,-4.454]	[-10.304,-3.384]	[-10.245,-3.442]	[-11.071,-3.693]
Age	[0.060,0.173]	[0.035,0.199]	[0.036,0.197]	[0.039,0.209]
NDRGFP1	[0.871,2.467]	[0.514,2.824]	[0.533,2.805]	[0.607,3.120]
NDRGFP2	[0.205,0.663]	[0.102,0.765]	[0.108,0.760]	[0.124,0.818]
IVHX2	[-1.220,-0.049]	[-1.482,0.213]	[-1.468,0.199]	[-1.481,0.156]
IVHX3	[-1.218,-0.192]	[-1.447,0.037]	[-1.435,0.025]	[-1.517,0.024]
Race	[0.166,1.202]	[-0.065,1.434]	[-0.053,1.421]	[-0.047,1.448]
Treat	[0.036,0.834]	[-0.143,1.013]	[-0.134,1.003]	[-0.149,1.035]
Site	[0.017,1.016]	[-0.207,1.239]	[-0.195,1.227]	[-0.244,1.219]
Age*NDRGFP1	[-0.027,-0.003]	[-0.032,0.002]	[-0.032,0.002]	[-0.035,0.001]
Race*Site	[-2.468,-0.391]	[-2.933,0.074]	[-2.907,0.049]	[-3.398,-0.065]

The pointwise and Bonferroni intervals are presented together with the Efron and bootstrap intervals for a comparison. As there is no obvious indexing of the parameters in this example, the maximal spanning tree with squared correlations as weights was used to optimally pair the estimators for the Efron method [13]. The normal-exact intervals are very similar to the Efron ones (having c(0.05) = 2.768 compared to 2.790 for Efron), hence are not shown. The Efron confidence intervals are shorter than Bonferroni’s but the improvement is quite small. This is because correlations among the estimators are not as large as in the previous example. The bootstrap intervals agree with the Efron and Bonferroni intervals in most coordinates, but deviate in few. A simulation study revealed that their coverage is somewhat less than the target 95% while the Efron intervals are quite accurate. Recentering the bootstrap intervals as discussed in the next section resulted in conservative coverage.

This example shows that the application of simultaneous confidence intervals in general and the bootstrap method in particular is not limited to discrete survival estimates. However, when the normal approximation is good, the bootstrap method is not really needed. Moreover, the example indicates that the simple Bonferroni correction method is satisfactory when the correlations are small.

5 Discussion

We have derived an algorithm to construct simultaneous confidence intervals by assigning ranks to the bootstrap samples and basing the SCI on the quantiles of the ranks. We compared the bootstrap SCI to two normal based SCI and showed that the bootstrap SCI requires more programming effort, but relies on fewer assumptions than the normal based approaches. The algorithm is based on the simple percentile bootstrap method which does not always work well (see [3] Section 5.3). Extension of the algorithm to adjusted percentile methods ([3] Section 5.3.2) is not straightforward and requires further investigation. However, one can shift the intervals by using for θ_j the interval

$$[2{\widehat{\theta }}_j-{\stackrel{\sim }{\theta }}_{(r_{1-\alpha /2})},2{\widehat{\theta }}_j-{\stackrel{\sim }{\theta }}_{(r_{\alpha /2})}]$$ (5.1)

(see Equation (5.6) of [3]). A small simulation study that compared the percentile intervals $[{\stackrel{\sim }{\theta }}_{(r_{\alpha /2})},{\stackrel{\sim }{\theta }}_{(r_{1-\alpha /2})}]$ to (5.1) using the logistic regression model discussed in Section 4, revealed that the latter is more conservative. Similar modifications can be used to calculate simultaneous studentized bootstrap confidence intervals.

The complexity of Step 1 of Algorithm 1 depends on the problem at hand, i.e., the time it takes to generate a bootstrap sample and to compute (θ̂₁, …, θ̂_m). In the simplest problems it is of order O(nmB), where n is the size of X. Among the remaining steps, Step 2 is most demanding; it requires sorting of all coordinates and has an average complexity of O(mB log(B)). In the MS example of Section 3, Step 1 of Algorithm 1 was quite complicated and was comprised of three steps: generating bootstrap samples, estimating the second order Markov model, and calculating the probabilities θ̃_b = (θ̃_b1, …, θ̃_bm). It took more than four hours to accomplish it. The time it took to run Algorithm 2 excluding Step 1 of Algorithm 1 was only two seconds. However, the time can be considerably longer when there are tied observations (or if the algorithm automatically checks and deals with ties). In our problem of B = 5000 and m = 10, checking for tied observations and assigning the maximum rank increased the running time to 27 seconds, still quite fast and much faster than Step 1.

When using normal based SCI, the bound due to [5] gives very close results to the normal exact method. This was also found in other simulated and real data sets that we have analyzed. Since the Efron SCI is easier to calculate than the normal exact method, we recommend its use when the normal approximation can be trusted. In cases where the correlations among the estimators are low, as in the logistic regression example of Section 4, the Bonferroni intervals are quite accurate.