Multilevel structure in behaviour and in the brain: a model of Fuster's hierarchy

Abstract

A basic question, intimately tied to the problem of action selection, is that of how actions are assembled into organized sequences. Theories of routine sequential behaviour have long acknowledged that it must rely not only on environmental cues but also on some internal representation of temporal or task context. It is assumed, in most theories, that such internal representations must be organized into a strict hierarchy, mirroring the hierarchical structure of naturalistic sequential behaviour. This article reviews an alternative computational account, which asserts that the representations underlying naturalistic sequential behaviour need not, and arguably cannot, assume a strictly hierarchical form. One apparent liability of this theory is that it seems to contradict neuroscientific evidence indicating that different levels of sequential structure in behaviour are represented at different levels in a hierarchy of cortical areas. New simulations, reported here, show not only that the original computational account can be reconciled with this alignment between behavioural and neural organization, but also that it gives rise to a novel explanation for how this alignment might develop through learning.

1. Introduction

In both psychology and neuroscience, the problem of action selection has often been characterized at the level of single actions. Although this approach has obviously been quite fruitful, it ultimately runs up against the fact that in everyday human behaviour worthwhile outcomes can rarely be attained with a single action. Instead, adaptive behaviour typically requires the selection of coherent sequences of action. Any comprehensive account of action selection must, therefore, grapple with the question of how action sequences are initiated and executed.

To some extent, the generation of routine sequential action can be explained on the basis of a perception–action cycle (see Fuster 1990) within which each action leads to a new percept, which in turn provides the basis for the subsequent action. However, although such a feedback loop undoubtedly plays a role, it has been recognized at least since the pioneering comments of Lashley (1951) that simple associations between perceptual inputs and actions, or between actions themselves, cannot explain the mass of human sequential behaviour. As Lashley (1951) noted, the current perceptual context and the identity of the preceding action are often inadequate cues to support action selection. One needs only to consider the situation of a pianist in the middle of a piece, for whom the last note played is generally not sufficient to indicate which note comes next. Instead, what is needed for the production of organized sequential action is an internal representation of temporal or task context, which—at a minimum—can span periods during which the environment provides an indeterminate cue (Fuster 1990, 1997, 2001; Botvinick & Plaut 2002).

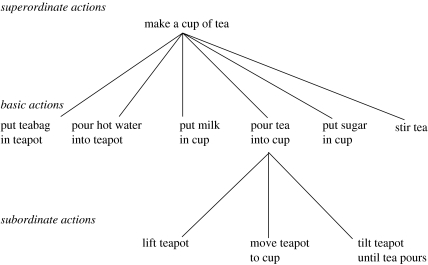
An additional characteristic of human action, which has often been emphasized in theories of sequential behaviour, is that it tends to assume a roughly hierarchical structure. Such hierarchical structure is evident, for example, in the everyday tasks of tea- and coffee-making, tasks that have become to some extent canonical in the cognitive neuropsychological literature on naturalistic sequential action (figure 1). Here, as in many other cases, an overall task, separable from surrounding behaviour, is composed of discrete subtasks (e.g. adding sugar and adding cream), which themselves are composed of more unitary actions. A key question is how representations of temporal or task context are structured and updated over time so as to support hierarchically structured action sequences of this kind.

Figure 1.

A hierarchical representation of the task of making tea. Adapted with permission from Humphreys & Forde (1998).

In recent work, the author and his colleagues have put forth a computational model of the mechanisms underlying routine sequential action production, which provides an account of how context information is maintained and exploited in the context of hierarchically structured tasks (Botvinick & Plaut 2002, 2004, 2006a; Botvinick & Bylsma 2005). As this paper shall review, the model builds directly on the idea of the perception–action cycle, but adds to it the simple assumption that the influence of perception on action is mediated by internal representations that have their own intrinsic dynamics. An important goal has been to implement this basic idea in a form that can be mapped, in a general way, onto neural circuitry. According to the resulting framework, routine sequential action arises from a massively parallel neural system that maps from perceptual inputs to action outputs via learned and distributed internal representations. It is assumed that this system is further characterized by extensive recurrent connectivity, which allows information about temporal or task context to be preserved and updated over time.

The first objective of this article is to review this computational proposal and the simulations and empirical data supporting it. The second objective is to relate this work to a set of empirical findings that may, at the first glance, appear to challenge it. As reviewed in what follows, a critical claim of the proposed computational framework, which differentiates it strongly from some competing accounts, is that the representations underlying hierarchically structured behaviour need not, and arguably cannot, themselves assume a strictly hierarchical form, a claim that has been emphasized by the use of a neural network architecture that is not itself hierarchically structured. In apparent contradiction to this stance, a growing body of evidence from cognitive neuroscience has led to the idea that there may be a link between the organization of the cerebral cortex and the hierarchical structure of action sequences, such that different levels of task structure are represented at different levels within a hierarchy of cortical areas. As reviewed further below, this idea has been most systematically developed by Fuster (1990, 1997, 2001, 2004) on the basis of neurophysiological work, but it has also received convergent support from neuroimaging work by Koechlin et al. (2003), Courtney (2004) and others.

This article, after reviewing the basic computational theory in its original formulation, presents new simulations that demonstrate how the claims of the theory about the role of hierarchy can be reconciled with such neuroscientific data. The basic approach in these simulations is to investigate the consequences of introducing hierarchical structure into the original processing architecture. In addition to allowing some important points to be made concerning the computational basis of sequential action, this enterprise had an additional and equally significant outcome, in that it yielded an insight into how hierarchical structure at the level of cortical connectivity might give rise to regional specialization in the representation of temporal or task context.

2. A model of routine sequential behaviour

Botvinick and Plaut (2004, henceforth BP04) reported a set of computer simulations articulating and validating a theory of naturalistic routine sequential action. As noted above, the implementation took the form of a recurrent neural network, and a primary question addressed in the simulations was whether the model, which did not assume an explicitly hierarchical structure, could nonetheless learn to perform hierarchically structured sequential tasks. An additional set of questions related to errors in routine sequential behaviour. In particular, it was asked whether the model could account for key properties of everyday slips of action, and for patterns of error seen in patients with action disorganization syndrome (ADS), a type of apraxia affecting performance in sequential routines (Schwartz et al. 1998).

(a) Model architecture and task domain

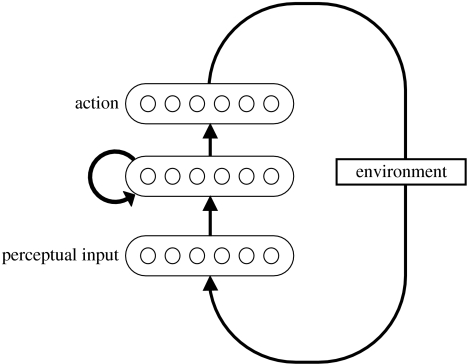
The structure of the model is diagrammed in figure 2. Like all connectionist-style neural network models, it is composed of simple processing units, each with a scalar activation value. These excite or inhibit one another through adjustable, weighted connections. In the BP04 model, units are organized into three groups. A group of input units serves to represent the perceptual features of objects in the environment. These units connect to an internal or ‘hidden’ group, which itself connects to an output group whose units represent simple actions (e.g. ‘pick-up’, ‘pour’ or ‘locate-spoon’). In order to capture the fact that actions affect perceptual inputs, the model communicates with a simulated environment, which updates inputs to the network contingent on selected actions.

Figure 2.

Architecture of the model used by Botvinick & Plaut (2004). Arrows indicate all-to-all connections. The input layer contained 39 input units, each coding for an object descriptor. Multiple units were activated in this layer to describe the currently viewed and held objects (e.g. ‘packet,’ ‘paper’ and ‘torn’). The output layer contained 19 units, each representing an action (e.g. ‘pour’ or ‘fixate-spoon’). The hidden layer contained 50 units.

A crucial feature of the model is that there are reciprocal connections between each pair of units in its internal layer. The presence of these ‘recurrent’ connections means that activation can flow over circuits within the network, allowing information to be preserved and transformed over multiple steps of processing. It also has important implications for the role of the model's internal units. Given their overall pattern of connectivity, these units play two roles. First, they serve as an intermediate stage in the stimulus–response mapping performed on each processing step. Second, because they carry all the information that will be conducted over the network's recurrent connections—and thus all the information that will be carried over to the next time-step—they are responsible for carrying the model's representation of temporal context.

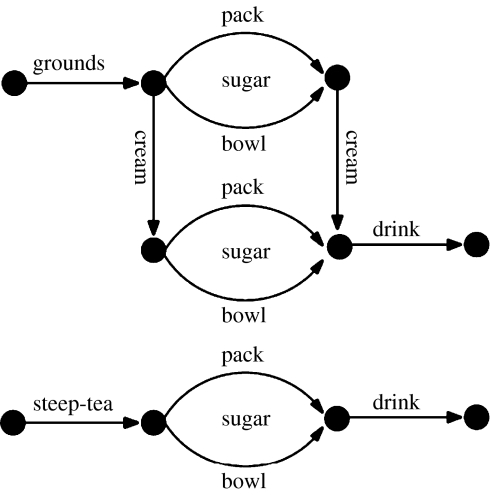
A number of studies have demonstrated the ability of recurrent networks to address aspects of human behaviour in the domains of language (e.g. Elman 1990), implicit learning (e.g. Cleeremans 1993) and memory (e.g. Botvinick & Plaut 2006). Our simulations investigated whether similar computational principles could be used to account for human behaviour in everyday, goal-oriented tasks involving the manipulation of objects. In order to facilitate comparison with another recent computational model, discussed below (Cooper & Shallice 2000), the task modelled was that of making a cup of instant coffee. Our implementation of the task is shown schematically in figure 3. It comprises four subtasks, each containing between 5 and 11 actions: (i) adding coffee grounds, (ii) adding cream, (iii) adding sugar (by one of two methods), and (iv) drinking. For reasons that will become clear in later discussion, the training corpus also contained a second task, tea-making. The model was trained to perform these tasks using a version of the back-propagation learning algorithm (Williams & Zipser 1995). The training was analogous to observing and attempting to predict the sequence of actions of a skilled individual repeatedly carrying out specific versions of each task. Testing involved successively presenting the trained model with perceptual input and using its generated action to modify the environment (and, hence, the model's subsequent perceptual input).

Figure 3.

Structure of the coffee and tea tasks used by Botvinick & Plaut (2004). Sugar could be added by either of the two means, and sugar and cream could be added in either order. Each labelled segment corresponds to a sequence containing between 5 and 11 individual actions. Adapted from Botvinick & Plaut (2002).

(b) Behaviour of the model

As noted earlier, our simulations were designed to address behavioural data from three domains: (i) normal, error-free performance in hierarchically structured tasks, (ii) everyday ‘slips of action’, and (iii) action disorganization syndrome. In our simulations of normal performance, we asked simply whether the model could learn to perform the target tasks, since some action researchers had expressed doubt concerning the ability of recurrent networks to deal with tasks that are hierarchically structured (Houghton & Hartley 1995). Consistent with earlier studies applying recurrent networks in hierarchical domains, the model proved quite capable of learning the target sequences and producing them autonomously following training. Our simulations of action slips and ADS were based on the assumption that both stem from disruptions to representations of temporal or task context. In our model, as noted above, such context information is carried by the hidden units. With this in mind, context information was degraded by randomly perturbing the activation values in the hidden layer on each cycle of processing. When this was done mildly, the model produced errors resembling human slips of action. In line with empirical observations concerning slips (Norman 1981; Reason 1990), the model made errors at decision points, behavioural ‘forks in the road’ where the actions just completed bear associations with multiple lines of subsequent behaviour. Also like typical human slips, the model's errors took the form of subtask sequences performed correctly, but in the wrong context. The model's errors fell into the same category as human slips: omissions, repetitions and lapses from one task into another. With increasingly severe disruption to the model's context representations, the model's behaviour became gradually more fragmented, coming to resemble the performance of ADS patients as characterized in relevant empirical studies (e.g. Schwartz et al. 1998; Humphreys et al. 2000).

(c) Internal representations

In order to understand how the model works, and why it makes the errors that it does, it is necessary to consider how the model represents task context within its internal or hidden layer. We now turn to a discussion of this issue.

Whether the model is used to simulate normal performance or errors, its behaviour is linked directly to the patterns of activation over the units in its internal layer. As noted above, these units play two roles. First, because they lie between input and output layers, they are responsible for facilitating the stimulus–response mapping being performed on each time-step. Second, because the internal units transmit information from one time-step to the next, via their recurrent connections, they also must serve to represent the current behavioural context. On each time-step, the information carried in this layer is integrated with information about external inputs to determine the context-appropriate action. Note that every unit in the hidden layer participates in each context representation. Unlike some competing models of action (described below) which use single units to represent entire task contexts, the present model employs distributed representations (Hinton et al. 1986); information is represented by an entire population of processing units, within which each unit participates in representing a variety of contexts. In order to understand the implications of the model's way of representing context, a spatial metaphor may be adopted. The model's internal layer contains 50 units, each of which carries an activation between zero and one. If these activations are thought of as spatial coordinates, then each pattern of activation (context representation) can be thought of as specifying a point in a 50-dimensional representational space. As the model steps through an action sequence, the successive patterns in its internal layer can be thought of as tracing out a trajectory in this space. Although it is impossible to visualize such trajectories in their original 50 dimensions, one can gain a sense of them using the technique of multidimensional scaling (MDS). This allows trajectories in high-dimensional space to be represented in two dimensions, while preserving as much information as possible about the original pattern (Kruskal & Wish 1978). Perhaps the most important aspect of the results yielded by MDS is that they carry information about the similarities among the model's internal representations. Such information is conveyed through the proximities of points within the diagram. To a first approximation, points located near to one another correspond to patterns of activation that are similar, while those located distant from one another correspond to more dissimilar patterns of activation.

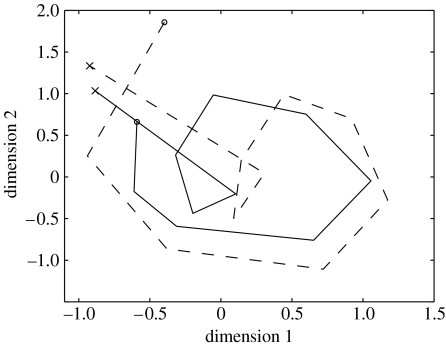
An example of the model's internal representations, visualized with MDS, is shown in figure 4. The plot shows two trajectories, both representing the sequence of internal states produced by the model as it stepped through the 11 actions of the sugar-adding subtask (the solid trace corresponds to the patterns produced when performing the subtask in the context of coffee-making, the dotted trace when performing it during tea-making). To be clear, this plot was created by recording the 50-element hidden-layer activation vectors arising during the relevant steps of processing, and entering all 22 of these vectors into a single MDS analysis.

Figure 4.

Multidimensional scaling analysis of the internal representations arising during performance of the sugarpack subtask, either in the context of coffee-making (solid lines) or tea-making (dotted lines). Adapted from Botvinick & Plaut (2002).

The first thing to note is that the two trajectories are similar in shape. This indicates that the series of internal representations the model uses when adding sugar to coffee are similar to those it uses when adding sugar to tea, an arrangement that makes sense since sugar-adding involves the same sequence of actions regardless of the overall task context. Note, however, that the two trajectories are not precisely identical. The minor differences between the two reflect the difference in overall task context; the model's internal representations on each step differ slightly according to whether it is coffee- or tea-making that is being performed. As earlier studies of recurrent networks (e.g. Servan-Schreiber et al. 1991) have expressed it, the network ‘shades’ its internal representations to reflect differences in context. It is in this way that the model manages to maintain important information about temporal context, while at the same time dealing with immediate stimulus–response mappings.

(d) Comparison with strict hierarchical models

The computational model of routine sequential behaviour just described differs in subtle but important ways from most other accounts. The majority of previous models take as foundational the observation that routine sequential action displays multiple levels of sequential structure (see figure 1). In response to this, such models begin with the assumption that the processing system underlying routine sequential behaviour is itself strictly and constitutively hierarchical in structure. Numerous influential models of sequential action have shared this assumption, both in the psychological literature (Estes 1972; Rumelhart & Norman 1982; Grossberg 1986a,b; Norman & Shallice 1986; Houghton 1990) and in the work on ethology (as reviewed by Tyrrell 1993; Seth 2007). The most recent, and arguably the most sophisticated, version of the hierarchical approach is by Cooper and Shallice (Cooper & Shallice 2000, 2006; Cooper 2003, in press; Cooper et al. 2005). Here, the processing system is composed of basic elements, referred to as schema nodes, which are arranged into an associative tree, with nodes representing simple actions making up the terminal leaves of the tree, and nodes representing higher levels of sequential structure (entire subtasks and tasks) at corresponding levels above.

The BP04 model differs from this and other hierarchical models in that it is not founded on the assumption that the processing system underlying routine sequential behaviour is strictly hierarchical. Instead, the model begins with large, unstructured and highly flexible representational space and dynamics, which are shaped by experience with specific task repertoires. Where distinctions between levels of structure are needed for successful control, the model is entirely capable of developing internal representations that capture them, as illustrated by the MDS data in figure 4. However, the model's internal representations are not constrained to be strictly hierarchical, and this allows them to respond to two other pervasive features of naturalistic human behaviour that pose problems for strict hierarchical accounts.

The first of these features is context-sensitivity. It is often the case that the way a subroutine is performed depends on the larger task context in which it occurs (Agre 1988). For example, the routine of adding sugar to a beverage may be performed differently, involving different amounts of sugar, depending on whether the beverage is coffee or tea. In order to see why such context-sensitivity raises a problem for strict hierarchical accounts, consider how this sugar-adding example would be implemented within the Cooper & Shallice (2000) model. The following question inevitably arises: should sugar-adding be represented by one schema node or two? Using one node leaves it unclear how the execution of this subtask is to vary with the higher-level task context. The other option, introducing two schema nodes, one for adding sugar to coffee and the other for adding sugar to tea, ignores the fact that these different versions of sugar-adding are likely to share a great deal of structure.

This example raises the second relevant characteristic of naturalistic sequential action, which is that different tasks often overlap in their details. Consider the interrelations among routines like spreading jam, spreading peanut butter, spreading sauerkraut on a hot dog, spreading icing on a cake, spreading wax on the floor, using a squeegee on a window, raking the lawn and so on. It seems likely that such routines are represented in a fashion that acknowledges and capitalizes upon their shared structure (Schank & Abelson 1977). Given the complex ways in which naturalistic tasks overlap, it is hard to see how a strictly hierarchical representational regime, where entire tasks and subtasks are represented in a discrete, unitary fashion, could satisfy this description (for further discussion of this point, see Botvinick & Plaut 2002).

The characteristics of context-sensitivity and structural overlap mean that naturalistic behaviour is, in fact, not strictly hierarchical, but might be better described as quasi-hierarchical. Unlike strict hierarchical accounts, the BP04 framework can accommodate this kind of structure. The internal representations it posits are not constrained to be strictly hierarchical and thus retain sufficient flexibility to allow for context-sensitivity and information-sharing between tasks (for demonstrative simulations, see Botvinick & Plaut 2002, 2004, 2006a). The system's representational flexibility also allows it to avoid other common pitfalls of strict hierarchical accounts, allowing it in principle to concurrently represent multiple, interacting contextual constraints (e.g. ‘close the door’ plus ‘do not wake the baby’; see Tyrrell 1993) and to balance the general need to inhibit completed actions against the occasional need to repeat actions.

In addition to these theoretical considerations, empirical evidence can be marshalled to support the BP04 account. To begin with, there is an obvious parallel between the massively recurrent connectivity involved in the BP04 model and the feedback loops connecting cerebral cortex with basal ganglia and thalamus (Middleton & Strick 2000), loops that have been proposed to play a critical role in guiding sequential action (Houk & Wise 1995; Redgrave et al. 1999; Tanji 2001). On a more specific level, there is neuroscientific support for the assertion that actions are represented in a context-dependent fashion: Aldridge & Berridge (1998) observed in rats that the set of basal ganglia neurons active during specific grooming movements differed dramatically depending on whether the relevant movement was executed inside or outside the context of the animal's grooming sequence (see also Salinas 2004). Finally, Botvinick & Bylsma (2005) tested and confirmed a counter-intuitive prediction of the BP04 model concerning the impact of momentary distraction on slips of action, and presented arguments for why the findings they obtained would be difficult to explain on the basis of a strictly hierarchical account of routine sequential behaviour.

3. Taking account of hierarchical structure in cerebral cortex

To recap, a central point demonstrated by the BP04 model is that despite the evidently hierarchical structure of everyday sequential behaviour, the representations underlying such behaviour need not be, and indeed are unlikely to be, strictly hierarchical. Instead, like the detailed structure of everyday behaviour itself, those representations are more likely to be quasi-hierarchical, capturing the distinctions between separable levels of sequential structure, while also allowing information to be shared across those levels and between interrelated task sequences. Having marshalled both computational observations and empirical evidence in support of this proposal, we now turn to address a set of findings that may appear, at first glance, to contradict it.

(a) Fuster's hierarchy

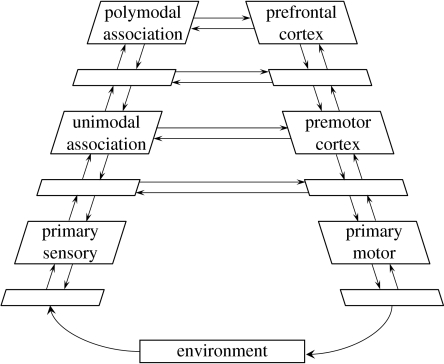
Drawing on neuroanatomical data, Fuster (1990, 1997, 2001, 2004) has characterized the system of cortical regions mapping from perceptual inputs to motor outputs as forming a ladder-like structure, with primary sensory and motor cortices at its base and prefrontal cortex (PFC) at its apex (figure 5).

Figure 5.

Fuster's hierarchy. Adapted from Fuster (2001).

According to Fuster, this structural hierarchy also contains a parallel functional hierarchy. Specifically, as one rises through the levels from the periphery to the PFC, successive levels play a smaller role in coding for immediate perceptual inputs and motor outputs, and a greater role in the representation of temporal context. According to Fuster's account, the PFC, lying at one extreme of this continuum, plays a functional role defined largely by its contribution to the ‘temporal integration’ of behaviour (Fuster 2004).

Consistent with Fuster's proposal, other researchers have suggested that different levels of sequential structure are represented at different levels of a cortical hierarchy culminating in the PFC. This has been proposed, for example, by Koechlin et al. (2003) on the basis of neuroimaging findings, and a similar account has also been put forth by Courtney (2004). Although the PFC is often associated with non-routine action, it is also believed to play a critical role in the coordination of routine sequential behaviour (Sirigu et al. 1995; Fuster 2001; Zalla et al. 2003), and Grafman (1995, 2002) has put forth an account of the representation of routine sequential behaviours that specifically proposes that different levels of task structure are represented at different levels of the neocortical hierarchy.

Returning to Fuster's version of this theory, it is worth noting that it is, in some regards, quite well aligned with the computational framework proposed by BP04. Specifically, these two share the basic idea that sequential behaviour arises from an elaborated perception–action cycle, within which a mediating role is played by internal representations capable of maintaining information about temporal or task context (see, in particular, Fuster 1990, 2004). Nevertheless, the emphasis on hierarchical structure in Fuster's and related accounts may appear to contradict the BP04 theory. It is true that the BP04 model was constructed in a pointedly non-hierarchical fashion. However, it is important to separate this implementational choice, which was made for the sake of simplicity and theoretical clarity, from the fundamental assertions of the account with regard to hierarchical structure. As has been noted, these are: (i) that the mechanisms underlying routine sequential action do not require that the processing system itself assumes a hierarchical form, and (ii) that the representations underlying sequential action do not relate to one another in a strict hierarchical fashion. Thus, in principle, there is no reason for the basic mechanisms at work in the BP04 model not to operate within a system displaying hierarchical structure, particularly if this structure were present at a level far above that of individual representational elements.

In order to substantiate this point, we implemented a neural network model based on the BP04 framework, but assuming a structure based on Fuster's hierarchy, and trained this on a task requiring the preservation of temporal context information. The results of this simulation study not only served to establish how the BP04 model can be reconciled with Fuster's and related accounts, but also suggested how the functional hierarchy Fuster described—and the special role of the PFC within it—might arise through learning.

(b) Simulation 1: modelling Fuster's hierarchy

In this simulation study, we constructed a recurrent neural network model that was similar to the one proposed by BP04, in that it mapped from perceptual inputs to action outputs via recurrently connected hidden units. However, unlike BP04, the model incorporated a pattern of connectivity resembling the ladder-like structure described by Fuster (1997). At the base of the ladder was a group that received external inputs representing environmental stimuli, and an output group representing motor commands. Connected to these were two internal unit groups, occupying an intermediate position. And connected to these was a final group of units, occupying the apex of the hierarchy, a position analogous to that of PFC in Fuster's hierarchy.

As explained below, this network was trained on a task that required both immediate input–output mappings and maintenance of context information over time. The question of interest was whether learning would result in the different unit groups serving different computational roles. Specifically, it was asked whether the ‘prefrontal’ group at the apex of the hierarchy would assume a special role in representing context information.

(i) Simulation methods

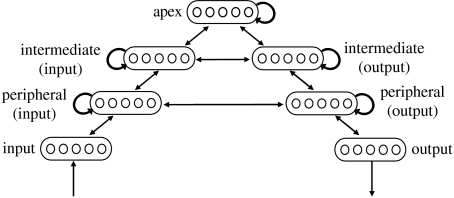
Network architecture The model architecture is diagrammed in figure 6. The input group contained 13 units, the output group 10 units and the remaining groups 15 units. Connections between groups were all-to-all and bidirectional. Each of the three internal groups was also internally connected, again in an all-to-all manner. All units in the network also received input from a bias unit with tonic activation of one.

Figure 6.

A recurrent neural network model based on Fuster's hierarchy. Reproduced with permission from Elsevier.

Units assumed activation values between zero and one, based on their inputs. The net input of each unit was computed as

$${\text{net}}_j(t)=(1-\tau ){\text{net}}_j(t-1)+\tau \sum _i{a}_i(t)w_{ij},$$ (3.1)

where a_i is the activation of unit i, w_ij is the weight of the connection from unit i to unit j, and the time constant τ was set equal to 0.2. Unit activations were based on the logistic function

$$a_j(t)=\frac{1}{1+{\text{e}}^{-{\text{net}}_j(t)}}.$$ (3.2)

External inputs to the input group were modelled by adding a value of either one or zero to the net input of the receiving unit.

Task and representations The task was chosen in order to allow a direct assessment of the degree to which units in the model coded for immediate inputs and outputs versus temporal context information. Specifically, we trained the model on the store-ignore-recall (SIR) task described by O'Reilly & Munakata (2000a). This involves presentation of an extended series of individual Arabic numerals. If the numeral presented is shown in black, the task is simply to read it aloud (‘ignore’ trials). If the numeral is shown in red (‘store’ trials), it is not only to be read aloud, but also to be held in memory until the appearance—following a variable number of intervening numerals—of a recall cue, in response to which the stored number is to be reported (‘recall’ trials). In order to simulate this task, the numerals zero to nine were represented using individual input units. The three remaining input units indicated the trial-type, with one unit indicating a black ‘ignore’ numeral, one indicating a red ‘store’ numeral and one representing the ‘recall’ cue. The output units were identified with the verbal responses ‘zero’ to ‘nine’. Stimulus sequences were randomly generated, except for the constraints that each recall trial was separated from the preceding store trial by between one and four ignore trials, and each store trial was separated from the preceding recall trial by between zero and two ignore trials.

Training Each trial lasted 25 time-steps. On each trial, an input of one was applied to the input units representing the appropriate numeral and the appropriate trial-type cue, and target values were identified for both input and output units (the model was trained not only to produce the correct response, but also to send activation to the input layer consistent with the present input). For output units, targets were one for the correct output and zero for all other units. Target values for input units were one for the correct numeral and cue units and zero otherwise, except on recall trials where no targets were applied to the numeral units. Activations at the beginning of each trial were simply those resulting from the last cycle of processing on the preceding trial. Prior to the first trial of training, all unit activations were set to 0.5.

Weights were initialized to random values between −0.6 and 0.6. Training was then conducted using recurrent back-propagation through time, as detailed in Williams & Zipser (1995), using sum-squared error as the error metric. A target radius of 0.1 was imposed, meaning that no error was incurred for activations within 0.1 of the current target value. A grace period of 10 time-steps was used, i.e. no error was incurred for the first two intervals after a change in input. Error back-propagation covered the interval from the end of each recall trial back to the end of the previous recall trial. The learning rate parameter was set to 0.001.

Response accuracy on each trial was judged by determining whether the target unit in the output group was the most active unit at the end of the trial. In initial simulations, training proceeded until the model produced perfect performance for a series of 10 consecutive recall trials. This criterion was typically reached by approximately 2 million training trials, and this duration of training was used in testing the model.

Testing and analysis Our interest was not so much in the model's overt performance, but rather in the representations underlying it. In particular, we wished to evaluate the degree to which each group of units in the model was involved in representing stored context information, as opposed to representing immediate inputs and outputs. To this end, we recorded the activation of each unit during processing of a set of ignore trials occurring between encode and recall trials. Twenty specific sequences were tested, including S(0)→I(1)→I(x)^* and S(x)→I(1)→I(0)^*, where S(·) indicates a store trial, I(·) an ignore trial, x ranged from 0 to 9, and the asterisk indicates the trial on which unit activations were recorded. Hidden unit activations were recorded on the final time-step of the relevant step. Based on the activations obtained, we evaluated the degree to which each unit's activity varied depending on: (i) the identity of the current ‘ignore’ numeral, and (ii) the identity of the earlier ‘store’ numeral, by measuring its standard deviation across the appropriate subset of trials (S(0)→I(1)→I(x)^* for the former case, S(x)→I(1)→I(0)^* for the latter). Both standard deviations were averaged across units within each unit group, and the mean for the second set of standard deviations was divided by the mean for the first set. The resulting measure, which we refer to as the coding ratio, provided an index of the degree to which units were involved in storing context information. The coding ratio was computed for each unit group, across 10 training runs. The higher the coding ratio, the more strongly the units in the relevant group coded for context information (i.e. the identity of stored items) relative to information about immediate input–output mappings.

(ii) Results

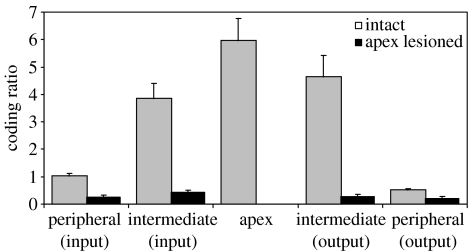
As shown in figure 7, the coding ratio was found to vary rather widely across groups, growing progressively larger with each step up in the architectural hierarchy. The largest coding ratio was observed in the group of units at the top of the hierarchy. Thus, the model developed through learning a regional differentiation of function like the one described by Fuster (1990, 1997, 2001, 2004), with processing structures at higher levels of the hierarchy—and in particular at its apex—coding preferentially for temporal context information. This division of labour was apparent in the behaviour of the model as well. When the units in the apical group were lesioned (i.e. inactivated), the model's performance changed dramatically. Although outputs remained correct on store and ignore trials, response accuracy on recall trials fell to chance levels. Lesioning the apex group also had a dramatic effect on the coding ratio for the groups lower in the hierarchy. As shown in figure 7, coding ratios in all of the remaining groups fell. This change in behaviour and internal representations indicates that the apex group, analogous to the PFC in Fuster's hierarchy, played an important functional role in maintaining information about temporal context and communicating it to lower levels of the hierarchy.

Figure 7.

Coding ratios observed in each unit group of the hierarchical model.

(iii) Discussion

A central point asserted with the BP04 model was that hierarchically structured behaviour need not require a hierarchically structured processing system and that certain aspects of human action can be better accommodated by an account that does not assume strict architectural hierarchy. However, as we have discussed, there is mounting evidence for a relationship between the hierarchical organization of the cerebral cortex and the representation of levels of task structure, with portions of cortex higher in the hierarchy representing successively higher levels of task structure. The present simulation provides an indication of how the computational framework discussed by BP04 can be reconciled with such neuroscientific evidence.

It is important to note that a hierarchical architecture is not required for performance of the SIR task. As shown by O'Reilly & Munakata (2000b), a non-hierarchical recurrent network almost identical in form to the BP04 model can learn to perform the task without error. However, we have shown here that when a hierarchical structure is present, a graded division of labour emerges, according to which unit groups higher in the hierarchy take on a disproportionate role in maintaining information about the temporal context. The resulting mechanism is not the same as that proposed in strict hierarchical models of sequential action, since context information is represented to some degree at all levels of the hierarchy. Instead, despite the presence of a hierarchical structure, the functioning of the network bears a closer relationship to the BP04 model. Indeed, considered as a group, the three upper layers of the present model perform precisely the same function as the hidden layer in the BP04 model.

Perhaps more important than what the model shows about the relationship between the BP04 model and hierarchical accounts is what it suggests about the origins of regional specialization in the cerebral cortex. Specifically, the network suggests a possible causal relationship between cortical connectivity and the regional division of labour increasingly thought to support hierarchically structured behaviour. It is important to emphasize, in this regard, that the division of labour illustrated in figure 7 emerged quite spontaneously as a result of learning. There was nothing in the construction of the model that prevented context information from being handled entirely at lower levels of the hierarchy. The emergence of the division of labour in the model appears to reflect differing pressures on unit groups during learning, as a function of their synaptic distance from the periphery. The groups directly connected to the input and output layers are immediately responsible for generating the correct pattern of activation in those layers, and are thus under pressure to strongly represent the current inputs and outputs. With immediate input–output mappings handled by lower-level groups, groups further from the periphery are freed up to represent context information. Indeed, it makes sense to represent such information away from the periphery, since there are many steps in the task during which context information is irrelevant to response selection.

Despite its simplicity, this simulation reveals an interesting possibility concerning the relationship between the function of the PFC and its connectivity with other parts of the brain. Fuster (1997) stressed, on the one hand, the involvement of the PFC in representing temporal context and, on the other, the position of the PFC at the apex of a hierarchy of cortical areas. Our simulation provides a motivation for the hypothesis that these two aspects of PFC are causally related: the connectivity of the PFC may itself provide part of the explanation for why this brain region comes to assume a role in representing temporal context.

To be sure, there are other distinctive characteristics of the PFC that may contribute to its assumption of this functional role. In particular, the PFC has been proposed to have ion channel properties, recurrent connectivity and a neuromodulatory environment conferring on it a special capacity to store information over time and in the face of distraction (Lisman et al. 1998; O'Reilly et al. 1999; Durstewitz et al. 2000; O'Reilly & Frank 2006). The present simulation introduces another possible explanation for the PFC's special role in context representation and temporal integration, not mutually exclusive with a contribution from these other factors.

Given the important role that learning plays in our theory, it must be asked to what extent the specific kind of learning involved in our simulations might correspond to learning in the brain. Our use of back-propagation, in particular, raises issues, since certain aspects of this learning algorithm have not yet been linked to known biological mechanisms. It is important to note that previous research (e.g. Zipser & Anderson 1988) has demonstrated that back-propagation can give rise to patterns of activity closely resembling those observed in actual neural systems. Indeed, this has been repeatedly shown in studies addressing prefrontal function (Zipser 1991; Zipser et al. 1993; Moody et al. 1998). Furthermore, there do exist biologically plausible learning algorithms operating in a manner very similar to back-propagation and which yield comparable results (Xiaohui & Seung 2003). Nevertheless, back-propagation through time is essentially the only currently available neural-network learning algorithm that is capable of robustly learning to preserve context information over time, and it is this consideration that necessitated the use of back-propagation in the present work. The question of how this problem is solved in the brain is a topic of active research (O'Reilly & Frank 2006; Hazy et al. 2006), and as answers take shape it will be interesting to investigate whether the relevant algorithms give rise to the same relationship between hierarchical connectivity and functional specialization that emerged within the present simulations.

Of interest in this regard are convergent results recently reported by Paine & Tani (2005). This work employed a genetic algorithm to train a hierarchically structured neural network on a task requiring preservation of context information. Consistent with the findings we obtained using back-propagation, Paine & Tani (2005) found that the set of connection weights that evolved in their simulations gave rise to a division of labour across the levels of the network, with higher levels playing a more central role in representing context. The close resemblance between the results obtained by Paine & Tani (2005), using a genetic algorithm, and our own results, using direct gradient-descent learning, suggests that the effect of interest does not depend on idiosyncratic properties of any specific training regime, but may instead show a considerable generality.

(c) Simulation 2: application to naturalistic action

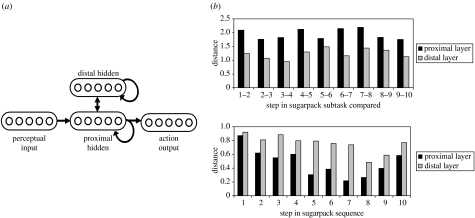
For clarity, simulation 1 addressed a relatively simple laboratory task, rather than the sort of naturalistic action sequences considered by BP04. In order to show how the results of simulation 1 might translate into the latter context, we performed a second simulation, investigating the effect of including a minimal architectural hierarchy in the BP04 model. The procedure was, in most regards, identical to that detailed in Botvinick & Plaut (2004). The only change was that an additional group of units was added to the original BP04 model, as shown in figure 8a. This group connected only to the original hidden layer and was thus at a greater synaptic distance from the periphery (input and output layers) than the latter. As in simulation 1, the question was whether units further from the periphery, i.e. those in this new layer, would assume a special role in representing task context. In order to evaluate this, the model was trained on the coffee and tea tasks, following the procedure used by BP04. Unit activations were then measured in each hidden layer during the performance of the sugarpack subtask. Sensitivity to immediate input–output mappings was measured in terms of the change in each hidden layer's pattern of activation with successive steps in the subtask (figure 8b, top). Sensitivity to task context was measured in terms of the degree to which the pattern of activation on each step of the subtask differed depending on the task context (coffee or tea; figure 8b, bottom). As in simulation 1, the unit group furthest from the periphery was found to code preferentially for context information.

Figure 8.

(a) Reimplementation of the Botvinick & Plaut (2004) model, with a new hidden layer. Each hidden layer contained 25 units. (b) Cartesian distances between pairs of internal representations.

4. Summary and conclusion

A critical question pertaining to human action selection is that of how actions are composed into sequences. The answer to this question turns in large part on the related problem of how temporal or task context is represented. This article has reviewed recent work proposing a computational account of naturalistic, routine sequential action selection. According to this account, implemented in the form of a recurrent neural network, familiar everyday tasks are accomplished by a system that maps from perceptual inputs to motor outputs via internal representations that maintain and integrate information concerning temporal or task context. A distinctive aspect of this account, emphasized in the present paper, is that it does not adopt the traditional assumption that the representations underlying sequential action, and the processing architecture within which they adhere, are strictly and constitutively hierarchical. This confers the advantage that the resulting model can capture stratified sequential structure, while at the same time supporting context-sensitive behaviour and capitalizing on task overlap. However, it also begs the question of how the model relates to neuroscientific data indicating the presence of hierarchical structure in the system of cortical areas supporting routine sequential behaviour. In order to clarify the relationship between the proposed computational framework and this empirical data, the original neural network model was reimplemented so as to incorporate a pattern of connectivity based on the neuroanatomic hierarchy described by Fuster. When the model was trained on a task that required it both to accomplish immediate input–output mappings and to maintain context information over time, it spontaneously developed a graded division of labour over its internal unit-groups, with groups further from periphery taking a larger role in context representation. The simulation results indicated how the original computational framework can be reconciled with the presence of a hierarchical arrangement of cortical regions, by showing how a regional division of labour might coexist with the same sorts of graded, distributed representations that defined the original computational model. Perhaps more important was the finding that this regional division of labour arose spontaneously as a result of learning within a hierarchically structured system. In view of this, the simulation results presented here provide a possible account for how different levels of temporal structure in behaviour may come to be represented at different levels within the hierarchy of cortical areas, and in particular how the PFC comes to assume its distinctive role in the representation of temporal or task context.

Given our initial assertion that such a spatial division of labour is not computationally necessary for the emergence of hierarchically structured behaviour, the question arises whether there might nonetheless be some advantage associated with it, which might have favoured its evolution. One possibility is that a hierarchical pattern of connectivity may facilitate learning of tasks with multiple levels of structure. Consistent with this, in their work using a genetic algorithm, Paine & Tani (2005) found that a hierarchically structured network learned to perform a multilevel task more efficiently than did a fully connected (i.e. non-hierarchical) network. Another possible advantage of a spatial division of labour relates to the top-down control of behaviour. Many theories of action selection assume that executive systems (Norman & Shallice 1986; Miller & Cohen 2001) and/or motivational systems (Tyrrell 1993; Joel & Weiner 1994; Redgrave et al. 1999; Haber et al. 2000; Cooper & Shallice 2006) provide top-down input to action-selection mechanisms. Logically speaking, such input is likely to be more relevant to action selection at relatively high levels of the task hierarchy, and this is indeed where it is imposed in most theories. To the extent that higher levels of the task hierarchy are represented in a spatially segregated manner, this may allow for more targeted input from executive and motivational systems (for related comments, see Cooper & Shallice 2006). Finally, a graded segregation of context information from lower-level codes may allow targeted input from neuromodulatory systems, in particular the dopaminergic system, which, as noted earlier, has been proposed to regulate the storage and release of action-relevant context information.