Spatial models of political competition with endogenous political parties

Abstract

Two important human action selection processes are the choice by citizens of parties to support in elections and the choice by party leaders of policy ‘packages’ offered to citizens in order to attract this support. Having reviewed approaches analysing these choices and the reasons for doing this using the methodology of agent-based modelling, we extend a recent agent-based model of party competition to treat the number and identity of political parties as an output of, rather than an input to, the process of party competition. Party birth is modelled as an endogenous change of agent type from citizen to party leader, which requires describing citizen dissatisfaction with the history of the system. Endogenous birth and death of parties transforms into a dynamic system even in an environment where all agents have otherwise non-responsive adaptive rules. A key parameter is the survival threshold, with lower thresholds leaving citizens on average less dissatisfied. Paradoxically, the adaptive rule most successful for party leaders in winning votes makes citizens on average less happy than under other policy-selection rules.

1. ‘Spatial’ models of political competition

Most people who analyse politics talk sooner or later about the positions of political actors, whether these are citizens, voters, politicians or behind-the-scenes éminences grises. It is hard to have a serious discussion about the substance of real politics without referring to where the key actors stand on important matters. Position implies distance (between two positions); distance implies movement; movement involves direction; movement can only be described relative to some benchmark. Indeed, it is difficult to analyse real political competition without using positional language and reasoning, which is why spatial models of political competition are among the ‘workhorse’ models of political science (Cox 2001).

Such spatial models typically involve two types of agents: citizens and politicians. Citizens have policy preferences; politicians compete for citizens' support by offering policy packages at elections. Citizen preferences are typically assumed to be single-peaked over the set of potential policy packages. This implies an ideal point for each citizen, characterizing his/her most-preferred policy package in a given choice setting and describing increasingly less-preferred policies as points in some cognitive space that are increasingly far from this ideal. Although this is not a logical necessity, spatial models of party competition almost always take the set of citizen ideal points as exogenously given and mapped into a common space. The basis vectors of real-world political spaces are typically interpreted in terms of policy dimensions such as: economic left–right; social liberal–conservative; foreign policy hawk–dove; and so on. Each citizen is typically assumed to support the politician offering the policy package closest to his/her ideal point. More complex models can be specified, involving strategic behaviours by citizens that do not always imply supporting the closest party, but these involve specifying and solving a model of post-electoral policy implementation and we do not consider these here (see Austen-Smith & Banks (2005) for a discussion). Each politician is assumed to be concerned with maximizing political support. The action selection problem for citizens is to support one of the policy packages on offer; the action selection problem for politicians is to offer a policy package that maximizes citizen support, subject to certain constraints. Hinich & Munger (1994, 1997) provide an accessible introduction to spatial models of party competition. Austen-Smith & Banks (2000, 2005) provide a comprehensive technical overview.

Most mainstream spatial models of party competition are static; key model parameters and rules of interaction are fixed exogenously; the core intellectual mission is to specify a model and solve analytically for equilibrium. Most informed observers of politics, however, see party competition as a system in continual motion and as a system with an endogenous dynamic: what agents do at tick t of the political process feeds back to affect the entire process at tick t+1. These observations characterize political competition as an evolving complex system. Recent work in political science has analysed this dynamic characterization using the techniques of agent-based modelling (ABM; Kollman et al. 1992, 1998, 2003a; De Marchi 1999, 2003; Fowler 2005; Fowler & Smirnov 2005; Laver 2005). A key feature of this work is that the number of political parties competing for votes is fixed exogenously. The innovation in this paper is a dynamic spatial model of political competition in which the number and identity of competing parties is an endogenous output of the model, not an exogenous input to it. We achieve this by modelling the birth and death of political parties.

In §2, we consider arguments for deploying ABM in this setting and review current agent-based models of party competition. In §3, we specify an agent-based model of party competition that comprehends the birth of new parties and the death of existing ones. In §4, we report results from the systematic interrogation of this model. In §5, we set out an agenda for future research on this problem.

2. Agent-based spatial models of party competition

(a) The shift from formal analytical models to agent-based computational models

Although this is still not fully articulated in the literature, there are several reasons to shift methodologies from the analytical game theoretic approach that underpins the traditional static spatial model to the systematic interrogation of computer simulations using dynamic ABM. The first reason concerns the analytical intractability of complex dynamic spatial models. Such intractability is significant if we assume a dynamic system of several parties competing in a multi-dimensional space; it becomes catastrophic when we add endogenous parties to the mix. Using ABMs allows us to build tractable models of multi-party competition as an evolving complex system.

The second reason for the shift to ABMs involves a reassessment, given the complexity of the decision-making environment sketched above, of plausible behavioural assumptions about agent rationality. Classical game theory tends to assume hyper-rational agents engaged in deep strategic look-forward; equilibrium strategy sets take account of every possible future choice that might be made by every agent. When agents are faced with potentially bewildering complexity in the decision-making environment, an alternative behavioural assumption might be more appropriate, stressing adaptive learning rather than deep strategic look-forward. On this account, a shift to ABM reflects this shift of behavioural assumption and the adoption of a methodology more suitable to modelling this. This leads to a third reason for the shift to ABM, which concerns the amount and quality of information available to decision-makers. Information requirements for many analytical spatial models are extremely high; many models, for example, assume all politicians know the ideal points of all citizens. If we assume a much lower-information world, adaptive learning models, implemented using ABM, might seem to offer a more empirically plausible description of how political agents select actions.

Thus, the potential shift in methodology from analytical game theory to ABM in modelling party competition involves changing several aspects of how party competition is characterized by the analyst—from a high-information static environment populated by forward-looking strategic agents to a low-information dynamic environment populated by backward-looking adaptive agents. The shift is thus not just a change in method, but a change in the entire characterization of political competition.

(b) Agent-based models of party competition with an exogenously fixed set of parties

The emerging literature on agent-based dynamic models of party competition can be traced to an influential early paper by Kollman et al. (1992), hereafter KMP, who developed an ABM of two-party, incumbent–challenger, competition in a multi-dimensional policy space that stimulated a programme of subsequent work. This work typically retains a US-oriented focus on two-party incumbent–challenger competition (Kollman et al. 1998; De Marchi 1999, 2003). The underlying spatial characterization of policy preferences is the same as in static spatial models, although computational implementations assume agents to occupy one of a small number of discrete positions on a finite set of issue dimensions. These authors follow the traditional spatial model in assuming voters to be both policy-motivated and well-informed about published party policy positions, and to support the party position that maximizes their utility. However, they depart from traditional static models in assuming that party leaders are not perfectly informed, either about the preferences of every single voter or about the uncertainties associated with these. Instead, party leaders are assumed to gather information, using private opinion poll and/or focus group feedback, on the impact of counterfactual policy moves on their electoral support levels, to select policy positions.

KMP propose and investigate three search algorithms for party leaders. A ‘random adaptive party’ generates a random set of counterfactual policy positions in the neighbourhood of its current position and uses private polling to select the alternative, attracting most support. A ‘climbing adaptive party’ envisages a systematic sequence of small counterfactual changes to its position, selecting any change that increases its support and iterating this process. A ‘genetic adaptive party’ uses a version of the genetic algorithm. Its policy package is described by a vector of p possible policy positions on d issue dimensions and treated as equivalent to its ‘policy DNA’. A finite set of counterfactual policy vectors is generated and subjected to the genetic operators of reproduction, crossover and mutation, with the resulting evolved positions selected if they increase party support—again measuring this using private polling. The key feature of the KMP results replicates a fundamental result of the analytical spatial model in that, regardless of search algorithm (Kollman et al. 1992) and the spatial distribution of voter ideal points (Kollman et al. 1998), the two party platforms systematically converge over a series of elections to positions that are centrist yet distinct. More ‘rugged,’ less smooth, profiles of voter preferences slow down party convergence towards the centre but do not change the strong tendency for this to happen.

The KMP action selection rules for party leaders look much less plausible when political competition is extended from a two- to a multi-party setting. Thus, Kollman et al. (2003b) deal with up to seven parties. In this context, the counterfactual question posed by each party in each round of private opinion polling must take the form: ‘assume all six other parties retain their current policy packages; assume we move our own policy package from x to x±ϵ; which party would you then support?’ A battery of similar questions, generating systematic sweeps of ϵ, must be asked by each party at each cycle of adaptation to select the best action in a given position. Laver (2005) argued this is a complicated and unrealistic assumption about how parties gather information, in addition to violating every professional canon on the type of question that can validly be posed in an opinion survey. The alternative model proposed by Laver (2005) defines behavioural rules for the selection of future party policy positions that do not involve complex counterfactual polling. In each of these, party leaders make use, when they select future actions, of freely available information about the history of the system. These action selection rules require no more, and often much less, information than the published policy positions of all parties, plus the levels of support these parties received, during the previous two cycles of competition. As with the traditional static spatial model, Laver assumes that citizen ideal points are located in a real policy space, with citizens supporting the party with the closest policy position to their ideal point. Following a random ‘cold start’ of the system, which is of course a model artefact, party policy positions and citizens' party support patterns evolve continuously in the forever loop described in figure 1. The citizens choose to support the closest party position; party leaders choose a policy position according to the profile of citizen support levels, using one of a number of adaptive rules. This process iterates continuously.

Figure 1.

Underlying dynamics of party competition.

The adaptive rules defined and investigated by Laver were as follows:

1. Sticker: never change position (an ‘ideological’ party leader).

2. Aggregator: set party policy on each dimension at the mean preference of all party supporters (a ‘democratic’ party leader).

3. Hunter: if the last policy move increased support, make the same move; else, reverse heading and make a unit move in a heading chosen randomly from the arc ±90° from the direction now being faced (an autocratic party leader who is a Pavlovian vote-forager).

4. Predator: identify largest party; if this is you, stand still; else, move towards largest party (an autocratic party leader who seeks votes by attacking larger parties).

Programming this system as an ABM, Laver investigated the effects of different adaptive rules on party system evolution. The most striking findings relate to the hunter rule, which significantly outperformed all other rules when it came to vote maximization. Hunters typically beat predators in the competition for votes and, less surprisingly, out-perform stickers and aggregators. Despite the fact that a predator is programmed to become the largest party, it is typically the smallest party in competition with a set of hunters. Hunters tend to go towards the centre of the policy space but not to the dead centre, where they tend to get attacked by other hunters responding to the resulting loss of votes by moving away from the centre. The other striking finding was that all aggregator systems quickly reach a steady state in which all parties have stable positions and support levels. Such steady states are easy to perturb, however, and are not robust to small random shocks to the ideal points of citizens. A final striking finding was that, in a system with both hunters and stickers, the hunters tend strongly to win more support than stickers at the same position in the policy space. This is because a sticker is occupying this position by applying an unconditional and non-responsive adaptive rule, while a hunter finds the same position as a result of being rewarded with higher support, given the configuration of other parties in the system.

Laver (2005) set out to fit this theoretical ABM of dynamic party competition to empirical opinion poll data on changing levels of party support in a real party system. Taking a period (1986–1997) of Irish politics when the number of political parties remained constant at five, and using independent empirical estimates of voter policy positions and the ‘starting’ policy positions of the political parties at the beginning of the period, the ABM was used to retrieve observed levels and variations in party support. The key parameter set in the model is the vector of adaptive rules used by each party. As a first pass, parties' adaptive rules were inferred from their public pronouncements. Two parties (Fianna Fáil and Fine Gael) characterize themselves as ‘parties of government’ and were designated as hunters; three parties (Labour, Democratic Left and the Progressive Democrats) describe themselves as ‘policy-driven’ and were designated as ideological stickers. A suite of simulations came close to retrieving the key observables using these behavioural assumptions about the parties. However, a sweep of all possible rule combinations revealed some substantively plausible combinations that generated voter support levels that better fit observed opinion poll series than results derived from the parties' declared strategies, potentially revealing information about what might be inferred to be parties' actual decision rules.

Overall, therefore, ABMs of dynamic party competition have replicated key findings of the canonical analytical static spatial model of party competition (notably a tendency of parties to converge on the centre of the policy space) and supplemented these with explanations of other systematically observed tendencies that are far more problematic for static models (notably a tendency for vote-seeking parties not to go to the dead centre of the policy space). In addition, the dynamic models offer the possibility of explaining times series features of party support that static models, more or less by definition, are unable to address, but which are nonetheless important aspects of the ways in which informed observers describe the process of party competition. This is clearly a promising start.

3. Modelling the birth and death of political parties

The models of party competition discussed above involve an important and unrealistic restriction; the set of political parties is fixed exogenously (in effect by nature). The distinction between static and dynamic models of party competition has particular significance, however, once we treat the set of political parties as an endogenous output of political competition, not an exogenous input to this. Dynamic models are obviously suited to describing the evolution of the set of competing parties as an intrinsic feature of the process of competition itself.

(a) ‘Static’ models of party ‘entry’

The possibility of new political parties has not been ignored by scholars developing static spatial models using traditional analytical methods. There is growing body of literature that sets out to extend the classical spatial model by treating the identity and number of parties as endogenous, analysing the comparative statics of actual or anticipated entry by new parties into an existing party configuration. Key features of the burgeoning literature on party entry and endogenous political parties are reviewed by Shepsle (1991); more recent writing, mostly by economists, is discussed by Dhillon (2005) and Austen-Smith & Banks (2005). The arguments put forward are surprisingly heterogeneous although one common thread is striking. Rigorous theoretical discussions of party systems with an endogenous number of political parties all analyse the entry and/or ‘exit’ of political parties as unitary actors. Thus, splits and fusions within the existing set of parties, which in the real world may be seen as quite frequent sources of change in the party system, tend not to be analysed (for an exception, see Laver & Benoit 2003). To a large extent, this flows from the lack within political science of any extensive body of work on rigorous analytical models of intra-party political bargaining in multi-party systems—an essential analytical precursor to modelling the logic of party splits and fusions.

Some scholars analysing party formation/entry have focused on the incentives for individual policy-motivated citizens to run as ‘citizen candidates’ (Osborne & Slivinski 1996; Besley & Coate 1997). This leads to a consideration of incentives for the citizen candidates to band together into parties, seen in effect as political clubs. These include: the value of a party ‘brand’ in signalling policy positions to voters (Snyder & Ting 2002); the value of a mechanism for politicians to commit to positions other than their ideal points when offering policy positions to voters (Levy 2004; Morelli 2004); and economies of scale in campaign costs (Osborne & Tourky 2004). Morelli extends the analysis beyond first-past-the-post to proportional representation electoral systems (Morelli 2004). Dealing explicitly with the entry into electoral competition by candidates rather than parties, Osborne modelled candidates who take up positions on a single policy dimension to deter entry of others into the competition (Osborne 1993, 2000).

This topic creates ferocious challenges for those working in the classical analytical tradition. One widely cited piece on candidate entry, for example, assumes an exogenously determined number of potential candidates, typically three, and a single dimension of policy. At the end of a heavy-duty analytical discussion, the substantive conclusion is that one candidate enters the race at the median of the voter distribution and no other candidate enters (Osborne 1993). When there are more than three potential candidates, the results of the model are, according to its author, ‘limited’. In another example, the setting is a legislature with three members who are assumed to form political parties to maximize expectations combining one-dimensional policy and some distributive private pay-off. Analysis of this model results in the conclusion that a majority party (i.e. the party with two legislators) will always form. Extending the approach to deal with legislatures with more than three members is acknowledged as presenting fundamental modelling issues that are not resolved (Jackson & Moselle 2002). Given the thinness and lack of generalizability of these results, it seems it is time to establish alternative lines of intellectual attack on this important problem.

Here, we extend Laver's (2005) ABM of dynamic party competition to a setting in which the identity and number of parties is endogenous to the process of political competition. New parties are ‘born’ as a result of this process; existing parties ‘die’. We model party birth as an endogenous change of agent type, from citizen to party leader, arising from dissatisfaction of an individual citizen with the existing offer of party policy positions. In this sense, our model can be seen as a dynamic ABM implementation of the intuitions of the ‘citizen candidate’ approach (Osborne & Slivinski 1996; Besley & Coate 1997). We leave for future work the development of a more explicit model of intra-party politics that could in turn form the basis of a dynamic model of party splits and fusions, thereby grounding a more comprehensive analysis of party systems with endogenous parties.

(b) Citizen dissatisfaction

To allow us to compare our work with static spatial models of party competition, we begin by modelling citizen dissatisfaction using the classic assumption about party choice used by these models. This is based on the Euclidean distance between the citizen ideal point and some characterization of the configuration of policy positions offered by party leaders. The first big question is thus to characterize the particular configuration of the party system that citizens are assumed to evaluate when becoming satisfied or dissatisfied.

The original spatial model (Downs 1957) and its direct intellectual descendents involve a description of ‘proximity’ voting by citizens. Each citizen is assumed to support the closest party, and to be more dissatisfied, the more distant this closest party. This assumes non-strategic behaviour by citizens who make no attempt, when they select a party to support at election time to anticipate the consequences of this for long-term post-electoral policy implementation. To do otherwise, citizens need a model of post-electoral politics and must then reason backwards from this when they choose how to vote. This may seem straightforward in settings, typically with a first-past-the-post electoral system, where one single party typically wins a legislative majority. The largest party ‘wins’ the election and can be assumed to form a government and implement its policy position; in this case all citizens have to forecast which party will win the election. However, strategic voting generates much deeper and more intractable problems in the far more common settings where there is a multi-party system and no single party wins a majority. Models assuming that citizens do all of this have certainly been proposed (Austen-Smith & Banks 1988; Kedar 2005). But they are analytically very complicated, posit extraordinarily high levels of citizen rationality and instrumental behaviour, and generate results that do not generalize further than three parties and one policy dimension. Since, as we have seen, the attraction of building ABMs of party competition is that we do not have to assume hyper-rational and perfectly informed citizens engaging in deep strategic look forward, in what follows, we assume citizens do not engage in complex forward calculations to anticipate the outcomes of future coalition bargaining and eventual policy implementation, but instead vote ‘non-strategically’ for the closest party.

We thus describe the level of a citizen C's dissatisfaction, D_c, during the current tick of the political process in terms of the distance between C's ideal point and the closest party policy position on offer. In this sense, we are modelling citizen dissatisfaction with the set of policies on offer at election time, as opposed to one of the many other possible sources of citizen dissatisfaction. An obvious alternative would be to measure citizens' dissatisfaction with the current, or some anticipated, government. However, this would require us to expand the model dramatically to generate a government with an agreed policy point from any given election result, as we have just seen, this would be a difficult and controversial extension of the model and we do not attempt it here. Thus, if the distance between C's ideal point and the position of Party P at tick t is δ_cpt, then C's dissatisfaction is D_ct=min_p(δ_cpt). The most basic measure of C's dissatisfaction with the party system at tick t of the political process is simply the distance of the closest party from C's ideal point at tick t.

(c) Updating citizen dissatisfaction

It seems substantively implausible in a dynamic setting, however, to assume that action selection by citizens (in this case party support) responds only to the current instantaneous state of the system. While this is never made explicit in existing accounts of party competition, it seems more plausible to treat citizens as using their observations of the system at tick t to update rather than completely determine their evaluations of the party system. In what follows, therefore, we propose a very simple updating model in equation (3.1), making a distinction between the instantaneous dissatisfaction of citizen C at tick t, D_ct and C's updated overall dissatisfaction with the history of the system, as of tick t, $D_{ct}^{*}$. We describe $D_{ct}^{*}$ in the following recursive fashion:

$$D_{ct}^{*}=D_{ct}+\alpha ·D_{c(t-1)}^{*}:0\le \alpha <1.$$ (3.1)

This type of update is analogous in some ways to updates modelled in the extensive literature on reinforcement learning, to which Sutton & Barto (1998) provide an excellent introduction. If α=0, then the updated citizen dissatisfaction reduces to D_ct, instantaneous dissatisfaction at tick t. As α approaches unity, then instantaneous dissatisfaction at tick t adds little to overall dissatisfaction, which is mainly affected by the past history of the system. If α=0.5, for example, then only one per cent of updated dissatisfaction contains information about states of the world earlier than t−6, and only 0.1 per cent contains information about states earlier that t−9, although a small amount of information about all previous states of the world remains impounded in current dissatisfaction.

(d) Updated citizen dissatisfaction and party switching

Existing dynamic models of party competition assume citizen C switches party support at the instant when some other party moves closer to his/her ideal point than the party currently supported, opening the possibility of ‘dithering’ when a citizen is almost equidistant from two parties. Once we move away from an instantaneous to an updated account of citizens' evaluations of the party system, however, we must reconsider the assumption of instantaneously responsive party-switching. Applying the model set out above, C's updated dissatisfaction with party P at tick t, ${\delta }_{cpt}^{*}$ (as opposed to dissatisfaction with the party system as a whole, $D_{ct}^{*}$) is given by equation (3.2).

$${\delta }_{cpt}^{*}={\delta }_{cpt}+\alpha ·{\delta }_{cp(t-1)}^{*}:0\le \alpha <1.$$ (3.2)

A ‘retrospective’ voter in this setting would always support the party minimizing ${\delta }_{cpt}^{*}$, updated dissatisfaction with each party. If α=0, then we model hyper-reactive citizens who always instantly switch to the closest party. This in effect is the answer adopted by existing dynamic models—the answer to a question that static models cannot comprehend. The larger is α, (the less the citizen discounts the past history of the system), the more ticks of the system for which a ‘new’ closest party must remain closest to C, other things being equal, before C switches parties. In other words, if α is relatively high, vote-switching by citizens will be ‘sticky’, with some citizens continuing to support the same party for some time after it has ceased to be the closest.

(e) Mean citizen dissatisfaction as a system output

Having defined citizen dissatisfaction at tick t in both an instantaneous (D_ct) and an updated ($D_{ct}^{*}$) form, both the mean and the variance of dissatisfaction across all citizens are of considerable substantive interest. Mean dissatisfaction measures the extent to which the set party positions on offer at election time reflects the ideal points of all citizens. Thus, the mean citizen dissatisfaction with the electoral offer will be zero when there is a party at the position of every citizen ideal point. Of course, given the threshold effects we discuss in the following section, there will never be one party per citizen in practice, but this nonetheless represents the theoretical limit of mean citizen dissatisfaction with the electoral offer. This is only one possible measure of citizen dissatisfaction, assuming non-strategic voters who do not try to anticipate both the government formation process and downstream policy implementation. For reasons we have already discussed, we do not deal here with more strategic citizens since we regard the required behavioural assumptions as substantively implausible in multi-party systems. The s.d. of $D_{ct}^{*}$ across all citizens is a measure of the level of inequality with which the party system reflects the ideal points of citizens. Neither of these substantively interesting measures is generated by those analysing traditional spatial models of party competition. Both are intractable to calculate analytically for an arbitrary configuration of citizen ideal points and party policy positions; both are trivial to calculate within a computational model and provide intuitively appealing measures of the output of any party system.

(f) De facto survival thresholds for political parties

If we treat the number and identity of political parties in the system as endogenous, we are forced to think about ‘threshold’ support levels—below which parties cannot survive or be born. While plausible in common sense terms and by analogy with biological systems, party survival thresholds raise surprisingly complicated issues.

Explicit and implicit vote thresholds for party representation in the legislature are embedded in all electoral systems, arising from the interaction of electoral formulae, constituency size and constituency-level concentrations of party support (Cox 1997), as well as matters such as campaign finance laws, the public funding of political parties, and so on. It is clear that many political parties continue to survive, however, even when they fall far below representational thresholds. One answer to this puzzle can be found in spatial models of party competition that include a ‘valence’ term (Ansolabehere & Snyder 2000; Adams 2001; Groseclose 2001; Aragones & Palfrey 2002; Schofield 2003; Aragones & Palfrey 2004; Schofield 2004, 2005). Valence captures ‘candidate quality’ viewed in a very general sense. It bundles together all non-policy candidate characteristics that enhance appeal to voters, which might include evaluations of the likely efficacy of prospective office-holders, their media profile and many other things besides. The crucial theoretical result in the present context, supported by some experimental evidence (Aragones & Palfrey 2004) is that, if two candidates take identical or very similar policy positions, the higher valence candidate wins all the votes that are available. Here, therefore, we propose a rule of thumb: parties that fall below a certain size threshold, T_s, measured as a percentage of the total vote, for T_t system ticks, have zero valence and are unable to win votes in policy competition with parties having non-zero valence. Such parties are ‘below the radar’ of mainstream party competition. They exist in some senses of the word, but in another sense they are the walking dead of insufficient consequence to affect action selection by other parties. Parties that sink below this threshold in effect die as far as mainstream party competition is concerned.

Turning to party birth, and assuming a citizen who considers forming a new party does not want to form a party that will operate below the radar of mainstream party competition, we apply the same threshold logic to party birth. A citizen contemplating forming a new party will not do so unless it would have achieved the threshold size, T_s, for the threshold number of ticks, T_t. (Note that, if birth and death thresholds are not set at the same level, the system will experience a secular growth, or decline, in the number of parties.) As we shall see the de facto survival threshold, T_s is one of the most important parameters in the model and the remainder of this paper is to a large extent concerned with analysing the impact of survival thresholds on party system configurations.

(g) The birth of political parties

So far, we have been regarding cumulative citizen dissatisfaction as an output from a dynamic model of party competition; we now treat it as feedback into the model. Our assumption about party birth is that, the more dissatisfied a citizen, the more likely he/she is to create a new party by changing type to party leader. (Recall that analyses of other types of change to the configuration of parties, arising from fission and fusion of existing parties, await future work that will require the specification of a model of intra-party bargaining.) Specifically, we assume every citizen always has the implicit option of forming a new party by changing type from citizen to party leader. For citizen C, the probability of doing this is p_c, where p_c is some function of updated dissatisfaction, $D_{ct}^{*}$, whereby relatively more dissatisfied citizens are more likely to become citizen candidates. Here, we assume that the probability C will form a new party increase in direct proportion to C's dissatisfaction relative to other citizens. Thus,

$$p_c=\frac{\beta ·D_{ct}^{*}}{\text{mean}\left(D_{ct}^{*}\right)}.$$

(We use the ratio $D_{ct}^{*}/\text{mean}(D_{ct}^{*})$ as opposed to the absolute value of $D_{ct}^{*}$, to remove any dependence of our results on the arbitrary units in which it is expressed, which would otherwise inflate over time, and to emphasize that it is citizens' relative dissatisfaction that affects their relative likelihood to form new parties.) Substantively, β describes the sensitivity of the probability that C will form a new party to his/her relative dissatisfaction with the system.

4. Analysing the birth and death of political parties

The model set of above was programmed as an ABM, using the Python implementation of the Repast modelling environment, and interrogated using suites of systematic simulation experiments. Before activating the birth and death of political parties in these experiments, we used Monte Carlo simulations to benchmark the impact of model parameters on our measures of system output. This benchmarking exercise is described and reported in the electronic supplementary material to this paper. We have already noted that one crucial system output is mean citizen dissatisfaction with the configuration of party positions. We characterize this configuration in terms of the ‘policy eccentricity’ of each party, defined as its Euclidean distance, measured in s.d. of the distribution of supporter ideal points, from the mean of the distribution of citizen ideal points. The headline result from these benchmarking runs that will aid the interpretation of subsequent findings is that mean citizen dissatisfaction with the party positions on offer tends to be lowest when these party positions are on average located 1.5 s.d. units from the centre of the voter distribution—in other words when party policy positions are quite decentralized.

(a) The impact of survival thresholds on birth-adapted party systems: citizen dissatisfaction

Our simulations of ‘birth-adapted’ party systems were designed to explore the impact of party survival thresholds T_s on: the number of parties in the system; mean citizen dissatisfaction; the spatial locations where new parties are born; and the mean policy eccentricity of all parties. Each experiment involved ten 2000-tick runs, for each parameter setting for each rule. Each run was initialized with a random-normal configuration of citizen ideal points and five parties with random policy positions, and each suite of experiments stepped through values of T_s, setting α at 0.5, β at 0.0001 and T_t at 10 ticks.

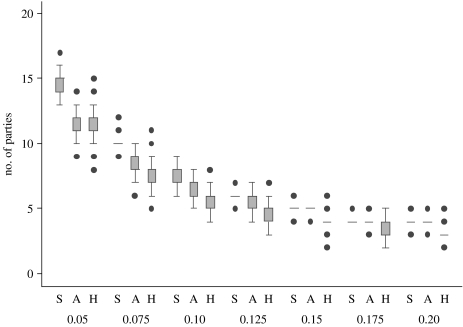
Figure 2 presents a box plot showing the impact of survival thresholds on the number of parties in the system, for each adaptive rule, for ‘ticks’ 1001–2000 of the 10 simulations for each rule and threshold—i.e. after any impact of the random cold start had burnt off and the simulated party system had reached a ‘mature’ state. Regardless of decision rule and survival threshold, the numbers of parties in the system had reached its ergodic state, and artificial start-up effects had ‘burnt off’, long before the half-way point in these 2000-tick runs (figures A2–A4 in the electronic supplementary material). For each survival threshold, the figure shows the distributions of the number of parties observed during the simulation experiments under each adaptive rule and survival threshold. The boxes in the centre of each distribution represent its inter-quartile range, with the lines above and below each box extending 1.5 times the inter-quartile range above and below this. Dots are outliers. Some ‘boxes’ in this and subsequent figures have no extension—reflecting a distribution of observations that is very tightly clustered around the median value. Parametric statistics (means plus associated standard errors and confidence intervals) for the distributions in figure 2 can be found in table A3 in the electronic supplementary material and show that each of the patterns we draw attention to here is statistically significant at the p<0.05 level at the very least, and typically at a very much higher level than that. Thus, the results in figure 2, summarizing data from 210 000 simulation ticks in all, represent a statistically reliable estimate of the ergodic number of parties for each combination of party decision rule and survival threshold. Figure 2 (confirmed by table A3 in electronic supplementary material) shows that, if the survival threshold is 0.20 (20%) of the vote, this tends to result in 3- or 4-party systems. A 15% threshold tends to result in a 4- or 5-party system, the 10% threshold in 6- or 7- party systems, the 7.5% threshold in 8–10-party systems and the 5% threshold in systems with 12–15 parties. This gives us a sense, for example, that real party systems with six or seven parties must have a de facto survival threshold, however, this might be realized in practice, of approximately 10 per cent.

Figure 2.

Birth-adapted numbers of parties (vertical axis) by survival threshold (lower horizontal axis label) and adaptive rule(upper horizontal axis label: S, sticker; A, aggregator; H, hunter); simulation tick greater than 1000.

The same basic pattern can be observed for all adaptive rules, though we expect party systems with parties using decision rules that themselves adapt to the system state to have systematically fewer parties, since they are less likely than parties with random locations to leave pools of dissatisfied citizens. This is what we observe. Especially at low levels of the de facto survival threshold, systems with hunters and aggregators tend to have fewer parties for any given survival threshold. With the exception of the 5% threshold, furthermore, all-hunter systems tend to sustain fewer parties than either of the other two rules.

Figure 3 shows the impact of survival thresholds on mean citizen dissatisfaction. (Statistics for this figure can be found in table A4. Figures A5–A7 in the electronic supplementary material confirm that mean citizen dissatisfaction has reached its ergodic state long before the 1000-cycle ‘burn in’ from a random start was over). Citizens in birth-adapted systems tend to be almost equally dissatisfied with stickers and aggregators, with a clear tendency to become more dissatisfied with aggregators than with stickers as survival thresholds decrease. Mean citizen dissatisfaction is significantly higher, as well as significantly more variable, in all-hunter systems, for all survival thresholds. For all decision rules, the strong pattern is for citizen dissatisfaction to increase as the survival threshold increases—higher survival thresholds imply fewer parties and thus a smaller chance, other things being equal, that a citizen finds a party close to his/her ideal point.

Figure 3.

Birth-adapted citizen dissatisfaction, measured in s.d. of the distribution of citizen ideal points (vertical axis), by survival threshold (lower horizontal axis label) and adaptive rule (upper horizontal axis label: S, sticker; A, aggregator; H, hunter); simulation tick greater than 1000.

The impact of party decision rules on citizen dissatisfaction can also be explained by the spatial locations typically occupied by birth-adapted parties, summarized in figure 4 and table A5. Hunters tend to locate much closer to the centre of the policy space (their policy eccentricity is lower) replicating in a more general context the pattern found by Laver (2005). Stickers tend to be found in more eccentric locations, and aggregators in more eccentric locations still. Thus, at all thresholds, birth-adapted hunters are tending to search for votes much ‘too close’ to the centre to minimize the mean dissatisfaction of all citizens. (Recall that we know, from the benchmarking runs summarized in figure A1 that citizen dissatisfaction tends to be minimized when parties tend to locate at approximately 1.5 s.d. units from the centre of the space). Although birth-adapted aggregators and sticker systems have similar effects on mean citizen dissatisfaction, stickers locate a little too close to the centre, and aggregators a little too far from the centre, to minimize mean citizen distances from the closest party.

Figure 4.

Birth-adapted party eccentricity measured in s.d. of the distribution of citizen ideal points (vertical axis), by survival threshold (lower horizontal axis label) and adaptive rule (upper horizontal axis label: S, sticker; A, aggregator; H, hunter); simulation tick greater than 1000.

Table 1 shows that enabling party birth and death can in some, but by no means all, circumstances make citizens more satisfied than they are in systems in which the number and identity of parties is fixed exogenously. To see this, since there is no survival threshold for the benchmark party systems with no birth and death, we must select birth-adapted systems with a given number of parties and compare citizen dissatisfaction in these with that in benchmark systems with the same decision rule and number of parties. Table 1 gives us a clear sense of the systematic effect of enabling party birth and death. Look first at all-sticker systems and compare birth-enabled systems with the static benchmark for systems with the same number of parties. Enabling sticker birth and death significantly reduces mean citizen dissatisfaction in a system for any given number of parties. This is because, while stickers never change policy position, the citizen–candidate dynamic means that sticker parties tend to die in areas where there are fewer citizen ideal points and to be born in areas where there are more. The pattern is quite different in all-aggregator and all-hunter systems, where we see no effective difference between the static benchmark and birth-adapted systems for any given number of parties. The reason is straightforward—while new hunter or aggregator births may occur at particular points in the policy space, the set of party positions as a whole quickly adapts away from this, so the impact of adding a new party at a particular policy location is quickly dissipated.

Table 1.

Birth-adapted means of mean citizen distances from closest party, by number of parties, by adaptive rule (tick>1000).

no. of parties	sticker				aggregator				hunter
	benchmark		birth-adapted		benchmark		birth-adapted		benchmark		birth-adapted
	mean	s.e.	mean	s.e.	mean	s.e.	mean	s.e.	mean	s.e.	mean	s.e.
3	1.70	0.009	1.35	0.0003	1.28	0.002	1.27	0.0008	1.57	0.002	1.53	0.0009
4	1.49	0.006	1.21	0.0003	1.14	0.002	1.14	0.0001	1.39	0.002	1.35	0.0007
5	1.36	0.005	1.09	0.0003	1.04	0.002	1.03	0.0002	1.25	0.001	1.22	0.0007
6	1.25	0.005	1.02	0.0002	0.96	0.002	0.96	0.0002	1.15	0.001	1.13	0.0007
7	1.17	0.004	0.93	0.0003	0.90	0.001	0.90	0.0002	1.07	0.001	1.06	0.0008
8	1.10	0.003	0.90	0.0003	0.85	0.001	0.84	0.0003	1.02	0.001	1.00	0.0007
9	1.05	0.003	0.85	0.0004	0.80	0.001	0.80	0.0003	0.96	0.001	0.95	0.0009
10	1.00	0.003	0.81	0.0002	0.76	0.001	0.76	0.0003	0.92	0.001	0.90	0.0010

Combining the results shown in table 1 with those reported in figures 2–4, we can see that enabling party birth and death has two quite distinct effects, each with a strong impact on citizen dissatisfaction. The strongest effect concerns the impact of the survival threshold on the number of parties in the system. Endogenizing party birth and death with lower survival thresholds makes the average citizen far more satisfied, in the sense of having an ideal point close to some party position on offer, than doing the same thing with higher survival thresholds. The endogenous number of parties in the system adapts to enhance citizen satisfaction, an effect that holds true for all adaptive rules under investigation. This is the main systematic effect of endogenizing party birth and death. In addition, enabling party birth and death also introduces a form of evolutionary adaptation for sticker parties, which tend to die in less popular locations in the policy space and to be born in more popular ones. This effect does not extend to aggregators and hunters, which tend to adapt away from their initial birth locations.

(b) The impact of survival thresholds: locations and rates of party births and deaths

Figure 5 and table A6 describe the policy eccentricity of births and deaths for various survival thresholds, for a mature party system (tick greater than 1000) in which all start-up effects have been burnt off. In all-aggregator systems, for example, party births tend strongly to occur towards the centre of the space, tending to become even more central as the survival threshold increases. Aggregator deaths tend to happen towards the periphery of the policy space, also becoming more central as the survival threshold increases. Looking back at figure 4, we see deaths tending to occur precisely where aggregators tend to be found, while births occur in a much more central location. Aggregators tend to arrange themselves in a dispersed pattern that most displeases more centrist citizens. Figures 4 and 5 thus show a continuous flow of aggregators through a mature party system, with new aggregators tending to be born towards the centre then evolving towards the periphery of the space, leaving centrist citizens once again dissatisfied and the centre once again ripe for party births. This process is much more pronounced for low birth and death thresholds, where it is also true that the rate of aggregator births and deaths is much higher than under larger survival thresholds (table A9 in the electronic supplementary material).

Figure 5.

Eccentricity of births and deaths, measured in s.d. of the distribution of supporter ideal points (vertical axis), by threshold (horizontal axis) and rule (panel), for simulation ticks greater than 1000.

The opposite pattern can be seen in all-hunter party systems, in which party births and deaths continue to occur at much higher rates than for other decisions rules, even under high survival thresholds (table A10). Hunter births tend strongly to occur at more eccentric locations than hunter deaths (table A6 shows hunter birth and death eccentricities plotted in figure 5 to be highly distinct statistically, using p<0.05 confidence intervals), though both births and deaths tend to occur at less eccentric locations as the survival threshold increases and this pattern is less striking than it is for aggregators. This is because, from the perspective of the average citizen, hunters are looking for votes too close to the centre (figure 4), leaving a larger number of dissatisfied citizens, and thus a larger number of party births, near the periphery of the space. Hunters thus tend to be born in the periphery of the space and to adapt towards the centre, leaving the periphery once more ripe for party births.

In a mature all-sticker system, there seems to be no systematic pattern in the locations of births and deaths (table A6 shows sticker birth and death eccentricities to be statistically indistinguishable.). It is also the case that births and deaths are very rare in a mature all-sticker system (figure A8). In this setting, most of the action arises in the immature system, immediately following a random cold start. Sticker births then systematically tend to occur closer to the centre than deaths, which is how a birth-enabled all-sticker system adapts to citizen preferences, and tends to reach something resembling an ergodic state.

5. Discussion and further work

The results reported above can be summarized quite crisply. Enabling endogenous party birth and death involves implementing a de facto survival threshold. Different survival thresholds imply different numbers of political parties for a given adaptive rule, with higher survival thresholds implying fewer parties. For all birth-enabled systems, the higher the survival threshold, the fewer parties, the less eccentric the mean party location and the less satisfied are citizens as a whole. We know from Laver (2005) that vote-seeking hunters (which are in effect run by autocratic voter-seeking leaders) tend very systematically to beat aggregators (which are in effect run according to a rule of intra-party democracy) and stickers (which are in effect run by unresponsive ideologues) in the competition for citizens' votes. The paradox that emerges from these results is that, in birth-adapted party systems, it is the parties most successful in winning votes, the hunters, who tend strongly to make citizens least happy. This is because hunter positions tend to be closer to the centre of the space, and thus less close to the ideal point of the average citizen, than the more dispersed positions of either stickers or aggregators.

Future work will investigate the impact of the updating parameter, stepping through values of α to explore the extent to which different party adaptive rules are affected by changing from an assumption that citizens switch to the party closest at any given instant, to an assumption that citizens switch only very slowly when the party they currently support is no longer closest to them. Low values of α correspond most closely to the implicit assumption in the current spatial model; higher values correspond to an assumption that citizens develop more long-standing party affiliations that respond only slowly to a changing configuration of party positions. Future work will also systematically interrogate the model to explore the implications with ‘mixed’ sets of party adaptive rules, exploring the performance of rules in competition with each other in birth-enabled party systems, moving on to look at the evolution of sets of rules in settings where the evolutionary fitness of a decision rule is conditioned on its past success in winning votes, before modelling the endogenous evolution of the adaptive rules themselves.

Supplementary Material

Spatial models of political competition with endogenous parties: supplementary statistical analysis, tables and figures

Spatial models of political competition with endogenous parties: supplementary statistical analysis, tables and figures