Abstract
Low- and high-frequency cochlear nonlinearity was studied by measuring DPOAE I/O functions at 0.5 and 4 kHz in 103 normal-hearing subjects. Behavioral thresholds at both f2's were used to set L2 in dB SL for each subject. Primary levels were optimized by determining the L1 resulting in the largest Ldp for each L2 for each subject and both f2's. DPOAE I/O functions were measured using L2 inputs from −10 dB SL (0.5 kHz) or −20 dB SL (4 kHz) to 65 dB SL (both frequencies). Mean DPOAE I/O functions, averaged across subjects, differed between the two frequencies, even when threshold was taken into account. The slopes of the I/O functions were similar at 0.5 and 4 kHz for high-level inputs, with maximum compression ratios of about 4:1. At both frequencies, the maximum slope near DPOAE threshold was approximately 1, which occurred at lower levels at 4 kHz, compared to 0.5 kHz. These results suggest that there is a wider dynamic range and perhaps greater cochlear-amplifier gain at 4 kHz, compared to 0.5 kHz. Caution is indicated, however, because of uncertainties in the interpretation of slope and because the confounding influence of differences in noise level could not be completely controlled.
I. INTRODUCTION
In this study, we were interested in comparing nonlinear properties for high frequencies and low frequencies in responses from the normal human cochlea. Interest in this question was based on observations from both behavioral data in humans and physiological measurements in lower animals, which suggest that the question of differences in nonlinear processing for low and high frequencies is not completely resolved. In this study, distortion product otoacoustic emissions (DPOAE) were measured at 0.5 and 4 kHz in a sample of subjects with normal hearing in an effort to provide data relevant to questions regarding the frequency dependence of nonlinear processing in humans.
Several physiological studies in lower animals indicate that there may be differences in cochlear processing at the base, compared to the apex, dating back to the seminal work of Kiang et al. (1965). Recordings of single-fiber tuning curves (more recently referred to as frequency-threshold curves, FTC) showed that fibers with high characteristic frequency (CF) innervating hair cells at the cochlear base had sharper tuning, compared to low-CF fibers innervating more apically located hair cells. Kiang and Moxon (1974) noted that high-CF fibers had long low-frequency tails where threshold remained relatively constant regardless of frequency. In contrast, low-CF fibers were characterized by more symmetrical tuning, and low-frequency tails (relative to CF) were less evident. These frequency-dependent patterns of sharpness of tuning and differences in symmetry have been demonstrated in many studies since the early work of Kiang and colleagues. Sewell (1984) recorded FTCs prior to and following administration of furosemide, which reversibly alters outer-hair cell (OHC) function through its action on the stria vascularis, which provides the driving potential for the OHCs. Soon after furosemide was administered, thresholds at CF (the tip of the FTC) were more elevated than thresholds on the tails, reflecting the frequency dependence of cochlear-amplifier gain relative to CF. Interestingly, greater threshold elevations at CF were observed for high-CF fibers, compared to fibers having lower CFs. Furosemide has also been shown to have an effect that has been interpreted as a reduction in cochlear-amplifier gain, based on direct measurements of basilar-membrane motion (Ruggero and Rich, 1991). Ruggero and Rich showed that following furosemide treatment, sensitivity was elevated at a given (basal) cochlear place to the frequency for which that place was the characteristic place (CP) prior to treatment. In contrast, the mechanical response of that same place to a frequency that was well below the best frequency for that place showed no influence from furosemide treatment. Taken together, the single-unit and basilar-membrane data indicate that cochlear-amplifier gain for any frequency is dependent on the condition of the cochlea (primarily the OHCs) at that tone's CP, and appears to be greater for high-CF regions and less for low-CF regions.
Direct measurements of basilar-membrane motion at the apical end of the cochlea, even in lower animals, is more difficult, compared to similar measurements at the cochlear base. Apparently, gaining access to cochlear structures at the apex is more traumatic. This situation might complicate the interpretation of measurements at the cochlear apex because damage to the cochlea would be expected to result in a loss of nonlinearity and a reduction in cochlear-amplifier gain. Thus, the direct observation of less nonlinearity at the cochlear apex may be the result of damage caused by experimental procedures, and, therefore, may not reflect apical cochlear processing in the normal state. Cooper and Yates (1994) indirectly estimated cochlear nonlinearity for a wide range of frequencies, based on single-unit rate-level functions. Their work was based on the hypothesis that the response to a low-frequency tone (relative to CF) would be linear at the CF place. Their results suggested that there was less nonlinearity at the apical end of the guinea-pig cochlea, compared to its base. More recently, Cooper and Rhode have made direct measurements of cochlear mechanics at the apical end of the cochlea (Cooper and Rhode, 1995, 1997, 1998; Rhode and Cooper, 1996). In general, these data demonstrate similar nonlinearities for apical and basal cochlear regions, although the nonlinear effects appear to exist for a wider range of frequencies for apical places and perhaps are less in magnitude. Zinn et al. (2000) concluded that negative feedback existed for the entire cochlear length, with gain at the base but not the apex. However, Zinn et al. observed no evidence for compressive nonlinearity at low and medium levels in the apical region of the guinea pig cochleae. The disagreement between this observation and those made by others may be due to the difficulty of the apical preparation.
For obvious reasons, direct measurements of cochlear nonlinearity are not possible at any cochlear place in humans. As a consequence, assessment of nonlinearity in the human cochlea must rely on non-invasive, indirect measurements. There are several psychophysical studies that have examined cochlear nonlinearity in humans, but the results are not in complete agreement. For example, some studies suggest that the human cochlea is more nonlinear at its base, compared to its apex (Hicks and Bacon, 1999; Plack and Oxenham, 1998), whereas other studies report data that suggest that there are no differences in cochlear nonlinearity for low and high frequencies (Plack and Drga, 2003; Plack and O'Hanlon, 2003; Lopez-Poveda et al., 2003; Schairer, Messersmith and Jesteadt, 2007). The apparent discrepancies across studies may be due to differences in the measures that were used to quantify nonlinearity, which, of necessity, must rely on indirect measurements. In some of the behavioral studies, comparisons were made for responses measured with on-frequency and low-frequency maskers, under the assumption that the response at any place along the cochlea is nonlinear only when stimulated with frequencies for which that place is the CP, and is linear in response to frequencies that are much lower than the CF for that place. However, several physiological studies (as described above) are consistent with the view that tuning is broader for apical cochlear places and that nonlinear response properties cover a wider range of frequencies, compared to more basal places. Behavioral studies (or any other indirect study, for that matter) that rely on comparisons between responses to CF tones and responses to tones much lower in frequency than CF might, therefore, underestimate the amount of nonlinearity for low-frequency, apical cochlear regions because the responses to the reference condition (a stimulus much lower than CF) are not entirely linear.
The present study represents an alternative effort to use non-invasive, indirect, but objective measures to determine if there are differences in cochlear nonlinearity across frequency in humans. Distortion product otoacoustic emission (DPOAE) input/output functions have been used as indirect measures of cochlear nonlinearity in humans (e.g., Dorn et al., 2001, Neely et al., 2003, 2007). These studies, as well as others, have provided estimates of compression ratio (the ratio of the change in output to the change in input) which are in the range of values observed in animal studies and in behavioral studies of humans with normal hearing. Furthermore, these ratios decrease (i.e., the response becomes less compressive) in the presence of hearing loss. Thus, DPOAE I/O functions have characteristics that are at least qualitatively similar to observations made in both normal and impaired animal preparations. In human ears with normal hearing, these functions are characterized by a linear segment as the response emerges from the noise floor, followed by a compressive region over which the output is no longer linearly related to the input. At its maximum, the compression ratio estimated from DPOAE I/O functions is approximately 4:1, at least for mid and high frequencies. In previous work, we have estimated the range of input levels over which compression takes place and the amount of compression in both normal and impaired ears (Dorn et al., 2001; Neely et al., 2003). Both the amount of compression and the range of input levels over which compression was observed decreased as hearing loss increased. Thus, those efforts were more concerned with changes in compression as a consequence of hearing loss, and did not focus on differences in cochlear nonlinearity between low-frequency and high-frequency primaries. In this study, we measured DPOAE I/O functions in subjects with normal hearing at two frequencies, 0.5 and 4 kHz, and then compared the I/O functions at those two frequencies to determine the extent to which they differed.
II. METHODS
A. Subjects
Data collection was completed on 103 subjects. Subjects ranged in age from 14 years to 47 years, with a mean age of 23.8 years (SD = 8.3). Each subject had audiometric thresholds of 15 dB HL or better (re: ANSI, 1996) for all octave and inter-octave frequencies from 250 to 8000 Hz and 10 dB HL or better for 250, 500, 2000, 3000, and 4000 Hz. The slightly more stringent threshold criteria were chosen to assure that hearing was well within normal limits at the frequencies related to the DPOAE measurements. In addition, each subject had normal 226-Hz tympanograms on each day on which DPOAE data were collected. For each subject, data were collected for only one ear (which was chosen as the one with the lowest thresholds; otherwise, the test ear was chosen randomly).
B. Stimuli
Experimental data were collected and analyzed for f2 frequencies of 0.5 and 4 kHz, with f2/f1= 1.22 in both cases. Thus, the DP frequencies were 0.32 kHz and 2.55 kHz when f2 = 0.5 kHz and 4 kHz, respectively. As a practical matter, 0.5 kHz was chosen because it is perhaps the lowest frequency for which reliable DPOAE data could be collected, due to problems associated with the increase in noise levels as frequency decreases. In general, the increase in noise level with decreasing frequency is a more significant problem for DPOAE measurements, compared to either stimulus frequency (SFOAE) or transient evoked otoacoustic emission (TEOAE) measurements, because predictions about cochlear responses at one frequency (f2) are based on measurements at a frequency that is about ½ octave lower in frequency (2f1-f2). It is likely that this factor underlies differences in the accuracy with which DPOAEs and TEOAEs identify auditory status at low frequencies (Gorga et al., 1993). In efforts to reduce the influence of noise level, averaging times were allowed to increase to unusually long times (see below) when f2 = 0.5 kHz to reduce noise levels to sufficiently low levels for reliable DPOAE measurements at low stimulus levels. The implications of this fact and its impact on the conclusions associated with this study will be described below. For comparison purposes, 4 kHz was selected because of its presumed basal characteristic place in the human cochlea. By focusing on these two frequencies, we hoped to obtain data on nonlinear processing from widely spaced regions, despite the fact that the CP for these two frequencies are probably not at the “extreme” opposite ends of the human cochlea (Greenwood, 1990). Recently, Shera et al. (2007) suggested that, in humans, frequencies above 1 kHz exhibit basal tuning properties whereas frequencies below 1 kHz exhibit apical characteristics. Thus, the 2 frequencies selected for the present study should provide information about basal and apical processing in humans.
C. Equating Stimulus Levels
One issue when comparing cochlear responses for low- and high-frequency stimulation relates to differences in the “internal” representation of the stimulus due to extraneous influences, such as the transfer of energy through the middle ear. Several steps were taken in an attempt to “equalize” the stimulation at 0.5 and 4 kHz. First, behavioral thresholds were measured at these two frequencies, using a two-interval, forced-choice, transformed up-down adaptive procedure that estimated the 71% correct point on the psychometric function (Levitt, 1971). Prior to behavioral threshold testing, a chirp was used to provide in-the-ear calibration of SPL for each subject. Calibration was repeated before each block of trials. Starting level was set to either 25 or 40 dB SPL, depending on f2 (0.5 and 4 kHz). In some cases, the starting level was increased by 10 dB above these levels if the subject was experiencing difficulty with the task. For each block of trials, the initial step size was 4 dB, which was reduced to 2 dB following the first four reversals. Following each block, threshold was defined as the average level for the last six reversals at the 2-dB step size. Three or more blocks were measured at each frequency until the standard deviation of these blocks was 4.5 dB or less. The final threshold for each frequency and each subject was defined as the average of at least 3 blocks of trials.
The level of f2 during DPOAE measurements (L2) was then set in dB SL, using each subject's behavioral thresholds as the reference. This approach was followed in an attempt to equate the level of the stimuli in the cochlea, accounting for factors such as differences in forward middle-ear transmission at 0.5 and 4 kHz, which presumably influences threshold differences as a function of frequency, at least in ears with normal hearing. If these assumptions are correct, equating stimulus levels based on behavioral thresholds should control for any differences in forward transmission through the middle ear. Even if threshold differences as a function of frequency are not solely determined by middle-ear energy transfer in the forward direction, this approach should result in equivalent cochlear representation (to the extent that the factors determining threshold are independent of frequency) across frequency and across subjects. On the other hand, threshold may depend on different mechanisms at the two f2 frequencies used in the present study. For example, phase locking may play a greater role at 0.5 kHz, compared to 4 kHz. However, there is no way this can be known and certainly no obvious approach for equating cochlear input or output. As a consequence, referencing stimulus level to the same psychophysical definition of behavioral threshold at both frequencies seems like a reasonable first approximation for equating stimulus levels at these frequencies.
D. Optimizing Stimulus Levels
Previously, several different approaches have been taken for setting primary levels. In some cases, L1 was set equal to L2 (e.g., Lonsbury-Martin et al., 1990; Smurzynski and Kim, 1992). L1 was set a constant number of dB higher than L2 (e.g., Stover et al., 1996), the difference between L1 and L2 decreased as L2 increased regardless of f2 (e.g., Kummer et al., 1998, 2000), or the difference between the two primary levels decreased as L2 increased in a way that depended on f2 (Neely et al., 2005; Johnson et al., 2006). With the exception of Neely et al. and Johnson et al., the same primary-level conditions were applied to all subjects in these studies. That is, the levels were not customized individually for each subject. In this study, we were interested in selecting stimulus-level conditions that optimized the response for each subject and for both f2 frequencies. We operationally defined optimal conditions as those primary levels that resulted in the largest DPOAE for each subject. The approach we took to determine these levels also obviates the need for us to take into account any differences in forward transmission for the f1 frequencies associated with 0.5 and 4 kHz. When f2 = 4 kHz, a procedure was used in which both L1 and L2 were continuously swept sinusoidally (Neely et al., 2005). We refer to this as the Lissajous-path procedure. At 4 kHz, this procedure was completed in 64 seconds. The L1 that resulted in the optimal (largest) DPOAE for each L2 was identified for each subject. Following the application of an inclusion criterion based on the signal-to-noise ratio (SNR, which we required to be ≥ 9 dB in order for the data point to be included), these optimal values were then fit with a linear model. The linear model was then solved to determine the L1 that would be used for each L2. In this way, we optimized the primary-level ratio at all L2 levels individually for each subject when f2 = 4 kHz.
The short averaging time associated with the Lissajous-path procedure was insufficient to identify optimal L1 conditions when f2 = 0.5 kHz. Without greater averaging times, the higher noise levels at this frequency made it impossible to explore the primary-level space because reliable measurements were seldom observed when the Lissajous-path procedure was used at 0.5 kHz. As a result, an alternative procedure was used at 0.5 kHz to determine optimal L1 levels for each L2 for each subject. At this frequency, measurements were made for discrete stimulus-level conditions, under which averaging could continue for extended periods of time that allowed for greater noise reduction. L2 was varied in discrete 10-dB steps from 40 to 70 dB SPL. These levels were chosen because of the increased likelihood that positive SNRs would be observed for these levels when f2 = 0.5 kHz. At each L2, L1 was varied in 5-dB steps from 10 dB below L2 to 20 dB above L2 (for L2 up to 60 dB SPL) or to 10 dB above L2 (for L2 = 70 dB SPL). For each L2, L1 pair, averaging continued until the noise floor was ≤ −20 dB SPL, the SNR exceeded 12 dB, or artifact-free averaging time exceeded 210 seconds, whichever occurred first. Just as was the case at 4 kHz (where the Lissajous-path procedure was used), the L1 at each L2 that resulted in the largest DPOAE was fit with a linear model, following the application of same data-point inclusion criterion (SNR ≥ 9 dB) that was used at 4 kHz. This model was then used to select the “optimal” L1 for each L2 when f2 = 0.5 kHz. Although this approach differs from the one used at 4 kHz, in both cases, procedures were followed that attempted to optimize stimulus-level conditions individually for each subject at both f2 frequencies. It could be argued that L1 could have been determined in the same manner as L2 was selected, namely by referencing L1 to the behavioral threshold for f1. However, this approach would not have provided the individualized information that was needed to select relative levels between L1 and L2 for the wide range of L2 levels that were used during measurements of I/O functions. Furthermore, relative level for optimal response level apparently depends on frequency (Neely et al., 2005; Johnson et al., 2006). By determining the optimal L1 for each L2 at both f2 frequencies, we not only took into account any differences in forward middle-ear transmission at f1, we hopefully also accounted for differences in optimal primary-level ratios across frequency.
E. Procedure for Measuring DPOAE I/O Functions
Prior to the collection of the DPOAE data, an in-the-ear calibration was performed with the same chirp stimulus that was used prior to behavioral-threshold measurements. While we recognize the issues associated with ear-canal SPL calibrations (Siegel and Hirohata, 1994; Siegel, 2002), we attempted to avoid problems by repositioning the probe more deeply whenever the calibration spectrum was characterized by notches near 4 kHz. This approach was favored over one in which measurements were restricted to frequencies below any observed notch in the calibration spectrum for several reasons. First, repositioning of the probe enabled us to assure that notches were not present at the frequency of interest. Second, it enabled us to collect all at the same f2 frequencies in all subjects. Third, it allowed us to make measurements at a higher frequency than might have been possible if measurements were restricted to frequencies below any observed notch in the spectrum. As might be expected from ear-canal geometry in relation to stimulus wavelength, notches in the calibration response were never observed around 0.5 kHz. DPOAE level was estimated in the frequency bin that corresponded to the distortion product (DP) frequency (2f1-f2) for each f2. Noise was estimated as the average power in the six frequency components adjacent to the DP frequency (three above and three below the DP frequency). The stimulus and response buffers were 0.25 s in duration, resulting in a 4-Hz spacing between adjacent frequency components. DPOAE I/O functions were measured for L2 levels ranging from −20 to 65 dB SL when f2 = 4 kHz, and from −10 to 65 dB SL when f2 = 0.5 kHz, using each subject's previously measured behavioral threshold as the reference for 0 dB SL. At both f2 frequencies, measurements commenced with the lowest stimulus level. L2 was incremented in 5-dB steps (resulting in I/O functions with either 16 or 18 points, depending on frequency), and L1 was set according to the individually optimized levels determined from either the continuously variable or discretely variable-level studies that were described above.
Measurement-based stopping rules were used in an effort to obtain reliable data at both f2 frequencies over a wide range of input levels. However, in the interest of reducing time commitments on the part of individual subjects, slightly different rules were used at 0.5 and 4 kHz. When f2 = 0.5 kHz, data collection continued until any one of the following conditions were met: measurements stopped for each L2 condition when either the noise floor was ≤ −25 dB SPL, the SNR was ≥ 12 dB, or 210 seconds of artifact-free averaging time had expired, whichever occurred first. At 4 kHz, the stopping rule was also based on three conditions, although the rules varied slightly from those used at 0.5 kHz. Data collection continued when f2 = 4 kHz until the noise floor was ≤ −25 dB SPL, the SNR ≥ 20 dB, or 210 seconds of artifact-free averaging had taken place, whichever occurred first. The inclusion of an SNR criterion at both f2 frequencies was intended to reduce test time for stimulus conditions in which the response was reliably measured well above the noise floor. The lower SNR stopping criterion when f2 = 0.5 kHz represents an additional compromise, given the longer time it took to collect data at this frequency due to the higher noise levels. The less stringent SNR criterion was viewed as a reasonable compromise, in that response levels with an SNR ≥ 12 dB would be expected to vary by less than 2 dB as a result of the noise. By relaxing the SNR rule, less data-collection time was needed for high-level stimuli at 0.5 kHz, when more robust responses were observed, with little or no effect on the reliability of the measurements. When measurements were made for low-level stimuli close to DPOAE threshold, the stopping rules for 0.5 and 4 kHz were identical because the measurements at neither frequency stopped on SNR; that is, the SNR did not exceed 12 dB (0.5 kHz) or 20 dB (4 kHz) for these low-level stimulus conditions. In reality, averaging times were always short when f2 = 4 kHz, typically 4 to 32 seconds, regardless of stimulus level. This occurred because it was common for the test to stop on the noise stopping criterion (≤ −25 dB SPL) at this frequency. The averaging times were much longer when f2 = 0.5 kHz for all stimulus levels, but especially for low-level stimuli, because of the higher noise levels at this frequency and the lower response levels at these stimulus levels. Frequently, it was the case that the measurement stopped when the (artifact-free) averaging time = 210 seconds at 0.5 kHz. Despite averaging times that were longer by an order of magnitude or more at 0.5 kHz, the noise floor was never as low at 0.5 kHz as it was at 4 kHz. Still, the use of slightly different measurement-based stopping rules at the two frequencies represented a compromise between total test time and reliability, thus allowing us to make measurements of DPOAE levels within reasonable amounts of time at both 0.5 and 4 kHz. Subjects were allowed to either sleep, read or watch a DVD (captioned with sound turned off) during data collection. Subjects were provided breaks as needed.
F. Middle-Ear Transmission
In an effort to validate the approach in which behavioral-threshold measurements were used to “equalize” cochlear input and (presumably) remove the influence of the middle ear on the transmission of energy in the forward direction, middle-ear reflectance was also measured (Keefe, 1997) in a subset of 91 subjects from the 103 subjects who also participated in the DPOAE studies. As will be shown subsequently, these measurements revealed a similar pattern of dependence on frequency, but also suggested that behavioral threshold cannot be completely predicted from forward middle-ear transmission (at least as it is described by reflectance). The middle-ear data, however, were not viewed as central to the goals of the study, and will be described here only briefly and only in relation to the behavioral-threshold data.
The collection of a complete set of data (including screening audiometric assessments, behavioral-threshold measurements used to set L2 in dB SL, determination of optimal primary-level for each subject at both f2 frequencies, measurement of DPOAE I/O functions at both frequencies, and measurements of middle-ear reflectance) took 4−6 hours per subject (two to three 2-hour sessions). Subjects were paid an hourly rate for their participation in the study. This study was approved the BTNRH Institutional Review Board.
III. RESULTS AND DISCUSSION
A. Behavioral Thresholds and Reflectance Measurements
Figure 1 plots the mean behavioral thresholds in dB SPL ± 1 standard deviation, shown as open symbols (referred to the left y-axis), when f2 was either 0.5 or 4 kHz. Not surprisingly, behavioral thresholds were lower (by about 8 dB) at 4 kHz, compared to 0.5 kHz. Filled symbols represent the mean reflectance converted to dB (referred to the right y-axis) at the same frequencies. Although the pattern is similar, there is less difference between middle-ear energy transfer in the forward direction (as estimated by reflectance) as a function of frequency, compared to the difference in behavioral threshold. The difference in reflectance between 0.5 and 4 kHz is about 5 dB. Interestingly, the variability in behavioral threshold was greater than the variability in reflectance. This finding also would be consistent with the view that behavioral thresholds cannot be completely explained by middle-ear transmission, although it also may be a consequence of greater inherent variability in behavioral-threshold measurements, compared to measures of energy reflectance. In any case, these data suggest that threshold is not entirely predictable from middle-ear energy reflectance. This finding does not negate the value of presenting stimuli (L2) in dB SL for DPOAE measurements. While these data indicate that behavioral thresholds are related to reflectance, they also suggest that other factors contribute to threshold. However, the use of behavioral thresholds to normalize stimulus levels was viewed as an approach in which the output of the cochlea (not just the transfer of energy through the middle ear) is held constant at the characteristic cochlear places at which the two f2 frequencies are represented for each subject.
Figure 1.
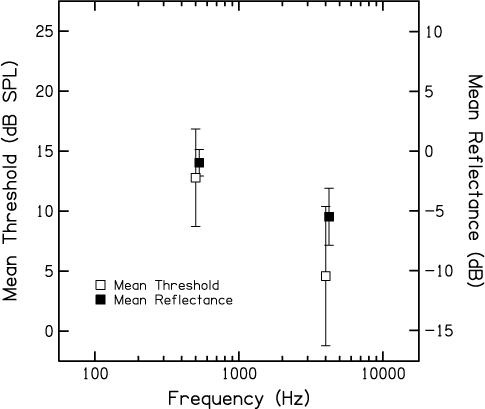
Mean behavioral threshold in dB SPL (left Y-Axis) and mean middle-ear reflectance in dB (right Y-Axis) as a function of frequency. Open symbols represent behavioral thresholds and filled symbols represent reflectance data. In both cases, error bars represent ± 1 SD. Data are shown for both f2 frequencies (0.5 and 4 kHz). Data points representing behavioral thresholds and reflectance are offset slightly to allow for easier visualization.
B. DPOAE I/O Functions – L2 in dB SPL
Figure 2 shows mean DPOAE and noise levels (in dB SPL) as a function of L2 (in dB SPL). The top panel shows data when f2 = 0.5 kHz and the bottom panel provides the data when f2 = 4 kHz. Squares represent DPOAE levels and circles represent noise levels. In all cases, error bars represent ±1 standard deviation. All data were included without regard to any inclusion criteria, such as SNR. We should note, however, that a re-analysis of the data restricted to those conditions for which the SNR ≥ 3 dB did not change the I/O functions in any significant way. Because individually measured behavioral thresholds were used to set L2, responses were not always measured at the exact same SPL in all subjects. For example, 0 dB SL (behavioral threshold) might have occurred at 6 dB SPL in one subject, 8 dB SPL in another subject, and 4 dB SPL in a third subject. Since L2 was set relative to each subject's behavioral threshold and measurements were made in 5-dB steps, data were never obtained at the exact same SPL for these three subjects. Given the goals of this study, we thought it was more important to make measurements for input stimuli that resulted in the same “cochlear output” in all subjects (as reflected in behavioral thresholds) rather than to make measurements at exactly the same input SPL in all subjects, which would ignore subtle threshold differences. However, it is more commonly the case that DPOAE I/O functions are plotted when L2 is specified in dB SPL. In order to provide this more typical representation, L2 was rounded to the nearest 5 dB and then averaged across subjects, which was done in the process of generating the data shown in Fig. 2. Despite this “rounding error” (which never exceeded 2.5 dB) and the fact that the measurement-based stopping rules did not result in the same noise levels at both f2 frequencies (see below), it can be seen that DPOAEs were measured over a wide range of input levels, perhaps as low as −5 dB SPL at 4 kHz and 20 dB SPL at 0.5 kHz. Measurements of DPOAEs extending down to these low stimulus levels are unusual, especially when f2 = 0.5 kHz. Having data for such low-level inputs demonstrates that the measurement-based stopping rules were successful in reducing noise to levels that are not typically observed. The results shown in Fig. 2 indicate that there is greater output (Ldp) at 4 kHz, compared to the output at 0.5 kHz for virtually every input level. Across conditions in which responses were observed, DPOAE level at 4 kHz exceeded DPOAE level at 0.5 kHz by between 5 and 13 dB.
Figure 2.
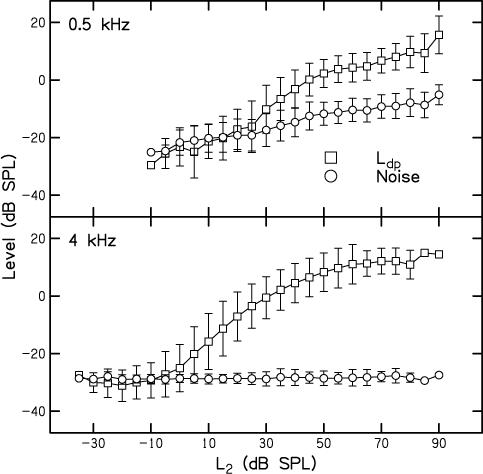
Top: Mean DPOAE level (Ldp) (circles) and noise level (squares) in dB SPL as a function of L2 in dB SPL when f2 = 4 kHz. Bottom: Mean DPOAE level (Ldp) (circles) and noise level (squares) in dB SPL as a function of L2 in dB SPL when f2 = 0.5 kHz. In all cases, error bars represent ± 1 SD. Because stimuli were presented relative to each subject's threshold, L2 was rounded to the nearest 5 dB prior to calculating the mean values shown in this figure.
C. DPOAE I/O Functions – L2 in dB SL
The top panel of Fig. 3 plots mean DPOAE level and noise levels(dB SPL) as a function of L2 (in dB SL). Thus, stimulus inputs were normalized to each subject's behavioral thresholds at the two f2 frequencies. In all other respects, the same conventions that were used in Fig. 2 are used here. Even when behavioral thresholds were used to create more equivalent input levels, the outputs still differed, with Ldp being greater and measurable over a wider dynamic range for 4 kHz, compared to 0.5 kHz. This is the first indication in our data (ignoring the results shown in Fig. 2) that the responses are not identical at 0.5 and 4 kHz, even after stimulus levels were chosen in a way that we thought would help to equate cochlear inputs. DPOAEs were measured down to −5 dB SL at 4 kHz; in contrast, DPOAEs were measured down to 10 dB SL at 0.5 kHz.
Figure 3.
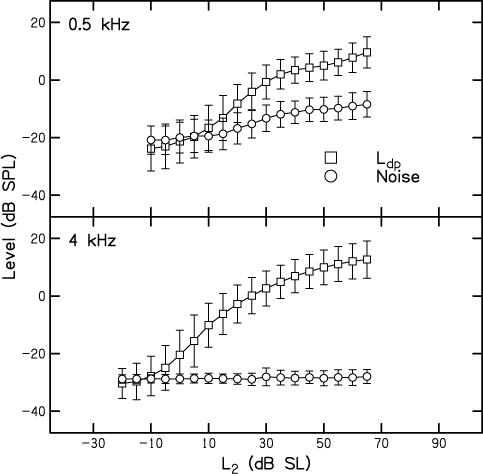
Top: Mean DPOAE level (Ldp) (circles) and noise level (squares) in dB SPL as a function of L2 in dB SL when f2 = 4 kHz. Bottom: Mean DPOAE level (Ldp) (circles) and noise level (squares) in dB SPL as a function of L2 in dB SL when f2 = 0.5 kHz. In all cases, error bars represent ± 1 SD. In all cases, error bars represent ± 1 SD.
Despite using a paradigm which allowed averaging time to vary in an effort to achieve similar noise levels at both 0.5 and 4 kHz, equivalent noise levels at the two frequencies were almost never achieved in individual subjects and certainly not in the mean data. Part of this effect was due to differences in the SNR stopping criteria for the two frequencies, but this factor would be expected to have no influence for low-level inputs, when the stopping rules were effectively identical, as described above. The noise levels were higher and more variable at all stimulus levels at 0.5 kHz, compared to 4 kHz. At 4 kHz, averaging stopped almost without exception when the noise-floor criterion (noise level ≤ −25 dB SPL) was met. However, at higher primary levels, testing sometimes stopped on SNR because the Ldp was so large. When this occurred, it resulted in slightly higher and more variable noise levels, which is evident from an examination of the noise data in the bottom panel of Fig. 3 (circles and error bars for L2 ≥ 25 dB SL when f2 = 4 kHz). At 4 kHz, it was never the case that data collection continued until the test-time criterion of 210 seconds was reached. At 0.5 kHz, averaging stopped more often when the SNR criterion was met at high stimulus levels, which is why the noise floor increases for L2 ≥ 20 dB SPL (circles in the top panel of Fig. 3). We are unconcerned with the higher noise levels for these higher level stimulus conditions because the influence of the noise on the measured DPOAE level is expected to be small, given the size of the response. However, at low-stimulus levels, the average noise floor still was higher when f2 = 0.5 kHz, despite the fact that data collection continued for as long as 210 seconds of artifact-free averaging time per measurement. In reality, the time spent collecting data at each of these lower levels at 0.5 kHz often exceeded 210 seconds because artifact rejection occurred frequently, thus making the effective test time greater. Theoretically, we could have increased averaging time by a factor of 4, which would presumably result in equivalent noise levels at both frequencies; however, this increase in averaging time would not have been tolerated by subjects. For this reason, increasing averaging time beyond 210 seconds was not considered a reasonable option for reducing the noise floor. Alternative techniques, currently unknown to us, would be needed to achieve lower noise levels at 0.5 kHz in practically feasible amounts of time. In any case, the implications of the difference in noise floors relative to our interpretation of the data will be discussed in a subsequent section.
D. Slopes of DPOAE I/O Functions
One explanation for the difference in cochlear output (DPOAE level) when inputs are “equated” could be differences in reverse transmission through the middle ear as a function of frequency. While behavioral thresholds were also measured at the DP frequency (2f1-f2), which is the frequency at which reverse transmission of the DPOAE takes place, the extent to which reverse middle-ear transmission can be estimated from behavioral thresholds is not known. Previous work has shown that horizontal shifts of the DPOAE I/O function can be used to provide estimates of relative forward middle-ear transmission, while vertical shifts in the I/O function can be used as an indirect, relative measure of reverse transmission (Keefe, 2002). For both horizontal and vertical shifts, it is assumed that the form of the cochlear nonlinearity is the same at every place along the cochlea, which, in turn, is related to the assumption of cochlear scaling symmetry that has been described by others (Shera et al., 2000; Zwieg, 1976). An assumption of scaling symmetry, however, would have been incompatible with the goals of the present study, which were to evaluate cochlear nonlinearity in humans for low- and high-frequency stimuli. This is one of the reasons why we referenced stimulus level to behavioral threshold as a way to “equate” effective excitation in the cochlea. Another reason for referencing L2 to behavioral thresholds was to remove middle-ear influences in the forward direction, as described in the Methods. We also needed an approach that would control or eliminate the influences of reverse middle-ear transmission on measured DPOAE level, but felt that there were too many uncertainties in using behavioral thresholds to estimate reverse transmission. As stated above, using vertical shifts in the I/O function was not viewed as an acceptable alternative, as it assumes the form of the nonlinearity is the same for high and low frequencies (which is the hypothesis we are attempting to test). We have opted instead to evaluate the slopes of I/O functions, which are independent of the relative placement of I/O functions along the Y axis and, therefore, presumably independent of reverse middle-ear energy transmission. Thus, we can compare DPOAE I/O function slopes as a way of determining if the functions differ at 0.5 and 4 kHz without worrying about the influence of reverse energy transmission through the middle ear.
Figure 4 plots the slope of the I/O functions as a function of L2 (dB SL), with circles representing data when f2 = 4 kHz and squares representing data when f2 = 0.5 kHz. These slopes were derived from the data plotted in the top panel of Fig. 3, calculated as the change in DPOAE level (Ldp) between adjacent L2 values. At both frequencies, the slopes are close to 1 within a few dB of DPOAE threshold (roughly defined as the level at which the DPOAE just exceeds the noise floor). More shallow slopes are observed for inputs below these levels; but, this observation may be a consequence of the fact that these estimates are dominated by the noise, which would be expected to make the slope more shallow. The slope of the DPOAE I/O functions are between 0 and 0.25 at high stimulus levels (40 to 60 dB SL), where the influence of noise is minimal. These slopes are consistent with previous estimates, and suggest that DPOAE I/O functions show about the same 4:1 or 5:1 compression at both frequencies for high-level inputs. Thus, there is little difference between slope estimates at the two frequencies for higher level inputs. In contrast, it appears that the maximum slope (approximately 1) is achieved for lower level inputs at 4 kHz, compared to 0.5 kHz, which represents a small deviation from scaling symmetry. This would suggest that there may be a wider dynamic range at 4 kHz, but we do not completely understand the meaning of the differences in slope, and we are cautious in our interpretation of these data because we cannot rule out the effects of differences in noise level. Recall that our efforts to reduce noise to equivalent levels were only moderately successful. This mattered little for high-level inputs, because the DPOAE level was well above the noise floor, even at 0.5 kHz. At low levels, however, the fact that the measurement-based stopping rules did not result in the same noise floor at both frequencies could have influenced the low-level differences in slope. This concern is relevant for comparisons of the slope estimates for stimulus levels of 0 dB SL or less, but is of less importance for comparisons between frequencies at levels ≥ 0 dB SL (4 kHz) and ≥ 10 dB SL (0.5 kHz). For these stimulus conditions, the responses were above the noise floor, and yet differences in slopes of the I/O function between the two f2 frequencies were still evident. Still, the influence of noise-floor differences at the two frequencies is a potentially important factor, and will be further discussed below.
Figure 4.

Slope (dB/dB) as a function of L2 in dB SL, calculated from the mean data shown in the top panel of Fig. 3. Circles represent data for 0.5 kHz and squares represent data for 4 kHz.
In an effort to smooth the mean data shown in Fig. 3, data were fit with a polynomial function. The mean data are reproduced as symbols in Fig. 5, with circles representing the data at 4 kHz, squares representing the data at 0.5 kHz, and the lines representing separate polynomial fits to the data for each frequency. These polynomial equations provide good fits to the mean data, accounting for 99% of the variance.
Figure 5.
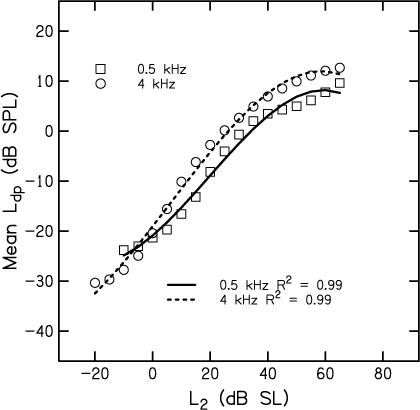
Mean Ldp in dB SPL as a function of L2 in dB SL, following the symbol conventions used in Figs. 2, 3, and 4. Lines represent polynomial fits to the mean data, with the solid line representing the fit to data at 0.5 kHz and the dashed line representing the fit to data at 4 kHz. Proportion of the variance accounted for is provided as an insert in the figure.
Figure 6 plots slopes as a function of L2 (dB SL) that were derived from polynomial fits shown in Fig. 5. As expected, these slopes follow a smoother path, compared to the data shown in Fig. 4, where the slopes were estimated from the actual mean data (as shown in Fig. 3), and not the fits to those data (shown in Fig. 5). In these smooth versions, differences in slope for inputs of 20 dB SL or greater are minimized. Slopes less than zero for inputs exceeding 55 dB SL are a consequence of the polynomial fits emphasizing non-monotonicities at high levels. In contrast to the similarities for stimulus levels ≥ 20 dB SL, there are large frequency-dependent differences in slope for lower level inputs. In an effort to quantify these differences, we estimated the level at which maximum slope was achieved from these fits. These points are represented by filled symbols on each function. At 4 kHz, this occurred for an input level of 6.5 dB SL, whereas maximum slope was observed at 19.7 dB SL when f2 = 0.5 kHz. Thus, maximum slope is achieved at a level that is 13 dB lower at 4 kHz, compared to 0.5 kHz. Given the similarity in responses at high levels, the dB difference at the low end might reflect differences in the dynamic range of response at the two test frequencies. As stated earlier, low-level stimulus conditions are particularly vulnerable to the influences of noise. For this reason, differences in slope for input levels less than about 0 dB SL at 4 kHz and less than about 10 or 15 dB SL at 0.5 kHz cannot be interpreted. For stimulus levels between these values and about 20−25 dB SL, it is difficult to see how the slope differences are due solely to frequency differences in background noise (see Figs. 3 and 4). Thus, the present data would be consistent with the view that this estimate of “dynamic range” is greater at 4 kHz, compared to 0.5 kHz.
Figure 6.
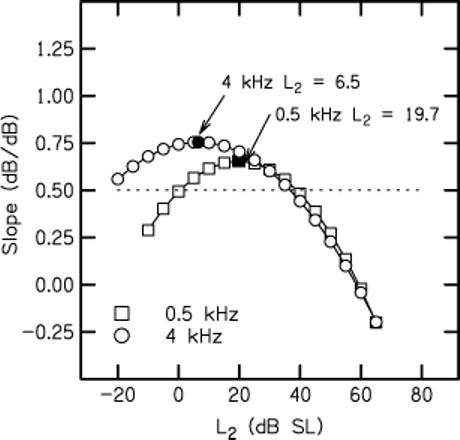
Slope (dB/dB) as a function of L2 in dB SL derived from the polynomial fits that were shown in Fig. 5. Symbol convention is the same as in previous figures. Filled symbols on each curve represent the point at which the maximum slope was achieved. Horizontal dashed line drawn at a slope of 0.5 was used as a definition of dynamic range.
An alternate way of estimating dynamic range, based on estimates of slope, is to define it as the range of input levels for which the slope exceeds some arbitrary value, such as the one shown by the dotted horizontal line in Fig. 6. The advantage of this approach is that it is derived from the polynomial fits to all of the data; as was seen in Fig. 5, these fits provide good descriptions of the mean data. The disadvantage of this approach is that it allows for extrapolation to extremely low-level inputs, where the influence of noise is greatest. Keeping in mind our concern that the extension towards low-level inputs based on the polynomial fits may have problems associated with it (given the potential influence of noise at these levels), we arbitrarily selected slopes of 0.5 as the inclusion criterion, mainly because the parabolas at both frequencies had slopes at or close to this value on both the low-level and high-level side of the stimulus level at which the maximum slope was observed. The range of levels between the intersections of the dashed line with each parabola was used as an estimate of the dynamic range. To the extent that this is an appropriate metric, the dynamic range at 0.5 kHz was 39 dB, while the dynamic range at 4 kHz was 61 dB.
The results shown in Fig. 6 might be consistent with the reduced differences between tip and tail thresholds as observed in frequency-threshold curves of auditory neurons (see, for example, Sewell, 1984), although we do not, as yet, have data that can be used to more directly test this hypothesis in humans. Tip-to-tail differences estimated from DPOAE suppression tuning curves have been interpreted as estimates of cochlear-amplifier gain (e.g., Pienkowski and Kunov, 2001; Mills, 1998; Gorga et al., 2002, 2003). If the interpretation of the data shown in Figs. 4 and 6 is correct, then the present results could be consistent with frequency differences in cochlear-amplifier gain, thus suggesting that nonlinear processing differs at the cochlear apex in humans, compared to its base. The present data suggest that the cochlea exhibits compressive growth at both 0.5 and 4 kHz (and, therefore, at its apex and at its base). These data would be inconsistent with the view that the human cochlea produces distortion at its base, but not its apex. Rather, the frequency differences noted here would be more a matter of the magnitude of the effect. Based on these data, we would predict that the human cochlear amplifier has less gain for low frequencies, compared to higher frequencies.
It is important to note that a level of uncertainty exists in how to interpret the differences in slope of the DPOAE I/O functions as a function of L2. However, it remains the case that slope estimates have the advantage that they require no assumptions regarding underlying cochlear processes (such as cochlear scaling symmetry, which is what we were evaluating in humans) and are independent of reverse middle-ear energy transmission (which, in any event, may be difficult to ascertain in humans). We remain concerned by the possible confounding influence of differences in noise levels on slope estimates. It is highly impractical, if not impossible, to reduce noise to the same levels at 0.5 and 4 kHz in humans. While the results suggest that differences exist in cochlear nonlinearity as a function of frequency in humans, we remain cautious in this interpretation, based on the present data. For practical reasons, the influence of noise could not be completely controlled, and the effect of its influence might lead to the potentially incorrect conclusion that the human cochlea is more nonlinear at its apex, compared to its base. Having said this, the differences in slopes of the I/O functions for stimulus levels between about 0 and 20 dB SL are less likely to be affected by noise levels (given that positive signal-to-noise ratios were observed for these conditions). In particular, the slope data shown in Fig. 4 suggest that there are real differences between 0.5 and 4 kHz in dynamic range that cannot be entirely attributed to differences in noise level. Still, additional studies in which a paradigm is used that results in equivalent noise levels or alternative measurements less susceptible to noise may be needed to determine if nonlinearity in humans differs at the cochlear base versus its apex with greater certainty.
With current technology and noise-reduction algorithms, it is unlikely that noise can be consistently reduced to the same low levels at 0.5 kHz as is routinely possible at 4 kHz. Further refinements in measurement or analysis techniques in the future, however, might result in more equivalent noise levels at these two frequencies. The use of experimental paradigms less affected by background noise (compared to the measurement of DPOAE I/O functions) might provide insights into cochlear-processing differences between 0.5 and 4 kHz in humans. For example, measurements of the decrease in DPOAE level due to the presence of a suppressor can be used to generate DPOAE suppressing tuning curves. Estimates of “tuning” and/or cochlear-amplifier gain derived from suppression tuning curves may be less affected by noise or middle-ear transfer and could, therefore, provide a way make base-apex comparisons that are more straightforward to interpret than I/O functions.
ACKNOWLEDGEMENTS
Work supported by the NIH (NIDCD R01 2251 and P30 4662). We thank Doug Keefe for providing the software that was used for measurements of middle-ear reflectance. We are grateful for informal discussions of this study with Chris Shera, and for two anonymous reviews that provided many helpful suggestions that improved the manuscript. We would also like to thank Sandy Estee, Alberto Cervantes and Gwen Watson for their help in recruiting subjects to participate in this study.
REFERENCES
- ANSI S3.6−1996 . Specifications for Audiometers. American Institute of Physics; New York: 1996. [Google Scholar]
- Cooper NP, Rhode WS. Nonlinear mechanics at the apex of the guinea-pig cochlea. Hear. Res. 1995;82:225–243. doi: 10.1016/0378-5955(94)00180-x. [DOI] [PubMed] [Google Scholar]
- Cooper NP, Rhode WS. Mechanical responses to two-tone distortion products in the apical and basal turns of the mammalian cochlea. J. Neurophys. 1997;78:261–270. doi: 10.1152/jn.1997.78.1.261. [DOI] [PubMed] [Google Scholar]
- Cooper NP, Rhode WS. Apical cochlear mechanics: A review of recent observations. In: Palmer AR, Rees A, Summerfield AQ, Meddis R, editors. Proc. International Symposium on “Psychophysical and Physiological Advances in Hearing”. Whurr Publishers Ltd.; London: 1998. pp. 11–18. [Google Scholar]
- Cooper NP, Yates GK. Nonlinear input-output functions derived from the responses of guinea-pig cochlear nerve fibers: Variations with characteristic frequency. Hear. Res. 1994;78:221–234. doi: 10.1016/0378-5955(94)90028-0. [DOI] [PubMed] [Google Scholar]
- Dorn PA, Konrad-Martin D, Neely ST, Keefe DH, Cyr E, Gorga MP. Distortion-product otoacoustic emission input/output functions in normal-hearing and hearing-impaired human ears. J. Acoust. Soc. Am. 2001;110:3119–3131. doi: 10.1121/1.1417524. [DOI] [PubMed] [Google Scholar]
- Gorga MG, Neely ST, Konrad-Martin D, Dorn PA. The use of DPOAE suppression as an estimate of response growth. J. Acoust. Soc. Am. 2002;111:271–284. doi: 10.1121/1.1426372. [DOI] [PubMed] [Google Scholar]
- Gorga MP, Neely ST, Dierking D, Dorn PA, Hoover BM, Fitzpatrick D. Distortion product otoacoustic emission tuning curves in normal-hearing and hearing-impaired human ears. J. Acoust. Soc. Am. 2003;114:263–278. doi: 10.1121/1.1575751. [DOI] [PubMed] [Google Scholar]
- Gorga MP, Neely ST, Bergman BM, Beauchaine KL, Kaminski JR, Peters J, Schulte L, Jesteadt W. A comparison of transient-evoked and distortion product otoacoustic emissions in normal-hearing and hearing-impaired subjects. J. Acoust. Soc. Am. 1993;94:2639–2648. doi: 10.1121/1.407348. [DOI] [PubMed] [Google Scholar]
- Greenwood DD. A cochlear frequency-position function for several species-29 years later. J. Acoust. Soc. Am. 1990;87:2592–2605. doi: 10.1121/1.399052. [DOI] [PubMed] [Google Scholar]
- Hicks ML, Bacon SP. Psychophysical measures of auditory nonlinearities as a function of frequency in individuals with normal hearing. J. Acoust. Soc. Am. 1999;105:285–296. doi: 10.1121/1.424526. [DOI] [PubMed] [Google Scholar]
- Johnson TA, Neely ST, Garner CA, Gorga MP. Influence of primary-level and primary-frequency ratios on human distortion product otoacoustic emissions. J. Acoust. Soc. Am. 2006;119:418–428. doi: 10.1121/1.2133714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keefe DH. Otoreflectance of the cochlear and middle ear. J. Acoust. Soc. Am. 1997;102:2849–2859. doi: 10.1121/1.420340. [DOI] [PubMed] [Google Scholar]
- Keefe DH. Spectral shapes of forward and reverse transfer functions between ear canal and cochlea estimated using DPOAE input/output functions. J. Acoust. Soc. Am. 2002;111:249–260. doi: 10.1121/1.1423931. [DOI] [PubMed] [Google Scholar]
- Kiang NY-S, Maxon EC. Tails of tuning curves of auditory-nerve fibers. J. Acoust. Soc. Am. 1974;55:620–630. doi: 10.1121/1.1914572. [DOI] [PubMed] [Google Scholar]
- Kiang NY-S, Watanabe T, Thomas EC, Clark LF. Discharge patterns of single fibers in the cat's auditory nerve. The MIT Press; Cambridge, MA: 1965. MIT Res. Monogr. No. 35. [Google Scholar]
- Kummer P, Janssen T, Arnold W. The level and growth behavior of the 2f1-f2 distortion product otoacoustic emission and its relationship to auditory sensitivity in normal hearing and cochlear hearing loss. J. Acoust. Soc. Am. 1998;103:3431–3444. doi: 10.1121/1.423054. [DOI] [PubMed] [Google Scholar]
- Levitt H. Transformed up-down methods in psychoacoustics. J. Acoust. Soc. Am. 1971;49:467–477. [PubMed] [Google Scholar]
- Lopez-Poveda EA, Plack CJ, Meddis R. Cochlear nonlinearity between 500 and 8000 Hz in listeners with normal hearing. J. Acoust. Soc. Am. 2003;113:951–960. doi: 10.1121/1.1534838. [DOI] [PubMed] [Google Scholar]
- Lonsbury-Martin BL, Harris MD, Stagner BB, Martin GK. Distortion product emissions in humans: I. Basic properties in normally hearing subjects. Ann. Otol. Rhinol., Laryngol. 1990;99(Supplement 147):3–13. [PubMed] [Google Scholar]
- Mills DM. Interpretation of distortion product otoacoustic emission measurements. II. Estimating tuning characteristics using three stimulus tones. J. Acoust. Soc. Am. 1998;103:507–523. doi: 10.1121/1.421101. [DOI] [PubMed] [Google Scholar]
- Neely ST, Gorga MP, Dorn PA. Cochlear compression estimates from measurements of distortion-product otoacoustic emissions. J. Acoust. Soc. Am. 2003;114:1499–1507. doi: 10.1121/1.1604122. [DOI] [PubMed] [Google Scholar]
- Neely ST, Johnson TA, Kopun JG, Converse C, Kennedy E, Dierking DM, Gorga MP. Quantitative estimates of DPOAE I/O functions in normal and impaired ears. 30th Midwinter Meeting of the Association for Research in Otolaryngology; Denver, CO. 2007. [Google Scholar]
- Neely ST, Johnson TA, Gorga MP. Distortion-product otoacoustic emissions with continuously varying stimulus level. J. Acoust. Soc. Am. 2005;117:1248–1259. doi: 10.1121/1.1853253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pienkowski M, Kunov H. Suppression of distortion product otoacoustic emissions and hearing thresholds. J. Acoust. Soc. Am. 2001;113:1574–1586. doi: 10.1121/1.1354202. [DOI] [PubMed] [Google Scholar]
- Plack CJ, Drga V. Psychophysical evidence for auditory compression at low characteristic frequencies. J. Acoust. Soc. Am. 2003;113:1574–1586. doi: 10.1121/1.1538247. [DOI] [PubMed] [Google Scholar]
- Plack CJ, O'Hanlon CG. Forward masking additivity and compression at low and high frequencies. J. Assoc. Res. Otol. 2003;4:405–415. doi: 10.1007/s10162-002-3056-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plack CJ, Oxenham AJ. Basilar membrane nonlinearity and the growth of forward masking. J. Acoust. Soc. Am. 1998;103:1598–1608. doi: 10.1121/1.421294. [DOI] [PubMed] [Google Scholar]
- Ruggero MA, Rich NC. Furosemide alters organ of corti mechanics: Evidence for feedback of outer hair cells upon the basilar membrane. J. Neuro. 1991;11:1057–1067. doi: 10.1523/JNEUROSCI.11-04-01057.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhode WS, Cooper NP. Nonlinear mechanics in the apical turn of the chinchilla cochlea in vivo. Aud. Neuro. 1996;3:101–121. [Google Scholar]
- Schairer KS, Messersmith J, Jesteadt W. Use of psychometric-function slopes for forward-masked tones to investigate cochlear nonlinearity. J. Acoust. Soc. Am. 2007 doi: 10.1121/1.2968686. in preparation. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sewell WF. The effects of furosemide on the endocochlear potential and auditory-nerve fiber tuning curves in cats. Hear. Res. 1984;14:305–314. doi: 10.1016/0378-5955(84)90057-1. [DOI] [PubMed] [Google Scholar]
- Shera CA, Guinan JJ, Oxenham AJ. Otoacoustic estimates of cochlear tuning: Validation in the chinchilla. 30th Midwinter Meeting of the Association for Research in Otolaryngology; Denver, CO. 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera CA, Talmadge CL, Tubis A. Interrelations among distortion-product phase-gradient delays: Their connection to scaling symmetry and its breaking. J. Acoust. Soc. Am. 2000;108:2933–2948. doi: 10.1121/1.1323234. [DOI] [PubMed] [Google Scholar]
- Siegel JH, Hirohata ET. Sound calibration and distortion product otoacoustic emissions at high frequencies. Hear. Res. 1994;80:146–152. doi: 10.1016/0378-5955(94)90106-6. [DOI] [PubMed] [Google Scholar]
- Siegel JH. In: Calibrating otoacoustic emission probes, in Otoacoustic Emissions: Clinical Applications. 2nd Edition Robinette MS, Glattke TJ, editors. Thieme Medical Publishers, Inc.; New York, NY: 2002. pp. 416–441. [Google Scholar]
- Smurzynski J, Kim DO. Distortion-product and click-evoked otoacoustic emissions of normally-hearing adults. Hear. Res. 1992;58:227–240. doi: 10.1016/0378-5955(92)90132-7. [DOI] [PubMed] [Google Scholar]
- Stover LJ, Gorga MP, Neely ST, Montoya D. Toward optimizing the clinical utility of distortion product otoacoustic emission measurements. J. Acoust. Soc. Am. 1996;100:956–967. doi: 10.1121/1.416207. [DOI] [PubMed] [Google Scholar]
- Zinn C, Maier H, Zenner HP, Gier AW. Evidence for active, nonlinear, negative feedback in the vibration of the apical region of the in vivo guinea-pig cochlea. Hear. Res. 2000;142:159–183. doi: 10.1016/s0378-5955(00)00012-5. [DOI] [PubMed] [Google Scholar]
- Zwieg G. Basilar membrane motion, in Cold Spring Harbor Symposia on Quantitative Biology. XL. Cold Spring Harbor Laboratory; Cold Spring Harbor, NY: 1976. pp. 619–633. [DOI] [PubMed] [Google Scholar]


