Wall shear stress as measured in vivo: consequences for the design of the arterial system

Abstract

Based upon theory, wall shear stress (WSS), an important determinant of endothelial function and gene expression, has been assumed to be constant along the arterial tree and the same in a particular artery across species. In vivo measurements of WSS, however, have shown that these assumptions are far from valid. In this survey we will discuss the assessment of WSS in the arterial system in vivo and present the results obtained in large arteries and arterioles. In vivo WSS can be estimated from wall shear rate, as derived from non-invasively recorded velocity profiles, and whole blood viscosity in large arteries and plasma viscosity in arterioles, avoiding theoretical assumptions. In large arteries velocity profiles can be recorded by means of a specially designed ultrasound system and in arterioles via optical techniques using fluorescent flow velocity tracers. It is shown that in humans mean WSS is substantially higher in the carotid artery (1.1–1.3 Pa) than in the brachial (0.4–0.5 Pa) and femoral (0.3–0.5 Pa) arteries. Also in animals mean WSS varies substantially along the arterial tree. Mean WSS in arterioles varies between about 1.0 and 5.0 Pa in the various studies and is dependent on the site of measurement in these vessels. Across species mean WSS in a particular artery decreases linearly with body mass, e.g., in the infra-renal aorta from 8.8 Pa in mice to 0.5 Pa in humans. The observation that mean WSS is far from constant along the arterial tree implies that Murray’s cube law on flow-diameter relations cannot be applied to the whole arterial system. Because blood flow velocity is not constant along the arterial tree either, a square law also does not hold. The exponent in the power law likely varies along the arterial system, probably from 2 in large arteries near the heart to 3 in arterioles. The in vivo findings also imply that in in vitro studies no average shear stress value can be taken to study effects on endothelial cells derived from different vascular areas or from the same artery in different species. The cells have to be studied under the shear stress conditions they are exposed to in real life.

Introduction

During left ventricular ejection the blood expelled into the arterial system exerts hemodynamic forces on the artery wall. The luminal side of the artery wall is subjected to a pressure pulse, i.e., the difference between diastolic and systolic blood pressure, and a tangential stress exerted by the flowing blood. The pressure pulse distends the artery wall, resulting in radial and circumferential wall strain, i.e., the systolic increase in diameter and cross-sectional area relative to the end-diastolic level, respectively. The radial strain compresses the artery wall during systole [36]. Besides, the pressure pulse generates an axial stress, but not necessarily an axial strain. The tangential stress is known as wall shear stress (WSS). It can be estimated as the product of wall shear rate (WSR) and local blood viscosity, WSR being defined as the radial derivative of blood flow velocity distribution at the wall.

These biomechanical forces are important determinants of endothelial cell function. By modifying the production of vasoactive mediators by endothelial cells, WSS regulates arterial diameter [6, 14, 23, 44], while WSS, and radial and circumferential strain are determinants of endothelial gene expression [10, 11, 16, 34, 42]. Endothelial genes can be transiently or more permanently up-regulated by shear stress [60]. The studies on the effect of shear stress on endothelial gene expression are mostly performed in vitro. In these experiments the level of shear stress applied is generally calculated based upon Poiseuille’s law, while WSS is assumed to be constant along the arterial tree, as predicted by theory, and to be about the same in a particular artery across species. Thus endothelial cells are exposed to average calculated shear stress values, no matter the area or the species they are derived from.

In vivo measurements in arterioles [2, 31, 46, 50] and large arteries [48], however, have shown that mean WSS is neither constant along the arterial tree in a particular species, nor the same in a particular artery across species [18]. These findings have shed new light on our concepts regarding the arterial system, among which, the flow-diameter relations at bifurcations, and do have consequences for the in vitro studies on shear stress and endothelial gene expression.

In this survey, we will discuss the assessment of WSS in the arterial system in vivo and present the results obtained in large arteries and arterioles. The consequences of these findings, especially regarding the concept of the flow-diameter relations in bifurcations along the arterial tree, will be addressed.

Determination of WSS in vivo

In arterioles

Direct assessment

In cat mesenteric arterioles WSS was determined by means of micropressure measurements upstream and downstream, and length and diameter measurements [31]. Measurements of micro pressure in vivo, however, need a lot of skill and can only be realized in a limited number of experienced centers. Pries and Secomb [46] used a similar approach to determine WSS in rat mesenteric arterioles, but to circumvent micro pressure measurements they computed the pressure differences along arteriolar segments using a mathematical model [47].

Bakker and colleagues [2] determined shear stress in rat cremaster muscle arterioles from length, diameter and viscosity measurements, assuming the presence of Poiseuille flow.

Assessment from velocity profiles

In arterioles optical techniques are employed, using fluorescent particles as velocity tracers. In this approach, pairs of flashes of light provide in a single video field two images of the same tracer displaced over a certain distance for the given interval between the flashes. The time interval between the two flashes is selected so that the concomitant images of the tracer show no or only little overlap. To construct velocity profiles, i.e., the velocity distribution over the cross-sectional area of the vessel, the centroids of the images of the tracers are identified and the displacement of the tracer in the preset time interval, yielding its velocity, and its relative radial position in the vessel are measured. By using sequences of illumination at a preset delay with respect to the ECG reference, systolic and diastolic velocity profiles can be determined. Originally, fluorescently labeled blood platelets were used as velocity tracers [58]. With these tracers no data points could be obtained closer to the wall than 0.5 μm due to their physical size [13] and their orientation [59]. In more recent years nanometer particles are in use as velocity tracers [32, 61]. Because of their smaller size (0.4–0.5 μm in diameter), flow velocities can be determined as close to the wall as about 0.2 μm. Originally the velocity of the tracers and their position were determined by hand, a time-consuming procedure, but recently a computerized two-dimensional correlation technique has been developed to assess displacement and position of the tracers [61].

The experimentally determined velocity profiles can be adequately described by a modification [58] of the equation as originally described by Roevros [52]:

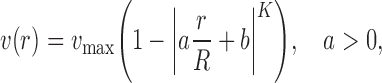1

where v(r) is the flow velocity at the radial position r, the vertical lines denote absolute values, v _max is the maximal center stream flow velocity in the vessel, R is the radius of the vessel, a is a scale factor allowing a non-zero intercept of the fit with the vessel wall, b is a parameter correcting for a shift of the top of the profile away from the vessel center (note that a and b are interrelated) and K describes the degree of flattening of the profile. K = 2 for a fully developed parabolic velocity profile; K will be higher the flatter the velocity profile is.

The platelet velocity profiles as described in this way are flattened parabolas in systole as well as in diastole [50, 58] with K factors varying between 2.3 and 4. Flattening of the profile is also indicated by the ratio of maximum and mean velocity of the profile, ranging from 1.39 to 1.54.This ratio is 2 in case of a parabolic profile. Differences in WSR at opposite walls may have to be appreciated due to asymmetry of the velocity profiles [57].

A least estimate of WSR can be obtained by determining the best fit through the measured velocity profile with the use of Eq. (1) and a linear extrapolation from the point closest to the wall, where velocity can be measured to zero flow at the wall [57]. Because in arterioles the velocity tracers are approaching the vessel wall closely, plasma viscosity, which can be accurately determined in vitro by means of glass capillary viscometry systems, is used to convert WSR to WSS.

In large arteries

Assessment from velocity profiles

Velocity profiles in large arteries can be recorded non-invasively by means of MRI [15, 40, 41, 55] and non-invasive ultrasound. In our studies the latter technique is used, because of its better spatial, and especially, temporal resolution [48].

To accurately determine velocity profiles in vivo, precise measurement of low blood flow velocities close to the vessel wall is required. This can only be achieved when the high amplitude low frequency signals reflected by the artery wall are adequately suppressed without losing the low blood flow velocity information near the wall. This can be accomplished by considering the time-dependent aspects of the reflections and using a band stop filter which adapts its rejection range to the mean frequency of the reflections from the artery wall [4]. In this adaptive filtering technique these reflections are suppressed by shifting the temporal frequency distribution toward zero frequency, the shift being given by the estimated mean frequency of the reflected signal. Subsequently, the reflections, then centered around zero frequency, are selectively suppressed by a high-pass filter with a low cut-off frequency.

To assess WSR, a conventional 2-D imager (Mark 9 HDI, ATL, Bothell, Washington, USA) with a C9-5 curved array is combined with dedicated signal processing to measure the blood flow velocity distribution along a selected line of observation across the center of the artery. After localization of the region of interest, the system is switched to a single line of observation (Motion mode; M-mode) with short emission bursts (2 periods) to retain spatial resolution and a high pulse repetition frequency to facilitate blood flow velocity detection. The radio frequency (RF) signals are captured at a sample rate of 20 MHz and stored on a computer for off-line analysis. After automatic identification of the wall-lumen interfaces, cursors, representing sample volumes, are positioned on the reflections from the anterior and posterior walls [35]. The time-dependent blood flow velocity distribution is obtained with the use of a modeled cross-correlation function applied to short segments of RF data between the cursors after suppression of the wall signals with an adaptive high pass filter. Calculation of mean blood flow velocity for all RF segments provides a time-dependent velocity profile (Fig. 1). The length of the RF segments is selected according to the actual bandwidth of the RF signals (2.5 MHz) and corresponds to 300 μm in depth; the segments are spaced at 150-μm intervals (50% overlap). For further details regarding this ultrasound technique the reader is referred to previous publications of our group [3, 4, 20].

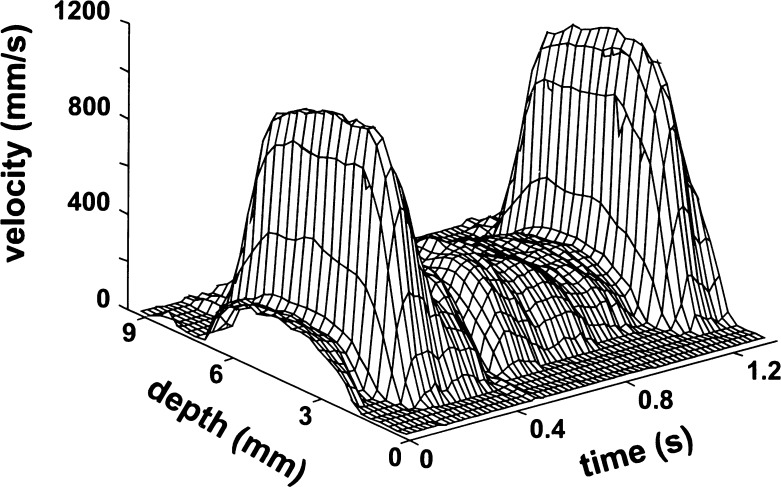
Fig. 1.

Velocity distribution in the common carotid artery of a presumed healthy volunteer. The velocities are high in the center of the artery, especially during systole, and decrease nearly linearly toward the artery wall. Note the very small velocity gradient in the center of the artery during systole

Using a similar analysis of profile shape as in arterioles, it could be demonstrated that in the common carotid artery the velocity profile is substantially flattened (Fig. 1) with a K factor of 4 in systole [8]. The systolic velocity profile is also flattened in the femoral artery [55]. In the brachial artery, however, the K factor was found to be 2.1 in systole [8], indicating that the velocity profile in this artery is close to parabolic [55]. The difference in shape of the velocity profile between the carotid and the brachial artery can likely be explained by the greater relative distension of the former artery [8, 43] and a relatively longer entrance length in the latter. The smaller diameter of the brachial artery, relative to the resolution of the ultrasound system, may contribute to the more parabolic profile measured in this vessel.

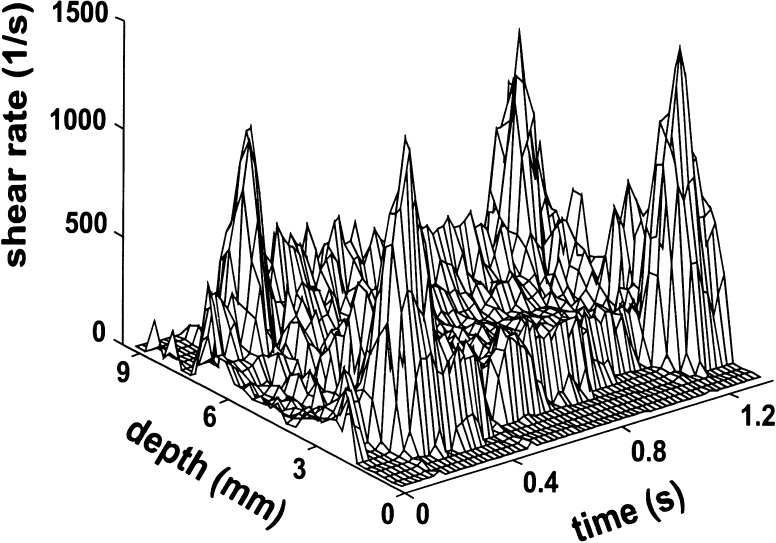
In the ultrasound systems presently in use, the shear rate distribution in an artery is derived from the radial derivative of the velocity profile at each site and each time instant (Fig. 2). Because blood flow velocities cannot be determined at the wall, the maximum value of the radial derivative of the velocity profile is considered as the estimate of instantaneous WSR [3, 20]. From the shear distribution mean WSR, the time-averaged shear rate over one cardiac cycle, and peak WSR, the value at peak systole, can be determined. When interested in WSR values in a particular artery in general, the values recorded near the anterior and the posterior walls are averaged to minimize the influence of skewness of the velocity profile and of secondary flows. In studies on the relation between WSR and artery wall structure, the shear rate values as assessed locally are used.

Fig. 2.

Shear rate distribution in the common carotid artery of a presumed healthy volunteer, as derived from the velocity profile in Fig. 1. The shear rate is substantially higher near the wall than in the center of the artery, especially during systole. The peaks near the wall represent the maximum dv/dr as measured 250–300 μm from the wall

In large arteries whole blood viscosity (WBV), which can be determined by using the approximation proposed by Weaver et al. [62], is used to calculate WSS:

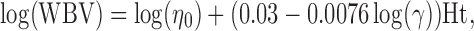2

where η _o is plasma viscosity, γ is WSR and Ht is hematocrit.

Under the shear rate conditions found in large arteries in vivo [48], the effect of changes in plasma viscosity on this estimation of WBV is negligible [8], leaving shear rate and hematocrit as the relevant parameters. In vitro WBV can be determined by means of a cone plate viscometer. The viscosity determined in this way, however, may lead to too high estimates of WBV, because it cannot be measured at appropriate and sufficiently high shear rates in all subjects studied [17].

WSS data obtained in vivo

In arterioles

The average WSS in mesenteric arterioles was found to be 1.82 Pa, with a range of 0.51–5.0 Pa, in rabbits [50], 4.71 ± 2.34 Pa (mean ± SD) in cats [31] and around 5 Pa, with a substantial variation, in rats, at least in arterioles larger than 15 μm in diameter [46]. In smaller arterioles, WSS rapidly increased to above 10 Pa in arterioles with a diameter of 6 μm [46]. The wide variation in WSS values found in these studies can likely be explained by the non-regulatory properties of mesenteric arterioles [5]; variations in blood flow velocity are not or inadequately compensated for by a change in arteriolar diameter. Besides, differences in anesthesia and variations in the site of measurement along the arterioles have to be considered.

Shear stress in the first order arterioles of rat cremaster muscle was found to be 3 ± 0.5 Pa (mean ± SEM) in the proximal part and 2.1 ± 0.5 Pa in the more distal part [2].

In large arteries

In humans

In human arteries mean WSS is far from constant along the arterial tree as predicted by theory (Table 1). In the common carotid artery of presumed healthy volunteers, mean WSS was found to vary on the average between 1.1 and 1.4 Pa in the different study populations [48], values within the limits of the theoretically predicted value of 1.5 Pa ± 50%. Mean WSS is substantially lower in muscular conduit arteries of presumed healthy volunteers, reaching average values in the common femoral artery, the superficial femoral artery and the brachial artery varying between 0.3 and 0.4 Pa, around 0.5 Pa and varying between 0.4 and 0.5 Pa, respectively (Table 1).

Table 1.

Average mean wall shear stress (Pa) in the common carotid (CCA), common (CFA) and superficial femoral (SFA) and brachial (BA) arteries at rest in healthy volunteers

	Men		Women
	Young	Old	Young	Old
CCA	1.3	1.2	1.2	1.1
CFA	0.4	0.3	–	–
SFA	0.5	0.5	–	–
BA	0.5	0.5	0.4	0.5

Derived from Reneman et al. [48]

The lower mean WSS in these conduit arteries at rest likely results from the high peripheral resistance in these vessels, reducing mean volume flow and inducing reflections. In the femoral artery, adaptation of the peripheral resistance during vasodilatation results in mean WSS values close to those in the common carotid artery [25]. Based upon these observations it may be concluded that at rest, mean WSS is regulated locally and depends on the characteristics of the peripheral circulation. Mean WSS will be higher in the absence of reflections, as in the brain circulation, and lower when reflections are dominantly present as in the arm and leg circulations at rest.

Mean shear stress in normal coronary arteries, as derived from intra-coronary velocity measurements and coronary angiography, assuming Poiseiulle flow, was found to be on the average 0.68 Pa (range 0.33–1.24 Pa) [12].

Peak WSS is not significantly different along the arterial tree, varying between 2.5 and 4.3 Pa in the common carotid artery, between 3.4 and 4.0 Pa in the femoral arteries and between 2.7 and 3.9 Pa in the brachial artery in the populations studied [48].

In humans, mean WSS also varies within artery bifurcations. At rest, mean WSS was found to be significantly lower in the common than in the superficial femoral artery; the former artery seeing reflections from both the superficial and the deep femoral artery, resulting in a longer-lasting negative flow during diastole in the common femoral artery [25]. Peak WSS is not significantly different between these arteries [25]. In the common carotid artery mean WSR, and, hence, mean WSS, was found to be lower near the bifurcation than about 3 cm more proximally. This can likely be explained by the influence of reflections from the external carotid artery at the former site, which has greatly disappeared at the latter site [27]. It is of interest to note that in both the femoral [26] and the carotid artery bifurcation [27] IMT at the posterior wall is greater in the areas with lower WSS. Also in normal coronary arteries, wall thickness and shear stress correlate negatively [63].

Mean WSS was not significantly different in men and women, either in the common carotid artery [53] or in the brachial artery [9].

In animals

Most of the shear stress data obtained in large arteries of anaesthetized animals are calculated from blood flow (as recorded optically, electromagnetically or by means of ultrasound), diameter and blood viscosity, using Poiseuille’s law. These mean shear stress data are likely to be underestimations and do not necessarily represent the shear stress value near the artery wall. Moreover, a substantial spread in the data is observed, for example, varying in the common carotid artery between 1.6 and 4.6 Pa in dogs and between 1.2 and 8.4 Pa in mice [7]. The error made in estimating the internal diameter of the artery likely contributes to this spread in the data. In dog coronary arteries shear stress was found to be around 1.0 Pa in arteries with a diameter larger than 160 μm and around 1.9 Pa in smaller ones [56]. Despite the spread in the data, it may be concluded that mean shear stress is not constant along the arterial tree in animals either [7].

Across species

Across species mean shear stress decreases with an increase in estimated internal arterial diameter. In their allometric scaling study, Greve and colleagues [18] showed that across species, including mice, rats, dogs and humans, mean WSS in the infra-renal aorta decreases linearly with body mass on a log/log scale. In this part of the aorta mean WSS was estimated to be about 0.5 Pa in men, about 7 Pa in rat and about 8.8 Pa in mice. In the common carotid artery mean shear stress varies on the average from about 1.2 Pa in humans to on the average about 7.0 Pa in mice [7]. Thus, the lesson to be learned is that in a particular artery mean shear stress will be higher, the smaller the animal is (Table 2).

Table 2.

Differences in mean wall shear stress (Pa) in a particular artery across species

	Man	Rat	Mouse
Infrarenal aortaa	0.5	7.0	8.8
Common carotid Ab	1.2	4.0	7.0

^aAccording to Greve et al. [18]

^bAccording to Cheng et al. [7]

Comments regarding the assessment of WSS in vivo

Using nanometer particles, shear rate can be determined close to the wall in arterioles. In large arteries, however, WSR is determined at some distance from the wall and, hence, the values obtained in arteries are least estimates, because shear rate increases toward the wall. Despite this underestimation, WSS as estimated at a distance from the wall will not be too different from the value at the wall, because viscosity decreases toward the wall. Shear stress can be more or less considered as a continuum from the center of the vessel to the wall. Although assessed in venules, extrapolation of the data on shear stress and shear rate as a function of vessel radius, as published by Long et al. [32], indicates that shear stress determined at 250–300 μm from the wall will underestimate wall shear stress by about 10%. For an artery with a lumen diameter of 6 mm, a distance of 300 μm, as in our ultrasound system, converts to a relative radial position of 0.9.

As indicated above, the in vivo recorded velocity profiles are generally flattened parabolas, in both large arteries and arterioles. It has been shown that in arterioles WSR is on the average 2.1 times lower (range: 1.5–3.9 times) when derived from a parabolic than from an actually measured velocity profile [57]. This underestimation of WSR, and, hence, of WSS, is even more pronounced when nanometer particles [32], allowing flow velocity assessments closer to the wall, rather than blood platelets [57, 58] are used as velocity tracers. Also in large arteries the WSR and WSS values calculated on the basis of a parabolic velocity profile are substantially lower than those derived from the actually measured profiles. In the common carotid artery mean WSR is underestimated by a factor of 2–3 [8, 20] and mean WSS by a factor of 2 [8], when assuming a parabolic velocity profile. In the brachial artery the underestimation of mean WSR and mean WSS is less pronounced [8], likely due to the more parabolic shape of the velocity profile in this artery. Such underestimations of WSR do not only affect calculated WSS, but also calculated or determined whole blood viscosity, which strongly depends on shear rate (Eq. 2).

Design of the arterial system with emphasis on the flow-diameter relations at bifurcations

The substantial differences in mean WSS along the arterial tree as found in vivo, in both man and animals, are in disagreement with the assumption that mean WSS is about constant along the arterial tree [22, 28]. As can be learned from Eq. (3), for fully developed flow, shear stress (τ) critically depends on the lumen diameter (d) of the artery:

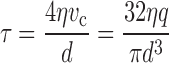3

where η is blood viscosity. To convert center stream velocity (v _c) to volume flow (q), use is made of the property that for a parabolic flow distribution v _c is twice the velocity averaged over the cross-sectional area (πd ² /4).

The concept of constant mean WSS is based upon the principle of minimal work according to Murray’s law [39], which implies that the cube diameter of a vessel should be proportional to the flow through it, converting the last part of Eq. (3) into a constant. Consequently, the cube of the diameter of a parent vessel equals the sum of the cubes of the diameters of the daughter vessels. The constant mean WSS requires adaptation of the arterial diameter to the tangential shear stress τ, i.e., any slight increase and decrease in WSS is counteracted by a proportional increase and decrease in arterial diameter, respectively [21, 51, 54, 64]. To date, it has been well established experimentally that indeed WSS is an important determinant of arterial diameter, both acutely and chronically, and that the adaptation process is of great importance in maintaining mean WSS within limits, in both large arteries and arterioles, despite changing peripheral blood flow requirements [6, 23, 24] and changes in blood viscosity [21, 37, 38].

In Murray’s law, however, it is assumed that Poiseuille’s law can be applied to the arterial system, which, among others, implies that the velocity profile is considered to be fully developed to a parabola. In general Poiseiulle’s law does not hold for the arterial system in vivo, because of the pulsatile nature of the flow, and branching, curving and tapering of the arteries. This is for instance demonstrated by the fact that the systolic velocity profile as recorded in vivo, is a flattened parabola rather than a fully developed one, in arteries due to flow unsteadiness and short entrance lengths and in arterioles mainly due to dominating viscous forces.

The validity of Murray’s “cube law” (q = cd ³) for the whole arterial tree has been challenged by Zamir and colleagues [65]. They showed that in the major branches of the aortic arch the relation between flow and diameter is governed by a “square law”, which would suggest (Eq. 3) that flow velocity is constant, independent of the diameter [65]. A “square law” for the whole arterial tree, however, is incompatible with the observation that mean blood flow velocity also varies along the arterial tree, in animals [30] as well as in man [49]. The observation that neither mean WSS, nor mean velocity is constant along the arterial tree indicates that the exponent in the power law may vary along the arterial tree, a concept already considered by Zamir and colleagues [65]. At the present state of the art, it may be concluded that Murray’s law does not hold for the whole arterial system and that the exponent of the power law varies along the arterial tree, possibly from 2 in larger arteries [65] to about 3 in arterioles [33]. In line with this idea is the earlier observation that the exponent of the power law was found to be 2.55 in coronary arteries [1].

One should bear in mind that the varying mean WSS values and the varying exponents of the power law along the arterial tree, as described above, refer to the situation at rest. During exercise the situation is likely to be different due to adaptation of the peripheral resistance during vasodilatation. In the femoral artery vasodilatation results in disappearance of reflections and in mean WSS values close to those in the common carotid artery [25]. The increased WSS values during vasodilatation indicate that the artery is incapable to fully counteract the increase in shear stress by lumen enlargement. During strenuous exercise the increase in mean WSS will even be more pronounced. Under these circumstances volume flow in the femoral artery may increase tenfold, which requires at least doubling of the arterial diameter (Eq. 3) to maintain shear stress at the same level. However, under sustained high flow conditions the increase in arterial diameter will maximally be about 20%, as indicated by flow-mediated dilatation experiments in the brachial artery. A tenfold increase in flow in combination with a 20% increase in diameter will cause a 5.8-fold increase in shear stress (Eq. 3), resulting in mean WSS values between 1.8 and 3.0 Pa in the femoral artery bifurcation during strenuous exercise.

Concluding considerations

The in vivo data presented clearly show that at rest mean WSS is far from constant along the arterial tree as predicted by theory, neither in man, nor in animals. In man mean WSS is about four times higher in the carotid artery than in the femoral and brachial arteries. The lower mean WSS in the latter arteries can be explained by the high peripheral resistance in these arteries at rest and is logical from a physiological point of view. It allows for an increase in mean WSS during exercise without reaching high levels that could be damaging to endothelial cells. During exercise, after all, the arteries may have to accommodate ten times higher blood flows, which would lead to too high WSS levels when starting at a high level already, because arteries can dilate maximally 20%. It is also shown that across species WSS in a particular artery is substantially different and will be higher, the smaller the animal is. Also along arterial bifurcations, and within arteriolar networks and a specific artery WSS may vary. The differences in WSS along the arterial tree as described in this review refer to developed arterial systems. In developing arterial systems WSS has been shown to be constant along the arterial system, at least in arteries with a diameter larger than about 60 μm [29]. Apparently, the diameter adapts to the flow to be carried during development. This does not imply that WSS is the sole determinant of importance in the developing arterial system. Model studies have shown that stable arterial systems can only develop and be maintained through interplay among WSS, arterial pressure, circumferential stress [19, 45, 46] and metabolic tissue status [45].

The differences in mean WSS along the arterial tree imply that Murray’s cube law of minimal energy discharge does not hold for the whole arterial system. A square law cannot be applied to the whole arterial tree either, because mean blood flow velocity also varies along this tree. At the present state of the art, it may be concluded that the exponent of the power law varies along the arterial tree, probably from 2 in large arteries near the heart to 3 in arterioles.

The in vivo observations on mean WSS also have consequences for the in vitro studies on the interaction between shear stress and endothelial cell gene expression. In these studies endothelial cells are exposed to an average shear stress value calculated based upon Poiseuille’s law and assuming shear stress to be constant along the arterial tree. Poiseuille’s law cannot be applied and, based upon the in vivo findings, no average shear stress value can be taken to study effects on endothelial cells derived from different vascular areas or from the same artery in different species. The cells have to be studied under the shear stress conditions they are exposed to in real life.

It should be kept in mind that the ultrasound techniques presently available to non-invasively assess WSR, and, hence, WSS, in vivo do have their limitations. Not only is the spatial resolution of the systems limited, but at the present state-of-the-art WSR can reliably be determined only in relatively straight arteries. This is a serious limitation, because information about the level of WSS and its direction in arterial bifurcations, especially opposite to flow dividers, is of utmost importance when studying the role of WSS in atherogenesis. In our institute we are working on a different approach to the assessment of velocity profiles, using multiple lines of observation (multiple M-line technique), that may allow assessment of the shear rate distribution in bifurcations as the carotid artery bulb.