Structure determination of a Galectin-3–carbohydrate complex using paramagnetism-based NMR constraints

Abstract

The determination of the location and conformation of a natural ligand bound to a protein receptor is often a first step in the rational design of molecules that can modulate receptor function. NMR observables, including NOEs, often provide the basis for these determinations. However, when ligands are carbohydrates, interactions mediated by extensive hydrogen-bonding networks often reduce or eliminate NOEs between ligand and protein protons. In these cases, it is useful to look to other distance- and orientation-dependent observables that can constrain the geometry of ligand–protein complexes. Here we illustrate the use of paramagnetism-based NMR constraints, including pseudo-contact shifts (PCS) and field-induced residual dipolar couplings (RDCs). When a paramagnetic center can be attached to the protein, field-induced RDCs and PCS reflect only bound-state properties of the ligand, even when averages over small fractions of bound states and large fractions of free states are observed. The effects can also be observed over a long range, making it possible to attach a paramagnetic center to a remote part of the protein. The system studied here is a Galectin-3–lactose complex. A lanthanide-binding peptide showing minimal flexibility with respect to the protein was integrated into the C terminus of an expression construct for the Galectin-3–carbohydrate-binding domain. Dysprosium ion, which has a large magnetic susceptibility anisotropy, was complexed to the peptide, making it possible to observe both PCSs and field-induced RDCs for the protein and the ligand. The structure determined from these constraints shows agreement with a crystal structure of a Galectin-3–N-acetyllactosamine complex.

Carbohydrate–protein interactions are primary mediators in the communication of a cell with its environment. They influence cell adhesion, modulate intracellular signaling, and provide a pathway for entry of several pathogens. Recently, these interactions have become targets for the development of drugs that can modulate cellular processes, and the determination of the structural characteristics of the complexes has become an issue (Greer et al. 1994; Barchi 2000; Henry 2001; Klyosov et al. 2006). Structure determination of complexes, particularly those of lectins with natural ligands, can be problematic. The interactions are often weak, with binding affinities in the range of 100 μM–1 mM. This works against crystallization of complexes for study by X-ray crystallography. NMR structure determination also has problems in that interactions are often dominated by hydrogen-bonding networks that place non-exchangeable proton pairs across the protein–ligand interface at distances too great for the measurement of useful NOEs. Here we present an alternative NMR approach that is not NOE-based. Instead, it relies on a combination of orientationally sensitive measurements (residual dipolar couplings [RDCs]) and long-range distance- and orientation-dependent measurements (pseudo-contact shifts [PCSs]), to conformationally constrain and locate a carbohydrate ligand in a protein-binding site.

The conventional NMR approach to determination of the structure of weakly binding ligands usually involves a combination of transferred NOEs (trNOEs) to determine bound ligand geometry (Poveda et al. 1998; Moore 1999; Post 2003) and saturation transfer difference (STD) spectra to determine parts of the ligand in closest contact with the protein surface (Mayer and Meyer 1999; Meyer and Peters 2003). Both of these approaches work very well, particularly in the case of complexes of small ligands in rapid exchange on and off the surface of large proteins. Here, the very efficient cross-relaxation properties of large systems allow information on the bound ligand to dominate measurements, even with a 10–100-fold excess of ligand over protein. However, neither method returns much information about the placement of the ligand on the protein surface. As mentioned above, intermolecular NOEs that could provide this placement are often difficult to observe because of the paucity of non-exchangeable pairs of protons at the carbohydrate–protein interface.

Residual dipolar couplings do provide a good complement to NOE measurements, and several examples of their measurement under conditions of rapid ligand exchange have appeared (Shimizu et al. 1999; Jain et al. 2003; Chen and Reif 2004; Zhuang et al. 2006; Seidel et al. 2007). Under ideal circumstances, RDCs can provide orientational information on both a protein and its ligands, making it possible to determine the relative orientations of ligand and protein. The development of reliable methods for their measurement has not, however, been straightforward. RDC measurements are normally achieved by aligning the protein and ligand in liquid crystal media, often by steric interactions of the anisotropically shaped molecules with elements of the alignment medium. Problems arise in that, unlike transferred NOEs, one cannot count on preferential orientation of the bound complex and domination of measurements by information on the ligand in this complex. The complex and free ligands are equally likely to have anisotropic shapes.

Methods developed in our laboratory to overcome this problem have so far relied on enhancing the alignment of the protein through addition of elements having specific interactions with the hydrophobic elements of the alignment medium. In one case, a short hydrophobic chain was attached to a cysteine at the C terminus of the protein, and in another case the incorporation of a chelate-carrying lipid was integrated into the orientation medium so that it could bind His-tag-terminated proteins (Zhuang et al. 2006; Seidel et al. 2007). In both cases, the enhancement in protein alignment results in the enhanced alignment of bound ligands and domination of measured ligand RDCs by the protein-bound fraction.

The applications of the above RDC enhancement strategies are, however, limited. In the case of the incorporation of a hydrophobic chain, the limitation is associated with a requirement for a single reactive cysteine in the protein sequence, and in the case of association between poly-histidine-tagged protein and chelate-carrying lipid, the limitation is associated with an excessive interaction of the protein with the alignment medium that results in severe line broadening of protein signals and an inability to determine protein orientation. In both cases, the requirement for an alignment medium with hydrophobic properties excludes applications to more hydrophobic ligands, which would have competitively strong interactions with the medium even as free molecules. The latter is particularly restrictive for drug discovery in which the addition of hydrophobic moieties is a common approach to increasing affinity. Also, methods based purely on orientational constraints cannot position ligands translationally. We hope to address all of these limitations in the methods described below.

Alignment without the use of hydrophobic liquid crystal media is possible if a molecule has a sufficiently high magnetic susceptibility anisotropy. In the presence of a magnetic field, a magnetic moment is induced in a substance in proportion to its magnetic susceptibility. This moment, in turn, interacts with the magnetic field to produce an energy of interaction that is proportional to the magnetic field squared. When the susceptibility is anisotropic, different orientations will have different energies, and orientational distributions become non-isotropic in accordance with Boltzmann statistics. For a protein–ligand system, the susceptibility of the protein can be made an order of magnitude or more larger than that of the ligand by attaching an appropriate paramagnetic tag. This will accomplish the desired enhanced alignment of the bound ligand without the use of a hydrophobic alignment medium.

The use of appropriate paramagnetic tags has an additional advantage in that they can also provide relatively long-range distance constraints (distance between the paramagnetic center and NMR observable sites of interest). Both paramagnetic enhanced relaxation and pseudo-contact shifts can provide this distance information. It is pseudo-contact shifts that we choose to use here. Pseudo-contact shifts have a distance dependence that is less steep than an NOE (proportional to 1/r ³). In combination with a large paramagnetic moment, this allows pseudo-contact shifts to be observed for nuclei up to 40 Å away from the metal center (Allegrozzi et al. 2000; Gaponenko et al. 2004).

There have been applications of paramagnetic constraints previously. Many of the early applications were to metalloproteins, since an appropriate paramagnetic metal ion can often be incorporated through replacement of an original ion with a suitable paramagnetic ion (Lee and Sykes 1980; Bertini et al. 2001a,b, 2005). However, among all proteins, only an estimated one-third are metalloproteins (Ascone et al. 2003), and it is useful to be able to introduce additional metal-binding sites. More recently, applications have used metal-binding tags. A metal-binding chelate can be chemically attached to a cysteine through a cysteine-specific reaction (Ikegami et al. 2004; Su et al. 2006) or a metal-binding peptide can be incorporated into the expression construct of the protein of interest (Ma and Opella 2000; Franz et al. 2003; Wohnert et al. 2003). It is this latter approach that we use here.

Using combinatorial screening, and beginning with a consensus sequence for calcium-binding motifs of EF-hand proteins, a short polypeptide (YIDTNNDGWYEGDELLA) had been previously developed to present a particularly high affinity for lanthanide ions (Nitz et al. 2003). Lanthanide ions have very useful properties for luminescence studies, X-ray crystallography, and NMR studies involving paramagnetic effects. This makes fusion constructs between polypeptides like this, and proteins of interest, particularly appealing (Martin et al. 2005). The properties of the original peptide have been thoroughly investigated, including production of an X-ray structure (Nitz et al. 2004). Second-generation tags have also been designed, including those with two lanthanide-binding sites that give greatly improved magnitudes of alignment (Martin et al. 2007). In this study, the original lanthanide-binding tag was added to the C terminus of the expression construct for our target protein. One issue that will become important is minimizing flexibility of the tag relative to the protein, while maintaining native protein structure. For this reason, minimizing the length of the linker was explored, and both N- and C-terminal tags were explored. The N-terminal tag was excluded from this study because of the formation of inclusion bodies on protein expression. The C-terminal-tagged protein proved to be soluble and well behaved. In the final construct, a C-terminal tag with no linker amino acid between the tag and the C terminus of the protein was used.

The target protein chosen is the carbohydrate-binding domain of Galectin-3. Galectin-3 is a mammalian protein that is found in the cytosol and the nucleus as well as extracellularly (Barondes 1984; Cooper and Barondes 1990). In its extracellular role, it has been implicated in modulation of inflammatory response, migration of malignant cells, and regulation of various growth factors. In its intracellular role, it has been implicated in various apoptotic events (Yang et al. 1996; Akahani et al. 1997; Nakahara et al. 2005).

Galectin-3 is normally a two-domain protein with both a C-terminal carbohydrate-binding domain and an N-terminal oligomerization domain. It is only the C-terminal domain that we study here. This domain has a molecular weight of ∼15 kDa. It has a high-resolution crystal structure (Seetharaman et al. 1998), and previous NMR studies have led to assignment of cross-peaks in its ¹⁵N–¹H NMR spectrum (Umemoto and Leffler 2001). Galactose-terminated cell surface oligosaccharides are believed to be its primary natural ligands. Here we study binding of lactose as a small soluble analog of these ligands. Lactose binds to the protein weakly with a K _d of 0.2 mM and undergoes fast exchange on and off the protein-binding site (Tejler et al. 2005). RDCs and pseudo-contact shifts of both the protein (Galectin-3–LBT) and the ligand are measured to allow a structure calculation of the ligand–protein complex.

Results

Protein RDCs and PCSs

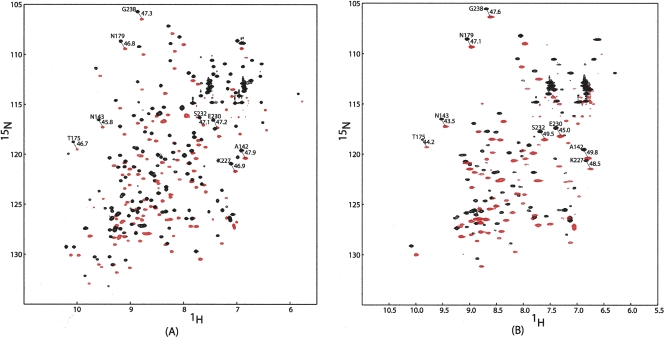
Figure 1 presents a comparison of HSQC and TROSY overlays for samples of tagged Galectin-3 with the diamagnetic metal Lu³⁺ (Fig. 1A) and the paramagnetic metal Dy³⁺ (Fig. 1B) at 600 MHz. HSQC cross-peaks (which are fully decoupled) are displaced from TROSY cross-peaks (which are not decoupled) by one-half the sum of scalar and dipolar couplings in both dimensions. The difference in the offsets between diamagnetic and paramagnetic cases yields one-half the RDC coupling at each site. It is readily apparent that both positive and negative couplings can be observed and that the approximate range of coupling at 600 MHz is ±6 Hz. These couplings are dependent on field squared, and similar measurements at 900 MHz show a range of ±15 Hz. Interpolating to 800 MHz for comparison, this is approximately twice the range seen in the original study of tagged ubiquitin (Wohnert et al. 2003), an indication that the mobility of the tag may be restricted. Cross-peaks for the non-tagged protein have been assigned previously, and in most cases, these assignments could be transferred unambiguously to the spectra in Figure 1. Based on the assignments, it is clear that for the paramagnetic sample, owing to the strong relaxation enhancement, the cross-peaks from residues close to the metal center (15 Å or less) are severely broadened or completely disappear. These effects are also field-squared dependent, and additional peaks are lost in spectra at 900 MHz.

Figure 1.

¹H–¹⁵N HSQC and TROSY overlays for 0.3 mM Galectin-3–LBT at a ¹H frequency of 600 MHz with (A) 0.3 mM Lu³⁺ and (B) 0.3 mM Dy³⁺.

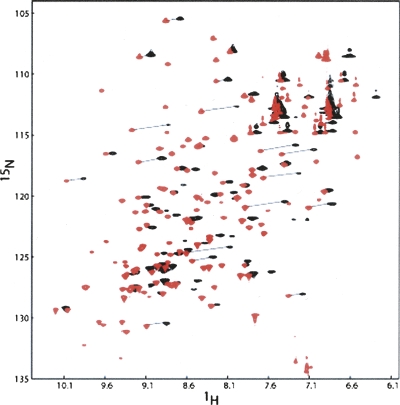
The dipolar interaction between the unpaired electrons of the lanthanide ion and the nuclei of the protein also causes changes in chemical shifts (pseudo-contact shifts) (see Fig. 2). The chemical shift changes in parts per million (ppm) are independent of the type of the nucleus (¹H or ¹⁵N) but depend on the length of the nucleus to metal ion vector, as well as on its orientation in the principal susceptibility frame (Jensen et al. 2006). For backbone ¹H and ¹⁵N pairs at long distances from the metal, similar chemical shifts changes (in ppm) are expected in both dimensions. On comparing spectra of complexes with paramagnetic ions (Dy³⁺) to spectra of complexes with diamagnetic ions (Lu³⁺), this leads to a characteristic diagonal shift in peak positions that helps pair the resonances of diamagnetic and paramagnetic samples. In principle, chemical shift anisotropy offsets, which occur on orientation of the protein, also lead to differences in chemical shifts (John et al. 2005). However, at 600 MHz, for the complexes studied here, these are estimated to be <5 Hz and do not significantly contribute to most shifts. The pseudo-contact shifts, however, are large enough to introduce a few additional ambiguities in assignments of shifted peaks. The ambiguities in assignments, accidental peak overlap, and peak broadening reduced the number of RDCs and PCSs that could be measured to 37 and 34, respectively. The values measured have been deposited in the BMRB (accession numbers: 15705 and 7422).

Figure 2.

¹H–¹⁵N HSQC spectra at a ¹H frequency of 600 Hz for 0.3 mM Galectin-3–LBT with 0.3 mM Lu³⁺ (red) or with 0.3 mM Dy³⁺ (black). Many peaks disappear for the protein sample with paramagnetic Dy³⁺. Peak assignments were accomplished by drawing a diagonal line between diamagnetic and paramagnetic peaks as shown in the figure.

Analysis of protein RDCs and PCSs

The equations connecting RDCs and PCSs with the magnetic susceptibility tensor share a very similar form. This can be seen in Equations 1 and 2, where θ and φ are polar angles of the interaction vectors in the principal susceptibility tensor frame, the Δχs are the axial and rhombic components of the susceptibility anisotropy tensor, and the rs are the lengths of the vectors between interacting pairs of nuclei and a nucleus and the paramagnetic center, respectively (Kurland and McGarvey 1970; Bertini et al. 2001b; Barbieri et al. 2004). Both equations are written here to give results in units of hertz.

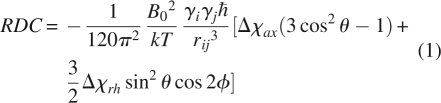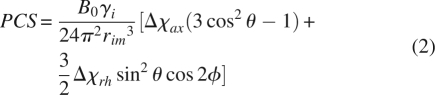The above equations assume one knows how to orient the principal frame of the susceptibility tensor in the molecular frame. This is usually not the case, and the equations can also be written in an arbitrary molecular frame (usually the frame of an available PDB file). These forms are given in Equations 3 and 4, where the θs are the angles of the interaction vector relative to the molecular frame axes.

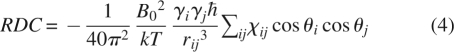The equations can, in turn, be related to the level of order induced in the molecule as represented by the order tensor elements, S_ij, using the relationship in Equation 5 (Prestegard et al. 2004).

While the susceptibility tensor elements (or order tensor elements) would appear to be the same in the two expressions above, there is a subtle difference. In both cases, the susceptibility tensor is an effective tensor, reduced in magnitude for NMR-detectable sites in the protein by any internal motion between the tag and the protein. The reduction is in principle different in the two cases because of the difference in distances and angles used, and this has led to a practice of separately fitting the two tensors (Keizers et al. 2007). Here we plan to exploit the potential difference in the tensors to assess the nature of any motion. In cases in which there appears to be no motion, use of a common set of tensor elements results in a reduction in the number of parameters to fit by a factor of 2.

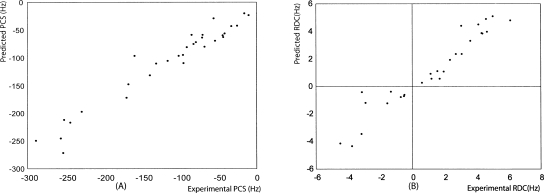
To assess the validity of a rigid model, we used an order tensor derived purely from RDC data to back-calculate PCSs for models that differed only in placement of the lanthanide ion. The program REDCAT was used to determine the order tensor elements from RDCs (Valafar and Prestegard 2004). At ¹H 600 MHz, these were S_zz = 2.4E-04, S_yy = −2.0E-04, and S_xx = −3.5E-05. Models used to back-calculate PCSs were generated by moving the ion over points on a 2 Å grid, and at each point Equation 3, as modified by substitution of order tensor elements, was used to back-calculate pseudo-contact shifts. Figure 3 shows correlation plots comparing experimental and calculated data for both PCSs (Fig. 3A) and RDCs (Fig. 3B). The fit of the PCS data are, in fact, reasonably good, giving confidence that a suitable model based on a single rigid structure could be found.

Figure 3.

Experimental RDCs and PCSs at a ¹H frequency of 600 Hz vs. back-calculated PCSs and RDCs using the structural coordinates determined by a 2 Å grid search.

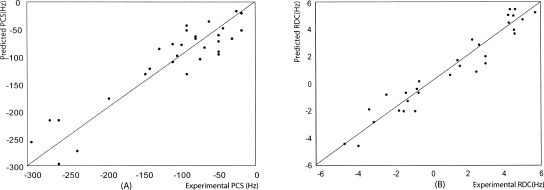
The above calculation does not take into account constraints imposed by bond connections between the tag and protein or by van der Waals contacts between tag and protein atoms. To introduce these constraints and improve the ion position, tools in the software package XPLOR-NIH were used. The position of the metal ion was adjusted using the internal variable module (Schwieters and Clore 2001) and PARArestraints module (Banci et al. 2004) as described in the Materials and Methods section. Both RDC and PCS constraints were used in conjunction with a single set of pseudo-atoms representing the alignment frame. By varying the number of flexible residues between the tag and protein, a structure was identified with good molecular contacts, only 1 PCS violation larger than 0.1 ppm, and no RDC violations >2 Hz. This was achieved by allowing a segment of 11 amino acids (from 244 to 254) to adopt a new conformation in the course of the simulation. The position of the lanthanide proved to be within 3 Å of that found by the grid search. The correlation plots for experimental PCSs plus RDCs and back-calculated PCSs plus RDCs show a very good agreement (Fig. 4A,B) with Q-factors (Bax 2003) of 0.23 and 0.27, respectively. The good agreement using only one structure suggests that the tag can be modeled as rigid with respect to the protein.

Figure 4.

Experimental PCSs and RDCs at a ¹H frequency of 600 MHz vs. back-calculated PCSs and RDCs using structural coordinates determined using XPLOR-NIH.

Ligand RDC and PCS measurements

RDCs and PCSs for the ligand were measured from ¹H–¹³C HSQC spectra taken with natural abundance material. An adequate signal-to-noise ratio is only achievable in these spectra if the ligand concentration can be in excess over that of the protein. Under these circumstances, ligand RDCs and PCSs are heavily weighted by the fraction in the free state, and measured values are much reduced from their bound values. A compromise between the signal-to-noise ratio and the size of measured values was reached at a 5:1 ratio of ligand over protein.

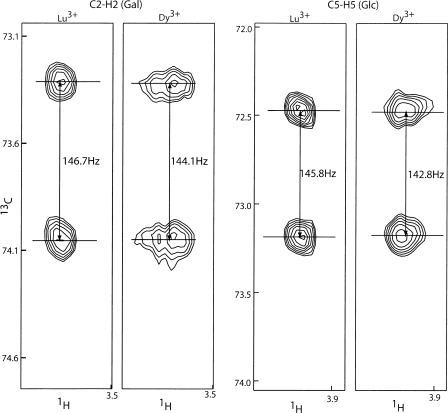
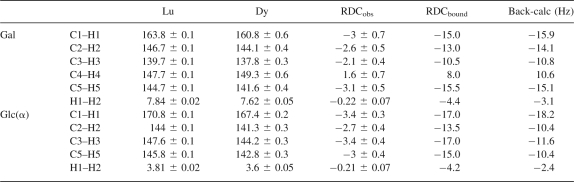
¹H–¹³C RDCs of ligand were obtained through the measurement of the splitting difference in the ¹³C dimension between the sample with diamagnetic Lu³⁺ and the sample with paramagnetic Dy³⁺. RDC measurements of C2–H2 of galactose and C5–H5 of glucose taken at 800 MHz are shown in Figure 5. To optimize the reliability of measured data, a Bayesian parameter estimation program, XRambo (Andrec and Prestegard 1998), was used for the extraction of RDCs and PCSs. The RDCs and PCSs of lactose measured by XRambo are presented in Tables 1 and 2. Bound lactose RDCs and PCSs were calculated using the following equations:

Figure 5.

RDCs measurement of C2–H2 of galactose and C5–H5 of glucose. RDCs were measured as the splitting difference in the ¹³C dimension between the sample with diamagnetic Lu³⁺ and the sample with paramagnetic Dy³⁺.

Table 1.

RDCs for 2.5 mM lactose with 0.5 mM Galectin-3–LBT at a ¹H frequency of 800 MHz

Table 2.

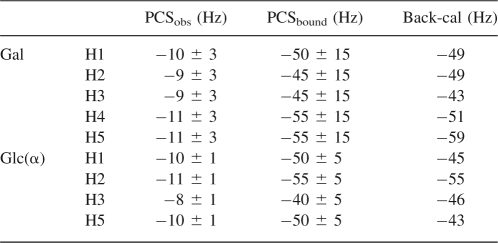
PCSs for 2.5 mM lactose with 0.5 mM Galectin-3–LBT at a ¹H frequency of 800 MHz

Here f _bound is the fraction of bound-state ligand that can be determined from a K _d along with total ligand and protein concentrations.

Ligand alignment determination

Coordinates for the heavy atoms in lactose were extracted from a crystal structure of a fungal galectin having lactose-bound (PDB ID:1ULC) (Walser et al. 2004). Hydrogens were added using standard geometries as provided in the Protonate Tool of the software program AMBER. Using the calculated ¹H–¹³C and ¹H–¹H RDCs for the bound ligand as presented in Table 1 and the extracted coordinates, principal order tensor elements (S_xx, S_yy, and S_zz) were determined for the ligand. REDCAT was used with error settings of ±4 Hz. If measurements and projections based on binding constants are accurate, the order tensors determined for the ligand should be identical to those determined for the protein. The order tensors found for the ligand after scaling down from ¹H 800 MHz to ¹H 600 MHz were (S_zz = 2.6E-04, S_yy = −2.4E-04, and S_xx = −2.2E-05). They are very close to those found for the protein (S_zz = 2.4E-04, S_yy = −2.0E-04, and S_xx = −3.5E-05). The actual alignment frame orientations should also be shared between the protein and lactose. When both the lactose coordinates and the protein coordinates are transformed to their principal alignment frames, the orientation of lactose relative to the protein can be examined. The transformation of lactose actually has a fourfold ambiguity because of the insensitivity of RDCs to inversion of axes (Al-Hashimi et al. 2000). However, only one of the possible orientations has an orientation of the galactose ring of lactose that would allow contacts seen in the crystal structure. The actual orientation is 10°–15° rotated from the galactose orientation found in the crystal structure.

Ligand-bound protein complex structure calculation

Actual docking of the lactose into the Galectin-3-binding site requires both orientational and translational constraints. Initially, we explored the ability of PCSs to add the required translational constraints. Because of broadening of the galactose proton resonances, these measurements have lower precision than for the glucose proton resonances. These are presented in Table 2. Using our optimized model for Galectin-3 with its lanthanide tag, we carried out an XPLOR-NIH calculation in which the ligand and protein were treated as separate rigid entities. The principal order parameters for the protein were used along with all measured RDCs and PCSs for both the protein and ligand. The set of 10 minimum energy structures showed the lactose positions to be closely clustered (<1 Å). However, the position relative to that of N-acetyllactosamine in a Galectin-3 crystal structure (1AK3) does deviate. When protein coordinates for a typical complex generated are superimposed on the protein coordinates for 1AK3, our lactose position deviates from that of the N-acetyllactosamine by an RMSD for lactose heavy atoms of 4.3 Å. This is clearly not high-accuracy positioning, but it does place the lactose well within the proper binding site.

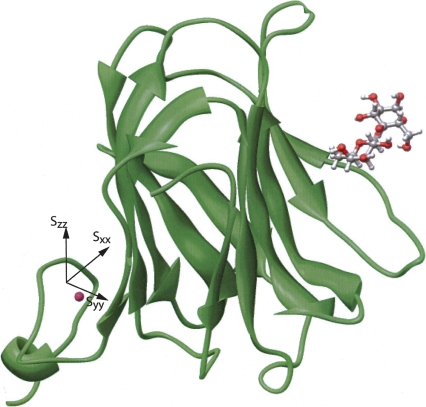
We were able to measure one intermolecular NOE for the lactose–Galectin-3 complex, that between H3 of galactose and the amine proton of the W181 side chain with an estimated distance of 2.5 ± 0.5 Å (Zhuang et al. 2006). We then added a constraint based on this NOE and repeated the XPLOR calculation. Figure 6 shows the final minimal energy structure of the lactose-bound Galectin-3 CRD. By comparison with the crystal structure of N-acetyllactosamine-bound Galectin-3 CRD, lactose showed a small degree (∼10°–15°) of rotation, but no van der Waals contacts or hydrogen-bond violations were observed. The RMSD (0.46 Å) of the bound ligand was calculated by superimposing 10 structures with minimal energy using VMD (Humphrey et al. 1996). The RMSD of the lactose relative to the X-ray structure for the average of these 10 structures is 1.91 Å when the protein coordinates were superimposed.

Figure 6.

Final ligand–protein complex structure determined by XPLOR-NIH using ligand and protein RDCs, PCSs, and a single ligand–protein NOE.

Discussion

In the above studies, we have shown that the incorporation of a lanthanide-binding tag to align a protein at high magnetic field can provide adequate RDC and PCS constraints to position and orient a ligand bound to the tagged protein. Agreement of the ligand position and orientation is acceptable despite the rather small magnitudes of PCSs and the resultant low precision of distance constraints. The use of PCSs proves to be very important as they provide distance constraints that translationally constrain the ligand in much the same way that a protein–ligand NOE would. However, unlike NOEs, which are proportional to 1/r ⁶, PCSs are proportional to 1/r ³. This, along with a much larger paramagnetic magnetic moment, allows distance constraints up to 35 Å to be measured with useful accuracy. In our case, the glucose residue for which we could accurately measure PCSs is more than 30 Å away from the metal center based on the calculated ligand-bound protein complex, and despite the small values of PCSs, the constraints prove to be useful. On inclusion of just a single NOE to the galactose ring, an excellent structure was obtained. PCSs, as an alternative source of distance information, are particularly important for carbohydrate–protein interaction as the number of observable NOE constraints is often small.

One caveat in the current combined use of RDCs and PCSs is that the model assumed in analysis was a rigid model, in which it is assumed that there is no internal motion between the lanthanide-binding tag and the protein. An attempt to minimize such motions was made in the present case by including no linkage amino acids between the protein and tag. This may not always produce viable constructs, and production of a system that fits a rigid model may not always be possible. There are examples in the literature where motion of tags clearly exists (Wohnert et al. 2003), and there is one other example where this motion appears to have been minimized (Su et al. 2006). Some investigators have also devised ways to deal with the averaging of some of the observables that result (Iwahara et al. 2004).

It is important to note that the fact that our data on the protein fit a rigid model well, does not necessarily mean that there is no motion. There are, in fact, very simple motional models for which averaging produces distance-dependent effects that are analytically identical to those of a rigid model. One involves the motion of the tag over the surface of a sphere having the lanthanide location for the rigid model at the center of the sphere. This can be understood by drawing an analogy between the magnetic field coming from the induced dipole at the lanthanide and the electric field from an electric dipole (A. Redfield, pers. comm.). The electric dipole can be represented as two point charges, and it is readily accepted that the field from a charge distributed uniformly over the surface of a sphere is identical to that from an equivalent point charge at the center. This accidental degeneracy of rigid and motional models was also pointed out for the case of rapid averaging of NOEs several years ago (Lemaster et al. 1988). For pseudo-contact shifts, there is the additional complication of averaging the orientation of the susceptibility tensor and whether such averaging would have the same effect on PCSs and RDCs. A qualitative argument can be made that these would have the same effect as long as the distance to the site of observation were larger than the radius of the sphere.

One of the main advantages of the lanthanide approach is the ability to collect data without the use of hydrophobic alignment media. One of the long-term objectives of applications like that described is the investigation of the bound geometry of drug candidates. Very frequently the binding affinities of drugs are enhanced by the incorporation of hydrophobic moieties (Sorme et al. 2002; Tejler et al. 2005). These modified compounds tend to associate directly with many of the hydrophobic media used for RDC alignment. Such associations make data coming from the free ligand dominate average measurements made on exchanging systems, and prevent analysis of bound state geometries.

One of the continuing limitations of approaches that heavily depend on orientational data is the requirement that sufficient data be collected to completely define the geometry of the system. For RDCs one must determine five parameters (order, asymmetry, and three angular terms) for each rigid unit that one wants to consider. A relatively large number of interaction vectors giving rise to RDCs must therefore be non-collinear. In carbohydrates, finding and measuring this number is often difficult because vectors such as ¹³C–¹H vectors in β-linked glucose rings are nearly parallel. PCSs, of course, help here as well. However, there is another potential advantage of lanthanide tags in that the use of different lanthanides can give distinctly different orientational alignment (Bertini et al. 2001b; Su et al. 2006; Pintacuda et al. 2007). We have presented only data on Dy³⁺ here. Data using Tb³⁺ were also collected successfully, but in our case the alignment tensor was not sufficiently different to warrant inclusion in the analysis. This may not be the case in other studies.

Materials and Methods

Galectin-3–LBT preparation

The lanthanide-binding tag is appended to the C terminus by regular cloning techniques. The nucleotide sequence of the lanthanide binding tag is 5′-TATATTGATACCAATAATGATGGCTGGTATGAAGGCGATGAACTGCTGGCG-3′. The incorporation of this 51-base polynucleotide cannot be achieved by a single-step PCR reaction. Instead, the polynucleotide was incorporated using three sequential polymerase chain reactions, each adding approximately a third of the sequence. No linker amino acid is introduced to prevent increasing the flexibility of the tag. One forward primer and three reverse primers were designed. These included 5′-AACGAGCGGCATATGCTGATTGTGCC-3′ (forward primer), 5′-CATCATTATTGGTATCAATATATATCATGGTATATGAAGCAC-3′ (first reverse primer), 5′-CATCGCCTTCATACCAGCCATCATTATTGGTATCAATATA-3′ (second reverse primer), and 5′-CGGCTCGAGTCACGCCAGCAGTTCATCGCCTTCATACCAGCC-3′ (third reverse primer). An Xho1 restriction site is included in the third primer. A PET-3c vector containing the gene encoding Galectin-3 CRD was used as the DNA template for the first PCR step. The PCR product was purified after each PCR step and was used for the subsequent PCR reaction. The complete PCR product after the third step and a PET-29a vector were double-digested by Nde1 and Xho1. The circular plasmid was obtained through ligation of the digested PCR product to the digested PET-29a vector using T4 DNA ligase (Bio-Rad). The correct sequence of the gene was verified by gene sequencing at IBL (UGA).

The same protein expression protocol was used here for the expression of both unlabeled and ¹⁵N-labeled protein as described in previous publications (Leffler et al. 1989; Zhuang et al. 2006). Since the lanthanide ion will precipitate at pH >7, a pH 5.4 MES buffer that contains 50 mM MES, 50 mM NaCl, 5 mM EDTA, and 2 mM DTT is used as the cell lysis buffer and storage buffer. The protein is purified by binding the protein to a lactosyl-agarose affinity column and eluting with 300 mM lactose. The protein after the affinity column is pure as tested through SDS-PAGE electrophoresis. The protein was concentrated and excess lactose was removed using an Amicon concentrator (Millipore). Before the protein was mixed with lanthanide ions, EDTA was removed by buffer exchange using 50 mM MES buffer (50 mM MES, 50 mM NaCl, pH 5.4).

To ensure that the protein has the tag and the protein conformation does not change significantly, mass spectrometry and ¹⁵N–¹H HSQC spectroscopy were performed to check the molecular weight of the protein and the chemical shifts of all the residues. The molecular weight shows very good agreement with the theoretical value (17,533 Da). The HSQC spectrum was compared with the spectrum of the Galectin-3 CRD, and except for a few belonging to the C terminus, the cross-peaks do not show chemical shift changes. Extra resonances are also observed, consistent in number with that expected for the lanthanide-binding tag.

NMR experiments

To prevent the nonspecific binding of the metal ion with the protein, the protein was mixed with dysprosium chloride in a 1:1 ratio. The same concentration of diamagnetic protein sample was prepared by mixing the protein with lutetium chloride in a 1:1 ratio. NMR experiments were recorded at 25°C in 50 mM MES buffer (pH 5.4) with 50 mM NaCl at a ¹H frequency of 800 MHz or 600 MHz on Varian Inova NMR spectrometers. Both are equipped with triple resonance gradient probes; in the case of the 800-MHz spectrometer, this is a cryogenic probe with enhanced sensitivity. Although the level of protein alignment is proportional to B₀ ², paramagnetic relaxation enhancement also increases with B₀ ², resulting in a greater loss of observable protein peaks at higher field. We therefore preformed all protein observe experiments at 600 MHz. For ligands, both RDCs and PCSs are the average of free and bound states. For accurate measurement, a higher field is required to achieve both better S/N and larger alignment of bound ligands. All the ligand experiments were performed at 800 MHz.

For protein RDC measurement, a ¹⁵N–¹H HSQC-TROSY spectrum was recorded (Kontaxis et al. 2000). For protein PCS measurement, a normal ¹⁵N–¹H HSQC spectrum was recorded at 600 MHz. 0.3 mM ¹⁵N-labeled protein was mixed with 0.3 mM diamagnetic lutetium to obtain a diamagnetic reference spectrum. A sample with the protein at the same 0.3 mM concentration was prepared with 0.3 mM paramagnetic dysprosium to obtain PCSs. Residual dipolar couplings were measured as observed differences in offsets in the ¹⁵N dimension between paramagnetic and diamagnetic samples. Pseudo-contact shifts were measured as differences in ¹H chemical shifts between diamagnetic and paramagnetic samples. The peak assignments were achieved by pairing the peaks of diamagnetic and paramagnetic samples along diagonal lines.

For lactose ¹³C–¹H RDCs, the diamagnetic sample was prepared by mixing 0.5 mM protein with 2.5 mM lactose and 0.5 mM lutetium ion in 50 mM deuterated MES buffer (50 mM D-MES, 50 mM NaCl, pH 5.4). For the paramagnetic sample, 0.5 mM dysprosium was mixed with 0.5 mM protein and 2.5 mM lactose in 50 mM deuterated MES buffer. Coupled ¹³C–¹H HSQC spectra were recorded at ¹H frequency of 800 MHz using a cryogenic triple resonance probe. For the diamagnetic spectrum, normally 256 t1 points over 9500 Hz were acquired with 100 acquisitions each. For the paramagnetic spectrum, owing to the severe line broadening by paramagnetic relaxation enhancement, 128 t1 points over 9500 Hz were acquired with 400 acquisitions each.

Constant time COSY spectra were also recorded at ¹H frequency of 800 MHz to obtain ¹H–¹H RDCs for the ligand (Tian et al. 1999). The same diamagnetic sample was used for the diamagnetic reference spectrum. The paramagnetic sample was prepared by mixing 0.5 mM protein with 10 mM lactose and 0.5 mM dysprosium in 50 mM deuterated MES buffer. The mixing time was arrayed from 0.1 to 0.3 s with time increments of 0.05 s.

For the lactose pseudo-contact shifts, the same samples as those used for RDC measurements were used except that 1 mM tetramethyl ammonium chloride (TMAC) was added to both samples for chemical shift referencing. Regular ¹³C–¹H HSQC spectra were recorded, and PCSs were measured as the difference in ¹H chemical shifts in diamagnetic and paramagnetic samples.

Data analysis

For proteins, the spectra were processed using NMRPipe (Delaglio et al. 1995). For protein RDCs and PCSs, nonlinear line shape curve fitting was applied to each peak to fit them to a Gaussian curve and extract the peak center. The peak assignments were achieved by comparison with the deposited Galectin-3 CRD spectrum (Umemoto and Leffler 2001). Only the peaks having unambiguous assignments were selected for alignment tensor determination.

For ligand RDCs and PCSs, since the magnitudes are small, data were extracted using a Bayesian curve-fitting program (XRAMBO) (Andrec and Prestegard 1998). A metropolis Monte Carlo algorithm was used to directly sample points in parameter space. Free-induction decays were modeled as sums of exponentially decaying sinusoids each described by four parameters (intensity, decaying constant, peak center position, and phase). The RDC was taken as the difference in splitting for diamagnetic and paramagnetic samples. XRAMBO requires the original FID and an estimation of peak position as input. The original FID for each or several peaks can be obtained by processing the 2D ¹H-¹³C HSQC spectrum routinely but keeping the imaginary part, and applying no weighting functions. This was followed by summing a region of interest perpendicular to the ¹³C dimension to get a 1D NMRpipe file. The 1D projection was then reformatted using an NMRPipe script and inverse Fourier transformed to reconstruct the FID file. The initial peak positions, intensities, and line widths can be estimated by NMRPipe auto-peak picking. The Monte Carlo search was set to 16,000 iterations, and the final parameter values and error estimation were obtained after the rejection rate fell between 60% and 70%.

For ¹H-¹H RDCs of the ligand, the same procedure as described by Tian et al. (1999) was used. The splitting was extracted by fitting the ratio of cross-peak and auto-peak intensities as a function of the constant time interval to a tangent function.

Structure calculation

The order tensors were determined using the program REDCAT (Valafar and Prestegard 2004). Since RDCs and PCSs share the same order tensors, if a diamagnetic reference is subtracted (Banci et al. 2004) and if a rigid model is appropriate, both RDCs and PCSs can be used simultaneously to determine the alignment tensors. One only needs to specify the correct RDC_max and PCS_max constants in the input files (24,350 Hz for ¹H-¹⁵N RDCs, and 1.26E + 10 Hz for ¹H PCSs at 600 MHz). However, the appropriateness of a rigid model and, for PCSs, the actual position of the metal ion must first be determined. Hence, we initially used only RDCs to determine the order tensor elements (S_xx, S_yy, and S_zz). The same tensor elements were then used to back-calculate PCSs as the ion was moved over the grid in 2 Å steps. The ability to find a position that fit both RDCs and PCSs well was taken as evidence of a rigid system, and both sets were combined to get an appropriate estimate of the order tensor.

Using the estimated order tensor (Da = 2.85 and Dr = −1.72), the position of the metal ion was then optimized using the internal variable module (Schwieters and Clore 2001) and PARArestraints module (Banci et al. 2004) available for the XPLOR-NIH program. To perform this simulation, the protein and the lanthanide-binding tag were grouped to two different clusters. The linker between the protein and the tag was set to be free for rotation and translation. PC6 was used as the molecular dynamics integration algorithm. The length of the linker was allowed to vary from 5 to 15 amino acids as attempts were made to find the position of the metal ion giving the best fit of the PCSs and RDCs. One structure with the fewest PCS and RDC violations was selected for the final ligand–protein complex determination.

The same procedures used for metal ion position optimization were applied when modeling the final ligand-bound protein complex structure (IVM and PARArestraints) (Schwieters and Clore 2001; Banci et al. 2004). RDCs and PCSs of ligand and protein were used as orientational and distance restraints. Since two ¹H–¹H ligand RDCs, which could have variable internuclear distances, were used for the final structure determination, XDIP was used to handle these ¹H–¹H couplings along with ¹H–¹³C and ¹H–¹⁵N couplings (Tjandra et al. 2000). The protein was grouped to one cluster. The pyranose rings of galactose and glucose were grouped to maintain the most stable chair form during simulated annealing. Previous experiments (Cambillau 1995; Alonso-Plaza et al. 2001) had shown that when the lactose binds to different lectins, lactose adopts a conformation near the local energy minimum with little alteration in glycosidic bond angles. Hence, the relative rotation of galactose and glucose rings was restrained by setting the dihedral angles of the glycosidic bond to φ = 50 and ψ = −116 with a ±5° variation. One intermolecular NOE was also included to accelerate the convergence in some of the calculations (Zhuang et al. 2006). The calculated structure was validated by checking for normal van der Waal contacts and appropriate hydrogen bonds between the ligand and the protein.