Structures, basins, and energies: A deconstruction of the Protein Coil Library

Abstract

Globular proteins adopt complex folds, composed of organized assemblies of α-helix and β-sheet together with irregular regions that interconnect these scaffold elements. Here, we seek to parse the irregular regions into their structural constituents and to rationalize their formative energetics. Toward this end, we dissected the Protein Coil Library, a structural database of protein segments that are neither α-helix nor β-strand, extracted from high-resolution protein structures. The backbone dihedral angles of residues from coil library segments are distributed indiscriminately across the φ,ψ map, but when contoured, seven distinct basins emerge clearly. The structures and energetics associated with the two least-studied basins are the primary focus of this article. Specifically, the structural motifs associated with these basins were characterized in detail and then assessed in simple simulations designed to capture their energetic determinants. It is found that conformational constraints imposed by excluded volume and hydrogen bonding are sufficient to reproduce the observed ϕ,ψ distributions of these motifs; no additional energy terms are required. These three motifs in conjunction with α-helices, strands of β-sheet, canonical β-turns, and polyproline II conformers comprise ∼90% of all protein structure.

Individual protein folds resist intuitive classification. This perception was captured memorably by Perutz, who characterized the earliest X-ray elucidated protein structures (Kendrew and Perutz 1957; Kendrew et al. 1958) as “visceral-looking” (Perutz 1964). Since that time, ∼45,000 protein structures have been accumulated in the Protein Data Bank (Berman et al. 2000), and it has become apparent that this number far exceeds current estimates of ∼1100 observed protein topologies (Murzin et al. 1995; Orengo et al. 1997). Indeed, one is no longer surprised to find that protein domains of dissimilar sequence and unrelated function share remarkably similar three-dimensional structures. With only modest extrapolation, this finding suggests that the total number of conceivable native topologies is intrinsically limited (Govindarajan and Goldstein 1996; Przytycka et al. 1999).

Protein comparison methods exploit this overall degeneracy of structure to good advantage. A common strategy for predicting the structure of a protein of known sequence but unknown structure is to “thread” it against a homolog of similar sequence and known structure (Kopp et al. 2007). Although similar sequences are expected to have similar structures (Doolittle 1986, 1989), deliberately constructed exceptions are possible (Alexander et al. 2007), and yet more powerful structure-based comparison strategies are needed because proteins with analogous structures can nevertheless have sequences that are dissimilar enough to evade sequence-based homology detection (Lesk and Chothia 1980).

All structure-based comparison approaches are grounded in the implicit assumption that locally organized assemblies maintain their structural integrity when embedded in ever larger superstructures (Crippen 1978; Rose 1979). The persistence of such hierarchically arranged substructures, together with the limited number of available topologies, imply that proteins can be decomposed into a limited number of recognizable “building blocks,” at least in principle. That this principle can be realized in practice was demonstrated by Jones and Thirup (1986), who determined the X-ray structure of a protein by fitting its experimentally determined electron density with short chain segments culled from a library of previously solved but unrelated protein structures, using an automated trial-and-error procedure. Their tour de force provided a persuasive demonstration that protein structures can be regarded as mix-and-match assemblies of a limited repertoire of recycled local motifs, common to many native folds (Fitzkee et al. 2005a).

Much ensuing work has sought to identify a repertoire of structural building blocks that can be combined to reproduce experimentally determined protein structures (Fetrow et al. 1988; Hunter and Subramaniam 2003). A few notable examples include work of Sussman and colleagues, who clustered 13,000 predominantly nonhomologous hexamers from 82 well-resolved proteins by C_α root-mean-square distances, yielding 103 unique building blocks that accurately represent ∼76% of all hexamers in refined protein structures (Unger et al. 1989; Unger and Sussman 1993). In a related approach, Bystroff and Baker (1998) parsed a collection of dissimilar protein structures into a library of 9- to 17-residue segments that were clustered into 82 unique local conformers based on a combination of C_α root-mean-square distances and differences in backbone torsion angles. Recently, this library was applied to solving the structure of a 112-residue protein (Qian et al. 2007). Similarly, de Brevern et al. (2000) isolated 16 distinct 5-residue “protein blocks” using a network trained to detect local backbone conformations in well-refined protein structures. In the approach of Kim and coworkers, multidimensional arrays of φ,ψ angles from high-resolution protein segments were projected onto three-dimensional vectors, partitioned into a small number of clusters, and used to classify corresponding protein fragments into topologically distinct backbone conformations (Sims et al. 2005). Focusing on the scaffold of α-helix and β-strand, Kamat and Lesk (2007) devised simple diagrams to classify and compare all possible patterns of repetitive secondary structures.

The variety and success of these methods support the proposition that proteins are constructed from a limited number of local backbone conformations, but none of the methods seek to provide a physical–chemical rationale for the conformations themselves. A recent analysis (Panasik Jr. et al. 2005) demonstrated that ∼80% of protein structure is composed of only four major building blocks—α-helices, β-strands, β-turns, and polyproline II—all governed by steric exclusion and hydrogen bond satisfaction (Fitzkee et al. 2005a). These same two physical principles were shown to rationalize the conformations of the 1- to 3-residue turns that interconnect adjacent segments of secondary structure (Street et al. 2007).

Here, we identify three structural motifs found in the coil regions of high-resolution protein structures. The extent to which sterics and hydrogen bonding can rationalize these motifs is explored via simulations. Two of these motifs—inverse γ-turns and proline-terminated helices—have been discussed previously (Rose et al. 1985; Milner-White 1990; MacArthur and Thornton 1991; Gunasekaran et al. 1998), and we revisit them with an emphasis on their physical–chemical origins. Sterics and hydrogen bonding are shown to account sufficiently for all three motifs. These three structures, together with α-helices, β-strands, canonical β-turns, and polyproline II conformers, comprise ∼90% of all protein structures.

Results

Our analysis was performed on the Protein Coil Library (Fitzkee et al. 2005b), a structural database of protein segments that are neither α-helix nor β-strand. The backbone dihedral angles of residues from these segments scatter indiscriminately across the φ,ψ map, but upon contouring, they cluster naturally into seven distinct basins. Five of these basins correspond to thoroughly familiar structures: hydrogen-bonded β-turns (Venkatachalam 1968; Rose et al. 1985) and polyproline II conformation (Sasisekharan 1959; Creamer and Campbell 2002; Shi et al. 2002). Although structures have also been associated with the remaining two basins (Milner-White 1990; MacArthur and Thornton 1991; Ho et al. 2003; Ho and Brasseur 2005), we focus on them here with two goals: developing a more precise structural characterization and rationalizing their underlying energetics. The local structures associated with these seven basins, together with α-helices and strands of β-sheet, are shown to account for ∼90% of high-resolution protein structures.

The coil library

All protein fragments from structures with resolution 2.0 Å or better and R-factor ≤0.25 were extracted from the Protein Coil Library (www.roselab.jhu.edu/Coil) (Fitzkee et al. 2005b). A total of 101,001 disjoint segments consisting of 693,771 residues satisfied these criteria and comprised the specific coil library used here.

A scatter plot of all backbone dihedral angles derived from these fragments reveals that the φ,ψ angles of most—but not all—residues fall within allowed regions of the Ramachandran plot (Fig. 1; Ramachandran and Sasisekharan 1968). Outliers in disallowed regions usually correspond to glycine residues, which can adopt backbone conformations that are inaccessible to residues with a β-carbon (Ramachandran and Sasisekharan 1968). Still, a population of 22,506 sterically proscribed φ,ψ-pairs remains after all clash-free glycines are eliminated (Fig. 1).

Figure 1.

Scatter plot of φ,ψ angles from the coil library (Fitzkee et al. 2005b). Outlined regions (in black) correspond to sterically allowed values of backbone torsion angles for the alanyl dipeptide, as described by Ramachandran and Sasisekharan (1968). It is apparent that many residues from the coil library have φ,ψ angles outside these “allowed” regions. Residues in allowed regions are subdivided into those with sterically restricting β-carbons (in yellow) and glycines (in red). The remaining 22,509 residues have φ,ψ angles that fall into “disallowed” regions are subdivided into those within a 30° radius of an allowed region (90%, in green) and all others (10%, in blue). Figure generated using Matlab.

A contour plot of these same data (Fig. 2A) reveals that almost all sterically disallowed outliers are situated near the margins of an allowed region. In particular, 73% of the outliers have φ,ψ angles within 15° of an allowed region, and 90% have φ,ψ angles within 30° of an allowed region. Previous work demonstrated that a slight adjustment of φ,ψ angles is sufficient to shift a significant population of β-turn-like conformers in the coil library into canonical β-turns while preserving overall chain topology (Panasik Jr. et al. 2005), and the same conclusion probably holds for the marginal outliers in Figure 2A. The remaining 10% of the outliers are sparsely distributed (Fig. 1) and statistically negligible. Accordingly, we focused on the prominent regions revealed by the contour map in Figure 2A.

Figure 2.

Basins extracted from the coil library (Fitzkee et al. 2005b). (A) Contour map of φ,ψ angles from the coil library. Populated regions lie largely within sterically allowed boundaries for the alanyl dipeptide, shown in black outline. Outliers correspond to glycines. The map is colored by population, as indicated by the color bar, which ranges from burgundy (most populated bins) to dark blue (least populated bins). The numerical population scale (measured in residues) is shown to the right of the color bar. Residues beyond the immediate margins of sterically allowed boundaries in Figure 1 are sparsely distributed, with populations that are insufficient to register on the color bar. (B) Contouring partitions the coil library into seven distinct φ,ψ basins. The contour map of backbone torsion angles, from panel A, clusters into seven discrete basins, shown in black outline and labeled: α, β, P_II, α_L, τ, γ, and δ. Most residues associated with a given basin participate in one of a few structural motifs. Motifs and basin boundaries are listed in Table 1. Note that the basin outlines in B were abstracted from the 2° × 2° bins used to contour the entire coil library in A. Figures 3–8 were produced from individual basins that have fewer data points than the entire library. Consequently, they were contoured at lower resolution (5° × 5° bins), and their basin outlines lack the fine structure shown here.

Populated regions in Figure 2A can be subdivided readily into seven discreet basins (Fig. 2B), labeled α, β, P_II, α_L, τ, γ, and δ. Of these, the α, β, P_II, α_L, and τ basins are populated largely by residues that participate in familiar motifs, specifically type I or type III turns, segments of β-strand, polyglycine, and polyproline II conformations together with residues from type II turns, type I′ and type III′ turns, and type II′ turns, respectively; all have been well described in the literature (Crick and Rich 1955; Sasisekharan 1959; Ramachandran et al. 1966; Venkatachalam 1968). Our analysis was confined to the γ and δ basins, as reported in the following two sections.

The γ basin

All 13,205 residues with φ,ψ angles in the γ basin (Table 1) were extracted from the coil library, and their backbone dihedral angles were contoured (Fig. 3). Over 90% of the residues in this basin (11,910) participate in inverse γ-turns (C₇ equatorial) (Rose et al. 1985; Milner-White 1990), a three-residue peptide chain turn that forms an (i + 1) N-H ••• O=C (i − 1) hydrogen bond, with residue i in the γ-basin (Fig. 4).

Table 1.

The seven coil library basins^a

Figure 3.

Contour map of the γ basin. Backbone torsions from the coil library that map to the γ basin (Table 1), colored by population. Note that the region has characteristics of an authentic basin, with a highly populated center and diminishing population toward the periphery. The coil library has 13,205 residues with backbone torsions that map to the γ basin (Table 1), and 99% (13,103) of these are the middle residue of an inverse γ-turn. Color coding as in Figure 2A.

Figure 4.

A three-residue, hydrogen-bonded inverse γ-turn. A residue at position i that adopts a backbone torsion angle from the γ basin results in an (i − 1) C=O ••• H-N (i + 1) hydrogen bond, illustrated here for Ace_i-1-Ala_i-Nme_i+1. Backbone atoms are shown as color-coded sticks, and transparent spheres depict the van der Waals overlap between N-H_i+1 and O_i-1. Color coding is by atom type: carbon, green; nitrogen, blue; oxygen, red; and hydrogen, white. Figure generated using PyMOL (DeLano Scientific).

The hypothesis that φ,ψ angles in the γ-basin are an automatic consequence of forming this hydrogen bond (Milner-White 1990) was tested by simulation. An exhaustive conformational search was performed using N-acetyl-Ala-N-methylamide (Fig. 4), a peptide model for which the conformation is governed by a single φ,ψ pair. All clash-free conformers were contoured (Fig. 5) if they formed an (i + 1) N-H ••• O=C (i − 1) hydrogen bond (see Materials and Methods) and all other polar groups were accessible to solvent. The γ-basin outline from Figure 3 was overlaid for comparison. Data from the coil library and its simulated counterpart trace markedly similar areas. The simulation also gives rise to a small population of γ-turns (C₇ axial) (Rose et al. 1985; Milner-White 1990), traces of which are also found in the coil library.

Figure 5.

Contour map of the γ basin from simulations. An overlay of the experimentally determined γ basin from Figure 3 is shown in black outline. It is apparent that the simulated and experimentally determined regions are similar. The small populated region in the southeast quadrant of the φ,ψ map corresponds to γ-turns (C₇ axial), traces of which are also evident in the coil library (Rose et al. 1985; Milner-White 1990). Color coding as in Figure 2A.

Residues that contribute to the γ-basin have marked sequence and structural preferences. Asp, Asn, and Pro have high γ-basin propensities; β-branched residues and Gly have low propensities (Table 2). γ-Turns are frequently—but not exclusively—adjacent to elements of repetitive secondary structure (Milner-White 1990).

Table 2.

Residue propensities in the γ and δ basins

The δ basin

The 11,653 residues with φ,ψ angles in the δ basin (Table 1) were extracted from the coil library, and their backbone dihedral angles were contoured (Fig. 6A). This basin is confluent with the adjacent β basin, suggesting that it is simply an extension of that region. On detailed examination, more than half (6349) of the residues in the δ region precede a proline, and when these are contoured separately, a distinct basin emerges (Fig. 6B), as noted previously (MacArthur and Thornton 1991; Gunasekaran et al. 1998; Ho and Brasseur 2005). Alternatively, a contour plot of those residues that do not precede a proline shows that the major population is distributed diffusely around the margins of the δ region, especially at the interface with the β basin (Fig. 6C), suggesting that these residues are most likely spillover from the β-strand population. An additional 2350 residues preceding proline belong in the latter category (for further details, see Materials and Methods) and were reclassified into the β basin.

Figure 6.

Contour map of the δ basin. Backbone torsions from the coil library that map to the δ region, colored by population and subdivided into two subpopulations. (A) Contour map of all 11,653 residues from the coil library that map to the δ region (Table 1). The area of highest population is confluent with the adjacent β basin (Fig. 2B), suggesting that some residues in the δ region are β-basin overflow. Accordingly, the δ region was subdivided into: (B) contour map of the 6349 residues in the δ region that precede proline, and (C) contour map of the 5304 residues that do not precede proline. It is apparent that residues in B form a distinct basin, while residues in C are preferentially distributed around the margins of the δ region, particularly along the boundary with the β basin. Color coding as in Figure 2A.

Of the remaining 3999 members of the δ basin, 3672 were classified into two related categories, both preceding proline residues: (1) δP_α, i.e., the residue preceding a proline residue in the α basin, and (2) ααδP, i.e., the residue directly following at least two residues in the α basin and preceding a proline residue. Both classes have focused populations concentrated at or near the center of the δ region similar to that in Figure 6B, validating their classification as distinct motifs.

In both categories, β-branched residues are disfavored (Table 2), and the adjacent proline residue is almost always in the trans isomer (three of 3672 are cis). Additionally, 52% of the residues in the ααδP category follow an α-helix and participate in a proline helix-capping motif (Aurora and Rose 1998). Some of these restrictions, extracted from the data, were utilized in simulations that seek to identify the underlying physical factors responsible for the basin, as described next.

The δP_α category was simulated using a blocked Ala-Pro peptide (Ace_i-1-Ala_i-Pro_i+1-Nme_i+2) in which the alanine sampled all sterically allowed backbone dihedral angles, but the proline was restricted to the α-basin (see Materials and Methods). The contour plot of all clash-free, hydrogen bond satisfied conformers shows that the δ region is sampled more frequently than the other six basins (Fig. 7A). In contrast, removing the restriction for hydrogen bond satisfaction of the amide hydrogen in the Nme blocking group enlarges the range of accepted regions to include the majority of the P_II and β basins (Fig. 7B). In other words, the amide nitrogen at i + 2 is accessible for hydrogen bonding (to solvent in this case) when the ith residue adopts a conformation in the δ region, but access to this amide is hindered when the ith residue adopts conformations in the β or P_II regions.

Figure 7.

Contour map of the δP_α motif from simulations. Distributions were generated using a blocked Ala-Pro peptide, Ace_i-1-Ala_i-Pro_i+1-NME_i+2 (see Materials and Methods). (A) Contour map of φ,ψ angles from Ala_i that result in sterically allowed, hydrogen-bond satisfied conformers. None are within the β and P_II basins. (B) Similar to A but without restricting N-H_i+2 to be hydrogen-bond satisfied. When the Ala at position i adopts backbone torsions from either the β or P_II basins, its C_β atom and the C_δ atom of Pro_i+1 hinder access, and therefore hydrogen bonding, to the N-H at i + 2. Color coding as in Figure 2A.

The ααδP category was simulated using a blocked Ala₃-Pro peptide (Ace_i-3-Ala_i-2-Ala_i-1-Ala_i-Pro_i+1-Nme_i+2) in which Ala_i-2 and Ala_i-1 were restricted to the α basin, Ala_i was a wildcard residue that sampled all sterically allowed backbone dihedral angles freely, and Pro_i+1 sampled the α and P_II basins uniformly (see Materials and Methods). All clash-free, hydrogen bond satisfied conformers were accepted. The contour plot of the resulting backbone dihedral angles sampled by the wildcard residue, Ala_i, shows that the population is concentrated in the α_L, δ, and P_II basins, with a tail that extends into the northwest corner of the plot (ϕ ∈ (−150°, −180°] and ψ ∈ [70°, 150°]) (Fig. 8A). Both this tail and the preference for the α_L basin are largely eliminated upon changing the residue at position i to a γ-branched residue (Fig. 8B), yielding a distribution that closely resembles the one produced by experimentally determined structures in the coil library (Fig. 8C).

Figure 8.

Contour map of the ααδP motif from simulations. Distributions were generated using a blocked tetrapeptide, Ace_i-3-Ala_i-2-Ala_i-1-X_i-Pro_i+1-Nme_i+2 (see Materials and Methods). Residues were restricted to conformations ααXP, where α lies within the α basin, P is a proline, and X was allowed to adopt any conformation for which the peptide was clash-free and hydrogen-bond satisfied. Contoured φ,ψ distributions for X_i are shown. (A) Contour map for Ala₃-Pro. When residue X is an alanine, the resulting distribution includes the α_L, P_II, and δ regions and a tail that extends into the northwest corner of the β basin. (B) Contour map for Ala₂-X_γ-branched-Pro. When residue X is γ branched, the tail is eliminated and the resultant distribution closely resembles that of experimentally determined ααXP motifs from coil library, shown in C. Color coding as in Figure 2A.

Several dominant interactions shape the distributions in Figure 8A,B. The O in Ace_i-3 clashes frequently with the C_δ of Pro_i+1 when Ala_i is in the α basin, disfavoring a helical conformation. Additionally, the O of Ace_i-3 clashes with the O of Ala_i when the latter residue is in the β basin (Fitzkee and Rose 2004b). Finally, when the residue at position i is γ branched, its C_δ atoms clash with the O of Ala_i-1, eliminating most of the tail seen in Figure 8A.

Significance of coil library statistics

The previous analysis was performed on the coil library, which consists of protein fragments after α-helices and β-strands are filtered from their parent structures. Upon filtering, remaining structures that would have been diluted below the threshold of detection in the parent population now become conspicuous. However, once such structures are identified, it is important to check whether motif statistics calculated from the coil library differ from corresponding statistics calculated from the parent data set. In other words, is there a coil library bias?

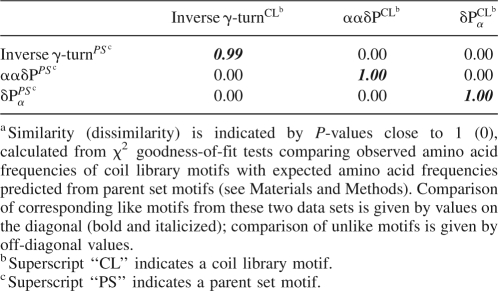
Accordingly, statistics reported in the previous subsections were recalculated for the parent population. Specifically, all residues with backbone torsions in the γ and δ regions that participated in either inverse γ-turns or ααδP and δP_α motifs, respectively, were extracted from the unfiltered parent set, grouped by motif, and analyzed. As expected, expansion to the full parent data set increased each motif's population by only 2%–10%, demonstrating that most of the population resides in the coil library, not in repetitive secondary structure. Additionally, each motif's amino acid frequencies were recalculated from the parent data set and compared with corresponding frequencies determined from the coil library by using a χ² goodness-of-fit test (Table 3). For all three motifs, the χ² values were low, resulting in P-values >0.99, a strong indication that coil library and parent library frequencies are similar. Cross-correlations between the amino acid frequencies of differing motifs were also calculated, and these yielded high χ² values, with P-values ≈ 0 (Table 3), an equally strong indication of dissimilarity between unlike motifs in the two data sets. Reassuringly, the comparisons in Table 3 indicate an absence of any significant coil library bias.

Table 3.

Similarity between motifs in the coil library and its parent data set^a

Are protein structures mix-and-match assemblies of motifs from this repertoire?

The prominent structural motifs found in the seven basins (Table 1) were grouped into five categories (β-turn, P_II, inverse γ-turns, δP_α, and ααδP) together with α-helix and β-strand, and tallied to determine how well they cover known protein structures (Table 4); 85.8% of all residues in the data set participate in at least one of these seven motifs. Relaxing β-strand and β-turn definitions (described in Materials and Methods) increases this total by an additional 3.6%, bringing the fraction of residues that participate in these seven local motifs to 89.4%.

Table 4.

Motif abundance^a

Discussion

Globular proteins are built on scaffolds of α-helix (Pauling et al. 1951) and β-sheet (Pauling and Corey 1951), characteristic motifs (Levitt and Chothia 1976) that comprise over 50% of protein structure (Fitzkee et al. 2005a). Inclusion of hydrogen-bonded β-turns (Venkatachalam 1968) and polyproline-II conformers (Creamer and Campbell 2002; Shi et al. 2002) brings this total to ∼80% (Fitzkee et al. 2005a). In the preceding, we extend this list by three more distinct categories extracted upon analysis of a Ramachandran plot: inverse γ-turns (Rose et al. 1985; Milner-White 1990), δP_α, and ααδP motifs (MacArthur and Thornton 1991; Gunasekaran et al. 1998). In sum, these seven building blocks, together with probable additions from marginal outliers, account for ∼90% of protein structure.

Pauling's approach to modeling, based on hydrogen bonding and steric constraints, led to the prediction of α-helix and β-sheet (Pauling and Corey 1951; Pauling et al. 1951). In contrast, much recent work has focused on identifying structural building blocks from the Protein Data Bank (Berman et al. 2000) using purely geometrical criteria (Unger et al. 1989; Unger and Sussman 1993; Bystroff and Baker 1998; de Brevern et al. 2000; Hunter and Subramaniam 2003; Sims et al. 2005), an approach that is deliberately indifferent to the issue of an underlying energetic rationale.

Our own approach, further developed here, seeks to combine identification with physicochemical understanding (Street et al. 2007). Motifs are identified by contouring and dissecting populated regions of the Ramachandran map. Then, their molecular origin is investigated via simulations of short, suitably constrained peptides, energy-weighted by hydrogen bonding and sterics. The several motifs described here are consistent with the hypothesis that short polypeptide chain segments populate only a limited repertoire of conformers (Fitzkee et al. 2005a).

Our analysis was performed on the coil library (Fitzkee et al. 2005b), the set of non-α-helix, non-β-strand protein segments thought to represent conformers present in the unfolded state (Serrano 1995; Swindells et al. 1995; Smith et al. 1996; Avbelj and Baldwin 2003; Jha et al. 2005). The coil library is assembled from folded proteins. To the degree that it also represents the unfolded state, it does so under conditions that bias the population toward the native state. Upon excluding helices and strands, 76% of residues participate in at least one of the five remaining motifs described here, indicative of clear conformational preferences in the coil library, and, most likely, in the unfolded state as well (Swindells et al. 1995; Avbelj and Baldwin 2003; Jha et al. 2005). The fact that a substantial fraction of the coil library can be parsed into a few local motifs is inconsistent with the classical picture of the unfolded state as a featureless random coil (Pappu et al. 2000; Fitzkee and Rose 2004a).

Already by 1936, Mirsky and Pauling had recognized an equivalence between protein denaturation and protein structure, postulating that “… a theory of denaturation is essentially a general theory of the structure of native and denatured proteins” (Mirsky and Pauling 1936). Many factors, both physical (temperature, pressure, and volume) and chemical (pH, mutations, and solvent quality), can shift the U(nfolded) ⇌ N(ative) equilibrium in two-state folding studies (Pace et al. 2004). However, following Tanford's compelling thermodynamic analysis of chemical denaturants (Tanford 1968), most folding studies have employed either urea or guanidinium chloride (GdmCl), where the U ⇌ N equilibrium is controlled by solvent quality (Bolen and Rose 2008).

Poor cosolvents, like TMAO, promote intrapeptide hydrogen bonds and, in turn, increased local structure; conversely, good cosolvents, like urea, promote peptide-solvent hydrogen bonds and, in turn, decreased local structure (Rose et al. 2006). Simulations that track the conformer distribution in short peptides as a function of solvent quality led to the testable prediction of a significant population of inverse γ-turns in a polyalanyl 7-mer under poor solvent conditions (Gong and Rose 2008). If this prediction proves to be correct, the finding demonstrates the emergence of a specific, hydrogen-bonded structure in the unfolded ensemble under solvent quality conditions that mimic those of the coil library (i.e., those of folded proteins).

The specific motifs reported here may provide a useful addition to protein structure prediction efforts based on fragment assembly methods. In particular, protein fragments drawn from conventional secondary structure categories (α-helix and β-sheet) are insufficient to cover the full three-dimensional structure of a protein. This deficit in fragment coverage is known to occur in “coil” regions of the protein (Etchebest et al. 2005). Even a highly approximate specification of the protein's backbone dihedral angles is sufficient to recover full tertiary structure for segments of α-helix or β-strand (Gong et al. 2005; Fleming et al. 2006)—but not the interconnecting loops. Consequently, recognizable motifs drawn from the coil library have the potential to expand the repertoire of known fragments and reduce the fraction of undifferentiated “coil.”

The remaining, unclassified 24% of the coil library includes noncanonical turns (Street et al. 2007), helix caps (Aurora and Rose 1998), and short segments (≤3 residues) that interconnect various motifs. Previous work demonstrated that hydrogen bonding and steric constraints impose significant conformational restrictions on these short linkers (Fitzkee and Rose 2005). It remains to be explored whether such segments can be further classified into a limited repertoire of motif connectors.

Materials and Methods

Structure selection

Coil segments and their parent protein structures were extracted from the Protein Coil Library (Fitzkee et al. 2005b) and the Protein Data Bank (Berman et al. 2000), respectively, based on the 9/3/07 PISCES list (Wang and Dunbrack Jr. 2003) of structures with resolution of 2 Å or better, R-factor ≤0.25, and sequence similarity ≤90%. Protein Data Bank segments with three or fewer residues and residues lacking defined φ,ψ angles or having nonstandard amino acids were removed from the data set, resulting in the 1,594,338 residues used in the analysis.

Contour plots

Contour plots were generated from binned φ,ψ distributions. In all cases except Figure 2, φ,ψ space was partitioned into 5° × 5° grid squares (i.e., 72 × 72 bins), and the φ,ψ angles under consideration were mapped into their appropriate bin. Bins were weighted on a relative scale with 11 levels, listed here in decreasing order: 95%–100% of the most populated bin, then nine equal decades descending from 95%–85% to 15%–5%, and a final 11th level of 5%–0%, that is not shown. Figure 2 was contoured similarly, using 2° × 2° grid squares (i.e., 180 × 180 bins) and 16 contour levels, analogously spaced with 3.3% increments in the first and 16th levels, and 6.7% increments in between.

Spillover of marginally disallowed conformers

An ostensibly disallowed backbone conformer was nevertheless classified as a clash-free conformation if its backbone dihedral angles fell within the same 5° × 5° bin as any sterically allowed point on the canonical Ramachandran plot (Ramachandran and Sasisekharan 1968). The conformer was considered to be within 15° (30°) of a sterically allowed conformation if its displacement from the closest allowed point spanned no more than three (six) contiguous bins.

Hydrogen bonding criteria

Hydrogen bond recognition was based on three criteria (Kortemme et al. 2003): (1) distance (donor, acceptor) ≤3.5 Å, (2) scalar angle N-H-O ≥ 100°, and (3) scalar angle H-O-C ≥ 90°. The distance and N-H-O angle criteria were tightened slightly for a hydrogen-bonded inverse γ turn by reducing the maximum hydrogen-bonding distance to 2.7 Å and increasing the minimum N-H-O scalar angle to 110°.

Precedence rules for δ-basin categories

The δ basin was defined as a rectangular region in the range −150° ≤ φ ≤ −110° and 45° ≤ ψ ≤ 90° (Fig. 6A). Residues in the δ basin were classified into one of three groups in the following order of precedence:

• (1) ααδP, where δ was any residue in the δ basin succeeding at least two residues in the α basin and preceding a proline residue (category 2 in Results section for the δ basin);

• (2) members of the β-basin, where the residue in question was one of at least three consecutive residues with −210° ≤ φ ≤ −30° and 90° ≤ ψ ≤ 210° or −150° ≤ φ ≤ −90° and 30° ≤ ψ ≤ 90°; and

• (3) δP_α, where δ was any residue in the δ basin preceding a proline residue in the α basin (category 1 in Results section for the δ basin).

The conventions adopted here for secondary structure and basin classification were those established in PROSS, a torsion-angle based algorithm for secondary structure identification (Gong et al. 2003).

Precedence rules for tallying motifs

Structural motifs were recognized and classified into one and only one of seven main groups in the following order of precedence: α-helices and β-strands, β-turns, inverse γ-turns, ααδP, δP_α, and P_II conformations. Remaining residues were then screened for motifs that could be further classified using slightly relaxed β-turn and β-strand definitions, respectively. In detail, residues were classified as belonging to α-helices or β-strands based on their backbone dihedral angles using definitions from PROSS (Gong et al. 2003). Residues were classified as β-turns if they made an N_i+3-H → O=C_i hydrogen bond (see hydrogen bond criteria above) and had backbone torsion angles within 30° of ideal values (Table 1; Rose et al. 1985,). Type VI and VI′ turns were not included in the count. Relaxed β-turns were defined using the less stringent torsion angle criteria of Hutchinson and Thornton (1994) in addition to a slightly relaxed hydrogen bonding criteria: (1) distance (donor, acceptor) ≤4.0 Å, (2) scalar angle N-H-O ≥ 85°, and (3) scalar angle H-O-C ≥ 75°. Relaxed β-strands were identified using rule 2 under Precedence Rules for δ-Basin Categories.

These precedence rules are sufficient to prevent double-counting. All residues in each motif were included in the motif census, i.e., all four residues in β-turns, all three residues in inverse γ-turns, etc.

Simulations

Simulations were performed using an Ace-(Ala)_n-Nme chain unless otherwise noted. All heavy atoms and backbone amide hydrogens were included. Hard sphere radii used throughout, from LINUS (Srinivasan and Rose 1995), were C(sp³) = 1.64 Å, C(sp²) = 1.5 Å, O (sp²) = 1.35 Å, N (sp²) = 1.35 Å, H = 1.0 Å, then scaled to 95% to ensure robust results. The C_γ, C_δ1, and C_δ2 atoms in γ-branched residues were treated as C(sp²). A water probe radius of 1.25 Å was used (i.e., 1.4 Å scaled to 90%). In all simulations, backbone ω angles were sampled uniformly in the range [170°,190°].

For residues constrained to be helical, φ,ψ angles were sampled uniformly over those 5° × 5° bins in the α basin having a population of at least , where , is the 5° × 5° bin with the largest population in the α basin. Applying this standard in δP_α simulations, proline torsions sampled were in the range φ ∈ [−65°,−55°] and ψ ∈ [−35°,−20°]. Again applying the standard in ααδP simulations, Ace_i-3-Ala_i-2-Ala_i-1-Ala_i-Pro_i+1-Nme_i+2, alanine torsions sampled were in the range φ ∈ [−75°,−60°]; ψ ∈ [−45°, −20°] and φ ∈ [−85°,−70°]; ψ ∈ [−40°,−25°], for Ala_i-2 and Ala_i-1, respectively, and proline sampled two regions with equal likelihood, φ ∈ [−85°,−40°]; ψ ∈ [−50°, 0°] and φ ∈ [−80°,−45°]; ψ ∈ [120°,175°].

χ² goodness-of-fit tests

χ² values were calculated as follows:

where is the expected frequency of amino acid i in coil library motif M_x, predicted from parent set motif, M_y, using

is the observed frequency of amino acid i in M_x; and n is the number of amino acid types. In three cases, n = 20, but in the other six cases, , so n was reduced to 19 to exclude proline and thus circumvent undefined values of χ². P-values of the resulting χ² statistics were calculated from χ² distributions with n − 1 degrees of freedom.