Identifying Persons with Treated Asthma Using Administrative Data via Latent Class Modelling

Abstract

Objective

To develop a parsimonious model of the respiratory patient population in British Columbia (BC), Canada through latent class modelling (LCM), using administrative data records and to assess conventional case definitions for asthma in relation to model-based case selection.

Data Sources

1996–2001 data from linked provincial databases containing fee-for-service physician billing records, hospital inpatient separation abstracts, and prescription drug purchase records for 1.9 million BC respiratory patients.

Study Design

This is a retrospective methodological/descriptive study that assesses case definitions for asthma in terms of sensitivity and specificity using a model fitted to seven physician, hospital and medication utilization markers in place of a conventional gold standard.

Data Collection

We computed values of the treatment markers for each of the 5 years for each patient aged 5–55 years who had had at least one occurrence of a respiratory diagnosis code.

Principal Findings

The marker for prescription of short-acting β agonists (SABAs) consistently had the highest sensitivity. Markers' specificities ranged from 0.97 to 1.0. The conventional case definitions' sensitivities were 0.41–0.87; specificities ranged from 0.98 to 0.997. Model-based estimates of asthma prevalence increased from 827/10,000 in 1996 to 992/10,000 in 2001. Conventional case definitions' estimates were consistently lower.

Conclusions

The linkage between utilization and case status is more complex than conventional case definitions allow for. LCM-based case classification was consistent over time and tends to lead to larger prevalence estimates than conventional definitions. The estimated increases in asthma prevalence are reliable. LCM provides health services planners with a useful probability-based approach for developing and assessing case definitions and estimating case prevalence.

Asthma is a chronic inflammatory disease of the human respiratory system. It is characterized by recurrent exacerbations of symptoms, which include coughing, wheezing, and shortness of breath. Worldwide, asthma is one of the most prevalent chronic diseases, affecting an estimated 300 million people and creating a burden in the order of 15 million disability-adjusted life years lost annually—approximately the level for diabetes or schizophrenia. Prevalence appears to be increasing (Masoli et al. 2004).

Researchers and health system planners frequently use administrative data (AD) to study the prevalence and burden of chronic conditions like asthma, to conduct population health surveillance, to allocate resources, to predict future health services utilization and to plan and evaluate prevention and treatment interventions (Peat et al. 2001).

The recent Breathing Easier study of the quality of asthma care in Saskatchewan by the province's Health Quality Council (Klomp et al. 2005) illustrates the latter point. Ten indicators related to hospitalization, spirometry testing, asthma control, and medication use were defined for the population of treated asthma patients selected from provincial linked databases. Comparisons across health regions and age groups highlighted population subgroups with whom substantial improvements in the quality of care could be made.

A variety of AD case definitions for asthma have been used by researchers and health care organizations. Examples can be found in Erzen et al. (1995), To et al. (2006), Senthilselvan et al. (2003), and National Committee for Quality Assurance (2001). These definitions are all based on counts of qualifying care events of different types—physician/outpatient visits, emergency room (ER) visits, inpatient hospital stays and asthma medication purchases—that occur during a defined interval. A simple example would be defining patients as having asthma if they have records during a 12-month period for ≥2 physician visits with an International Classification of Disease, 9th Revision (ICD-9) code of 493 and/or ≥1 hospital inpatient stay with ICD-9 code 493 for the principal diagnosis. A key premise in the development of such definitions is that physicians' diagnosis of asthma, recorded as a code on a record of service, is accurate. Pekkanen and Pearce (1999) note that “although clinical assessment cannot be considered to be a true gold standard of asthma, it currently represents the most appropriate standard for use in validating instruments for clinical studies.” Definitions differ in terms of the amount and type of recorded evidence that is considered to be sufficient to classify a patient as a case.

VALIDATION OF AD CASE DEFINITIONS

A common and important problem in selecting cohorts from administrative databases is that the misclassification errors of the criteria used are seldom known. In the case of asthma, very little research on comparison and validation of existing AD-based definitions of the condition has been reported in the literature. Most validation work on these case definitions has involved using classifications based on survey or chart review data as a “gold standard”—see, for example, Huzel et al. (2002) and To et al. (2004).

Conducting chart reviews or surveys is expensive, so validation using these types of criteria is often not feasible. A more important problem, however, is the fact that there are unknown components of measurement error in such criterion data—the criteria may not provide true gold standards—leading to biased estimates of case prevalence and of the AD definition's sensitivity and specificity.

LATENT CLASS MODELLING (LCM) AND CASE DEFINITIONS

LCM is a technique for assigning individuals to discrete homogeneous classes using scores on a set of observed categorical variables (often binary) where the number of classes (usually small) and the classes' characteristics are initially unknown. The methodology offers several advantages, described below, compared with more familiar classification approaches like cluster analysis. As we hope to demonstrate, LCM is well suited to the problem of evaluation of AD case definitions in the absence of a gold standard.

The key idea in LCM, often referred to as the assumption of local independence, is that the associations among the observed variables are the result of individuals' differences on an unobserved or latent variable, i.e., class membership. In other words, for individuals within a given class, the associations among the observed variables vanish. Based on an individual's set of values on the observed variables—their profile—and the fitted model, their probability of belonging to each class can be estimated. In addition, a fitted model produces a prevalence estimate, with a standard error, for each class and class-related conditional probabilities for each value of each observed variable. LCM provides assistance in determining the appropriate number of classes, e.g., indices of model fit and measures of the contribution of each of the observed variables to the classification process (Uebersax 1988; Magidson and Vermunt 2002).

There is a growing number of very accessible discussions of LCM theory and practice in the literature—see, for example, Dayton (1998) and McCutcheon (1987)—and space limitations do not permit a review of the foundations here. As with any statistical technique, a variety of issues can arise during the course of a latent class analysis, including interpretation of classes, model (mis)specification, dependence among the observed variables and suboptimal model fitting, i.e., failure to find a global maximum during maximum likelihood estimation. Helpful practical advice on addressing these issues is available from Uebersax (2000a, b), Garrett and Zeger (2000) and Formann (1994, 2003).

LCM is increasingly being used in the health sciences (Rindskopf and Rindskopf 1986; Formann and Kohlmann 1996) to estimate prevalence of medical conditions and to assess the sensitivity and specificity of imperfect clinical diagnostic tests (see for example, Faraone and Tsuang 1994, in the case of psychiatric diagnoses). LCM is also used in epidemiology, e.g., O'Rand and Hamil-Luker's (2005) work on childhood disadvantage and the risk of heart attacks later in life, as well as in studies of health care utilization—see d'Uva (2006), for example—and substance abuse, e.g., Carlson et al. (2005).

An important contributor to the increased use of the technique is the availability of free LCM software such as LEM (Vermunt 1997) and WinLTA (Collins et al. 2002). The User's Guide for the latter, in particular, has step-by-step examples for conducting LC analyses and practical suggestions for resolving issues that can arise.

The problem of identifying asthma or other patients on the basis of event count marker variables derived from AD—in the absence of a gold standard—is analogous to the task of classifying patients on the basis of fallible clinical tests. To the best of our knowledge, there is no published research on the use of LCM in identifying chronic disease cohorts with AD.

OBJECTIVES OF THE STUDY

The objectives of this study were: (a) to develop a parsimonious model of the respiratory patient population in British Columbia (BC), Canada through LCM, using treatment marker variables derived from counts of event records in administrative databases; (b) to use this model to create and evaluate a case definition of treated asthma; (c) to compute a model-based estimate of the prevalence of asthma in BC; and (d) to assess a set of conventional AD case definitions for asthma in relation to the model-based definition.

METHODOLOGY

Subjects and Data

Ethical approval for this study was obtained from the University of British Columbia's Behavioural Research Ethics Board. All data files used in the analyses were provided without variables that would permit the personal identification of individuals.

The primary data sources used in this study were three linked BC Ministry of Health databases: the Medical Services Plan (MSP) database containing fee-for-service general practitioner (GP) and specialist physician billing records, the Discharge Abstracts Database (DAD) of hospital inpatient separation records, and the PharmaNet database that captures all prescription drug purchases in community pharmacies throughout BC. Complete ER utilization data were unavailable, however, so they were not used in any of the analyses reported here.

The base population of respiratory patients whose data records we analyzed is defined as follows: Any BC MSP enrollee who was between 5 and 55 years old during the 5 fiscal years from April 1, 1996 through March 31, 2001 and who had ≥1 MSP or DAD records between 1991 and 2001 that satisfy either or both of the following broad criteria:

1. MSP database: An ICD-9 diagnosis code from the set {466—acute bronchitis; 472—chronic pharyngitis; 490—bronchitis, not specified; 491—chronic bronchitis; 492—emphysema; 493—asthma; 494—bronchiectasis; 496—chronic airway obstruction} is the reason for visit on the record.

2. DAD: Any of the above ICD-9 codes occurs in any of the diagnosis fields.

The number of respiratory patients in the 5–55 age range satisfying these conditions was 1.36 million. The total population of MSP enrollees grew from 3.92 million in 1996/1997 to 4.02 million in 2000/2001. About 94 percent of respiratory patients met a continuous enrollment requirement (≥ 271 days) in any given year.

For all respiratory patients, we obtained all relevant MSP and DAD records dated within the time frame as well as all PharmaNet records dated during the study period for a set of asthma-related medications. (This list of medications is available from the first author.) We also obtained individuals' MSP enrollment records and summary comorbidity measures, namely aggregated diagnosis group (ADG) indicators. The latter variables were generated using the Johns Hopkins ACG Case-Mix System (Weiner, Abrams, and Bodycombe 2003).

Fitting Alternative Models and Selecting One for Further Use

We first created seven categorical marker variables, each with two or four event count categories (labeled A–D), to summarize individuals' asthma-related service and medication use during each fiscal year. These markers and categories are defined in Table 1. We assigned values for the variables to each respiratory patient for each fiscal year.

Table 1.

Marker Variables and Categories Used in Latent Class Modelling

		Categories and Interpretations
Marker Variable	Description of Variable (Event Type)	A	B	C	D
GP	Number of GP visits in year with ICD-9 code 493	0	1	2	≥3
OP	Number of other physician visits coded 493	0	≥1	—	—
Dx1	Number of hospitalizations in year with ICD-9 code 493 as the primary diagnosis	0	≥1	—	—
Dx2	Number of hospitalizations in year with ICD-9 code 493 as a secondary diagnosis	0	≥1	—	—
SABA	Number of short-acting beta agonist (SABA) prescription fills in year	0	1	2	≥3
ICS	Number of inhaled corticosteroid (ICS) fills in year	0	1	2	≥3
OAD	Number of other (non-SABA, non-ICS) asthma drug fills, including oral steroids, long-acting beta agonists, xanthines, leukotriene receptor antagonists, and anti-allergic agents	0	1	2	≥3

Note: Category A for a marker is assigned to patients with 0 events during a year of that particular type. Categories B, C, and D are assigned to patients with, in the case of the GP marker, 1, 2, or ≥3 GP visits for asthma (ICD-9 code 493), respectively. In the case of the OP, Dx1, and Dx2 variables—markers for relatively uncommon events—only categories A and B were assigned. The B category is used for these variables when patients had ≥1 event of their respective types.

GP, general practitioner; ICD-9, International Classification of Disease, 9th Revision.

We used markers that split physician, hospital, and medication use into subcomponents so that we could check for the possibility of differential effects in distinguishing cases from noncases that would be masked within markers of the type used in the definitions cited earlier.

With this set of variables and their numbers of score categories (i.e., 2 or 4), 2,048 distinct patient score profiles can be obtained. We chose the number of score categories and the cutpoints for each marker after examining the count distribution for each type of event, balancing the desire not to lose information with the need to avoid a large number of low-frequency profiles. Even so, only about half of the 2,048 potential profiles were actually observed to occur in any given year.

The individual-level data for all qualified respiratory patients—individuals from the base population who met the age and continuous enrollment requirements for a particular year—were aggregated to produce counts of patients having each profile. The profiles and their counts were the input data used in LC model fitting.

With each year's profile counts we fitted unrestricted latent class models involving 2, 3, and 4 latent classes using WinLTA version 3.0 software (Collins et al. 2002). We obtained the following statistics for each model: (1) The unconditional probability of belonging to each of the latent classes, i.e., estimated class prevalences; (2) the conditional probability of obtaining a particular score on a particular marker variable for members of each of the latent classes—providing, in two-class models, estimates of each marker's sensitivity and specificity; (3) the probability of belonging to each latent class for each of the observed profiles, i.e., each patient's probability of belonging to a particular class; and (4) measures of goodness of fit. For each model fitted we performed nonparametric bootstrapping (10 replications per model) to provide estimates of the standard errors of all statistics of interest.

Because the number of patients used in fitting the models is so large, the usual tests of fit such as the likelihood ratio chi-square (χ²) measure suggest that the fit is acceptable for only the four-class model. It is desirable, however, to fit a more parsimonious model if possible. We examined three other indices of fit and an index of predictive accuracy—all described by Dayton (1998)—for each model using 1996/1997 data (see electronic supplemental material in Appendix A1).

The I_D is a dissimilarity index whose values represent the sum over all profiles of the absolute values of the differences between the observed and expected numbers of cases divided by the total number of cases. Values <0.05 are considered to be acceptable (Dayton 1998). The AIC′ and BIC′ indices (Akaike 1973; Schwartz 1978) are related to χ², but involve applying a penalty for greater model complexity. (The larger the number of classes, the greater the complexity, all else being equal.) Smaller values indicate a better fitting model. The λ criterion (Goodman and Kruskall 1954), related to the percentage of cases correctly classified, is a measure of the model's improvement over chance assignment of cases to classes.

All three models have acceptable I_D values with the three-class model having the best value. The AIC′ criterion and BIC′ criteria favor the four-class and two-class models, respectively. The largest improvement on chance assignment results from using the two-class model.

The models' rankings in terms of each of the four fit indices are identical in all bootstrap replications. Estimated standard errors for these indices are all very small. Values for two-class models were similar across years. The fact that the probabilities and fit measures replicate so well in different data sets suggests that these are all very stable models with generally good fit.

Assessing Conventional Case Definitions

Having found that the two-class model had an acceptable fit, we assessed the performance of three conventional AD case definitions for asthma relative to the two-class model-based case selection (referred to as 2CMS). The three definitions are as follows:

• A modified HEDIS (MH) definition of persistent asthma (National Committee for Quality Assurance 2001) in which the ER visit criterion was omitted.

• A set of three criteria similar to those used for identifying asthma patients to include in the BC's Provincial Asthma Registry (AR) (British Columbia Ministry of Health 2004), namely ≥2 physician visits with an ICD-9 code of 493; or ≥1 inpatient hospitalization with ICD-9 code 493 as the principal diagnosis; or ≥3 prescription fills from a list of asthma medications.

• The Senthilselvan–Suissa (SS) definition tested in the Breathing Easier study, i.e., ≥1 physician visit with an ICD-9 code of 493 or ≥3 asthma medication fills during a year.

We compared definition-based subgroups of 1996/1997 respiratory patients on the following seven variables: gender, age, indicators of (a) acute upper respiratory tract infection (URTI), (b) acute bronchitis/bronchiolitis, and (c) other bronchitis and ADG indicators of chronic medical stable and unstable conditions (ADG 10 and ADG 11, respectively). Adult onset type 1 diabetes and essential hypertension are examples of ADG 10 conditions; multiple sclerosis and ischemic heart disease are examples of ADG 11 conditions. The three indicators of respiratory conditions were constructed by counting physician visit records during the target year coded with ICD-9 codes 465, 466, and 490, respectively.

Note that patients could belong to more than one subgroup, and most did. The bootstrapping method used for testing intergroup differences on the seven variables accounted for the covariation in the groups' values.

RESULTS

Model Selection and Stability Assessment

As noted earlier, we found that a two-class model fit acceptably well in comparison with the three- and four-class models, so we used the former in addressing study objectives (b), (c), and (d) because of its parsimony. We labeled the two classes TA (treated asthma) and NA (nonasthma).

Consistency in the assignment of patients to classes across samples and years is an important consideration in applying a case definition. Conventional case definitions are deterministic—the assignment rule is the same regardless of the data, so consistency is an automatic consequence. In contrast, the LCM approach is data driven—the patients' marker score distributions and covariation determine the probability that patients with a particular profile belong to a particular class—so consistency must be evaluated.

No profile changed from the TA class to the NA class or vice versa across replications under the two-class model. Further, profiles' classes were completely consistent across years.

Conditional Probabilities for the Two-Class Models

Electronic supplemental material in Appendix B shows the conditional probabilities for the two-class model fitted to the 1996/1997 data. Values for the other years are very similar. Patients in latent class 1 have very high probabilities of having a value of 0 (visits/fills) on each of the seven markers. Patients in class 2 have lower probabilities of 0s. A patient in class 2, for example, has only a 20 percent chance of having no short-acting β agonist (SABA) fills and a 41 percent chance of having no inhaled corticosteroid (ICS) fills. It is thus reasonable to interpret the latter class as the TA class for this model.

Because hospitalizations for asthma are rare, as expected, patients in the TA class have only a 1.5 percent chance of having ≥1 hospitalization with ICD-9 code 493 as the principal diagnosis. Patients in the NA class have a 0 percent chance of having such a hospitalization.

If we group marker categories B, C, and D together and add their corresponding probabilities, the resulting conditional probabilities for each marker (now a binary variable) have an additional interpretation related to screening test characteristics. The sensitivity analog of each marker individually is the conditional probability that TA class patients have >0 events for the marker, and the specificity analog is the conditional probability that NA class patients have 0.

For each marker we also computed likelihood ratio values LR+ and LR− and a single LR value for each of its two or four categories (Sackett et al. 1991). The general likelihood ratio is defined as follows: LR=probability that a person with the condition has a particular test result/probability that a person without the condition has the test result.

LR+ refers to a positive result on a diagnostic test (in this context, a marker variable) and is equal to sensitivity/(1−specificity); LR− refers to a negative result and equals (1−sensitivity)/specificity. Likelihood ratios are useful in part because they quantify the extent to which a test (marker) increases or decreases a patient's odds of having the condition: Posttest Odds=LR × Pretest Odds. LR values that are >10 or <0.1 are considered to produce a large increase (decrease) in the odds. Table 2 shows the sensitivities, specificities, and LR values.

Table 2.

Sensitivity, Specificity, and Likelihood Ratios of Markers (1996/97 Data)

	Marker Variable
Parameter	GP	OP	Dx1	Dx2	SABA	ICS	OAD
Specificity	0.989	0.997	1.000	0.999	0.975	0.993	0.975
Sensitivity	0.605	0.117	0.015	0.015	0.801	0.592	0.255
LR+ overall	55.0	39.0	>105	66.2	32.0	84.6	10.2
LR− overall	0.40	0.89	0.99	0.99	0.20	0.41	0.76
LR category A	0.40	0.89	0.99	0.99	0.20	0.41	0.76
LR category B	31.0	44.3	>105	42.8	18.5	46.9	7.0
LR category C	>105	—*	—	—	69.0	281	15.3
LR category D	>105	—	—	—	274	>105	37.5

^*The dashes in the table indicate that score categories C and D were not used for the OP, Dx1, and Dx2 markers.

LR, Likelihood ratio.

Marker abbreviations are defined in Table 1.

The SABA marker has the highest sensitivity and smallest LR− value among the seven, and the two hospital markers have the highest specificities and LR+ values. Hospitalization with an asthma diagnosis is the surest way to rule in membership in the TA class, and absence of any SABA fills is the best (though not particularly strong) way to rule out membership in this class. In this model, each marker is useful in assigning patients to the TA class: all LR+ values are >10. Although none of the markers individually has a very small LR− value, the capacity to assign patients to the NA class, and thus to discriminate effectively, results from using the markers together, particularly the SABA, ICS, and GP markers.

Patient Classification and Comparison of Definitions

In each year, under the two-class model only the 12 profiles classified patients as not having asthma (see electronic supplemental material in Appendix B). All but two of these involve a single marker, and none involve the Dx1 marker; having even a single hospital visit with the principal diagnosis of asthma leads to classification as asthmatic under the model. The last column in the table gives the probability that a person with a given profile is nonasthmatic. (These probabilities are computed using the estimated conditional and class probabilities that result directly from fitting a model.) The probability that a patient with only 1 SABA fill is nonasthmatic is 0.85; the probability for a patient with two SABA fills is 0.63, i.e., lower, as we would expect. Interestingly, a patient with ≥3 other drugs would be classified as asthmatic under the AR and SS definitions while having a high probability under the model of belonging to the NA class.

The other 2,036 profiles generated by this set of markers and categories consistently assigned patients to the TA class, i.e., the probability in any particular year that a patient with one of these profiles belonged to the TA class was >0.5. Note that even profiles that were not observed for any patients in this particular sample have calculable class assignment probabilities.

We compared the classification of patients by the conventional MH, AR, and SS case definitions referred to earlier treating model-based (2CMS) selection as a gold standard. Table 3a shows the sensitivity, specificity, and likelihood ratios we estimated with the 1996/1997 data.

Table 3a.

Sensitivity, Specificity, and Likelihood Ratios (LRs) of Conventional Case Definitions Relative to Model-Based Selection (1996/1997 Data)

	Case Definition
Parameter	AR	MH	SS
Sensitivity	0.632 (0.005)	0.413 (0.024)	0.865 (0.007)
Specificity	0.997 (<0.001)	0.997 (<0.001)	0.983 (<0.001)
LR+	212.5 (3.7)	139.0 (9.0)	50.8 (0.6)
LR−	0.369 (0.005)	0.588 (0.024)	0.137 (0.007)

AR, asthma registry; MH, modified HEDIS; SS, Senthilselvan–Suissa.

Table 3b shows the proportions of cases that were classified as asthmatic by the four definitions applied in concert. In the latter table, the first row indicates that 90.8 percent of the 1.22 million qualified respiratory patients in 1996/1997 were not classified as asthmatic by any definition, and the last row indicates that 3.1 percent were classified as asthmatic by all definitions.

Table 3b.

Classification of Patients by Four Case Definitions (1996/1997 Data)

Case Definition
AR	MH	SS	2CMS	N Patients	% Patients
NA	NA	NA	NA	1,111,245	90.79
NA	NA	TA	NA	14,594	1.19
TA	NA	TA	NA	1,789	0.15
TA	TA	TA	NA	2,075	0.16
NA	NA	NA	TA	14,538	1.19
NA	NA	TA	TA	21,374	1.75
TA	NA	TA	TA	20,505	1.68
TA	TA	NA	TA	23	<0.01
TA	TA	TA	TA	37,861	3.09

TA, classified as asthmatic; NA, nonasthmatic; AR, asthma registry; MH, modified HEDIS; SS, Senthilselvan–Suissa; 2CMS, 2-class model-based selection.

The SS definition is considerably more sensitive than the more complex AR and MH definitions. The latter two definitions, on the other hand, have greater specificity than the former. The AR and MH definitions are best in terms of ruling in TA but worst at ruling it out. There is a greater degree of agreement between the SS definition and model-based selection than between any other pair of definitions.

Asthma Prevalence

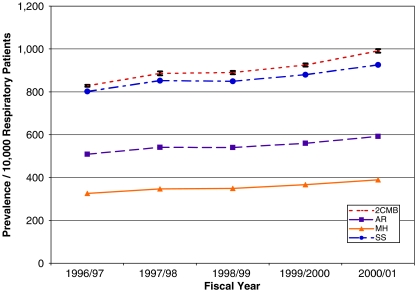
On the basis of class membership probabilities for the two-class model, the estimated prevalence of TA patients among respiratory patients aged 5–55 increased significantly from 828/10,000 (SE=2/10,000) in 1996/1997 to 991/10,000 (SE=4/10,000) in 2000/2001 (see Figure 1). As expected, the 2CMS and SS prevalence estimates are most similar each year, and the MH estimates are consistently smallest: the 2CMS prevalence estimates are approximately 2.55, 1.65, and 1.05 times larger than the MH, AR, and SS values, respectively.

Figure 1.

Trend in Estimated Asthma Prevalence (per 10,000 Respiratory Patients) 1996/1997 to 2000/2001 for Four Definitions.

Notes: AR, asthma registry; MH, modified HEDIS; SS, Senthilselvan–Suissa; 2CMS, two-class model-based selection.

Patients Classified as Asthmatic by Model-Based Selection and Conventional Definitions

Table 4 shows the means and proportions for the seven variables used to compare the four definition-based subgroups and a fifth group consisting of respiratory patients who satisfied none of the definitions—the NA group. As noted earlier, patients could belong to more than one definition-based subgroup.

Table 4.

Characteristics of Patients Classified as Asthmatic by the Four Case Definitions

	Case Definition
Sample Characteristic	NA Patients	AR	MH	SS	2CMS
(1) % male	45.4 (45.0, 45.8)	45.8 (45.3, 46.3)	45.0 (44.7, 45.3)	45.0 (44.7, 45.4)	44.9 (44.8, 45.0)
(2) Mean age (years)	29.2 (29.1, 29.3)	30.8 (30.7, 31.0)	27.6 (27.5, 27.7)	27.9 (27.8, 28.0)	30.1 (30.0, 30.1)
(3) % with ≥1 physician visit with ICD-9=465	16.5 (16.2, 16.8)	15.6 (15.2, 16.0)	16.8 (16.6, 17.1)	17.1 (16.8, 17.3)	11.8 (11.7, 11.9)
(4) % with ≥1 physician visit with ICD-9=466	17.9 (17.6, 18.2)	17.8 (17.4, 18.1)	16.5 (16.2, 16.7)	17.9 (17.7, 18.2)	10.8 (10.7, 10.8)
(5) % with ≥1 physician visit with ICD-9=490	11.7 (11.5, 12.0)	11.7 (11.4, 12.0)	10.8 (10.8, 11.0)	12.1 (11.9, 12.3)	6.3 (6.25, 6.34)
(6) % with a chronic medical (stable) condition (ADG 10)	22.0 (21.7, 22.3)	23.4 (23.0, 23.9)	19.7 (19.4, 19.9)	19.7 (19.5, 20.0)	16.2 (16.1, 16.3)
(7) % with a chronic medical (unstable) condition (ADG 11)	15.0 (14.7, 15.2)	16.7 (16.3, 17.0)	12.1 (11.9, 12.3)	11.2 (11.0, 11.4)	6.3 (6.29, 6.38)

Notes: Bootstrap 95% confidence intervals are in parentheses.

AR, asthma registry; ADG, aggregated diagnosis group; MH, modified HEDIS; SS, Senthilselvan–Suissa; 2CMS, 2-class model-based selection; NA, nonasthmatic.

All subgroups consisted of about 45 percent males. The 2CMS and SS subgroups were most similar to the NA group. The AR, SS, and 2CMS subgroups were all significantly younger than the NA group—the mean age for the latter was 30.1 years—but the MH subgroup was significantly older by 0.8 years.

The proportion of patients with ≥1 physician visit for acute URTI during 1996/1997 was significantly lower in the NA group (11.8 percent) than in each of the other subgroups (range 15.6–17.1 percent). The 2CMS subgroup had the largest proportion, and this differed significantly from the other groups. Similar patterns of proportions for the two other respiratory diagnoses indicate that the model-based asthma subgroup was the most different from the NA group.

The NA group had significantly lower levels of comorbidity than the four asthmatic subgroups: the proportions of NA cases with indications of chronic medical stable (ADG10) and chronic medical unstable (ADG11) conditions—16.2–6.3 percent, respectively—were smaller than the corresponding proportions for the other subgroups. With proportions of 19.7 percent and 11.7 percent, the 2CMS patients were the most similar to the NA patients in terms of chronic comorbidity.

DISCUSSION

Developing or choosing a case definition to use in selecting AD records for an analysis is a critical operation in many types of health services research, planning, and evaluation. The accuracy of the results of the analysis is directly linked to the validity of the case definition, but often even the basic operating characteristics of candidate definitions—sensitivity and specificity—are unknown, let alone the magnitude of potential biases. As Kephart et al. (2004) point out, the problem of bias is compounded in longitudinal analyses in which cases, once identified, remain in their cohort; false-positive cases accumulate over time.

It is often not feasible to validate a potential AD definition with a criterion measure such as a survey; furthermore, the criterion itself is almost certainly affected by measurement error, which as Vacek (1985) notes, would bias the estimates of the definition's sensitivity and specificity. As a range of clinical variables become more readily available in electronic form to health services researchers, and as diagnostic procedures improve, the accuracy of case selection algorithms would be expected to increase due to reductions in measurement error in algorithms' input marker variables. In our view, however, the “no gold standard” problem (and the need for evidence-combining methodologies to address it) is likely to remain for asthma until such time as a definitive indicator of the condition is developed and data based on this indicator become generally available.

Garrett, Eaton, and Zeger (2002) have demonstrated the utility of using two- and three-class latent class models in validating Diagnostic and Statistical Manual of Mental Disorders (DSM) and International Classification of Diseases (ICD-10) diagnostic criteria for depression. As they conclude, “…although LCMs are not definitive indicators of true disease, they are useful for helping to understand the operating characteristics of diagnostic tests” (p. 1291).

We have examined the utility of using LCM to develop an AD case definition for TA and have concluded that this approach is useful at least in creating a large population-based cohort of asthma patients. We found that a simple well-fitting model—a two-class model based on the full set of marker variables we examined—provided a very high level of consistency for class assignment across years. While the physician visit, hospitalization, and prescription fill markers we used differed considerably in both sensitivity and specificity, each contributed to discrimination among cases. The hospitalization markers were most effective in ruling in a classification of TA while the GP visits, SABA fills and ICS fills markers were most useful in ruling out such a classification.

Modelling with multicategory markers enabled us to better understand the contribution to classification that results from a patient's change in categories on a particular marker as well as the relative impact of different combinations of marker values on case selection. All else being equal, for example, having ≥3 SABA fills increases the odds of being classified as asthmatic over 3 times as much as having 2 SABA fills.

Further, two marker profiles involving the same total number of utilization events, e.g., three drug purchases, can have markedly different probabilities of belonging to the asthma class. Combining a prescription fill with a single physician visit increases the probability of being classified as asthmatic. This is consistent with the findings of Rector et al (2004). Thus the linkage between utilization and case status is more complex than most conventional case definitions allow for.

The fact that each marker profile is associated with a calculable probability of belonging to the asthma class reminds us that patients with different profiles belonging to the same class are not homogeneous; they have (sometimes considerably) different probabilities of having the condition of interest. As Embretson and Reise (2000) have observed in a related context, LCM is analogous to clinical inference with markers functioning as diagnostic signs and symptoms; their patterns of co-occurrence are consistent to varying degrees with the ultimate diagnosis of the patient.

As we expected, given the conventional definitions' significantly different sensitivities, the cohorts selected by the four definitions differ considerably in size. The annual prevalences estimated using the Senthilselvan–Suissa definition are almost as large as their model-based counterparts but are more than double the values obtained using the modified HEDIS definition.

In choosing a case definition for a particular analysis, researchers and health planners must balance the importance of including as many patients as is reasonably possible within a cohort—an effect of a definition with a high sensitivity—and limiting the number of false positives while possibly missing some true positives. Once a model has been cross-validated and accepted, its probability-based case selection rule provides a benchmark against which a set of other potential definitions can be compared. The resulting sensitivity and specificity estimates for each definition can be used to make an evidence-based choice among the options considered. The magnitude of the prevalence differences resulting from the different case selection approaches we examined underscores, in our view, the importance of a careful analysis of the properties of alternative case definitions, using LCM as a tool, at the start of a program of health services research based on a cohort selected from AD.

For longitudinal analyses, it is important to examine the effects of applying candidate definitions across multiple years and examining the proportions of patients who are identified repeatedly. As we have seen, the definition that is most sensitive on a single occasion may not be best in terms of identifying persistent cases. Applying a definition to a 2-year period rather than a single year would be a way to increase its sensitivity.

Health services researchers and planners need to be aware that their choice of case definition has implications beyond just the size of the cohort selected. Our comparisons of the patient subgroups selected by each definition and by no definition showed that while asthmatic patients are significantly different from NA respiratory patients in a number of important respects, the definitions' subgroups are also distinctive. In particular, patients classified as asthmatic by our two-class model were the most different from the NA patients in terms of having a significantly greater probability of receiving another different respiratory diagnosis. On the other hand, while the model-selected asthmatic patients were significantly more likely to have another chronic condition than the NA patients, the asthmatic patients selected by the other definitions were even sicker. Understanding these observations requires further investigation.

In choosing a suitable case definition after a systematic comparison along the lines outlined here, researchers and planners will be able to have increased confidence in the results of their analyses involving their selected cohorts—whether they be regional comparisons of health care quality indicators or projections of future health system utilization, for example. Using a model-based approach in the process of selecting a cohort helps to quantify the uncertainty in the selection process. The sensitivity and specificity of the different variables in the model can be assessed. Markers that do not contribute usefully can be refined, e.g., by collapsing categories, or deleted. Prevalence estimates with estimated standard errors are a key direct product of the model-based approach. Finally, each case/profile is assigned a probability of belonging in the model's class of primary interest. The consistency of profiles' probabilities can be tracked over time when multiple years of data are available, providing evidence about the stability (or lack thereof) of the model's class assignments.

The methodological framework we have described is generalizable across jurisdictions in that it can be applied to the task of case selection wherever sufficient relevant data are available. It must be tailored to the particulars of a research or planning situation, however, and we see the assessment of the feasibility of doing so in different jurisdictions and health care organizations as an area for further study. The choice of marker variables to use as inputs in the modeling, for example, will depend on the types, completeness, and quality of the data available. (Examining the effects of adding a marker for ER utilization for asthma to the set we tested would be a useful investigation, for example.) Marker choices will affect outcomes, but this is true for any case selection procedure.

In terms of the statistical results and case selection outcomes from the application of the methodology, we would expect both similarities and differences across jurisdictions. For other jurisdictions with large heterogeneous populations like BC's and with data concerning physician visits, hospitalization, and drug dispensing, we would expect that replication of the steps we outlined in “Methodology” would lead to some results that are similar to ours. For example, we would predict that a SABA marker like ours would have a higher sensitivity than an ICS marker, although we could not predict the exact sensitivities. On the other hand, because true asthma prevalence varies considerably across jurisdictions, we would expect interjurisdictional differences in model-based estimates of prevalence.

A limitation in the current study—our focus on a single chronic condition—suggests a second avenue for further investigation. Rector et al. (2004) systematically compared a series of AD definitions for each of six chronic medical conditions—diabetes, hypertension, heart failure, arthritis, chronic lung disease, and glaucoma—and found that sensitivities and specificities for particular types of definitions varied considerably across conditions. It would be useful to assess the latent class modeling approach as a tool for assisting in the selection of cases with other conditions.

SUPPLEMENTARY MATERIAL

The following supplementary material for this article is available online:

Appendix A

Indices of Model Fit for Unrestricted 2-, 3-, and 4-Class Models (1996/97 Data).

Appendix B

Marker Categories' Conditional Probabilities for a 2-Class Model (1996/97 Data).

Appendix C

Profiles That Assign a Patient to the Nonasthma Class (1996/97 Data).

This material is available as part of the online article from http://www.blackwell-synergy.com/doi/abs/10.1111/j.1475-6773.2007.00775.x (this link will take you to the article abstract).

Please note: Blackwell Publishing is not responsible for the content or functionality of any supplementary materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.