Structural analyses of a hypothetical minimal metabolism

Abstract

By integrating data from comparative genomics and large-scale deletion studies, we previously proposed a minimal gene set comprising 206 protein-coding genes. To evaluate the consistency of the metabolism encoded by such a minimal genome, we have carried out a series of computational analyses. Firstly, the topology of the minimal metabolism was compared with that of the reconstructed networks from natural bacterial genomes. Secondly, the robustness of the metabolic network was evaluated by simulated mutagenesis and, finally, the stoichiometric consistency was assessed by automatically deriving the steady-state solutions from the reaction set. The results indicated that the proposed minimal metabolism presents stoichiometric consistency and that it is organized as a complex power-law network with topological parameters falling within the expected range for a natural metabolism of its size. The robustness analyses revealed that most random mutations do not alter the topology of the network significantly, but do cause significant damage by preventing the synthesis of several compounds or compromising the stoichiometric consistency of the metabolism. The implications that these results have on the origins of metabolic complexity and the theoretical design of an artificial minimal cell are discussed.

1. Introduction

One century ago, the challenge of synthesizing a living cell was considered the ‘ideal goal’ of biology (Loeb 1906). Nowadays, while working on the development of the appropriate technology for actually ‘synthesizing life’, scientists are trying to design artificial minimal life forms in two opposite but complementary ways, defined as the bottom-up and the top-down approaches (Luisi 2002; Szathmáry 2005). The bottom-up approach aspires at constructing the artificial simplest chemical supersystem or protocell by assembling the basic non-living components that confer a system the properties of living matter (Szostak et al. 2001; Luisi et al. 2006). Although no such experimental system exists yet, the recent advances in genomic technology and membrane biophysics make the possibility of synthesizing protocells an imaginable goal (Pohorille & Deamer 2002; Rasmussen et al. 2004; Szathmáry 2005), which will provide fascinating insights into the essence of cellular life and may give some clues about how life first evolved on earth. On the other side, the top-down approach aims at constructing a living cell by simplifying existing small genomes, taking the information about minimal genomes already obtained from computational and experimental studies as a start. It is generally admitted that a top-down approach will not achieve the construction of the minimal possible cell in chemical terms, since all extant cells have very complex transcription and translation systems, and it seems unrealistic that the simplest living chemical system would require such components. However, this approach is helping to understand which functions are essential for modern cells, an information that can be applied to the synthesis of modern living cells. The underlying idea, presented a few years ago by Craig Venter, is to build a synthetic chromosome containing the necessary information to perform all the essential living functions, and insert it into a cell to generate a semi-synthetic minimal living cell (Zimmer 2003).

Several challenges must be overcome before such a goal is achieved. On one hand, with our current knowledge, it is not completely obvious which genes should be encoded by this genome, in which order they must be present, which regulatory sequences must be included, or how to put the genome to work once it is introduced into a cell. On the other hand, it is necessary to improve the present technology in order to be able to accurately synthesize the long stretch of DNA necessary to make a minimal genome. While recent methodological advances in long DNA molecule synthesis, improving both accuracy and pace, have been reported (Smith et al. 2003; Kodumal et al. 2004; Shevchuk et al. 2004), several attempts have been made to define the minimal genome, i.e. the repertoire of genes that is necessary and sufficient to support cellular life, as a first step towards the synthesis of such a minimal semi-synthetic living cell.

Even the simplest unicellular organisms on earth display an amazing degree of complexity. But such complexity does not seem to be a necessary attribute of cellular life, since modern cells possess many functions that would be dispensable in an ideally controlled environment. A minimal genome must contain the smallest number of genetic elements sufficient to allow the cells to maintain metabolic homeostasis, reproduce and evolve, the three main properties of living beings (Luisi et al. 2002, 2006; Islas et al. 2004; Ruiz-Mirazo et al. 2004), in the most favourable scenario, i.e. in a rich environment in which all essential nutrients are provided, and in the absence of any adverse factors (Koonin 2000).

The increasing knowledge on complete genomes from bacteria makes these prokaryotes a suitable model to try to define what a modern minimal genome should be like. Comparative genomic analyses have proven to be very useful to understand the essential functions that define a living cell, based on the assumption that genes conserved across large phylogenetic distances are good candidates to be considered essential. The first comparative genomic analysis was performed soon after the two first bacterial genome sequences, those from Haemophilus influenzae (Fleischmann et al. 1995) and Mycoplasma genitalium (Fraser et al. 1995), were completed. This comparison resulted in the reconstruction of a first minimal gene set comprising only 256 genes (Mushegian & Koonin 1996). More recent approaches to the minimal gene set have been based in the comparison of the reduced genomes of insect endosymbionts and intracellular parasites. All these species have experienced a massive genome reduction after the establishment of their respective bacteria–host relationships, due to a relaxed selection on the maintenance of genes that are rendered unnecessary in the protected environment provided by the host. Therefore, most of the genes shared by these genomes are likely to code for essential cellular functions. The comparison among five endosymbionts and the epicellular parasite, M. genitalium, revealed that they share only 180 housekeeping protein-coding genes (Gil et al. 2004). This number was further reduced to 156 when the intracellular parasites Rickettsia prowazekii and Chlamydia trachomatis were included in the comparison (Klasson & Andersson 2004). When 21 complete genomes of bacteria, archaea and eukaryotes were compared (Koonin 2000), it was suggested that a set of approximately 150 genes would be sufficient to maintain a living cell.

Complementarily, experimental approaches have been used to identify genes that are essential under particular growth conditions. Several genome-wide analyses have been performed using three different strategies: massive transposon mutagenesis, use of antisense RNA to inhibit gene expression and systematic inactivation of each individual gene present in a genome (reviewed in Gil et al. 2004). Recently, Glass et al. (2006) have defined a set of essential genes in M. genitalium using transposon mutagenesis. The authors proposed that 387 protein-coding and 43 structural RNA genes would suffice to support cellular, heterotrophic life in a chemically complex environment.

In summary, all experimental approaches yield minimal gene sets that are compatible with the comparative genomics inferences. However, since all present living cells possess common genetic information-processing systems, both computational and experimental approaches provide sets of essential genes that are enriched in genes involved in such function, mainly encoding the components of the transcriptional apparatus, and contain relatively few genes for metabolic enzymes. Yet, the minimal genome must include the necessary genes to maintain a minimal metabolism in order to achieve metabolic homeostasis, one of the essential functions that define life (Peretó 2005; Szathmáry et al. 2005). It should be stressed that, from a metabolic point of view, there is no conceptual or experimental support for the existence of just one form of minimal bacterial cell and, therefore, a diversity of minimal ecologically dependent metabolic charts could sustain a universal genetic machinery. Nevertheless, taking into account all previous computational and experimental approaches to define a minimal genome, we proposed a minimal set for life composed by 206 protein-coding genes (Gil et al. 2004) in which all genes involved in essential pathways to maintain one possible form of a coherent minimal metabolism were included.

In the present paper, we emphasize and deepen our previous work on that minimal genome, exploring some structural properties of the inferred metabolic network, namely the stoichiometric and topological consistency and the robustness of the proposed minimal metabolism.

2. Material and methods

(a) Metabolic network inference

To investigate the topological properties of a minimal metabolism and compare it with the metabolisms from extant bacteria, the metabolic network of each genome was inferred from the corresponding annotated gene functions. The metabolic network reconstruction procedure used here was initially described in Gabaldón & Huynen (2003) and consists of an automatic mapping of the annotated gene functions onto KEGG metabolic pathways (Kaneisha & Goto 2000). The reaction database was derived from the Ligand v. 35.0 database, from which polymerization reactions and reactions involving macromolecules were filtered out. To eliminate connections through frequent metabolites such as cofactors (Schuster et al. 2002), we only considered connections through metabolites represented in the pathway maps of the KEGG database. When more than one substrate, or more than one product, were represented for a given reaction in a pathway map, we included connections only through pairs of compounds that have at least one carbon atom in common on the two sides of the reaction. For this purpose, we used the atomic mappings of the corresponding reactions annotated in the Rpair database (Hattori et al. 2003). Finally, we automatically checked for errors in the directionality of the reaction detected by Ma & Zeng (2003) and made efforts to correct additional obvious inconsistencies. The final database comprised a total 8115 reactions. To reconstruct the metabolic network of a genome, the annotated functions of all encoded genes were mapped onto the above-mentioned reaction database, and a file describing the existing network connections was generated. This information was represented in the form of a directed graph in which nodes and edges represent metabolites and enzymatic connections between them, respectively. This allows for the use of mechanical statistics and graph theory to describe the main topological properties of the reconstructed networks (see below).

(b) Topological analysis

The following topological properties of the reconstructed networks were computed.

Connection degree (k_i) distribution. The connection degree of a given node is defined as the number of metabolites directly linked to it. When the direction of the reaction is considered, k_i can be decomposed into input and output connection degrees representing the number of connections starting or ending at that metabolite, respectively. The frequency distribution of all types of connection degrees was investigated to ascertain whether they followed a power-law distribution (P(x)=Kx^a, where x is the variable and K and a are constants). Power laws were detected as linear relations in logarithmic scales.

Clustering coefficient (C). For a given metabolite i, directly connected to k_i metabolites in the network, the clustering coefficient (C_i) is defined as the ratio between the number of connecting edges existing among the k_i metabolites and the theoretical maximum of connections (every node in a cluster connected to all the others), k_i(k_i−1)/2. The clustering coefficient of the network (C) is the average of all individual C_i's. Note that, in this case, directionality of the connection is not taken into account to compute the clustering coefficient; therefore, networks are treated as undirected graphs. In a random network with n nodes and e edges, since edges are distributed randomly, the average clustering coefficient is C=2e/n² (Albert & Barabasi 2002).

Average path length (L). The path length (l_ij) is defined as the number of edges in the shortest pathway from metabolite i to metabolite j. Note that directionality of the reaction is considered in this case, so that the path from metabolite i to j is not necessarily the same as the path from j to i. All reachable metabolites in the network were identified by the ‘breath first searching’ algorithm (Broder et al. 2000), and the average path length of the network (L) was computed averaging path lengths over all pairs of connected metabolites in the network.

Network diameter (D) is defined as the length of the longest pathway among all shortest pathways in the network (Albert & Barabasi 2002).

(c) Stoichiometric analysis

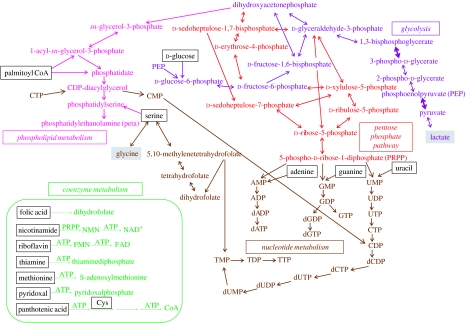
A reduced theoretical network, derived from a revised version of the minimal genome proposed by Gil et al. (2004) (figure 1 and table 1), composed by 208 protein-coding genes, was expressed as a set of stoichiometrically adjusted reactions, and the reversible/irreversible character of each reaction was assigned (table 2). Although coenzymes are essential chemical reagents for some metabolic reactions (e.g. thiamine pyrophosphate for transketolase) their metabolism (except folate reactions linked to TTP biosynthesis, see figure 1 and inset) was not considered in the following analysis because coenzymes play essentially a catalytic function and do not affect the stoichiometric analysis. To perform the structural analysis of the metabolic network, we used Metatool (Pfeiffer et al. 1999), an efficient algorithm for computing all metabolic pathways that are feasible in an inferred network, using reaction equations as input. Once the set of metabolites (external—source substrates k with an input flux Jik, and k sink products with an output flux Jok—and internal) and reactions of the network are defined, Metatool calculates the stoichiometric matrix and several structural properties of the system. Among those, the following are remarkable (Pfeiffer et al. 1999; Schuster et al. 2002).

Figure 1.

A simplified overview of the metabolic network implemented by a hypothetical minimal genome of 208 protein-coding genes derived by an integrated approach (modified from Gil et al. 2004). Names of substrates freely available for the hypothetical minimal cell are represented inside a frame. Two sink metabolites are labelled in grey. Coenzyme metabolism (except the folate metabolism linked to TTP biosynthesis) is shown in the inset and was not considered in the stoichiometric analysis. Wider arrows in the glycolytic pathway indicate the two steps where ATP is synthesized by substrate-level phosphorylation.

Table 1.

Classification of genes, and enzymatic steps catalysed by the associated encoded proteins, included in a minimal metabolism for bacterial life (modified from Gil et al. 2004).

pathways	genes	enzymatic steps
glycolysis from glucose to lactate	13	11
pentose phosphate pathway	5	7
phospholipid biosynthesis	6	6
biosynthesis of nucleotides	15	26
total	39	50

Table 2.

Metabolite and reaction input for the network shown in figure 1. (Metabolite abbreviations are the usual in biochemistry, except for pal (palmitoyl CoA), peta (phosphatidylethanolamine), pser (phosphatidylserine), mthf (5,10-methylene-tetrahydrofolate). Input fluxes (for k source substrate) and output fluxes (for k sink product) are indicated by Jik and Jok, respectively. For redox coenzyme NAD⁺/NADH, a reversible flux Jk is defined. Reversible and irreversible reactions are indicated, in the reaction equations, by the symbols ↔ and →, respectively. Last column shows the corresponding Mycoplasma genitalium genes considered as essential by Glass et al. (2006). The four cases in boldface correspond to non-essential genes. n.i., non-identified in M. genitalium. Input file for Metatool is available upon request to the corresponding author.)

external metabolites		internal metabolites
metabolite input
sources: glc (Ji1), pal (Ji2), ade (Ji3), gua (Ji4), ura (Ji5), ser (Ji6), p (Ji7), nadh (Jk1), nad (Jk2) sinks: lac (Jo1), peta (Jo2), atp (Jo3), ctp (Jo4), gtp (Jo5), utp (Jo6), datp (Jo7), dctp (Jo8), dgtp (Jo9), ttp (Jo10), gly (Jo11)		g6p, f6p, fbp, gdp, dhp, bpg, 3pg, 2pg, pep, pyr, g3p, mag, dag, cdp-dag, pser, sbp, s7p, rip, xip, e4p, rup, prpp, amp, gmp, cmp, ump, tmp, adp, gdp, cdp, udp, dump, dadp, dgdp, dcdp, dudp, dutp, tdp, mthf, dhf, thf, pp

EC	name	abbreviation	input reaction equations	Glass et al. (2006)
enzyme and reaction input
2.7.1.69	phosphotransferase system	PTS	glc+pep→g6p+pyr	MG041, 069, 429
5.3.1.9	glucose-6-phosphate isomerase	PGI	g6p↔f6p	MG111
2.7.1.11	6-phosphofructokinase	PFK	f6p+atp →fbp+adp	MG215
4.1.2.13	fructose-1,6-bisphosphate aldolase	FBA	fbp↔gdp+dhp	MG023
5.3.1.1	triose-phosphate isomerase	TPI	gdp↔dhp	MG431
1.2.1.12	glyceraldehyde-3-phosphate dehydrogenase	GAP	gdp+nad+p↔bpg+nadh	MG301
2.7.2.3	phosphoglycerate kinase	PGK	bpg+adp↔3pg+atp	MG300
5.4.2.1	phosphoglycerate mutase	GPM	3pg↔2pg	MG430
4.2.1.11	enolase	ENO	2pg↔pep	MG407
2.7.1.40	pyruvate kinase	PYK	pep+adp→pyr+atp	MG216
1.1.1.27	lactate dehydrogenase	LDH	pyr+nadh↔lac+nad	MG460
1.1.1.94	sn-glycerol-3-phosphate dehydrogenase	GPS	dhp+nadh→g3p+nad	n.i.a
2.3.1.15	sn-glycerol-3-phosphate acyltransferase	PLSb	g3p+pal→mag	n.i.
2.3.1.51	1-acyl-sn-glycerol-3-phosphate acyltransferase	PLSc	mag+pal→dag	MG212
2.7.7.41	phosphatidate cytidyltransferase	CDS	dag+ctp→cdp-dag+pp	MG437
2.7.8.8	phosphatidylserine synthase	PSS	cdp-dag+ser→pser+cmp	n.i.
4.1.1.65	phosphatidylserine decarboxylase	PSD	pser→peta	n.i.
4.1.2.13	fructose-1,6-bisphosphate aldolase	FBA2	gdp+e4p↔sbp	MG023
3.1.3.37b	sedoheptulose-1,7-bisphosphatase	SPH	sbp→s7p+p	n.i.
2.2.1.1	transketolase	TKT	gdp+s7p↔rip+xip	MG066
2.2.1.1	transketolase	TKT2	e4p+xip↔f6p+gdp	MG066
5.1.3.1	ribulose-phosphate 3-epimerase	RPE	xip↔rup	MG112
5.3.1.6	ribose-5-phosphate isomerase	RPI	rup↔rip	MG396
2.7.6.1	phosphoribosylpyrophosphate synthase	PRS	rip+atp→prpp+amp	MG058
2.4.2.8	hypoxanthine phosphoribosyltransferase	HPT	prpp+ade→amp+pp	MG276
2.4.2.8	hypoxanthine phosphoribosyltransferase	HPT2	prpp+gua→gmp+pp	MG458
2.4.2.9	uracil phosphoribosyltransferase	UPP	prpp+ura→ump+pp	MG030
3.6.1.1	inorganic pyrophosphatase	PPA	pp→2p	MG351
2.7.4.3	adenylate kinase	ADK	amp+atp→2adp	MG171
2.7.4.8	guanylate kinase	GMK	gmp+atp→gdp+adp	MG107
2.7.4.14b	cytidylate kinase	CMK	ump+atp→udp+adp	MG330
2.7.4.14	cytidylate kinase	CMK2	cmp+atp→cdp+adp	MG330
2.7.4.6	nucleoside diphosphate kinase	NDK	gdp+atp↔gtp+adp	MG216c
2.7.4.6	nucleoside diphosphate kinase	NDK2	udp+atp↔utp+adp	d
2.7.4.6	nucleoside diphosphate kinase	NDK3	dadp+atp↔datp+adp	MG216c
2.7.4.6	nucleoside diphosphate kinase	NDK4	dgdp+atp↔dgtp+adp	MG216c
2.7.4.6	nucleoside diphosphate kinase	NDK5	ctp+adp↔cdp+atp	d
2.7.4.6	nucleoside diphosphate kinase	NDK6	dcdp+atp↔dctp+adp	d
2.7.4.6	nucleoside diphosphate kinase	NDK7	dutp+adp↔dudp+atp	d
2.7.4.6	nucleoside diphosphate kinase	NDK8	tdp+adp↔ttp+adp	MG034
1.17.4.1	ribonucleoside diphosphate reductase	NRD	adp+nadh→dadp+nad	MG229–MG231
1.17.4.1	ribonucleoside diphosphate reductase	NRD2	gdp+nadh→dgdp+nad	MG229–MG231
1.17.4.1	ribonucleoside diphosphate reductase	NRD3	cdp+nadh→dcdp+nad	MG229–MG231
6.3.4.2	CTP synthase	PYR	utp→ctp	n.i.
3.5.4.13	dCTP deaminase	DCD	dctp→dutp	n.i.
2.7.4.9	thymidylate kinase	TMK	dudp+adp↔dump+atp	MG006
2.7.4.9	thymidylate kinase	TMK2	tmp+atp↔tdp+adp	MG006
2.1.1.45	thymidylate synthase	THY	dump+mthf→dhf+tmp	MG227
1.5.1.3	dihydrofolate reductase	DFR	dhf+nadh↔thf+nad	MG228
2.1.2.1	glycine hydroxymethyltransferase	GHT	ser+thf↔gly+mthf	MG394

^aMG039 codes for a non-essential FAD-dependent glycerol-3-phosphate dehydrogenase.

^bSedoheptulose-1,7-bisphosphatase and cytidylate kinase are missing in table 1 of Gil et al. (2004).

^cMG216 encodes pyruvate kinase. This glycolytic enzyme can also catalyse the phosphorylation of purine dinucleotides using PEP as a phosphate donor.

^dMushegian & Koonin (1996) proposed MG264 (dephospho-CoA kinase, EC 2.7.1.24) and MG268 (conserved hypothetical protein) as candidates for the role of NDK. Both genes are independently dispensable after Glass et al. (2006).

The ‘enzyme subsets’ (ES) are groups of enzymes that, in all steady states of the system, operate together in fixed flux proportions, i.e. with a constant stoichiometry.

The ‘elementary flux modes’ (EFM) are flux patterns which can be accomplished at steady state (with all the irreversible reactions proceeding in the appropriate direction) and that cannot be decomposed into simpler flux distributions. An EFM can be characterized by indicating which enzymes are involved and their respective flux proportions. Except for internal cycles, the EMF set informs on the possible pathways that convert input substrates into output products throughout the system. Each EMF disappears when any of its associated enzymes is eliminated.

The ‘convex basis’ informs on the vectorial space dimension in which all the system solutions can be represented. It also displays a base of that space for which all the elements are EFM. Any steady-state solution can thus be represented as a linear combination of elements of the convex basis with all coefficients being positive.

3. Results

(a) Topological consistency of a minimal metabolic network

Several groups have recently investigated the system properties that emerge from the network organization of natural metabolisms to gain insights on the organizational and evolutionary principles of the metabolism of living organisms (Jeong et al. 2000; Wagner & Fell 2001; Ma & Zeng 2003; Arita 2004; Tanaka 2005). Albeit deriving quite different conclusions, they all found that natural metabolisms can be described as networks following a power-law distribution of connectivities, i.e. most metabolites exhibit few connections, while a few densely connected metabolites act as hubs in the network. We have previously proposed a minimal metabolism based on different theoretical and experimental approaches (Gil et al. 2004). To assess whether the reconstructed minimal metabolism is consistent in terms of its topological organization, and to investigate whether certain topological parameters of the inferred metabolisms are dependent on the genome size, we compared the topology of the automatically reconstructed metabolic network from the theoretically inferred minimal genome with those inferred from 21 natural bacterial genomes, which represent different bacterial taxa and genome sizes (table 3). In terms of the size of the inferred network (n) as well as all topological measures analysed, the metabolism of the theoretically inferred minimal gene set behaves as expected for a natural genome of its size. We found that, amid a great degree of variation, some topological properties, such as the average path length (L) and the network diameter (D), tend to decrease with the size of the network (n) rather than that of the genome (table 3; see Gabaldón et al. in press for details).

Table 3.

Topological parameters of the inferred metabolic networks from the minimal gene set and natural genomes ordered from high to small size. The size of the genome is expressed by the number of protein-coding genes (p-c genes). n, Number of nodes; L, average path length; D, network diameter; C, clustering coefficient; C_r, clustering coefficient for random network.

species	p-c genes	n	L	D	C	Cr
Bradyrhizobium japonicum	8317	1282	10.20	35	0.044	0.00150
Streptomyces coelicolor	8154	1119	10.10	29	0.064	0.00174
Mesorhizobium loti	7272	1209	9.71	33	0.055	0.00165
Anabaena sp.	6131	970	9.76	29	0.041	0.00192
Nocardia farcinica	5936	1089	9.79	30	0.047	0.00174
Agrobacterium tumefaciens (w)	5402	1147	9.45	33	0.056	0.00171
Escherichia coli (CFT073)	5379	1120	10.20	34	0.075	0.00201
Escherichia coli (K-12)	4237	1215	10.30	35	0.067	0.00570
Mycobacterium tuberculosis	3991	1139	9.98	31	0.051	0.00167
Clostridium acetobutylicum	3848	784	9.56	25	0.061	0.00246
Synechocystis sp.	3264	918	10.50	30	0.044	0.00192
Brucella melitensis	3198	1197	8.54	31	0.049	0.00161
Lactobacillus plantarum	3059	864	9.64	26	0.067	0.00220
Haemophilus influenzae (d)	1657	775	10.00	30	0.065	0.00250
Prochlorococcus marinus	1760	844	10.50	30	0.045	0.00210
Wolbachia (Bma)	1195	516	8.76	28	0.075	0.00321
Rickettsia prowazekii	886	517	8.41	24	0.042	0.00299
Tropheryma whipplei	839	426	11.60	43	0.027	0.00475
Wigglesworthia brevipalpis	617	561	11.40	35	0.035	0.00308
Blochmannia floridanus	583	634	8.47	26	0.046	0.00273
Buchnera aphidicola	504	443	7.76	25	0.042	0.00395
Mycoplasma genitalium	484	207	7.49	23	0.043	0.00826
Minimal gene set	208	165	5.34	18	0.031	0.00977

(b) Clustering coefficient analysis of natural and randomized metabolic networks

A general characteristic of some complex networks is the existence of cliques, groups of nodes that are more densely interconnected between them than with the rest of the network. This is quantified by the clustering coefficient of the network (C). In our case, the network clustering coefficient of all studied genomes range from 0.027 to 0.075, with a slight tendency to increase with the size of the network (table 3). We compared these values with the expected clustering coefficient for the corresponding randomized networks (C_r), i.e. a network with the same number of nodes and edges in which connections are distributed randomly. In all cases, the expected clustering coefficient for the random networks is much smaller than the natural ones, ranging from 0.00150 to 0.00977 (table 3). However, the deviation from the random scenario (measured as the ratio between the observed clustering coefficient and the expected value for a randomized network) is far from uniform, showing a linear relationship with the network size (figure 2). These differences are achieved despite a great similarity in the average number of connections per node, which was found to be in the range of 1.2–1.6 for all studied networks, including that of the minimal genome (1.25).

Figure 2.

Effect of network size on the deviation of the clustering coefficient from the expected random scenario.

(c) Robustness analysis of a minimal metabolic network

As a direct consequence of their power-law connectivity distribution, complex networks are sensitive to directed attacks but resistant to random errors. That is, the sequential removal of the most connected nodes (directed attack) leads to sharp variations in some topological parameters such as the average path length, whereas random removal of nodes and/or edges do not alter the topology of the network significantly. These tendencies have also been reported for natural metabolic networks, which have been shown to be robust and error tolerant (Jeong et al. 2000).

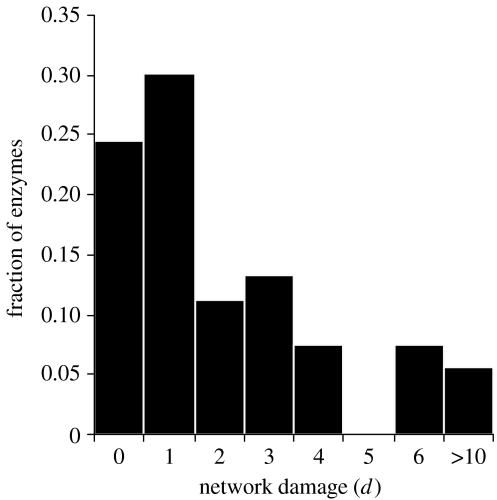
To investigate the robustness of the minimal metabolic network against random mutations, we previously simulated a series of random mutation attacks in which up to 20 enzymatic activities encoded by the minimal genome were sequentially removed (Gabaldón et al. in press). The results showed a behaviour similar to natural networks: most mutations had a limited effect in the overall topology, varying in less than 10% the average path length and network diameter, while the removal of few key enzymatic activities triggered abrupt reductions of up to 50% in both parameters. The small size of the network, however, makes it sensitive to sustained random attacks, and most simulations (90%) produced a collapsed network after 20 random mutations. In contrast, a significant fraction (8–12%) of the simulations resulted in variations lower than 10% in the topological parameters of the network. One might be tempted to conclude from these results that subtracting those genes whose mutations do not significantly alter the network topology might further reduce the proposed minimal gene set. We must keep in mind, however, that retaining the global topological properties of a network does not necessarily mean that the resulting mutated networks are viable. Recently, Lemke et al. (2004) have introduced a new quantitative criterion to evaluate the deleterious effect of the removal of an enzyme from a metabolic network. They showed, for the metabolic network of Escherichia coli, that the ‘network damage’ (d), a parameter defined as the number of metabolites whose production is prevented by the absence of a given enzyme, correlates well with the experimentally determined viability of that mutant. To ascertain whether the proposed minimal metabolism is also robust regarding this new parameter, we conducted the same experiment using the algorithm described by Lemke et al. (2004). The results (figure 3) indicate that most mutations (76%) in metabolic enzymes encoded in the minimal genome prevent the synthesis of at least one compound. This is in sharp contrast to what was found for the E. coli metabolic network, in which the vast majority of the mutations produced no network damage (Lemke et al. 2004). Thus, it appears that a lower redundancy in enzyme activities in the minimal genome, coupled with a lack of alternative pathways for the synthesis of most compounds, compromises the robustness of the emerging metabolism in terms of the metabolic damage caused by random mutations. A fragile metabolism is more in line with the idea of a minimal genome, in which, by definition, all genes would be essential.

Figure 3.

Network damage analysis for the minimal metabolic network. Frequency of deletions causing a given network damage (d), measured as the number of metabolites whose synthesis is prevented by that mutation.

(d) Stoichiometric consistency of a minimal metabolic network

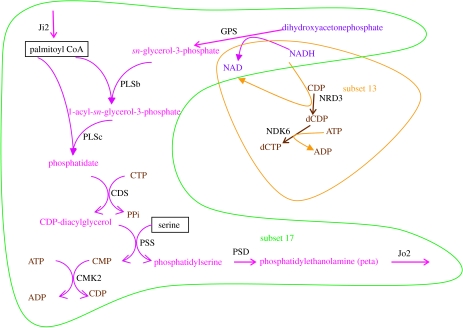
Although the topological analyses of computationally inferred networks provide important insights into the system-level organization of the metabolism, it should be considered that such networks are still a rough approximation to real metabolisms. For instance, a network graph representation does not take into account the stoichiometry of the reactions, a parameter that might be relevant for assessing the consistency of a reconstructed network or establishing the effects of a given mutation. In order to gain further insight into the proposed minimal metabolism, we derived a reduced but more realistic model, which includes information on the stoichiometry of the reactions considered. By manually editing the automatically reconstructed network, we eliminated isolated reactions caused by wide substrate specificity, to retain, for each enzyme, only those reactions that made sense in the context of the other enzymes present in the minimal genome. Additionally, the stoichiometric relationships of the reactions were included in the model and a set of input and output metabolites were defined based on the current knowledge of biochemical pathways. Table 2 presents all 50 enzymatic steps with stoichiometric reactions corresponding to the activities associated with 39 protein-coding genes, accepting that some of them exhibit wide substrate specificity. Figure 1 represents the metabolic network derived from this reaction set. The reaction set was structurally analysed for stoichiometric consistency using the Metatool program. As shown in table 4, there are 26 ES, some of which include just one input or output reaction, and 11 EFM. The EFM can be represented as a function of the ES (figure 4). A detailed inspection of ES reveals that those including input or output fluxes, or that are present in all EFM, cannot be eliminated. Furthermore, ES that simultaneously participate in EFM 9 and 11 (the only two containing output fluxes Jo10 and Jo11) are not dispensable. Therefore, only ES 12 can be eliminated, since the removal of EFM 1, 8 and 9 still leaves EFM 11, which contains the output fluxes Jo10 and Jo11. A closer look to the remaining EFM reveals that EFM 10 and 11 both contain ES 13 and 17 with the same stoichiometry, by which they can be grouped into a single ES (NDK6, NDR3, Jo2, (2 Ji2), PLSb, PLSc, CDS, PSS, PSD, GPS and CMK2) represented in figure 5. This transformation results in a new metabolic map comprising 24 ES when compared with the initial 26. By systematically eliminating each one of the 50 enzymatic reactions, and repeatedly running the Metatool program with the remaining 49, we found that only NDK5 can be removed while maintaining a coherent metabolism. In all other cases, inconsistencies of the network were revealed by sets of enzymes not participating in any EFM, inconsistent sets of input and output metabolites, and significant reductions in the number of resulting EFM. Thus, NDK5 activity is clearly dispensable from the stoichiometric point of view and a reorganized network can be conceived.

Table 4.

ES and EFM for the minimal network depicted in figure 1. (The enzymes participating in the ES and EFM are weighted with their fractional flux. Negative values indicate the reaction is used in the reverse sense. For abbreviations, see table 2. Schemes for all the ES can be retrieved from: http://bioinfo.cipf.es/tgabaldon/minimal_metabolism.html.)

ES	overall reaction	participating enzymes and fluxes
1	nadh+ser+dctp→nad+Jo10+Jo11	DFR GHT NDK7 NDK8 TMK1 TMK2 Jo11 Jo10 DCD THY
2	gdp+pyr+adp+p→pep+atp+Jo1	ENO GAP GPM LDH PGK Jo1
3	f6p+atp→gdp+dhp+adp	FBA PFK
4	gdp↔dhp	TPI
5	pep+Ji1→f6p+pyr	PGI PTS Ji1
6	nadh+Jk2↔nad+Jk1	−Jk1 Jk2
7	f6p+3 gdp+3 atp→p+3 amp+3 prpp	TKT1 –TKT2 FBA2 (2 RPE) (2 RPI) SPH (3 PRS)
8	atp+gdp→adp+Jo5	NDK1 Jo5
9	2 atp+prpp+Ji5→pp+2 adp+utp	NDK2 Ji5 UPP CMK
10	atp+nadh→nad+Jo7	NDK3 Jo7 NRD1
11	atp+nadh+gdp→adp+nad+Jo9	NDK4 Jo9 NRD2
12	adp+ctp↔atp+cdp	NDK5
13	atp+nadh+cdp→adp+nad+dctp	NDK6 NRD3
14	Ji7↔p	Ji7
15	pp→2 p	PPA
16	pep+adp→pyr+atp	PYK
17	dhp+atp+nadh+ctp+ser+2 Ji2→pp+adp+nad+cdp+Jo2	Jo2 (2 Ji2) PLSb PLSc CDS PSS PSD GPS CMK2
18	atp→Jo3	Jo3
19	prpp+Ji3→pp+amp	Ji3 HPT1
20	atp+prpp+Ji4→pp+adp+Gdp	Ji4 HPT2 GMK
21	Ji6→ser	Ji6
22	atp+amp→2 adp	ADK
23	ctp→Jo4	Jo4
24	utp→Jo6	Jo6
25	dctp→Jo8	Jo8
26	utp→ctp	PYR

EFM	overall reaction	participating enzymes	function
1	2 glc+2 pal+ser+p+nadh=3 lac+peta+nad	(3 ENO) (2 FBA) –TPI (3 GAP) (3 GPM) (3 LDH) (2 PGI) (3 PGK) –NDK5 PPA (2 PTS) (2 PFK) PYK PLSb PLSc CDS PSS PSD GPS CMK2	membrane phospholipid synthesis
2	21 glc+6 ade+18p=32 lac+6 atp	(16 ENO) (9.5 FBA) (−9.5 TPI) (16 GAP) (16 GPM) (16 LDH) (10.5 PGI) (16 PGK) TKT1 –TKT2 FBA2 (2 RPE) (2 RPI) (3 PPA) (10.5 PTS) (9.5 PFK) (5.5 PYK) SPH (3 PRS) (6 ADK) (3 HPT1)	ATP synthesis
3	21 glc+6 ade+18 p+6nadh=32 lac+6 datp+6 nad	(16 ENO) (9.5 FBA) (−9.5 TPI) (16 GAP) (16 GPM) (16 LDH) (10.5 PGI) (16 PGK) TKT1 –TKT2 FBA2 (2 RPE) (2 RPI) (3 NDK3) (3 PPA) (10.5 PTS) (9.5 PFK) (5.5 PYK) SPH (3 PRS) (6 ADK) (3 HPT1) (3 NRD1)	dATP synthesis
4	21 glc+6 gua+18p=32 lac+6 gtp	(16 ENO) (9.5 FBA) (−9.5 TPI) (16 GAP) (16 GPM) (16 LDH) (10.5 PGI) (16 PGK) TKT1 –TKT2 FBA2 (2 RPE) (2 RPI) (3 NDK1) (3 PPA) (10.5 PTS) (9.5 PFK) (5.5 PYK) SPH (3 PRS) (3 ADK) (3 HPT2) (3 GMK)	GTP synthesis
5	21 glc+6 gua+18 p+6 nadh=32 lac+6 dgtp+6 nad	(16 ENO) (9.5 FBA) (−9.5 TPI) (16 GAP) (16 GPM) (16 LDH) (10.5 PGI) (16 PGK) TKT1 –TKT2 FBA2 (2 RPE) (2 RPI) (3 NDK4) (3 PPA) (10.5 PTS) (9.5 PFK) (5.5 PYK) SPH (3 PRS) (3 ADK) (3 HPT2) (3 GMK) (3 NRD2)	dGTP synthesis
6	21 glc+6 ura+18 p=32 lac+6 utp	(16 ENO) (9.5 FBA) (−9.5 TPI) (16 GAP) (16 GPM) (16 LDH) (10.5 PGI) (16 PGK) TKT1 –TKT2 FBA2 (2 RPE) (2 RPI) (3 NDK2) (3 PPA) (10.5 PTS) (9.5 PFK) (5.5 PYK) SPH (3 PRS) (3 ADK) (3 UPP) (3 CMK)	UTP synthesis
7	21 glc+6 ura+18 p=32 lac+6 ctp	(16 ENO) (9.5 FBA) (−9.5 TPI) (16 GAP) (16 GPM) (16 LDH) (10.5 PGI) (16 PGK) TKT1 –TKT2 FBA2 (2 RPE) (2 RPI) (3 NDK2) (3 PPA) (10.5 PTS) (9.5 PFK) (5.5 PYK) SPH (3 PRS) (3 ADK) (3 UPP) (3 CMK) (3 PYR)	CTP synthesis
8	21 glc+6 ura+18 p+6 nadh=32 lac +6 dctp +6 nad	(16 ENO) (9.5 FBA) (−9.5 TPI) (16 GAP) (16 GPM) (16 LDH) (10.5 PGI) (16 PGK) TKT1 –TKT2 FBA2 (2 RPE) (2 RPI) (3 NDK2) (3 NDK5) (3 NDK6) (3 PPA) (10.5 PTS) (9.5 PFK) (5.5 PYK) SPH (3 PRS) (3 ADK) (3 UPP) (3 CMK) (3 NRD3) (3 PYR)	dCTP synthesis
9	21 glc+6 ura+6 ser +18 p+12 nadh=32 lac+6 ttp+12 nad+6 gly	(3 DFR) (3 GHT) (16 ENO) (9.5 FBA) (−9.5 TPI) (16 GAP) (16 GPM) (16 LDH) (10.5 PGI) (16 PGK) TKT1 –TKT2 FBA2 (2 RPE) (2 RPI) (3 NDK2) (3 NDK5) (3 NDK6) (3 NDK7) (3 NDK8) (3 TMK1) (3 TMK2) (3 PPA) (10.5 PTS) (9.5 PFK) (5.5 PYK) SPH (3 PRS) (3 ADK) (3 UPP) (3 CMK) (3 NRD3) (3 PYR) (3 DCD) (3 THY)	TTP synthesis
10	33 glc+12 pal+6 ura+6 ser+24 p+12 nadh=50 lac+6 peta+6 dctp+12 nad	(25 ENO) (15.5 FBA) (−12.5 TPI) (25 GAP) (25 GPM) (25 LDH) (16.5 PGI) (25 PGK) TKT1 –TKT2 FBA2 (2 RPE) (2 RPI) (3 NDK2) (3 NDK6) (6 PPA) (16.5 PTS) (15.5 PFK) (8.5 PYK) (3 PLSb) (3 PLSc) (3 CDS) (3 PSS) (3 PSD) (3 GPS) SPH (3 PRS) (3 ADK) (3 UPP) (3 CMK) (3 CMK2) (3 NRD3) (3 PYR)	membrane phospholipid and dCTP synthesis
11	33 glc+12 pal+6 ura+12 ser+24 p+18 nadh=50 lac+6 peta+6 ttp+18 nad+6 gly	(3 DFR) (3 GHT) (25 ENO) (15.5 FBA) (−12.5 TPI) (25 GAP) (25 GPM) (25 LDH) (16.5 PGI) (25 PGK) TKT1 –TKT2 FBA2 (2 RPE) (2 RPI) (3 NDK2) (3 NDK6) (3 NDK7) (3 NDK8) (3 TMK1) (3 TMK2) (6 PPA) (16.5 PTS) (15.5 PFK) (8.5 PYK) (3 PLSb) (3 PLSc) (3 CDS) (3 PSS) (3 PSD) (3 GPS) SPH (3 PRS) (3 ADK) (3 UPP) (3 CMK) (3 CMK2) (3 NRD3) (3 PYR) (3 DCD) (3 THY)	membrane phospholipid and TTP synthesis

Figure 4.

Elementary flux modes (EFM) as a function of the ES. v_i Represents denormalized rate of the subset i at every EFM. The input (Ji) and output (Jo) fluxes involved in each ES are also indicated.

Figure 5.

The new ES emerging as a consequence of deleting the NDK5 reaction. See table 2 for abbreviations.

The convex vectorial space for the minimal metabolism under study shows a dimension (kernel) of 9. The space basis can be arbitrarily chosen among the EFM, and since EFM 11 is a linear combination of EFM 1 and 9, we selected all EFM except these two. The inspection of this general solution for the minimal network reveals that if ES 12 (NDK5) is eliminated, the system still keeps all the inputs and output fluxes. As a consequence, EFM 8 disappears and the kernel dimension turns into 8, the same as the new number of EFM.

4. Discussion

Altogether, our results show that some topological properties of metabolic networks scale down with their size in natural reduced genomes, although a significant degree of variation does exist. Most importantly, the metabolic network from the theoretically inferred minimal gene set appears to behave as would be expected for a natural reduced genome of its size. Regarding the clustering coefficient of the reconstructed networks, it is remarkable that smaller networks are closer to the randomized situation than larger ones. This finding suggests that the emergence of a power-law organization from an unorganized, randomly connected network would be easier for networks with fewer nodes. In terms of the origin of the complex organization of metabolic networks, it can then be conceived a model in which power-law organization could have emerged from a random network comprising few enzymes. If power-law organization would render benefits, this protometabolism could have been expanded in a way that this topological property would be maintained. The ratio C/C_r observed for the proposed minimal metabolism (165 nodes) is close to three, suggesting that the transition from random to power-law networks could occur in further reduced networks. Given the diversity of architectures exhibiting power-law connectivity distribution and the different mechanisms to originate them (Fox Keller 2005), it will be worth further study of those transitions in the smallest chemically coherent networks. At any rate, if we assume some sort of chemical determinism, the structure of the simplest networks would not be completely random (Morowitz 1992; Luisi 2003; de Duve 2005).

The robustness of metabolic networks has usually been evaluated by measuring the effects on several topological parameters caused by the removal of enzymes from the network. Attending to such measures, the proposed minimal network is robust to random isolated attacks. However, when more subtle effects are measured, such as the so-called metabolic damage or effects on the elementary fluxes of the network, the minimal metabolism turns out to be fragile. This indicates that although a given mutation can have little or no effect on the overall topological properties of a metabolic network, it may indeed disturb the metabolism in a very drastic way. The use of simulated mutagenesis and metabolic network reconstruction to predict essentiality of proteins, to subsequently use this information to identify drug targets, has been gaining ground in recent years (Lemke et al. 2004). Our results advocate for the use of more complex models in such studies, in order to capture the non-topological effects of the removal of metabolic enzymes.

The metabolic fragility observed for the minimal genome is expected for a network in which, by definition, all components are essential. Yet, we have shown that the NDK5 activity can be removed, leading to a smaller metabolic subset potentially able to maintain metabolic homeostasis. Nevertheless, the net effect of NDK5 suppression is a more constrained metabolism (the kernel dimension is 9 for the initial network and 8 for the new version). In terms of biochemical functions, our theoretical minimal metabolism allows the independent syntheses of phospholipid, dCTP and TTP (EFM 1, 8 and 9, respectively, table 4), whereas its modified version links the biosynthesis of phospholipid either to dCTP or TTP biosynthesis, due to the combination of ES 13 and 17 (figure 5). Since enzymes of the same ES usually share common regulatory circuits (Klamt & Stelling 2003), the smaller network could eventually represent a less advantageous condition, forcing a tied regulation of former independent metabolic fluxes. On the other hand, the concerted biosynthesis of phospholipid and dCTP (EFM 10) or TTP (EFM 11) (table 4) might be a fundamental way of preparing cell division through the stoichiometric linking of membrane synthesis and DNA replication, in a more primary way than other sophisticated mechanisms observed in living cells (for a review, see Boeneman & Crooke 2005). In fact, this property of our minimal metabolic network represents a structural link between the three Gánti's subsystems (Gánti 2003; Szathmáry et al. 2005): the metabolic connection between physical boundary and genetic replication in a minimal cell.

We compared our minimal enzyme set with the list of essential M. genitalium genes provided by Glass et al. (2006) (last column on the enzyme and reaction section of table 4). Some activities have no correspondence with any annotated gene. Non-orthologous gene displacement could explain some of such discrepancies. In some other instances (e.g. phospholipid or ribose biosyntheses), the obvious explanation is that M. genitalium can use a different set of source substrates and/or it performs an anabolism displaying a different set of sink products. Nonetheless, most of the enzymatic steps in our minimal set have a direct correspondence with proteins encoded by essential genes in M. genitalium, with a few exceptions, as follows. (i) The biochemical function of lactate dehydrogenase (LDH) in our minimal metabolism can be replaced with many different solutions (e.g. an electron transport chain). (ii) CDS acts in the context of phospholipid biosynthesis, and its essentiality depends dramatically on the medium, which in the above-mentioned experiment was a rich one (SP4 glucose broth). (iii) RPE catalyses an essential step in pentose phosphate pathway and, as a consequence, this activity participates in all the EFM related to nucleotide anabolism (all except EFM 1, table 4); thus, M. genitalium either takes up ribose from the medium or catalyses the epimerase reaction with an enzyme coded by a non-orthologous gene. (iv) The same explanation applies to THY, an essential activity for TTP biosynthesis (EFM 9 and 11), since M. genitalium could either use thymine from the medium or synthesize it with a non-orthologous enzyme.

In our analysis, we have defined, based on current knowledge on natural metabolisms, a set of input substrates and output products that would be needed or rendered, respectively, by the proposed minimal metabolism. As we have previously said, variations in the hypothetical set of substrates provided by the environment would lead to alternative, perhaps smaller, minimal metabolisms. Since essentiality, viability and minimal complexity are context-dependent concepts, it would be worth exploring how the complexities of a minimal metabolism and its corresponding environment are related. We completely agree with the necessity to define a ‘hierarchy of minimal cells’ as expressed by Luisi et al. (2006, see especially footnote 2). That is, what degree of complexity should the surrounding environment gain to compensate for the loss of an essential component in a minimal metabolism? Is there an optimum, limit or critical value in this relationship? All these considerations will have deep implications, not only for the design of a semi-synthetic minimal cell or the speculations on primitive protocells, but also for our understanding of biological processes such as symbiosis and parasitism.