Emergence of protocellular growth laws

Abstract

Template-directed replication is known to obey a parabolic growth law due to product inhibition (Sievers & Von Kiedrowski 1994 Nature 369, 221; Lee et al. 1996 Nature 382, 525; Varga & Szathmáry 1997 Bull. Math. Biol. 59, 1145). We investigate a template-directed replication with a coupled template catalysed lipid aggregate production as a model of a minimal protocell and show analytically that the autocatalytic template–container feedback ensures balanced exponential replication kinetics; both the genes and the container grow exponentially with the same exponent. The parabolic gene replication does not limit the protocellular growth, and a detailed stoichiometric control of the individual protocell components is not necessary to ensure a balanced gene–container growth as conjectured by various authors (Gánti 2004 Chemoton theory). Our analysis also suggests that the exponential growth of most modern biological systems emerges from the inherent spatial quality of the container replication process as we show analytically how the internal gene and metabolic kinetics determine the cell population's generation time and not the growth law (Burdett & Kirkwood 1983 J. Theor. Biol. 103, 11–20; Novak et al. 1998 Biophys. Chem. 72, 185–200; Tyson et al. 2003 Curr. Opin. Cell Biol. 15, 221–231). Previous extensive replication reaction kinetic studies have mainly focused on template replication and have not included a coupling to metabolic container dynamics (Stadler et al. 2000 Bull. Math. Biol. 62, 1061–1086; Stadler & Stadler 2003 Adv. Comp. Syst. 6, 47). The reported results extend these investigations. Finally, the coordinated exponential gene–container growth law stemming from catalysis is an encouraging circumstance for the many experimental groups currently engaged in assembling self-replicating minimal artificial cells (Szostak 2001 et al. Nature 409, 387–390; Pohorille & Deamer 2002 Trends Biotech. 20 123–128; Rasmussen et al. 2004 Science 303, 963–965; Szathma´ry 2005 Nature 433, 469–470; Luisi et al. 2006 Naturwissenschaften 93, 1–13).1

1. Lipid-associated template-directed replication

Our simple protocell model consists of a lipid container (e.g. a large micelle) with amphiphilic replicating protogene molecules and an associated hydrophobic metabolic system as discussed in Rasmussen et al. (2003). However, the details of the coupling between the genes and the container are not important as long as the container defines a localized and restrictive volume or area for the genes (Szostak et al. 2001; Pohorille & Deamer 2002; Rasmussen et al. 2004; Szathmáry 2005; Luisi et al. 2006). In our current minimal representation, only the replicator and container kinetics are modelled explicitly. We can assume that all lipophilic replicators are bound to the exterior surfaces of the lipid aggregates and that both single- and double-stranded templates coexist at these lipid interfaces (figure 1a). For the following arguments, it is only necessary to localize the genes. In our model, we can, for example, assume that the replicator molecules are peptide nucleic acid (Pschl et al. 1998; Nielsen 1999; Mattes & Seitz 2001) oligomers with decorated (lipophilic) backbones. We can further assume that the single- and double-stranded templates are at equilibrium with each other as long as the template replication rate is much slower than the hybridization and dehybridization processes.

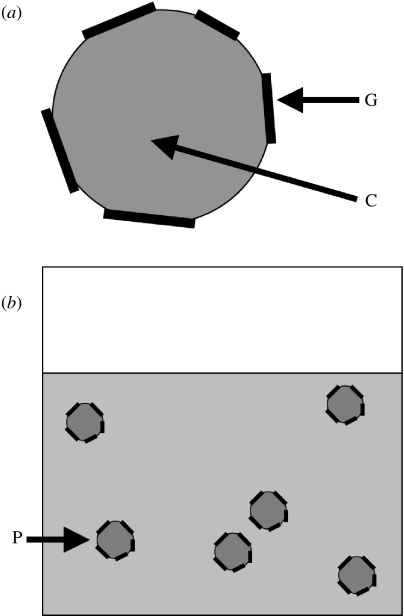
Figure 1.

(a) A protocell consists of a lipid container C (e.g. a large micelle) with amphiphilic gene molecules G at local aggregate concentration $T_{\text{tot}}^{\text{l}}$ attached to the surface (Rasmussen et al. 2004). (b) The average aggregate of each protocell P is composed of m₀ lipid molecules. The (global) aggregate concentration is A and the global template concentration $T_{\text{tot}}^{\text{g}}=T_{\text{tot}}^{\text{l}}A{V}_{\text{A}}$, where $T_{\text{tot}}^{\text{l}}$ denotes the local aggregate template concentration (template molecules per aggregate volume).

The local replication reaction can then be written as

$$T_{\text{s}}+\alpha O\to T_{\text{d}}\rightleftharpoons T_{\text{s}}+T_{\text{s}},$$ (1.1)

where O is a resource replicator substrate molecule and α is the number of such molecules used in each replication. Denoting these local template concentrations by $T_{\text{s}}^{\text{l}}$ and $T_{\text{d}}^{\text{l}}$ for the single- and double-stranded templates, respectively, the local equilibrium condition for the single- and double-stranded templates is then given by

$$K_t=\frac{{\left(T_{\text{s}}^{\text{l}}\right)}^2}{T_{\text{d}}^{\text{l}}},$$ (1.2)

where K_t defines the equilibrium constant. In the following, we assume that K_t≪1. If $T_{\text{tot}}^{\text{l}}$ defines the total local template concentration, single- or double stranded, we have

$$T_{\text{tot}}^{\text{l}}=T_{\text{s}}^{\text{l}}+2T_{\text{d}}^{\text{l}}.$$ (1.3)

$T_{\text{s}}^{\text{l}}$ and $T_{\text{d}}^{\text{l}}$ can now be expressed as a function of $T_{\text{tot}}^{\text{l}}$ by combining equations (1.2) and (1.3),

$$T_{\text{s}}^{\text{l}}=\frac{-K_t+\sqrt{K_t^2+8K_t{T}_{\text{tot}}^{\text{l}}}}{4}=\sqrt{\frac{K_t{T}_{\text{tot}}^{\text{l}}}{2}}+O_1(K_t),$$ (1.4)

$$T_{\text{d}}^{\text{l}}=\frac{T_{\text{tot}}^{\text{l}}}{2}-\frac{T_{\text{s}}^{\text{l}}}{2}=\frac{T_{\text{tot}}^{\text{l}}}{2}-\frac{-K_t+\sqrt{K_t^2+8K_t{T}_{\text{tot}}^{\text{l}}}}{8}=\frac{T_{\text{tot}}^{\text{l}}}{2}-\sqrt{\frac{K_t{T}_{\text{tot}}^{\text{l}}}{8}}-\frac{O_2(K_t)}{2},$$ (1.5)

where we have used that K_t≪T_tot (K_t≪1) and $O_i(K_t),i=1,2$ is small in terms of K_t.

The left side of equation (1.1) defines the template-directed replication of $T_{\text{s}}^{\text{l}}$ using some background precursor template molecules with the local aggregate concentration O^l. The template replication rate equation then becomes

$$\frac{\text{d}{T}_{\text{tot}}^{\text{l}}}{\text{d}t}=k_{\text{T}}f(O^{\text{l}})T_{\text{s}}^{\text{l}}=\frac{1}{\alpha }{k}_{\text{T}}{O}^{\text{l}}{T}_{\text{s}}^{\text{l}},$$ (1.6)

where f(·) is a reaction mechanism dependent, which is O^l/α in the case where α resource oligomers are added sequentially to the template one at the time, while k_T is the single oligomer addition rate constant. Substituting equation (1.4) into equation (1.6)

$$\frac{\text{d}{T}_{\text{tot}}^{\text{l}}}{\text{d}t}=k_{\text{T}}f(O^{\text{l}})\left(\sqrt{\frac{K_t{T}_{\text{tot}}^{\text{l}}}{2}}+O_{\text{1}}(K_t)\right),$$ (1.7)

where $O_1(K_t)$ is small, which to the leading order results in parabolic growth

$$T_{\text{tot}}^{\text{l}}(t)=\frac{f{(O^{\text{l}})}^2{K}_t{k}_{\text{T}}^2}{8}{t}^2+\frac{\sqrt{T_{\text{tot}}^{\text{l}}(0)K_t}f(O^{\text{l}})k_{\text{T}}}{\sqrt{2}}t+T_{\text{tot}}^{\text{l}}(0)={\left(\frac{f(O^{\text{l}})\sqrt{K_t}{k}_{\text{T}}}{2\sqrt{2}}t+\sqrt{T_{\text{tot}}^{\text{l}}(0)}\right)}^2,$$ (1.8)

where $T_{\text{tot}}^{\text{l}}(0)$ is the concentration at t=0. This result is an example of the well-known growth law for product inhibition in template-directed replication (Sievers & Von Kiedrowski 1994) in an unlimited system.

2. Template catalysed container reproduction

In our model, the aggregate-associated lipid production L is template catalysed and can be described by

$$pL+T_{\text{d}}\to T_{\text{d}}+L,$$ (2.1)

where pL is the precursor lipid. We assume that the catalysis is dominated by the double-stranded template (Rasmussen et al. 2003). The lipid production rate equation is then

$$\frac{\text{d}{L}^{\text{l}}}{\text{d}t}=k_{\text{L}}p{L}^{\text{l}}{T}_{\text{d}}^{\text{l}},$$ (2.2)

where k_L is the lipid production rate constant and pL^l is the local (background) lipid precursor concentration.

This simple gene–container coupling can be generalized to explicitly account for a variety of details involved in the metabolic processes as discussed in Munteanu et al. (2007). In this paper, we focus on a detailed discussion of the above minimal gene–container connection.

We assume the average number of lipid molecules per average aggregate volume V_A to be m₀. An average aggregate number can, for example, be maintained through a natural micellar size distribution (Rosen 1988). The relative local (dimensionless) aggregate growth rate can now be expressed as

$$\frac{V_{\text{A}}}{m_0}\frac{\text{d}{L}^{\text{l}}}{\text{d}t}=k_{\text{L}}p{L}^{\text{l}}{T}_{\text{d}}^{\text{l}}\frac{V_{\text{A}}}{m_0}.$$ (2.3)

Let A be the global aggregate concentration. Since each aggregate is assumed to divide following growth in order to maintain an average of m₀ lipid molecules per aggregate, the growth in the global aggregate concentration due to the local lipid production in the aggregates can be expressed as

$$\frac{\text{d}A}{\text{d}t}=\frac{A{V}_{\text{A}}}{m_0}\frac{\text{d}{L}^{\text{l}}}{\text{d}t}=k_{\text{L}}p{L}^{\text{l}}{T}_{\text{d}}^{\text{l}}\frac{A{V}_{\text{A}}}{m_0}.$$ (2.4)

In the above expression, we have implicitly assumed that the volume of the templates and its change are small (constant) compared with the volume of lipid in an aggregate. We can now transform the local aggregate concentration of templates into the corresponding global concentrations using the simple relation between local and global template concentrations

$$T^{\text{g}}=T^{\text{l}}A{V}_{\text{A}},$$ (2.5)

noting that T^l is measured in template molecules per lipid aggregate volume V_A and A is measured in the number of lipid aggregates (of average size V_A) per system volume. Substituting equation (2.5) into equation (2.4) and taking into account that T_tot≈2T_d, we obtain

$$\frac{\text{d}A}{\text{d}t}=\frac{k_{\text{L}}p{L}^{\text{l}}}{m_0}{T}_{\text{d}}^{\text{g}}={\gamma }_{\text{A}}{T}_{\text{tot}}^{\text{g}},$$ (2.6)

where

$${\gamma }_{\text{A}}=\frac{k_{\text{L}}p{L}^{\text{l}}}{2m_0}.$$ (2.7)

It should be noted that we can just as well express the local concentrations in molecules per aggregate, in molecules per aggregate volume using an average aggregate volume of V_A or in molecules per aggregate surface area S_A.

3. Global template reproduction

The growth equation for the local total template concentration $T_{\text{tot}}^{\text{l}}$ corresponding to equation (1.6) is given by

$$\frac{\text{d}{T}_{\text{tot}}^{\text{l}}}{\text{d}t}=k_{\text{T}}f(O^{\text{l}})T_{\text{s}}^{\text{l}}-\frac{\text{d}A}{\text{d}t}\frac{T_{\text{tot}}^{\text{l}}}{A},$$ (3.1)

where the second term stems from the effect the volume change has on the local concentration. Since equation (3.1) is central to the argument, we discuss it in detail. The question that needs to be answered is what happens to the concentrations when one goes from a well-stirred solution to many small containers. This has to do with the origin of the second term in equation (3.1). The volume of the container grows with time and hence the concentration can change, and decreases with increasing container volume as A is measured in aggregates of average size V_A per litre. The volume growth of the container must be equal to the growth in the (global) concentration of the aggregates. One also needs a normalization factor to go from the change in container volume to the change in template concentration. All together, this yields a minus sign (the concentration goes down with increasing volume) multiplied by the ratio of the concentration of templates divided by the concentration of aggregates.

Now, since equation (1.2) holds for the local concentration (not the global), we can use the approximate form of equation (1.4) to rewrite the growth equation as

$$\frac{\text{d}{T}_{\text{tot}}^{\text{l}}}{\text{d}t}=k_{\text{T}}f(O^{\text{l}})\sqrt{\frac{K_t{T}_{\text{tot}}^{\text{l}}}{2}}-\frac{\text{d}A}{\text{d}t}\frac{T_{\text{tot}}^{\text{l}}}{A}.$$ (3.2)

To rewrite the growth in terms of global concentrations, we multiply the growth equation (3.2) by A, and get

$$\frac{\text{d}\left(A{T}_{\text{tot}}^{\text{l}}\right)}{\text{d}t}-\frac{\text{d}A}{\text{d}t}{T}_{\text{tot}}^{\text{l}}=k_{\text{T}}f(O^{\text{l}})\sqrt{\frac{K_t{T}_{\text{tot}}^{\text{l}}}{2}}A-\frac{\text{d}A}{\text{d}t}{T}_{\text{tot}}^{\text{l}}.$$ (3.3)

Note that the volume compensation term vanishes as it should. We then use the relation T^g=T^lAV_A to rewrite the growth in terms of global concentrations

$$\frac{\text{d}{T}_{\text{tot}}^{\text{g}}}{\text{d}t}={\gamma }_{\text{T}}\sqrt{T_{\text{tot}}^{\text{g}}A},$$ (3.4)

where

$${\gamma }_{\text{T}}=k_{\text{T}}f(O^{\text{l}})\sqrt{\frac{K_t{V}_{\text{A}}}{2}}.$$ (3.5)

4. Coupled template and container reproduction

The coupled growth equations (2.6) and (3.4) can be solved by separation of variables, which can be used to rewrite equation (3.4) where we are seeking the solution for large $T_{\text{tot}}^{\text{g}}$ values. We obtain (Appendix A) the solution,

$$T_{\text{tot}}^{\text{g}}(t)=\frac{{\left(\text{exp}\left(\frac{3}{2}at+D_0\right)-b\right)}^{2/3}}{a^{2/3}}\sim \text{exp}(at),$$ (4.1)

where

$$a={\gamma }_{\mathrm{T}}^{2/3}{\gamma }_{\mathrm{A}}^{1/3},$$ (4.2)

and

$$b=\frac{{\gamma }_{\text{T}}^{5/3}{C}_0}{3{\gamma }_{\text{A}}^{2/3}},C_0=A{(0)}^{3/2}-\frac{{\gamma }_{\text{A}}}{{\gamma }_{\text{T}}}{T}_{\text{tot}}^{\text{g}}{(0)}^{3/2},\text{and}{D}_0=\text{ln}\left(a{T}_{\text{tot}}^{\text{g}}{(0)}^{3/2}+b\right).$$ (4.3)

Substituting equation (4.1) into equation (2.6) yields

$$\frac{\text{d}A}{\text{d}t}\sim {\gamma }_{\text{A}}\text{exp}(at),$$ (4.4)

which means that

$$A(t)\sim \text{exp}(at)\sim T_{\text{tot}}^{\text{g}}(t).$$ (4.5)

Thus, to a leading order, both the coupled template and the aggregate grow exponentially with the same exponent (a). As equations (2.7) and (3.5) are substituted into equation (4.2), we note that the exponent in a direct manner depends on the template and lipid production rate constants, k_T and k_L, the local background precursor concentration, pL, the background template substrate concentration and the order of the template reaction, f(O^l), the template duplex equilibrium constant, K_t and the average number of lipids per aggregate, m₀.

$$a={\left(\frac{1}{4}{k}_{\text{T}}^2{k}_{\text{L}}p{L}^{\text{l}}f{(O^{\text{l}})}^2\frac{K_t{V}_{\text{A}}}{m_0}\right)}^{1/3}.$$ (4.6)

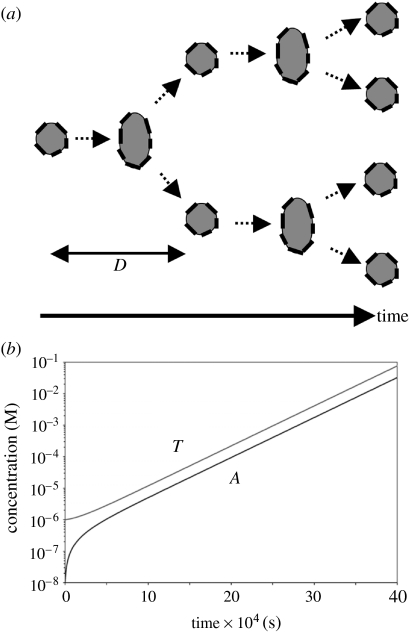
In figure 2, a simulation of the original kinetic equations (2.6) and (3.4) illustrates these findings. It should be noted that at least one gene duplex must be present in each aggregate for the derived kinetic growth equations to be valid, which is ensured if γ_A< γ_T.

Figure 2.

(a) The template catalyses the lipid production, while the lipid aggregate makes possible (catalyses) the template replication. Since the local template concentration is kept approximately constant due to the aggregate growth, the template replicates exponentially. The generation (doubling) time is given by $D={\left[(1/4)k_{\text{T}}^2{k}_{\text{L}}f{(O^{\text{l}})}^{2}p{L}^{\text{l}}(K_t{V}_A)/m_0\right]}^{-(1/3)}\text{ln}2$. See §5 in the text. (b) The results of a numerical simulation of the original coupled template–container replication system equations (2.6) and (3.4) illustrating the derived coupled asymptotic exponential growth law. Parameter values: m₀∼1000, K_tV_A∼10⁻³, pL^l∼10⁻³ M, f(O^l)∼2×10⁻⁴ M, k_L∼25 Ms⁻¹ and k_T∼10 Ms⁻¹. Note how the gene and the container concentrations converge to a coordinated growth rate after an initial transient adjustment period, due to an unbalanced set of initial concentrations. The protocell population doubles approximately once a day with these parameter values.

5. Discussion

A kinetic analysis of a minimal protocell model shows that the local parabolic template growth law is compensated by parallel aggregate division dynamics, which results in an overall exponential growth for the whole system. In simple terms, the coupled replication/container growth through equations (1.1) and (2.1) assures that at steady-state conditions the average local value of the template concentration $T_{\text{d}}^{\text{l}}$ is kept constant as the volume of the system (the number of containers) grow concertedly. Consequently, no shift in the equilibrium of equation (1.1) for the system as a whole is occurring during growth and replication (in contrast to solution replication at constant volume). A second consequence is that the average concentration of single-stranded templates $T_{\text{s}}^{\text{l}}$ and thus the replication rate is kept constant, allowing the system as such (genes+container) to grow exponentially. This result holds for any coupled genetic growth law as well as for an explicit inclusion of the metabolic kinetics or any other detailed intracellular growth dynamics (Munteanu et al. 2007). We have expressed analytically how the generation time is affected by the internal gene replication kinetics.

Thus, a detailed stoichiometric growth control of the individual protocell components is not necessary as conjectured, for example, by Gánti (2004). A coupled autocatalytic feedback between the template and the aggregate replication processes generates a coordinated growth of the main components. This result is also an extension of the exponential growth law in the low template concentration limit as discussed by Stadler (Stadler & Stadler 2003) and others. As long as the effective 2 average local replicator concentration is kept constant, in this case by growing the system's total lipid volume, exponential growth is also possible. A discussion of the detailed growth dynamics in modern cells can be found in e.g. Burdett & Kirkwood (1983); Novak et al. (1998) and Tyson et al. (2003).

Appendix A.

The coupled growth equations (2.6) and (3.4) can be solved by separation of variables, i.e. by dividing equation (3.4) by equation (2.6)

$$\frac{\text{d}{T}_{\text{tot}}^{\text{g}}}{\text{d}A}=\frac{{\gamma }_{\text{T}}}{{\gamma }_{\text{A}}}\frac{\sqrt{A}}{\sqrt{T_{\text{tot}}^{\text{g}}}}.$$ (A1)

Note that equation (A 1) is a special case of a Bernoulli differential equation. From equation (A 1), we obtain

$${(A(t))}^{3/2}=\frac{{\gamma }_{\text{A}}}{{\gamma }_{\text{T}}}{\left(T_{\text{tot}}^{\text{g}}(t)\right)}^{3/2}+C_0,$$ (A2)

where $C_0=A{(0)}^{3/2}-\frac{{\gamma }_{\text{A}}}{{\gamma }_{\text{T}}}{T}_{\text{tot}}^{\text{g}}{(0)}^{3/2}$. We use this to rewrite equation (3.4) as

$$\frac{\text{d}{T}_{\text{tot}}^{\text{g}}}{\text{d}t}={\gamma }_{\text{T}}\sqrt{T_{\text{tot}}^{\text{g}}}{\left(\frac{{\gamma }_{\text{A}}}{{\gamma }_{\text{T}}}{\left(T_{\text{tot}}^{\text{g}}\right)}^{3/2}+C_0\right)}^{1/3}={\gamma }_{\text{T}}\sqrt{T_{\text{tot}}^{\text{g}}}\left(\frac{{\gamma }_{\text{A}}^{1/3}}{{\gamma }_{\text{T}}^{1/3}}\sqrt{T_{\text{tot}}^{\text{g}}}+\frac{C_0{\gamma }_{\text{T}}^{2/3}}{3{\gamma }_{\text{A}}^{2/3}{T}_{\text{tot}}^{\text{g}}}+\text{O}\left[{\left(T_{\text{tot}}^{\text{g}}\right)}^{-5/2}\right]\right),$$ (A3)

where we have expanded the expression for large $T_{\text{tot}}^{\text{g}}$ relative to C₀. Ignoring the last term, which is small in order $T_{\text{tot}}^{\text{g}-5/2}$, the simplified expression has the solution

$$T_{\text{tot}}^{\text{g}}(t)=\frac{{\left(\text{exp}\left(\frac{3}{2}at+D_0\right)-b\right)}^{2/3}}{a^{2/3}}\sim \text{exp}(at),$$ (A4)

to the leading order in $T_{\text{tot}}^{\text{g}}$, where $a={\gamma }_{\text{A}}^{1/3}{\gamma }_{\text{T}}^{2/3}$, $b=({\gamma }_{\text{T}}^{5/3}{C}_0)/3{\gamma }_{\text{A}}^{2/3}$ and $D_0=\text{ln}(b+a{T}_{\text{tot}}^{\text{g}}{(0)}^{3/2})$. Substituting equation (4.1) into equation (2.6) yields

$$\frac{\text{d}A}{\text{d}t}\sim {\gamma }_{\text{A}}\text{exp}(at),$$ (A5)

which means that

$$A(t)\sim \text{exp}(at)\sim T_{\text{tot}}^{\text{g}}(t).$$ (A6)

Thus, to leading order, the coupled template and aggregate grow exponentially with the same exponent. Simulation of equations (2.6) and (3.4) verifies these findings (figure 2).