Iterative Relative Fuzzy Connectedness for Multiple Objects with Multiple Seeds

Abstract

In this paper we present a new theory and an algorithm for image segmentation based on a strength of connectedness between every pair of image elements. The object definition used in the segmentation algorithm utilizes the notion of iterative relative fuzzy connectedness, IRFC. In previously published research, the IRFC theory was developed only for the case when the segmentation was involved with just two segments, an object and a background, and each of the segments was indicated by a single seed. (See Udupa, Saha, Lotufo [15] and Saha, Udupa [14].) Our theory, which solves a problem of Udupa and Saha from [13], allows simultaneous segmentation involving an arbitrary number of objects. Moreover, each segment can be indicated by more than one seed, which is often more natural and easier than a single seed object identification.

The first iteration step of the IRFC algorithm gives a segmentation known as relative fuzzy connectedness, RFC, segmentation. Thus, the IRFC technique is an extension of the RFC method. Although the RFC theory, due to Saha and Udupa [19], is developed in the multi object/multi seed framework, the theoretical results presented here are considerably more delicate in nature and do not use the results from [19]. On the other hand, the theoretical results from [19] are immediate consequences of the results presented here. Moreover, the new framework not only subsumes previous fuzzy connectedness descriptions but also sheds new light on them. Thus, there are fundamental theoretical advances made in this paper.

We present examples of segmentations obtained via our IRFC based algorithm in the multi object/multi seed environment, and compare it with the results obtained with the RFC based algorithm. Our results indicate that, in many situations, IRFC outperforms RFC, but there also exist instances where the gain in performance is negligible.

1 Introduction

Image segmentation—the process of partitioning (in a hard or fuzzy manner) the image domain into meaningful object regions—is perhaps the most challenging and critical problem in image processing and analysis. Research in this area will probably continue indefinitely long because the solution space is infinite dimensional, and since any single solution framework is unlikely to produce an optimal solution (in the sense of the best possible precision, accuracy, and efficiency) for a given application domain. It is important to distinguish between two types of activities in segmentation research—the first relating to the development of application domain-independent general solution frameworks, and the second pertaining to the construction of domain-specific solution starting from a known general solution framework. The latter is not a trivial task most of the time. Both these activities are crucial, the former for advancing the theoretical aspects of, and shedding new light on, segmentation research, and the latter for bringing the theoretical advances to actual practice. The topic of this paper pertains to the former.

General segmentation frameworks [1]-[12] may be broadly classified into three groups: boundary-based [1]-[5], region-based [6]-[10], and hybrid [11,12]. As the nomenclature indicates, in the first two groups the focus is on recognizing and delineating the boundary or the region occupied by the object in the image. In the third group, the focus is on exploiting the complementary strengths of each of boundary-based and region-based strategies to overcome their individual shortcomings. The segmentation framework discussed in the present paper belongs to the region-based group and constitutes an extension of the fuzzy connectedness (abbreviated from now on as FC) methodology [9].

In the FC framework [9], a fuzzy topological construct, called fuzzy connectedness, characterizes how the spatial elements (abbreviated as spels) of an image hang together to form an object. This construct is arrived at roughly as follows. A fuzzy relation called affinity is defined on the image domain; the strength of affinity between any two spels depends on how close the spels are spatially and how similar their intensity-based properties are in the image. Affinity is intended to be a local relation. A global fuzzy relation called fuzzy connectedness is induced on the image domain by affinity as follows. For any two spels c and d in the image domain, all possible paths connecting c and d are considered. Each path is assigned a strength of fuzzy connectedness which is simply the minimum of the affinities of consecutive spels along the path. The level of fuzzy connectedness between c and d is considered to be the maximum of the strengths of all paths between c and d. For segmentation purposes, FC is utilized in several ways as described below. See [13] for a review of the different FC definitions and how they are employed in segmentation and applications.

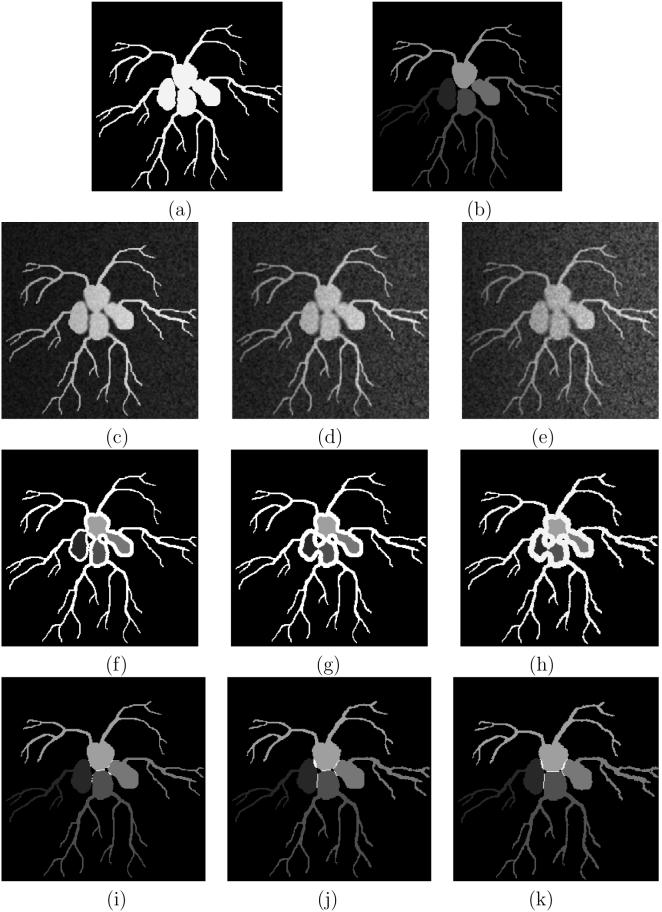
In absolute FC (abbreviated AFC) [9], the support of a segmented object is considered to be the maximal set of spels, containing one or more seed spels, within which the level of FC is at or above a specific threshold. To obviate the need for a threshold, relative FC (or RFC) [19] was developed by letting all objects in the image to compete simultaneously via FC to claim membership of spels in their sets. Each co-object is identified by one or more seed spels. Any spel c in the image domain is claimed by that co-object with respect to whose seed spels c has the largest level of FC compared to the level of FC with the seed sets of all other objects. To avoid treating the core aspects of an object (that are very strongly connected to its seeds) and the peripheral subtle aspects (that may be less strongly connected to the seeds) in the same footing, an iterative refinement strategy is devised in iterative RFC (or IRFC) [14]-[16]. The superior performance of IRFC over RFC and the underlying reasons are illustrated in Figures 11 and 9(e-f). Another advantage of IRFC is that the objects it generates are topologically nicer than those generated by RFC or AFC—any IRFC object generated by a single seed has no “holes” (i.e., is simply connected), unless a “hole” contains a seed of another object. This feature is illustrated in Figure 1.

Figure 11.

(a) A hand drawn scene with four iso-intensity objects and a dark background. (b) Object labeling in the true scene. (c)-(e) Three phantom scenes generated from (a) at different levels of blur, noise, and inhomogeneity. (f)-(h) Multi-object segmentations of (c)-(e), respectively, by using RFC. (i)-(k) Segmentation of (c)-(e) by using IRFC.

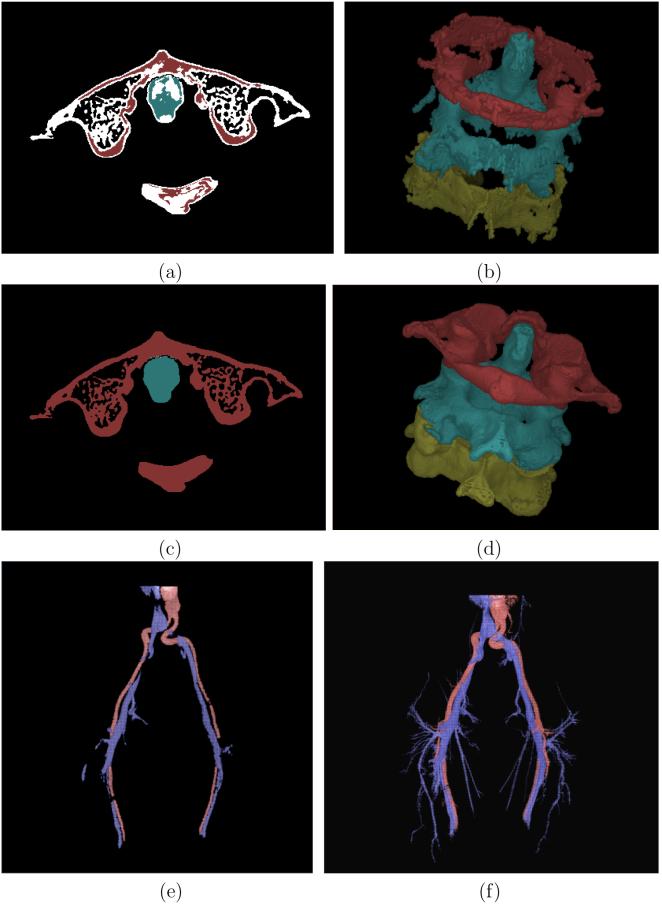
Figure 9.

(a) A slice display of the separation of cervical vertebra by applying RFC for the slice shown in Figure 8(a). White spels are not assigned to any specific vertebra. (b) Color surface rendition of the three vertebra segmented by RFC. (c)-(d) Same as (a)-(b), respectively, but by using IRFC. (e) Color surface rendition of arterial (red) and veinous (blue) trees segmented by RFC. (f) Same as (e) but by using IRFC.

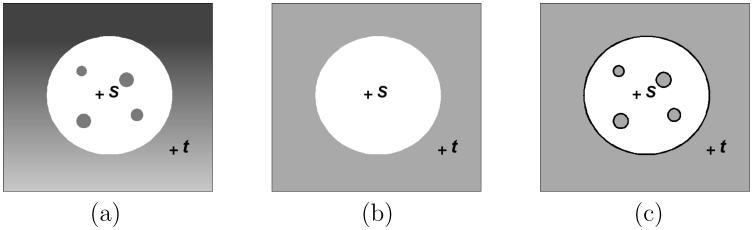
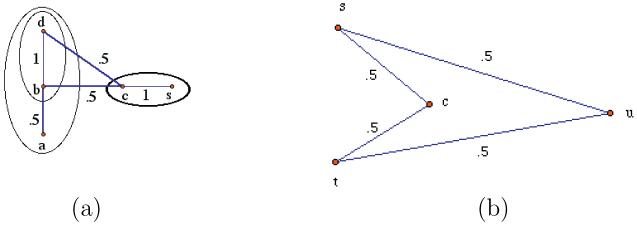
Figure 1.

(a) Original image, with seeds s and t indicating the object and the background, respectively. (b) The foreground object (in white) generated by RFC. (c) The foreground object (in white) generated by IRFC. (We used the same homogeneity based affinity in both cases.)

In general, IRFC leads to better object definition than RFC with a theoretical construct similar to that of RFC. The proper design of affinity is crucial to the effectiveness of the segmentations that ensue, no matter what type of FC is used. In scale-based FC [13], which is applicable to all of AFC, RFC, and IRFC, affinity is defined not based just on the properties of the two spels under question but also on the properties of all spels in the local scale region around the two spels. In vectorial FC [27], affinity is constructed in a vectorial manner, allowing spels to assume not just scalar values but any vectorial values, which may come from the original acquisition of the image owing to multiple image properties at every spel or that may arise from vector-valued features estimated from the given scalar or vectorial image. By using S and V to abbreviate “scale-based” and “vectorial,” and by allowing a combination of these indexes with different types of FC referred to above, we may describe the FC family that is developed to date by methods denoted by AFC, SAFC, VAFC, VSAFC, RFC, SRFC, VRFC, VSRFC, IRFC, SIRFC, VIRFC, and VSIRFC. See [13] and the original articles cited therein for further details on each member of this family.

In the present paper, we make two sets of fundamental contributions. (1) The original IRFC was devised, due to theoretical challenges, in a 2-object (foreground-background) scenario. We now overcome this theoretical challenge and generalize its theory to multiple objects. (2) In this process of generalization, several most fundamental properties of AFC, RFC, and IRFC have been uncovered. They allow us to better understand the behavior of the FC process in general, and IRFC in particular, and give us a single unified theoretical framework within which all members of FC family methods can be described elegantly. This may lead us to more effective segmentation strategies in the future. These fundamental theoretical advances are described in Section 2. For ease of reading, most long proofs are pooled together in Section 3, so that skipping this section will not affect the understandability of the new results presented in the paper. The new algorithm is described in Section 4. Some examples and comparison with RFC are presented in Section 5 to demonstrate the behavior of the multi-object strategy of generalized IRFC. Our concluding remarks are stated in Section 6.

2 Theory

In this section we present the theoretical framework of generalized IRFC. The terminology and notation employed in this paper follow in spirit that of previously published FC papers. However, we slightly deviate from the previous notation in several aspects, and we believe that the new approach is more precise and elegant.

2.1 Basic definitions and notation

The most fundamental notion in our theory is that of the strength of connectedness between a pair of image elements. In its definition, we will use a notation that is only a slight modification of that used by Udupa and Samarasekera [9].

In this paper we will use the following interpretation of the notions of (hard) functions and relations, which is standard in set theory and is used in many calculus books. A binary relation R from a set X into a set Y is identified with its graph; that is, R is equal to {〈x, y〉 ∈ X × Y : xRy holds} . Since a function f : X → Y is a (special) binary relation from X to Y , in particular we have f = {〈x, f(x)〉: x ∈ X}. With this interpretation, handling fuzzy sets and fuzzy relations becomes quite natural and less cumbersome than usual. In particular, let $\mathcal{Z}$ be a fuzzy subset of a hard set X with a membership function μ_Z: X → [0, 1]. For x ∈ X, we interpret ${\mu }_{\mathcal{Z}}\left(x\right)$ as the degree to which x belongs to $\mathcal{Z}$. Usually such a fuzzy set $\mathcal{Z}$ is defined [17] as $\{\langle x,{\mu }_{\mathcal{Z}}\left(x\right)\rangle :x\in X\}$, which is the graph of ${\mu }_{\mathcal{Z}}$. Thus, according to our interpretation,$\mathcal{Z}$ is actually equal to ${\mu }_{\mathcal{Z}}$. Note that this interpretation fits also quite well the situation when $\mathcal{Z}$ is the hard subset Z of X, as then $\mathcal{Z}={\mu }_{\mathcal{Z}}$ is equal to the characteristic function χ_Z (defined as χ_Z(x) = 1 for x ∈ Z and χ_Z(x) = 0 for x ∈ X\ Z), and the identification of Z with χZ is quite common in analysis and set theory. Notice also, that a fuzzy binary relation ρ from X to Y is just a fuzzy subset of X × Y , so it is equal to its membership function μ_ρ: X × Y → [0, 1].

Let n ≥ 2. A binary fuzzy relation α on ${\mathbb{Z}}^n$ is said to be a fuzzy adjacency binary relation if α = μ_α is symmetric (i.e., μ_α(c, d) = μ_α(d, c)) and reflexive (i.e., μ_α(c, c) = 1). The value of μ_α(c, d) depends only on the relative spatial position of c and d. Usually μ_α(c, d) is decreasing with respect to the distance function ||c - d||. In most applications, α is just a hard case relation like 4-adjacency relation for n = 2 or 6-adjacency in the three-dimensional case. By an n-dimensional fuzzy digital space we will understand a pair $\langle {\mathbb{Z}}^n,\alpha \rangle$. The elements of digital space are called spels. (For n = 2 also called pixels, while for n = 3 - voxels.) A scene over a fuzzy digital space ${\mathbb{Z}}^n$ is a pair $\mathcal{C}=\langle C,f\rangle$, where $C={\prod }_{j=1}^n[-b_j,b_j]\subset {\mathbb{Z}}^n$, each b_j > 0 being an integer, and $f:C\to \mathbb{R}$ is a scene intensity function. In this paper, symbols $\mathcal{C}$ and C will always stand for a scene and its domain, respectively, as defined above.

The most fundamental measure of local “hanging togetherness” of any pair of spels is an affinity relation κ. It is a fuzzy binary relation defined on C; that is, μ_κ: C × C → [0, 1]. Affinity relation κ is defined to be symmetric and reflexive. The value of μ_κ(c, d) depends not only on the adjacency strength μ_κ(c, d), but also on the intensity function f. There are many methods of finding the affinity relation for a given scene. (See the survey paper [13].) In this paper, we will always assume that an appropriate affinity has already been specified for the segmentation task on hand.

A translation of the local strength of connectedness given by κ into the global strength of connectedness is done with the help of the notion of a path and its strength. A path in A ⊆ C is any sequence p = 〈c₁, . . . , c_l〉, where l > 0 and c_i∈ A for every i = 1, . . . , l. The family of all paths in A is denoted by ${\mathcal{P}}^A$. If c, d ∈ A, then the family of all paths 〈c₁, . . . , c_l〉 in A from c to d (i.e., such that c₁ = c and c_l = d) is denoted by ${\mathcal{P}}_{cd}^A$. The strength μ(p) of a path $p=\langle c_1,\dots ,c_l\rangle \in {\mathcal{P}}^C$ is defined as the strength of its κ-weakest link; that is,

$$\mu \left(p\right)=\min \{{\mu }_{\kappa }(c_{i-1},c_i):1<i\le l\},$$ (1)

when l > 1, and μ(p) = 1 for l = 1. For c, d ∈ A ⊆ C the fuzzy κ-connectedness strength in A between c and d is defined as the strength of a strongest path in A between c and d; that is,

$${\mu }^A(c,d)=\max \{\mu \left(p\right):p\in {\mathcal{P}}_{c,d}^A\}.$$ (2)

If κ is a hard binary relation, κ: C × C → {0, 1}, then the relation μ^A is known as a transitive closure of κ ∩ (A × A). Note that

$${\mu }^A(c,d)\le {\mu }^B(c,d)\text{for every}c,d\in A\subseteq B\subseteq C.$$ (3)

Notice also that μ^A(c, d) ≥ μ_κ(c, d). A path $p\in {\mathcal{P}}_{c,d}^A$ with μ(p) = μ^A(c, d) is referred to as a strongest path (in A) from c to d.

It is easy to see that, for every c, d ∈ A ⊆ C and paths $p,q\in {\mathcal{P}}^A$, we have

(i) μ(〈c, d〉) = μ_κ(c, d) and μ(p)≤ μ(q) if p is either an initial or a terminal extension of q; and

(ii) μ^A is reflexive and symmetric on A.

It is also not difficult to see (and it follows easily from Proposition 2.1 below) that

(iii) μ^A is transitive on A; that is, μ^A (c, d) ≥ min{μ^A (c, x), μ^A(x, d)} for every c, d, x ∈ A.

A very interesting fact is that if μ^A is defined from μ via formula (2) and the properties (i)-(iii) hold, then one might assume as well μ is defined by a formula (1), since under this conditions, independent of the actual definition of μ(p), we still have ${\mu }^A(c,d)={\max }_{\langle c_1,\dots ,c_l\rangle \in {\mathcal{P}}_{c,d}^A}{\min }_{1<i\le l}{\mu }_{\kappa }(c_{i-1},c_i)$. This was proved by Saha and Udupa in [18].

For paths $p=\langle c_1,\dots ,c_l\rangle \in {\mathcal{P}}^A$ and $q=\langle d_1,\dots ,d_n\rangle \in {\mathcal{P}}^A$, we will use symbol p + q to denote the path $\langle c_1,\dots ,c_l,d_1\dots ,d_n\rangle \in {\mathcal{P}}^A$. We will use this symbol only when c_l = d₁. Notice that in such a situation, by the definition in (1), we have μ(p + q) = min{μ(p), μ(q)}, as μ_α(c_l, d₁) = 1.

The following result is a slight refinement of [15, Prop. 2.3].

Proposition 2.1

For any spels a, b, c ∈ A ⊆ C,

$${\mu }^A(a,b)>{\mu }^A(b,c)\Rightarrow {\mu }^A(a,c)={\mu }^A(b,c).$$ (4)

Proof

If p_ab and p_bc are the strongest paths between a and b and between b and c, respectively, then the path p_ab + p_bc justifies μ^A(a, c) ≥ μ^A(b, c), as μ^A(a, c) ≥ μ(p_ab+p_bc) = min{p_ab, p_bc} ≥ μ^A(b, c). If we had μ^A(a, c) > μ^A(b, c), with path p_ca being the strongest path between c and a, then we would have μ(p_ca + p_ab) = min{μ(p_ca), μ(p_ab)} > μ^A(b, c), which is impossible.

2.2 Fuzzy connected objects: absolute and relative

By a segmentation of a scene $\mathcal{C}=\langle C,f\rangle$ we will understand any family {P₁, . . . , P_m} of pairwise disjoint hard subsets of C. Although this is a departure from the terminology used in the previous papers on fuzzy connectedness, the change is only superficial. This is the case since the algorithms from all previous papers were also designed to create the hard segmentations of C, while, in the last step, each set P from the segmentation was assigned a membership function μ_P: C → [0, 1] of the form μ_P(c) = η(f(c)) · χ_P(c), where η is a function (like Gaussian) that maps the image intensity function into objectness values. Although this last step could be done also in the case of our segmentation, we will confine ourselves up to the step of hard segmentation only since, from the viewpoint of the new theory and algorithms, this is what matters.

To translate the notion of a path strength into an actual segmentation of a given scene $\mathcal{C}=\langle C,f\rangle$, one must indicate each object with one or more seeds. So, assume that we have a nonempty set S ⊂ C of seeds such that each seed represents a different object. (The case of multiple seeds per object will be discussed later.)

The simplest way to define a segmentation of a scene $\mathcal{C}$ is to choose a threshold θ ∈ (0, 1] and for each seed s ∈ S define an object in $\mathcal{C}$ associated with s as

$$P_{s\theta }=\{c\in C:{\mu }^C(c,s)\ge \theta \}.$$

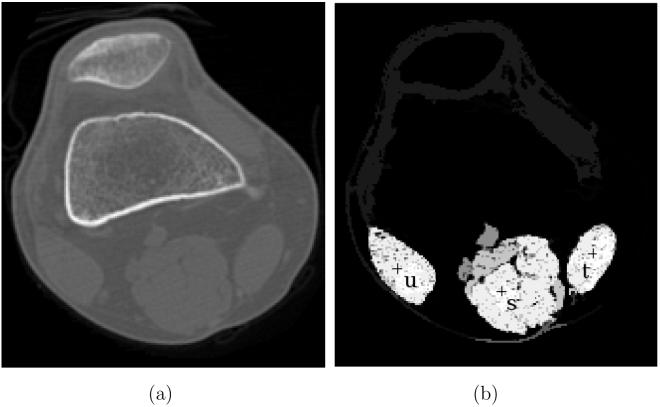
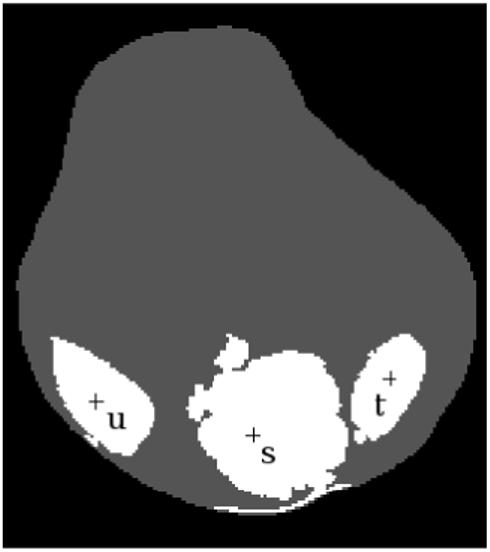
These objects were first studied by Udupa and Samarasekera in [9]. It is easy to see that s ∈ P_sθ for every s ∈ S. Also, for s, t ∈ S, if θ ≤ μ^C(s, t), then P_sθ and P_tθ are disjoint; on the other hand, if θ ≤ μ^C(s, t), then P_sθ = P_tθ. Thus, to make the objects disjoint, one must choose θ greater than every number μ^C(s, t), for all distinct s, t ∈ S. This is the underlining mechanism of AFC. This phenomenon is illustrated in Figure 2 on a CT slice of a human knee, wherein three seed spels s, t, and u are chosen, one in each of three muscle regions. Since the strength of connectedness between any two seeds is much lower than the strength of connectedness within each object (Figure 2(b)), for the individual muscle regions a threshold can be selected to specify P_sθ.

Figure 2.

Illustration of AFC segmentation of the muscles of a knee. (a) A CT slice of a human knee. (b) Each pixel has a strength of connectedness with respect to each seed, u, s, and t, chosen within muscle regions. The largest of these strengths is shown as a scene.

A considerably more powerful segmentation tool is that of RFC. For any s ∈ C and T ⊂ C, define

$$P_{sT}=\{c\in C:{\mu }^C(c,s)>{\mu }^C(c,t)\text{for every}t\in T\backslash \left\{s\right\}\}.$$

Then, the segmentation generated by seeds S ⊂ C is defined as {P_sS: s ∈ S}.

It is easy to see that the objects {P_sS: s ∈ S} are pairwise disjoint. In addition, s ∈ P_sS as long as there is no t ∈ S, t ≠ s, with μ^C(s, t) = 1; if there is such a t, then P_sS is empty. Note also, that if θ > max{μ^C(s, t): s, t ∈ S, s ≠ t} (so that the sets {P_sθ: s ∈ S} are pairwise disjoint), then P_sθ ⊂ P_sS for every s ∈ S. Thus, the RFC method of segmentation is indeed more refined than the AFC method. Again, by using the example in Figure 2, we demonstrate in Figure 3 the results P_sS of RFC. Note that these segmented regions are generally larger than those in Figure 2. Note also that the spels that are not in the muscle regions all have the same strength of connectedness with respect to at least two objects.

Figure 3.

RFC segmentation of the knee muscles from Figure 2, where the same seed points were used as in the AFC segmentation shown in Figure 2(b).

One of the important properties of the above described methods of segmentation (AFC and RFC) is known as robustness. This property states that the segmentation does not change if different seeds are chosen within the same objects, which, for the practice of these segmentation methods, is a very desirable property to have. The following result, due to Saha and Udupa [19], is the precise statement of this property in case of RFC segmentation. (This result follows also from our Corollary 2.7.)

Proposition 2.2 (Robustness)

Let S = {s₁, . . . , s_m} ⊂ C and for every i ∈ {1, . . . , m} let t_i ∈ P_siS. If T = {t₁, . . . , t_m}, then P_tiT = P_siS for every i ∈ {1, . . . , m}.

The objects P_sS are often referred to as connected components. The following fact justifies the word connected in this term. Moreover, this fact will be used in what follows as a motivational tool and in the actual proofs.

Fact 2.3

If p = 〈c₁, . . . , c_l〉 is a strongest path from c ∈ P_sS to an s ∈ S, then c_i ∈ P_sS for every i ∈ {1, . . . , l}; that is, $p\in {\mathcal{P}}^{P_{sS}}$.

Proof

Fix an i ∈ {1, . . . , l} and a t ∈ S\ {s}. Since c ∈ P_sS, we know that μ^C(c, s) > μ^C(c, t). We need to show that μ^C(c_i, s) > μ^C(c_i, t). But, by (4), we have μ^C(s, t) = μ^C(c, t). Since also

$${\mu }^C(c_i,s)\ge \mu \left(\langle c_i,\dots ,c_l\rangle \right)\ge \mu \left(p\right)={\mu }^C(c,s)>{\mu }^C(c,t)={\mu }^C(s,t),$$

by (4) we have μ^C(c_i, s) > μ^C(s, t) = μ^C(c_i, t).

It is sometimes difficult to pinpoint a single seed in a desired object, and often, it is convenient, or becomes necessary, to choose multiple seeds for each object under consideration. So, let $\mathcal{S}$ be a family of nonempty pairwise disjoint sets of seeds. For each $S\in \mathcal{S}$, we like to find an object $P_{S\mathcal{S}}$ containing S in a way similar to that described above. To define $P_{S\mathcal{S}}$, it is convenient to have the following notation for every c ∈ A ⊂ C and D ⊂ A:

$${\mu }^A(c,D)=\underset{d\in D}{\max }{\mu }^A(c,d).$$

(Note that μ^A(c, ∅) = -∞, as max ∅ = ∞ according to a convention that, for a finite $Z\subset \mathbb{R}$, max Z is the smallest b ∈ [-∞, ∞] for which z ≤ b for every z ∈ Z.) We define

$$\begin{array}{cc}\hfill P_{S\mathcal{S}}=& \{c\in C:{\mu }^C(c,S)>{\mu }^C(c,T)\text{for every}T\in \mathcal{S}\backslash \left\{S\right\}\}\hfill \\ \hfill =& \{c\in C:\underset{s\in S}{\max }{\mu }^C(c,s)>{\mu }^C(c,t)\text{for every}t\in W\},\hfill \end{array}$$

where $W=\bigcup (\mathcal{S}\backslash \left\{S\right\})$. Although this multi seed approach is useful in practice, it is worth to note that this theory is quite close to, and readily ensues from, the single seed theory, as each $P_{S\mathcal{S}}$ can be easily expressed in terms of objects generated by singleton seeds:

$$P_{S\mathcal{S}}=\bigcup _{s\in S}{P}_{sW},$$ (5)

since $P_{S\mathcal{S}}={\bigcup }_{s\in S}\{c\in C:{\mu }^C(c,s)>{\mu }^C(c,t)\text{for every}t\in W\}={\bigcup }_{s\in S}{P}_{sW}$.

2.3 Iterative Relative Fuzzy Connectedness: motivation, definition, and properties

The RFC segmentation {P_sS: s ∈ S of a scene can still leave quite a sizable “boundary” set B = C\ ∪_s∈S P_sS; that is, the set of all spels c outside any of the objects P_sS wherein the strengths of connectedness are equal with respect to the seeds. An example is provided in Figure 4 to illustrate this concept of “boundary” spels left unclaimed. The goal of what follows is to find a way to naturally redistribute some of the spels from B among the object regions in a new generation (iteration) of segmentation. Another motivation for IRFC, also explained in Figure 4, is to overcome the problem of “path strength dilution within the same object,” of paths that reach the peripheral subtle and thin aspects of the object.

Figure 4.

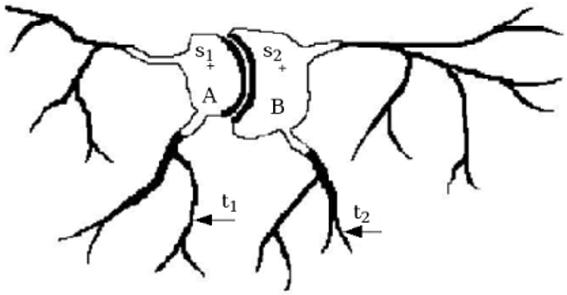
Illustration of the phenomenon of “path strength dilution within the same object.” The strongest paths from s₁ to t₁, s₁ to t₂, s₂ to t₁, and s₂ to t₂ are likely to have the same strength because of partial volume effects.

In Figure 4, two object regions A and B, each with its core and peripheral subtle parts, are shown. Owing to blur and other artifacts introduced into the scene by the imaging device due to partial volume effect and other shortcomings, the strongest paths from s₁ to t₁, s₁ to t₂, s₂ to t₁, and s₂ to t₂ are all likely to assume similar strengths. As a consequence, the spels in the dark areas may fall in B, the unclaimed “boundary” set.

A basic idea behind the definition of relative fuzzy connected objects P_sS, s ∈ S, is that each seed s ∈ S competes for each spel: a spel c goes to the object P_sS provided c is connected to s in a stronger way than to any other seed t ∈ S. Here the strength of connectedness between c and d is expressed by a number μ^C(c, d), the strength of a strongest path (in C) between c and d. Thus, the fact that a spel c belongs to P_sS means that

c is connected to s within the object P_sS with a strength μ^C(c, s) and any appropriate path between c and t ∈ S\ {s} is weaker than μ^C(c, s).

Although the clause “within the object P_sS” may not seem obvious from the definition of P_sS, it is justified both by intuition and by Fact 2.3. It is also not clear what we have in mind by an “appropriate path,” but at this stage it does not matter, since the strength inequality holds for any path between c and t ∈ S\ {s}.

The importance of the clause “appropriate path” comes to light when we examine the spels c from the “boundary” set B = C\ ∪_s∈S P_sS. If we like to refine our definition and to extend each object P_sS, s ∈ S, to a possible larger object $P_{sS}^{\prime }$, what would be the “appropriate” paths between c ∈ B and s ∈ S that we should consider? Since the “strongest path” justifying $c\in P_{tS}^{\prime }$, for t ∈ S, should be contained in $P_{tS}^{\prime }\subset B\cup P_{tS}$, it seems should that we should restrict our attention to the paths between c and t only from B ∪ P_tS. Thus, to obtain a definition of $P_{sS}^{\prime }$, we should modify the definition of P_sS by replacing each number μ^C(c, t), t ∈ S\ {s}, with μ^B∪P_tS(c, t). This leads to

$$P_{sS}^{\prime }=P_{sS}\cup \{c\in B:{\mu }^{B\cup P_{sS}}(c,s)>{\mu }^{B\cup P_{tS}}(c,s)\text{for every}t\in S\backslash \left\{s\right\}\}.$$

Although this definition could be used as the engine for the iteration described below, it turns out that it will be more convenient to use its equivalent form:

$$P_{sS}^{+}=P_{sS}\cup \{c\in C\backslash P_{sS}:{\mu }^C(c,s)>{\mu }^{C\backslash P_{sS}}(c,t)\text{for every}t\in S\backslash \left\{s\right\}\}.$$

The equality $P_{sS}^{\prime }=P_{sS}^{+}$ follows from Theorem 3.7.

Figure 5 illustrates these ideas pictorially. The initial segmentation is defined by RFC conservatively, so that P_sS corresponds to the core aspects of the object identified by seed s (illustrated by the hatched area containing s in Figure 5). This leaves a large boundary set B where the strengths of connectedness with respect to the different seeds are equal (illustrated by the shaded area containing s in Figure 5). In the next iteration, the segmentation is improved incrementally by grabbing those spels of B that are connected more strongly to P_sS than to P_tS. When considering the object associated with s, the “appropriate” path from s to any c ∈ B is any path in C. However, all objects have to compete with the object associated with s by allowing paths from their respective seeds t to c not to go through P_sS since this set has already been declared to be part of the object of s.

Figure 5.

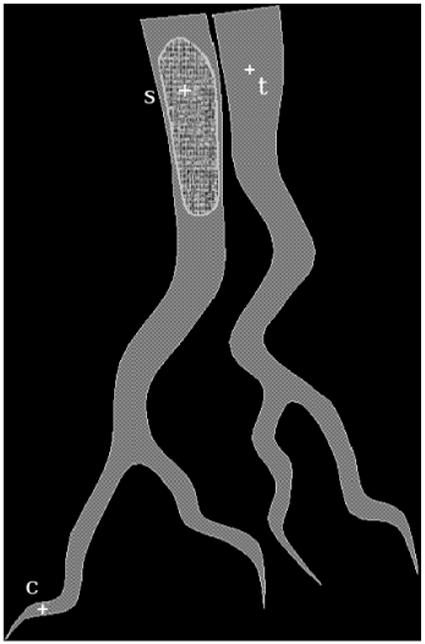
Pictorial illustration of IRFC advantages over RFC.

The advantage of the formula for $P_{sS}^{+}$ over that for $P_{sS}^{\prime }$ comes from the fact that, unlike the case of $P_{sS}^{\prime }$, we can compute $P_{sS}^{+}$ without knowing sets P_tS for t ≠ s. This makes the implementation of the algorithm easier and more efficient. In addition, the two object IRFC theory in earlier papers discussing this subject [15] was done in the format of $P_{sS}^{+}$, which makes our ($P_{sS}^{+}$ based) theory its natural generalization. However, the formalism underlining $P_{sS}^{\prime }$ also has its advantages. First of all, it is more intuitive from the connectedness point of view. Also, the disjointness of the new generation of segments (see Theorem 2.4) is obvious in the $P_{sS}^{\prime }$ setting, while it requires a complicated argument in the $P_{sS}^{+}$ formalism.

Now, the iterative version of sets P_sS can be defined as follows. For each s ∈ C let $P_{sS}^0$ be the empty set and define iteratively sets P^j_sS by a formula $P_{sS}^{j+1}=P_{sS}^j\cup Q_{sS}^j$, where

$$Q_{sS}^j=\{c\in C\backslash P_{sS}^j:{\mu }^C(c,s){>}^{C\backslash P_{sS}^j}(c,t)\text{for every}t\in S\backslash \left\{s\right\}\}.$$

This definition works fine if we assume that each object is connected and is generated by a single seed. However, we like to develop this theory also in the case when each object in the segmentation is generated by a set S of seeds where the different resulting segments may be disconnected. So, let ${\mu }_{\mathcal{S}}$ be a nonempty family of nonempty pairwise disjoint sets of seeds. For every A ⊂ C let $P_{AS}^0=\varnothing$ and for j = 0, 1, 2, . . . define $P_{AS}^{j+1}=P_{AS}^j\cup Q_{AS}^j$, where

$$\begin{array}{cc}\hfill Q_{A\mathcal{S}}^j=& \{c\in C\backslash P_{A\mathcal{S}}^j:{\mu }^C(c,A)>{\mu }^{C\backslash P_{A\mathcal{S}}^j}(c,T)\text{for every}T\in \mathcal{S}\backslash \left\{A\right\}\}\hfill \\ \hfill =& \{c\in C\backslash P_{A\mathcal{S}}^j:{\mu }^C(c,A)>{\mu }^{C\backslash P_{A\mathcal{S}}^j}(c,t)\text{for every}t\in \bigcup (\mathcal{S}\backslash \left\{A\right\})\}\hfill \\ \hfill =& \{c\in C\backslash P_{A\mathcal{S}}^j:{\mu }^C(c,A)>{\mu }^{C\backslash P_{A\mathcal{S}}^j}(c,\bigcup (\mathcal{S}\backslash \left\{A\right\})\}.\hfill \end{array}$$

The equality between the sets defining $Q_{A\mathcal{S}}^j$ follows immediately from the definition μ^A(c, D) = max_d∈D μ^A(c, d). (For alternative definitions of $P_{A\mathcal{S}}^{j+1}$ see also Subsection 3.2.)

Clearly $P_{A\mathcal{S}}^j\subseteq P_{A\mathcal{S}}^{j+1}$ for every j and for any A ⊂ C. Since the scene domain C is finite, the growth must stop at some stag j. In particular, there is a k for which $P_{S\mathcal{S}}^{k+1}=P_{S\mathcal{S}}^k$ for all $S\in \mathcal{S}$. We will denote such terminal iterative $P_{S\mathcal{S}}^k$ as $P_{S\mathcal{S}}^I$. The IRFC segmentation (of $\mathcal{C}$ with respect to $\mathcal{S}$) is defined as $\{P_{S\mathcal{S}}^I:S\in \mathcal{S}\}$.

Note that the result of the first iteration $P_{S\mathcal{S}}^1$ is equal to $P_{S\mathcal{S}}$ as defined by the RFC formula. Thus, $P_{S\mathcal{S}}\subseteq P_{S\mathcal{S}}^I$. In particular, the iterative technique is a refinement of the RFC method. Also, for every s ∈ S ⊂ C and j, we have

$$P_{sS}^j=P_{\left\{s\right\}\mathcal{S}}^j,$$

where $\mathcal{S}=\{\left\{s\right\}:s\in \mathcal{S}\}$. Thus, every family $\{P_{sS}^j:s\in S\}$ of single seed generated IRFC segmentation can be easily represented in the formalism of multi seed generated IRFC segmentations. In other words, the theory of IRFC segmentations $\{P_{S\mathcal{S}}^j:S\in \mathcal{S}\}$ contains, as special cases, the theories of RFC and IRFC segmentations generated by singleton seeds, as well as the theory of RFC in the case of multi seed generated objects.

Equation (5) shows a beautiful relation between the RFC objects, P_sS, generated by singleton seeds and their multi seed generated counterparts P_SS. Could we also prove its iterative analog? This certainly would give a hope that a large part of multi seed IRFC theory could be easily deduced from its single seed counterpart. However, the iterative analog of (5) is false as can be seen in Example 3.14. Thus, we need to prove our results in a full multi seed setting.

The most fundamental property of any segmentation is that the objects it creates are pairwise disjoint. For IRFC segmentation, this is given by the following theorem.

Theorem 2.4

For any family $\mathcal{S}$ of subsets of a scene C, we have $P_{S\mathcal{S}}^I\cap P_{U\mathcal{S}}^I=\varnothing$ for every distinct $S,U\in \mathcal{S}$.

Since the iteration leading to the sets $P_{S\mathcal{S}}^j$ uses the formula as in $P_{sS}^{+}$ rather than as in $P_{sS}^{\prime }$, the proof of Theorem 2.4 is rather complicated and it will be postponed till the next section. It is also worth to notice that, in our proof of the equation $P_{sS}^{+}=P_{sS}^{\prime }$ (see Theorem 3.7), we need to use Theorem 2.4 in the $P_{sS}^{+}$ formalism.

Notice that, in the formulation of Theorem 2.4, we assumed almost nothing about the family $\mathcal{S}$ of sets of seeds. We will continue with these minimal assumptions about $\mathcal{S}$ throughout most of the theoretical development that follows, since this does not make the proofs any more difficult. Moreover, in some cases (e.g., when we modify $\mathcal{S}$ to form another family of seeds $\mathcal{T}$ to compare the $\mathcal{S}$-segmentation with $\mathcal{T}$-segmentation), it saves us the trouble of checking any extra properties we could impose on the generating families of seeds. However, in practical applications, we will apply our algorithm only when the sets in $\mathcal{S}$ are nonempty and pairwise disjoint.

Notice that allowing the empty set to be in $\mathcal{S}$ does not change much, since $P_{\varnothing \mathcal{S}}^j$ is empty for any $\mathcal{S}$ and j. The fact that allowing overlapping sets in $\mathcal{S}$ also changes little is more subtle. It is true that if a seed s belongs to distinct $S,T\in \mathcal{S}$, then s does not belong to $P_{S\mathcal{S}}^I$, or any other $P_{US}^I$. This is certainly an undesirable situation, since we would like the generating seeds S to be in the object $P_{S\mathcal{S}}^I$ they generate. Unfortunately, a simple assumption that the sets in $\mathcal{S}$ be pairwise disjoint does not solve the problem: if $S,T\in \mathcal{S}$ are distinct and there are s ∈ S and t ∈ T with μ^C(s, t) = 1, then neither s nor t belongs to ${\bigcup }_{V\in \mathcal{S}}{P}_{V\mathcal{S}}^I$. Then the question arises as to what part of S belongs to $P_{S\mathcal{S}}^I$. In Lemma 3.2, we will show that the missing seeds are precisely those from the above example: if $E_{\mathcal{S}}={\bigcup }_{S\in \mathcal{S}}\{s\in S:{\mu }^C(s,t)=1\text{for some}t\in T\in \mathcal{S}\backslash \left\{S\right\}\}$, then $S\backslash E_{\mathcal{S}}\subseteq P_{S\mathcal{S}}^1$, while $E_{\mathcal{S}}$ is disjoint with ${\bigcup }_{V\in \mathcal{S}}{P}_{V\mathcal{S}}^I$. We will also show in Proposition 3.12 that, even if $E_{\mathcal{S}}$ is nonempty, it is possible to redistribute its elements (i.e., to find a family $\mathcal{T}=\{T_S\supseteq S\backslash E_S:S\in \mathcal{S}\}$ with $\bigcup \mathcal{T}=\bigcup \mathcal{S}$) in such a way that $T\subseteq P_{T\mathcal{T}}^1$ for every $T\in \mathcal{T}$. Moreover, we can ensure that $P_{S\mathcal{S}}^I\subseteq P_{T_s\mathcal{T}}^I$ for every $S\in \mathcal{S}$.

The second fundamental property of our segmentation method is its stability with respect to different choices of seeds initializing the segmentation process. This will be discussed in the next subsection.

2.4 Robustness of IRFC segmentation

The most natural impulse for a formulation of a robustness theorem in our setting is to state it in the compact format of Proposition 2.2: “For a family $\mathcal{S}=\{S_1,\dots ,S_m\}$ of seeds and nonempty sets $T_i\subseteq P_{S_i\mathcal{S}}^I$, $P_{T_i\mathcal{T}}=P_{S_i\mathcal{S}}$, where $\mathcal{T}=\{T_1,\dots ,T_m\}$.” However, in a multiple seed setting, there is no hope for such a result even in the case of RFC or AFC. To verify this, consider a scene $\mathcal{C}=\langle C,f\rangle$ that contains three uniform circles C₁, C₂, and C₃ which are pairwise completely separated. (This means that for any c ∈ C_i and d ∈ C_j we have μ^C(c, d) = 1 for i = j and μ^C(c, d) = 0 for i ≠ j.) If we choose S₁ = T₁ = C₁, S₂ = C₂ ∪ C₃ and T₂ =C₂, then $P_{s_2\mathcal{S}}^I=P_{S_2\mathcal{S}}=C_2\cup C_3$, while $P_{T_2\mathcal{T}}^I=P_{T_2\mathcal{T}}=C_2$ is smaller. The difficulty outlined in this example comes from the fact that an object $P_{S_i\mathcal{S}}^I$ may have more than one connected component, while T_i may intersect only one of them. Thus, to insure that this will not happen, we will assume that S_i ⊆ T_i, leading to the following result.

Theorem 2.5

Let $\mathcal{S}=\{S_1,\dots ,S_m\}$ be a family of subsets of C, fix k ∈ {1, 2, 3, . . .}, and let $S_i\subseteq T_i\subseteq S_i\cup P_{S_{i}S}^k$ for every i ∈ {1, . . ., m}. If $\mathcal{T}=\{T_1,\dots ,T_m\}$, then $P_{S_i\mathcal{S}}^I=P_{T_i\mathcal{T}}^I$ for every i ∈ {1, . . . , m}. Moreover, if k = 1, then $P_{S_i\mathcal{S}}^j=P_{T_i\mathcal{T}}^j$ for every i ∈ {1, . . . , m} and j ∈ {0, 1, 2, . . .}.

This theorem shows that there is considerable flexibility in the choice of seeds used to iteratively generate an object $P=P_{S\mathcal{S}}^I$: as long as we choose the seeds inside P and ensure that they contain some minimal set of generators, the final result will always be the same. The version of the theorem when k = 1 has even nicer conclusion. However, the assumption that $T_i\subset S_i\cup P_{S_i\mathcal{S}}^1$ may be somewhat restrictive—it may be difficult to guess which spels be in the “core part” $P_{S_i\mathcal{S}}^1$ of the object, even in the case when the entire object, $P_{S_i\mathcal{S}}^I$, can be guessed with a good approximation. Note also that, in fact Theorem 2.5 remains true, if we assume that each T_i contains only a subset T_Si of S_i described in Proposition 3.10.

The only version of Theorem 2.5 that was previously proved in the literature (see [15]) was done only for two components, in a single seed format, and in the version with k = 1 (i.e., Corollary 2.7 below for m = 2).

Theorem 2.5 directly leads to the following corollary.

Corollary 2.6

Let $\mathcal{S}=\{S_1,\dots ,S_m\}$ and $\mathcal{T}=\{T_1,\dots ,T_m\}$ be the families of subsets of C, fix k ∈ {1, 2, 3, . . .}, and assume that for every i ∈{1,...,m} we have $T_i\subseteq S_i\cup P_{S_i\mathcal{S}}^k$ and $S_i\subseteq T_i\cup P_{T_i\mathcal{T}}^k$. Then $P_{S_i\mathcal{S}}^I=P_{T_i\mathcal{T}}^I$ for every i ∈ {1, . . . , m}. Moreover, if k = 1, then $P_{S_i\mathcal{S}}^j=P_{T_i\mathcal{T}}^j$ for every i ∈ {1 , . . . , m} and j ∈ {0, 1, 2, . . .}.

Proof

For i ∈ {1, . . . , m}, put U_i = S_i ∪ T_i and let $\mathcal{U}=\{U_1,\dots ,U_m\}$. Then, the pairs $\langle \mathcal{S},\mathcal{U}\rangle$ and $\langle \mathcal{T},\mathcal{U}\rangle$ satisfy the assumptions of Theorem 2.5, so, $P_{S_i\mathcal{S}}^I=P_{U_i\mathcal{U}}^I=P_{T_I\mathcal{T}}^j$ for every i ∈ {1, . . . , m}. If k = 1, we also have $P_{S_i\mathcal{S}}^j=P_{U_i\mathcal{U}}^j=P_{T_i\mathcal{T}}^j$ for every j ∈ {0, 1, 2, . . .}.

When we restrict our attention to the segmentation generated with only singleton seeds, one of the inclusions in the assumptions of Corollary 2.6 can be dropped and we obtain an analog of Proposition 2.2.

Corollary 2.7

Let S = {s₁, . . . ,s_m} and T = {t₁, . . . , t_m} be some m-element subsets of C and assume that for every i ∈ {1, . . . , m} we have $t_i\in P_{s_{i}S}^1$. Then $P_{t_{i}T}^j=P_{s_{i}S}^j$ for every i ∈ {1, . . . , m} and j ∈ {0, 1, . . .}.

It is not accidental that in Corollary 2.7 we assume that each t_i belongs to a smaller set $P_{s_{i}S}^1$ rather than to a bigger set $P_{s_{i}S}^I$, as in our other robustness results—the version of Corollary 2.7 with assumption $t_i\in P_{s_{i}S}^I$ is false, even if we weaken the conclusion to $P_{t_{i}T}^I=P_{s_{i}S}^I$. A simple example of such a situation is given in Example 3.15, where $t_i\in P_{s_{i}S}^I$ for all i while $P_{t_{1}T}^I⊊P_{s_{1}S}^I$. This is yet another reason why in Theorem 2.5 we need the assumption S_i ⊆ T_i.

3 The proofs and the examples

This section is designed mainly to prove the results announced in the previous section. This will require an introduction of some new concepts and proving several auxiliary results, some of which are of independent interest and are fundamental to the FC phenomenon. Unless otherwise explained, in what follows, $\mathcal{C}=\langle C,f\rangle$ will always stand for a digital scene with fixed adjacency and affinity relations, and $\mathcal{S}$ for a nonempty family of subsets of C.

3.1 Disjointness of the segments

The following simple fact will be used (often implicitly) many times in this section.

Fact 3.1

If c, d ∈ A ⊆ B ⊆ C and p is a path in A from c to d such that μ(p) = μ^B(c, d), then μ^A(c, d) = μ^B(c, d).

Proof

This follows immediately from μ^A(c, d) ≤ μ^B(c, d) = μ(p) ≤ μ^A(c, d), where the first inequality is justified by (3) and the last is a consequence of the definition of μ^A.

The next lemma describes precisely what portion of S must belong to $P_{S\mathcal{S}}^1$.

Lemma 3.2

For $S\in \mathcal{S}$ let $E=\{s\in S:{\mu }^C(s,T)=1\text{for some}T\in \mathcal{S}\backslash \left\{S\right\}\}$. Then $S\backslash E\subseteq P_{S\mathcal{S}}^1$ and E is disjoint with ${\bigcup }_{V\in \mathcal{S}}{P}_{V\mathcal{S}}^I$.

Proof

Clearly $S\backslash E\subseteq P_{S\mathcal{S}}^1$ as μ^C(s, S) = 1 > μ^C(s, T) for any s ∈ S\ E and $T\in \mathcal{S}\backslash \left\{S\right\}$.

We will prove $P_{S\mathcal{S}}^j\subseteq C\backslash E$ by induction on j ∈ {0, 1, 2, . . .}. For j = 0 it is obvious, as $P_{S\mathcal{S}}^0=\varnothing$. So, assume that for some j we have $P_{S\mathcal{S}}^j\subseteq C\backslash E$. We need to show that $P_{S\mathcal{S}}^{j+1}\subseteq C\backslash E$. For this, choose a $c\in P_{S\mathcal{S}}^{j+1}$ and, by way of contradiction, assume that c ∈ E. Then there is a $T\in \mathcal{S}\backslash \left\{S\right\}$ for which μ^C(c, T) = 1. Moreover, any strongest path from c to T is in E, so, by Fact 3.1, we have μ^E(c, T) = 1. Also, $E\subseteq C\backslash P_{S\mathcal{S}}^j$, which follows from the inductive assumption, and (3) imply that ${\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)\ge {\mu }^E(c,T)$. So, ${\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)=1$. However, this contradicts ${\mu }^C(c,S)>{\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)$, which is a consequence of $c\in P_{S\mathcal{S}}^{j+1}$. So, indeed c ∈ C\ E.

Now, if $V\in \mathcal{S}\backslash \left\{S\right\}$, then the inclusion $P_{V\mathcal{S}}^j\subseteq C\backslash S\subseteq C\backslash E$ is proved by even easier induction. Indeed, if $P_{V\mathcal{S}}^j\subseteq C\backslash S$ is true for some j, then ${\mu }^C(s,V)\le 1={\mu }^C(s,s)={\mu }^{C\backslash P_{V\mathcal{S}}^j}(s,s)={\mu }^{C\backslash P_{V\mathcal{S}}^j}(s,S)$ for every s ∈ S; that is, no s ∈ S is in $P_{V\mathcal{S}}^{j+1}$.

Let c ∈ A ⊂ C and S ⊂ A. We say that a path $p=\langle c_1,\dots ,c_l\rangle \in {\mathcal{P}}^A$ is a nice path (in A) from c to S provided c₁ = c, c_l ∈ S, and for every k ∈ {1, . . . , l}, we have μ(〈c_k, . . . , c_l〉) = μA(c_k, S), that is, 〈c_k, . . . , c_l〉 is a strongest possible path in A from c_k to S. If S = {s}, then we will say that p is a nice path (in A) from c to s, rather than to S.

Lemma 3.3

For every c ∈ A ⊂ C and S ⊂ A, there exists a nice path in A from c to S.

Proof

We will start with the following simple remark. In its statement, by a one-to-one path we understand any path in which no spel appears more than once.

(I) For every d ∈ A ⊂ C and S ⊂ A there exists a one-to-one path $p\in {\mathcal{P}}^A$ from d to an s ∈ S with μ(p) = μ^A(d, S).

Indeed, let $p=\langle c_1,\dots ,c_l\rangle \in {\mathcal{P}}^A$ be a shortest path in A from d to an s ∈ S with μ(p) = μ^A(d, S). Then p must be one-to-one. Otherwise, there would exist 1 ≤ i < j ≤ l for which c_i = c_j. But then the path 〈c₁, . . . , c_i, c_j+1, . . . , c_l〉 would be a strongest path in A from d to an s ∈ S of shorter length than p, which contradicts the choice of p.

Next we will prove, by induction on n = 1, 2, 3, . . ., the following statement.

I_n: For every c ∈ A ⊂ C and S ⊂ A there exists a one-to-one path $p=\langle c_1,\dots ,c_l\rangle \in {\mathcal{P}}^A$ from c to S such that for every i ∈ {1, . . . , n}

$$\text{if}i\le l,\text{then}\mu \left(\langle c_i,\dots ,c_l\rangle \right)={\mu }^A(c_i,S).$$ (*)

For n = 1 the statement is true: it is just the condition (I) we proved above. So, assume that I_n holds. We need to prove I_n+1.

So, pick c ∈ A ⊂ C and S ⊂ A. Let p = 〈c₁, . . . , c_l〉 be a path satisfying I_n. If l ≤ n, then p satisfies also I_n+1 and we are done. So, assume that l ≥ n+1. Let x = μ(〈c_n, . . . , c_l〉) = μ^A(c_n, S), y = μ(〈c_n+1, . . . ,c_l〉)), and z = μ^A(c_n+1, S). Then x ≤ y < z. If y = z, then p satisfies also I_n+1 and, again, we are done. So, assume that x ≤ y ≤ z. Let $q=\langle d_1,\dots ,d_m\rangle \in {\mathcal{P}}^A$ be a path from c_n+1 to S with μ(q) = μ^A(d₁, S). By (I) we can assume that q is one-to-one. Let $p^{\prime }=\langle c_1,\dots ,c_n,d_1,\dots ,d_m\rangle \in {\mathcal{P}}^A$. We will show that p’ satisfies I_n+1.

Indeed, clearly p’ is a path in A from c to S. To see that p’ is one-to-one assume, by way of contradiction, that this is not the case. Then there exist 1 ≤ i ≤ n and 1 ≤ j ≤ m such that c_i = d_j. But then

$${\mu }^A(c_i,S)={\mu }^A(d_j,S)\ge \mu \left(\langle d_j,\dots ,d_m\rangle \right)\ge \mu \left(\langle d_1,\dots ,d_m\rangle \right)=z.$$

Thus, z ≤ μ^A(c_i, S) = μ(〈c_i, . . . , c_l〉) ≤ μ(〈c_n, . . . , c_l〉) = x, contradicting x ≤ y < z. So, q is one-to-one.

To see (*) take an i ≤ n + 1, then condition (*) becomes μ(〈d1, . . . , d_m〉) = μ^A(d₁, S) and it is ensured by μ(q) = μ^A(d₁, S). So, assume i ≤ n. Then μ(〈c_i, . . . , c_n, d₁, . . . , d_m〉) ≥ μ(〈c_i, . . . , c_l〉) = μ^A(c_i, S), since μ(〈d₁, . . . , d_m〉) = μ^A(〈c_n+1,S) ≥ μ(〈c_n+1, ...,c_l〉). Thus, (*) holds. This finishes the inductive proof of I_n.

Finally, note that if N is the size of A, then I_N implies the lemma, since for any one-to-one path $p=\langle c_1,\dots ,c_l\rangle \in {\mathcal{P}}^A$ we have l ≤ N, so a path satisfying and I_N must be nice.

The following fact is the iterative version of Fact 2.3.

Fact 3.4

If $S\in \mathcal{S}$ and p = 〈c₁, . . . , c_l〉 is a nice path from $c\in P_{S\mathcal{S}}^j$ to S, then $c_i\in P_{S\mathcal{S}}^j$ for every i ∈ {1, . . . , l}, that is, $p\in {\mathcal{P}}^{P_{S\mathcal{S}}^j}$.

Proof

The proof goes by induction on j. For j = 1 it follows from Fact 2.3 and (5). So, assume that it is true for some j ≤ 1. We need to prove it for j + 1.

So, fix an $S\in \mathcal{S}$ and a nice path p = 〈c₁, . . . , c_l〉 from $c\in P_{S\mathcal{S}}^{j+1}$ to S. First notice thatthere is an i ∈ {1, . . . , l} for which $c_i\in P_{S\mathcal{S}}^j$.

Indeed otherwise p is in $C\backslash P_{S\mathcal{S}}^j$ and c_l ∈ E, where E is as in Lemma 3.2. Pick a $T\in \mathcal{S}\backslash \left\{S\right\}$ for which μ^C(c_l, T) = 1 and let q be a path from c_l to T with μ(q) = 1. Then q is in $E\subseteq C\backslash P_{S\mathcal{S}}^j$. Thus, p + q is a path in $C\backslash P_{S\mathcal{S}}^j$ from c to T and ${\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)\ge \mu (p+q)=\mu \left(p\right)={\mu }^C(c,S)$, contradicting $c\in P_{S\mathcal{S}}^{j+1}$.

Let k ∈ {1, . . . , l} be the smallest number such that $c_k\in P_{S\mathcal{S}}^j$. Since 〈c_k, . . . , c_l〉 is a nice path from $c_k\in P_{S\mathcal{S}}^j$ to S, by the inductive assumption we have that $c_i\in P_{S\mathcal{S}}^j\subset P_{S\mathcal{S}}^{j+1}$ for every i ∈ {k, . . . , l}. Thus, we just need to prove that, for each i ∈ {1, . . , k - 1}, the spel c_i belongs to $Q_{S\mathcal{S}}^j$.

If k = 1 there is nothing to prove. So, assume that k > 1. Then the proof is almost identical to that for Fact 2.3.

Fix an i ∈ {1, . . . , k - 1}, a $T\in \mathcal{S}\backslash \left\{S\right\}$, and a t ∈ T. Since $c_1\in Q_{S\mathcal{S}}^j$, we know that ${\mu }^C(c_1,S)>{\mu }^{C\backslash P_{S\mathcal{S}}^j}(c_1,T)\ge {\mu }^{C\backslash P_{S\mathcal{S}}^j}(c_1,t)$. We need to show that ${\mu }^C(c_i,c_l)>{\mu }^{C\backslash P_{S\mathcal{S}}^j}(c_i,t)$,as ${\mu }^C(c_i,c_l)={\mu }^C(c_i,S)$. Since

$${\mu }^{C\backslash P_{S\mathcal{S}}^j}(c_1,c_i)\ge \mu \left(\langle c_1,\dots ,c_i\rangle \right)\ge \mu \left(\langle c_1,\dots ,c_l\rangle \right)={\mu }^C(c_1,S)>{\mu }^{C\backslash P_{S\mathcal{S}}^j}(c_1,t),$$

by (4) we have ${\mu }^{C\backslash P_{S\mathcal{S}}^j}(c_1,t)={\mu }^{C\backslash P_{S\mathcal{S}}^j}(c_i,t)$. Thus

$${\mu }^C(c_i,c_l)\ge \mu \left(\langle c_1,\dots ,c_l\rangle \right)\ge \mu \left(p\right)={\mu }^C(c_1,S)>{\mu }^{C\backslash P_{S\mathcal{S}}^j}(c_1,t)={\mu }^{C\backslash P_{S\mathcal{S}}^j}(c_i,t),$$

completing the proof.

It would be nice if the conclusion of Fact 3.4 was true for any strongest path from c to S, rather than just for nice paths. This, however, is not the case. In the above proof, the place we used the stronger assumption is where we claimed that $c_i\in P_{S\mathcal{S}}^j$ for every i ∈ {k, . . . , l}. If p is just any strongest path from c to S, then 〈c_k, . . . , c_l〉 does not need to be a strongest path from $c_k\in P_{S\mathcal{S}}^j$ to S and it might happen that $c_{k+1}\notin P_{S\mathcal{S}}^{j+1}$. A specific example of such a situation is a given in Example 3.13.

Fact 3.4 says, in particular, that if $S\in \mathcal{S}$ is a singleton, say S = {s}, then for every $c\in P_{S\mathcal{S}}^j$ there is a strongest path in $P_{S\mathcal{S}}^j$ from c to s. The following remark gives a stronger version of this fact.

Remark 3.5

If $S\in \mathcal{S}$ is a singleton, then for every $c,d\in P_{S\mathcal{S}}^j$, there is a strongest path r in $P_{S\mathcal{S}}^j$ from c to d, that is, ${\mu }^C(c,d)={\mu }^{P_{S\mathcal{S}}^j}(c,d)$.

Proof

Let S = {s} and let p = 〈c₁, . . . , c_l〉 be a nice path from c to s and q = 〈d₁, . . . , d_m〉 be a nice path from d to s. Then, by Fact 3.4, $p,q\in {\mathcal{P}}^{P_{S\mathcal{S}}^j}$. If μ^C(c, d) = min{μ^C(c, s), μ^C(d, s) = min μ(p), μ(q), then r = 〈c₁, . . . , c_l, d_m, . . . , d₁〉 is as desired. So, assume that μ^C(c, d) is greater than min {μ^C(c, s), μ^C(d, s)}. Then, in particular, μ^C(c, d) > μ^C(d, s) = μ(q). Let 〈b₁, . . . , b_n〉 be a nice path from c to d and put r = 〈b₁, . . . , b_n, d₁, . . . , d_m〉. We claim that r is a nice path from c to s. Indeed, clearly for any index i ∈ {1, . . . , m}, the path 〈d_i, . . . , d_m〉 is a strongest from d_i to d_m = s, since q was nice. Next, fix an i ∈ {1, . . . , n}. Since

$${\mu }^C(b_i,d)\ge \mu \left(\langle b_i,\dots ,b_n\rangle \right)\ge \mu \left(\langle b_1,\dots ,b_n\rangle \right)={\mu }^C(c,d)>{\mu }^C(d,s)=\mu \left(q\right)$$

we have, by (4), that μ^C(b_i, s) = μ^C(d, s) and

$$\begin{array}{cc}\hfill & \hfill \\ \hfill \mu \left(\langle b_i,\dots ,b_n,d_1,\dots ,d_m\rangle \right)& =\min \{\mu \left(\langle b_i,\dots ,b_n\rangle \right),\mu \left(\langle d_1,\dots ,d_m\rangle \right)\}\hfill \\ \hfill & =\min \{\mu \left(\langle b_i,\dots ,b_n\rangle \right),\mu \left(q\right)\}\hfill \\ \hfill & =\mu \left(q\right)={\mu }^C(d,s)={\mu }^C(b_i,s).\hfill \end{array}$$

Thus, r is a nice path from c to s and as such, by Fact 3.4, it is in $P_{S\mathcal{S}}^j$. In particular, 〈b₁, . . . , b〉 is in $P_{S\mathcal{S}}^j$.

Assume that $U,S,T\in \mathcal{S}$ are distinct and that there exists a spel c ∈ C for which μ^C(c, U) < μ^C(c, S) = μ^C(c, T). Then $c\notin {\bigcup }_{V\in \mathcal{S}}{P}_{V\mathcal{S}}^1$. Is it possible that $c\in P_{U\mathcal{S}}^j$ for some j > 1? This certainly would be counter intuitive. The next fact ensures us that this is impossible.

Fact 3.6

If $S,U\in \mathcal{S}$ and $c\in P_{S\mathcal{S}}^I$, then μ^C(c, S) s≥ μ^C(c, U).

Proof

By way of contradiction assume that μ^C(c, S) < μ^C(c, U). Choose a nice path p = 〈c₁, . . . , c_l〉 from c to U and let k ∈ {1, . . . , l} be the largest index with $c_k\in P_{S\mathcal{S}}^I$. Let s ∈ S. Since

$${\mu }^C(c,c_k)\ge \mu \left(\langle c_1,\dots ,c_k\rangle \right)\ge \mu \left(p\right)={\mu }^C(c,U)>{\mu }^C(c,S)\ge {\mu }^C(c,s),$$

(4) implies that μ^C(c_k, s) = μ^C(c, s). Therefore, for every s ∈ S,

$${\mu }^C(c_k,s)={\mu }^C(c,s)<{\mu }^C(c,U)=\mu \left(p\right)\le \mu \left(\langle c_k,\dots ,c_l\rangle \right)\le {\mu }^C(c_k,U).$$

Thus, μ^C(c_k, S) < μ^C(c_k, U). Let i ∈ {0, 1, 2, . . .} be the smallest index with the property that $c_k\in P_{S\mathcal{S}}^i$. Note that i > 1 since μ^C(c_k, S) < μ^C(c_k, U). But, by the maximality of k, we have that $\langle c_k,\dots ,c_l\rangle \in {\mathcal{P}}^{C\backslash P_{S\mathcal{S}}^{i-1}}$. Therefore, ${\mu }^C(c_k,s)<{\mu }^C(c_k,U)=\mu \left(\langle c_k,\dots ,c_l\rangle \right)\le {\mu }^{C\backslash P_{uS}^{i-1}}(c_k,U)$ implying $c_k\notin Q_{S\mathcal{S}}^{i-1}$. Since the minimality of i implies also that $c_k\notin P_{S\mathcal{S}}^{i-1}$, we conclude $c_k\notin P_{S\mathcal{S}}^i$, contradicting choice of i.

Proof of Theorem 2.4

We prove that $P_{S\mathcal{S}}^j\cap P_{U\mathcal{S}}^j=\varnothing$ by induction on j = 0, 1, 2, . . ..

Clearly the result is true for j = 0 since sets $P_{S\mathcal{S}}^0$ are empty. Also, definition the of $P_{S\mathcal{S}}^1=P_{S\mathcal{S}}$ clearly insures that the result is true for j = 1. So, assume that the result is true for some j. We need to show that the sets $P_{S\mathcal{S}}^{j+1}=P_{S\mathcal{S}}^j\cup Q_{S\mathcal{S}}^j$, with $S\in \mathcal{S}$, are pairwise disjoint.

For this first notice that $P={\bigcup }_{S\in \mathcal{S}}{P}_{S\mathcal{S}}^j$ is disjoint with $Q={\bigcup }_{S\in \mathcal{S}}{Q}_{S\mathcal{S}}^j$. Indeed, take a c∈ P and let $S\in \mathcal{S}$ be such that $c\in P_{S\mathcal{S}}^j$. By Lemma 3.3 there exists a nice path p (in C) from c to S. Fact 3.4 then shows that $p\in {\mathcal{P}}^{P_{S\mathcal{S}}^j}$. Now, take a $U\in \mathcal{S}$. We need to show that $c\notin Q_{U\mathcal{S}}^j$.

This is obvious if U = S, since $Q_{S\mathcal{S}}^j\subset C\backslash P_{S\mathcal{S}}^j$. So, assume that U ≠ S. Then, by the inductive assumption, $P_{S\mathcal{S}}^j\subset C\backslash P_{U\mathcal{S}}^j$, so $p\in {\mathcal{P}}^{C\backslash P_{U\mathcal{S}}^j}$. In particular, ${\mu }^{C\backslash P_{U\mathcal{S}}^j}(c,S)=\mu \left(p\right)={\mu }^C(c,S)$. Now, by way of contradiction, assume that $c\in Q_{U\mathcal{S}}^j\subset P_{U\mathcal{S}}^{j+1}$. Then, in particular, ${\mu }^C(c,U)>{\mu }^{C\backslash P_{U\mathcal{S}}^j}(c,S)$. Therefore, μ^C(c, U) > μ^C(c, S). But this, together with $c\in P_{S\mathcal{S}}^j$, contradicts Fact 3.6. So, indeed P ∩ Q = ∅.

Let B^j = C\ P . To finish the proof of the theorem it is enough to show that every c ∈ B^j belongs to at most one of $Q_{S\mathcal{S}}^j$ with $S\in \mathcal{S}$. So, fix a c ∈ B^j and let $U\in \mathcal{S}$ be such that ${\mu }^C(c,U)={\max }_{T\in \mathcal{S}}{\mu }^C(c,T)$. Let p = 〈c₁, . . . , c_l〉 be a nice path from c to U. If $p\in {\mathcal{P}}^{B^j}$, then for every $S\in \mathcal{S}$ we have ${\mu }^C(c,S)\le {\mu }^C(c,U)=\mu \left(p\right)\le {\mu }^{B^j}(c,U)\le {\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,U)$ insuring that $c\notin Q_{S\mathcal{S}}^j$ for every $S\in \mathcal{S}\backslash \left\{U\right\}$. So, we can assume that $p\notin {\mathcal{P}}^{B^j}$, that is, that there is an i ≤ l with c_i ∈ P. Let k ∈ {1,...,l} be the smallest index such that c_k ∈ P. Let $S\in \mathcal{S}$ be such that $c_k\in P_{S\mathcal{S}}^j$. We claim that

$$\text{there is a path}r\in {\mathcal{P}}^{B^j\cup P_{S\mathcal{S}}^j}\text{from}c\text{to}S\text{such that}\mu \left(r\right)={\mu }^C(c,U).$$ (6)

To see this notice first that μ(〈c_k, . . . , c_l〉) = μ^C(c_k, U), since 〈c_k, . . . , c_l〉 is a nice path from c_k to U. Note also that μ^C(c_k, S) ≥ μ^C(c_k, U). This is obvious if S = U. Otherwise, this follows from Fact 3.6, as $c_k\in P_{S\mathcal{S}}^j$. Let q = 〈d₁, . . . , d_m〉 be a nice path from c_k to S. We claim that the path r= 〈c₁, . . . , c_k-1, d₁, . . . , d_m〉 satisfies (6).

Clearly r is a path from c to S and $r\in {\mathcal{P}}^{B^j\cup P_{S\mathcal{S}}^j}$, since {c₁, . . . , c_k-1} ⊂ B^j, while $q\in {\mathcal{P}}^{P_{S\mathcal{S}}^j}$ follows from Fact 3.4. Also, μ(q) = μ^C(c_k, S) μ (c_k, U) = μ(〈c_k, . . . , c_l〉) implies that

$$\mu \left(r\right)=\min \{\mu \left(\langle c_1,\dots ,c_k\rangle \right),\mu \left(q\right)\}\ge \min \{\mu \left(\langle c_1,\dots ,c_k\rangle \right),\mu \left(\langle c_k,\dots ,c_l\rangle \right)\}=\mu \left(p\right).$$

Combining this with μ^C(c, U)≥ μ^C(c, S), which follows from the maximality of μ^C(c, U), we get

$${\mu }^C(c,S)\ge \mu \left(r\right)\ge \mu \left(p\right)={\mu }^C(c,U)\ge {\mu }^C(c,S).$$

Thus, μ(r) = μ^C(c, U), completing the proof of (6).

To finish the proof of the theorem, notice that, by (6), for every $T\in \mathcal{S}\backslash \left\{S\right\}$ we have ${\mu }^C(c,T)\le {\mu }^C(c,U)=\mu \left(r\right)\le {\mu }^{B^j\cup P_{S\mathcal{S}}^j}(c,S)\le {\mu }^{C\backslash P_{T\mathcal{S}}^j}(c,S)$ insuring that $c\notin Q_{T\mathcal{S}}^j$.

3.2 Alternative definitions of $P_{S\mathcal{S}}^j$

Theorem 3.7

Let j ∈ {0, 1, 2, . . .}, $B^j=C\backslash {\bigcup }_{S\in \mathcal{S}}{P}_{S\mathcal{S}}^j$, and $S\in \mathcal{S}$. If

$$R=\{c\in B^j:{\mu }^C(c,S)>{\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)\backslash \text{for every}\backslash T\in \mathcal{S}\backslash \left\{S\right\}\},$$

$$W=\{c\in B^j:{\mu }^{B^j\cup P_{S\mathcal{S}}^j}(c,S)>{\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)\text{for every}T\in \mathcal{S}\backslash \left\{S\right\}\},$$

$$Z=\{c\in B^j:{\mu }^{B^j\cup P_{S\mathcal{S}}^j}(c,S)>{\mu }^{B^j\cup P_{T\mathcal{S}}^j}(c,T)\text{for every}T\in \mathcal{S}\backslash \left\{S\right\}\},$$

then $Q_{S\mathcal{S}}^j=R=W=Z$.

Proof

Since

$$Q_{S\mathcal{S}}^j=\{c\in C\backslash P_{S\mathcal{S}}^j:{\mu }^C(c,S)>{\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)\text{for every}T\in \mathcal{S}\backslash \left\{S\right\}\},$$

by Theorem 2.4 we have $Q_{S\mathcal{S}}^j\subset B^j\subset C\backslash P_{S\mathcal{S}}^j$. So, $Q_{S\mathcal{S}}^j=Q_{S\mathcal{S}}^j\cap B^j=R$.

Clearly W ⊂ R, since ${\mu }^C(c,S)\ge {\mu }^{B^j\cup P_{S\mathcal{S}}^j}(c,S)$. To see that R ⊂ W take a $c\in R=Q_{S\mathcal{S}}^j$. Let p be a nice path from c to S and notice that, by Fact 3.4,

$${\mu }^C(c,S)=\mu \left(p\right)\le {\mu }^{B^j\cup P_{S\mathcal{S}}^j}(c,S)\le {\mu }^C(c,S).$$

This implies that c ∈ W . So $W=R=Q_{oS}^j$. Now, in order to prove the theorem it is enough to show that W = Z.

By Theorem 2.4, we have $B^j\cup P_{T\mathcal{T}}^j\subset C\backslash P_{S\mathcal{S}}^j$ for every $T\in \mathcal{S}\backslash \left\{S\right\}$. Thus, ${\mu }^{B^j\cup P_{T\mathcal{S}}^j}(c,T)\le {\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)$ for every $T\in \mathcal{S}\backslash \left\{S\right\}$ and c ∈ C. So, W ⊂ Z.

To see that Z ⊂ W take a c ∈ Z and by way of contradiction assume c ∉ W. Then, there is a $T\in \mathcal{S}\backslash \left\{S\right\}$ such that ${\mu }^{B^j\cup P_{S\mathcal{S}}^j}(c,S)\le {\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)$. Also, ${\mu }^{B^j\cup P_{S\mathcal{S}}^j}(c,S)>{\mu }^{B^j\cup P_{T\mathcal{S}}^j}(c,T)$ since c ∈ Z. So, ${\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)>{\mu }^{B^j\cup P_{T\mathcal{S}}^j}(c,T)$.

Let p = 〈c₁ , . . . , c_l〉 be a nice path in $C\backslash P_{S\mathcal{S}}^j$ from c to T. Notice that p cannot be a path contained in $B^j=C\backslash \backslash {\bigcup }_{S\in \mathcal{S}}{P}_{S\mathcal{S}}^j$, since this would imply ${\mu }^{B^j\cup P_{T\mathcal{S}}^j}(c,T)\ge {\mu }^{B^j}(c,T)\ge \mu \left(p\right)={\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)$ which contradicts the inequality ${\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)>{\mu }^{B^j\cup P_{T\mathcal{S}}^j}(c,T)$. Thus, p intersects ${\bigcup }_{S\in \mathcal{S}}{P}_{S\mathcal{S}}^j$. Let k ∈ {1, . . . , l} be the smallest index such that $c_k\in {\bigcup }_{S\in \mathcal{S}}{P}_{S\mathcal{S}}^j$. Let $U\in \mathcal{S}$ be such that $c_k\in P_{U\mathcal{S}}^j$. Then U ≠ S, since $p\in {\mathcal{P}}^{C\backslash P_{S\mathcal{S}}^j}$. If U = T, then $p\in B^j\cup P_{T\mathcal{S}}^j$ since 〈c_k, . . . , c_l〉 be a nice path from $c_k\in P_{U\mathcal{S}}^j=P_{T\mathcal{S}}^j$ to T. Thus, ${\mu }^{B^j\cup P_{T\mathcal{S}}^j}(c,T)\ge \mu \left(p\right)={\mu }^{C\backslash P_{oS}^j}(c,T)$ which contradicts the inequality ${\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)>{\mu }^{B^j\cup P_{T\mathcal{S}}^j}(c,T)$. Thus, we can assume that U ≠ T.

Let q be a nice path from $c_k\in P_{U\mathcal{S}}^j$ to U. Then, by Fact 3.4, $q\in {\mathcal{P}}^{P_{U\mathcal{S}}^j}$. Also, by Fact 3.6, μ^C(c_k, U) ≥ μ^C(c_k, T). Then

$$\mu \left(q\right)={\mu }^C(c_k,U)\ge {\mu }^C(c_k,T)\ge \mu \left(\langle c_k,\dots ,c_l\rangle \right)\ge \mu \left(p\right).$$

Thus, if r = 〈c₁, . . . , c_k-1〉 + q, then μ(r) ≥ μ(p) and $r\in {\mathcal{P}}^{B^j\cup P_{U\mathcal{S}}^j}$. So

$${\mu }^{B^j\cup P_{U\mathcal{S}}^j}(c,U)\ge \mu \left(r\right)\ge \mu \left(p\right)={\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,T)\ge {\mu }^{B^j\cup P_{S\mathcal{S}}^j}(c,S),$$

contradicting c ∈ Z.

Theorem 3.7 justifies our earlier claim that the iterative definition of $P_{A\mathcal{S}}^{j+1}$ can be obtained by using an approach as in the formula for $P_{sS}^{\prime }$ instead of the one in the formula for $P_{sS}^{+}$. More precisely, we have $P_{A\mathcal{S}}^{j+1}=P_{A\mathcal{S}}^j\cup Z_{A\mathcal{S}}^j$, where

$$Z_{A\mathcal{S}}^j=\{c\in B^j:{\mu }^{B^j\cup P_{S\mathcal{S}}^j}(c,A)>{\mu }^{B^j\cup P_{T\mathcal{S}}^j}(c,T)\text{for every}T\in \mathcal{S}\backslash \left\{A\right\}\}.$$

Recall also that in (2) we defined ${\mu }^A(c,d)=\max \{\mu \left(p\right):p\in {\mathcal{P}}_{c,d}^A\}$ only for spels c, d ∈ A, since in any other case the sets ${\mathcal{P}}_{c,d}^A$ and $\{\mu \left(p\right):p\in {\mathcal{P}}_{c,d}^A\}$ are empty. However, it is standard to define max ∅ to equal -∞ With this agreement in hand, we can consider μ^A given by (2) as a function from C × C into [-∞, ∞]. Then the definition of $P_{A\mathcal{S}}^{j+1}$ can be written in a slightly more compact form:

$$P_{A\mathcal{S}}^{j+1}=\{c\in C:{\mu }^C(c,A)>{\mu }^{C\backslash P_{A\mathcal{S}}^j}(c,T)\text{for every}T\in \mathcal{S}\backslash \left\{A\right\}\}.$$ (7)

The formula is valid since $c\in P_{A\mathcal{S}}^j$ if and only if ${\mu }^{C\backslash P_{A\mathcal{S}}^j}(c,T)=-\infty$ for every $T\in \mathcal{S}\backslash \left\{A\right\}$.

For A, B, D ⊂ C let

$$\begin{array}{cc}\hfill & \hfill \\ \hfill P_{AB}^D& =\{c\in C:{\mu }^C(c,A)>{\mu }^{C\backslash D}(c,b)\text{for every}b\in B\}\hfill \\ \hfill & =\{c\in C:{\mu }^C(c,A)>{\mu }^{C\backslash D}(c,B)\}.\hfill \end{array}$$

We are introducing this notation since it is easier to work with it (see Fact 3.8) than with the other definitions of $P_{A\mathcal{S}}^{j+1}$, including (7). At the same time $P_{A\mathcal{S}}^{j+1}$ can be easily expressed in this language:

$$P_{A\mathcal{S}}^{j+1}=P_{AB}^D,$$

where $D=P_{A\mathcal{S}}^j$ and $B=\bigcup (\mathcal{S}\backslash \left\{A\right\})$.

3.3 The robustness results

We start here with a list of the properties of $P_{AB}^D$.

Fact 3.8

Let A, B, D, V ⊂ C. Then,

1. $P_{AB}^D={\bigcap }_{b\in B}{P}_{A\left\{b\right\}}^D$,

2. $P_{A{B}^{\prime }}^D\supseteq P_{AB}^D$ for every B^’ ⊂ B,

3. $P_{A^{\prime }B}^D\subseteq P_{AB}^D$ for every A^’ ⊂ A,

4. $P_{AB}^{D^{\prime }}\subseteq P_{AB}^D$ for every D^’ ⊂ D,

5. If $D=P_{A\left\{B\right\}}^k$ for some k ∈{0, 1, 2, . . .} and $R\subseteq A\cup P_{AB}^D$, then $P_{RB}^D\subseteq P_{AB}^D$.

Proof

(a) is obvious from the definition of $P_{AB}^D$. (b) follows immediately from (a). (c) holds, since μ^C(c, A) ≥ μ^C(c, A^’). To see that (d) holds notice that D^’⊂ D implies C\D^’⊃ C\D. Thus, by (3), μ^C\D’(c, b) ≥ μ^C\D(c, b), implying (d).

(e) Fix a $c\in P_{RB}^D$ and a b ∈ B. We need to show that

$${\mu }^C(c,A)>{\mu }^{C\backslash D}(c,b).$$ (8)

Notice that μ^C(c, R) > μ^C\D(c, b), since $c\in P_{RB}^D$. Let p = 〈c₁, . . . , c_l〉 be a strongest path from c to R and let m ∈ {1,...,l}be minimal such that r = c_m ∈ R. Then μ^C (c, r) ≥ μ(〈 c₁,...,c_m〉) ≥ μ(p)= μ^C (c, R) ≥ μ^C(C, r). Thus, we have μ(〈c₁,..c_m 〉) = μ^C (c, R) > μ^C\D (c,b). If r ∈ A, then μ^C (C, A) ≥ μ^C (c, r) > μ^C\D (c, b), proving (8). So, we can assume that $r\in P_{AB}^D=P_{A\left\{B\right\}}^{k+1}={\bigcup }_{n\le k}{Q}_{A\left\{B\right\}}^n$. Thus, there exists an n ≤ k with the property that $r\in Q_{A\left\{B\right\}}^n=\{c\in C\backslash P_{A\left\{B\right\}}^n:{\mu }^C(c,A)>{\mu }^{C\backslash P_{A\left\{B\right\}}^n}(c,b)\text{for every}b\in B\}$. In particular,

$${\mu }^C(r,A)>{\mu }^{C\backslash P_{A\left\{B\right\}}^n}(r,b).$$ (9)

Also, since $r\in C\backslash P_{A\left\{B\right\}}^n$, path 〈c₁, . . . , c_m〉 is in $C\backslash P_{A\left\{B\right\}}^n$. So, by Fact 3.1,

$${\mu }^{C\backslash P_{A\left\{B\right\}}^n}(c,r)={\mu }^C(c,r)>{\mu }^{C\backslash D}(c,b).$$ (10)

Next we will prove that

$${\mu }^C(r,A)>{\mu }^{C\backslash D}(c,b).$$ (11)

If ${\mu }^{C\backslash P_{A\left\{B\right\}}^n}(c,r)>{\mu }^{C\backslash P_{A\left\{B\right\}}^n}(r,b)$, then, by (4), ${\mu }^{C\backslash P_{A\left\{B\right\}}^n}(r,b)={\mu }^{C\backslash P_{A\left\{B\right\}}^n}(c,b)$. So, by (9), ${\mu }^C(r,A)>{\mu }^{C\backslash P_{A\left\{B\right\}}^n}(c,b)\ge {\mu }^{C\backslash D}(c,b)$, where the last inequality is justified by (3) and an inclusion $C\backslash P_{A\left\{B\right\}}^n\supseteq C\backslash P_{A\left\{B\right\}}^k=C\backslash D$. Thus, in this case, (11) holds. So, assume that ${\mu }^{C\backslash P_{A\left\{B\right\}}^n}(c,r)\le {\mu }^{C\backslash P_{A\left\{B\right\}}^n}(r,b)$. Then, by (9) and (10), we get ${\mu }^C(r,A)>{\mu }^{C\backslash P_{A\left\{B\right\}}^n}(r,b)\ge {\mu }^{C\backslash P_{A\left\{B\right\}}^n}(c,r)>{\mu }^{C\backslash D}(c,b)$, finishing the proof of (11).

Now, by (10) and (11), μ^C(c, r) > μ^C\D(c, b) and μ^C(r, A) > μ^C\D(c, b). Let p₁ be a strongest path from c to r and p₂ be a strongest path from r to A. Then μ(p₁+ p₂) = min{μ(p₁), μ(p₂)} = min{μ^C(c, r), μ^C(r, A)} and so

$${\mu }^C(c,A)\ge \mu (p_1+p_2)=\min \{{\mu }^C(c,r),{\mu }^C(r,A)\}>{\mu }^{C\backslash D}(c,b),$$

finishing the proof of (8) and (e).

Lemma 3.9

Let ${\mathcal{S}}_0=\mathcal{S}\backslash \left\{A\right\}$, where $A\in \mathcal{S}$ is fixed. If j, k∈ {0, 1, 2, . . .}, $A\subseteq R\subseteq A\cup P_{A\mathcal{S}}^{k+1}$, and $\mathcal{T}={\mathcal{S}}_0\cup \left\{R\right\}$, then the following holds.

1. $P_{A\mathcal{S}}^j\subset P_{R\mathcal{T}}^j$.

2. $P_{R\mathcal{T}}^j\subseteq P_{A\mathcal{S}}^{k+j}$.

3. If $V\in {\mathcal{S}}_0$, then $P_{V\mathcal{T}}^j\subseteq P_{V\mathcal{S}}^j$.

4. If $V\in {\mathcal{S}}_0$, then $P_{V\mathcal{S}}^j\subseteq P_{V\mathcal{T}}^j$.

5. If either k = 0 or $P_{A\mathcal{S}}^k=P_{A\mathcal{S}}^{k+1}$, then $P_{A\mathcal{S}}^j=P_{R\mathcal{T}}^j$ and $P_{V\mathcal{S}}^j=P_{V\mathcal{T}}^j$ for every j ≥ k and $V\in {\mathcal{S}}_0$. In, particular, $\{P_{S\mathcal{S}}^I:S\in \mathcal{S}\}=\{P_{T\mathcal{T}}^I:T\in \mathcal{T}\}$. Moreover, if k = 0, then also all intermediate segmentations are equal: $\{P_{S\mathcal{S}}^j:S\in \mathcal{S}\}=\{P_{T\mathcal{T}}^j:T\in \mathcal{T}\}$ for all j ≥ 0.

Proof

All properties (a)-(d) are proved by induction on j and they are obvious for j = 0.

(a) To make an inductive step, assume that $D^{\prime }=P_{A\mathcal{S}}^j$ is a subset of $D=P_{R\mathcal{T}}^j$ and put $B=\bigcup {\mathcal{S}}_0$. Since A ⊂ R, conditions (c) and (d) from Fact 3.8 give $P_{A\mathcal{S}}^{j+1}=P_{AB}^{D^{\prime }}\subseteq P_{RB}^{D^{\prime }}\subseteq P_{RB}^D=P_{R\mathcal{T}}^{j+1}$.

(b) To make an inductive step, assume that $D^{\prime }=P_{R\mathcal{T}}^j$ is a subset of $D=P_{A\mathcal{S}}^{k+j}$. First note that $\mathcal{T}\backslash \left\{R\right\}={\mathcal{S}}_0$. To see this, it is enough to show that $R\notin {\mathcal{S}}_0$. But if there is an $S\in {\mathcal{S}}_0$ such that S = R, then $S\backslash A\subseteq P_{A\mathcal{S}}^{k+1}\cap (E\cup P_{S\mathcal{S}}^1)$, where E is as in Lemma 3.2. Since, by Lemma 3.2 and Theorem 2.4, this last set is empty, we get S ⊆ A. But we have also A ⊆ R = S, so $A=S\in {\mathcal{S}}_0$, contradicting the definition of ${\mathcal{S}}_0$.

Let $B=\bigcup {\mathcal{S}}_0=\bigcup (\mathcal{S}\backslash \left\{A\right\})=\bigcup (\mathcal{T}\backslash \left\{R\right\})$, put $D^{″}=P_{A\mathcal{S}}^k\subseteq D$, and notice that $R\subseteq A\cup P_{A\mathcal{S}}^{k+1}=A\cup P_{AB}^{D^{″}}\subseteq A\cup P_{AB}^D$ follows from from Fact 3.8(d). Then conditions (d) and (e) from Fact 3.8 give $P_{R\mathcal{T}}^{j+1}=P_{RB}^{D^{\prime }}\subseteq P_{RB}^D\subseteq P_{AB}^D=P_{A\mathcal{S}}^{k+j+1}$, completing the proof of (b).

(c) To make an inductive step, assume that it is true for some j, that is, that $D=P_{V\mathcal{S}}^j$ contains $D^{\prime }=P_{V\mathcal{T}}^j$. Since $B^{\prime }=\bigcup (\mathcal{S}\backslash \left\{V\right\})=A\cup \bigcup ({\mathcal{S}}_0\backslash \left\{V\right\})$ is a subset of $B=\bigcup (\mathcal{T}\backslash \left\{V\right\})=R\cup \bigcup ({\mathcal{S}}_0\backslash \left\{V\right\})$, conditions (b) and (d) from Fact 3.8 give $P_{V\mathcal{T}}^{j+1}=P_{VB}^{D^{\prime }}\subseteq P_{V{B}^{\prime }}^{D^{\prime }}\subseteq P_{V{B}^{\prime }}^D=P_{V\mathcal{S}}^{j+1}$.

(d) To make an inductive step, assume that $D^{\prime }=P_{V\mathcal{S}}^j$ is a subset of $D=P_{V\mathcal{T}}^j$. Let $B_0=\bigcup ({\mathcal{S}}_0\backslash \left\{V\right\})$. Then $B^{\prime }=\bigcup (\mathcal{S}\backslash \left\{V\right\})=B_0\cup A$ is a subset of $B=\bigcup (\mathcal{T}\backslash \left\{V\right\})=B_0\cup R$. Notice that it is enough to prove that $P_{V{B}^{\prime }}^{D^{\prime }}\subseteq P_{VB}^{D^{\prime }}$ since this and Fact 3.8(d) imply $P_{V\mathcal{S}}^{j+1}=P_{V{B}^{\prime }}^{D^{\prime }}\subseteq P_{VB}^{D^{\prime }}\subseteq P_{VB}^D=P_{V\mathcal{T}}^{j+1}$.

To show $P_{V{B}^{\prime }}^{D^{\prime }}\subseteq P_{VB}^{D^{\prime }}$ take a $c\in P_{V\mathcal{S}}^{j+1}=P_{V{B}^{\prime }}^{D^{\prime }}$. Then μ^C(c, V) > μ^C\D’(c, B’). We need to prove that

$${\mu }^C(c,V)>{\mu }^{C\backslash D^{\prime }}(c,B).$$ (12)

If μ^C\D’(c, B’) ≥ μ^C\D’(c, B), then μ^C(c, V) > μ^C\D’(c, B’) ≥ μ^C\D’(c, B) proving inequality (12). Thus, by way of contradiction, we can assume that μ^C\D’ (c, B’) < μ^C\D’ (c, B). We will find v ∈ V , r ∈ B, a ∈ A, and D₀ ⊆ C such that

$${\mu }^{C\backslash D^{\prime }}(c,a)={\mu }^{C\backslash D^{\prime }}(r,a)={\mu }^C(r,a)>{\mu }^{C\backslash D_0}(r,v)={\mu }^C(c,V).$$ (13)

First notice that (13) gives us a desired contradiction, since then a ∈ B’ implies μ^C\D’(c, B’) ≥ μ^C\D’(c, a) > μ^C(c, V) contradicting $c\in P_{V{B}^{\prime }}^{D^{\prime }}$. Thus to finish the proof it is enough to show (13).

First, we will choose an appropriate r. Let p₀ = 〈c₁, . . . , c_l〉 be a strongest path in C\ D’ from c to B and let m ∈ {1, . . . , l} be minimal such that r = c_m ∈ B. Then μ^C\D’(c, r) ≥ μ(p₀) = μ^C\D’ (c, B) ≥ μ^C\D’ (c, r), where p = 〈C₁, ..., C_m 〉. In particular, μ(p) = μ^C\D’(c, r) = μ^C\D’(c, B).

Let a ∈ A be such that there is a path q from r to a which is a nice path from r to A. Since μ^C\D’(c, r) = μ^C\D’(c, B) > μ^C\D’(c, B’) ≥ μ^C\D’(c, a) the equation μ^C\D’(c, a) = μ^C\D’(r, a) follows from (4).

To show μ^C\D’(r, a) = μ^C(r, a) note that $r\in B\backslash B^{\prime }=R\backslash A\subseteq P_{A\mathcal{S}}^{k+1}\subseteq P_{A\mathcal{S}}^I$, since μ^C\D’(c, r) = μ^C\D’(c, B) > μ^C\D’(c, B’). In particular, since q is a nice path from r to A, then, by Fact 3.4, q is in $P_{A\mathcal{S}}^I\subseteq C\backslash P_{V\mathcal{S}}^I\subseteq C\backslash P_{V\mathcal{S}}^j=C\backslash D^{\prime }$. As μ^C(r, a) = μ(q), Fact 3.1 implies μ^C\D’(r, a) = μ^C (r, a).

Next, we need to choose D₀ and v ∈ V. Let q be a path from c to v which is a nice path from c to V . Then μ^C(c, v) = μ^C(c, V). Since $r\in P_{A\mathcal{S}}^{k+1}={\bigcup }_{n\le k}{Q}_{A\mathcal{S}}^n$, there is an n ≤ k with $r\in Q_{A\mathcal{S}}^n=\{c\in C\backslash P_{A\mathcal{S}}^n:{\mu }^C(c,A)>{\mu }^{C\backslash P_{A\mathcal{S}}^n}(c,\bigcup {\mathcal{S}}_0)\}$. We put $D_0=P_{A\mathcal{S}}^n$. Then ${\mu }^C(r,a)={\mu }^C(r,A)>{\mu }^{C\backslash D_0}(r,\bigcup {\mathcal{S}}_0)\ge {\mu }^{C\backslash D_0}(r,v)$.

To prove μ^C\D₀(r, v) = μ^C(c, V) it is enough to show μ^C\D₀(r, v) = μ^C\D₀(c, v) and μ^C\D₀(c, v) = μ^C(c, V). Recall that μ(p) = μ^C\D’(c, r) = μ^C\D’(c, B), where p is in $C\backslash D_0=C\backslash P_{A\mathcal{S}}^n$ since {c₁, . . . , c_m-1} is disjoint with $B\supseteq P_{A\mathcal{S}}^n$, while $c_m=r\in Q_{A\mathcal{S}}^n\subset C\backslash P_{A\mathcal{S}}^n$. By this and a part of (13) proved so far μ^C\D₀(c, r)≥μ(p) = μ^C\D’(c, B) > μ^C\D’(c, B’)≥ μ^C\D’(c, a) > μ^C\D₀(r, v). So, by (4), we get μ^C\D₀(r, v) = μ^C\D₀(c, v).

The equation μ^C\D₀(c, v) = μ^C(c, V) follows from Fact 3.1, since q, as a nice path from $c\in P_{V\mathcal{S}}^{j+1}$ to V , is in $P_{V\mathcal{S}}^{j+1}\subseteq C\backslash P_{A\mathcal{S}}^n=C\backslash D_0$. This finishes the proof of (d).

(e) Parts (c) and (d) imply that $P_{V\mathcal{S}}^j=P_{V\mathcal{T}}^j$ for every $V\in {\mathcal{S}}_0$ and j ≥ 0.

If j ≥ k, then $P_{A\mathcal{S}}^j=P_{R\mathcal{T}}^j$ follows from $P_{R\mathcal{T}}^j\subseteq P_{A\mathcal{S}}^{k+j}=P_{A\mathcal{S}}^j\subseteq P_{R\mathcal{T}}^j$. Here $P_{R\mathcal{T}}^j\subseteq P_{A\mathcal{S}}^{k+j}$ follows from (b); equation $P_{A\mathcal{S}}^{k+j}=P_{A\mathcal{S}}^j$ is obvious when k = 0 and is proved by an easy induction when $P_{A\mathcal{S}}^k=P_{A\mathcal{S}}^{k+1}$; inclusion $P_{A\mathcal{S}}^j\subseteq P_{R\mathcal{T}}^j$ is a restatement of (a).

Proof of Theorem 2.5

First notice that Lemma 3.9(e) implies that (*) the theorem is true if T_i = S_i for every i ≥ 2.

Now, the general form of the theorem follows from (*) by induction on m. Indeed, for 0 ≤ l ≤ m and i ∈ {1, . . . , m} put $T_i^l=T_i$ for i ≤ l and $T_i^l=S_i$ otherwise. Let ${\mathcal{T}}_l=\{T_1^l,\dots ,T_m^l\}$. Then ${\mathcal{T}}_0=\mathcal{S}$, ${\mathcal{T}}_m=\mathcal{T}$. and to every pair $\langle {\mathcal{T}}_k,{\mathcal{T}}_{k+1}\rangle$ we can apply (*). Thus, applying it m-times, we get that $P_{S_i\mathcal{S}}^j=P_{T_i^0{\mathcal{T}}_0}^j=P_{T_i^1{\mathcal{T}}_1}^j=\cdots =P_{T_i^m{\mathcal{T}}_m}^j=P_{T_i\mathcal{T}}^j$ for every i ∈ {1, . . . m} and an appropriate j.

Proof of Corollary 2.7

Let U_i = {s_i, t_i} and put $\mathcal{U}=\{U_1,\dots ,U_m\}$, $\mathcal{S}=\{\left\{s_1\right\},\dots ,\left\{s_m\right\}\}$, and $\mathcal{T}=\{\left\{T_1\right\},\dots ,\left\{t_m\right\}\}$. Then, by Theorem 2.5 (version with k = 1), for every i ∈ {1, . . . ,m} we have $P_{s_{i}S}^j=P_{\left\{s_i\right\}\mathcal{S}}^j=P_{U_i\mathcal{U}}^j$. To finish the proof is enough to show that

$$s_i\in P_{t_{i}T}^1\text{for every}i\in \{1,\dots ,m\},$$ (†)

since then, again by Theorem 2.5, $P_{t_{i}T}^j=P_{\left\{t_i\right\}\mathcal{T}}^j=P_{U_i\mathcal{U}}^j=P_{s_{i}S}^j$ for every i ∈ {1, . . . , m}.

First notice that for every distinct i, k ∈ {1, . . . , m}

$${\mu }^C(s_i,t_k)={\mu }^C(t_i,s_k).$$ (14)

Indeed, since $t_k\in P_{s_{k}S}^1$ we have μ^C (t_k, s_k) > μ^C (t_k, s_i). Therefore, by (4), μ^C(t_k, s_i) = μ^C(s_i, s_k). Similarly, $t_i\in P_{s_{i}S}^1$ implies μ^C(t_i, s_i) > μ^C (t_i, s_k) so, by (4), μ^C(t_i, s_k) = μ^C(s_i, s_k). This proves (14).

Now, to prove (†) take distinct i, k ∈ {1, . . . , m}. We need to show that μ ^C (s_i, t_i) > μ^C(s_i, t_k). But $t_i\in P_{s_{i}S}^1$ implies μ^C (t_i, s_i) > μ^C (t_i, s_k). Combining this with (14) gives μ^C(s_i, t_i) = μ^C(t_i, s_i) > μ^C(t_i, s_k) = μ^C(s_i, t_k).

3.4 How to choose seed generating families S?

In a general setting, the title question is well beyond the scope of this paper. What we will discuss here is only its very restricted version: Given $\mathcal{S}$, how to modify it to get either the same or a better segmentation?

The first of the results presented here estimates the size of minimal subsets T_S of $P_{S\mathcal{S}}^1$ for which the segmentations $\{P_{S\mathcal{S}}^I:S\in \mathcal{S}\}$ and $\{P_{T_S\mathcal{T}}^I:S\in \mathcal{S}\}$ are equal, where $\mathcal{T}=\{T_S:S\in \mathcal{S}\}$.

Proposition 3.10

For every $A\in \mathcal{S}$ let ${\mathcal{U}}_A=\{P_{\left\{s\right\}{\mathcal{S}}_A}^1:s\in A\}\backslash \left\{\varnothing \right\}$, where ${\mathcal{S}}_A=\mathcal{S}\backslash \left\{A\right\}$. Then

1. Sets in ${\mathcal{U}}_A$ are pairwise disjoint.

2. If $T\subseteq P_{A\mathcal{S}}^1=P_{A{\mathcal{S}}_A}^1$, then $P_{T{\mathcal{S}}_A}^1=P_{A{\mathcal{S}}_A}^1$ if and only if T intersects every $P\in {\mathcal{U}}_A$.

In particular, if for every $A\in \mathcal{S}$ we choose a $T_A\subseteq P_{A\mathcal{S}}^1$ which intersects every $P\in {\mathcal{U}}_A$ and put $\mathcal{T}=\{T_A:A\in \mathcal{S}\}$, then $\{P_{S\mathcal{S}}^j:S\in \mathcal{S}\}=\{P_{T_s\mathcal{T}}^j:S\in \mathcal{S}\}$ for every j ≥ 0.

Proof

(a) If $u\in P_{\left\{s\right\}{\mathcal{S}}_A}^1\cap P_{\left\{t\right\}{\mathcal{S}}_A}^1$ for some s, t ∈ A, then, by Corollary 2.7, $P_{\left\{s\right\}{\mathcal{S}}_A}^1=P_{\left\{u\right\}{\mathcal{S}}_A}^1=P_{\left\{t\right\}{\mathcal{S}}_A}^1$.

(b) Let A₀ ⊂ A be minimal such that $\{P_{\left\{s\right\}{\mathcal{S}}_A}^1:s\in A_0\}={\mathcal{U}}_A$. By (5) we have $T\subseteq P_{A\mathcal{S}}^1=\bigcup {\mathcal{U}}_A$. Thus, for every t ∈ T there is a unique a_t ∈ A₀ such that $t\in P_{\left\{a_t\right\}{\mathcal{S}}_A}^1$. Note that $P_{\left\{t\right\}{\mathcal{S}}_A}^1=P_{\left\{a_t\right\}{\mathcal{S}}_A}^1$ follows from Corollary 2.7. Let A₁ = {a_t: t ∈ T }. Then, by (5), $P_{T{\mathcal{S}}_A}^1={\bigcup }_{a\in A_1}{P}_{\left\{a\right\}{\mathcal{S}}_A}^1\subseteq {\bigcup }_{a\in A_0}{P}_{\left\{a\right\}{\mathcal{S}}_A}^1=P_{A{\mathcal{S}}_A}^1$ and the equation holds precisely when A₁ = A₀, that is, when T intersects every $P\in {\mathcal{U}}_A$.

The value of Proposition 3.10 comes from the fact that, usually, the size of ${\mathcal{U}}_A$ is quite small, even if the set A is quite big. Note also, that it is possible that the equation $\{P_{S\mathcal{S}}^I:S\in \mathcal{S}\}=\{P_{T_s\mathcal{T}}^I:S\in \mathcal{S}\}$ may hold for sets $T_A\subseteq P_{A\mathcal{S}}^1$ which do not intersect every $P\in {\mathcal{U}}_A$. Such a situation is described in Example 3.16.

Lemma 3.11

Let $A\in \mathcal{S}$ and $E=\{s\in A:{\mu }^C(s,T)=1\text{for some}T\in {\mathcal{S}}_0\}$, where ${\mathcal{S}}_0=\mathcal{S}\backslash \left\{A\right\}$. If A₀ = A\ E, then $P_{A_0{\mathcal{S}}_0}^j=P_{A{\mathcal{S}}_0}^j$ for every j ≥ 0.

Proof

Inclusion $P_{A_0{\mathcal{S}}_0}^j\subseteq P_{A{\mathcal{S}}_0}^j$ follows from Lemma 3.9(a). We just need to show that $P_{A{\mathcal{S}}_0}^j\subseteq P_{A_0{\mathcal{S}}_0}^j$. This will be proved by induction on j ≥ 0.

For j = 0 it is obvious, as both sets are empty. So, assume that for some j we have $P_{A{\mathcal{S}}_0}^j\subseteq P_{A_0{\mathcal{S}}_0}^j$. We need to prove that $P_{A{\mathcal{S}}_0}^{j+1}\subseteq P_{A_0{\mathcal{S}}_0}^{j+1}$. For this, choose a $c\in P_{A{\mathcal{S}}_0}^{j+1}$. We need to show that $c\in P_{A_0{\mathcal{S}}_0}^{j+1}$.

So, fix a $T\in {\mathcal{S}}_0$. We need to prove ${\mu }^C(c,A_0)>{\mu }^{C\backslash P_{A_0{\mathcal{S}}_0}^j}(c,T)={\mu }^{C\backslash P_{A{\mathcal{S}}_0}^j}(c,T)$, where the equation follows from our inductive assumption that $P_{A{\mathcal{S}}_0}^j=P_{A_0{\mathcal{S}}_0}^j$. However, since $c\in P_{A{\mathcal{S}}_0}^{j+1}$, we have ${\mu }^C(c,A)>{\mu }^{C\backslash P_{A{\mathcal{S}}_0}^j}(c,T)$. Thus, to finish the proof, it is enough to show that

$${\mu }^C(c,A_0)\ge {\mu }^C(c,A).$$ (15)

By way of contradiction, assume that (15) is false. Then μ^C(c, A) > μ^C(c, A₀). Let a ∈ A\ A₀ ⊆ E be such that μ^C(c, a) = μ^C(c, A). Let $T\in {\mathcal{S}}_0$ be such that μ^E(a, T) = μ^C(a, T) = 1 and let q be a path in E from a to T with μ(q) = 1. Also, let p = 〈c₁, . . . , c_l〉 be a strongest path from c to a. Thus, μ(p) = μ^C(c, a) = μ^C(c, A) > μ^C(c, A₀). If p is disjoint with $P_{A{\mathcal{S}}_0}^j$ then so is p + q and ${\mu }^{C\backslash P_{A{\mathcal{S}}_0}^j}(c,T)\ge \mu (p+q)=\mu \left(p\right)={\mu }^C(c,A)$ contradicting $c\in P_{A{\mathcal{S}}_0}^{j+1}$. So, assume that p intersects $P_{A{\mathcal{S}}_0}^j=P_{A_0{\mathcal{S}}_0}^j={\bigcup }_{k<j}{Q}_{A_0{\mathcal{S}}_0}^k$. Let k < j be minimal that p intersects $Q_{A_0{\mathcal{S}}_0}^k$ and let n ∈ {1,...,l} be such that $c_n\in Q_{A_0{\mathcal{S}}_0}^k$. Then ${\mu }^C(c_n,A_0)>{\mu }^{C\backslash P_{A{\mathcal{S}}_0}^k}(c_n,T)\ge \mu (\langle c_n,\dots ,c_l\rangle +q)=\mu \left(\langle c_n,\dots ,c_l\rangle \right)\ge \mu \left(p\right)={\mu }^C(c,A)$. Also, μ^C(c, c_n) ≥ μ(〈c₁, . . . , c_n〉) ≥ μ(p) = μ^C(c, A). So, μ^C(c, A₀) ≥ min{μ^C(c, c_n), μ^C(c_n, A₀)} ≥ μ^C(c, A), finishing the proof.

Recall that $E_{\mathcal{S}}={\bigcup }_{A\in \mathcal{S}}\{s\in S:{\mu }^C(s,t)=1\text{for some}t\in T\in \mathcal{S}\backslash \left\{A\right\}\}$.

Proposition 3.12

For every $S\in \mathcal{S}$, there exists a T_S containing $S\backslash E_{\mathcal{S}}$ such that if $\mathcal{T}=\{T_S:S\in \mathcal{S}\}$, then $\bigcup \mathcal{T}=\bigcup \mathcal{S}$, $T\subseteq P_{T\mathcal{T}}^1$ for every $T\in \mathcal{T}$, and $P_{S\mathcal{S}}^j\subseteq P_{T_S\mathcal{T}}^j$ for every $S\in \mathcal{S}$ and j ≥ 0.

Proof

For s ∈ C let [s] = {t ∈ C : μ^C(s, t) = 1}. Thus, each [s] is an equivalence class of an equivalence relation ∼ on C defined by s ∼ t if and only if μ^C(s, t) = 1. In particular, the sets in $\mathcal{F}=\{\left[s\right]\cap \bigcup \mathcal{S}:s\in \bigcup \mathcal{S}\}$ are nonempty and pairwise disjoint. Let $W\subseteq \bigcup \mathcal{S}$ be a selector of $\mathcal{F}$, that is, such that W intersects each $\left[s\right]\cap \bigcup \mathcal{S}$ at precisely one element. Define $T_S=\bigcup \{\left[s\right]\cap \bigcup \mathcal{S}:s\in S\cap W\}$. We will just sketch the proof that these sets are as desired.

Clearly $\bigcup \mathcal{T}=\bigcup \mathcal{S}$, as for every $s\in \bigcup \mathcal{S}$ there are $S\in \mathcal{S}$ and w ∈ W ∩ S such that s ∈ [w], so $s\in \left[w\right]\cap \bigcup \mathcal{S}\subseteq T_S\subseteq \bigcup \mathcal{T}$.

Next, fix an $S\in \mathcal{S}$. To see that $P_{S\mathcal{S}}^j\subseteq P_{T_S\mathcal{T}}^j$ put ${\mathcal{S}}_0=\mathcal{S}\backslash \left\{S\right\}$ and notice that $S\backslash E_{\mathcal{S}}\subseteq T_S$ and that $Z=C\backslash (S\backslash E_{\mathcal{S}})$ contains union of ${\mathcal{T}}_0=\mathcal{T}\backslash \left\{T_S\right\}$. Thus

$$P_{S\mathcal{S}}^j=P_{S{\mathcal{S}}_0}^j=P_{S\backslash E_{\mathcal{S}}{\mathcal{S}}_0}^j=P_{S\backslash E_{\mathcal{S}}\left\{Z\right\}}^j\subseteq P_{T_S\left\{Z\right\}}^j\subseteq P_{T_S{\mathcal{T}}_0}^j=P_{T_S\mathcal{T}}^j.$$

Here, the second equation follows from Lemma 3.11, the first inclusion from Fact 3.8(c), while the second inclusion is a consequence of Fact 3.8(b). The proof of the third equation is very similar to that of Lemma 3.11 and uses the fact that any [c] intersecting Z intersects also $\bigcup {\mathcal{S}}_0$. (This proof relies also on the fact that every strongest path p between spels in [c] is in ${\mathcal{P}}^{\left[c\right]}$ and that $\left[c\right]\cap P_{S\mathcal{S}}^j\ne \varnothing$ implies $\left[c\right]\subseteq P_{S\mathcal{S}}^j$.)

The inclusion $T\subseteq P_{T\mathcal{T}}^1$ follows from Lemma 3.2 and the fact that $E_{\mathcal{T}}=\varnothing$.

3.5 Examples

In this subsection, we will present the examples announced earlier in this paper, which show different limitations for our results. The examples are presented in a graphical form, where vertices represent spels from a given scene while a number next to an edge of a graph represents the affinity between the connected vertices. Lack of an edge between vertices means that the affinity between the spels they represent is equal to 0.

Our first example shows that, unlike a nice path, a strongest path from an $a\in P_{dS}^j$ to d need not to be contained in $P_{dS}^j$.

Example 3.13

Assume that a scene $\mathcal{C}$ contains spels a, b, c, d, and s, connected as in Figure 6(a). Let S = {d, s}. Then $P_{sS}^1=\{c,s\}$ and $P_{dS}^1=\{b,d\}$. Also, $a\in P_{dS}^2$, since ${\mu }^C(a,d)=.5>0={\mu }^{C\backslash P_{dS}^1}(a,s)$. However, the path p = 〈a, b, c, d〉 is strongest between $a\in P_{dS}^2$ and d, but it is not inside $P_{dS}^2$.

Figure 6.

Affinities for Examples 3.13 and 3.14.

The following example shows that the iterative analog of formula (5) is false.

Example 3.14

Assume that a scene $\mathcal{C}$ contains spels s, t, u, and c, connected as in Figure 6(b). Let S = {s, t}, U = {u}, and $\mathcal{S}=\{S,U\}$. Then $P_{U\mathcal{S}}^I=\left\{u\right\}$, $P_{S\mathcal{S}}^1=\{s,t\}$, and $P_{S\mathcal{S}}^I=P_{S\mathcal{S}}^2=\{s,t,c\}$. However, $P_{s\{s,u\}}^I=P_{s\{s,u\}}^1=\left\{s\right\}$ and $P_{t\{t,u\}}^I=P_{t\{t,u\}}^1=\left\{t\right\}$, showing that ${\bigcup }_{s\in S}{P}_{s\{s,u\}}^I=\{s,t\}\ne \{s,t,c\}=P_{S\mathcal{S}}^I$.

The following example shows that, in Corollary 2.7, we cannot weaken the assumptions to $t_i\in P_{s_{i}S}^I$, even if we also weaken the conclusion to $P_{t_{i}T}^I=P_{s_{i}S}^I$.

Example 3.15

Assume that a scene $\mathcal{C}$ contains spels a, s, and t, connected as in Figure 7(a). Let S = {s, t}. Then for j > 1 we have $P_{sS}^1=\left\{s\right\}⊊P_{sS}^j=\{a,s\}$ and $P_{tS}^1=P_{tS}^j=\left\{t\right\}$. However, if we replace a seed s with $a\in P_{sS}^2$ and put T = {a, t}, then for every i > 0 and j > 1, we have $P_{tT}^i=P_{tS}^i=\left\{t\right\}$, and $P_{aT}^i=\left\{a\right\}\ne P_{sS}^j$.

Figure 7.

Affinities for Examples 3.15 and 3.16.

The next example shows the limitations of the result from Proposition 3.10.

Example 3.16

Assume that a scene $\mathcal{C}$ contains spels s, t, u, and c, connected as in Figure 7(b). Let S = {s, t}, U = {u}, and $\mathcal{S}=\{S,U\}$. Then $P_{sU}^1=\{s,c\}$ is disjoint with $P_{tU}^1=\left\{t\right\}$. However, although T_S = {s} does not intersect $P_{tU}^1$, we still have $P_{T_{S}U}^I=P_{tU}^2=\{s,c,t\}=P_{S\mathcal{S}}^I$.

4 The algorithm

In this section, we present an algorithm, called κIRMOFC (abbreviation for iterative relative multi object fuzzy connectedness), allowing a set of seeds for each object. Within this algorithm, the algorithm κFOEMS as described in [18] for multi seeded AFC is called. κFOEMS takes as an input a given scene $\mathcal{C}=\langle C,f\rangle$, an affinity function κ, and a set S ⊂ C of seeds. Its output is a connectivity scene ${\mathcal{C}}_{\kappa ,S}=\langle C,f_{\kappa ,S}\rangle$, where f_κ,S(c) represents the strength of a κ-strongest path from c to S. Aspects related to the computational efficiency of algorithm κFOEMS have been addressed in [20,21]. For A ∈ C, by the restriction of κ to A we will understand an affinity κ’ on C such that, for every distinct c, d ∈ C, we have κ’(c, d) = κ(c, d) for c, d ∈ A, and κ(c, d) = 0 otherwise. In the algorithm κIRMOFC, we will use the fact that, for distinct c, d ∈ C, the number μ^A(c, d) is equal to μ^C(c, d) calculated with respect to the restriction of κ to A.

Algorithm κIRMOFC

Input

$\mathcal{C}=\langle C,f\rangle$, κ as defined in Section 2, a family $\mathcal{S}=\{S_1,S_2,\dots ,S_m\}$ of pairwise disjoint sets of seed spels such that κ(s, t) < 1 for any s and t from distinct sets from $\mathcal{S}$.

Output

For each S in $\mathcal{S}$, iteratively defined fuzzy κ-object $P_{S\mathcal{S}}^I$ containing S and relative to a background containing $W=\bigcup (\mathcal{S}\backslash \left\{S\right\})$.

Auxiliary Data Structures

For each $S\in \mathcal{S}$, the κ-connectivity scene ${\mathcal{C}}_{\kappa ,S}=\langle C,f_{\kappa ,S}\rangle$, the κ_S-connectivity scenes ${\mathcal{C}}_{{\kappa }_S,W}=\langle C,f_{{\kappa }_S,W}\rangle$, where κ_S is the restriction of κ to $C\backslash P_{S\mathcal{S}}^j$, and the temporary scenes ${\mathcal{C}}_S=\langle C,f_S\rangle$ such that f_S corresponds to the characteristic function of $P_{S\mathcal{S}}^j$. Index j refers to the iteration level; that is, the number of completed while loops, in Steps 5-16, for each fixed S.

begin

1. for each $S\in \mathcal{S}$ do

2. compute ${\mathcal{C}}_{\kappa ,S}$ by using κFOEMS;

3. set all elements of ${\mathcal{C}}_S$ to 0 (this corresponds to setting $P_{S\mathcal{S}}^0=\varnothing$);

4. set κ_S = κ and flag = true;

5. while flag = true do

6. set flag = false;

7. compute ${\mathcal{C}}_{{\kappa }_S,W}$ by using κFOEMS;

8. for all c ∈ C do

9. if f_S(c) = 0 and f_κ,S(c) > f_κS,W(c) then

10. set f_S(c) = 1;

11. set flag = true;

12. for all d ∈ C, d ≠ c, do

13. set κ_S(c, d) = 0;

14. endfor;

15. endif;

16. endfor;

17. endwhile;

18. output $P_{S\mathcal{S}}^I=\{c\in C:f_S\left(c\right)=1\}$;

19. endfor;

end

In the above algorithm each run of the loop of Steps 2-18 is independent of the other runs and can be considered as a subroutine (similar to algorithm κIFROE from [15]) which for seeds S and W returns an IRFC object containing S and relative to a background containing W. The value of flag determines whether in the previous run of the loop in Steps 6-16 there was at least one spel which was added to the object $P_{S\mathcal{S}}^I$ (i.e., changed value of f_S(c) from 0 to 1). Since the number of spels c ∈ C is finite, eventually no change is made and the loop terminates. Each time the algorithm enters the loop in Steps 6-16, f_S is the characteristic function of the previous stage, say jth stage, $P_{S\mathcal{S}}^j$ is the approximation of $P_{S\mathcal{S}}^I$, while κ_S is the restriction of κ to $C\backslash P_{S\mathcal{S}}^j$. Notice that this situation remains true when Steps 6-16 of the next stage are completed. Indeed, the loop of Steps 9-15 is entered for each c and the if statement is performed only if c was not yet in $P_{S\mathcal{S}}^j$, but the inequality ${\mu }^C(c,S)=f_{\kappa ,S}\left(c\right)>f_{{\kappa }_S,W}\left(c\right)={\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,W)$ indicates that c is added to $P_{S\mathcal{S}}^{j+1}$. This is done at Step 10, while the loop in Steps 12-14 restricts current κ_S to C\ {c}. Thus, when Steps 9-15 are finished, all seeds from $C\backslash P_{S\mathcal{S}}^j$ for which ${\mu }^C(c,S)>{\mu }^{C\backslash P_{S\mathcal{S}}^j}(c,W)$ are added to $P_{S\mathcal{S}}^{j+1}$, and the new κ_S is the restriction of the old κ_S to ${\bigcap }_{c\in P_{S\mathcal{S}}^{j+1}\backslash P_{S\mathcal{S}}^j}(C\backslash \left\{c\right\})$, so it is the restriction of κ to the set $(C\backslash P_{S\mathcal{S}}^j)\cap {\bigcap }_{c\in P_{S\mathcal{S}}^{j+1}\backslash P_{S\mathcal{S}}^j}(C\backslash \left\{c\right\})=C\backslash P_{S\mathcal{S}}^{j+1}$. The argument from this paragraph justifies the following result.

Proposition 4.1

For any scene $\mathcal{C}=\langle C,f\rangle$ over $\langle {\mathbb{Z}}^n,\alpha \rangle$, for any fuzzy affinity relation κ in $\mathcal{C}$, and for any non-empty family of $\mathcal{S}$ non-empty pairwise disjoint subsets of C such that κ(s, t) < 1 for any s and t from distinct sets from $\mathcal{S}$, algorithm κIRFCMO terminates, $S\subset P_{S\mathcal{S}}^I$ for every $S\in \mathcal{S}$, and the family $\{P_{S\mathcal{S}}^I:S\in \mathcal{S}\}$ is the IRFC segmentation of $\mathcal{C}$.

5 Results and evaluation

5.1 Qualitative Evaluation

In this section, we present the results of application of the IRFC method and compare them with the results obtained by using RFC. Specifically, we present qualitative results of the following three experiments: (1) segmentation of individual vertebra from a 3D CT scene of a human cervical spine; (2) artery/vein separation in contrast-enhanced MR angiograms; (3) segmentation of white matter (WM), gray matter (GM), and cerebro-vascular fluid (CSF) in simulated MR scenes obtained from BrainWebMR simulator [22].

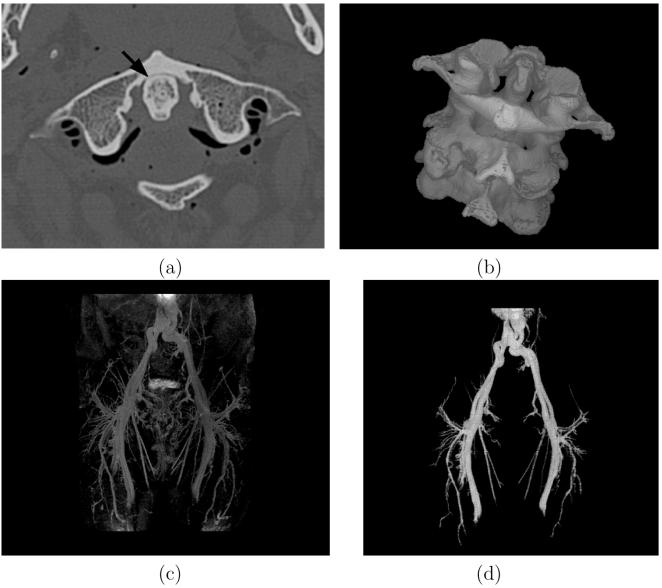
The contact area between the two cervical vertebrae C1 and C2 is shown by an arrow. (b) A surface rendition of the vertebral column consisting of three vertebrae segmented by using AFC. (c) A Maximal Intensity Projection (MIP) rendition of a 3D contrast enhanced MR angiography scene of the body region from belly to knee. (d) A surface rendition of the entire vascular tree segmented by AFC from this scene.

The aim of our first experiment is to compare the performances of RFC and IRFC in segmenting the individual vertebrae. Figure 8(a) displays a region of interest from a slice in the 3D CT data (size: 512 × 512 × 77, voxel size 0.23×0.23×1.0 mm³). In CT scenes, bones appear bright, and it is not difficult to segment them from the rest of the body region. Figure 8(b) displays a surface rendition of the cervical spine column after segmenting it from other bones and soft tissues by using AFC. Here, AFC is used instead of simple thresholding since the former simultaneously removes other non-vertebral bone regions which otherwise would have to be segmented by using a subsequent connectivity analysis. Also, AFC outperforms simple thresholding and connectivity analysis for spels with partial bone occupancy. Our aim in this experiment is to segment the three vertebrae (C1-C3) from the spinal section shown in Figure 8(b). The major challenges in separating the individual vertebrae are: (1) complex shape and geometry of the contact regions between two successive vertebrae; (2) the fuzzy fusion at these junctions (see Figure 8(a)); (3) porous interior of the vertebrae due to the existence of cancellous trabecular bone. It is difficult to separate these vertebrae by using intensity-based features. Therefore, we applied a morphology-based separation through the use of RFC and IRFC methods. The following preprocessing steps were applied first. The cavities created by the trabecular bone network were separately filled in each slice to generate the bone region R_B. We used R_B to define an affinity relation κ utilized in the RFC and IRFC separations of the vertebrae as follows.

Figure 8.

(a) An axial slice from the CT scene of a patient’s cervical spine.

First, for a given scene 〈C, f〉, a separate bone volume fraction scene 〈C, f_B〉 was computed by setting

$$f_B\left(c\right)=\{\begin{array}{cc}\hfill 1\hfill & \text{for}c\in R_B\text{and}f\left(c\right)\ge {\text{Bone}}_{\mathit{max}},\hfill \\ \hfill \frac{f\left(c\right)-{\text{Bone}}_{\mathit{min}}}{{\text{Bone}}_{\mathit{max}}-{\text{Bone}}_{\mathit{min}}}\hfill & \text{for}c\in R_B\text{and}{\text{Bone}}_{\mathit{min}}<f\left(c\right)<{\text{Bone}}_{\mathit{max}},\hfill \\ \hfill 0\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$

where Bone_max and Bone_min represent maximal and minimal intensities of spels in R_B, respectively.

For a path p = 〈c₁, c₂, . . . , c_l〉 in C, wherein the consecutive spels are 26-adjacent, we define its fuzzy length as

$${\pi }_B\left(p\right)=\sum _{i=1}^{l-1}\frac{1}{2}(f_B\left(c_i\right)+f_B\left(c_{i+1}\right))\cdot \text{distance}(c_i,c_{i+1}).$$

$(\text{If}\frac{1}{2}(f_B\left(c_i\right)+f_B\left(c_{i+1}\right))\cdot \text{distance}(c_i,c_{i+1})$ is interpreted as an average bone density of the link 〈c_i, c_i+1 〉, then π_B(p) is approximately the total bone mass of p.) The fuzzy distance transform [23] is derived from f_B as follows:

$${\Omega }_B\left(c\right)=\underset{d\notin R_B}{\min }\{{\pi }_B\left(p\right):p\text{is a path with adjacent consecutive spels from}c\text{to}d\}.$$

(Under the interpretation as above, Ω_B(c) is the smallest mass of a path connecting c with the complement of R_B.) Now, affinity between spels c and d is defined as given below, where N = max_{c ∈ C}Ω_B(c):

$${\mu }_{\kappa }(c,d)=\{\begin{array}{cc}\hfill \max \{{\Omega }_B\left(c\right),{\Omega }_B\left(d\right)\}∕N\hfill & \text{for adjacent}c\ne d,\hfill \\ \hfill 1\hfill & c=d,\hfill \\ \hfill 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (16)

Next, RFC and IRFC algorithms were applied to 〈C, f〉 by using the affinity relation defined above on 〈C, f_B〉. The same set of seeds, selected manually, was used for both methods. The results of vertebral separation obtained by using RFC and IRFC are illustrated in Figures 9(a)-(d), (a) and (c) showing the results on a slice, and (b) and (d) depicting the result via 3D surface rendering. In both figures, voxels segmented as part of a specific vertebra are assigned the same color. In the slice display, spels shown white indicate that they were not assigned to any specific bone. Although RFC has succeeded in capturing the skeletal core of each vertebra after segmentation, it has lost most of the regions of each bone (too many white spels in the slice display) and the results are obviously not acceptable. Despite fuzzy fusion at contact regions between the vertebrae, IRFC has successfully separated them. IRFC stopped after 8, 14, and 15 iterations, respectively, for the first, second, and third vertebra. For the particular affinity function defined above, the results of RFC-based vertebral separation are similar to the results that may be obtained by using morphological erosion with a ball of appropriate size. The beauty of RFC is that, effectively, the radius of the eroding ball is automatically computed by the RFC method. The results obtained by IRFC cannot be produced by using a simple morphological operation.

The aim of our second experiment is to demonstrate how IRFC can be employed to separate arteries and veins in contrast-enhanced MR angiography scenes. MR imaging approaches [25] exist which attempt to elicit different types of signals from the arteries and veins through carefully designed imaging protocols and thereby to distinguish arteries from veins. Here, we use RFC and IRFC to separate artery/vein trees from MR scenes that are acquired by using long resident blood-pool contrast agents [26] which do not produce different signals from the arteries and veins, but which provide a better overall definition of the vessels themselves. Figure 8(c) shows a maximum intensity projection (MIP) rendition from a patient MRA scene (size: 512 × 512 × 60; resolution: 0.94 × 0.94 × 1.8 mm³) of the body region from belly to knee. Figure 8(d) shows a surface rendition of the whole fuzzy vascular structure that was segmented by using AFC from the original MRA data set. Figures 9(e) and (f) show renditions of the fuzzy arterial and veinous trees separated via RFC and IRFC, respectively. Note that, in this experiment, RFC (or, IRFC) was applied between arteries and veins so that when the arterial tree was segmented the veinous tree served as the background and vice versa.

For this experiment, a morphology-based affinity was computed in a manner similar to the first experiment Equation (16), except that no 2D cavity filling was necessary. In this case, the algorithm stopped after nine iterations. Clearly, IRFC has captured more thin branches in segmented arterial and veinous tress than those captured by RFC. Also, RFC segmentation of the main arterial branch on the right appears largely broken and the same is true for the main veinous branch on the left. On the other hand, the main branches in IRFC segmentation of both arterial and veinous trees appear complete, continuous, and smooth.

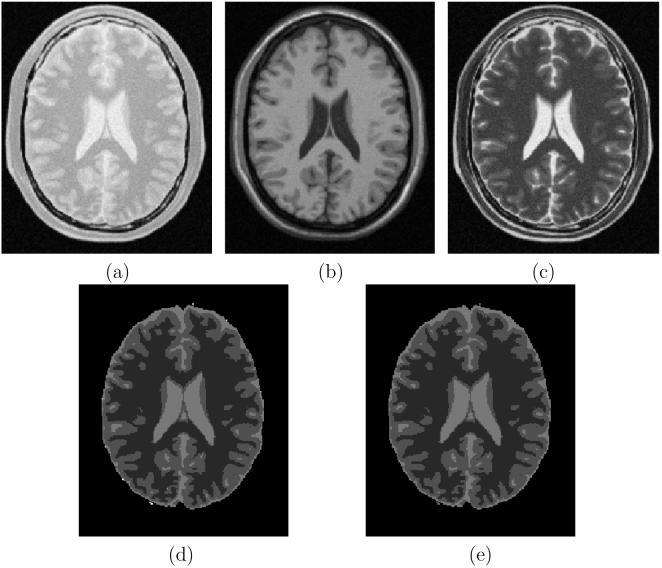
The results of segmentation, by using RFC and IRFC, of WM, GM, CSF in a simulated MR scene produced by the BrainWebMR simulator [22] are presented in Figure 10. Figures 10(a)-(c) show corresponding slices from the simulated proton density, T1-, and T2-weighted MR data sets. Affinity was computed from the three MR data sets after combining them into one vectorial scene [27]. A set of seeds was manually specified for each of the three regions, and the regions were segmented by using RFC and IRFC. These results are shown in Figures 10(d) and (e). It may be noted that there is not much difference between the segmentation results for RFC and IRFC. As in this example, when one object wraps around the entire boundary of the other object, the scope of refinement of segmentation by using IRFC is reduced. Generally, IRFC outperforms RFC when a relatively large part of one object comes close to a large part of another object, forming a fuzzy interface between them, but otherwise the remaining smaller aspects of the objects have a clean association with the two objects, as in our second example above. This situation can also occur in a multi object setting, as in our first example.

Figure 10.

Results of WM, GM, and CSF segmentation on simulated MR scenes produced by BrainWebMR simulator. (a)-(c) Matching slices from simulated PD, T1-, and T2-weighted MR data sets. (d) Segmentation of WM (dark), GM (intermediate brightness), and CSF (bright) regions obtained by using RFC. (e) Same as (d) but for IRFC.

5.2 A Quantitative Evaluation

The purpose of this experiment is to quantitatively evaluate the performance of IRFC and compare it with the performance of RFC under various levels of noise, blurring, and intensity inhomogeneity in the scene. Toward this goal, five 2D scenes ${\mathcal{C}}^T=\langle C,f^T\rangle$, T ∈ {1, 2, 3, 4, 5}, were created by using the drawing tools supported by 3DVIEWNIX [24]. Each of these scenes contained four separate objects and a background. The object regions and the background were assigned different constant intensities. One such scene is shown in Figure 11(a). Next, each scene ${\mathcal{C}}^T$ was modified by: blurring it (via a 2D Gaussian kernel) at one of three fixed blur levels B₁ > B₂ > B₃; adding noise at one of three fixed levels N₁ > N₂ > N₃; and introducing to it intensity inhomogeneity from one of three fixed levels I₁, I₂, I₃. A scene ${\mathcal{C}}^T$ with added blur B ∈ {B₁, B₂, B₃}, noise N ∈ {N₁, N₂, N₃}, and intensity inhomogeneity I ∈ {I₁, I₂, I₃}, is denoted as ${\mathcal{C}}_{\mathit{BNI}}^T=\langle C,f_{\mathit{BNI}}^T\rangle$. Thus, from each of the five scenes ${\mathcal{C}}^T$, we generated 27 modified phantom scenes ${\mathcal{C}}_{\mathit{BNI}}^T$. Three of these 135 phantom scenes, generated from the scene ${\mathcal{C}}^T$ of Figure 11(a), are illustrated in Figures 11(c)-(e).

In each scene ${\mathcal{C}}^T=\langle C,f^T\rangle$, each spel c ∈ C is assigned to a unique object. Let L^T : C → {0, 1, 2, 3, 4} denote the true object labeling function; that is, the set {c ∈ C : L^T (c) = i} is the i-th object for i ∈ {1, 2, 3, 4} and the background, when i = 0. Figure 11(b), used as a reference, presents the true object labeling for Figure 11(a). We will denote by O^T the set of all spels with non-zero label in ${\mathcal{C}}^T$.

Object labeling of the phantom scenes is accomplished in two steps—separation of the foreground from background, and separation among the four objects. This is because the nature of the segmentation task between background and foreground is entirely different from segmentation among objects within the foreground. In the former case, there is a clear intensity difference, and a simpler approach like AFC works fine. On the other hand, among the different foreground objects there is no clear intensity difference and intensity-based approaches will not work. After segmenting the foreground from the background by using AFC, a fuzzy membership scene was created as follows. Let $O_{\mathit{BNI}}^T$ denote the set of spels in the foreground region and let ρ and σ denote the mean and standard deviation of spel intensity values over $O_{\mathit{BNI}}^T$.

A foreground fuzzy membership value ${\phi }_{\mathit{BNI}}^T\left(c\right)$ at a spel $c\in O_{\mathit{BNI}}^T$ was then created, defined by

$${\phi }_{\mathit{BNI}}^T\left(c\right)=\{\begin{array}{cc}\hfill e^{-\frac{{(f_{\mathit{BNI}}^T\left(c\right)-\rho )}^2}{2{\sigma }^2}}\hfill & \text{if}{f}_{\mathit{BNI}}^T\left(c\right)<\rho ,\hfill \\ \hfill 1\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

A fuzzy distance transformation map was then computed from $\langle C,{\phi }_{\mathit{BNI}}^T\rangle$, which was utilized to define affinity as described previously Equation (16). Finally, RFC and IRFC methods were applied to obtain multi-object segmentations within the foreground region. Segmentations resulting from RFC and IRFC for scenes in Figures 11(c)-(e) are shown, respectively, in Figures 11(f)-(h) and (i)-(k). In these displays, white colored spels represent foreground spels that are not assigned to any specific region. (Those were referred to as “boundary spels” in our theoretical discussion.) Clearly IRFC has successfully separated the objects while preserving the thin branches, and RFC has captured only the core of the objects and the results are similar to those that can be obtained via morphological erosion.

Let $\mathit{RFC}-L_{\mathit{BNI}}^T\left(c\right)$ and $\mathit{IRFC}-L_{\mathit{BNI}}^T\left(c\right)$ denote the object labels estimated at a spel c from a phantom scene ${\mathcal{C}}_{\mathit{BNI}}^T$ by using RFC and IRFC, respectively. We use here the label value 5 for the foreground spels which are not assigned to any of the four objects. A similarity measure between L^T (c) and $\mathit{RFC}-L_{\mathit{BNI}}^T\left(c\right)$ (or $\mathit{IRFC}-L_{\mathit{BNI}}^T\left(c\right)$) is necessary to assess the performance of the two methods. Unlike the one object case, establishing agreement with truth in the case of multiple objects simultaneously is tricky. Here, we have used a figure-of-merit (FOM) that gives a full score only when the label of a spel in the segmentation matches with the true label at that spel; otherwise the score is 0. Specifically, the figure of merit $X-{\mathit{FOM}}_{\mathit{BNI}}^T$, with X ∈ {RFC, IRFC}, for the phantom scene ${\mathcal{C}}_{\mathit{BNI}}^T$ is defined as

$$X-{\mathit{FOM}}_{\mathit{BNI}}^T=\frac{{\Sigma }_{c\in C}F(X-L_{\mathit{BNI}}^T\left(c\right),L^T\left(c\right))}{\parallel O^T\cup O_{\mathit{BNI}}^T\parallel }\times 100,$$

where symbol $\parallel O^T\cup O_{\mathit{BNI}}^T\parallel$ denotes the number of spels in $O^T\cup O_{\mathit{BNI}}^T$, and F(a, b) = 1 for a = b and F(a, b) = 0 for a ≠ b . Finally, at any given blur, noise, and inhomogeneity level BNI, the mean and the standard deviation values of $X-{\mathit{FOM}}_{\mathit{BNI}}^T$, for T ∈ {1, 2, 3, 4, 5}, are computed. Tables 1 and 2 list the mean and standard deviation of these FOM values for RFC and IRFC methods, respectively. It is clear from these tables that the performance of IRFC is superior to that of RFC.

Table 1.

The mean and standard deviation (in parenthesis) of the similarity measure ${\mathrm{RFC}-\mathrm{FOM}}_{\mathit{BNI}}^T$, T ∈ {1, 2, 3, 4, 5}, are shown for each blur, noise, and inhomogeneity condition.

B1N1I1	31.29(4.36)	B2N1I1	26.23(4.90)	B3N1I1	25.56(5.36)
B1N1I2	26.67(3.78)	B2N1I2	24.83(5.12)	B3N1I2	21.72(5.78)
B1N1I3	26.51(4.68)	B2N1I3	21.92(5.23)	B3N1I3	20.31(6.09)
B1N2I1	26.69(3.89)	B2N2I1	24.42(4.89)	B3N2I1	21.73(5.45)
B1N2I2	24.28(5.11)	B2N2I2	19.89(5.13)	B3N2I2	17.93(5.85)
B1N2I3	22.47(3.96)	B2N2I3	18.29(5.24)	B3N2I3	15.92(6.12)
B1N3I1	25.49(5.21)	B2N3I1	21.92(4.99)	B3N3I1	18.00(5.54)
B1N3I2	22.58(4.76)	B2N3I2	18.18(5.33)	B3N3I2	15.78(6.02)
B1N3I3	20.09(4.59)	B2N3I3	16.03(5.02)	B3N3I3	15.93(6.11)

Table 2.

The mean and standard deviation (in parenthesis) of the similarity measure ${\mathrm{IRFC}-\mathrm{FOM}}_{\mathit{BNI}}^T$, T ∈ {1, 2, 3, 4, 5}, are shown for each blur, noise, and inhomogeneity condition.

B1N1I1	98.93(0.31)	B2N1I1	98.38(0.37)	B3N1I1	97.30(0.46)
B1N1I2	98.08(0.39)	B2N1I2	96.78(0.40)	B3N1I2	93.12(0.42)
B1N1I3	97.91(0.42)	B2N1I3	94.49(0.34)	B3N1I3	90.42(0.50)
B1N2I1	97.90(0.38)	B2N2I1	95.91(0.29)	B3N2I1	91.73(0.49)
B1N2I2	96.65(0.45)	B2N2I2	90.60(0.40)	B3N2I2	85.89(0.53)
B1N2I3	94.40(0.42)	B2N2I3	87.41(0.38)	B3N2I3	82.81(0.50)
B1N3I1	97.34(0.40)	B2N3I1	92.62(0.35)	B3N3I1	87.69(0.56)
B1N3I2	93.80(0.46)	B2N3I2	86.70(0.42)	B3N3I2	82.09(0.48)
B1N3I3	90.50(0.49)	B2N3I3	83.30(0.46)	B3N3I3	78.90(0.55)

6 Concluding remarks

The theory of IRFC segmentation presented in this paper consolidates all earlier versions of FC segmentation theories in a unified framework. This is especially the case for the RFC theory, since any segmentation obtained with the RFC algorithm is just a first iteration step in the IRFC based algorithm. Since our exposition of the IRFC theory is presented with the iteration number as a parameter, the RFC results (viewed as the first-iteration-level-IRFC results) are readily accessible due to the format of our presentation of the IRFC theory.

It should also be stressed that the IRFC theory presented here is self contained. We were not able to use the theoretical results from earlier papers in this connection, because of the intricacy of the arguments needed for the IRFC theory. Thus, from a theoretical point of view, this paper supplants previous papers on FC theory.

Note also that, once the IRFC algorithm is implemented, there is no reason to implement also an RFC based algorithm separately. There are two reasons in support of this statement. First, it is easy to implement an IRFC algorithm that will ask an operator whether to impose a maximal number N of iterations. Then such an algorithm used with “no bound for N” is just our standard IRFC algorithm, and when run with N = 1, it becomes a standard RFC algorithm. Although this allows an implementation of RFC algorithm as a restricted version of IRFC, we do not believe that there is much benefit in running RFC segmentation once an IRFC program is at hand. It is true that, in principle, the RFC algorithm is simpler than IRFC, and in some cases (as demonstrated in Figures 10(d) and (e)) the RFC program works just as well as IRFC. However, in such cases, the first iteration of IRFC will already give the RFC “good enough” segmentation; that is, the IRFC algorithm will stop after just one iteration. Since the expense of running IRFC algorithm in the case it stops after just one iteration is only slightly higher than running the RFC algorithm, the benefit of an operator deciding whether to use IRFC or RFC is minimal, even when there is no better performance of IRFC over RFC.

Apart from its generality, IRFC is a more powerful technique than RFC. Our experiments indicate that there are potentially many situations wherein IRFC would perform better than RFC, especially when multiple objects come close to each other without one completely surrounding the other.

One area that requires careful scrutiny and that can make an impact on the practical utility of FC methods in segmentation is the proper design of affinity. In this paper, we have utilized mostly image-based strategies for defining affinity, as described in previous publications. We have also shown (see Equation (16)) that morphology-based strategies can also be employed to devise effective affinities. It is also conceivable that affinities can be constructed by utilizing information available in statistical shape models [28]. A question naturally arises then as to whether these three strategies can be combined in a FC-driven segmentation task to construct affinities. We are currently studying some of these issues in the context of specific imaging applications.