Abstract
In this paper we present a new theory and an algorithm for image segmentation based on a strength of connectedness between every pair of image elements. The object definition used in the segmentation algorithm utilizes the notion of iterative relative fuzzy connectedness, IRFC. In previously published research, the IRFC theory was developed only for the case when the segmentation was involved with just two segments, an object and a background, and each of the segments was indicated by a single seed. (See Udupa, Saha, Lotufo [15] and Saha, Udupa [14].) Our theory, which solves a problem of Udupa and Saha from [13], allows simultaneous segmentation involving an arbitrary number of objects. Moreover, each segment can be indicated by more than one seed, which is often more natural and easier than a single seed object identification.
The first iteration step of the IRFC algorithm gives a segmentation known as relative fuzzy connectedness, RFC, segmentation. Thus, the IRFC technique is an extension of the RFC method. Although the RFC theory, due to Saha and Udupa [19], is developed in the multi object/multi seed framework, the theoretical results presented here are considerably more delicate in nature and do not use the results from [19]. On the other hand, the theoretical results from [19] are immediate consequences of the results presented here. Moreover, the new framework not only subsumes previous fuzzy connectedness descriptions but also sheds new light on them. Thus, there are fundamental theoretical advances made in this paper.
We present examples of segmentations obtained via our IRFC based algorithm in the multi object/multi seed environment, and compare it with the results obtained with the RFC based algorithm. Our results indicate that, in many situations, IRFC outperforms RFC, but there also exist instances where the gain in performance is negligible.
Keywords: image segmentation, path strength, path connectedness, fuzzy connectedness
1 Introduction
Image segmentation—the process of partitioning (in a hard or fuzzy manner) the image domain into meaningful object regions—is perhaps the most challenging and critical problem in image processing and analysis. Research in this area will probably continue indefinitely long because the solution space is infinite dimensional, and since any single solution framework is unlikely to produce an optimal solution (in the sense of the best possible precision, accuracy, and efficiency) for a given application domain. It is important to distinguish between two types of activities in segmentation research—the first relating to the development of application domain-independent general solution frameworks, and the second pertaining to the construction of domain-specific solution starting from a known general solution framework. The latter is not a trivial task most of the time. Both these activities are crucial, the former for advancing the theoretical aspects of, and shedding new light on, segmentation research, and the latter for bringing the theoretical advances to actual practice. The topic of this paper pertains to the former.
General segmentation frameworks [1]-[12] may be broadly classified into three groups: boundary-based [1]-[5], region-based [6]-[10], and hybrid [11,12]. As the nomenclature indicates, in the first two groups the focus is on recognizing and delineating the boundary or the region occupied by the object in the image. In the third group, the focus is on exploiting the complementary strengths of each of boundary-based and region-based strategies to overcome their individual shortcomings. The segmentation framework discussed in the present paper belongs to the region-based group and constitutes an extension of the fuzzy connectedness (abbreviated from now on as FC) methodology [9].
In the FC framework [9], a fuzzy topological construct, called fuzzy connectedness, characterizes how the spatial elements (abbreviated as spels) of an image hang together to form an object. This construct is arrived at roughly as follows. A fuzzy relation called affinity is defined on the image domain; the strength of affinity between any two spels depends on how close the spels are spatially and how similar their intensity-based properties are in the image. Affinity is intended to be a local relation. A global fuzzy relation called fuzzy connectedness is induced on the image domain by affinity as follows. For any two spels c and d in the image domain, all possible paths connecting c and d are considered. Each path is assigned a strength of fuzzy connectedness which is simply the minimum of the affinities of consecutive spels along the path. The level of fuzzy connectedness between c and d is considered to be the maximum of the strengths of all paths between c and d. For segmentation purposes, FC is utilized in several ways as described below. See [13] for a review of the different FC definitions and how they are employed in segmentation and applications.
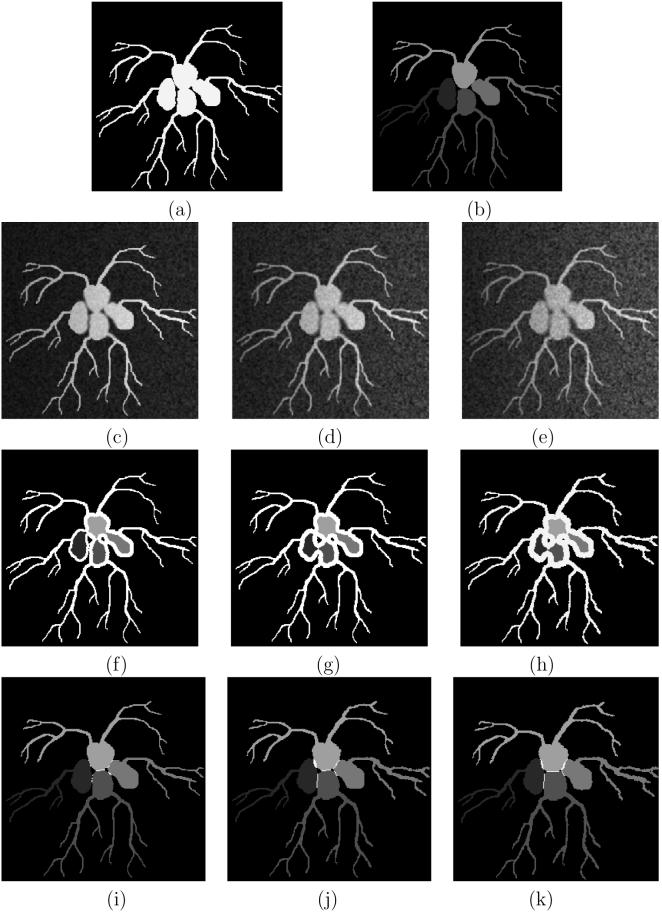
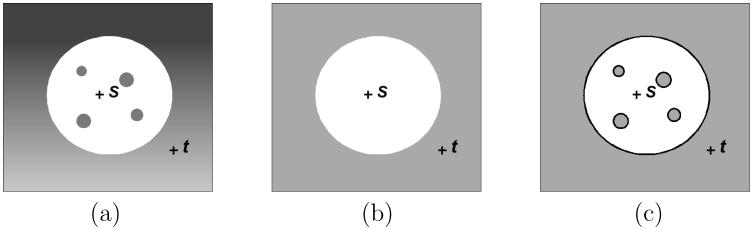
In absolute FC (abbreviated AFC) [9], the support of a segmented object is considered to be the maximal set of spels, containing one or more seed spels, within which the level of FC is at or above a specific threshold. To obviate the need for a threshold, relative FC (or RFC) [19] was developed by letting all objects in the image to compete simultaneously via FC to claim membership of spels in their sets. Each co-object is identified by one or more seed spels. Any spel c in the image domain is claimed by that co-object with respect to whose seed spels c has the largest level of FC compared to the level of FC with the seed sets of all other objects. To avoid treating the core aspects of an object (that are very strongly connected to its seeds) and the peripheral subtle aspects (that may be less strongly connected to the seeds) in the same footing, an iterative refinement strategy is devised in iterative RFC (or IRFC) [14]-[16]. The superior performance of IRFC over RFC and the underlying reasons are illustrated in Figures 11 and 9(e-f). Another advantage of IRFC is that the objects it generates are topologically nicer than those generated by RFC or AFC—any IRFC object generated by a single seed has no “holes” (i.e., is simply connected), unless a “hole” contains a seed of another object. This feature is illustrated in Figure 1.
Figure 11.
(a) A hand drawn scene with four iso-intensity objects and a dark background. (b) Object labeling in the true scene. (c)-(e) Three phantom scenes generated from (a) at different levels of blur, noise, and inhomogeneity. (f)-(h) Multi-object segmentations of (c)-(e), respectively, by using RFC. (i)-(k) Segmentation of (c)-(e) by using IRFC.
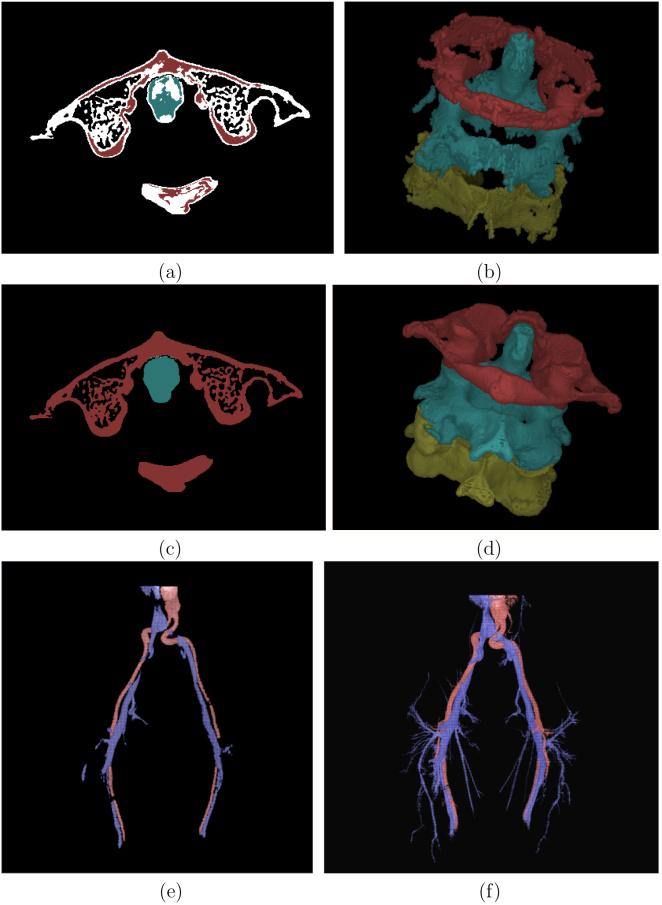
Figure 9.
(a) A slice display of the separation of cervical vertebra by applying RFC for the slice shown in Figure 8(a). White spels are not assigned to any specific vertebra. (b) Color surface rendition of the three vertebra segmented by RFC. (c)-(d) Same as (a)-(b), respectively, but by using IRFC. (e) Color surface rendition of arterial (red) and veinous (blue) trees segmented by RFC. (f) Same as (e) but by using IRFC.
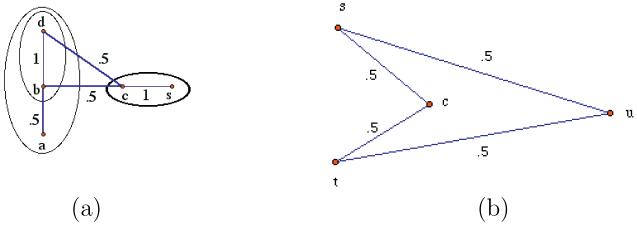
Figure 1.
(a) Original image, with seeds s and t indicating the object and the background, respectively. (b) The foreground object (in white) generated by RFC. (c) The foreground object (in white) generated by IRFC. (We used the same homogeneity based affinity in both cases.)
In general, IRFC leads to better object definition than RFC with a theoretical construct similar to that of RFC. The proper design of affinity is crucial to the effectiveness of the segmentations that ensue, no matter what type of FC is used. In scale-based FC [13], which is applicable to all of AFC, RFC, and IRFC, affinity is defined not based just on the properties of the two spels under question but also on the properties of all spels in the local scale region around the two spels. In vectorial FC [27], affinity is constructed in a vectorial manner, allowing spels to assume not just scalar values but any vectorial values, which may come from the original acquisition of the image owing to multiple image properties at every spel or that may arise from vector-valued features estimated from the given scalar or vectorial image. By using S and V to abbreviate “scale-based” and “vectorial,” and by allowing a combination of these indexes with different types of FC referred to above, we may describe the FC family that is developed to date by methods denoted by AFC, SAFC, VAFC, VSAFC, RFC, SRFC, VRFC, VSRFC, IRFC, SIRFC, VIRFC, and VSIRFC. See [13] and the original articles cited therein for further details on each member of this family.
In the present paper, we make two sets of fundamental contributions. (1) The original IRFC was devised, due to theoretical challenges, in a 2-object (foreground-background) scenario. We now overcome this theoretical challenge and generalize its theory to multiple objects. (2) In this process of generalization, several most fundamental properties of AFC, RFC, and IRFC have been uncovered. They allow us to better understand the behavior of the FC process in general, and IRFC in particular, and give us a single unified theoretical framework within which all members of FC family methods can be described elegantly. This may lead us to more effective segmentation strategies in the future. These fundamental theoretical advances are described in Section 2. For ease of reading, most long proofs are pooled together in Section 3, so that skipping this section will not affect the understandability of the new results presented in the paper. The new algorithm is described in Section 4. Some examples and comparison with RFC are presented in Section 5 to demonstrate the behavior of the multi-object strategy of generalized IRFC. Our concluding remarks are stated in Section 6.
2 Theory
In this section we present the theoretical framework of generalized IRFC. The terminology and notation employed in this paper follow in spirit that of previously published FC papers. However, we slightly deviate from the previous notation in several aspects, and we believe that the new approach is more precise and elegant.
2.1 Basic definitions and notation
The most fundamental notion in our theory is that of the strength of connectedness between a pair of image elements. In its definition, we will use a notation that is only a slight modification of that used by Udupa and Samarasekera [9].
In this paper we will use the following interpretation of the notions of (hard) functions and relations, which is standard in set theory and is used in many calculus books. A binary relation R from a set X into a set Y is identified with its graph; that is, R is equal to {〈x, y〉 ∈ X × Y : xRy holds} . Since a function f : X → Y is a (special) binary relation from X to Y , in particular we have f = {〈x, f(x)〉: x ∈ X}. With this interpretation, handling fuzzy sets and fuzzy relations becomes quite natural and less cumbersome than usual. In particular, let be a fuzzy subset of a hard set X with a membership function μZ: X → [0, 1]. For x ∈ X, we interpret as the degree to which x belongs to . Usually such a fuzzy set is defined [17] as , which is the graph of . Thus, according to our interpretation, is actually equal to . Note that this interpretation fits also quite well the situation when is the hard subset Z of X, as then is equal to the characteristic function χZ (defined as χZ(x) = 1 for x ∈ Z and χZ(x) = 0 for x ∈ X\ Z), and the identification of Z with χZ is quite common in analysis and set theory. Notice also, that a fuzzy binary relation ρ from X to Y is just a fuzzy subset of X × Y , so it is equal to its membership function μρ: X × Y → [0, 1].
Let n ≥ 2. A binary fuzzy relation α on is said to be a fuzzy adjacency binary relation if α = μα is symmetric (i.e., μα(c, d) = μα(d, c)) and reflexive (i.e., μα(c, c) = 1). The value of μα(c, d) depends only on the relative spatial position of c and d. Usually μα(c, d) is decreasing with respect to the distance function ||c - d||. In most applications, α is just a hard case relation like 4-adjacency relation for n = 2 or 6-adjacency in the three-dimensional case. By an n-dimensional fuzzy digital space we will understand a pair . The elements of digital space are called spels. (For n = 2 also called pixels, while for n = 3 - voxels.) A scene over a fuzzy digital space is a pair , where , each bj > 0 being an integer, and is a scene intensity function. In this paper, symbols and C will always stand for a scene and its domain, respectively, as defined above.
The most fundamental measure of local “hanging togetherness” of any pair of spels is an affinity relation κ. It is a fuzzy binary relation defined on C; that is, μκ: C × C → [0, 1]. Affinity relation κ is defined to be symmetric and reflexive. The value of μκ(c, d) depends not only on the adjacency strength μκ(c, d), but also on the intensity function f. There are many methods of finding the affinity relation for a given scene. (See the survey paper [13].) In this paper, we will always assume that an appropriate affinity has already been specified for the segmentation task on hand.
A translation of the local strength of connectedness given by κ into the global strength of connectedness is done with the help of the notion of a path and its strength. A path in A ⊆ C is any sequence p = 〈c1, . . . , cl〉, where l > 0 and ci∈ A for every i = 1, . . . , l. The family of all paths in A is denoted by . If c, d ∈ A, then the family of all paths 〈c1, . . . , cl〉 in A from c to d (i.e., such that c1 = c and cl = d) is denoted by . The strength μ(p) of a path is defined as the strength of its κ-weakest link; that is,
| (1) |
when l > 1, and μ(p) = 1 for l = 1. For c, d ∈ A ⊆ C the fuzzy κ-connectedness strength in A between c and d is defined as the strength of a strongest path in A between c and d; that is,
| (2) |
If κ is a hard binary relation, κ: C × C → {0, 1}, then the relation μA is known as a transitive closure of κ ∩ (A × A). Note that
| (3) |
Notice also that μA(c, d) ≥ μκ(c, d). A path with μ(p) = μA(c, d) is referred to as a strongest path (in A) from c to d.
It is easy to see that, for every c, d ∈ A ⊆ C and paths , we have
(i) μ(〈c, d〉) = μκ(c, d) and μ(p)≤ μ(q) if p is either an initial or a terminal extension of q; and
(ii) μA is reflexive and symmetric on A.
It is also not difficult to see (and it follows easily from Proposition 2.1 below) that
(iii) μA is transitive on A; that is, μA (c, d) ≥ min{μA (c, x), μA(x, d)} for every c, d, x ∈ A.
A very interesting fact is that if μA is defined from μ via formula (2) and the properties (i)-(iii) hold, then one might assume as well μ is defined by a formula (1), since under this conditions, independent of the actual definition of μ(p), we still have . This was proved by Saha and Udupa in [18].
For paths and , we will use symbol p + q to denote the path . We will use this symbol only when cl = d1. Notice that in such a situation, by the definition in (1), we have μ(p + q) = min{μ(p), μ(q)}, as μα(cl, d1) = 1.
The following result is a slight refinement of [15, Prop. 2.3].
Proposition 2.1
For any spels a, b, c ∈ A ⊆ C,
| (4) |
Proof
If pab and pbc are the strongest paths between a and b and between b and c, respectively, then the path pab + pbc justifies μA(a, c) ≥ μA(b, c), as μA(a, c) ≥ μ(pab+pbc) = min{pab, pbc} ≥ μA(b, c). If we had μA(a, c) > μA(b, c), with path pca being the strongest path between c and a, then we would have μ(pca + pab) = min{μ(pca), μ(pab)} > μA(b, c), which is impossible.
2.2 Fuzzy connected objects: absolute and relative
By a segmentation of a scene we will understand any family {P1, . . . , Pm} of pairwise disjoint hard subsets of C. Although this is a departure from the terminology used in the previous papers on fuzzy connectedness, the change is only superficial. This is the case since the algorithms from all previous papers were also designed to create the hard segmentations of C, while, in the last step, each set P from the segmentation was assigned a membership function μP: C → [0, 1] of the form μP(c) = η(f(c)) · χP(c), where η is a function (like Gaussian) that maps the image intensity function into objectness values. Although this last step could be done also in the case of our segmentation, we will confine ourselves up to the step of hard segmentation only since, from the viewpoint of the new theory and algorithms, this is what matters.
To translate the notion of a path strength into an actual segmentation of a given scene , one must indicate each object with one or more seeds. So, assume that we have a nonempty set S ⊂ C of seeds such that each seed represents a different object. (The case of multiple seeds per object will be discussed later.)
The simplest way to define a segmentation of a scene is to choose a threshold θ ∈ (0, 1] and for each seed s ∈ S define an object in associated with s as
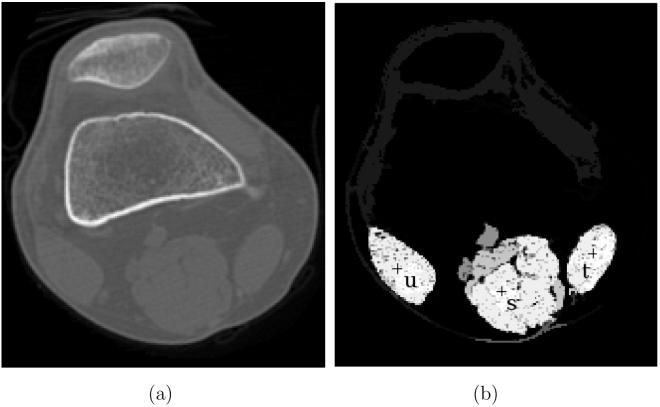
These objects were first studied by Udupa and Samarasekera in [9]. It is easy to see that s ∈ Psθ for every s ∈ S. Also, for s, t ∈ S, if θ ≤ μC(s, t), then Psθ and Ptθ are disjoint; on the other hand, if θ ≤ μC(s, t), then Psθ = Ptθ. Thus, to make the objects disjoint, one must choose θ greater than every number μC(s, t), for all distinct s, t ∈ S. This is the underlining mechanism of AFC. This phenomenon is illustrated in Figure 2 on a CT slice of a human knee, wherein three seed spels s, t, and u are chosen, one in each of three muscle regions. Since the strength of connectedness between any two seeds is much lower than the strength of connectedness within each object (Figure 2(b)), for the individual muscle regions a threshold can be selected to specify Psθ.
Figure 2.
Illustration of AFC segmentation of the muscles of a knee. (a) A CT slice of a human knee. (b) Each pixel has a strength of connectedness with respect to each seed, u, s, and t, chosen within muscle regions. The largest of these strengths is shown as a scene.
A considerably more powerful segmentation tool is that of RFC. For any s ∈ C and T ⊂ C, define
Then, the segmentation generated by seeds S ⊂ C is defined as {PsS: s ∈ S}.
It is easy to see that the objects {PsS: s ∈ S} are pairwise disjoint. In addition, s ∈ PsS as long as there is no t ∈ S, t ≠ s, with μC(s, t) = 1; if there is such a t, then PsS is empty. Note also, that if θ > max{μC(s, t): s, t ∈ S, s ≠ t} (so that the sets {Psθ: s ∈ S} are pairwise disjoint), then Psθ ⊂ PsS for every s ∈ S. Thus, the RFC method of segmentation is indeed more refined than the AFC method. Again, by using the example in Figure 2, we demonstrate in Figure 3 the results PsS of RFC. Note that these segmented regions are generally larger than those in Figure 2. Note also that the spels that are not in the muscle regions all have the same strength of connectedness with respect to at least two objects.
Figure 3.
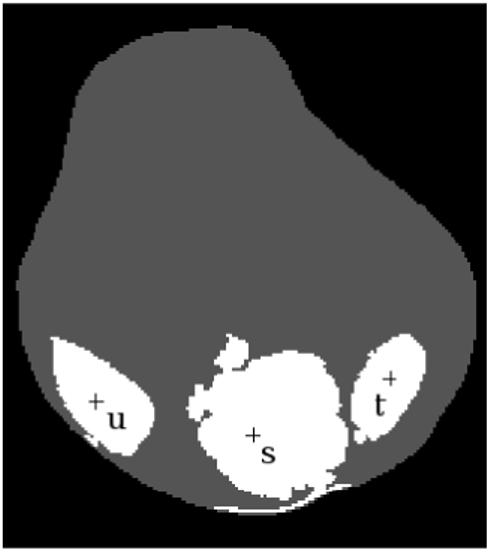
RFC segmentation of the knee muscles from Figure 2, where the same seed points were used as in the AFC segmentation shown in Figure 2(b).
One of the important properties of the above described methods of segmentation (AFC and RFC) is known as robustness. This property states that the segmentation does not change if different seeds are chosen within the same objects, which, for the practice of these segmentation methods, is a very desirable property to have. The following result, due to Saha and Udupa [19], is the precise statement of this property in case of RFC segmentation. (This result follows also from our Corollary 2.7.)
Proposition 2.2 (Robustness)
Let S = {s1, . . . , sm} ⊂ C and for every i ∈ {1, . . . , m} let ti ∈ PsiS. If T = {t1, . . . , tm}, then PtiT = PsiS for every i ∈ {1, . . . , m}.
The objects PsS are often referred to as connected components. The following fact justifies the word connected in this term. Moreover, this fact will be used in what follows as a motivational tool and in the actual proofs.
Fact 2.3
If p = 〈c1, . . . , cl〉 is a strongest path from c ∈ PsS to an s ∈ S, then ci ∈ PsS for every i ∈ {1, . . . , l}; that is, .
Proof
Fix an i ∈ {1, . . . , l} and a t ∈ S\ {s}. Since c ∈ PsS, we know that μC(c, s) > μC(c, t). We need to show that μC(ci, s) > μC(ci, t). But, by (4), we have μC(s, t) = μC(c, t). Since also
by (4) we have μC(ci, s) > μC(s, t) = μC(ci, t).
It is sometimes difficult to pinpoint a single seed in a desired object, and often, it is convenient, or becomes necessary, to choose multiple seeds for each object under consideration. So, let be a family of nonempty pairwise disjoint sets of seeds. For each , we like to find an object containing S in a way similar to that described above. To define , it is convenient to have the following notation for every c ∈ A ⊂ C and D ⊂ A:
(Note that μA(c, ∅) = -∞, as max ∅ = ∞ according to a convention that, for a finite , max Z is the smallest b ∈ [-∞, ∞] for which z ≤ b for every z ∈ Z.) We define
where . Although this multi seed approach is useful in practice, it is worth to note that this theory is quite close to, and readily ensues from, the single seed theory, as each can be easily expressed in terms of objects generated by singleton seeds:
| (5) |
since .
2.3 Iterative Relative Fuzzy Connectedness: motivation, definition, and properties
The RFC segmentation {PsS: s ∈ S of a scene can still leave quite a sizable “boundary” set B = C\ ∪s∈S PsS; that is, the set of all spels c outside any of the objects PsS wherein the strengths of connectedness are equal with respect to the seeds. An example is provided in Figure 4 to illustrate this concept of “boundary” spels left unclaimed. The goal of what follows is to find a way to naturally redistribute some of the spels from B among the object regions in a new generation (iteration) of segmentation. Another motivation for IRFC, also explained in Figure 4, is to overcome the problem of “path strength dilution within the same object,” of paths that reach the peripheral subtle and thin aspects of the object.
Figure 4.
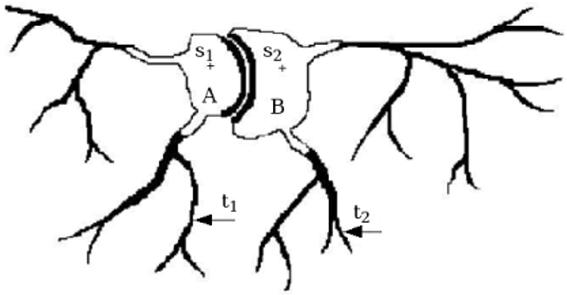
Illustration of the phenomenon of “path strength dilution within the same object.” The strongest paths from s1 to t1, s1 to t2, s2 to t1, and s2 to t2 are likely to have the same strength because of partial volume effects.
In Figure 4, two object regions A and B, each with its core and peripheral subtle parts, are shown. Owing to blur and other artifacts introduced into the scene by the imaging device due to partial volume effect and other shortcomings, the strongest paths from s1 to t1, s1 to t2, s2 to t1, and s2 to t2 are all likely to assume similar strengths. As a consequence, the spels in the dark areas may fall in B, the unclaimed “boundary” set.
A basic idea behind the definition of relative fuzzy connected objects PsS, s ∈ S, is that each seed s ∈ S competes for each spel: a spel c goes to the object PsS provided c is connected to s in a stronger way than to any other seed t ∈ S. Here the strength of connectedness between c and d is expressed by a number μC(c, d), the strength of a strongest path (in C) between c and d. Thus, the fact that a spel c belongs to PsS means that
c is connected to s within the object PsS with a strength μC(c, s) and any appropriate path between c and t ∈ S\ {s} is weaker than μC(c, s).
Although the clause “within the object PsS” may not seem obvious from the definition of PsS, it is justified both by intuition and by Fact 2.3. It is also not clear what we have in mind by an “appropriate path,” but at this stage it does not matter, since the strength inequality holds for any path between c and t ∈ S\ {s}.
The importance of the clause “appropriate path” comes to light when we examine the spels c from the “boundary” set B = C\ ∪s∈S PsS. If we like to refine our definition and to extend each object PsS, s ∈ S, to a possible larger object , what would be the “appropriate” paths between c ∈ B and s ∈ S that we should consider? Since the “strongest path” justifying , for t ∈ S, should be contained in , it seems should that we should restrict our attention to the paths between c and t only from B ∪ PtS. Thus, to obtain a definition of , we should modify the definition of PsS by replacing each number μC(c, t), t ∈ S\ {s}, with μB∪PtS(c, t). This leads to
Although this definition could be used as the engine for the iteration described below, it turns out that it will be more convenient to use its equivalent form:
The equality follows from Theorem 3.7.
Figure 5 illustrates these ideas pictorially. The initial segmentation is defined by RFC conservatively, so that PsS corresponds to the core aspects of the object identified by seed s (illustrated by the hatched area containing s in Figure 5). This leaves a large boundary set B where the strengths of connectedness with respect to the different seeds are equal (illustrated by the shaded area containing s in Figure 5). In the next iteration, the segmentation is improved incrementally by grabbing those spels of B that are connected more strongly to PsS than to PtS. When considering the object associated with s, the “appropriate” path from s to any c ∈ B is any path in C. However, all objects have to compete with the object associated with s by allowing paths from their respective seeds t to c not to go through PsS since this set has already been declared to be part of the object of s.
Figure 5.
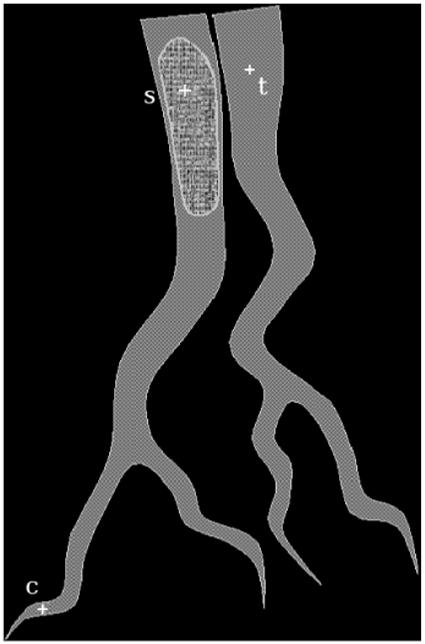
Pictorial illustration of IRFC advantages over RFC.
The advantage of the formula for over that for comes from the fact that, unlike the case of , we can compute without knowing sets PtS for t ≠ s. This makes the implementation of the algorithm easier and more efficient. In addition, the two object IRFC theory in earlier papers discussing this subject [15] was done in the format of , which makes our ( based) theory its natural generalization. However, the formalism underlining also has its advantages. First of all, it is more intuitive from the connectedness point of view. Also, the disjointness of the new generation of segments (see Theorem 2.4) is obvious in the setting, while it requires a complicated argument in the formalism.
Now, the iterative version of sets PsS can be defined as follows. For each s ∈ C let be the empty set and define iteratively sets PjsS by a formula , where
This definition works fine if we assume that each object is connected and is generated by a single seed. However, we like to develop this theory also in the case when each object in the segmentation is generated by a set S of seeds where the different resulting segments may be disconnected. So, let be a nonempty family of nonempty pairwise disjoint sets of seeds. For every A ⊂ C let and for j = 0, 1, 2, . . . define , where
The equality between the sets defining follows immediately from the definition μA(c, D) = maxd∈D μA(c, d). (For alternative definitions of see also Subsection 3.2.)
Clearly for every j and for any A ⊂ C. Since the scene domain C is finite, the growth must stop at some stag j. In particular, there is a k for which for all . We will denote such terminal iterative as . The IRFC segmentation (of with respect to ) is defined as .
Note that the result of the first iteration is equal to as defined by the RFC formula. Thus, . In particular, the iterative technique is a refinement of the RFC method. Also, for every s ∈ S ⊂ C and j, we have
where . Thus, every family of single seed generated IRFC segmentation can be easily represented in the formalism of multi seed generated IRFC segmentations. In other words, the theory of IRFC segmentations contains, as special cases, the theories of RFC and IRFC segmentations generated by singleton seeds, as well as the theory of RFC in the case of multi seed generated objects.
Equation (5) shows a beautiful relation between the RFC objects, PsS, generated by singleton seeds and their multi seed generated counterparts PSS. Could we also prove its iterative analog? This certainly would give a hope that a large part of multi seed IRFC theory could be easily deduced from its single seed counterpart. However, the iterative analog of (5) is false as can be seen in Example 3.14. Thus, we need to prove our results in a full multi seed setting.
The most fundamental property of any segmentation is that the objects it creates are pairwise disjoint. For IRFC segmentation, this is given by the following theorem.
Theorem 2.4
For any family of subsets of a scene C, we have for every distinct .
Since the iteration leading to the sets uses the formula as in rather than as in , the proof of Theorem 2.4 is rather complicated and it will be postponed till the next section. It is also worth to notice that, in our proof of the equation (see Theorem 3.7), we need to use Theorem 2.4 in the formalism.
Notice that, in the formulation of Theorem 2.4, we assumed almost nothing about the family of sets of seeds. We will continue with these minimal assumptions about throughout most of the theoretical development that follows, since this does not make the proofs any more difficult. Moreover, in some cases (e.g., when we modify to form another family of seeds to compare the -segmentation with -segmentation), it saves us the trouble of checking any extra properties we could impose on the generating families of seeds. However, in practical applications, we will apply our algorithm only when the sets in are nonempty and pairwise disjoint.
Notice that allowing the empty set to be in does not change much, since is empty for any and j. The fact that allowing overlapping sets in also changes little is more subtle. It is true that if a seed s belongs to distinct , then s does not belong to , or any other . This is certainly an undesirable situation, since we would like the generating seeds S to be in the object they generate. Unfortunately, a simple assumption that the sets in be pairwise disjoint does not solve the problem: if are distinct and there are s ∈ S and t ∈ T with μC(s, t) = 1, then neither s nor t belongs to . Then the question arises as to what part of S belongs to . In Lemma 3.2, we will show that the missing seeds are precisely those from the above example: if , then , while is disjoint with . We will also show in Proposition 3.12 that, even if is nonempty, it is possible to redistribute its elements (i.e., to find a family with ) in such a way that for every . Moreover, we can ensure that for every .
The second fundamental property of our segmentation method is its stability with respect to different choices of seeds initializing the segmentation process. This will be discussed in the next subsection.
2.4 Robustness of IRFC segmentation
The most natural impulse for a formulation of a robustness theorem in our setting is to state it in the compact format of Proposition 2.2: “For a family of seeds and nonempty sets , , where .” However, in a multiple seed setting, there is no hope for such a result even in the case of RFC or AFC. To verify this, consider a scene that contains three uniform circles C1, C2, and C3 which are pairwise completely separated. (This means that for any c ∈ Ci and d ∈ Cj we have μC(c, d) = 1 for i = j and μC(c, d) = 0 for i ≠ j.) If we choose S1 = T1 = C1, S2 = C2 ∪ C3 and T2 =C2, then , while is smaller. The difficulty outlined in this example comes from the fact that an object may have more than one connected component, while Ti may intersect only one of them. Thus, to insure that this will not happen, we will assume that Si ⊆ Ti, leading to the following result.
Theorem 2.5
Let be a family of subsets of C, fix k ∈ {1, 2, 3, . . .}, and let for every i ∈ {1, . . ., m}. If , then for every i ∈ {1, . . . , m}. Moreover, if k = 1, then for every i ∈ {1, . . . , m} and j ∈ {0, 1, 2, . . .}.
This theorem shows that there is considerable flexibility in the choice of seeds used to iteratively generate an object : as long as we choose the seeds inside P and ensure that they contain some minimal set of generators, the final result will always be the same. The version of the theorem when k = 1 has even nicer conclusion. However, the assumption that may be somewhat restrictive—it may be difficult to guess which spels be in the “core part” of the object, even in the case when the entire object, , can be guessed with a good approximation. Note also that, in fact Theorem 2.5 remains true, if we assume that each Ti contains only a subset TSi of Si described in Proposition 3.10.
The only version of Theorem 2.5 that was previously proved in the literature (see [15]) was done only for two components, in a single seed format, and in the version with k = 1 (i.e., Corollary 2.7 below for m = 2).
Theorem 2.5 directly leads to the following corollary.
Corollary 2.6
Let and be the families of subsets of C, fix k ∈ {1, 2, 3, . . .}, and assume that for every i ∈{1,...,m} we have and . Then for every i ∈ {1, . . . , m}. Moreover, if k = 1, then for every i ∈ {1 , . . . , m} and j ∈ {0, 1, 2, . . .}.
Proof
For i ∈ {1, . . . , m}, put Ui = Si ∪ Ti and let . Then, the pairs and satisfy the assumptions of Theorem 2.5, so, for every i ∈ {1, . . . , m}. If k = 1, we also have for every j ∈ {0, 1, 2, . . .}.
When we restrict our attention to the segmentation generated with only singleton seeds, one of the inclusions in the assumptions of Corollary 2.6 can be dropped and we obtain an analog of Proposition 2.2.
Corollary 2.7
Let S = {s1, . . . ,sm} and T = {t1, . . . , tm} be some m-element subsets of C and assume that for every i ∈ {1, . . . , m} we have . Then for every i ∈ {1, . . . , m} and j ∈ {0, 1, . . .}.
It is not accidental that in Corollary 2.7 we assume that each ti belongs to a smaller set rather than to a bigger set , as in our other robustness results—the version of Corollary 2.7 with assumption is false, even if we weaken the conclusion to . A simple example of such a situation is given in Example 3.15, where for all i while . This is yet another reason why in Theorem 2.5 we need the assumption Si ⊆ Ti.
3 The proofs and the examples
This section is designed mainly to prove the results announced in the previous section. This will require an introduction of some new concepts and proving several auxiliary results, some of which are of independent interest and are fundamental to the FC phenomenon. Unless otherwise explained, in what follows, will always stand for a digital scene with fixed adjacency and affinity relations, and for a nonempty family of subsets of C.
3.1 Disjointness of the segments
The following simple fact will be used (often implicitly) many times in this section.
Fact 3.1
If c, d ∈ A ⊆ B ⊆ C and p is a path in A from c to d such that μ(p) = μB(c, d), then μA(c, d) = μB(c, d).
Proof
This follows immediately from μA(c, d) ≤ μB(c, d) = μ(p) ≤ μA(c, d), where the first inequality is justified by (3) and the last is a consequence of the definition of μA.
The next lemma describes precisely what portion of S must belong to .
Lemma 3.2
For let . Then and E is disjoint with .
Proof
Clearly as μC(s, S) = 1 > μC(s, T) for any s ∈ S\ E and .
We will prove by induction on j ∈ {0, 1, 2, . . .}. For j = 0 it is obvious, as . So, assume that for some j we have . We need to show that . For this, choose a and, by way of contradiction, assume that c ∈ E. Then there is a for which μC(c, T) = 1. Moreover, any strongest path from c to T is in E, so, by Fact 3.1, we have μE(c, T) = 1. Also, , which follows from the inductive assumption, and (3) imply that . So, . However, this contradicts , which is a consequence of . So, indeed c ∈ C\ E.
Now, if , then the inclusion is proved by even easier induction. Indeed, if is true for some j, then for every s ∈ S; that is, no s ∈ S is in .
Let c ∈ A ⊂ C and S ⊂ A. We say that a path is a nice path (in A) from c to S provided c1 = c, cl ∈ S, and for every k ∈ {1, . . . , l}, we have μ(〈ck, . . . , cl〉) = μA(ck, S), that is, 〈ck, . . . , cl〉 is a strongest possible path in A from ck to S. If S = {s}, then we will say that p is a nice path (in A) from c to s, rather than to S.
Lemma 3.3
For every c ∈ A ⊂ C and S ⊂ A, there exists a nice path in A from c to S.
Proof
We will start with the following simple remark. In its statement, by a one-to-one path we understand any path in which no spel appears more than once.
(I) For every d ∈ A ⊂ C and S ⊂ A there exists a one-to-one path from d to an s ∈ S with μ(p) = μA(d, S).
Indeed, let be a shortest path in A from d to an s ∈ S with μ(p) = μA(d, S). Then p must be one-to-one. Otherwise, there would exist 1 ≤ i < j ≤ l for which ci = cj. But then the path 〈c1, . . . , ci, cj+1, . . . , cl〉 would be a strongest path in A from d to an s ∈ S of shorter length than p, which contradicts the choice of p.
Next we will prove, by induction on n = 1, 2, 3, . . ., the following statement.
In: For every c ∈ A ⊂ C and S ⊂ A there exists a one-to-one path from c to S such that for every i ∈ {1, . . . , n}
| (*) |
For n = 1 the statement is true: it is just the condition (I) we proved above. So, assume that In holds. We need to prove In+1.
So, pick c ∈ A ⊂ C and S ⊂ A. Let p = 〈c1, . . . , cl〉 be a path satisfying In. If l ≤ n, then p satisfies also In+1 and we are done. So, assume that l ≥ n+1. Let x = μ(〈cn, . . . , cl〉) = μA(cn, S), y = μ(〈cn+1, . . . ,cl〉)), and z = μA(cn+1, S). Then x ≤ y < z. If y = z, then p satisfies also In+1 and, again, we are done. So, assume that x ≤ y ≤ z. Let be a path from cn+1 to S with μ(q) = μA(d1, S). By (I) we can assume that q is one-to-one. Let . We will show that p’ satisfies In+1.
Indeed, clearly p’ is a path in A from c to S. To see that p’ is one-to-one assume, by way of contradiction, that this is not the case. Then there exist 1 ≤ i ≤ n and 1 ≤ j ≤ m such that ci = dj. But then
Thus, z ≤ μA(ci, S) = μ(〈ci, . . . , cl〉) ≤ μ(〈cn, . . . , cl〉) = x, contradicting x ≤ y < z. So, q is one-to-one.
To see (*) take an i ≤ n + 1, then condition (*) becomes μ(〈d1, . . . , dm〉) = μA(d1, S) and it is ensured by μ(q) = μA(d1, S). So, assume i ≤ n. Then μ(〈ci, . . . , cn, d1, . . . , dm〉) ≥ μ(〈ci, . . . , cl〉) = μA(ci, S), since μ(〈d1, . . . , dm〉) = μA(〈cn+1,S) ≥ μ(〈cn+1, ...,cl〉). Thus, (*) holds. This finishes the inductive proof of In.
Finally, note that if N is the size of A, then IN implies the lemma, since for any one-to-one path we have l ≤ N, so a path satisfying and IN must be nice.
The following fact is the iterative version of Fact 2.3.
Fact 3.4
If and p = 〈c1, . . . , cl〉 is a nice path from to S, then for every i ∈ {1, . . . , l}, that is, .
Proof
The proof goes by induction on j. For j = 1 it follows from Fact 2.3 and (5). So, assume that it is true for some j ≤ 1. We need to prove it for j + 1.
So, fix an and a nice path p = 〈c1, . . . , cl〉 from to S. First notice thatthere is an i ∈ {1, . . . , l} for which .
Indeed otherwise p is in and cl ∈ E, where E is as in Lemma 3.2. Pick a for which μC(cl, T) = 1 and let q be a path from cl to T with μ(q) = 1. Then q is in . Thus, p + q is a path in from c to T and , contradicting .
Let k ∈ {1, . . . , l} be the smallest number such that . Since 〈ck, . . . , cl〉 is a nice path from to S, by the inductive assumption we have that for every i ∈ {k, . . . , l}. Thus, we just need to prove that, for each i ∈ {1, . . , k - 1}, the spel ci belongs to .
If k = 1 there is nothing to prove. So, assume that k > 1. Then the proof is almost identical to that for Fact 2.3.
Fix an i ∈ {1, . . . , k - 1}, a , and a t ∈ T. Since , we know that . We need to show that ,as . Since
by (4) we have . Thus
completing the proof.
It would be nice if the conclusion of Fact 3.4 was true for any strongest path from c to S, rather than just for nice paths. This, however, is not the case. In the above proof, the place we used the stronger assumption is where we claimed that for every i ∈ {k, . . . , l}. If p is just any strongest path from c to S, then 〈ck, . . . , cl〉 does not need to be a strongest path from to S and it might happen that . A specific example of such a situation is a given in Example 3.13.
Fact 3.4 says, in particular, that if is a singleton, say S = {s}, then for every there is a strongest path in from c to s. The following remark gives a stronger version of this fact.
Remark 3.5
If is a singleton, then for every , there is a strongest path r in from c to d, that is, .
Proof
Let S = {s} and let p = 〈c1, . . . , cl〉 be a nice path from c to s and q = 〈d1, . . . , dm〉 be a nice path from d to s. Then, by Fact 3.4, . If μC(c, d) = min{μC(c, s), μC(d, s) = min μ(p), μ(q), then r = 〈c1, . . . , cl, dm, . . . , d1〉 is as desired. So, assume that μC(c, d) is greater than min {μC(c, s), μC(d, s)}. Then, in particular, μC(c, d) > μC(d, s) = μ(q). Let 〈b1, . . . , bn〉 be a nice path from c to d and put r = 〈b1, . . . , bn, d1, . . . , dm〉. We claim that r is a nice path from c to s. Indeed, clearly for any index i ∈ {1, . . . , m}, the path 〈di, . . . , dm〉 is a strongest from di to dm = s, since q was nice. Next, fix an i ∈ {1, . . . , n}. Since
we have, by (4), that μC(bi, s) = μC(d, s) and
Thus, r is a nice path from c to s and as such, by Fact 3.4, it is in . In particular, 〈b1, . . . , b〉 is in .
Assume that are distinct and that there exists a spel c ∈ C for which μC(c, U) < μC(c, S) = μC(c, T). Then . Is it possible that for some j > 1? This certainly would be counter intuitive. The next fact ensures us that this is impossible.
Fact 3.6
If and , then μC(c, S) s≥ μC(c, U).
Proof
By way of contradiction assume that μC(c, S) < μC(c, U). Choose a nice path p = 〈c1, . . . , cl〉 from c to U and let k ∈ {1, . . . , l} be the largest index with . Let s ∈ S. Since
(4) implies that μC(ck, s) = μC(c, s). Therefore, for every s ∈ S,
Thus, μC(ck, S) < μC(ck, U). Let i ∈ {0, 1, 2, . . .} be the smallest index with the property that . Note that i > 1 since μC(ck, S) < μC(ck, U). But, by the maximality of k, we have that . Therefore, implying . Since the minimality of i implies also that , we conclude , contradicting choice of i.
Proof of Theorem 2.4
We prove that by induction on j = 0, 1, 2, . . ..
Clearly the result is true for j = 0 since sets are empty. Also, definition the of clearly insures that the result is true for j = 1. So, assume that the result is true for some j. We need to show that the sets , with , are pairwise disjoint.
For this first notice that is disjoint with . Indeed, take a c∈ P and let be such that . By Lemma 3.3 there exists a nice path p (in C) from c to S. Fact 3.4 then shows that . Now, take a . We need to show that .
This is obvious if U = S, since . So, assume that U ≠ S. Then, by the inductive assumption, , so . In particular, . Now, by way of contradiction, assume that . Then, in particular, . Therefore, μC(c, U) > μC(c, S). But this, together with , contradicts Fact 3.6. So, indeed P ∩ Q = ∅.
Let Bj = C\ P . To finish the proof of the theorem it is enough to show that every c ∈ Bj belongs to at most one of with . So, fix a c ∈ Bj and let be such that . Let p = 〈c1, . . . , cl〉 be a nice path from c to U. If , then for every we have insuring that for every . So, we can assume that , that is, that there is an i ≤ l with ci ∈ P. Let k ∈ {1,...,l} be the smallest index such that ck ∈ P. Let be such that . We claim that
| (6) |
To see this notice first that μ(〈ck, . . . , cl〉) = μC(ck, U), since 〈ck, . . . , cl〉 is a nice path from ck to U. Note also that μC(ck, S) ≥ μC(ck, U). This is obvious if S = U. Otherwise, this follows from Fact 3.6, as . Let q = 〈d1, . . . , dm〉 be a nice path from ck to S. We claim that the path r= 〈c1, . . . , ck-1, d1, . . . , dm〉 satisfies (6).
Clearly r is a path from c to S and , since {c1, . . . , ck-1} ⊂ Bj, while follows from Fact 3.4. Also, μ(q) = μC(ck, S) μ (ck, U) = μ(〈ck, . . . , cl〉) implies that
Combining this with μC(c, U)≥ μC(c, S), which follows from the maximality of μC(c, U), we get
Thus, μ(r) = μC(c, U), completing the proof of (6).
To finish the proof of the theorem, notice that, by (6), for every we have insuring that .
3.2 Alternative definitions of
Theorem 3.7
Let j ∈ {0, 1, 2, . . .}, , and . If
then .
Proof
Since
by Theorem 2.4 we have . So, .
Clearly W ⊂ R, since . To see that R ⊂ W take a . Let p be a nice path from c to S and notice that, by Fact 3.4,
This implies that c ∈ W . So . Now, in order to prove the theorem it is enough to show that W = Z.
By Theorem 2.4, we have for every . Thus, for every and c ∈ C. So, W ⊂ Z.
To see that Z ⊂ W take a c ∈ Z and by way of contradiction assume c ∉ W. Then, there is a such that . Also, since c ∈ Z. So, .
Let p = 〈c1 , . . . , cl〉 be a nice path in from c to T. Notice that p cannot be a path contained in , since this would imply which contradicts the inequality . Thus, p intersects . Let k ∈ {1, . . . , l} be the smallest index such that . Let be such that . Then U ≠ S, since . If U = T, then since 〈ck, . . . , cl〉 be a nice path from to T. Thus, which contradicts the inequality . Thus, we can assume that U ≠ T.
Let q be a nice path from to U. Then, by Fact 3.4, . Also, by Fact 3.6, μC(ck, U) ≥ μC(ck, T). Then
Thus, if r = 〈c1, . . . , ck-1〉 + q, then μ(r) ≥ μ(p) and . So
contradicting c ∈ Z.
Theorem 3.7 justifies our earlier claim that the iterative definition of can be obtained by using an approach as in the formula for instead of the one in the formula for . More precisely, we have , where
Recall also that in (2) we defined only for spels c, d ∈ A, since in any other case the sets and are empty. However, it is standard to define max ∅ to equal -∞ With this agreement in hand, we can consider μA given by (2) as a function from C × C into [-∞, ∞]. Then the definition of can be written in a slightly more compact form:
| (7) |
The formula is valid since if and only if for every .
For A, B, D ⊂ C let
We are introducing this notation since it is easier to work with it (see Fact 3.8) than with the other definitions of , including (7). At the same time can be easily expressed in this language:
where and .
3.3 The robustness results
We start here with a list of the properties of .
Fact 3.8
Let A, B, D, V ⊂ C. Then,
,
for every B’ ⊂ B,
for every A’ ⊂ A,
for every D’ ⊂ D,
If for some k ∈{0, 1, 2, . . .} and , then .
Proof
(a) is obvious from the definition of . (b) follows immediately from (a). (c) holds, since μC(c, A) ≥ μC(c, A’). To see that (d) holds notice that D’⊂ D implies C\D’⊃ C\D. Thus, by (3), μC\D’(c, b) ≥ μC\D(c, b), implying (d).
(e) Fix a and a b ∈ B. We need to show that
| (8) |
Notice that μC(c, R) > μC\D(c, b), since . Let p = 〈c1, . . . , cl〉 be a strongest path from c to R and let m ∈ {1,...,l}be minimal such that r = cm ∈ R. Then μC (c, r) ≥ μ(〈 c1,...,cm〉) ≥ μ(p)= μC (c, R) ≥ μC(C, r). Thus, we have μ(〈c1,..cm 〉) = μC (c, R) > μC\D (c,b). If r ∈ A, then μC (C, A) ≥ μC (c, r) > μC\D (c, b), proving (8). So, we can assume that . Thus, there exists an n ≤ k with the property that . In particular,
| (9) |
Also, since , path 〈c1, . . . , cm〉 is in . So, by Fact 3.1,
| (10) |
Next we will prove that
| (11) |
If , then, by (4), . So, by (9), , where the last inequality is justified by (3) and an inclusion . Thus, in this case, (11) holds. So, assume that . Then, by (9) and (10), we get , finishing the proof of (11).
Now, by (10) and (11), μC(c, r) > μC\D(c, b) and μC(r, A) > μC\D(c, b). Let p1 be a strongest path from c to r and p2 be a strongest path from r to A. Then μ(p1+ p2) = min{μ(p1), μ(p2)} = min{μC(c, r), μC(r, A)} and so
finishing the proof of (8) and (e).
Lemma 3.9
Let , where is fixed. If j, k∈ {0, 1, 2, . . .}, , and , then the following holds.
.
.
If , then .
If , then .
If either k = 0 or , then and for every j ≥ k and . In, particular, . Moreover, if k = 0, then also all intermediate segmentations are equal: for all j ≥ 0.
Proof
All properties (a)-(d) are proved by induction on j and they are obvious for j = 0.
(a) To make an inductive step, assume that is a subset of and put . Since A ⊂ R, conditions (c) and (d) from Fact 3.8 give .
(b) To make an inductive step, assume that is a subset of . First note that . To see this, it is enough to show that . But if there is an such that S = R, then , where E is as in Lemma 3.2. Since, by Lemma 3.2 and Theorem 2.4, this last set is empty, we get S ⊆ A. But we have also A ⊆ R = S, so , contradicting the definition of .
Let , put , and notice that follows from from Fact 3.8(d). Then conditions (d) and (e) from Fact 3.8 give , completing the proof of (b).
(c) To make an inductive step, assume that it is true for some j, that is, that contains . Since is a subset of , conditions (b) and (d) from Fact 3.8 give .
(d) To make an inductive step, assume that is a subset of . Let . Then is a subset of . Notice that it is enough to prove that since this and Fact 3.8(d) imply .
To show take a . Then μC(c, V) > μC\D’(c, B’). We need to prove that
| (12) |
If μC\D’(c, B’) ≥ μC\D’(c, B), then μC(c, V) > μC\D’(c, B’) ≥ μC\D’(c, B) proving inequality (12). Thus, by way of contradiction, we can assume that μC\D’ (c, B’) < μC\D’ (c, B). We will find v ∈ V , r ∈ B, a ∈ A, and D0 ⊆ C such that
| (13) |
First notice that (13) gives us a desired contradiction, since then a ∈ B’ implies μC\D’(c, B’) ≥ μC\D’(c, a) > μC(c, V) contradicting . Thus to finish the proof it is enough to show (13).
First, we will choose an appropriate r. Let p0 = 〈c1, . . . , cl〉 be a strongest path in C\ D’ from c to B and let m ∈ {1, . . . , l} be minimal such that r = cm ∈ B. Then μC\D’(c, r) ≥ μ(p0) = μC\D’ (c, B) ≥ μC\D’ (c, r), where p = 〈C1, ..., Cm 〉. In particular, μ(p) = μC\D’(c, r) = μC\D’(c, B).
Let a ∈ A be such that there is a path q from r to a which is a nice path from r to A. Since μC\D’(c, r) = μC\D’(c, B) > μC\D’(c, B’) ≥ μC\D’(c, a) the equation μC\D’(c, a) = μC\D’(r, a) follows from (4).
To show μC\D’(r, a) = μC(r, a) note that , since μC\D’(c, r) = μC\D’(c, B) > μC\D’(c, B’). In particular, since q is a nice path from r to A, then, by Fact 3.4, q is in . As μC(r, a) = μ(q), Fact 3.1 implies μC\D’(r, a) = μC (r, a).
Next, we need to choose D0 and v ∈ V. Let q be a path from c to v which is a nice path from c to V . Then μC(c, v) = μC(c, V). Since , there is an n ≤ k with . We put . Then .
To prove μC\D0(r, v) = μC(c, V) it is enough to show μC\D0(r, v) = μC\D0(c, v) and μC\D0(c, v) = μC(c, V). Recall that μ(p) = μC\D’(c, r) = μC\D’(c, B), where p is in since {c1, . . . , cm-1} is disjoint with , while . By this and a part of (13) proved so far μC\D0(c, r)≥μ(p) = μC\D’(c, B) > μC\D’(c, B’)≥ μC\D’(c, a) > μC\D0(r, v). So, by (4), we get μC\D0(r, v) = μC\D0(c, v).
The equation μC\D0(c, v) = μC(c, V) follows from Fact 3.1, since q, as a nice path from to V , is in . This finishes the proof of (d).
(e) Parts (c) and (d) imply that for every and j ≥ 0.
If j ≥ k, then follows from . Here follows from (b); equation is obvious when k = 0 and is proved by an easy induction when ; inclusion is a restatement of (a).
Proof of Theorem 2.5
First notice that Lemma 3.9(e) implies that (*) the theorem is true if Ti = Si for every i ≥ 2.
Now, the general form of the theorem follows from (*) by induction on m. Indeed, for 0 ≤ l ≤ m and i ∈ {1, . . . , m} put for i ≤ l and otherwise. Let . Then , . and to every pair we can apply (*). Thus, applying it m-times, we get that for every i ∈ {1, . . . m} and an appropriate j.
Proof of Corollary 2.7
Let Ui = {si, ti} and put , , and . Then, by Theorem 2.5 (version with k = 1), for every i ∈ {1, . . . ,m} we have . To finish the proof is enough to show that
| (†) |
since then, again by Theorem 2.5, for every i ∈ {1, . . . , m}.
First notice that for every distinct i, k ∈ {1, . . . , m}
| (14) |
Indeed, since we have μC (tk, sk) > μC (tk, si). Therefore, by (4), μC(tk, si) = μC(si, sk). Similarly, implies μC(ti, si) > μC (ti, sk) so, by (4), μC(ti, sk) = μC(si, sk). This proves (14).
Now, to prove (†) take distinct i, k ∈ {1, . . . , m}. We need to show that μ C (si, ti) > μC(si, tk). But implies μC (ti, si) > μC (ti, sk). Combining this with (14) gives μC(si, ti) = μC(ti, si) > μC(ti, sk) = μC(si, tk).
3.4 How to choose seed generating families S?
In a general setting, the title question is well beyond the scope of this paper. What we will discuss here is only its very restricted version: Given , how to modify it to get either the same or a better segmentation?
The first of the results presented here estimates the size of minimal subsets TS of for which the segmentations and are equal, where .
Proposition 3.10
For every let , where . Then
Sets in are pairwise disjoint.
If , then if and only if T intersects every .
In particular, if for every we choose a which intersects every and put , then for every j ≥ 0.
Proof
(a) If for some s, t ∈ A, then, by Corollary 2.7, .
(b) Let A0 ⊂ A be minimal such that . By (5) we have . Thus, for every t ∈ T there is a unique at ∈ A0 such that . Note that follows from Corollary 2.7. Let A1 = {at: t ∈ T }. Then, by (5), and the equation holds precisely when A1 = A0, that is, when T intersects every .
The value of Proposition 3.10 comes from the fact that, usually, the size of is quite small, even if the set A is quite big. Note also, that it is possible that the equation may hold for sets which do not intersect every . Such a situation is described in Example 3.16.
Lemma 3.11
Let and , where . If A0 = A\ E, then for every j ≥ 0.
Proof
Inclusion follows from Lemma 3.9(a). We just need to show that . This will be proved by induction on j ≥ 0.
For j = 0 it is obvious, as both sets are empty. So, assume that for some j we have . We need to prove that . For this, choose a . We need to show that .
So, fix a . We need to prove , where the equation follows from our inductive assumption that . However, since , we have . Thus, to finish the proof, it is enough to show that
| (15) |
By way of contradiction, assume that (15) is false. Then μC(c, A) > μC(c, A0). Let a ∈ A\ A0 ⊆ E be such that μC(c, a) = μC(c, A). Let be such that μE(a, T) = μC(a, T) = 1 and let q be a path in E from a to T with μ(q) = 1. Also, let p = 〈c1, . . . , cl〉 be a strongest path from c to a. Thus, μ(p) = μC(c, a) = μC(c, A) > μC(c, A0). If p is disjoint with then so is p + q and contradicting . So, assume that p intersects . Let k < j be minimal that p intersects and let n ∈ {1,...,l} be such that . Then . Also, μC(c, cn) ≥ μ(〈c1, . . . , cn〉) ≥ μ(p) = μC(c, A). So, μC(c, A0) ≥ min{μC(c, cn), μC(cn, A0)} ≥ μC(c, A), finishing the proof.
Recall that .
Proposition 3.12
For every , there exists a TS containing such that if , then , for every , and for every and j ≥ 0.
Proof
For s ∈ C let [s] = {t ∈ C : μC(s, t) = 1}. Thus, each [s] is an equivalence class of an equivalence relation ∼ on C defined by s ∼ t if and only if μC(s, t) = 1. In particular, the sets in are nonempty and pairwise disjoint. Let be a selector of , that is, such that W intersects each at precisely one element. Define . We will just sketch the proof that these sets are as desired.
Clearly , as for every there are and w ∈ W ∩ S such that s ∈ [w], so .
Next, fix an . To see that put and notice that and that contains union of . Thus
Here, the second equation follows from Lemma 3.11, the first inclusion from Fact 3.8(c), while the second inclusion is a consequence of Fact 3.8(b). The proof of the third equation is very similar to that of Lemma 3.11 and uses the fact that any [c] intersecting Z intersects also . (This proof relies also on the fact that every strongest path p between spels in [c] is in and that implies .)
The inclusion follows from Lemma 3.2 and the fact that .
3.5 Examples
In this subsection, we will present the examples announced earlier in this paper, which show different limitations for our results. The examples are presented in a graphical form, where vertices represent spels from a given scene while a number next to an edge of a graph represents the affinity between the connected vertices. Lack of an edge between vertices means that the affinity between the spels they represent is equal to 0.
Our first example shows that, unlike a nice path, a strongest path from an to d need not to be contained in .
Example 3.13
Assume that a scene contains spels a, b, c, d, and s, connected as in Figure 6(a). Let S = {d, s}. Then and . Also, , since . However, the path p = 〈a, b, c, d〉 is strongest between and d, but it is not inside .
Figure 6.
Affinities for Examples 3.13 and 3.14.
The following example shows that the iterative analog of formula (5) is false.
Example 3.14
Assume that a scene contains spels s, t, u, and c, connected as in Figure 6(b). Let S = {s, t}, U = {u}, and . Then , , and . However, and , showing that .
The following example shows that, in Corollary 2.7, we cannot weaken the assumptions to , even if we also weaken the conclusion to .
Example 3.15
Assume that a scene contains spels a, s, and t, connected as in Figure 7(a). Let S = {s, t}. Then for j > 1 we have and . However, if we replace a seed s with and put T = {a, t}, then for every i > 0 and j > 1, we have , and .
Figure 7.
Affinities for Examples 3.15 and 3.16.
The next example shows the limitations of the result from Proposition 3.10.
Example 3.16
Assume that a scene contains spels s, t, u, and c, connected as in Figure 7(b). Let S = {s, t}, U = {u}, and . Then is disjoint with . However, although TS = {s} does not intersect , we still have .
4 The algorithm
In this section, we present an algorithm, called κIRMOFC (abbreviation for iterative relative multi object fuzzy connectedness), allowing a set of seeds for each object. Within this algorithm, the algorithm κFOEMS as described in [18] for multi seeded AFC is called. κFOEMS takes as an input a given scene , an affinity function κ, and a set S ⊂ C of seeds. Its output is a connectivity scene , where fκ,S(c) represents the strength of a κ-strongest path from c to S. Aspects related to the computational efficiency of algorithm κFOEMS have been addressed in [20,21]. For A ∈ C, by the restriction of κ to A we will understand an affinity κ’ on C such that, for every distinct c, d ∈ C, we have κ’(c, d) = κ(c, d) for c, d ∈ A, and κ(c, d) = 0 otherwise. In the algorithm κIRMOFC, we will use the fact that, for distinct c, d ∈ C, the number μA(c, d) is equal to μC(c, d) calculated with respect to the restriction of κ to A.
Algorithm κIRMOFC
Input
, κ as defined in Section 2, a family of pairwise disjoint sets of seed spels such that κ(s, t) < 1 for any s and t from distinct sets from .
Output
For each S in , iteratively defined fuzzy κ-object containing S and relative to a background containing .
Auxiliary Data Structures
For each , the κ-connectivity scene , the κS-connectivity scenes , where κS is the restriction of κ to , and the temporary scenes such that fS corresponds to the characteristic function of . Index j refers to the iteration level; that is, the number of completed while loops, in Steps 5-16, for each fixed S.
begin
1. for each do
2. compute by using κFOEMS;
3. set all elements of to 0 (this corresponds to setting );
4. set κS = κ and flag = true;
5. while flag = true do
6. set flag = false;
7. compute by using κFOEMS;
8. for all c ∈ C do
9. if fS(c) = 0 and fκ,S(c) > fκS,W(c) then
10. set fS(c) = 1;
11. set flag = true;
12. for all d ∈ C, d ≠ c, do
13. set κS(c, d) = 0;
14. endfor;
15. endif;
16. endfor;
17. endwhile;
18. output ;
19. endfor;
end
In the above algorithm each run of the loop of Steps 2-18 is independent of the other runs and can be considered as a subroutine (similar to algorithm κIFROE from [15]) which for seeds S and W returns an IRFC object containing S and relative to a background containing W. The value of flag determines whether in the previous run of the loop in Steps 6-16 there was at least one spel which was added to the object (i.e., changed value of fS(c) from 0 to 1). Since the number of spels c ∈ C is finite, eventually no change is made and the loop terminates. Each time the algorithm enters the loop in Steps 6-16, fS is the characteristic function of the previous stage, say jth stage, is the approximation of , while κS is the restriction of κ to . Notice that this situation remains true when Steps 6-16 of the next stage are completed. Indeed, the loop of Steps 9-15 is entered for each c and the if statement is performed only if c was not yet in , but the inequality indicates that c is added to . This is done at Step 10, while the loop in Steps 12-14 restricts current κS to C\ {c}. Thus, when Steps 9-15 are finished, all seeds from for which are added to , and the new κS is the restriction of the old κS to , so it is the restriction of κ to the set . The argument from this paragraph justifies the following result.
Proposition 4.1
For any scene over , for any fuzzy affinity relation κ in , and for any non-empty family of non-empty pairwise disjoint subsets of C such that κ(s, t) < 1 for any s and t from distinct sets from , algorithm κIRFCMO terminates, for every , and the family is the IRFC segmentation of .
5 Results and evaluation
5.1 Qualitative Evaluation
In this section, we present the results of application of the IRFC method and compare them with the results obtained by using RFC. Specifically, we present qualitative results of the following three experiments: (1) segmentation of individual vertebra from a 3D CT scene of a human cervical spine; (2) artery/vein separation in contrast-enhanced MR angiograms; (3) segmentation of white matter (WM), gray matter (GM), and cerebro-vascular fluid (CSF) in simulated MR scenes obtained from BrainWebMR simulator [22].
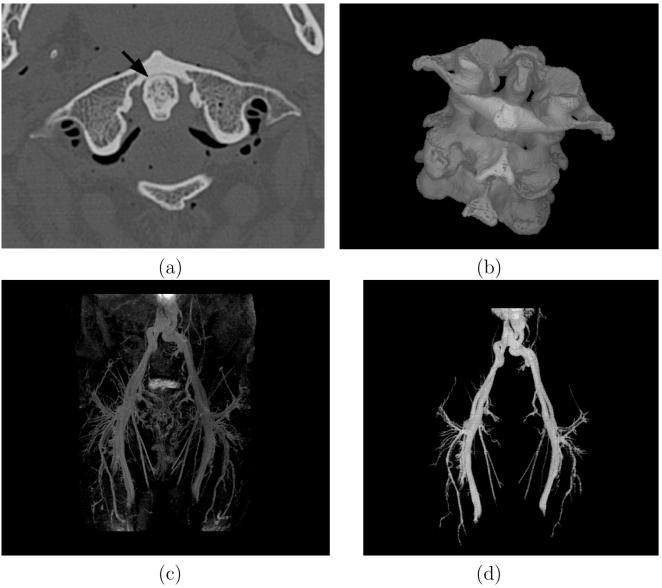
The contact area between the two cervical vertebrae C1 and C2 is shown by an arrow. (b) A surface rendition of the vertebral column consisting of three vertebrae segmented by using AFC. (c) A Maximal Intensity Projection (MIP) rendition of a 3D contrast enhanced MR angiography scene of the body region from belly to knee. (d) A surface rendition of the entire vascular tree segmented by AFC from this scene.
The aim of our first experiment is to compare the performances of RFC and IRFC in segmenting the individual vertebrae. Figure 8(a) displays a region of interest from a slice in the 3D CT data (size: 512 × 512 × 77, voxel size 0.23×0.23×1.0 mm3). In CT scenes, bones appear bright, and it is not difficult to segment them from the rest of the body region. Figure 8(b) displays a surface rendition of the cervical spine column after segmenting it from other bones and soft tissues by using AFC. Here, AFC is used instead of simple thresholding since the former simultaneously removes other non-vertebral bone regions which otherwise would have to be segmented by using a subsequent connectivity analysis. Also, AFC outperforms simple thresholding and connectivity analysis for spels with partial bone occupancy. Our aim in this experiment is to segment the three vertebrae (C1-C3) from the spinal section shown in Figure 8(b). The major challenges in separating the individual vertebrae are: (1) complex shape and geometry of the contact regions between two successive vertebrae; (2) the fuzzy fusion at these junctions (see Figure 8(a)); (3) porous interior of the vertebrae due to the existence of cancellous trabecular bone. It is difficult to separate these vertebrae by using intensity-based features. Therefore, we applied a morphology-based separation through the use of RFC and IRFC methods. The following preprocessing steps were applied first. The cavities created by the trabecular bone network were separately filled in each slice to generate the bone region RB. We used RB to define an affinity relation κ utilized in the RFC and IRFC separations of the vertebrae as follows.
Figure 8.
(a) An axial slice from the CT scene of a patient’s cervical spine.
First, for a given scene 〈C, f〉, a separate bone volume fraction scene 〈C, fB〉 was computed by setting
where Bonemax and Bonemin represent maximal and minimal intensities of spels in RB, respectively.
For a path p = 〈c1, c2, . . . , cl〉 in C, wherein the consecutive spels are 26-adjacent, we define its fuzzy length as
is interpreted as an average bone density of the link 〈ci, ci+1 〉, then πB(p) is approximately the total bone mass of p.) The fuzzy distance transform [23] is derived from fB as follows:
(Under the interpretation as above, ΩB(c) is the smallest mass of a path connecting c with the complement of RB.) Now, affinity between spels c and d is defined as given below, where N = maxc ∈ CΩB(c):
| (16) |
Next, RFC and IRFC algorithms were applied to 〈C, f〉 by using the affinity relation defined above on 〈C, fB〉. The same set of seeds, selected manually, was used for both methods. The results of vertebral separation obtained by using RFC and IRFC are illustrated in Figures 9(a)-(d), (a) and (c) showing the results on a slice, and (b) and (d) depicting the result via 3D surface rendering. In both figures, voxels segmented as part of a specific vertebra are assigned the same color. In the slice display, spels shown white indicate that they were not assigned to any specific bone. Although RFC has succeeded in capturing the skeletal core of each vertebra after segmentation, it has lost most of the regions of each bone (too many white spels in the slice display) and the results are obviously not acceptable. Despite fuzzy fusion at contact regions between the vertebrae, IRFC has successfully separated them. IRFC stopped after 8, 14, and 15 iterations, respectively, for the first, second, and third vertebra. For the particular affinity function defined above, the results of RFC-based vertebral separation are similar to the results that may be obtained by using morphological erosion with a ball of appropriate size. The beauty of RFC is that, effectively, the radius of the eroding ball is automatically computed by the RFC method. The results obtained by IRFC cannot be produced by using a simple morphological operation.
The aim of our second experiment is to demonstrate how IRFC can be employed to separate arteries and veins in contrast-enhanced MR angiography scenes. MR imaging approaches [25] exist which attempt to elicit different types of signals from the arteries and veins through carefully designed imaging protocols and thereby to distinguish arteries from veins. Here, we use RFC and IRFC to separate artery/vein trees from MR scenes that are acquired by using long resident blood-pool contrast agents [26] which do not produce different signals from the arteries and veins, but which provide a better overall definition of the vessels themselves. Figure 8(c) shows a maximum intensity projection (MIP) rendition from a patient MRA scene (size: 512 × 512 × 60; resolution: 0.94 × 0.94 × 1.8 mm3) of the body region from belly to knee. Figure 8(d) shows a surface rendition of the whole fuzzy vascular structure that was segmented by using AFC from the original MRA data set. Figures 9(e) and (f) show renditions of the fuzzy arterial and veinous trees separated via RFC and IRFC, respectively. Note that, in this experiment, RFC (or, IRFC) was applied between arteries and veins so that when the arterial tree was segmented the veinous tree served as the background and vice versa.
For this experiment, a morphology-based affinity was computed in a manner similar to the first experiment Equation (16), except that no 2D cavity filling was necessary. In this case, the algorithm stopped after nine iterations. Clearly, IRFC has captured more thin branches in segmented arterial and veinous tress than those captured by RFC. Also, RFC segmentation of the main arterial branch on the right appears largely broken and the same is true for the main veinous branch on the left. On the other hand, the main branches in IRFC segmentation of both arterial and veinous trees appear complete, continuous, and smooth.
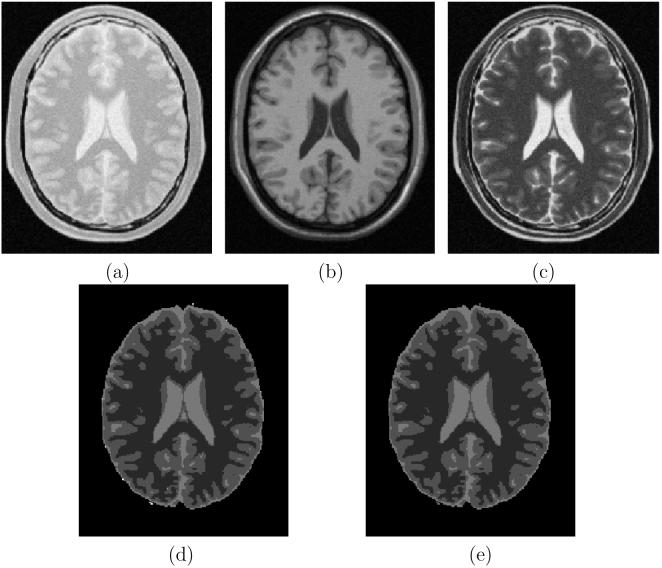
The results of segmentation, by using RFC and IRFC, of WM, GM, CSF in a simulated MR scene produced by the BrainWebMR simulator [22] are presented in Figure 10. Figures 10(a)-(c) show corresponding slices from the simulated proton density, T1-, and T2-weighted MR data sets. Affinity was computed from the three MR data sets after combining them into one vectorial scene [27]. A set of seeds was manually specified for each of the three regions, and the regions were segmented by using RFC and IRFC. These results are shown in Figures 10(d) and (e). It may be noted that there is not much difference between the segmentation results for RFC and IRFC. As in this example, when one object wraps around the entire boundary of the other object, the scope of refinement of segmentation by using IRFC is reduced. Generally, IRFC outperforms RFC when a relatively large part of one object comes close to a large part of another object, forming a fuzzy interface between them, but otherwise the remaining smaller aspects of the objects have a clean association with the two objects, as in our second example above. This situation can also occur in a multi object setting, as in our first example.
Figure 10.
Results of WM, GM, and CSF segmentation on simulated MR scenes produced by BrainWebMR simulator. (a)-(c) Matching slices from simulated PD, T1-, and T2-weighted MR data sets. (d) Segmentation of WM (dark), GM (intermediate brightness), and CSF (bright) regions obtained by using RFC. (e) Same as (d) but for IRFC.
5.2 A Quantitative Evaluation
The purpose of this experiment is to quantitatively evaluate the performance of IRFC and compare it with the performance of RFC under various levels of noise, blurring, and intensity inhomogeneity in the scene. Toward this goal, five 2D scenes , T ∈ {1, 2, 3, 4, 5}, were created by using the drawing tools supported by 3DVIEWNIX [24]. Each of these scenes contained four separate objects and a background. The object regions and the background were assigned different constant intensities. One such scene is shown in Figure 11(a). Next, each scene was modified by: blurring it (via a 2D Gaussian kernel) at one of three fixed blur levels B1 > B2 > B3; adding noise at one of three fixed levels N1 > N2 > N3; and introducing to it intensity inhomogeneity from one of three fixed levels I1, I2, I3. A scene with added blur B ∈ {B1, B2, B3}, noise N ∈ {N1, N2, N3}, and intensity inhomogeneity I ∈ {I1, I2, I3}, is denoted as . Thus, from each of the five scenes , we generated 27 modified phantom scenes . Three of these 135 phantom scenes, generated from the scene of Figure 11(a), are illustrated in Figures 11(c)-(e).
In each scene , each spel c ∈ C is assigned to a unique object. Let LT : C → {0, 1, 2, 3, 4} denote the true object labeling function; that is, the set {c ∈ C : LT (c) = i} is the i-th object for i ∈ {1, 2, 3, 4} and the background, when i = 0. Figure 11(b), used as a reference, presents the true object labeling for Figure 11(a). We will denote by OT the set of all spels with non-zero label in .
Object labeling of the phantom scenes is accomplished in two steps—separation of the foreground from background, and separation among the four objects. This is because the nature of the segmentation task between background and foreground is entirely different from segmentation among objects within the foreground. In the former case, there is a clear intensity difference, and a simpler approach like AFC works fine. On the other hand, among the different foreground objects there is no clear intensity difference and intensity-based approaches will not work. After segmenting the foreground from the background by using AFC, a fuzzy membership scene was created as follows. Let denote the set of spels in the foreground region and let ρ and σ denote the mean and standard deviation of spel intensity values over .
A foreground fuzzy membership value at a spel was then created, defined by
A fuzzy distance transformation map was then computed from , which was utilized to define affinity as described previously Equation (16). Finally, RFC and IRFC methods were applied to obtain multi-object segmentations within the foreground region. Segmentations resulting from RFC and IRFC for scenes in Figures 11(c)-(e) are shown, respectively, in Figures 11(f)-(h) and (i)-(k). In these displays, white colored spels represent foreground spels that are not assigned to any specific region. (Those were referred to as “boundary spels” in our theoretical discussion.) Clearly IRFC has successfully separated the objects while preserving the thin branches, and RFC has captured only the core of the objects and the results are similar to those that can be obtained via morphological erosion.
Let and denote the object labels estimated at a spel c from a phantom scene by using RFC and IRFC, respectively. We use here the label value 5 for the foreground spels which are not assigned to any of the four objects. A similarity measure between LT (c) and (or ) is necessary to assess the performance of the two methods. Unlike the one object case, establishing agreement with truth in the case of multiple objects simultaneously is tricky. Here, we have used a figure-of-merit (FOM) that gives a full score only when the label of a spel in the segmentation matches with the true label at that spel; otherwise the score is 0. Specifically, the figure of merit , with X ∈ {RFC, IRFC}, for the phantom scene is defined as
where symbol denotes the number of spels in , and F(a, b) = 1 for a = b and F(a, b) = 0 for a ≠ b . Finally, at any given blur, noise, and inhomogeneity level BNI, the mean and the standard deviation values of , for T ∈ {1, 2, 3, 4, 5}, are computed. Tables 1 and 2 list the mean and standard deviation of these FOM values for RFC and IRFC methods, respectively. It is clear from these tables that the performance of IRFC is superior to that of RFC.
Table 1.
The mean and standard deviation (in parenthesis) of the similarity measure , T ∈ {1, 2, 3, 4, 5}, are shown for each blur, noise, and inhomogeneity condition.
| B1N1I1 | 31.29(4.36) | B2N1I1 | 26.23(4.90) | B3N1I1 | 25.56(5.36) |
| B1N1I2 | 26.67(3.78) | B2N1I2 | 24.83(5.12) | B3N1I2 | 21.72(5.78) |
| B1N1I3 | 26.51(4.68) | B2N1I3 | 21.92(5.23) | B3N1I3 | 20.31(6.09) |
| B1N2I1 | 26.69(3.89) | B2N2I1 | 24.42(4.89) | B3N2I1 | 21.73(5.45) |
| B1N2I2 | 24.28(5.11) | B2N2I2 | 19.89(5.13) | B3N2I2 | 17.93(5.85) |
| B1N2I3 | 22.47(3.96) | B2N2I3 | 18.29(5.24) | B3N2I3 | 15.92(6.12) |
| B1N3I1 | 25.49(5.21) | B2N3I1 | 21.92(4.99) | B3N3I1 | 18.00(5.54) |
| B1N3I2 | 22.58(4.76) | B2N3I2 | 18.18(5.33) | B3N3I2 | 15.78(6.02) |
| B1N3I3 | 20.09(4.59) | B2N3I3 | 16.03(5.02) | B3N3I3 | 15.93(6.11) |
Table 2.
The mean and standard deviation (in parenthesis) of the similarity measure , T ∈ {1, 2, 3, 4, 5}, are shown for each blur, noise, and inhomogeneity condition.
| B1N1I1 | 98.93(0.31) | B2N1I1 | 98.38(0.37) | B3N1I1 | 97.30(0.46) |
| B1N1I2 | 98.08(0.39) | B2N1I2 | 96.78(0.40) | B3N1I2 | 93.12(0.42) |
| B1N1I3 | 97.91(0.42) | B2N1I3 | 94.49(0.34) | B3N1I3 | 90.42(0.50) |
| B1N2I1 | 97.90(0.38) | B2N2I1 | 95.91(0.29) | B3N2I1 | 91.73(0.49) |
| B1N2I2 | 96.65(0.45) | B2N2I2 | 90.60(0.40) | B3N2I2 | 85.89(0.53) |
| B1N2I3 | 94.40(0.42) | B2N2I3 | 87.41(0.38) | B3N2I3 | 82.81(0.50) |
| B1N3I1 | 97.34(0.40) | B2N3I1 | 92.62(0.35) | B3N3I1 | 87.69(0.56) |
| B1N3I2 | 93.80(0.46) | B2N3I2 | 86.70(0.42) | B3N3I2 | 82.09(0.48) |
| B1N3I3 | 90.50(0.49) | B2N3I3 | 83.30(0.46) | B3N3I3 | 78.90(0.55) |
6 Concluding remarks
The theory of IRFC segmentation presented in this paper consolidates all earlier versions of FC segmentation theories in a unified framework. This is especially the case for the RFC theory, since any segmentation obtained with the RFC algorithm is just a first iteration step in the IRFC based algorithm. Since our exposition of the IRFC theory is presented with the iteration number as a parameter, the RFC results (viewed as the first-iteration-level-IRFC results) are readily accessible due to the format of our presentation of the IRFC theory.
It should also be stressed that the IRFC theory presented here is self contained. We were not able to use the theoretical results from earlier papers in this connection, because of the intricacy of the arguments needed for the IRFC theory. Thus, from a theoretical point of view, this paper supplants previous papers on FC theory.
Note also that, once the IRFC algorithm is implemented, there is no reason to implement also an RFC based algorithm separately. There are two reasons in support of this statement. First, it is easy to implement an IRFC algorithm that will ask an operator whether to impose a maximal number N of iterations. Then such an algorithm used with “no bound for N” is just our standard IRFC algorithm, and when run with N = 1, it becomes a standard RFC algorithm. Although this allows an implementation of RFC algorithm as a restricted version of IRFC, we do not believe that there is much benefit in running RFC segmentation once an IRFC program is at hand. It is true that, in principle, the RFC algorithm is simpler than IRFC, and in some cases (as demonstrated in Figures 10(d) and (e)) the RFC program works just as well as IRFC. However, in such cases, the first iteration of IRFC will already give the RFC “good enough” segmentation; that is, the IRFC algorithm will stop after just one iteration. Since the expense of running IRFC algorithm in the case it stops after just one iteration is only slightly higher than running the RFC algorithm, the benefit of an operator deciding whether to use IRFC or RFC is minimal, even when there is no better performance of IRFC over RFC.
Apart from its generality, IRFC is a more powerful technique than RFC. Our experiments indicate that there are potentially many situations wherein IRFC would perform better than RFC, especially when multiple objects come close to each other without one completely surrounding the other.
One area that requires careful scrutiny and that can make an impact on the practical utility of FC methods in segmentation is the proper design of affinity. In this paper, we have utilized mostly image-based strategies for defining affinity, as described in previous publications. We have also shown (see Equation (16)) that morphology-based strategies can also be employed to devise effective affinities. It is also conceivable that affinities can be constructed by utilizing information available in statistical shape models [28]. A question naturally arises then as to whether these three strategies can be combined in a FC-driven segmentation task to construct affinities. We are currently studying some of these issues in the context of specific imaging applications.
Acknowledgments
The first author was partially supported by NSF grant DMS-0623906, while working on this project.
The second author was partially supported by DHHS grant NS 37172, while working on this project.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Kass M, Witkin A, Terzopoulos D. Snakes: Active contour models. Int. J. Comput. Vision. 1987;1:321–331. [Google Scholar]
- [2].Falcão AX, Udupa JK, Samarasekera S, Sharma S. User-steered image segmentation paradigms: live wire and live lane. Graph. Models Image Process. 1998;60(4):233–260. [Google Scholar]
- [3].Cootes T, Taylor C, Cooper D. Active shape models-their training and application. Computer Vision and Image Understanding. 1995;61:38–59. [Google Scholar]
- [4].McInerney T, Terzopoulos D. Deformable models in medical image analysis: A survey. Medical Image Analysis. 1996;1(2):91–108. doi: 10.1016/s1361-8415(96)80007-7. [DOI] [PubMed] [Google Scholar]
- [5].Cootes T, Edwards G, Taylor C. Active appearance models. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2001;23(6):681–685. [Google Scholar]
- [6].Trivedi M, Bezdek J. Low-level segmentation of aerial images with fuzzy clustering. IEEE Trans. Systems, Man, and Cybernetics. 1986;16(4):589–598. [Google Scholar]
- [7].Beucher S. The watershed transformation applied to image segmentation; 10th Pfefferkorn Conf. Signal and Image Processing in Microscopy and Microanalysis; 1992.pp. 299–314. [Google Scholar]
- [8].Sethian JA. Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science. Cambridge Univ. Press; 1999. Fast Marching Methods and Level Sets Methods. [Google Scholar]
- [9].Udupa JK, Samarasekera S. Fuzzy connectedness and object definition: theory, algorithms, and applications in image segmentation. Graphical Models and Image Processing. 1996;58(3):246–261. [Google Scholar]
- [10].Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2001;23(11):1222–1239. [Google Scholar]
- [11].Chakraborty A, Staib L, Duncan J. Deformable boundary finding in medical images by integrating gradient and region information. IEEE Trans. Med. Imag. 1996;15(6):859–870. doi: 10.1109/42.544503. [DOI] [PubMed] [Google Scholar]
- [12].Imielinska C, Metaxas D, Udupa JK, Jin Y, Chen T. Hybrid segmentation of anatomical data; Proceedings of MICCAI; 2001.pp. 1048–1057. [Google Scholar]
- [13].Udupa JK, Saha PK. Fuzzy connectedness in image segmentation. Proceedings of the IEEE. 2003;91(10):1649–1669. [Google Scholar]
- [14].Saha PK, Udupa JK. Iterative relative fuzzy connectedness and object definition: theory, algorithms, and applications in image segmentation; Proceedings of IEEE Workshop on Mathematical Methods in Biomedical Image Analysis; Hilton Head, South Carolina. 2002.pp. 28–35. [Google Scholar]
- [15].Udupa JK, Saha PK, Lotufo RA. Relative fuzzy connectedness and object definition: Theory, algorithms, and applications in image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2002;24:1485–1500. [Google Scholar]
- [16].Herman GT, De Carvalho BM. Multiseeded segmentation using fuzzy connectedness. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2001;23:460–474. [Google Scholar]
- [17].Kaufmann A. Introduction to the Theory of Fuzzy Subsets 1. Academic Press; New York: 1975. [Google Scholar]
- [18].Saha PK, Udupa JK. Fuzzy connected Object Delineation: Axiomatic Path Strength Definition and the Case of Multiple Seeds. Computer Vision and Image Understanding. 2001;83:275–295. [Google Scholar]
- [19].Saha PK, Udupa JK. Relative fuzzy connectedness among multiple objects: Theory, algorithms, and applications in image segmentation. Computer Vision and Image Understanding. 2001;82(1):42–56. [Google Scholar]
- [20].Carvalho BM, Gau CJ, Herman GT, Kong TY. Algorithms for fuzzy segmentation. Pattern Analysis and Applications. 1999;2:73–81. [Google Scholar]
- [21].Nyúl LG, Falcão AX, Udupa JK. Fuzzy-connected 3D image segmentation at interactive speeds. Graphical Models. 2002;64:259–281. [Google Scholar]
- [22].Kwan RK-S, Evans AC, Pike GB. An extensible MRI simulator for post-processing evaluation. Proceedings of Visualization in Biomedical Computing, Lecture Notes in Computer Science. 1996;1131:135–140. [Google Scholar]
- [23].Saha PK, Wehrli FW, Gomberg BR. Fuzzy distance transform—theory, algorithms, and applications. Computer Vision and Image Understanding. 2002;86:171–190. [Google Scholar]
- [24].Udupa JK, Odhner D, Samarasekera S, Goncalves R, Iyer K, Venugopal K, Furuie S. 3DVIEWNIX: an open, transportable, multidimensional, multimodality, multiparametric imaging software system; Proceedings of Proceedings of SPIE: Medical Imaging; San Diego, CA, 2164. 1994.pp. 58–73. [Google Scholar]
- [25].Bluemke DA, Darrow RD, Gupta R, Tadikonda SK, Dormoulin CL. 3D contrast enhanced phase contrast angiography: utility for artery/vein separation. ISMRM Proc. 1999;2:1237. [Google Scholar]
- [26].Lei T, Udupa JK, Saha PK, Odhner D. Artery-vein separation via MRA—an image processing approach. IEEE Transactions on Medical Imaging. 2001;20(20):689–703. doi: 10.1109/42.938238. [DOI] [PubMed] [Google Scholar]
- [27].Zhuge Y, Udupa JK, Saha PK. Vectorial scale-based fuzzy connected image segmentation. Computer Vision and Image Understanding. 2006;101(3):177–193. [Google Scholar]
- [28].Cootes TF, Taylor CJ, Cooper DH, Graham J. Active shape sodels their training and application. Computer Vision and Image Understanding. 1995;61:38–59. [Google Scholar]