A unified view of ligand-protected gold clusters as superatom complexes

Abstract

Synthesis, characterization, and functionalization of self-assembled, ligand-stabilized gold nanoparticles are long-standing issues in the chemistry of nanomaterials. Factors driving the thermodynamic stability of well documented discrete sizes are largely unknown. Herein, we provide a unified view of principles that underlie the stability of particles protected by thiolate (SR) or phosphine and halide (PR₃, X) ligands. The picture has emerged from analysis of large-scale density functional theory calculations of structurally characterized compounds, namely Au₁₀₂(SR)₄₄, Au₃₉(PR₃)₁₄X₆⁻, Au₁₁(PR₃)₇X₃, and Au₁₃(PR₃)₁₀X₂³⁺, where X is either a halogen or a thiolate. Attributable to a compact, symmetric core and complete steric protection, each compound has a filled spherical electronic shell and a major energy gap to unoccupied states. Consequently, the exceptional stability is best described by a “noble-gas superatom” analogy. The explanatory power of this concept is shown by its application to many monomeric and oligomeric compounds of precisely known composition and structure, and its predictive power is indicated through suggestions offered for a series of anomalously stable cluster compositions which are still awaiting a precise structure determination.

In Mendeleev's periodic table of elements, atoms are arranged according to their chemical nature. The periodic arrangement and properties are fully explained by the electronic theory of atoms and the universal aufbau sequence of electrons in a centrosymmetric Coulomb potential. Closed electronic shells appear for the noble gases, which are chemically inert. The electronic configuration of any other atom with atomic number Z in the periodic table can be expressed in terms of the maximum valence Z − n_rg*, where n_rg* is the shell-closing number of the underlying noble-gas configuration. Considering metals, all of the Z − n_rg* valence electrons can be transferred to suitable ligands, opening the possibility to restore the noble-gas electronic configuration in formation of stable maximum-valence complexes (1).

Analogously to the atomic theory, the “superatom electronic theory” predicts the stability and chemical nature of simple metal clusters and nanoparticles (2, 3). This theory has been successful explaining the mass abundances of uncoordinated gas-phase metallic clusters (4), gas-phase metallic clusters coordinated with a small number of simple ligands (5–7), and Ga-based “metalloid” clusters (8). It has also been speculatively proposed (9) as a possible explanation for the compositions of the distinct thermodynamically stable cluster sizes of various monolayer-protected metal clusters that form by a self-organized process in solution.

The appropriate aufbau rule of delocalized “superatomic orbitals” of metal clusters is 1S² | 1P⁶ | 1D¹⁰ | 2S² 1F¹⁴ | 2P⁶ 1G¹⁸ | 2D¹⁰ 3S² 1H²² | …, wherein S–P–D–F–G–H– denote the angular-momentum characters. In the case of medium-size gold clusters, the delocalized orbitals are derived mainly from atomic 6s orbitals (10, 11), representing a finite-system analogy to the bulk conduction electron states, which have 6s-character close to the Fermi surface. Exceptional stability is associated with a total count of

electrons, corresponding to strong electron shell closures in an anharmonic mean-field potential (depending on the details of the mean-field potential, 20 and 40 electrons can also account for a stable cluster; see ref. 4).

Similarly to atom–ligand complexes, superatoms may be electronically stabilized by adsorption of ligands. These ligands X may either withdraw electrons (or localize electrons into covalent bonds) from the metal core or be attached as weak Lewis base (L) ligands that coordinate to the core surface by dative bonds that do not withdraw electrons from the core metal atoms A. The requirement for an electronically closed shell superatom complex, therefore, formulated as (L_s · A_NX_M)^z, is

where the shell-closing electron count (n*) of the metallic core has to satisfy one of the shell-closing numbers given in Eq. 1. n* is deduced from the superatomic number (i.e., the product of the number (N) of core metal atoms, A, and the atomic valence, v_A), from the number M of electron-localizing (or electron-withdrawing) ligands (assuming here a withdrawal of one electron per each X), and from the overall charge on the complex (z). The weak ligands L_s may be needed for completion of the steric protection of the core surface.

The predictive value of the simple arithmetic embodied in Eq. 2 has been demonstrated in the case of gas-phase metallic clusters coordinated with small numbers of simple ligands (5–7) and for Ga-based metalloid clusters (8). However, it has been challenging to adapt the similar arithmetic for “solution”-phase clusters, which besides satisfying expressions 1 and 2 must also have a sterically complete protective ligand shell compatible with a compact atomic shell structure for the metallic core. It has not been at all obvious how the three requirements of compact geometry, electron shell closing in the metal core, and complete steric shielding can be simultaneously achieved. Even worse, the ill defined nature of the surface chemical bond in some of the most important cases (e.g., the metal-rich gold- and silver-thiolate cluster compounds) leaves even the identity of the actual X groups uncertain.

The recent breakthrough in total-structure determination of an all-thiolate-protected 102-atom gold cluster 1, Au₁₀₂(p-MBA)₄₄ (p-MBA, para-mercaptobenzoic acid, SC₇O₂H₅), (12) presents an opportunity to rectify this problem. We present here large-scale density-functional calculations that solve the electronic structure of the 102-atom cluster starting from the experimentally determined coordinates, including the relevant p-MBA ligand. Analysis of the results and comparisons to the homologous compound 2, Au₁₀₂(SMe)₄₄ (Me, methyl), to the experimentally characterized phosphine-halide-protected Au₃₉ cluster (13), formulated here as 3, Au₃₉(PR₃)₁₄Cl₆⁻, to the undecagold compounds 4, Au₁₁(PR₃)₇Cl₃, and 5, Au₁₁(PR₃)₇(SMe)₃, and to the tridecagold compound 6, Au₁₃(PR₃)₁₀Cl₂³⁺ (refs. 14–17) unambiguously show that the superatom concept is valid irrespective of the chemical differences in the protection in 1–6. Compounds 4–6 correspond to n* = 8, compound 3 to n* = 34, and 1 and 2 to n* = 58; in all cases v_A = 1 for gold. We discuss the relevance of our findings with respect to identification of the precise compositions of other known all-thiolate-protected gold clusters, as well as the importance of the atomic structure of the interface of the gold core and the gold-thiolate shell in compounds 1 and 2 regarding the structure of the interface of the bulk Au(111) and the self-assembled monolayer (SAM). The theoretical concepts laid out here provide a solid background for further understanding of the distinct electrical, optical, and chemical properties of the stable monolayer-protected Au nanoclusters (MPCs) (18–30), which eventually can parallel the wealth of information gained from investigations of nanosized gold clusters in the gas phase (10, 11, 31–35) and should facilitate engineering of nano-applications, made out of MPC building blocks, for catalysis, sensing, photonics, biolabeling, and molecular electronics.

Results and Discussion

The All-Thiolate Monolayer-Protected 102-Atom Gold Cluster.

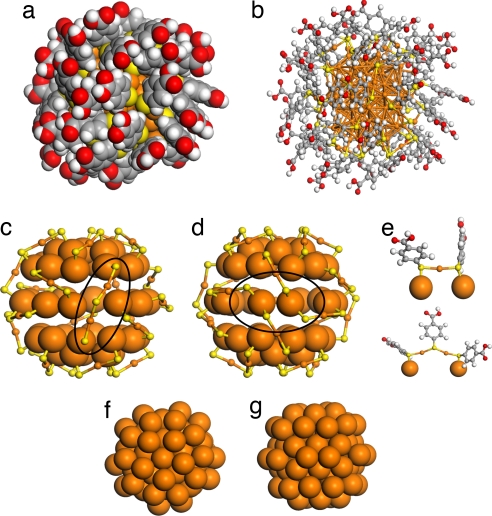
The atomic structure of the Au₁₀₂(p-MBA)₄₄ compound (Fig. 1) is best described as consisting of an approximately D_5h-symmetric Au₇₉ metallic core with a protective gold-thiolate layer of composition Au₂₃(p-MBA)₄₄. Hence Au₁₀₂(p-MBA)₄₄ is more accurately described in the formulation Au₇₉[Au₂₃(p-MBA)₄₄]. The gold atoms in the cluster are in two distinct chemical states: the 79 core Au atoms (Au_core) are in a metallic (charge-neutral) state, whereas the 23 Au atoms (Au_ligand) that belong to the RS–(AuSR)_x oligomeric units are oxidized. Consequently, the composition evokes the “divide and protect” structure motif recently predicted by some of the authors of this study (36). The Au₂₃(p-MBA)₄₄ layer can further be decomposed into 19 RS–AuSR units and 2 RS–(AuSR)₂ units, which are anchored to the core by sulfur in atop positions. The Au_core–S–Au_ligand angle is close to 90°, and the Au_ligand atoms are linearly coordinated with two sulfurs. The local structure in the ligand shell therefore resembles that of (AuSR)_x oligomers (37). The 21 units require 42 anchoring points on the 40 atoms on the surface of the Au₇₉ core. This is accomplished by two cases of “double anchoring” as highlighted in Fig. 1. The total number of units, 21, is intimately related to the stability derived from the electronic structure analysis below.

Fig. 1.

Core-shell structure of the Au₁₀₂(p-MBA)₄₄ cluster. (a and b) Space-filling (a) and ball-and-stick (b) representations of the Au₁₀₂(p-MBA)₄₄ nanoparticle. Au, orange; S, yellow; C, gray; O, red; H, white. (c and d) Two views of the 40-atom surface of the Au₇₉ core, together with the passivating Au₂₃(p-MBA)₄₄ mantle. The cationic Au atoms in the mantle are depicted by the smaller orange spheres. The “structure defects” at the core–mantle interface [two Au atoms with two Au–S bonds, and a long RS–(AuSR)₂ unit] are highlighted by the ellipse. (e) Close-up of the protecting RS–(AuSR)_x unit with x = 1 or 2. (f and g) Two views of the Au₇₉ core, which has a symmetry of D_5h (within 0.4-Å tolerance).

The calculated electronic density of states is shown in supporting information (SI) Fig. S1. The calculated energy gap between the HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) states is significant, 0.5 eV, given the large size of the system (close to 3,400 valence electrons). This gap indicates an electronic stability of the compound.

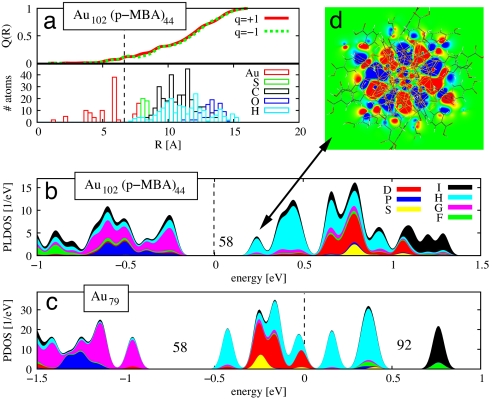
The metallicity and the closed-electron-shell configuration of the Au₇₉ core emerge in a natural way from the analysis of radial difference in the cumulative induced charge, Q(R), when the Au₁₀₂(p-MBA)₄₄ compound is made either cationic or anionic. Fig. 2a compares Q(R) for the cationic (red curve) and anionic (green curve) cases. In both cases, the major portion (90%) of the induced charge is located in the Au₂₃(p-MBA)₄₄ shell. Virtually no charge is observed inside a radius of 5 Å, and only 10% of the induced charge resides at the interface between the Au₇₉ core and the Au₂₃(p-MBA)₄₄ protective layer (5 Å < R < 7 Å), indicating a metallic and electronically stable character of the core.

Fig. 2.

Electronic structure analysis of the Au₁₀₂(p-MBA)₄₄ cluster. (a) The radial dependence of the integrated induced charge Q(R) upon removing (red curve) and adding (green curve) one electron to the neutral Au₁₀₂(p-MBA)₄₄ cluster (Upper), and the radial distribution of atoms (Lower). The dashed line indicates a midpoint between the surface of Au₇₉ core and the Au-thiolate layer. Q(R) = 4π ∫^R Δρ(r) r² dr, where Δρ(r) = ρ⁰(r) − ρ^q(r) is the induced charge difference from two density functional theory (DFT) calculations for the neutral and charged particle. (b) The angular-momentum-projected local electron density of states (PLDOS) (projection up to the I symmetry, i.e., l = 6) for the Au₇₉ core in Au₁₀₂(p-MBA)₄₄. (c) The angular-momentum-projected electron density of states (PDOS) for the bare Au₇₉ without the Au-thiolate layer. (d) A cut-plane visualization of the LUMO state of the Au₁₀₂(p-MBA)₄₄ cluster. Note the H symmetry (10 angular nodes) at the interface between the Au₇₉ core and the Au-thiolate layer. In b, the zero energy corresponds to the middle of the HOMO–LUMO gap, whereas in c the zero energy is at the HOMO level (dashed lines). For plotting PLDOS/PDOS curves, each individual electron state is displayed by a Gaussian smoothing of 0.03 eV. Shell-closing electron numbers are indicated in b and c.

To understand the metallic part of the electronic structure of Au₁₀₂(p-MBA)₄₄ we first consider the isolated Au₇₉ core (Fig. 2c). In particular, we subsequently base the discussion of the electronic structure on the analysis of the major angular momentum components of the electron states around the HOMO and LUMO. The technical details of this analysis are given in the SI Text. An isolated Au₇₉ has an odd number of valence electrons, consequently, the HOMO and LUMO states are degenerate (we neglect here the exchange splitting that would arise from a spin-dependent calculation). The HOMO/LUMO state (at energy zero in Fig. 2c) is in the middle of a set of states that span the energy range between −0.5 eV and 0.5 eV in Fig. 2c. In this band we find 34 single-electron states, of which 2 states show S symmetry, 10 states D symmetry, and 22 states H symmetry. This set of states is separated from other states by rather large energy gaps: 0.5-eV gap to deeper-lying (occupied) states with a dominant G character, and 0.33-eV gap to higher-lying (empty) states with I character. The symmetries and the energy ordering of the states in the energy region shown in Fig. 2c correspond well to the delocalized conduction-electron model, where angular symmetries of 3S, 2D, and 1H appear between major electron shell closings at 58 delocalized electrons (closing the 1G shell and opening a gap of 0.5 eV in Fig. 2c) and at 92 delocalized electrons (0.33-eV gap in Fig. 2c) (4).

As noted above, the bare Au₇₉ core is a spin-open-shell system without a HOMO–LUMO gap. What stabilizes then the large 0.5-eV HOMO–LUMO gap (Fig. S1) for the fully passivated compound? The answer is found by comparing Fig. 2b to Fig. 2c. From Fig. 2b we see that the 3S + 2D + 1H band of states is visible in the electronic structure of the full compound, but the states are now empty and a large HOMO–LUMO gap of 0.5 eV is exposed. In other words, 21 electrons are depleted from the highest electron states of the Au₇₉ core (Fig. 2c), exposing the large gap after the 1G shell, which corresponds to the gap closing at 58 delocalized electrons. The 21 electrons are localized from the delocalized states by hybridization with sulfur states to make surface covalent bonds to the 21 protecting gold-thiolate units; therefore, 21 new electron states appear at higher binding energies in the energy region not shown in Fig. 2.

We have confirmed this mechanism by an analysis of the electronic structure of a Au₈₀(p-MBA)₂ [= Au₇₉(Au(p-MBA)₂)] model cluster (removing all but one RS–AuSR unit from the full compound): in this case, one electron (the electron occupying the HOMO state of Au₇₉) is rehybridized to a deeper-lying Au–S bonding state and thus removed from the delocalized electron shells of the Au₇₉ core. We thus conclude that the protective gold-thiolate layer is organized in such a way that the surface of the Au₇₉ core is chemically fully passivated (each surface gold atom has at least one covalent bond to sulfur) and, at the same time, a major shell closing of the core is exposed and a large HOMO–LUMO gap is obtained for the full compound. A visual impression of the 1H angular symmetry of the LUMO state is conveyed by Fig. 2d (note the 10 nodes in the perimeter of the Au₇₉ core).

The reorganization of the electronic structure of the gold core upon passivation is achieved without any significant charge transfer from the gold core to the ligands. The surface covalent bond between gold in the Au₇₉ core and the sulfur in RS–AuSR is only weakly polarized. Bader charge analysis (see Table S1) yields the total charge in the core to be +2.2 e; i.e., only 0.055 electron per surface gold atom in the core has been transferred to the gold-thiolate layer outside the core. The charge transfer has contributions both from Au(6s) and Au(5d) electrons. The weak positive charging of the surface gold atoms induces formation of holes in the atomic 5d¹⁰ shell of Au. This indicates magnetic behavior; indeed, it was recently shown that thiolate-protected 1.4-nm Au particles exhibit permanent magnetism up to room temperature (38). The measured magnetic moment of 0.036 μ_B per Au atom agrees well with the d-hole generation found in this work.

Phosphine-Halide-Protected 39-Atom Gold Cluster.

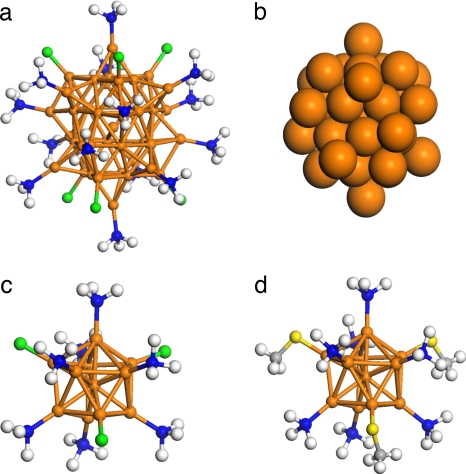
In 1992, the Au₃₉(PPh₃)₁₄Cl₆^z compound was isolated and crystallized, and for 15 years remained the largest “soluble” cluster with an unambiguously determined structure (13). Although density-functional theory results on its atomic structure were discussed recently (36), a detailed electronic structure analysis of the bonding mechanism or of the factors underlying its stability has not been presented. As discussed in ref. 36, we constructed a model cluster Au₃₉(PH₃)₁₄Cl₆ based on the experimental structure (13) and fully relaxed it in its anionic charge state (z = −1). The geometrical arrangement of the Au₃₉ gold core of this cluster is close to D₃ symmetry and can be also described as two hexagonal close-packed (hcp) crystallites, joined together by 30° twist (see Fig. 3a and refs. 13 and 36). There is only one fully coordinated gold atom in the center of a hexagonal antiprismatic cage. The calculated HOMO–LUMO gap is as large as 0.8 eV. The angular momentum analysis of the electron states around the gap (Fig. 4c) shows that the gap closes a band of states that have dominantly F character, whereas the states above the gap have a major G character. The F-shell closing indicates an effective conduction electron count of 34 in the gold core. This is consistent with the fact that there are six ionocovalent AuCl bonds at the surface, thereby reducing the effective count of delocalized electrons from 40 to 34, and satisfying Eq. 2 for n* = 34.

Fig. 3.

Structure of phosphine-chloride- and phosphine-thiolate-protected Au₃₉ and Au₁₁ clusters. (a) The Au₃₉Cl₆(PH₃)₁₄⁻ cluster. (b) The Au₃₉ core. (c) The Au₁₁Cl₃(PH₃)₇ cluster. (d) The Au₁₁(SMe)₃(PH₃)₇ cluster. The Au core symmetries (with tolerance) are as follows: a, Au₃₉, D₃ (within 0.2 Å); c, Au₁₁, C_3v (0.2 Å); d, Au₁₁, C_3v (0.2 Å). Au, orange; Cl, green; S, yellow; P, blue; H, white.

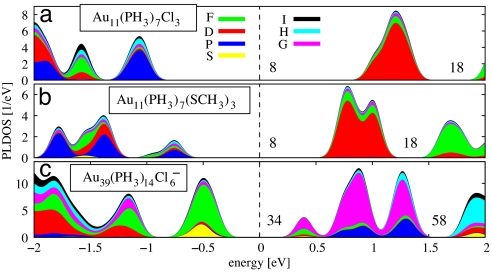
Fig. 4.

Superatom shell closures for 8 and 34 electrons in Au₁₁ and Au₃₉ clusters. The angular-momentum-projected local density of electron states (PLDOS) (projection up to the I symmetry, i.e., l = 6) for the gold core of phosphine-halide- and phosphine-thiolate-protected clusters is shown. (a) Au₁₁(PH₃)₇Cl₃. (b) Au₁₁(PH₃)₇(SMe)₃. (c) Au₃₉(PH₃)₁₄Cl₆⁻. The zero energy in each figure corresponds to the middle of the HOMO–LUMO gap (dashed line). Shell-closing electron numbers are indicated. Each individual electron state is displayed by a Gaussian smoothing of 0.07 eV.

Undecagold and Tridecagold Compounds.

Various Au₁₁- and Au₁₃-based phosphine-halide-passivated clusters have been characterized in solid state by x-ray diffraction since the late 1970s (14–17). The undecagold compounds generally have the formula Au₁₁(PR₃)₇X₃, where X = halide or thiolate, and the gold skeleton often has an approximate C_3v symmetry. We have investigated here the electronic structure of clusters Au₁₁(PH₃)₇(SMe)₃ and Au₁₁(PH₃)₇Cl₃, which are homologous models for a recently reported thiolate-stabilized cluster Au₁₁(S-4-NC₅H₄)₃(PPh₃)₇ (17). The optimized structures of these clusters are shown in Fig. 3 c and d.

The HOMO–LUMO gaps of these compounds are 1.5 eV for X = SMe and 2.1 eV for X = Cl (Table 1). Comparing Fig. 4 a and b, one notes that the dominant angular momentum character of the states around the gap changes from P symmetry to D symmetry. In the delocalized electron model this corresponds to closing of the 8-electron (in configuration 1S²1P⁶) gap. This gap exposure is due to the fact that the three halide or thiolate ligands localize one electron each of the 11 conduction electrons from the gold core, therefore satisfying n* = 8 in Eq. 2. It is interesting to note that a halide and a thiolate ligand act here in analogous roles, although the character of the Au–Cl bond is more “ionocovalent” than that of the Au–SR bond (Bader charge decomposition given in Table S1). The seven phosphine ligands act as weak surfactants in both systems, without modifying the electron shell structure of the gold core.

Table 1.

Experimentally determined band gaps for free gas-phase gold cluster anions from photoelectron spectroscopy vs. theoretical DFT values (PBE functional) for HOMO–LUMO gaps of passivated gold cluster compounds that correspond to 8, 34, and 58 conduction-electron shell closings

Shell closing	Experiment		Theory (this work)
	Cluster	Gap, eV	Cluster compound	Gap, eV
8e (1S21P6)			Au11(PH3)7(SMe)3	1.5
8e			Au11(PH3)7Cl3	2.1
8e			Au13(PH3)10Cl23+*	1.8
8e			Au25(SMe)18−†	1.2
34e (8e + 1D102S21F14)	Au34−‡§	1.0	Au39Cl6(PH3)14−	0.8
58e (34e + 2P61G18)	Au58−‡¶	0.6	Au102(p-MBA)44	0.5
58e			Au102(SMe)44	0.5‖

*Ref. 16; the cationic charge is compensated by 3 non-coordinated PF₆⁻ anions in the experimental crystal structure.

^†Ref. 41.

^‡Ref. 32.

^§Ref. 34.

^¶Ref. 33.

^‖The calculation of the optical gap by a single-pole approximation in linear-response time-dependent DFT yields 0.55 eV for compound 2.

A tridecagold compound, [Au₁₃(PMe₂Ph)₁₀Cl₂][PF₆]₃, was experimentally characterized in 1981 (16), confirming earlier theoretical predictions of stable ligand-protected icosahedral gold clusters (14, 15). The three hexafluorophosphate anions stabilize the triple-cationic gold compound in the crystal structure. Our calculated HOMO–LUMO gap for the homologous relaxed Au₁₃(PH3)₁₀Cl₂³⁺ compound is 1.8 eV (Table 1), very similar to that of the undecagold compounds. Analysis similar to that shown in Fig. 4 shows unambiguously that the large gap separates states with P and D symmetry in the Au₁₃ core, therefore signaling n* = 8 shell closure (M = 2, z = 3 in Eq. 2).

Superatom Concept and the 8-, 34-, and 58-Electron Shell Closures Found Here.

We have demonstrated here that the experimentally well characterized, structure-resolved, thermodynamically stable species of thiolate-, phosphine-halide-, and phosphine-thiolate–protected gold nanoparticles share common factors that underlie their stability. The chemical passivation in the fully thiolate-protected clusters 1 and 2 is achieved by RS–(AuSR)_x units (x = 1 or 2), which each localize one conduction-electron from the metal core to share for the formation of the surface-chemical bond between this unit and the gold core. In the phosphine-halide 3, 4, 6 or phosphine-thiolate 5-protected clusters, the phosphine ligands act as weak surfactants, whereas the role of each halide or each thiolate SR unit in 3–6 is analogous to the RS–(AuSR)_x units in 1 and 2. The number of the (pseudo)halides derives from two requirements: (i) the surface gold atoms in the core each must have at least one surface-chemical bond (Au–S, Au–Cl, Au–I, …) (or be covered by the phosphine surfactant) and (ii) the gold core has to exhibit a strong conduction-electron shell closing. [We note that the decahedral structure motif found here for the core of the Au₁₀₂ particle has been found to be energetically competitive also for bare 1- to 2-nm gold clusters (39).] We have disclosed here the closings at 8, 34, and 58 electrons, which are also the well known major shell closings occurring in the mean-field conduction-electron model of the bare metal clusters, and are known to survive under various deformations in the radial or axial shapes (4). Each of these closings leads to an enhanced HOMO–LUMO gap for the passivated compound that can well be compared with the known gaps for corresponding 34- and 58-electron shell closings measured for gas-phase gold clusters (32–34) (Table 1). We note here that by using a single particle-hole approximation (40) in the linear-response time-dependent DFT, we have estimated the magnitude of the optical gap in compound 2 to be quite similar (0.55 eV) to the HOMO–LUMO gap (0.5 eV). Taking into account the tendency of the Perdew, Burke, and Ernzerhof (PBE) functional to underestimate the optical gaps by 0.2–0.3 eV, the true optical gap of compounds 1 and 2 should be of the order of 0.7–0.8 eV. It will be of interest to compare these predictions to future experimental optical and electrochemical measurements.

Other Electron Shell Closures for Known All-Thiolate-Protected Au Clusters.

From gas-phase studies, many other shell closings, such as those for 18, 20, or 92 electrons (10, 32, 35), are known for gold clusters. We expect that these shell closings will be discovered in other stable ligand-protected compounds where the mass and even elemental composition are already known. Prominent candidates are Au₄₄(SR)₂₈²⁻ (7) (8 kDa) (27) and Au₇₅(SR)₄₀^(z) (8) (14 kDa) clusters (30). Although these compounds are still awaiting total structure determination, the suggested elemental compositions together with the stability rule (Eq. 2) strongly indicate that the electron-shell closures are 18 electrons for compound 7 and 34 electrons for compound 8 (assuming z = +1 for compound 8). The 8-electron shell closing has very recently been confirmed for the Au₂₅(SR)₁₈⁻ compound (41, 42). Independent DFT calculations with R = SMe (41) and x-ray crystallography with R = S(CH₂CH₂Ph)₁₈ (42) revealed that Au₂₅(SR)₁₈⁻ has a slightly distorted icosahedral Au₁₃ core protected by 6 RS–(AuSR)₂ units. Because each unit localizes one electron, an 8-electron shell closing is obtained for the anion, which can account for its more preferable formation (43, 44). However, the computations demonstrated (41) that the geometry of this compound is robust also in neutral and cationic charge states, in qualitative agreement with earlier experimental findings of refs. 43 and 44.

Cluster Materials Made out of MPC Superatoms.

One can also envisage a host of stable cluster materials, made out of ligand-protected gold nanoclusters that are electronically stable species or “superatoms,” bound together by bridging ligands. One such recent realization is an experimental (28) and theoretical (29) demonstration of dimers and trimers of oligomeric icosahedral vertex-sharing clusters that make compounds [Au₂₅(PR₃)₁₀(SR)₅Cl₂]²⁺ and [Au₃₇(PR₃)₁₀(SR)₁₀Cl₂]⁺, which can be understood as compositions of two and three electronically stable units, each stabilized by 8e conduction-electron shell closure (the former one yields, according to Eq. 2, n* = 25 (Au) − 5 (SR) − 2 (Cl) − 2 (z) = 16 = 2 × 8; the latter one n* = 37 (Au) − 10 (SR) − 2 (Cl) − 1 (z) = 24 = 3 × 8; phosphine groups serve the role of weak ligands L in Eq. 2 and do not affect the conduction-electron count.

Connection to Au(111)/SAM Interface Structure.

Finally, the structural motif of the protection of the Au₁₀₂(p-MBA)₄₄ compound, protection by RS–(AuSR)_x units, makes an intriguing connection to current developments in surface-science studies of the hidden Au–S interface of SAMs on the Au(111) surface. Recent experimental and theoretical (45–49) studies have challenged the conventional model (50) of an interface comprising an unreconstructed Au(111) surface. X-ray standing wave experiments have indicated the existence of AuSMe monomers at the Au(111) surface (47), and RS–Au–SR units have been detected in low-temperature scanning tunneling microscope (STM) studies of early stages of SAM formation on Au(111) (48). DFT calculations by some of us (49) have shown that structural relaxations of the RS/Au(111) interface into motifs based on (AuSR)_x units indeed are energetically preferred.

Methods

The first-principles calculations were performed within DFT by using the approximation proposed by Perdew, Burke, and Ernzerhof (PBE) for the exchange-correlation energy functional (51).

Au₁₀₂(p-MBA)₄₄ was calculated with the QUICKSTEP/CP2K program (52). The Kohn–Sham orbitals are in this method expanded with localized Gaussian functions and an efficient treatment of the electrostatic interactions is achieved by an additional plane-wave representation of the electron density. Scalar-relativistic pseudopotentials are used to model the interaction between the valence electrons [Au(5d¹⁰6s¹), C(2s²2p²), Cl(3s²3p⁵), O(2s²2p⁴), P(3s²3p⁵), S(3s²3p⁴), and H(1s)] and the atomic cores (53). The calculations were performed in a periodic cubic simulation box of 35 Å.

Au₁₀₂(SMe)₄₄, Au₃₉(PH₃)₁₄Cl₆⁻, Au₁₁(PH₃)₇Cl₃, Au₁₁(PH₃)₇(SMe)₃, the Au₇₉ core of 1 and 2, Au₈₀(p-MBA)₂, and isolated p-MBA units were treated with GPAW (54), which implements the projector augmented wave (PAW) method (55) in a real space grid. In this method, the atomic cores are treated within the frozen core approximation.

The SI Text, Table S1, and Figs. S1–S5 give a full description of computational methods, Bader charge analysis of compounds 1–6, electronic density of states of 1, and relaxed configurations of Au₂(p-MBA) and Au₃(p-MBA)₂.