Visualizing single molecules interacting with nuclear pore complexes by narrow-field epifluorescence microscopy

Abstract

The utility of single molecule fluorescence (SMF) for understanding biological reactions has been amply demonstrated by a diverse series of studies over the last decade. In large part, the molecules of interest have been limited to those within a small focal volume or near a surface to achieve the high sensitivity required for detecting the inherently weak signals arising from individual molecules. Consequently, the investigation of molecular behavior with high time and spatial resolution deep within cells using SMF has remained challenging. Recently, we demonstrated that narrow-field epifluorescence microscopy allows visualization of nucleocytoplasmic transport at the single cargo level. We describe here the methodological approach that yields 2 ms and ∼15 nm resolution for a stationary particle. The spatial resolution for a mobile particle is inherently worse, and depends on how fast the particle is moving. The signal-to-noise ratio is sufficiently high to directly measure the time a single cargo molecule spends interacting with the nuclear pore complex. Particle tracking analysis revealed that cargo molecules randomly diffuse within the nuclear pore complex, exiting as a result of a single rate-limiting step. We expect that narrow-field epifluorescence microscopy will be useful for elucidating other binding and trafficking events within cells.

1. Introduction

1.1. Visualizing single cargo molecules interacting with nuclear pore complexes

The method described here provides a means to determine fundamental mechanistic properties of the nuclear pore complex (NPC) by studying the dynamic behavior of single molecules interacting with NPCs in intact nuclear envelopes (NEs). Monitoring single particle behavior in the complex environment of an NPC is challenging for a number of reasons. First, high localization precision is necessary. NPCs are large (∼60–120 MDa), octagonally rotationally symmetric structures comprised of at least 30 different nuclear pore proteins (Nups) [1–3]. The pore itself is ∼90 nm in length and is ∼50 nm wide at its narrowest point. Flexible filaments extend ∼50 nm into the cytoplasm, and a filamentous open basket structure extends ∼75 nm into the nucleoplasm (Fig. 1) [1,4]. High localization precision for cargos moving within these NPC structures (spanning ∼200 nm) is most easily obtained from micrometer-scale images using particle tracking algorithms. It is certainly desirable to be able to track more than one cargo molecule simultaneously as they traffic through distinct NPCs within the same imaging field. Second, image acquisition must be rapid. Diffusing molecules move quickly, and thus, are inherently difficult to track in three dimensions. The transport event itself occurs in <10 ms [5,6]. Third, sensitive, high-quality instrumentation is necessary to maximize the signal-to-noise ratio (S/N). The signals arising from a single molecule are inherently weak, especially for the desired time and spatial resolution. And fourth, the imaging technique must allow deep cell penetration and must provide accurate positional information perpendicular to, rather than within, the plane of the NE. NEs are typically embedded deep within cells, and the desired spatial tracking dimension is perpendicular to the NE surface.

Fig. 1.

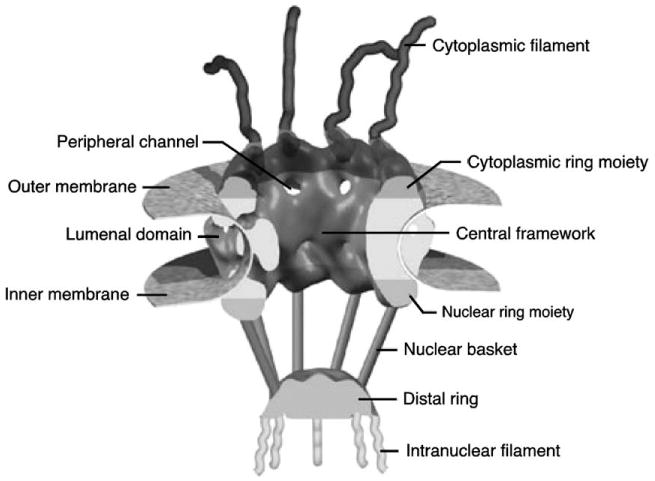
The nuclear pore complex. Reproduced and modified with permission from the authors and from Nature Reviews (www.nature.com/reviews) Molecular Cell Biology [1] copyright (2003) Macmillan Magazines Ltd. The original figure was modeled and prepared by D. Stoffler using ViPEr, a Visual Programming Environment, that was developed by D. Stoffler and M. Sanner at The Scripps Research Institute, La Jolla, California, USA.

In this paper, we describe a fluorescence imaging approach that provides 2 ms and ∼15 nm resolution on immobile particles and allows direct observation of molecules interacting with NPCs. The fundamental characteristics of cargo movement determined via this technique have provided an advanced molecular understanding of NPC function and transport dynamics [5].

1.2. Overview of nuclear transport

NPCs are permeable to molecules smaller than ∼20–40 kDa (∼4–5 nm diameter) without specific recognition (“signal-independent transport,” or “passive diffusion”). Larger molecules, up to ∼25 MDa (∼40 nm diameter), must form a complex with at least one transport receptor to transit through the NPC (“carrier-mediated, signal-dependent transport,” or “facilitated translocation”) [7–9]. Importins and exportins are soluble protein cofactors that recognize and bind to import and export cargos through nuclear localization sequences (NLSs) and nuclear export sequences (NESs), respectively. Import complexes (ICs), consisting of cargo and importin(s), are disassembled after transit through the NPC by Ran-GTP, the GTP-bound form of the G-protein Ran. In contrast, export complexes, consisting of cargo, exportin and Ran-GTP, disassemble upon Ran-GTP activation (leading to GTP hydrolysis) by Ran's cytoplasmically localized GTPase activating protein, RanGAP [8]. The Ran-GTP concentration gradient is established and maintained by cytoplasmic RanGAP and nucleoplasmic RanGEF, the chromosome-bound guanine-nucleoside exchange factor for Ran, which catalyzes GDP/GTP exchange (Fig. 2) [8]. Model cargos can be generated by attaching an NLS and/or an NES to a molecule of interest. Expression plasmids are available for transport cofactors (including Ran, RanGAP, and many importins and exportins), and thus, the role of these transport cofactors can be directly tested in in vitro assays with permeabilized cells.

Fig. 2.

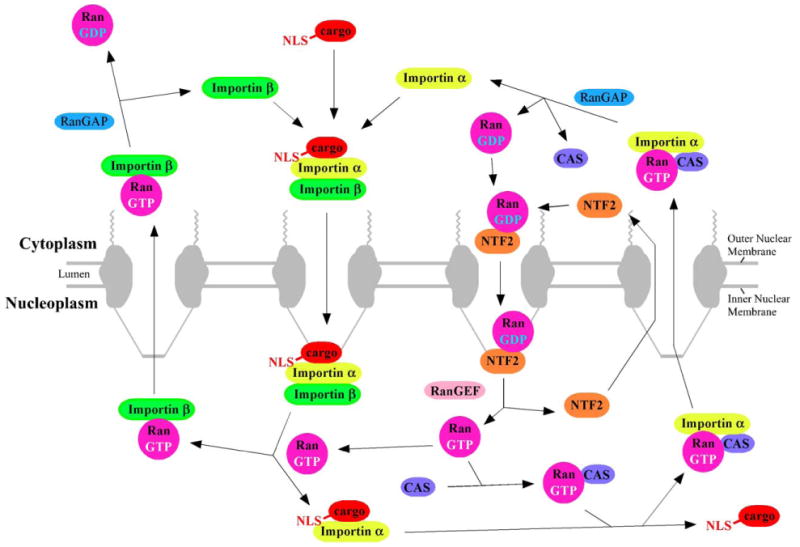
Transport pathways involved in NLS-mediated nuclear import. Nuclear localization sequences (NLSs) are typically recognized by a member of the importin-β family of import receptors. Sometimes an adaptor protein is required. In the case of the NLS of the SV40 large T antigen, this adaptor protein is importin-α [38]. The import complex (importin(s) plus cargo) is dissociated by Ran-GTP. Importins are recycled by export from the nucleus in a complex with Ran-GTP; as for import, sometimes an additional cofactor is required (e.g., CAS for importin-α). RanGAP activates the Ran GTPase, leading to GTP hydrolysis and dissociation of export cargo. Ran-GDP is recycled back to the nucleus with the assistance of NTF2. The chromosome-bound RanGEF catalyzes GDP/GTP exchange. See text for additional details.

An extensive network of thousands of phenylalanine–glycine (FG) repeat motifs located on almost half the Nups (FG-Nups) provides binding sites for importins and exportins and thereby provide the NPC interaction sites for cargo complexes [2]. These FG-Nups are distributed throughout the NPC structure on both the cytoplasmic filaments and nuclear basket, and in the pore itself [3,10,11]. The FG-repeat regions are highly unfolded (disordered) and highly flexible [12]. The structure, distribution and properties of the FG-Nup filaments within the NPC central pore (invisible in Fig. 1) have been intensely debated. It is clear that these filaments play critical roles in selectivity and permeability regulation.

1.3. Why single molecules?

There are at least four main advantages of single molecule experiments. First, reactions do not need to be synchronized. This avoids a main drawback of ensemble kinetic experiments where it is often difficult to obtain a homogeneous population that can be instantaneously triggered to begin the reaction of interest. Second, fluctuations and distributions of dynamical processes and kinetic parameters can be extracted from studies on single molecules that are simply lost by ensemble averaging. Thus, short-lived and minor reaction intermediates can be identified. Third, the relationship between multiple competing or possible reactions can often be directly distinguished in single molecule experiments, but lost by ensemble averaging [13]. The cause and effect of individual binding and release events, or the effects of energy or force input at well-defined positions can often give important clues to molecular level rearrangements [13–16]. And fourth, a long series of connected reactions can be examined without the often insurmountable experimental necessity of trapping reaction intermediates that is so crucial for obtaining accurate kinetic information from ensemble experiments. In some cases, one single molecule experiment can provide a dramatic direct visualization of a picture that was painstakingly constructed from many ensemble experiments. The rotation of the F₁F₀-type ATP synthase [17,18] and the movement of the motor proteins myosin and kinesin [14,19–21] are excellent examples.

In the case of nuclear transport, single molecule studies have provided, or are expected to provide, information on all of the above levels. The movement of signal-dependent cargos through the NPC requires a series of weak interactions with the FG-Nups, so transport is clearly a result of a long series of connected interactions. Transport begins at the moment of first interaction with the NPC and there is no known way to trap transport intermediates at this early stage. Consequently, ensemble measurements have not yielded direct information on the dynamic migration of cargos within the pore. In contrast, single molecule measurements have demonstrated the potential for deciphering the spatial and kinetic connection between steps of transport, as well as for probing the existence of different reaction paths [5,6].

2. Description of the method

2.1. Motivation

Common approaches used in single molecule fluorescence (SMF) experiments are: (1) wide-field epifluorescence microscopy; (2) fluorescence correlation spectroscopy (FCS); (3) scanning confocal microscopy; and (4) total internal reflection fluorescence (TIRF) microscopy [13,22–24]. In conventional wide-field epifluorescence microscopy, the entire field of view is bathed in light by an illumination beam that passes through the imaging objective and reaches a focus beyond the image plane. The fluorescence from molecules outside the image plane decreases the S/N, which translates into lower image quality. Nonetheless, single molecules can be observed under dilute conditions. FCS addresses the issue of noise contributions from out-of-focus fluorescence by focusing the illumination beam to a diffraction-limited volume. In this approach, the most intense fluorescence arises from within the diffraction-limited volume, thus enhancing the desired signal over that from other molecules within the beam path. A pinhole in a conjugate image plane within the emission path further reduces the contribution from out-of-focus fluorescence. The limitation here is that no spatial information is obtained about the molecules of interest (they are either in, or out of, the focal volume). Scanning confocal microscopy takes the FCS approach one step further and scans the diffraction-limited illumination volume across the sample, collecting the image plane fluorescence in point-by-point fashion. Thus, spatial information is gained. However, since only a small fraction of the sample is illuminated at any one time, time resolution suffers and high photon fluxes, which can be quite damaging to the sample, are required. Modern confocal approaches include scanning slits or microlens arrays to increase time resolution for large image areas (instruments are available from major microscope manufacturers). Multiphoton approaches eliminate the need for a pinhole in FCS- and confocal-type experiments and allow a greater penetration depth, but they do not reduce the spatial and temporal limitations of the techniques [25]. TIRF microscopy takes advantage of the evanescent wave that is developed when light is totally internally reflected at the interface between two media having dissimilar refractive indices, such as that between a glass coverslip surface and an aqueous sample. Since the evanescent wave intensity decays exponentially with distance away from the surface interface, typically over a distance of ∼100–300 nm [13], appreciable fluorescence arises only from molecules close to the surface. Thus, this approach has the advantage of excellent S/N in a constantly illuminated plane near the surface. Spatial resolution can be as high as ∼1.5 nm, though the time resolution necessary to achieve this precision is relatively lengthy (∼500 ms) or requires highly fluorescent particles [26–28]. Disadvantages include the technical limitation that TIRF microscopy can only provide information about reactions close to a surface, and the spatial information obtained is typically in the plane of the surface. Three-dimensional sectioning by changing the evanescent field penetration depth is possible, but at decreased time resolution [29]. None of these approaches is ideally suited for observing molecules deep within a cell as they briefly interact with NPCs.

2.2. Narrow-field epifluorescence microscopy

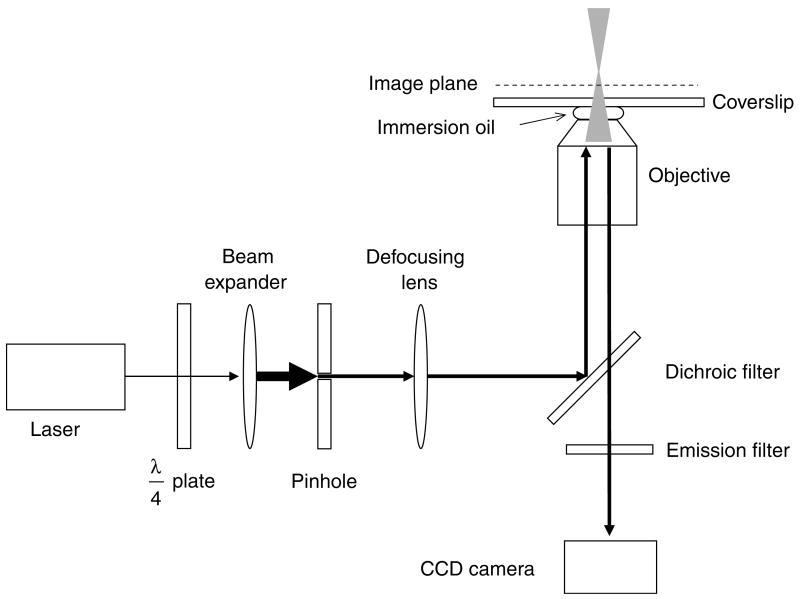
Images obtained via confocal microscopy display an increased S/N as compared to those obtained by wide-field microscopy due to the use of pinholes at conjugate image planes in the excitation and emission beam paths to decrease the noise from out-of-focus fluorescence. However, these pinholes (<1 μm), which do not allow passage of much more than a focused beam waist, represent an extreme: there is no need for the apertures to be so small and still yield an increased S/N. In narrow-field epifluorescence microscopy, a circular aperture (pinhole) is placed in a conjugate image plane within the excitation path, reducing the illuminated area at the sample image plane (Fig. 3). Modern Zeiss research microscopes (e.g., the Axiovert 200 series) are constructed with an adjustable aperture (field stop) at the appropriate location within the normal epifluorescence illumination path. Due to technical constraints, this adjustable aperture cannot be closed smaller than ∼1 mm. However, fixed diameter pinholes are available (e.g., from Newport, Irvine, CA) in a range of sizes, and can be mounted directly within the microscope (we use a home-built holder). Laser illumination is necessary to provide the high photon fluxes required for high time resolution, but mercury or xenon lamp excitation is sufficient for long time integrations. In typical experiments using our microscopy systems, a 400 μm pinhole reduced the excitation laser beam width such that an area of 8–11 μm diameter (depends on laser divergence and microscope optics of our two systems) was illuminated within the sample plane.

Fig. 3.

Narrow-field epifluorescence microscopy. This schematic shows the essential features of a narrow-field epifluorescence microscope setup that can be used for SMF. A quarter-wave (λ/4) plate is used to convert linearly polarized laser light to a circularly polarized beam, which is expanded to overfill the back aperture of the objective. A pinhole (typically 200–500 μm diameter) at a conjugate image plane confines the laser beam, reducing the illumination area within the image plane. The laser beam is converted to a diverging beam such that it focuses beyond the image plane.

The S/N in narrow-field epifluorescence microscopy is at least ∼1.8-fold better than that in wide-field epifluorescence microscopy (Fig. 4). As expected, smaller pinholes yield a better S/N. However, there is only a weak dependence of S/N on pinhole size over the 200–500 μm diameter range. Since the limiting (minimum) S/N for reliable Gaussian fit localization (see below) is ∼4 [30] and SMF signals are inherently weak, increasing the S/N by ∼2-fold can easily make the difference between a feasible and unfeasible experiment. Further, this difference in S/N is considered an underestimate since it was obtained with dye molecules only in the focal plane, i.e., with no contributions from out-of-focus fluorescence emission. When visualization of single molecule nuclear transport was attempted without a pinhole in the excitation beam path, it was very difficult to observe the interaction of individual cargo molecules with NPCs, whereas with a pinhole, these events became fairly obvious.

Fig. 4.

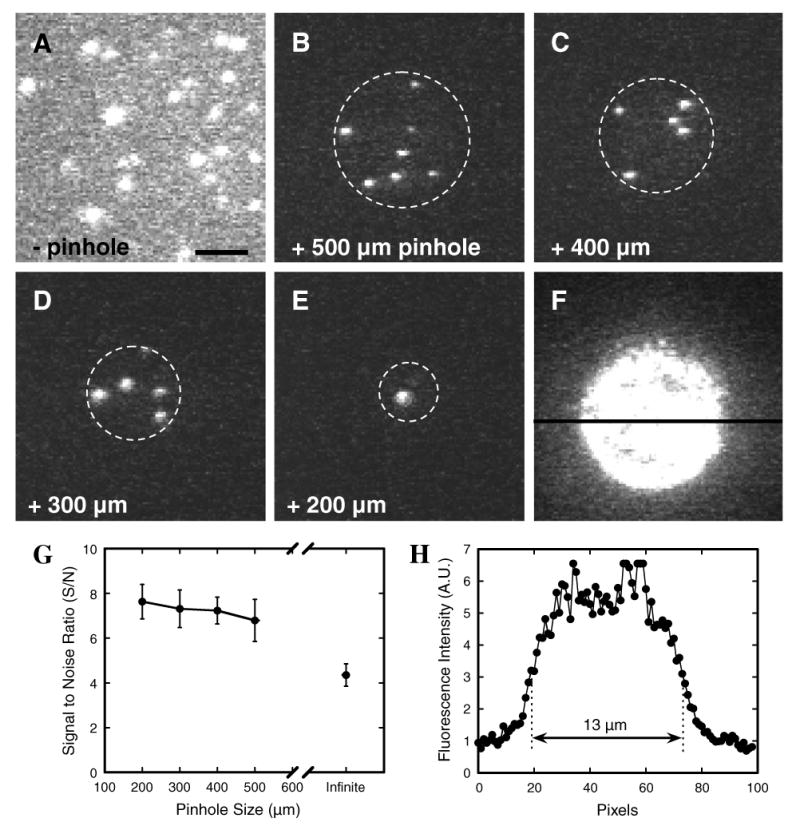
Effect of pinhole size in narrow-field epifluorescence microscopy. The model cargo NLS-2×GFP(4C) labeled with four Alexa647 molecules was absorbed onto a coverslip surface. The effect of illumination area on S/N was then examined by narrow-field epifluorescence microscopy: (A) without pinhole; (B–E) with pinholes ranging from 200 to 500 μm as indicated; (F) 500 μm pinhole with higher protein concentration to coat surface, showing the effective illumination area. Dashed circles show the approximate illumination area. Camera gain was identical for all images, and optical densities (laser power/illumination area) were kept approximately constant (∼2 kW/ μm²) by adjusting the laser power as necessary. Note the significant reduction in background noise when a pinhole was present. Bar: 5 μm. (G) S/N as a function of pinhole size. Data (mean ± SE; N = 20 for each point) were collected as in A–E. “Infinite” denotes the condition with no pinhole. (H) Emission intensity across the illuminated area in (F) at the position defined by the black horizontal line. The full-width at half-maximum was ∼13 μm, and the intensity distribution was nearly flat for the central ∼9 μm diameter area.

The effective focal plane thickness can be measured by examining coverslip adsorbed molecules and then z-stepping (the z-axis is normal to the focal plane) until individual fluorescent spots can no longer be resolved. The accuracy of this procedure clearly depends on the magnitude of the available z-stepping system. Our microscopes are capable of z-stepping in 100 nm increments. Fluorescent spots from single molecules were detectable ±1 z-step away from the plane of best focus, but undetectable ±2 z-steps away from the focal plane. Thus, we estimate that our effective focal plane thickness spans from −1.5 to +1.5 z-steps, yielding a thickness of ∼300 nm.

2.3. Narrow-field epifluorescence microscopy with an emission-side pinhole

The S/N can be increased further by including an aperture in the emission beam path. This aperture has the same function as the emission side pinhole in confocal microscopy, i.e., the rejection of out-of-focus fluorescence. However, due to the larger focal area, the emission side pinhole must allow passage of a significantly wider cone of light than a tightly focused beam waist. Consequently, the rejection selectivity is not as good as in confocal microscopy. Nonetheless, a noticeable improvement in S/N was obtained, resulting in a corresponding increase in localization precision. For example, with an illumination area of ∼8 μm and 2 ms frames, an emission side pinhole of ∼300 μm increased the S/N from ∼11 to ∼14, and the precision from ∼20 to ∼16 nm. The emission-side pinhole must be mounted and aligned in-house (i.e., it is not part of commercial epifluorescence microscopes), and therefore, this approach is more challenging technically.

3. Description of the equipment

3.1. Microscope

Two Zeiss inverted microscopes were used to perform our SMF experiments (Axiovert 200M; Zeiss, Germany). The microscopes were equipped with 1.45 NA 100× oil-immersion objectives, and Zeiss low-fluorescence, 1.51 refractive index immersion oil was used. High NA objectives are essential for maximizing photon collection efficiency in SMF experiments. Home-made coverslip holders were used to mount the samples in Zeiss sample holders. Optical axis image plane movement was controlled by an objective z-stepping motor (100 nm resolution). Sample plane (x and y) movement was controlled by a motorized stage (10 nm resolution; model H107, Prior Scientific, Rockland, MA). A 20 W halogen lamp was used for bright-field illumination: a bandpass filter was used to select an excitation band of 600–650 nm to reduce short wavelength cell damage, and a short pass (heat) filter (<800 nm) was used to prevent infrared excitation. A 100 W mercury lamp was mounted to the epifluorescence excitation port for ensemble transport experiments. The entire SMF microscope systems were mounted on an 8″ thick research grade optical table mounted on pneumatic isolators (Newport, Irvine, CA) to reduce vibrational noise.

3.2. Laser illumination

Two lasers were used with the above microscope systems to provide the intensities necessary for rapid image acquisition of SMF signals. One set-up included a 300 mW, 532 nm solid-state laser (Coherent Radiation, Palo Alto, CA). The other set-up included a 2.5 W ArKr mixed-gas ion laser (Spectra-Physics, Mountain View, CA) running in single-line mode. Laser output was controlled manually, and beam intensity was additionally modulated with neutral density filters as necessary. Sample illumination was software controlled via a Uniblitz (Rochester, NY) mechanical shutter system (∼5 ms open/close time constant).

Linearly polarized laser light was converted to circularly polarized light with a quarter-wave plate to allow homogeneous (polarization-independent) fluorophore excitation within the xy-plane. A 10× (rail-mounted Newport optics) or 20× (Melles-Griot, Carlsbad, CA) beam expander was used to over-fill the back aperture of the objective. A filled back aperture insured that the entire microscope field was illuminated for sample positioning. Since the laser beams were monochromatic, an epifluorescence excitation filter was not necessary, although an emission filter was retained to block scattered laser light that penetrated the dichroic filter (Fig. 3).

3.3. CCD cameras

Charged-coupled device (CCD) cameras were used for signal detection. CCDs provide wide-field spatial information that cannot be obtained with photomultiplier tubes or avalanche photodiodes. Initial experiments were performed with the I-Pentamax (Roper Scientific, Duluth, GA) intensified CCD (ICCD) camera [5]. However, the ICCD technology has been replaced for most applications by on-chip electron multiplying CCDs (EMCCDs; available from Roper Scientific, and Andor Technology, South Windsor, CT among others). Since frame rates are largely limited by readout speed and the number of pixels, we chose a 128 pixel × 128 pixel CCD camera (Cascade128+; Roper Scientific) to monitor the fast nuclear import process. For this camera, full-frame, continuous image acquisition occurs at 510 frames per second (fps), with ∼90% quantum efficiency. Faster frame rates can be obtained by limiting the acquisition area through software: e.g., for a 32 × 32 area, 1684 fps can be acquired. Readout noise is a major factor limiting image quality for EMCCDs, especially at high frame rates. The solution is to cool down the detection chip. The Cascade128+ camera is cooled to −30 °C, leading to a readout noise of <1 e⁻ rms with the on-chip multiplication gain enabled.

For high-resolution images, or for larger area imaging (e.g., for alignment, or whole cell/many cell experiments), it is useful to have a second camera with a larger chip. In addition to the Cascade128+ camera, we utilize Cascade512B and CoolSnapES cameras (both from Roper Scientific). The Cascade512B camera contains a 512 × 512 chip, with 16 × 16 μm pixels. This camera has similar sensitivity to the Cascade128+ camera (24 μm square pixels) and both provide 16-bit data, but full frame acquisition is slower (29 fps), and the viewing area is about seven times larger with greater pixel density (higher resolution image). Again, faster frame rates are possible through region of interest selection, but, due to hardware limitations arising from the larger chip size, the Cascade512B camera is ∼5 times slower than the Cascade128+ camera for 128 × 128 images. We make use of a CoolSnapES camera (6.45 μm square pixels; 1392 × 1040 chip) for higher spatial resolution images, but since this camera has lower sensitivity, it cannot be used for high time resolution SMF experiments. A word of caution is necessary here on the comparison of images acquired with different cameras. Ideally, one could directly align images from different cameras, and this approach is reasonable accurate if spatial resolution is not that critical. However, problems arise from different pixel sizes, and image alignment must be done with care to correct for any non-linearities. For image alignment, we recommend multicolor fluorescent beads (e.g., 0.5–1 μm from Molecular Probes, Carlsbad, CA) that can be visualized in multiple fluorescent channels and/or in transmitted light images. The image alignment matrix should be obtained on the day of the experiment since small displacements arising over time (or due to other users) have significant effects [39]. An alternative approach is to obtain all necessary images on the same camera and sacrifice resolution in one of the images. We currently obtain both bright-field and single-molecule fluorescence images with the Cascade128+ camera (alignment precision ∼ 13 ± 2 nm), and use the other cameras for instrument alignment and control experiments (e.g., bulk transport experiments with many nuclei simultaneously).

3.4. Imaging software

Basic image acquisition software is typically obtained with the microscope from the manufacturer. It is desirable to obtain a software package that not only will run the image acquisition by the microscope, but also will control motorized microscope functions such as a z-stepper, objective changer, filter changer, and emission path changer (e.g., eye to camera, or camera to camera) as well as instrumentation add-ons (obtained initially or through expansion), such as (in our case) a laser shutter, microinjector, and motorized stage. We use the Metamorph (Universal Imaging, Media, PA) software package for data acquisition, instrument control and most image processing. Matlab (The MathWorks, Natick, MA), and Igor (WaveMetrics, Inc., Portland, OR) are commercially available software packages that can be used to fit fluorescent emission spots with two-dimensional Gaussian distributions for particle tracking purposes. We use Glimpse, a Matlab-based program written by Jeff Gelles and freely available from his lab website (http://www.brandeis.edu/projects/gelleslab/glimpse/glimpse.html).

4. Experimental procedures

4.1. Cargo purification and fluorescent labeling

Numerous model nuclear transport cargos have been described in the literature, and many model cargos are possible depending on exactly what is to be experimentally tested. For our studies [5], we constructed a fusion protein (NLS-2×GFP) comprised of two green fluorescent protein (GFP) domains, the nuclear localization signal (NLS) of the large T-antigen of the SV40 virus at the N-terminus and a 6×His-tag for purification at the C-terminus (Fig. 5A). The GFP used is a modified “superglow” variant (S65T, Q80R, V163A). Two GFP domains were used since a single GFP domain (∼27 kDa) is small enough to transit through the NPC in a signal-independent fashion [31]. Protein was expressed from the pTrcHisB vector (Invitrogen, Carlsbad, CA) in Escherichia coli (JM109) at 30 °C overnight, and purified by nickel–nitrilotriacetic acid Superflow (Qiagen, Valencia, CA), Mono Q, and Superdex 200 (GE Healthcare, Piscataway, NJ) chromatography. The three chromatographic steps were necessary to yield a single band by Coomassie-stained polyacrylamide gel electrophoresis.

Fig. 5.

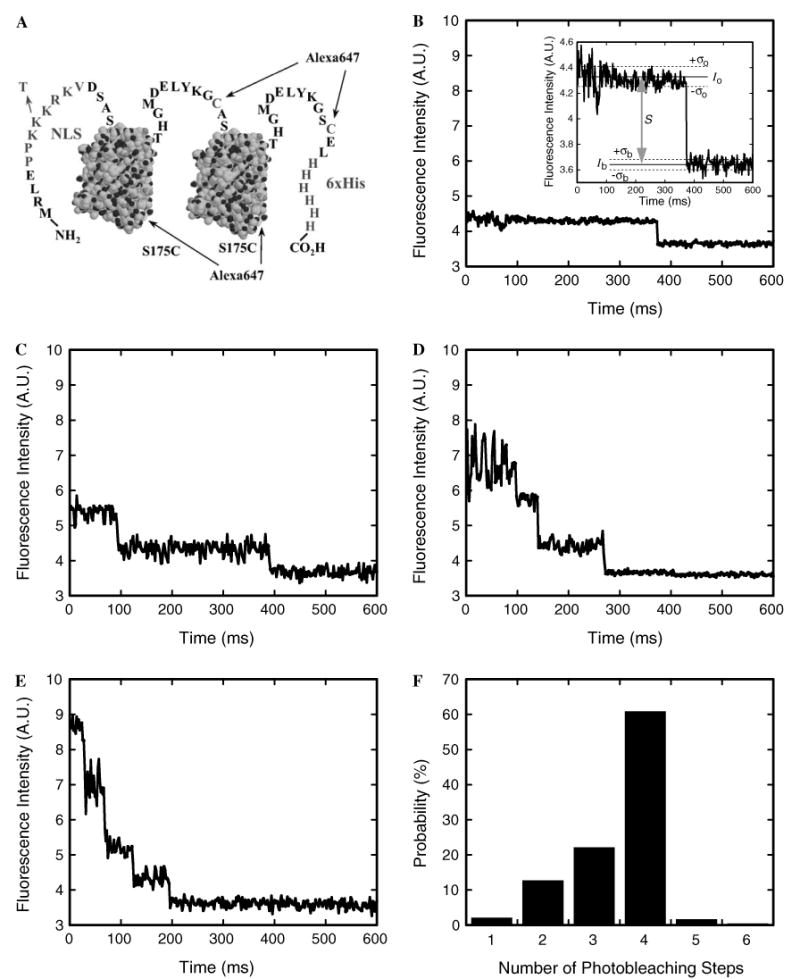
Photobleaching of NLS-2×GFP(4C) labeled with four Alexa647 molecules. (A) The NLS-2×GFP(4C) model cargo. Two identical GFP domains, represented here by structural models (PDB accession number 1C4F), have N- and C-terminal extensions and are linked by the peptide shown. The four identified cysteines (one in the linker, one in the C-terminal extension, and the S175C mutations in each of the two GFP domains) can each be labeled with a molecule of Alexa647 maleimide. The two wildtype cysteines in each GFP domain are unreactive toward maleimides. The N-terminal extension contains a nuclear localization sequence (NLS; PPKKKRKV) that targets the protein for importin-α/β-dependent transport. The indicated K → T mutation in the NLS blocks recognition by importin-α. The 6×His-tag assists with purification. (B–E) Photobleaching profile of an NLS-2×GFP(4C) cargo molecule labeled with (B) one, (C) two, (D) three, or (E) four Alexa647 molecules. Since each Alexa647 molecule exhibits quantized photobleaching, the number of dyes on the cargo can be determined by counting the number of photobleaching steps. The fluorescence intensity was integrated over a 6 × 6 pixel area. Inset in (B): expanded view of the photobleaching event. The signal intensity (S = I_o − I_b) is estimated from the average intensities observed before (I₀) and after (I_b) photobleaching. The standard deviation in the intensity while the dye is fluorescent (σ_o) is typically larger than the baseline noise (σ_b). The S/N is defined by Eq. (2). (F) Probability histogram for the number of photobleaching steps observed for individual cargo molecules. A sample from a preparation of NLS-2×GFP(4C) labeled with Alexa647 was immobilized on a coverslip surface, and the photobleaching profiles were determined as in B–E (N = 235). From these data, the average labeling ratio was calculated as 3.5 dye molecules per cargo molecule, in excellent agreement with the ratio (also 3.5) determined from absorption measurements of the labeled protein stock solution.

The intrinsic green fluorescence emission of NLS-2×GFP was unsuitable for single molecule detection in our NPC transport experiments due to blinking (interconversion between fluorescence “on” and “off” states) [32], rapid photobleaching of the chromophore, and its overlap with the autofluorescence of permeabilized cells. Therefore, the NLS-2×GFP protein was labeled with an excess of a cysteine-reactive organic dye (Alexa555 or Alexa647 maleimide, the Molecular Probes' more photochemically stable versions of Cy3 and Cy5, respectively—the CyDyes are available from GE Healthcare) for 2 h at room temperature in 50 mM sodium phosphate, 150 mM NaCl, pH 7.5. Reactions were quenched with 2-mercaptoethanol, and the protein solutions were dialyzed to remove the free dye.

4.2. Photobleaching, brightness, and the dye-to-protein ratio

In SMF experiments, it is important to distinguish loss of signal due to photobleaching, from loss of signal due to another reason. For example, in nuclear transport experiments, the photobleaching rate should ideally be significantly longer than the time required for transport, or loss of signal due to photobleaching could be mistakenly interpreted as loss of signal due to transport. To determine the photobleaching properties of a dye-labeled protein, ∼0.1 nM protein can be incubated in flow cells constructed on a glass coverslip. We use size 0 thickness (∼100 μm) coverslips to maximize our focal depth in nuclear transport experiments, since the working distance of the 1.45 NA objective used is ∼280 μm. Most proteins will adsorb to a glass surface (which is typically negatively charged due to ionized silanol groups, SiOH, pK_a ∼ 4–5). The time course of the fluorescence intensity for single, well-dispersed cargo molecules immobilized on a glass surface can then be measured. The typical photobleaching behavior of a single fluorophore is shown in Fig. 5B. Loss of fluorescence intensity was observed suddenly in a single step, since emission is quantized at the molecular level (either the molecule emits fluorescence or it does not). When the protein molecule was labeled with more than one dye molecule, multi-step photobleaching was typically observed, with each step corresponding to the photobleaching of a single dye molecule (Fig. 5C–E).

To avoid concerns of heterogeneity, we strive to only use proteins fully labeled at all accessible dye labeling sites. To insure saturation, a series of labeling reactions are performed in which the dye-to-protein ratio is progressively increased. When the reactant dye concentration is high enough such that all available protein sites are labeled, the number of dye molecules covalently attached to the protein will not increase with an increase in reactant dye concentration. For example, NLS-2×GFP(2C) has two engineered cysteines, one in the linker between the GFP domains and one in the C-terminal extension [5]. Only these cysteines are reactive with maleimides yielding a maximum dye-to-protein ratio of ∼2; the two cysteines in each of the GFP domains are unreactive. To obtain a brighter cargo, two additional cysteine residues were added to NLS-2×GFP(2C) by mutating surface serines on the bottom of the two GFP β-barrel domains (S175C) to yield NLS-2×GFP(4C) (Fig. 5A). NLS-2×GFP(4C) tagged with four Alexa647 molecules is ∼1.8-fold more fluorescent than doubly-labeled NLS-2×GFP(2C). While dye-to-protein ratios can easily be estimated from the absorption bands of the GFP and dye chromophores for the NLS-2×GFP cargo, the average number of dyes per protein molecule can, in general, be confirmed at the single molecule level by counting the number of photobleaching steps for single protein molecules. In addition to an average dye-to-protein ratio, the single molecule approach also yields the frequency distribution for the number of dye molecules per protein molecule (Fig. 5F). For NLS-2×GFP(4C) labeled with four Alexa 647 molecules, average photobleach times for the first, second, third and fourth dye molecules were 30 ± 12 ms, 80 ± 18 ms, 201 ± 27 ms, and 291 ± 43 ms when the illumination intensity was ∼2 kW/cm². Thus, under these conditions, NLS-2×GFP(4C) cargo molecules labeled with Alexa647 display fluorescence intensity from 3-4 dye molecules for ∼80 ms, significantly longer than the time that cargos interact with NPCs [5].

4.3. Cell culture, permeabilization, and microinjection

In our experiments, freshly split HeLa cells (American Type Culture Collection, Manassas, VA) were grown overnight on glass coverslips at 37 °C with 5% CO₂ in Dulbecco's modified Eagle's medium (D-MEM; Gibco, Grand Island, NY) supplemented with 4.5 g/L glucose, 862 mg/L GlutaMAX-I, 15 mg/mL phenol red, 100 U/mL penicillin, 100 μg/mL streptomysin, and 10% (v/v) newborn calf serum. For microscopy, flow-chambers were constructed by adding a top coverslip together with two lines of silicone grease as spacers. This procedure is not as simple as it sounds since, on the one hand, grease will not stick to a wet surface, and, on the other hand, if the surface dries out, the cells die. Our approach was as follows. The top coverslip (actually, just a small sliver of a glass coverslip cut with a diamond knife) was placed upside down on a Kimwipe^®. Two lines of silicone grease were placed along the edges of the coverslip with a 10 mL plastic syringe that had a pipet tip tightly attached with Parafilm^® to control the size of the grease bead. The HeLa cell-coated slide, was then drip-dried and mounted with grease (as glue) in a home-machined aluminium frame, which served to hold the slide in the microscope sample holder. The top coverslip with the two lines of grease was then picked up with a pointed tweezers and then inverted over the cell-coated slide, forming a flow chamber. A relatively firm attachment was made by pressing gently over the greased edges of the coverslip. Buffer was added to the flow-chamber, and a reservoir was then made at the end of the flow cell out of grease, if desired. Solution flow was promoted with a small piece of filter paper to wick the fluid out of the exit side of the flow-chambers. With steady hands, solution could be added simultaneously by pipette to one side of the flow-chamber with one hand, and absorbed on the other side by filter paper held with the other hand. For single molecule experiments, it was found necessary to place an additional strip of grease between flow-chambers to prevent cross-contamination. After flow-chamber construction, the bottom of the slide was washed with a wetted cotton-tipped swab, twice with water, and then twice with 100% ethanol. Then, cells were washed with 2 × 20 μL import buffer (20 mM Hepes, 110 mM KOAc, 5 mM NaOAc, 2 mM MgOAc, 1 mM EGTA, pH 7.3), permeabilized for two minutes with 2 × 10 μL 40 μg/mL digitonin in import buffer, and washed again with 2 × 20 μL import buffer supplemented with 1.5% polyvinylpyrrolidone (PVP; 360 kDa). Using differential interference contrast microscopy, a noticeable swelling of nuclei was observed to begin ∼2 min after digitonin treatment began. Therefore, PVP was included in all import buffer solutions after digitonin treatment to prevent osmotic swelling of nuclei.

4.4. Transport cofactors and ensemble transport experiments

For import experiments in permeabilized HeLa cells, the cargo and essential transport cofactors were added together. Typical import reactions contained 1 mM GTP, 0.5 μM importin-α, 0.5 μM importin β, 2 μM Ran and 1 μM NTF2 [5]. Fluorescent cargo concentrations were ≥ 100 nM in ensemble (bulk) experiments, and ∼100 pM for single molecule transport assays. At these cargo and cofactor concentrations, >99% of the cargo was expected to be complexed with importin-α and importin-β [33].

A functional transport assay can be demonstrated by ensemble experiments. When determining simply whether transport occurs under a given set of conditions (e.g., whether a given model cargo transports, or whether a given set of transport cofactors are functional), a single time point is sufficient. Thus, the external cargo was washed away after a 10 min incubation period and the efficiency of transport was estimated by comparing the nuclear fluorescence intensity for a series of different conditions. Fixation was unnecessary as the NLS-2×GFP cargo was retained by the nuclei for minutes with minimal loss of signal. Transport kinetics was monitored by epifluorescence (if only relative rates were important), or confocal fluorescence microscopy (if absolute rates were desired; confocal microscopy is necessary to convert fluorescence intensities to concentrations [31]). The initial transport rate of our NLS-2×GFP cargos in permeabilized HeLa cells in the presence of transport factors and energy was ∼10-fold higher than in their absence. Therefore, these cargos are predominantly transported by the facilitated transport mechanism. Permeabilized cell assays were performed at room temperature (∼20 °C).

4.5. Localization precision

Thompson et al. [34] analyzed the sources contributing to localization precision in light microscopy images. They determined that the localization precision (or error), Δx, can be approximated as:

$${\langle {\left(\Delta x\right)}^2\rangle }^{1/2}=\sqrt{\frac{s^2+a^2/12}{N}+\frac{8\pi s^4{\sigma }_{\text{b}}^2}{a^2{N}^2}},$$ (1)

where s is the point spread function, a is the pixel width, σ_b is the background noise (standard deviation of the background signal), and N is the number of photons collected. When the signal is high (N large), the first term dominates, and the localization precision is limited by the shot noise of the photons in the spot, scaling as (1/N)^1/2. When the signal is low (N small), the second term dominates, and the localization precision is limited by background noise (arising from out-of-focus fluorescence, CCD readout noise, dark current, and other factors), scaling as 1/N. Since the determination of N requires a cumbersome set of calibration measurements (unless the camera manufacturer's measurements are considered sufficiently reliable), it would be useful if precision could be correlated with an easier-to-obtain parameter. Fortunately, this is possible.

The S/N is commonly used as a measure of the quality of an image. Details in a higher quality image are better resolved. Thus, it should be no surprise that single molecules can be better localized when they yield fluorescent intensity spots with a higher S/N. The theoretical calculation of localization precision was discussed above. In practice, the precision for an immobilized particle is typically estimated from repeated position determinations. The standard deviation of the position measurements is considered the precision. There are four commonly used localization and tracking algorithms: the cross-correlation, sum-absolute difference, centroid, and Gaussian fit methods. For a sub-wavelength diameter particle, the Gaussian fit is the superior algorithm in terms of both accuracy and precision [30]. The localization precision of a moving particle is inherently worse than that of an immobilized particle due to errors that arise from movement during image acquisition. Further, it is more difficult to estimate, since the error due to particle motion must be deconvolved from localization precision and the particle may only be detected fleetingly. To address these difficulties, we first determined the localization precision for a series of immobilized particles with varying S/N. The localization precision of a mobile particle was then estimated from the S/N of that particle, using the S/N vs. precision correlation for the immobile particles.

Numerous definitions of S/N exist in the literature due to disagreement over what is the best measure of the noise level. The primary complicating factor is the fact that the noise in the presence (σ_o) and absence (σ_b) of signal is different, due to the presence of photon shot noise only when a fluorescent object is present [34]. One approach is to propagate the noise error as $\sqrt{{\sigma }_{\text{o}}^2+{\sigma }_{\text{b}}^2}$ [35]. This error propagation formula assumes that the errors are independent, which they are not since σ_o contains contributions from both shot noise and background noise errors [34]. Furthermore, for low signal levels, such as those typically observed in SMF experiments, this expression reduces to $\sim \sqrt{2}{\sigma }_{\text{b}}$, which is a conservative (over)estimate of the true noise. A second approach is to estimate the noise with that arising from the higher noise level measurement, σ_o [30]. The problem with this approach is that σ_o may be poorly defined because the measurement is fleeting, e.g., nuclear transport events can occur within a few frames. We found that the geometrically averaged noise works well for our purposes, i.e.:

$$\frac{S}{N}=\frac{\left(I_{\text{o}}-I_{\text{b}}\right)}{\sqrt{{\sigma }_{\text{o}}{\sigma }_{\text{b}}}},$$ (2)

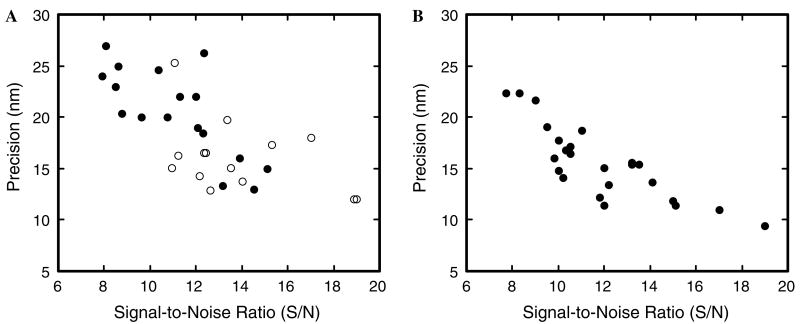
where I_o and I_b are the average measured intensities in the presence and absence of the fluorescent object, respectively, and σ_o is the standard deviation of I_o. This definition does not require σ_o to be well-defined (if ill- or un-defined, σ_o can be approximated with σ_b), and the limiting noise level at low signal is σ_b, as expected. Under our conditions, a S/N of ∼12 yields a localization precision of ∼15 nm for a stationary particle (Fig. 6).

Fig. 6.

Precision depends on the S/N. (A) Localization precision for coverslip-adsorbed NLS-2×GFP(4C) molecules labeled with Alexa555. The S/N likely depended on the number of attached dye molecules and differential effects of surface adsorption (which can affect dye orientation and focal clarity). A modest improvement in average S/N (from ∼11.1 to ∼13.7) was observed when a pinhole (300 μm) was included in the emission path (open circles), compared to the S/N obtained without such a confocal-type arrangement (filled circles). The corresponding increase in average precision was ∼4 nm (from ∼20 to ∼16 nm). The Cascade128+ camera chip was cooled to −5 °C. Illumination area: ∼8 μm (400 μm excitation side pinhole). Acquisition speed: 2 ms per frame. (B) Localization precision for coverslip-adsorbed NLS-2×GFP(4C) molecules labeled with Alexa647. The CCD camera chip was cooled to −30 °C and the images were Gaussian filtered (3 × 3 kernel) before further processing. As a result of the additional cooling and Gaussian filtering, the average S/N increased by ∼0.8 (from ∼11.1 to ∼11.9), and the precision increased by ∼5 nm (from ∼20 to ∼15 nm; compare the filled circles in A and B). The significant increase in precision with only a minor increase in the S/N is largely a consequence of the Gaussian filtering, a processing technique that does not substantially change the S/N but does significantly improve the localization precision. Acquisition speed: 2 ms per frame.

The localization precision for a moving particle is inherently worse than that of a stationary particle, and depends on how fast the particle is moving and the camera frame rate. What is meant by the precision with which one can locate a stationary particle is fairly straightforward, i.e., how similar is the position determined from the measurement to the actual position. In contrast, it is not so obvious what the precision is for a moving particle. Since the particle moves during image acquisition, how accurate can a single position measurement be? We estimate the precision of a moving particle's position measurement as follows. A moving particle will migrate from point A to point B during image acquisition, and the obtained image will be an integration of the fluorescence emission over all positions (within the focal plane) during the image acquisition time. Without knowing what point A and point B are (which cannot be known), the question really becomes how accurately can we estimate where points A and B are? Or, more precisely, how accurately can we estimate the path from point A to point B? A good estimate of both points A and B is the point exactly midway between points A and B, which we shall call point C. We can then define the precision of a moving particle as the precision with which we can determine point C (through which the particle might never pass). Given a sufficiently fast image acquisition (diffusion constants are underestimated if the frame rate is too slow [36]), the majority of a diffusing particle's movement during image acquisition will be most likely somewhere between points A and B (because the particle has to get from point A to point B). The integrated intensity, then, should have a maximum between points A and B (though not necessarily on the straight line path from A to B). Thus, the error due to movement between the position determined experimentally from the integrated intensity and point C is expected to be at most about half the distance from point A to point B (i.e., σ_m ≤ [A(x, y, z) − B(x, y, z)]/2). The experimental measurement will, of course, also have an error associated with it that arises from the Gaussian fit; this error should be approximately the precision with which a stationary particle with the same S/N can be localized (σ_g). Since these errors are expected to be independent, the total error (σ_t) can be approximated as follows:

$${\sigma }_{\text{t}}\le \sqrt{{\sigma }_{\text{m}}^2+{\sigma }_{\text{g}}^2}.$$ (3)

For example, a cargo diffuses within the NPC with a diffusion constant (D) of ∼1 μm²/s. Thus, the cargo moves ∼90 nm (r² = 4Dt, for movement within the image plane) within 2 ms (i.e., σ_m ≤ ∼45 nm). As discussed above, the precision with which a stationary particle can be located is ∼15 nm. In this case, σ_t is largely limited by the particle's movement, and is approximated with Eq. (3) as ∼40–50 nm. Since transiting cargo molecules are confined within the NPC and therefore not freely diffusing, σ_t may in fact be lower.

4.6. Nuclear envelope localization

In lieu of direct NPC localization, NPCs can be inferred to exist at those points on the NE at which cargo is observed interacting with the NE. While this approach provides some measure of the position of the NPC within the plane of the NE, it does not provide information on the position of the NPC structure along the normal to the NE. Based on electron microscopy data [10,37], we have assumed that the path of the NE in equatorial nuclear cross-sections passes through the center of NPCs. The position of the NE was determined by bright-field microscopy as follows. The pixel intensities within a row or column approximately perpendicular to the NE were fit to a Gaussian. The peak position of the Gaussian for a particular set of pixel intensities was considered the NE position for that row or column. The peak positions of a series of such Gaussians were then fit with a second-degree polynomial, yielding the path of the NE within the entire image.

5. Typical results

The narrow-field epifluorescence method and experimental procedures described above allowed observation of single cargo molecules interacting with NPCs [5]. Control experiments confirmed that cargo molecules transported through the NPCs under these conditions. When the microscope focus was adjusted such that the NE was visualized in cross-section at the nuclear equator of a permeablized HeLa cell nucleus, and 0.1 nM NLS-2×GFP cargo was added by flow along with the necessary transport cofactors, transient spots of fluorescence emission from cargo molecules were occasionally observed in the cytoplasmic compartment. These events were typically rare (e.g., ∼0.007 events s⁻¹ μm⁻²), as is expected for molecules that are free in solution and thus diffuse micron-scale distances on the timescale of a single, short duration video frame (e.g., 3 ms). In contrast, transient, localized emission spots appeared far more frequently (∼1 events s⁻¹ μm⁻²) at the NE. More than one such interaction event was observed at the same location on the NE, consistent with the hypothesis that multiple cargos interacted with the same NPC. The distribution of interaction times was approximately exponential, consistent with a single, rate-limiting kinetic step.