Microsatellite signature of ecological selection for salt tolerance in a wild sunflower hybrid species, Helianthus paradoxus

Abstract

The hybrid sunflower species Helianthus paradoxus inhabits sporadic salt marshes in New Mexico and southwest Texas, USA, whereas its parental species, Helianthus annuus and Helianthus petiolaris, are salt sensitive. Previous studies identified three genomic regions — survivorship quantitative trait loci (QTLs) — that were under strong selection in experimental hybrids transplanted into the natural habitat of H. paradoxus. Here we ask whether these same genomic regions experienced significant selection during the origin and evolution of the natural hybrid, H. paradoxus. This was accomplished by comparing the variability of microsatellites linked to the three survivorship QTLs with those from genomic regions that were neutral in the experimental hybrids. As predicted if one or more selective sweeps had occurred in these regions, microsatellites linked to the survivorship QTLs exhibited a significant reduction in diversity in populations of the natural hybrid species. In contrast, no difference in diversity levels was observed between the two microsatellite classes in parental populations.

Introduction

A central interest in evolutionary biology is to understand the genetic basis of population divergence and adaptation. This issue can be addressed directly by testing the fitness effects of allelic variants in the wild (e.g. Bradshaw & Schemske 2003; Lexer et al. 2003; Weinig et al. 2003) or indirectly through the search for molecular signatures of positive selection from genome scans (Harr et al. 2002; Schlötterer 2002). This latter approach not only makes it possible to infer the strength and direction of historical bouts of selection, but it also provides a means for identifying genes of interest to ecology, agriculture, and medicine.

Selection leaves several different kinds of signatures on patterns of molecular variation. Perhaps the most striking of these is the reduction of diversity at neutral sites linked to loci under directional selection. When an advantageous mutation appears at a very low frequency in a population, it may rapidly increase in prevalence, resulting in the loss of less fit alleles. Due to linkage or ‘genetic hitchhiking’, variability is predicted to be lowest near the target of selection and to rise with increasing genetic distance from the selected site (Maynard Smith & Haigh 1974). The physical size of the hitchhiked fragment will depend on the selection coefficient of the favourable mutation and on the local recombination rate; strong selection and low recombination will increase the size of affected regions. Hence hitchhiking increases correlations in diversity levels among linked loci (Kim & Stephan 2002) and creates a local skew in the frequency spectrum (first tested by Tajima 1989). Directional selection may also increase genetic differentiation between populations at selected loci and adjacent genomic regions (Lewontin & Krakauer 1973).

Numerous statistics have been developed to quantify levels of genetic diversity and distance for tests of selection, including nucleotide diversity π (Nei & Li 1979), gene diversity He (Nei 1978), F_ST-based estimators (first introduced by Lewontin & Krakauer 1973), and the lnRV and lnRH statistics (Schlötterer 2002; Schlötterer & Dieringer 2005). The latter were recently developed to screen for reductions in variability at microsatellite loci.

However, confident detection of selection remains challenging because changes in variability or differentiation may have multiple causes. As a consequence, a broad array of methods have been developed to minimize false positives caused by differences in mutation and/or recombination rates among loci or by genome-wide effects on variation due to population size expansions or contractions, sampling design, population structure, and population admixture (reviewed in Storz 2005). These methods include both model-based approaches that account for population structure (e.g. Beaumont & Nichols 1996; Beaumont & Balding 2004) and model-free approaches based on the distribution of summary statistics (e.g. Schlötterer 2002). Evaluation of these methods by computer simulation indicates that loci detected by multiple tests (each with different parameters and assumptions) represent robust candidates for further study (Schlötterer & Dieringer 2005).

As predicted by theory (Barton 1999; McKay & Latta 2002; Le Corre & Kremer 2003), selective sweeps appear to be frequent in genomic regions that contain quantitative trait loci (QTLs) or genes known to be under directional selection. These include sweeps associated with plant domestication (Vigouroux et al. 2002, 2005; Clark et al. 2004, 2006; Burke et al. 2005), animal breeding (Wiener et al. 2003), and parasite resistance to antibiotics (Wootton et al. 2002; Nair et al. 2003). The signature of selection also appears to be widespread in natural populations of organisms as diverse as fruit flies (Harr et al. 2002; Kauer et al. 2003), mice (Storz & Nachman 2003; Storz & Dubach 2004), salmon (Vasemägi et al. 2005) and humans (Kayser et al. 2003; Storz et al. 2004). Here, we test for the signature of ecological selection around major QTLs involved in adaptation to saline stress during the origin and evolution of a wild, annual sunflower, Helianthus paradoxus.

Helianthus paradoxus belongs to a complex of five annual sunflower species. Three of these (Helianthus anomalus, Helianthus deserticola and H. paradoxus) are stabilized diploid hybrid derivatives of the same two parental species, Helianthus annuus and Helianthus petiolaris (Rieseberg 1991). A remarkable feature of the hybrid neospecies is their adaptation to severe environments: sand dunes, deserts and salt marshes. The two parental species cannot survive in the salt marsh habitat of H. paradoxus (Lexer et al. 2003) and do not grow well in the sand dune (Ludwig et al. 2004) and desert habitats (Gross et al. 2004) of H. anomalus and H. deserticola, respectively. This implies that despite their outcrossing breeding system, gene flow between the hybrid lineages and their parental taxa must have been low relative to the strength of environmental selection during the establishment of the hybrid species. The necessary reduction in gene flow appears to have been aided by karyotypic restructuring during hybrid speciation (Rieseberg et al. 1995; Lai et al. 2005). Despite the karyotypic changes, the species are closely related and synteny extends over large genomic regions of all 17 linkage groups (Lai et al. 2005). As a consequence, it is possible to recreate many aspects of the genotype and phenotype of the hybrid species by crossing contemporary populations of the parental species and tracing parentage and phenotypic effects in synthetic hybrid lineages (Rieseberg et al. 1996; Rieseberg et al. 2003; Rosenthal et al. 2005). These synthetic hybrids also represent valuable experimental material for locating QTLs or candidate genes responsible for adaptation to extreme habitats currently occupied by the hybrid species (Lexer et al. 2003; Lexer et al. 2004).

In the present study we focused on three QTLs that had a significant effect on the survivorship of BC₂ synthetic hybrids of H. annuus × H. petiolaris that were grown in the brackish salt marsh habitat of H. paradoxus in New Mexico (Lexer et al. 2003). To determine whether these same regions were also under selection during the origin and/or subsequent evolution of H. paradoxus, we compared levels of polymorphism and differentiation for six microsatellite markers close to the three survivorships QTLs with six from elsewhere in the genome.

Materials and methods

Study organisms and populations

The progenitor species (Helianthus annuus and Helianthus petiolaris) are abundant throughout the central and western USA. In contrast, Helianthus paradoxus is restricted to a handful of brackish salt marshes in New Mexico and southwestern Texas and is listed as an endangered species by the US government. We collected achenes (one-seeded fruits) from three populations of H. paradoxus from across its range in the fall of 2001 (Table 1). In addition, three populations of each parental species were sampled from the same general area (Table 1); we assumed that geographically local populations would be most similar genetically to the ancestral parental populations that gave rise to H. paradoxus. Note that while the three species are broadly sympatric, because of differences in habitat preferences they typically are parapatric or allopatric locally. Indeed, we know of only two locations where habitat variation is sufficiently fine-grained that H. paradoxus grows intermixed with one of its parental species (H. annuus).

Table 1.

Populations, sample sizes n, gene diversity He, allelic richness Rs and variance of repeat number V of the parental species Helianthus annuus and Helianthus petiolaris and their hybrid derivative Helianthus paradoxus, at Putative Selected Regions (PSRs) and Putative Unselected Regions (PURs). For comparative purposes, we also included gene diversity He corrected for sample size over 17 microsatellites from Welch & Rieseberg (2002). Collections were made by Loren H. Rieseberg (LHR) or Mark E. Welch (MEW)

		He		Rs		V		He (Welch &Rieseberg 2002)
Name	n	PSR	PUR	PSR	PUR	PSR	PUR		Location	Reference
H. annuus
ANNcap	18	0.86	0.79	9.00	7.96	66.95	44.30	0.77	Capitan, Lincoln Co., NM	MEW 1–1998
ANNchi	25	0.85	0.83	8.89	8.74	81.71	56.97	0.77	Chinle, Apache Co., AZ	LHR 1297
ANNhop	25	0.78	0.84	6.30	7.44	64.07	52.41	0.73	Hopi Indian Reservation, AZ	LHR 1294
H. paradoxus
PARgra	64	0.37	0.52	3.06	3.53	2.32	18.85	0.42	Grants, Cibola Co., NM	LHR 1300
PARsan	64	0.35	0.49	2.59	3.00	7.46	23.39		Santa-Rosa, Guadalupe Co., NM	LHR 1302
PARbit	64	0.67	0.89	5.61	9.59	12.40	53.99	0.76	Bitterlake NWR, Chaves Co., NM	LHR 1303
H. petiolaris
PEThop	24	0.79	0.82	7.45	8.43	30.33	61.82	0.82	Hopi Indian Reservation, AZ	LHR 1283
PETlin	14	0.83	0.83	7.77	8.45	29.22	49.34	0.77	Lincoln Co., NM	MEW 10 –1998
PETokl	25	0.73	0.77	6.91	9.27	11.36	115.97	0.82	Cotton Co., OK	LHR 1220

For H. paradoxus, 64 achenes from each population were germinated in the Indiana University greenhouses and fresh leaf tissue was collected for DNA extraction. Genomic DNA from the parental species was derived from a previous study (Welch & Rieseberg 2002). Sample sizes ranged from 14 to 25 individuals per population for the parental species (Table 1).

Microsatellite choice and genotyping

Because synteny relationships are mostly conserved across the three species (Lai et al. 2005), we were able to employ a detailed map of the cultivated sunflower, H. annuus (Tang et al. 2002), as well as a second-generation backcross (BC₂) map of H. annuus × H. petiolaris (Lexer et al. 2003), to identify markers within the 1-LOD confidence intervals of the QTLs of interest. Note that the BC₂ map was also employed for mapping the survivorship and mineral ion uptake QTLs that are the focus of the present study (Lexer et al. 2003). We chose six microsatellites (ORS728, ORS1128, ORS235, ORS784, ORS727 and ORS845) that were linked to the three survivorship QTLs on linkage groups (LG) 1, 4 and 17b (hereafter referred to as Putative Selected Regions or PSRs). For comparative purposes, six microsatellite loci [ORS386 (LG17a), ORS484 (LG5), ORS519 (LG16), ORS525 (LG3), ORS733 (LG11) and ORS1011 (LG2)] were chosen from regions that had no effect on survivorship in the H. paradoxus habitat (i.e. Putative Unselected Regions or PURs) and that did not contain mineral uptake QTLs whether tested under natural (Lexer et al. 2003) or greenhouse conditions (Rieseberg et al. 2003). Primer sequences are available at http://cropandsoil.oregonstate.edu/knapp-lab/. The 12 microsatellites chosen were codominant, readily amplified in all three species, and present in a single copy.

Total genomic DNA was isolated using the DNeasy Plant Kit (QIAGEN 2001), from 30 to 40 mg of fresh leaf tissue collected in the greenhouse (3 × 64 H. paradoxus individuals). After extraction, DNA concentration was quantified using a TKO-100 fluorometer (Hoefer Scientific Instruments). Polymerase chain reactions (PCRs) were run in a 10-μL total volume, following protocols described in Burke et al. (2002). To reduce nonspecific amplification, touchdown PCR (Don et al. 1991) was used. Reactions were given an initial denaturation step of 3 min at 95 °C. This was followed by 10 cycles of 30 s at 94 °C, 30 s at the annealing temperature plus 10 °C (minus 1 °C at each cycle), and 45 s at 72 °C, and then 30 cycles of 30 s at 94 °C, 30 s at the annealing temperature, and 45 s at 72 °C. A final extension step cycle of 20 min at 72 °C was employed to ensure full-length amplification of all fragments. Annealing temperatures varied between 48 °C and 57 °C depending on the best average amplification. All PCRs were run in 96 Well Flexible Plates (Fisherbrand). Microsatellite fragments were separated by electrophoresis on an ABI PRISM 3700 capillary sequencer (Applied Biosystems 2000). PCR products from different loci were pooled on the basis of size or fluorophore. Between two and six PCR products were combined after 20-fold (forward labelled primer system) or 10-fold (M13 three-primer system for ORS845, ORS1011, and ORS1128) dilutions. Samples were then prepared by mixing 1 μL of the diluted PCR pool with 9.8 μL ddH₂O and 0.20 μL GenSize R500 ROX standard sizes (GenPak), heated for 5 min at95°C, chilled on ice, and placed on the ABI PRISM 3700. Chromatographs were generated using GENESCAN 3.7 software (Applied Biosystems 2000) and microsatellite fragment lengths were scored with GENOTYPER 3.6 (PE Biosystems 2000).

Analysis of genetic diversity

Allele frequencies were computed for each locus and a principal components analysis (PCA) was performed on allele size to provide an initial overview of the data.

Levels of genetic diversity (or differentiation) were compared between the two classes of loci in each species using four estimators: He, Rs, lnRV and lnRH. Gene diversity or expected heterozygosity He (Nei 1978) corrected for sample size was estimated with the software MICROSATELLITE ANALYSER (MSA) (Dieringer & Schlötterer 2003). Allelic richness Rs (El Mousadik & Petit 1996), which is a measurement of number of alleles per locus corrected by the rarefaction index (Hurlbert 1971), was calculated with the software FSTAT (Goudet 2001). The ratio of variance in repeat number corrected for sample size, lnRV, between two populations at a locus

$$\left(\text{here}ln\mathit{RV}=ln\frac{V_{\mathit{hybrid}}}{V_{\mathit{parent}}}\right)$$

(Schlötterer 2002) was calculated with the software MSA (Dieringer & Schlötterer 2003). This statistic assumes that mutations at microsatellite loci follow an unbiased stepwise model (Ohta 1973), in which mutations are confined to single repeat unit changes. However, this model is violated for two microsatellites, ORS1128 and ORS784 (some alleles had deletions in flanking regions), so these were excluded from analyses of lnRV. The ratio of the expected heterozygosity, lnRH

$$\left(\text{approximated}\text{by}ln\mathit{RH}=ln\frac{{\left(\frac{1}{1-H_{\mathit{hybrid}}}\right)}^2-1}{{\left(\frac{1}{1-H_{\mathit{parent}}}\right)}^2-1}\right),$$

was also calculated. Note that when a locus was monomorphic within a population, a single allele that differed by a single repeat unit change from the common allele was added to the data set so that both lnRV and lnRH could be calculated.

Mann–Whitney tests (JMP SAS Institute 1997) were used to test for differences in He and Rs among species. To determine within species whether the diversity indices He, Rs, lnRV and lnRH differed among populations or between PSRs and PURs, we employed a mixed linear model for each species: y_ijk = μ + Class_i + Pop_j + (Class_i × Pop_j) + ε_ijk, where i = 1 to 2 is the microsatellite class (PSRs vs. PURs), j = 1 to 3 refers to the population of a given species and, k = 1 to 6 represents the microsatellite loci from each class, with loci treated as independent replicates. The lnRV and lnRH statistics were calculated separately for comparisons of H. paradoxus with H. annuus and H. paradoxus with H. petiolaris, and ratios derived from comparisons with each of the three populations of a given parental species were considered to be independent replicates. Hence, k = 1 to 18 (three populations × six loci) for comparisons among populations of H. paradoxus. To test for differences in diversity between classes of loci, we employed nonparametric tests (despite lower statistical power relative to their parametric counterparts) because assumptions of normality and equality of variance were violated by some of our data. The significance of population, marker class, and interaction effects was tested by random permutations of the data (R Development Core Team 2004). Population effects were tested by permuting microsatellites among populations, class effects by permuting microsatellites between classes, and interaction effects by permuting microsatellites globally. For marker class and interaction effects, the statistic

$$S=\frac{\mathit{MST}}{\mathit{MSR}}$$

was computed, whereas for the population effects

$$S=\frac{\mathit{MST}}{\mathit{MSI}}$$

was employed because populations were considered as a random effect (MST is the mean square of the effect being tested, MSR is the mean square of the residual and MSI is the mean square of the interaction). P values were calculated as the proportion of permutations with S values that exceed observed values.

Because levels of variation at markers linked to QTLs under selection in H. paradoxus are expected to be influenced by hitchhiking, we developed regression models for the diversity estimators He, Rs, lnRH and lnRV that considered the strength of selection on QTLs and the recombination distance of a given marker from the most likely QTL position: y_ij = μ + (1 − r_i)s_i + ε_ij, where i is the microsatellite locus, j the hybrid species populations considered as replicates, and r the recombination rate. r was approximated here by the Haldane function

$$r=\frac{1}{2}[1-e^{(-2d)}],$$

with d the distance of a microsatellite to the most likely QTL position (d_ORS728 = 1 cM, d_ORS1128 = 13.5 cM, d_ORS235 = 10 cM, d_ORS784 = 1 cM, d_ORS727 = 10.7 cM, d_ORS845 = 19.9 cM), and s is the selection coefficient estimated at ORS728 (s = 0.126), ORS784 (s = −0.084), and ORS727 (s = −0.097) (Lexer et al. 2003). For microsatellites located in PURs, r and s were approximated by r = 0.5 and s = 0.

Differentiation among populations

Pairwise F_ST values (Weir & Cockerham 1984) were estimated with the software _MSA (Dieringer & Schlötterer 2003). Mean F_ST values for the two classes of microsatellites were compared among populations of the same species or populations of different species using Mann–Whitney tests (JMP SAS Institute 1997).

Blind test for microsatellite loci with reduced diversity

One possible approach for identifying loci that have been subject to selection within a population is to identify outliers in the distribution of a given summary statistic under the null hypothesis of random genetic drift. In our data set, two classes of microsatellites, PSR and PUR, were defined a priori and tested for a difference in genetic diversity. Under a null hypothesis of pure drift, there should be no more difference between PSR and PUR for genetic diversity than expected by chance between two subsets of six microsatellites chosen at random from the genome. The difference between classes for the level of genetic diversity (He, Rs, lnRV and lnRH) was assessed by the summary statistic S (see above). All

$$n=C_{12}^6=924$$

possible permutations were tested and S_0.05 was computed as the threshold value for rejecting the null hypothesis at the probability level α = 0.05. To control for false-positive results, the nα = 46 significant permutations were stored and for each permutation, the class with the significantly lower diversity level was defined as the blind-PSR class. Thereafter, the number of times a given microsatellite appeared in the blind-PSR class was tabulated. If our hypothesis of selection near survivorship QTLs is correct, then we expect the blind-PSR class to be enriched with microsatellites belonging to the PSR class defined in terms of genomic location.

Admixture proportion

The software LEADMIX (Wang 2003) performs maximum-likelihood estimation of admixture proportions in a model where an ancestral species P₀ is split into two parental populations P₁ (here H. annuus) and P₂ (here H. petiolaris), which evolve independently before they contribute in genetic proportion p₁ and (1 − p₁) to form a hybrid population P_h (here H. paradoxus). In our analysis, the admixture proportion p₁ was defined as the contribution of the species H. annuus to the hybrid species H. paradoxus. After the admixture event, P₁, P₂ and P_h evolve independently (no gene flow) before a sample is taken from each species. From allelic frequencies in each species, _LEADMIX estimates different parameters: the time before the admixture event, the time from the admixture event to present, and the admixture proportion. As time is measured in units of generations per effective population size (2Ne), there are two different estimates for the time before the admixture event, one for H. annuus (t₁) and one for H. petiolaris (t₂). Similarly, there are three estimates for the time after the admixture event: T₁ for H. annuus, T₂ for H. petiolaris and T_h for H. paradoxus. Differences between t₁ and t₂ or between T₁, T₂ and T_h represent differences in effective population sizes, with higher estimates of T corresponding to lower relative population sizes. The estimates can be used to provide a rough approximation of the number of generations τ_A since the admixture event, compared to the total number of generations τ_A + τ_B since the divergence of the parental species H. annuus and H. petiolaris:

$$\frac{{\tau }_A}{{\tau }_A+{\tau }_B}=\frac{1}{1+\frac{t}{T}\frac{N_B}{N_A}},$$

where N_B is the effective population size before the admixture event and N_A is the effective population size after the admixture event.

$$\frac{T_{\mathit{PARENT}}}{T_h}=\frac{N_h}{N_{\mathit{PARENT}}}$$

is the ratio of the effective population size of the hybrid species relative to that of the parental species.

Results

Microsatellite polymorphism over all individuals

The 12 microsatellite loci genotyped in this study have either di- or trinucleotide repeats, with motif lengths varying from 10 to 71 nucleotides and allele sizes from 111 to 492 nucleotides. The number of alleles detected across the 12 loci ranged from 147 alleles in Helianthus paradoxus, to 206 alleles in Helianthus annuus, to 218 alleles in Helianthus petiolaris, despite the fact that close to three times as many individuals were genotyped in H. paradoxus than its parental species. The polymorphism level for the three species is comparable to that reported by Welch & Rieseberg (2002). Also, the paucity of allelic variation in the hybrid species is concordant with observations from this earlier study (Table 1).

The two microsatellite classes, from PSRs and PURs, do not have intrinsic properties that might lead to reduced diversity at PSR loci. For example, allele numbers are often correlated with repeat numbers at a given locus because of increased slippage and reading frame shifts (Wierdl et al. 1997). In the present study, the average motif length was lower in the PSR (25 nucleotides) than in the PUR (42 nucleotides). However, the difference between the two microsatellite classes is not significant (t₅ = 1.651, P = 0.080). Also, interruptions within a motif and irregular repeats are known to decrease microsatellite variability (Petes et al. 1997; Brinkmann et al. 1998). In our study, microsatellites from the PURs were interrupted more frequently (ORS484, ORS519, ORS525 and ORS733 have interrupted motifs) than those linked to the survivorship QTLs (only ORS728 is interrupted). Thus, in the absence of selection, microsatellites from PURs would be predicted to have less diversity.

The distributions of allele frequencies are significantly different between species (P < 0.01 for all chi-squared tests) and among populations within each species (P < 0.01 for all tests). The most obvious difference among species is that microsatellite length variance is reduced in H. paradoxus relative to the parental species, as was previously reported by Welch & Rieseberg (2002).

A PCA of allele size variation across the 12 microsatellite loci clusters individuals from the same species together (Fig. 1). The PCA graphically illustrates the reduced allelic diversity in H. paradoxus populations relative to its parents. The first component separates the parental species from the hybrid taxon, whereas the second component distinguishes the parental species from each other. On this second component, the hybrid species’ populations are projected between the parental species, a placement consistent with their hybrid origin.

Fig. 1.

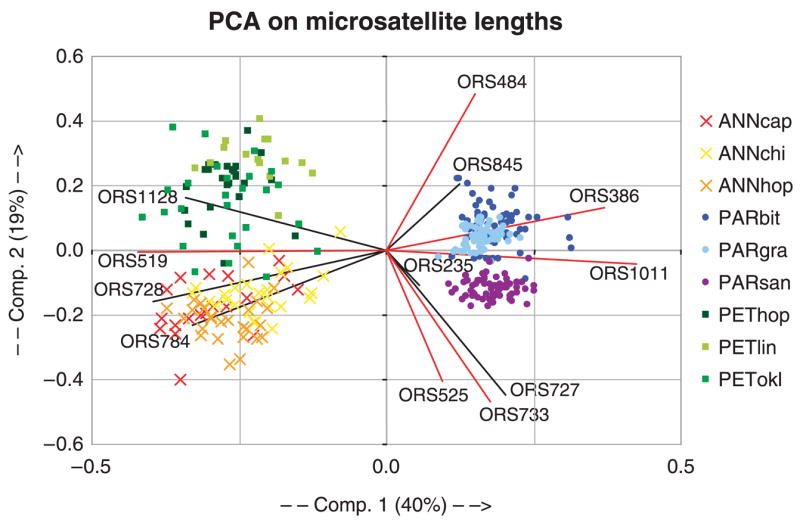
Principal components analysis of allele size variation across the 12 microsatellite loci in Helianthus annuus (crosses), Helianthus paradoxus (closed circles), and Helianthus petiolaris (squares). The contribution of each microsatellite to each component is computed to maximize the difference between individuals. Vectors represented by black lines indicate the contribution of PSR microsatellites, whereas red line vectors show the contribution of PUR markers. The first two components explain 59% of the total variation for allele sizes.

Genetic variation among populations and between microsatellite classes

Gene diversity, He, and allelic richness, Rs, do not differ between parental species for either PSRs or PURs (Fig. 2a, b; U_He,PSR = 316, P = 0.602; U_He,PUR = 354, P = 0.517; U_Rs,PSR = 312, P = 0.517; U_Rs,PUR = 190, P = 0.380). By contrast, the hybrid species H. paradoxus has less diversity as measured by He or Rs than either parental species and for both PSR and PUR markers (Fig. 2a, b; U_He,PSR = 208, P < 0.001; U_He,PUR = 260, P = 0.022; U_Rs,PSR = 200, P < 0.001; U_Rs,PUR = 242, P = 0.012 for the comparisons between H. paradoxus and H. annuus and U_He,PSR = 433, P = 0.002; U_He,PUR = 411, P = 0.014; U_Rs,PSR = 438.5, P = 0.001; U_Rs,PUR = 242, P = 0.012 for the comparisons between H. paradoxus and H. petiolaris).

Fig. 2.

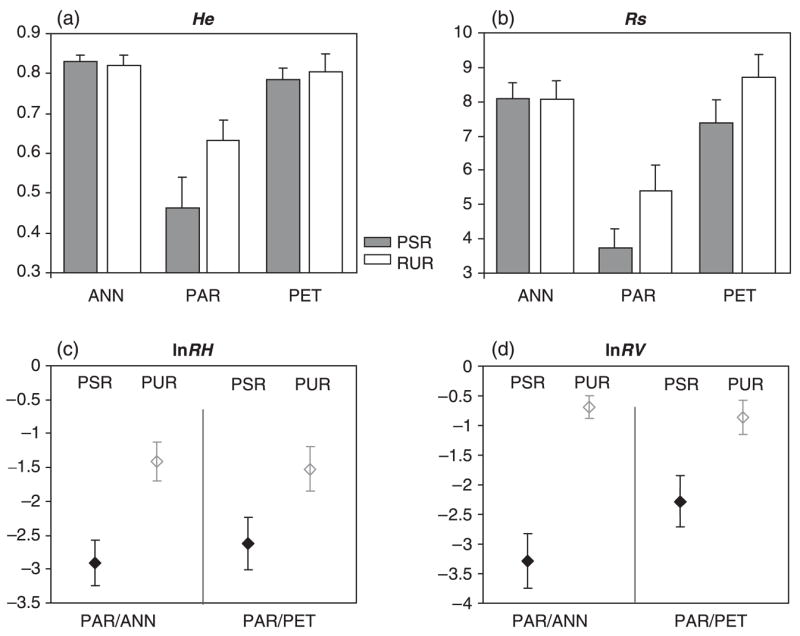
Comparison of variability levels (means and standard errors) between microsatellites in PSRs (grey) and in PURs (white). (a) gene diversity, He; (b) allelic richness, Rs; (c), lnRH of Helianthus paradoxus over Helianthus annuus and over Helianthus petiolaris, respectively; (d) lnRV of H. paradoxus over each one of its parents. Note that standard errors do not take into account population effects and therefore cannot be used to test for differences between microsatellite classes in H. paradoxus.

Within the two parental species, none of the factors tested (population, marker class or interaction) had a significant effect on either He, or Rs. By contrast, in the hybrid species, H. paradoxus, population and class significantly affected variability levels. The population effect was significant when tested on He (S = 73.643, P = 0.014), Rs (S = 28.532, P < 0.001) and both lnRH ratios (S = 49.007, P = 0.015 for H. paradoxus vs. H. annuus and S = 49.007, P = 0.022 for H. paradoxus vs. H. petiolaris). This effect is a consequence of the greater diversity of H. paradoxus from Bitter Lake relative to the two other populations. Permutations on microsatellite classes revealed significant differences between PSR and PUR microsatellites. However, despite the trend toward lower diversity at PSRs than PURs for all four diversity estimators (Fig. 2), significant differences between PSR and PUR microsatellites are found only for Rs (S = 8.038, P = 0.050) and lnRV of H. paradoxus vs. H. annuus (S = 41.801, P = 0.017). No interaction effects were found.

The blind search for loci that have been under selection deviated somewhat from the predictions based on the locations of survivorship QTLs. Consistent with expectations, four out of the six microsatellites linked to survivorship QTLs were repeatedly found in the blind-PSR class (Table 2): ORS728 and ORS1128 (LG1), ORS235 (LG4) and ORS727 (LG17b). However, two microsatellites, ORS525 and ORS484, from the PUR class appear in the blind-PSR class for He (Fig. 3) and lnRH, but in the blind-PUR for Rs or lnRV. These two microsatellites are interrupted in their repeat motif and may have a lower mutation rate. Also, six microsatellites occur most commonly in the blind-PUR class (ORS386, ORS733, ORS845, ORS1011, ORS519, and ORS784), two of which (ORS845 and ORS784) were initially assigned to the PSR class. In summary, the blind search confirmed the initial assignments to PSR and PUR classes for eight of the 12 microsatellites. The four microsatellites that failed the blind-test were excluded from some of the analyses described below.

Table 2.

Results from blind classifications of microsatellite loci performed over the 924 permutations for each of the four diversity estimators. Proportions in cells indicate the frequency at which the corresponding microsatellites were detected by the blind-test. Cells with crosses denote microsatellites that were discarded because they violated the stepwise mutation model in Helianthus paradoxus

		Status before blind-test	Status after blind-test	He	Rs	lnRH		lnRV
				PAR	PAR	ANN	PET	ANN	PET
ORS728	LG1	PSR	blind-PSR	1	1	1	1	1	1
ORS1128	LG1	PSR	blind-PSR	0.79	0.90	0.75	0.88	X	X
ORS235	LG4	PSR	blind-PSR	1	1	1	0.96	1	1
ORS727	LG17b	PSR	blind-PSR	0.68	0.79	0.82		0.71
ORS525	LG3	PUR	excluded	0.67		0.66	0.65
ORS484	LG5	PUR	excluded	0.78		0.67	0.66
ORS386	LG17a	PUR	blind-PUR						0.68
ORS733	LG11	PUR	blind-PUR
ORS1011	LG2	PUR	blind-PUR
ORS519	LG16	PUR	blind-PUR				0.65		0.54
ORS845	LG17b	PSR	excluded
ORS784	LG4	PSR	excluded		0.56			X	X

Fig. 3.

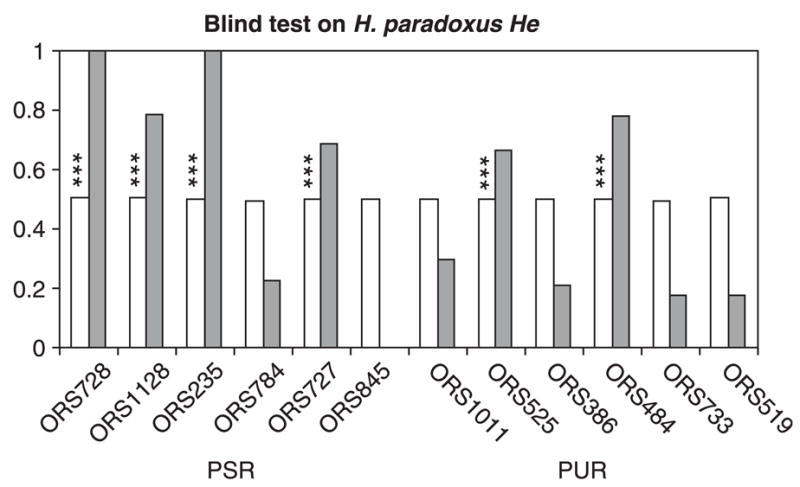
Results of a blind-test performed on the genetic diversity estimator (He) in Helianthus paradoxus. For each microsatellite, the frequency of the marker in the class with the lower diversity is in white. The difference between classes for the level of genetic diversity was assessed by the summary statistic S, and S_0.05 was computed as the threshold value for rejecting the null hypothesis of no diversity differences between classes at the probability level α = 0.05. The frequency at which S exceeds S_0.05 is in grey, stars indicate when S exceeds S_0.001.

Within H. paradoxus, the linear regression models showed a significant linear relationship between He, lnRH, lnRV and (1 − r)s and marginal significance for comparisons with Rs (Table 3). This indicates that levels of variation are correlated with the strength of selection on QTLs in the wild and with the distance to the selected site. Values of R² are higher and relationships between all four diversity statistics and (1-r)s are significant when these models are applied to the subset of eight microsatellites identified by the blind-test (Table 3).

Table 3.

R² and P associated with linear regression models of four diversity estimators in Helianthus paradoxus. The models take into account the strength of selection on QTLs and distance of markers from the putative selected sites to better account for differences in variability among microsatellite loci, either with the initial microsatellite classes (upper rows) or with the blind-test markers only (lower rows)

		He	Rs	ln RH ANN	ln RH PET	ln RV ANN	ln RV PET
All markers	R2	0.112	0.096	0.142	0.099	0.399	0.13
	P	0.046	0.066	< 0.001	< 0.001	< 0.001	< 0.001
blind-test markers	R2	0.315	0.155	0.383	0.487	0.519	0.635
	P	0.004	0.024	< 0.001	< 0.001	< 0.001	< 0.001

Differentiation among populations

Levels of genetic differentiation, as measured by F_ST for the blind-test microsatellites, did not differ between blind-PSRs and blind-PURs for comparisons among populations within species (Table 4). In contrast, for comparisons between the hybrid and parental species, mean F_ST was significantly greater for loci located in blind-PSRs than blind-PURs: H. paradoxus vs. H. annuus (U = 1009, P < 0.001) and H. paradoxus vs. H. petiolaris (U = 969, P < 0.001) (Table 4).

Table 4.

Mean F_STs within (diagonal) or between species performed after the blind-test. Values above the diagonal are for microsatellites located in the blind-PSR, whereas those below the diagonal are derived from markers in the blind-PUR.

PUR/PSR	ANN	PAR	PET
ANN	0.080/0.038	0.433*	0.158
PAR	0.251*	0.211/0.257	0.478*
PET	0.132	0.273*	0.116/0.117

^*= P < 0.05

Admixture

Our analyses of demographic history employed the eight blind-test microsatellites only (Table 3). For each parameter of the admixture model applied by LEADMIX, there were six different estimates: three populations of H. paradoxus times two microsatellite classes.

Estimates of time (generations/N_e) before admixture differed according to microsatellite class for H. petioliaris [t_2(PUR) = 0.074; C.I. 0.045 – 0.113 and t_2(PSR) = 0.136; C.I. 0.093 –0.195], but not for H. annuus (mean t₁ = 0.115; C.I. 0.080 –0.167). Estimates of time after the admixture event did not significantly differ between microsatellite classes in the parental species and the estimates were T₁ = 0.00053 (C.I. < 0.00001–0.010) for H. annuus, and T₂ = 0.00162 (C.I. < 0.00001–0.011) for H. petiolaris. Those different estimates gave a ratio t/T ranging from 46 to 216; therefore, the relative number of generations after the admixture event ranged from 0.005 to 0.021, assuming N_e did not change dramatically after the admixture event. This implies that H. paradoxus arose recently relative to the origin of its parental species. Estimates of the time after admixture for H. paradoxus varied significantly among populations and between microsatellite classes (0.157 ≤ T_h ≤ 0.470). In all cases, T_h was significantly higher than T₁ or T₂, the ratio

$$\frac{T_{\mathit{PARENT}}}{T_h}$$

ranged from 0.001 to 0.007, indicating that N_e is much lower in the hybrid species than its parents.

Interestingly, admixture proportions (i.e. the proportion of genes in the hybrid species that were inherited from H. annuus) depends on the microsatellite class. For the PUR class, the admixture proportions were 0.757, 0.809 and 0.708 for populations PARgra, PARsan and PARbit, respectively; thus H. annuus is the major contributor. For the PSR class, in contrast, the corresponding admixture proportions were 0.201, 0.004, and 0.325, and H. petiolaris is the primary donor.

Discussion

Species history

Our results are largely consistent with previous estimates of the phylogenetic and demographic history of Helianthus paradoxus (Rieseberg et al. 1990; Welch & Rieseberg 2002; Lai et al. 2005). The lower overall genetic diversity in H. paradoxus compared to its parents suggests that the species experienced a narrow bottleneck during its origin, a demographic event previously implied by large-scale karyotypic re-patterning detected in the hybrid lineage (Lai et al. 2005). Likewise, the estimated time since admixture, as computed by LEADMIX, suggests that H. paradoxus arose recently, a conclusion in agreement with previous microsatellite (Welch & Rieseberg 2002) and chloroplast DNA studies (Rieseberg et al. 1991), which place the origin of H. paradoxus within the past 210 000 years. Even if populations of the parental species were 10 times smaller before than after the hybridization event, the proportion of generations after the admixture event never exceeds 20% of the total number of generations since the divergence of the parental species, which has been estimated at between 750 000 and 1 million years ago (Rieseberg et al. 1991).

Paradoxically, F_ST values between H. paradoxus and its progenitors are higher than between the two parental species themselves (Table 4). This result is most likely due the large reduction in allelic diversity in H. paradoxus, which may inflate estimates of F_ST (Hedrick 2005). However, it might also be that H. annuus and H. petiolaris continue to exchange genes with each other, but not with H. paradoxus. H. annuus and H. petiolaris are partially sympatric and average genetic differentiation between them is less than for a pair of more closely related but historically allopatric congeners, H. annuus vs. H. bolanderi (Gardner 2004; Yatabe & Rieseberg, in review). In contrast, H. paradoxus comes into contact with its parental species only sporadically. Thus, despite a stronger sterility barrier between parental species than between the parental species and H. paradoxus (Lai et al. 2005), interspecific gene flow may be more important in the former.

The three hybrid populations differ significantly in diversity, with the most southerly population (Bitter Lake) exhibiting the greatest variability. This pattern, which is opposite that predicted by passive colonization along rivers, was also reported by Welch & Rieseberg (2002). The higher genetic diversity of the Bitter Lake population could be due to its large population size. Surprisingly, H. paradoxus from Bitter Lake is more similar to the Grants population than to Santa Rosa (Fig. 1), despite the fact that Bitter Lake and Grants are on different drainages and are separated by the tail end of the Rocky Mountain chain. The lack of congruence between geographical and genetic distance could be explained by multiple origins of H. paradoxus or by a single origin followed by long distance dispersal by animals. Welch & Rieseberg (2002) favoured the latter hypothesis since H. paradoxus had a single chloroplast DNA haplotype and was monophyletic for nuclear loci. Our results also favour this hypothesis since estimates of time since admixture are highly consistent across the three populations of H. paradoxus.

Testing for differences in diversity levels among markers

To test for the molecular signature of the adaptation to an extreme environment, we used four different diversity estimators He, Rs, lnRV and lnRH with the hope of minimizing biases associated with each individual statistic. For example, gene diversity He is sensitive to the mutation rate (or frequency of rare alleles), whereas allelic richness Rs is sensitive to population size changes caused by bottlenecks and admixture (Petit et al. 1998; Comps et al. 2001). The lnRV and lnRH statistics, which were developed for the analysis of microsatellite data, are robust to genome-wide effects such as population expansions, bottlenecks, and admixture (Schlötterer & Dieringer 2005) and control for variation in mutation rates (Schlötterer 2002).

Thus, it is perhaps not surprising that the four statistics provide slightly different estimates of diversity differences between marker classes. While all four statistics show the same trend, with PSR markers exhibiting lower diversity than PUR markers (Fig. 2), these differences were significant only for Rs and lnRV for H. paradoxus over H. annuus. These two estimators were also most discriminating when performing the blind-test (Table 2). They both take into account the number of alleles rather than their frequencies and may therefore be more sensitive to bottlenecks (whether caused by selection or drift) than the other two estimators, He and lnRH. A similar result was reported in European Beech, where a greater decrease in Rs than He was observed following postglacial colonization (Comps et al. 2001). These authors concluded that Rs might be more suited for identifying population historical processes.

The blind-test provided an alternative means for identifying loci with low relative diversity and explaining differences in diversity levels. For example, we were able to confirm the predicted reduction in diversity for four of six candidate PSR loci and show that reduced variation in two candidate PUR loci was likely due to a low mutation rate. More generally, the blind-test represents a promising method for identifying subsets of loci with reduced diversity, even in the absence of mapping data or other predictive information.

Signature of selection around three survivorship QTLs in H. paradoxus

The loss of diversity at markers associated with the three survivorship QTLs in H. paradoxus is consistent with the hypothesis that these regions have been subjected to one or more selected sweeps, presumably due to ecological adaptation to salt marsh conditions. This conclusion is supported by observations that the hybrid species is more differentiated from its parental species for PSR than PUR microsatellites. The fact that intraspecific F_STs are not significantly different between PSR and PUR microsatellites suggests that the selective sweeps occurred prior to geographical expansion of the species or that selection was homogeneous in the three H. paradoxus populations.

An alternative hypothesis is that the observed distribution of variability across the H. paradoxus genome is a byproduct of one or more population bottlenecks, which are known to increase the variance in diversity among loci. In this scenario, the low variability of loci from selected regions simply represents the extreme values in such a distribution. However, this hypothesis seems unlikely because of the correlation between variability levels and selected regions (above) and because the selective sweep hypothesis is supported by multiple lines of evidence (below).

BC₂ synthetic hybrid populations descended from contemporary populations of H. annuus and H. petiolaris have already helped to recreate many aspects of the genotype and phenotype of the ancient hybrid (Rieseberg et al. 2003; Rosenthal et al. 2005). In our study, the three survivorship QTLs detected in BC₂s were good predictors of regions under selection in the natural hybrid species. Interestingly, H. petiolaris alleles for two of the three survivorship QTLs were favoured in the BC₂s (Lexer et al. 2003), which is in agreement with the high proportion of H. petiolaris alleles from PSRs in the present study. Paradoxically, H. petiolaris is even more salt sensitive than H. annuus (Lexer et al. 2003). However, previous work indicates that the origin of H. paradoxus and other homoploid hybrid sunflower species was facilitated by transgressive segregation, whereby complementary genes from both parental species were combined to colonize extreme environmental conditions (Rieseberg et al. 2003). That is, despite being salt sensitive, H. petiolaris does contain alleles that contribute to salt tolerance and these alleles appear to have facilitated ecological adaptation of H. paradoxus.

We find significant differences between microsatellite classes for the level of genetic diversity within H. paradoxus. It is noteworthy that these differences are much better explained by regression models that account for selection coefficients and recombination distances to selected sites. This result strongly supports our interpretation that the lower diversity of PSR markers is a consequence of selection and genetic hitchhiking (Maynard Smith & Haigh 1974).

So when did these sweeps occur? One possibility is that we have detected the footprint of very strong sweeps that occurred during the origin of H. paradoxus. This hypothesis is supported by the observation that diversity is reduced at PSR loci for all three H. paradoxus populations and that very large chromosomal segments, such as those created by admixture (Ungerer et al. 1998), seemed to have been affected by the sweeps. This would also imply that the admixture event was recent, since the molecular signature of selection will be eroded quickly over time (Slatkin 1995; Wiehe 1998).

An alternative hypothesis is that the survivorship QTLs are rich in genes that contribute to salt adaptation and have been subjected to repeated selective sweeps since the origin of H. paradoxus. This explanation would not require a recent origin of H. paradoxus, but it would imply that selection was homogenous across the three H. paradoxus populations. Genetic modelling as well as fine-scale analyses of genetic diversity levels within these QTL regions are currently underway in an attempt to distinguish between these possibilities and to account for the seemingly large width of the sweeps observed.

Biography

Loren Rieseberg and Christian Lexer study the genetics of hybridization and speciation in plants. Christine Dillmann and Delphine Sicard are working on the genetics and evolution of quantitative traits. This study is part of Cecile Edelist’s PhD project carried out in collaboration between the laboratories of Rieseberg and Dillmann. Cecile studies the genetic basis of adaptation to saline stress to explore the origin of the homoploid hybrid species Helianthus paradoxus.