Reducing Bias from Test Misclassification in Burden of Disease Studies: Use of Test to Actual Positive Ratio – New Test Parameter

Abstract

Aim

To address the problem of estimating disease frequency identified by a diagnostic test, which may not represent the actual number of persons with disease in a community, but rather the number of persons who tested positive. Those two values may be very different, their relationship depending on the properties of the diagnostic test applied and true prevalence of the disease in a population.

Methods

We defined a new test parameter, the ratio of Test to Actual Positives (TAP), which summarizes the properties of the diagnostic test applied and true prevalence of the disease in a population, and propose that is the most useful summary measure of the potential for bias in disease frequency estimates.

Results

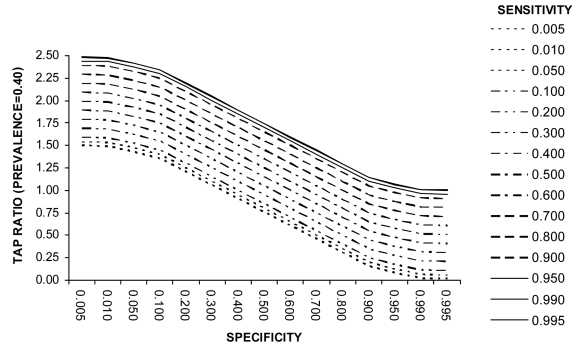
A consideration of the relationship between the sensitivity (Se) and specificity (Sp) of the diagnostic test and the true prevalence of disease in a population can inform study design by highlighting the potential for disease misclassification bias. The effects of a decrease in Sp on the TAP ratio at very low disease prevalence are dramatic, as at 80% Sp (and any Se value including 100%), the measured disease frequency will represent a 25-fold overestimate. At a disease prevalence of 0.10, the Sp needs to be 90% or greater to achieve a TAP ratio of 1.0. However, unlike at lower levels of disease prevalence, the test Se is also an important determinant of the TAP ratio. A TAP ratio of 1.0 can be achieved by a Sp of 95% and intermediate Se (40%-60%); or a Sp of 99% and very high Se (over 90%). This illustrates how a test with poor performance characteristics in a clinical setting can perform well in a disease burden study in a population. In circumstances in which the TAP ratio suggests a potential for a large bias, we suggest correction procedures that limit disease misclassification bias and which are often counter-intuitive. We also illustrate how these methods can improve the power of intervention studies which define outcomes by use of a diagnostic test.

Conclusions

Optimal screening test characteristics for use in a population-based survey are likely to be different to those when the test is utilized in a clinical setting. Calibrating the test a priori to bring the TAP ratio closer to unity deals with the possible large bias in disease burden estimates based on application of diagnostic (screening) test.

Observational studies estimate burden of disease and are increasingly used to inform health planning and resource allocation decisions at both the global and local level (1-4). However, measures of disease frequency (eg, prevalence and incidence) reported in these studies typically do not represent the actual number of persons with disease in a community, rather they show the number of persons who tested positive for a diagnostic test (including verbal autopsies). Those two values may be very similar, but may also be very different, depending on the properties of the diagnostic test applied (5).

Evaluations of diagnostic or screening tests within public health programs have concentrated on the test parameters – sensitivity (Se) and specificity (Sp) – since these describe performance within the overall program. They are independent of disease prevalence and thus estimates of these parameters in one setting may retain relevance in a variety of settings. Evaluations of diagnostic tests within clinical settings often focus on positive and negative predictive values and likelihood ratios of the test, as these guide the interpretation of the test to individual patients (6). However, in this paper we consider a different use of a test, where the primary aim is estimating the prevalence or incidence of disease in a population.

In our recent review which aimed to produce global burden estimate of a specific childhood disease (pneumonia) for the World Health Organization (WHO) (7), we realized that large potential problems exist when diagnostic tests designed for use in clinical settings are applied in community settings to measure disease frequencies (5,8-10). In this study, we aimed to define the relationships between diagnostic test validity, disease prevalence, and accuracy of disease frequency estimates. We considered potential implications of these relationships on study design and interpretation and illustrated these with examples from the literature and our own work. We also generalized these findings to discuss the impact of an imperfect screening or diagnostic test in:

1) yielding inaccurate estimates of disease prevalence and incidence (as well as invalid comparisons across groups); and

2) limiting the power of a study to detect differences in disease prevalence and incidence across groups.

Methods

We used a 2 × 2 table in which “D present” and “D absent” represent the true state of presence or absence of disease (D). “D test positive” represents all examined cases that tested positive on examination with the chosen diagnostic test. “D test negative” represents all examined cases that did not fulfill all the required criteria to establish a diagnosis. Definitions of sensitivity, specificity, positive predictive value, negative predictive value, and probability of test-positive (T) are given in Table 1.

Table 1.

Table of distribution of diagnosed cases according to diagnostic test result and true disease status*

	D present	D absent
D test positive	“a”	“b”
D test negative	“c”	“d”

*Cell “a” represents examinees with D (true positives) who tested positive; cell “b” represents examinees without D (true negatives) who tested positive; cell “c” represents examinees with D (true positives) who tested negative; and cell “d” represents examinees without D (true negatives) who tested negative. Sensitivity of diagnostic test is thus generally given by [a/(a + c)]; specificity by [d/(b + d)]; positive predictive value by [a/(a + b)]; negative predictive value by [d/(c + d)]; disease prevalence by [(a + c)/(a + b+c + d)]; the number of examinees (N) by (a + b+c + d). The probability of a test-positive is given by (a + b)/N. The probability of a true positive is given by (a + c)/N is equivalent to disease prevalence.

Published community-based cohort studies seeking to estimate disease incidence or prevalence (especially in regions with limited resources) can only measure the number of examinees who tested positive for disease (a + b) as a proxy for the true number of examinees with disease (a + c) (7). For the purpose of estimating disease frequency it would be advantageous for the test to be configured in a particular setting so that (a + b) is approximately equal to (a + c), and thus that the number of false positives (b) and false negatives (c) were equivalent. We considered the parameter (a + b)/(a + c), defined as the ratio of the number of examinees who tested positive to the number of examinees with actual disease, and designated here as the ratio of Test to Actual Positives (TAP):

1) TAP = (a + b)/(a + c)

For example, if the TAP ratio equals 3 for a given test, then the observed incidence or prevalence is a 3-fold overestimate of truth (Box 1) or alternatively, the TAP ratio is the ratio of the probability of test positive to the probability of true positive, ie,

Box 1. Screening for clinical pneumonia in children using World Health Organization diagnostic criteria (prevalence=0.01).

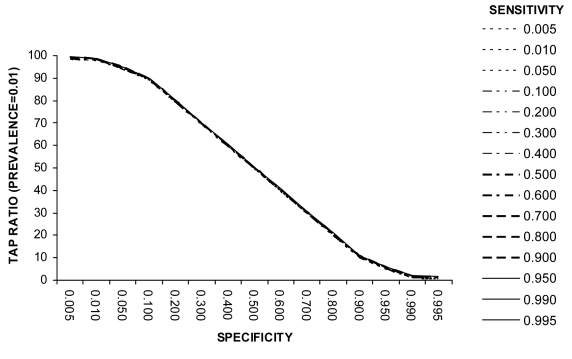
Pneumonia and bronchiolitis are together one of the most important causes of global burden of disease and one of the largest causes of death in young children (11). The WHO diagnostic test for the assessment of clinical pneumonia in young children has been frequently applied to estimate disease incidence in community-based studies in developing countries (7). The test is positive if a child (with a cough or difficult breathing) is found to have a raised respiratory rate or lower chest wall indrawing. Estimates of clinical pneumonia incidence from cohort studies with weekly surveillance fall in the range 0.1-0.5 episodes per child-year, with median duration of clinical pneumonia episode from 1-4 weeks, suggesting a weekly point prevalence of disease between 0.002 and 0.04 (12). Reported values for the sensitivity and specificity of this test fall in the range 40-95% (13,14). Figure 1 shows how the properties of this test can affect the incidence estimate when the point prevalence of disease in the study population is close to 1%. Even at very high test specificity of 99% (and regardless of test sensitivity), the Test to Actual Positives ratio will still be about 3.0. This means that the measures of incidence resulting from the application of this test are 3-fold overestimates.

2) TAP = (a + b)/N, or alternatively

(a + c)/N.

3) TAP = T/P

where T is the probability of test positive, P is the probability of true positive (or disease prevalence), and N is the number of examinees (Table 1).

When estimating disease frequency using a screening test, the values (a + b) and (a + c) should ideally be equal, resulting in a TAP ratio value of 1.0. When the TAP ratio exceeds 1, it represents the amount by which the true disease frequency in the studied population has been overestimated. When less than 1, it is the amount by which the true disease frequency in the studied population has been underestimated.

The relationships between TAP ratio and test sensitivity, specificity, and disease prevalence can be derived algebraically. TAP can be rewritten in a number of ways, eg, as a function of Se, Sp, and the typically unknown P:

4) TAP = [1-Sp-P(1-Sp-Se)]/P

TAP can also be written as a function of only the known quantities Se, Sp, and T:

5) TAP = T(Se+Sp-1)/[T-(1-Sp)]

The TAP ratio will equal 1.0 when:

6) P = (1-Sp)/[(1-Sp)+(1-Se)]

Any imbalance between the number of false positives and false negatives creates inaccuracy between true cases and test-positives. The key condition for the probability of test positive (T) to equal the true probability of disease (P) is

7) (1-Sp)/(1-Se) = P/(1-P)

ie, the ratio of the false-positive rate (1-Sp) to the false-negative rate (1-Se) should equal the true odds of disease. If the false positive/false negative ratio is greater than the odds of disease, then the probability of test positive will overestimate the true probability of disease (t > P); on the other hand, if the false positive/false negative ratio is smaller than the odds of disease, then the probability of test positive will underestimate the true disease prevalence (t < P). Thus, TAP equals unity if and only if equation (7) is true. This implies that P can be computed if T and TAP are known (ie, P = T/TAP).

From equation 6 it can be seen that at a disease prevalence of 50%, specificity will need to equal sensitivity to achieve TAP ratio of 1.0. At any true disease prevalence lower than 50%, specificity will need to be greater than sensitivity.

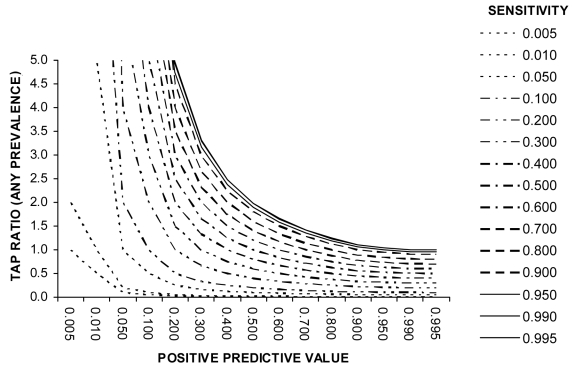
Finally, the TAP ratio can be expressed in terms of sensitivity and positive predictive value (PPV) of the test, which can be useful in some circumstances, as follows:

8) TAP = Se/PPV

Results

Use of TAP ratio in summarizing the potential for disease misclassification bias in disease frequency estimates

It is well known that an imperfect test may yield a biased estimate of the disease prevalence. However, the size of this effect and hence the need to limit or correct for this bias is not always clearly appreciated. We present several examples of diseases with varying point prevalences (Boxes 1-5) to demonstrate how the properties of a diagnostic test affect the accuracy of the disease frequency estimate. These examples illustrate how the TAP ratio can summarize the potential for bias in disease frequency estimates. We have selected examples relevant to developing countries and other resource-poor areas since the use of a simple diagnostic test result without further investigative confirmation is typical in disease burden studies in these settings.

Box 5. Screening for iodine deficiency by the rapid urinary iodide test (RUIT) (prevalence>0.50).

The situations in which human diseases reach a population point prevalence greater than 50% are unusual but several examples exist (such as hypertension or cardiovascular disease among the elderly in European countries) (15,20). In addition, serious disease risk factors can reach very high prevalences in developing countries. One example is iodine deficiency, the most common preventable cause of mental retardation and brain damage, which has also been associated with lower mean birth weight, impairment of hearing and motor skills and neurological dysfunction (15). It is estimated that more than one third of the world’s population may be at risk of iodine deficiency, so the prevalence in some areas of the developing world can be exceptionally high (21). The gold standard for identifying iodine deficiency in children is by performing the Sandell-Kolthoff reaction in urine specimens. Recently, the performance of a new semi-quantitative method, affordable and simple to perform, was assessed in a developing country setting (22). The RUIT method showed a sensitivity of 96% and a specificity of 61%. At a prevalence of iodine deficiency among children of 90% or more, this test would have Test to Actual Positives ratio of very close to 1.0. However, at a lower true prevalence, eg, of 70% or 50%, the test will overestimate prevalence of iodine deficiency in the population by 13% and 35%, respectively.

Example 1 (Box 1): Screening for clinical pneumonia in children using WHO diagnostic criteria (prevalence = 0.01. Example 1 (Figure 1) shows that at low disease prevalence (0.01) in the population, the specificity of the test needs to be very high if measured disease frequency is not to be overestimated by one or two orders of magnitude. The accuracy of the disease frequency estimate relies almost entirely upon test specificity. Sensitivity of the diagnostic test is not an important determinant of the TAP ratio (at very low disease prevalence) and hence the ability of the test to produce accurate disease estimates. The effects of a decrease in test specificity on the TAP ratio at very low disease prevalence are dramatic, as at 80% specificity (and any sensitivity value including 100%), the measured disease frequency will represent a 25-fold overestimate. Thus, when the expected disease frequency is very low, a diagnostic test for disease burden estimates should only be employed if positives can be checked (see use of positive predictive value below).

Figure 1.

Relationship between test sensitivity, specificity, and Test to Actual Positives ratio at a disease prevalence of 0.01

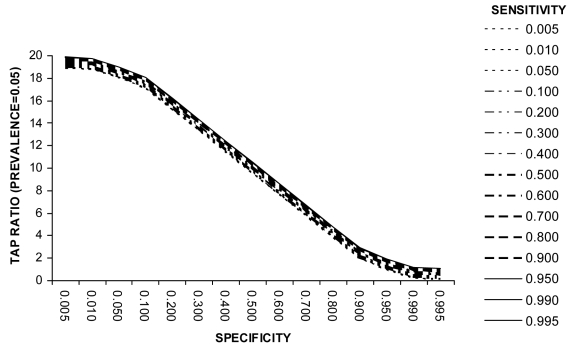
Example 2 (Box 2). Screening for diabetes mellitus using WHO diagnostic criteria (prevalence = 0.05). Example 2 (Figure 2) presents the relationship between sensitivity, specificity, and TAP ratio when the disease prevalence is 0.05. It can be seen from Figure 2 that if small modifications were made to the recommended WHO test cut-off levels such that test specificity falls to 95% and test sensitivity rises, the TAP ratio would move closer to 1 and thus the test would yield more accurate disease frequency estimates. This illustrates that the most appropriate test specification is not always intuitively obvious. In this example a small reduction of test specificity (and consequent small rise in test sensitivity) would yield better test performance in a disease burden study.

Box 2. Screening for diabetes mellitus using World Health Organization (WHO) diagnostic criteria (prevalence=0.05).

Diabetes prevalence is rising in many developing countries and the true prevalence in the adult population in many settings is of the order of 5% (15). Figure 2 presents the relationship between sensitivity, specificity, and Test to Actual Positives (TAP) ratio when the disease prevalence is 0.05. When measuring prevalence in population-based studies, investigators frequently use fasting blood glucose, random blood glucose or the oral glucose tolerance test. WHO criteria state that the diagnosis of diabetes mellitus can be established if the value of fasting glucose is greater than 7.8 mmol/L, or value after 2 hours is greater or equal 11.1 mmol/L. Yudkin estimated the sensitivity of the oral glucose tolerance test to be 32%, and specificity to be 99% (16).

The TAP ratio for these values of specificity and sensitivity is about 0.5 (Figure 2). Thus community-based studies of the prevalence of diabetes mellitus using oral glucose tolerance test and WHO diagnostic criteria will underestimate true disease frequency by 50%.

Figure 2.

Relationship between test sensitivity, specificity and Test to Actual Positives ratio at a disease prevalence of 0.5

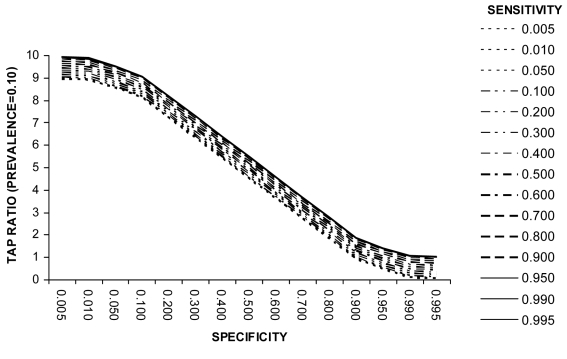
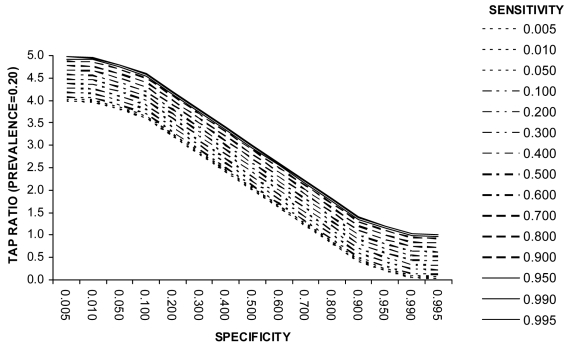
Example 3 (Box 3). Screening for Trichomoniasis using Papanicolau Test (prevalence = 0.10). Example 3 (Figure 3) shows that at a disease prevalence of 0.10 the specificity needs to be 90% or greater to achieve a TAP ratio of 1.0. However, unlike at lower levels of disease prevalence, the test sensitivity is also an important determinant of the TAP ratio. A TAP ratio of 1.0 can be achieved for example by (a) a specificity of 95% and intermediate sensitivity (40%-60%) or (b) a specificity of 99% and very high sensitivity (over 90%). This example illustrates how a test with poor performance characteristics in a clinical setting can perform well in a disease burden study. It also shows that a combination of very high sensitivity and very high specificity is not necessarily the only suitable test specification. Figure 4 illustrates the relationship at a disease prevalence of 0.20.

Box 3. Screening for trichomoniasis using Papanicolau Test (prevalence=0.10).

Trichomonas vaginalis is the most frequent non-viral cause of sexually transmitted disease in the world. Its prevalence in developing country settings is estimated at about 0.1 among women of reproductive age (4). In western countries, the definitive diagnosis of the disease is established using polymerase chain reaction (PCR) technology to detect T. vaginalis in cervicovaginal DNA samples using sets of specific primers. However, in developing countries, the disease is detected mainly through the use of the Papanicolau test. A recent study validated it on over 1000 cervicovaginal swab specimens from a randomized sample of women in Brazil, using PCR to confirm true disease status (17). The study showed that the sensitivity of the Papanicolau test to detect T. vaginalis is 61%, and specificity 98%. Figure 3 shows that this screening test, apparently of limited value in clinical setting, would still be excellent for population-based disease prevalence estimates (carried out, for example, as part of a cervical cancer screening program). At a disease prevalence of about 10% in a population, this combination of sensitivity and specificity yields Test to Actual Positives ratio of 0.98, thus the proportion of infected cases measured by this test will very nearly equal the true proportion of infected in the population (Figure 3).

Figure 3.

Relationship between test sensitivity, specificity, and Test to Actual Positives ratio at a disease prevalence of 0.1

Figure 4.

Relationship between test sensitivity, specificity, and Test to Actual Positives ratio at a disease prevalence of 0.2

Example 4 (Box 4). Screening for tuberculosis in HIV-infected persons using Mantoux, polymerase chain reaction, and amplified mycobacterium direct (AMDT) tests (prevalence = 0.40). Example 4 (Figure 5) illustrates that the most appropriate combination of values of test sensitivity and specificity can be counter-intuitive and need special consideration. This may reveal that the use of cheaper or more efficient alternative test strategies in circumstances where resources are limited may be acceptable in disease burden studies. It also illustrates that underestimation may be more likely at high prevalence, since diagnostic tests in developing countries often have moderately high specificity and only moderate sensitivity yielding a TAP ratio of <1.

Box 4. Screening for tuberculosis in HIV-infected persons using Mantoux, polymerase chain reaction, and amplified mycobacterium direct (AMDT) tests (prevalence=0.40).

Tuberculosis disease is a common complication of HIV in developing countries. In some countries significant parts of entire populations are affected with HIV, and prevalence of tuberculosis among HIV infected adults is about 40% (18). Concerns over the validity of the Mantoux test in HIV-infected patients has resulted in the investigation of the utility of tests based on nucleic amplification for diagnosis of pulmonary tuberculosis in resource-poor settings with high prevalence of HIV (19). The low-cost one-tube nested PCR test showed a sensitivity of 80% and specificity of 40% (which would yield a Test to Actual Positives (TAP) ratio of 1.7, Figure 5), while more costly and sophisticated AMDT had a sensitivity of 92% and specificity of 60% (which would yield a TAP ratio of 1.5) (Figure 5).

Figure 5.

Relationship between test sensitivity, specificity, and Test to Actual Positives ratio at a disease prevalence of 0.4

Example 5 (Box 5). Screening for iodine deficiency by the rapid urinary iodide test (prevalence >0.50). Example 5 illustrates that at a high disease prevalence level the magnitude of over- or under-estimation is much lower than at lower disease prevalence levels (see example 4 also).

Limiting bias from test misclassification

A preliminary estimate of the TAP ratio in the design of a study can be helpful. It may be difficult to make a precise estimate since this may require detailed information on various test configurations (ie, how sensitivity and specificity vary with varying cutpoints or definitions of test criteria) and an accurate estimate of the underlying true probability of disease before the study is performed. However, even a rough estimate of the TAP ratio will help identify situations in which there is a very large potential for bias (such as in the case of studies of diseases in low prevalence – Boxes 1 and 2). This important information may suggest the need for an alternative diagnostic test (or reconfiguration of the test to have a more favorable TAP ratio) or study design or the need to employ the direct correction approach described below in order to reduce bias in disease frequency estimates. Table 2 provides the combinations of test sensitivity and specificity at given values of disease prevalence required to yield a TAP ratio of 1.0.

Table 2.

Levels of test specificity required for various levels of test sensitivity and disease prevalence to achieve a Test to Actual Positives (TAP) ratio of 1.0*

Sensitivity	Prevalence of disease in a population
	0.01	0.03	0.05	0.10	0.15	0.20	0.25	0.30	0.40	0.50
0.100	0.991	0.972	0.953	0.900	0.841	0.775	0.700	0.614	0.400	0.100
0.200	0.992	0.975	0.958	0.911	0.858	0.800	0.733	0.657	0.466	0.200
0.300	0.993	0.978	0.963	0.922	0.876	0.825	0.766	0.700	0.533	0.300
0.400	0.994	0.981	0.968	0.933	0.894	0.850	0.800	0.743	0.600	0.400
0.500	0.995	0.984	0.973	0.944	0.911	0.875	0.833	0.786	0.666	0.500
0.600	0.996	0.987	0.978	0.955	0.929	0.900	0.866	0.830	0.733	0.600
0.700	0.997	0.990	0.983	0.966	0.947	0.925	0.900	0.872	0.800	0.700
0.800	0.998	0.993	0.988	0.977	0.964	0.950	0.933	0.914	0.866	0.800
0.900	0.999	0.996	0.994	0.988	0.982	0.975	0.966	0.957	0.933	0.900
0.950	1.000	0.998	0.997	0.994	0.991	0.987	0.983	0.979	0.967	0.950
0.990	1.000	0.999	0.999	0.999	0.998	0.997	0.997	0.996	0.993	0.990
0.995	1.000	1.000	1.000	1.000	0.999	0.999	0.998	0.998	0.997	0.995

*Very high test specificity cannot always be achieved realistically since many inexpensive screening tests are not highly specific. For a low disease prevalence of around 1% (0.01), if the highest specificity achievable is 95% then the sensitivity in the control group would have to be lowered to <5% in order for the test configuration to have a TAP of 1. Such extremes would be undesirable.

Estimating the TAP ratio. As noted above, an accurate estimation of the TAP ratio (equations 2-4 and Figures 1-5) requires that the properties of diagnostic test (sensitivity and specificity) are established before the study and that the expected true prevalence (or incidence) of disease is also known, either from previous published studies in same population or from studies in similar populations. Typically, all these data are not available. In these circumstances the TAP ratio can be estimated by measuring the test positive predictive value. This will involve further investigation of the cases which were identified as positive by the diagnostic test. All, or a random sample of all, who tested positive should be referred to local hospital or research center, where the diagnosis can be confirmed or excluded by physicians with more experience, using more sophisticated and valid diagnostic methods. Dividing the sensitivity of the diagnostic test (known from published reports or past experience with the test before the study is undertaken) by the positive predictive value (established through this further investigation of those who tested positive – which can be performed during the study) will yield an estimate of the TAP ratio (see equation 8). Alternatively, limits within which the TAP ratio must lie can than be defined over a range of plausible test sensitivity values.

It is important to note that whereas Se and Sp are more stable across studies at least within levels of disease and covariates such as age, sex, and socioeconomic status, PPV values depend heavily on disease prevalence, which varies from study to study. So the use of PPV should be limited to studies in which internal validation data are available (13,23,24). Figure 6 shows how the TAP ratio depends on different combinations of diagnostic test sensitivity and positive predictive value.

Figure 6.

Relationship between test sensitivity, positive predictive value, and Test to Actual Positives ratio

Using the TAP ratio to make a direct correction for bias from test misclassification. From above,

P = T/TAP

Once the TAP ratio has been estimated then the disease prevalence can be obtained by prevalence = T/TAP or prevalence = number of true positives divided by the TAP ratio.

Alternatively, substituting the expression for TAP given in (5),

9) P = [T-(1-Sp)]/(Se+Sp-1)

Thus, this equation can be applied to correct the inaccuracy of any test with known sensitivity and specificity (14). For example, suppose that we want to survey a population and we assume that the disease prevalence will be around 20%. Further suppose that a standard screening test has been used extensively and has properties in the target population which are known (sensitivity of 90% and specificity of 80%). When the true prevalence is 20%, the standard test configuration would be expected to label 34% of the population as positive, a serious overestimate of the true disease prevalence. If the true prevalence is 10%, the standard test configuration would yield a 27% test-positive prevalence, a serious overestimate. These could be corrected with the above equation to obtain the corrected value of 20% and 10% respectively.

This direct correction can eliminate bias irrespective of the true (but unknown) disease prevalence. In addition, standard statistical inference procedures can be applied to compute confidence intervals (assuming that Se and Sp are fixed known parameters). Even when the test sensitivity and specificity are not known precisely in the study population, direct correction estimates may typically be more accurate than those without correction. However, this may not necessarily be the case and examples of problems with direct correction have been published (25,26). To improve the validity of this approach a validation substudy could be carried out in the target population and this could take place concurrently with the main study. This direct correction approach is essentially a two-stage design, with relatively straight-forward statistical inference. The main study and substudy could be combined and analyzed together via maximum likelihood methods thus yielding valid estimates for disease prevalence, as well as sensitivity and specificity of the test. This can give estimates with confidence intervals (11,27).

Corrections could be applied in different exposure cohorts and within strata; if Se and Sp are the same in all groups then this is non-differential disease misclassification; if they vary across groups then this is differential misclassification. Results of repeated corrections with different estimates of Se and Sp could be tabulated to give a sensitivity analysis.

If the validation standard is measured with error then the corrected error will be biased. Any bias in the corrected estimate will be less than that in the uncorrected estimate if the Se and Sp of the validation measure is higher than that of the regular measurement. However, it is better to have a sensitivity analysis with formal correction methods even when internal validation methods are available (28,29). Correction methods which are more efficient and more general can be obtained using likelihood-based approaches (27).

Influence of the TAP ratio on the power of a randomized controlled trials

Disease episodes defined by diagnostic test results are commonly measured in controlled trials. Measurement error theory suggests that the higher the misclassification of the outcome, the lower the power to detect differences across groups. Consider a trial in a population in which the disease prevalence is known to be 5% from previous studies and in which the test employed has been shown to have a sensitivity of 80% and specificity of 95%. Assume also that the trial includes 5000 participants per group, with a targeted reduction in outcome events due to the intervention from 250/5000 episodes (0.05) to 125/5000 episodes (0.025) over the study period. If the intervention group had 125 actual cases, it would be measured as 344 positive tests in the study cohort; analogously, 250 actual cases of disease in the control group would be measured as 438 positive tests. Instead of a reduction of 50% in incidence (125 vs 250 cases) due to the intervention, it will appear that a reduction of only 22% has been achieved (344 vs 438 cases). This could result in an underestimation of the impact of the intervention or even an incorrect conclusion that the intervention is ineffective due to inadequate power to reject the null hypothesis.

In this example, Fisher exact test with α of 0.05 suggests that the sample size needed for 80% power is N = 3312 per group (if a test with 80% sensitivity and 95% specificity is used).

In this case, the test would be expected to label 8.75% of the control group and 6.88% in the control group as positives (OR, 0.77, instead of the true 0.49). In contrast, the direct correction approach would still yield unbiased estimates of 5% and 2.5%, but the study would have needed thousands of subjects.

However, the TAP ratio approach could be used to reconfigure the test before the start of the trial. Ideally, this would involve configuring and applying the test separately for control and intervention groups. Thus, for the control group, TAP = 1 implies that (1-Sp)/(1-Se) should be equal to 0.0526; this could be achieved, for example, with sensitivity of 62% and specificity of 98%. In the intervention group, TAP = 1 implies that (1-Sp)/(1-Se) should be equal to 0.0256, and this could be achieved with for example a sensitivity of 22% and specificity of 98% or a sensitivity of 61% and specificity of 99%.

This approach could, in theory, result in the expected test positives equaling the true positives in each group (ie, 5% and 2.5%). If this were possible to achieve in practice then in theory the required sample size would be N = 960 per group, if appropriate test configurations (having TAP of 1) are used.

If there were good data (for example from a validation substudy in the same population) to support the choice of the most appropriate test sensitivity and specificity, and if feasible in practice, using test configurations with TAPs close to unity would be advantageous from the viewpoint of efficiency. However, some uncertainty would remain about test performance characteristics and therefore the extent of remaining bias.

Summarizing the limitations of the use of TAP ratio

We already stated that the primary aim of the use of TAP ratio is in situations where an estimate of the prevalence or incidence of disease in a population is being made. However, there are some caveats, limitations, and special considerations associated with its potential use, to which we would like to point systematically in this section. For example, there will be situations when there are several screening test available for one diagnosis. In these cases, TAP ratio can be particularly helpful when deciding which one to apply in burden measure studies, because a combination of test sensitivity and specificity that renders it useful in clinical setting may not be ideal for its application in community-based studies, where tests with different properties may do better. Furthermore, when the disease of interest is very rare, the effects of a decrease in test specificity on the TAP ratio at very low disease prevalence can be dramatic and a diagnostic test for disease burden estimates should only be employed if positives can be checked and established with nearly 100% accuracy, which would allow calculation of positive predictive value. When the disease is known to often be under-reported, especially if this is due to lack of availability of highly accurate screening test from clinical settings, a consideration should be given to the possible use of cheaper or more efficient alternative test strategies in circumstances where resources are limited. This is because even if their sensitivity and specificity are very low, they may still do very well in estimating disease burden in the population, depending on disease prevalence.

Cost-effectiveness of use of TAP ratio should be very high, because it only takes a very limited sub-sample of positively tested cases to be verified at a secondary facility to establish positive predictive value. Once this parameter becomes available, there are no further costs in applying TAP ratio, and the expected benefits in terms of improving accuracy of the estimates and ensuring adequate power of the planned research study will outweigh the costs of the pilot study under large majority of assumptions.

There are also some special circumstances that could limit the use of TAP ratio. One possible concern is how TAP ratio would apply to verbal autopsy data, given that all causes of death must add to 100%. If TAP was appropriately applied to correct for each reported cause individually, their proportions may change but they would still need to add to 100%. If such corrected cause-specific estimates considerably exceed the overall number of recorded deaths after the correction using TAP is made, that would imply that the use of TAP ratio highlighted the problem of multiple causes leading to a single death (which is often the case). If they fall well below 100% of all recorded deaths when added up, that would imply that there are further causes of mortality that were not picked up by verbal autopsy tool (which is, again, often the case).

Theoretically, it may be possible that sensitivity and specificity is different for the same instrument used in different settings. This consideration again justifies the use of a pilot-study to establish all the necessary key parameters needed for the application of the TAP ratio. Finally, there will be cases when prevalence rate will be reported, but the screening procedure used will be unknown. In those cases, contacting the authors of the study about the tool they used to establish the prevalence is the safest way to correct their estimate (if necessary), as TAP ratio cannot be applied.

Discussion

In studies where the aim is to measure disease frequency in a population, a diagnostic test may be used to identify disease episodes when it is not possible to make a definitive diagnosis of the disease. This is typically the case in community-based studies (especially in resource poor settings, where access to hospitals or research facilities may be poor), where disease prevalence is low and where resources do not permit highly trained staff to participate directly in the disease surveillance. To interpret the results of such studies, it is important to have information about the extent of misclassification from the test. Misclassification itself does not inevitably result in inaccurate estimates. It is the imbalance between the number of false positives and false negatives which creates inaccuracy (30). Somewhat counter-intuitively, in some circumstances a decrease in sensitivity or specificity may actually result in more accurate estimates being reached (30).

Diagnostic test parameters are estimated typically in clinical settings and test specifications are set to meet clinical requirements (where high sensitivity is often accorded relatively higher priority than in epidemiological studies). The application of such test specifications to population-based epidemiological research is problematic. First, as we illustrate, the differing test populations and settings can yield very different test performance (even when disease prevalence is constant). For clinical pneumonia, the specificity of the WHO test in community-based clinical pneumonia studies is very high (at least 95%), whereas it has been repeatedly reported to be in the range of 70%-80% in hospital out-patients studies (7,10). This is most likely to be because the study populations are quite different, with the majority of children being completely well (and with low respiratory rates) in the community-based studies, whereas most children are ill (with a variety of conditions other than clinical pneumonia that may tend to increase respiratory rate) in the hospital-based studies.

The relationship between test positives, positive predictive value, and true prevalence has been considered in a study of health interview surveys. This study made suggestions on how to correct the apparent prevalence in a survey for shortcomings in the methods used to estimate them and to take into account their absolute values (14). The Australian Institute of Health and Welfare used routine data to monitor the incidence of major cardiovascular events in Australia and derived corrected numerators by multiplying counts of events by sensitivity and dividing by the positive predictive value of clinical diagnoses as judged against criteria developed for the World Health Organization MONICA Project (http://www.health.nsw.gov.au/public-health/chorep/cvd/cvd_intro.htm). However, adjustment for misclassification bias has proven unsuccessful when information from an appropriate study population has not been available or applied incorrectly (26,31). An example of this are verbal autopsy studies which are commonly used to define causes of death in disease burden studies in developing countries and which form an important part of the evidence base of global burden of disease estimates. These studies have often taken sensitivity and specificity estimates from study populations with substantially different patterns of cause-specific mortality (25) and this has led to incorrect conclusions being reached from the data. Second, optimal test characteristics for use in a population-based survey are likely to be different from those when the test is utilized in a clinical setting. In the example of community-based studies reporting clinical pneumonia incidence in young children, the respiratory rate threshold for the definition of clinical pneumonia was lowered by WHO from 50 breaths per minute or above to 40 in children 1-4 years of age. This revised test specification, which has higher sensitivity but lower specificity for clinical pneumonia, was introduced so that an increased percentage of children with clinical pneumonia would be identified and treated appropriately. Although this change has benefits for clinical practice the revised test specification will result in less accurate overall clinical pneumonia frequency estimates when used in disease burden studies, as lower test specificity at low disease prevalence will inflate estimates of clinical pneumonia incidence (32-34).

However, by understanding the relationship between sensitivity, specificity, and disease prevalence the TAP ratio can be calculated. We suggest that the TAP ratio is the most useful summary measure of the potential for disease misclassification bias. In some studies it may be possible to estimate test sensitivity and specificity for various test configurations and use these data to set the test specification to result in roughly equivalent numbers of false positives and false negatives. This may improve study efficiency and is still compatible with later direct correction of the final estimates. It is important to note that improving test sensitivity and specificity alone may not improve the accuracy of disease frequency estimates.

In studies in which the TAP ratio shows a large potential for bias it is important to consider the implications for study design and to plan to apply a direct correction approach (see equation 9). In surveys measuring rare disease events or in regular surveillance of common disease events (such that events are rare in each survey), the potential for over-estimation is high. It is particularly important to maximize test specificity and advisable to check a sample of test positives (to estimate the test positive predictive value) to assess the level of possible over-estimation (as described above). An alternative strategy would be to avoid application of the test in settings of very low disease prevalence, since the TAP ratio may be markedly different from 1.0.

In practice, test sensitivity and specificity information over a range of test specifications is often not available. In these circumstances it may be possible to estimate a plausible range for the TAP ratio. One example, when disease prevalence is low, would be to check the validity of all or a sample of test positives to measure the test positive predictive value. Limits within which the TAP ratio must lie can then be defined over a range of plausible test sensitivity values.

When a diagnostic test result is used to define outcome events in a controlled trial, then test misclassification has important implications for the power of the trial and for the estimation of the size of difference in disease frequency in intervention groups (34,35). We have suggested a use for the TAP ratio by calibrating the test a priori to bring it closer to a TAP of unity. This would realize certain efficiency benefits. Then, at the end of the study, one could still apply the appropriate direct correction (equation 9) to eliminate the remaining bias (due to the test configuration not being entirely appropriate because of missed assumptions).