Sensitive and fast T₁ mapping based on two inversion recovery images and a reference image

Abstract

We developed a fast method to obtain T₁ relaxation maps in magnetic resonance imaging (MRI) based on two inversion recovery acquisitions and a reference acquisition, while maintaining high sensitivity by utilizing the full dynamic range of the MRI signal. Optimal inversion times for estimating T₁ in the human brain were predicted using standard error propagation theory. In vivo measurements on nine healthy volunteers yielded T₁ values of 1094±18 ms in gray matter and 746±40 ms in white matter, in reasonable agreement with literature values using conventional approaches. The proposed method should be useful for clinical studies because the T₁ maps can be obtained within a few seconds.

I. INTRODUCTION

Spin-lattice relaxation times (T₁) measured with magnetic resonance imaging (MRI) can provide important information about normal and pathological conditions. Furthermore, various MRI applications, such as arterial spin labeling perfusion imaging,^1,2 magnetization transfer imaging,³ and temperature monitoring⁴ require estimates of T₁ for quantification. A large number of different methods have been proposed to measure T₁ relaxation (for an extensive review see Refs. ⁵ and ⁶). Conventionally, an inversion recovery (IR) experiment is repeated with multiple inversion times to estimate T₁.⁷ This approach requires relatively long scan times and may compromise accuracy because of involuntary subject motion during data acquisition. In addition, the precise timing of the negative-to-positive zero crossing of the IR signal is usually not easily identified in conventional MRI, because in general only magnitude images are stored. Finally, multi-time point methods are generally very sensitive to image noise, especially at inversion times (TI) where the signal is close to zero (TI > T₁ *ln 2).⁸

To reduce these problems, several two-point methods were introduced to measure T₁ using either a combination of saturation-recovery (SR) and IR spin preparations,^8,9 or two different repetition times, or two different pulse flip angles without SR and IR preparations.^10,11 However, these methods have certain limitations. If a combination of SR and IR spin preparation is used, dynamic range is sacrificed, because SR experiments yield only 50% of the signal range of IR experiments. Moreover, differences in rf power between SR and IR pulses can introduce systematic errors for T₁ measurements. If different repetition times or flip angles are used, dynamic range is also reduced and/or systematic errors in T₁ can be introduced by deviations of actual flip angles from their nominal settings. Dependency on flip angles is also a problem for inversion recovery methods using a Look–Locker acquisition,¹² which furthermore diminishes signal-to-noise ratio because fast repetitions of excitation pulse are employed.

The primary objective of this study was to develop a method for T₁ mapping based on two IR images and a reference image, thus allowing the maximum measurement dynamic range to be used within a very short scan time. Another objective was to eliminate complications with zero crossing of the signal for T₁ measurements. Using single-shot echo planar imaging (EPI) (Ref. ¹³) to further reduce scan time, multislice T₁ maps of human brain were obtained within a few seconds.

II. THEORY

The magnetic resonance signal, S_e, of a single-shot gradient-echo (GE) EPI sequence at echo time TE with repetition time, TR (TR ≫ T₁ of brain tissue) can be expressed as $S_{\text{e}}=S_{0}exp(-\text{TE}/T_2^{\ast })$, where S₀ is the initial equilibrium magnetization and $T_2^{\ast }$ is the transverse relaxation time due to both random magnetic field fluctuations and static magnetic susceptibility. If an inversion pulse is applied prior to the GE-EPI acquisition, the signal is then subject to T₁ relaxation for an inversion time TI, according to

$$S_{\text{IR}}(\text{TI})=S_e\left[1-(1-k)exp\left(-\frac{\text{TI}}{T_1}\right)\right],$$ (1)

where k=cos(α_eff) accounts for imperfect inversion by a pulse with effective flip angle α_eff.⁶ Note that full relaxation is assumed (TR > seven times the T₁ of brain tissue). To estimate T₁, at least two measurements at two different inversion times TI₁ and TI₂ are required. From the two measurements shown in Fig. 1, yielding S_IR1 at TI₁ and S_IR2 at TI₂, two difference signals, S_e − S_IR1 and S_e − S_IR2, can be obtained. By taking their ratios (S_e − S_IR1)/(S_e − S_IR2), and rear-ranging the components, T₁ can then be estimated from the expression

Fig. 1.

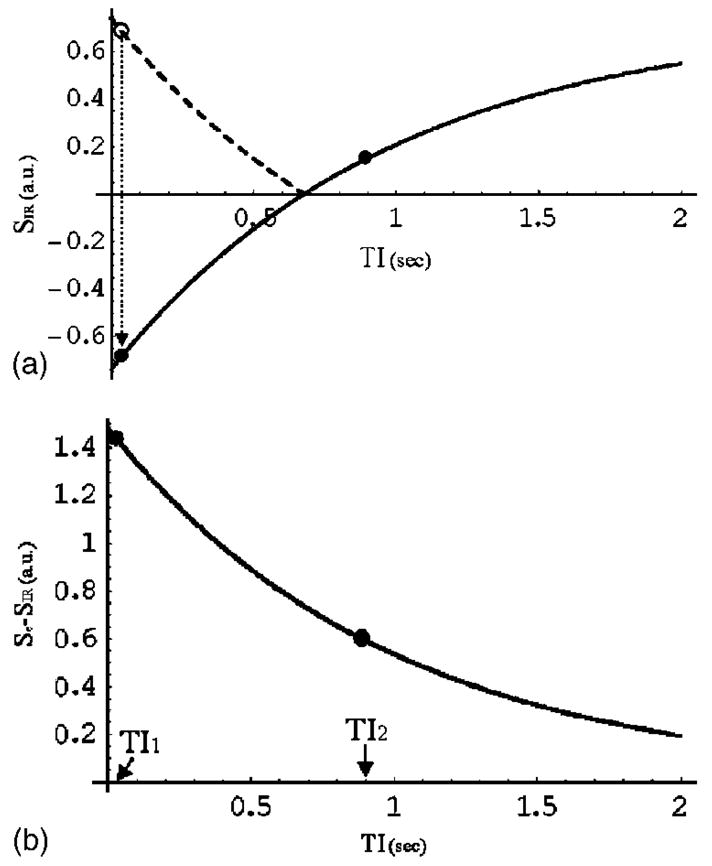
Simulation of the signal intensity of the inversion recovery sequence as a function of inversion time (TI) (A) and the difference signal intensity of S_e − S_IR (B). The parameters used were TE=15 ms, S₀ =1.0, T₂ * =50 ms, and T₁ =980 ms for human gray matter at 1.5 T. In (A), the heavy dashed line before the zero crossing represents the absolute value of S_IR. The two dots represent the inversion times, TI₁ and TI₂, used to calculate T_1m from the difference signal.

$$T_{1m}=\frac{{\text{TI}}_2-{\text{TI}}_1}{ln\left(\frac{S_e-(-S_{\text{IR}1})}{S_e-S_{\text{IR}2}}\right)},$$ (2)

with T_1m indicating an estimated value of T₁. By taking the ratio (S_e − S_IR1)/(S_e − S_IR2), the (1− k) term disappears, achieving insensitivity to inversion pulse imperfections.⁶ Note, standard MR acquisitions produce magnitude images only, but since it is obvious that spins must have a negative magnetization at the shortest TI₁, the sign of S_IR1 can be reversed in Eq. (2) to gain the full range of magnetization, as shown in Fig. 1.

To minimize the error in computing T_1m of gray and white matter in the human brain, first-order error propagation theory was applied to determine an optimum combination of TI₁ and TI₂ values, assuming a perfect inversion rf pulse. With the assumption that the measurement errors of S_IR1, S_IR2, and S_e are uncorrelated and that each has the same standard of deviation (σ_S, the standard of deviation of the error in the T_1m measurement, (σ_T1m, is

$$\begin{array}{l}\frac{{\sigma }_{T1m}}{T_1}\left(\frac{1}{2}\right)\left(\frac{{\sigma }_s}{S_e}\right)\left(\frac{T_1}{{\text{TI}}_2-{\text{TI}}_1}\right)\\ \times \left\{\frac{\sqrt{exp(-2^{\ast }{\text{TI}}_2/T_1)+exp(-2^{\ast }{\text{TI}}_1/T_1)}}{exp[-({\text{TI}}_1+{\text{TI}}_2)/T_1]}\right\}.\end{array}$$ (3)

The derivation of first-order error propagation for Eq. (3) can be found in references by Kurland⁸ and Imran et al.¹⁰ Obviously, TI₂ must be different from TI₁ to avoid a singularity from the 1/(TI₂ −TI₁) term in Eq. (3). On the other hand, their difference should not be too large, because 1/(TI₂ −TI₁) is counterbalanced by 1/exp(− (TI₁ +TI₂)/T₁), indicating that the error increases if the signal-to-noise ratio (SNR) of the second IR measurement becomes too small as TI₂ increases. From Eq. (3), the SNRs of T_1m and S_e are defined as SNR_T1 = T₁/(σ_T1m and SNR_Se = S_e/(σ_S, respectively.¹⁴ Equation (3) also implies that if T₁ of gray matter and white matter are roughly known a priori, TI₁ and TI₂ values can be carefully optimized to maximize SNR_T1 in human brain.

III. METHODS

A. Simulations

From Eq. (3) it is obvious that TI₁ should be as short as possible. To determine the optimal inversion time of TI₂ for human brain T₁ measurements, computer simulations were performed to evaluate Eq. (3) with the following parameters: SNR_Se =50 and T₁ =980 ms (Ref. ⁷) for gray matter and SNR_Se =30 and T₁ =640 ms (Ref. ⁷) for white matter in human brain at 1.5 T. The SNR_Se values are typical for the single-shot GE-EPI acquisitions described below. Optimized values found for TI₁ and TI₂ were then used in studies with normal volunteers to measure the pixel-wise T_1m of brain tissue. The simulations were performed using MATHEMATICA software (Wolfram Research, Champaign, IL).

B. Experiments in human brain

In order to minimize motion artifacts and noise differences between measurements, a sequence was developed to obtain three sets of images in a single scan using a series of 2D multislice EPI data acquisitions, as shown in Fig. 2. Here, 180° indicates a nonselective inversion pulse; 90° indicates a slice-selective 90° sinc-shaped pulse with duration of 2.56 ms. TE is the echo time between the 90° pulse and the center of EPI k space. Each slice is acquired with a 52 ms single-shot GE-EPI readout. TD is a variable delay time to maintain a constant TR for all three acquisitions [TR=slices*(TE+EPI/2) +TD₀ =TI_{1 or 2} +slices*(TE+EPI/2) +TD_{1 or 2}]. The first image acquisition, which provides the reference image used to calculate S_e, does not involve an IR-preparation rf pulse. The second and third acquisitions are identical to the first except that a non-selective hyperbolic secant inversion pulse (12.8 ms duration, 50 μT of B₁ field strength) was applied to invert spins on the whole volume of interest, followed by multislice acquisitions with two different inversion times, TI₁ and TI₂. In all three acquisitions, TR=7000 ms (about seven times T₁ in gray matter) and TE=15 ms.

Fig. 2.

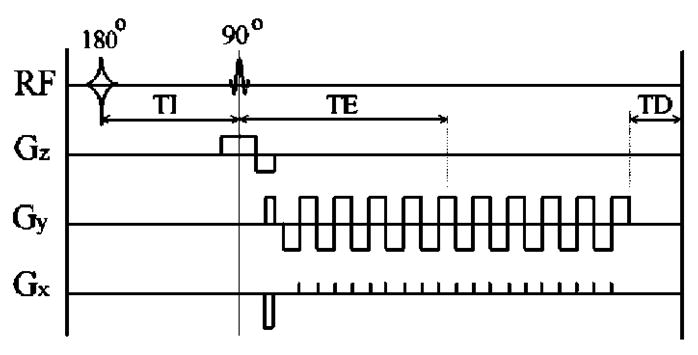
Pulse sequence timing diagram showing radio frequency (rf) pulses and gradients (G_r) along each spatial direction r=x, y, z. A nonselective hyperbolic inversion (180°) rf pulse is followed after the inversion time TI by a slice-selective sinc-shaped excitation (90°) pulse. G_z is the slice selective gradient. An echoplanar image (EPI) is generated by gradients G_y and G_x. TE is the echo time, and TD is a variable delay time and was adjusted to yield the same repetition time (TR=7000 ms) for all three images. The first image S_e according to Eq. (2) is obtained without applying a 180° pulse, while the second S_IR1 and third S_IR2 images are acquired each with a 180° pulse at delays TI₁ =40 ms and TI₂ =900 ms, respectively.

To demonstrate the utility of this approach for the in vivo T_1m measurement, nine normal volunteers (mean age and standard deviation=61±15 years and age range =37–80 years) were studied using a 1.5 T MR system (Vision, Siemens, Germany). A circularly polarized head coil was used for radio frequency transmission and reception. Seven 8 mm thick slices with a 3.4 × 3.4 mm² in-plane resolution and a 2 mm gap were acquired in an interleaved fashion to minimize cross-talk effects between slices. The bottom slice was located 1 cm above the Circle of Willis for all subjects. Inversion times of TI₁ =40 ms and TI₂ =900 ms were chosen based on simulation results. The total acquisition time for seven slices was 21 s. The T_1m value for each pixel was calculated using Eq. (2).

Regions of interest (ROIs) of gray matter and deep white matter in each subject were selected in the four slices (3 to 6) of the S_e (reference) images using the OSIRIS software package (Geneva University Hospital, Geneva, Switzerland; http://www.sim.hcuge.ch). The gray and white matter T₁ values for each subject were obtained by averaging over these ROIs. Note that images from the subjects were not normalized into a standard space; therefore, the size and anatomical locations of the ROIs used to obtain T₁ values were different for each subject. Representative ROIs are shown in Fig. 4.

Fig. 4.

Images from one normal volunteer without inversion preparation (reference S_e images, top row) and corresponding T_1m maps (bottom row) for seven slices. Representative ROIs of gray matter and white matter were drawn on the middle slice out of seven slices as indicated in the figure. Slices 3 to 6 were used to measure average T₁ values in each subject.

IV. RESULTS

A. Simulations

SNR_T1, calculated according to Eq. (3), is plotted in Fig. 3 as a function of TI₁ and TI₂ for gray matter (A) and white matter (B). With longer TI₁, the SNR_T1 for gray matter and white matter decreased, indicating that the shortest possible TI₁ (in this case, 40 ms) should be used. With TI₁ =40 ms, the maximum SNR_T1 was achieved, TI₂ =1100 ms for gray matter and TI₂ =700 ms for white matter. For the in vivo studies, it was decided to use the average of the optimal TI₂ inversion times for gray and white matter, which was 900 ms.

Fig. 3.

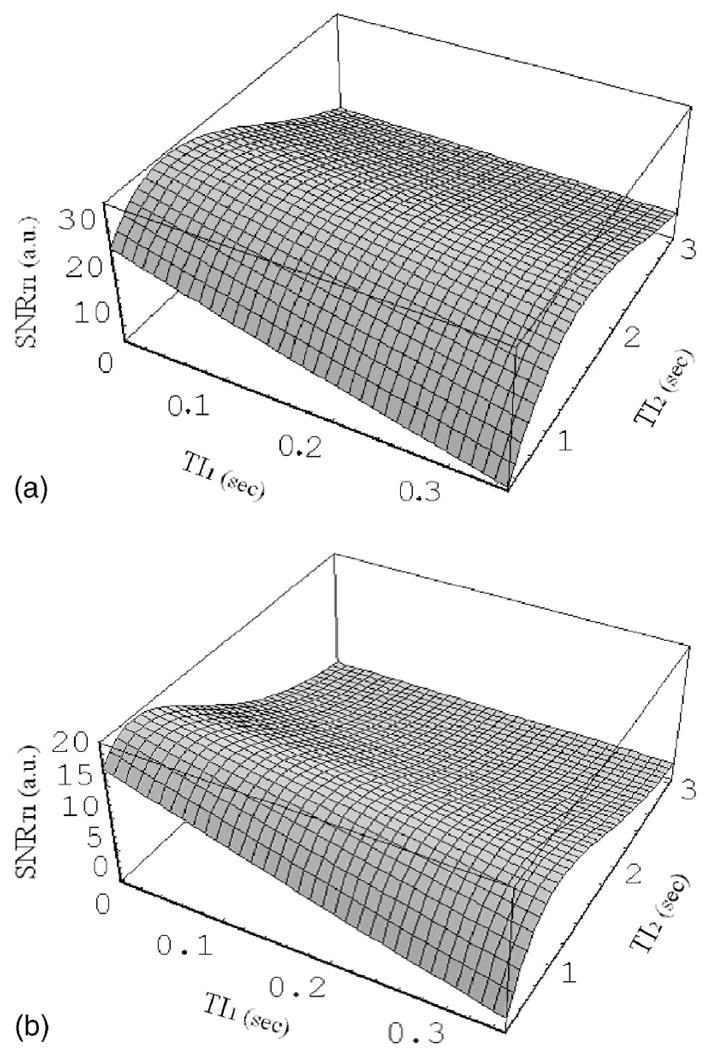
Simulation of SNR_T1, calculated according to Eq. (3), as a function of inversion times TI₁ and TI₂, assuming a perfect inversion pulse. The simulation parameters used were SNR_Se =50 and T₁ =980 ms for human gray matter (A) and SNR_Se =30 and T₁ =640 ms for human white matter (B) at 1.5 T. SNR_T1 reached a maximum at TI₂ =1100 ms for gray matter and at TI₂ =700 ms for white matter with TI₁ =40 ms.

B. Studies on human brain

Figure 4 shows single shot GE-EPI (S_e) images and corresponding T_1m maps from seven axial sections through the brain of a volunteer. Overall, the T_1m maps show reasonable contrast between gray and white matter. Results of T_1m estimates averaged over gray matter and white matter, respectively, from nine volunteer studies are listed in Table I. Averaged over all subjects, the proposed method yielded T_1m values of 1094±18 ms for gray matter and 746±40 ms for white matter.

Table I.

T_1m estimates for gray and white matter from nine volunteers.

Subject	Graymatter T1m (ms)	Whitematter T1m (ms)
1	1080±26	720±16
2	1075±55	750±9
3	1100±71	770±8
4	1110±57	703±12
5	1101±68	772±25
6	1090±63	682±33
7	1073±56	730±18
8	1130±82	810±25
9	1090±61	780±23
Mean±STD	1094±18	746±40
Referencea	980±63	640±30

^aReference from phase-sensitive multipoint inversion recovery sequence published by Cho et al. (Ref. ⁷).

V. DISCUSSION

We have demonstrated that a new acquisition method with carefully selected values of two inversion times provides maps of T₁ estimates of gray matter and white matter that are comparable to those obtained from a phase-sensitive multi-point inversion recovery technique.⁷ Compared to published two-point methods for T₁ measurements,^8–11 the proposed method has several advantages: (1) The method makes use of the full dynamic range of both S_IR1 and S_IR2, which should improve the SNR (Ref. ¹⁵) and therefore improve accuracy for T₁ measurements. (2) By choosing TI₁ and TI₂ so that reasonable assumptions can be made about the signs of S_IR1 and S_IR2, the problem of identifying the negative-to-positive zero crossing of the IR signal is avoided, because both (S_e−S_IR1) and (S_e − S_IR2) always yield positive values.¹⁶ However, the proposed method has several limitations: Because nonselective inversion pulses are used, successive slices have different TI₁’s and TI₂’s. Therefore, although TI₂−TI₁ remains the same for all slices, not all slices will have the optimal inversion time for the highest SNR_T1 and the dynamic range will decrease for successive slices. In addition, different slices will sample a different part of the relaxation curve, allowing accurate estimation of only monoexponential relaxation, To the extent that longitudinal relaxation in the human brain tissue is multiexponential, including effects due to partial volumes of gray matter, white matter, and CSF, slice-dependent errors in estimating T₁ are introduced. Especially, when data acquisition occurs on a later part of a multiexponential curve, T₁ will appear prolonged. The presence of partial volumes of brain tissue with CSF may have contributed to slightly higher T₁ values in gray and white matter in this study than previously reported. Partial volume effects can be reduced with the acquisition of a higher resolution multishot EPI sequence.

Finally, one should note that the optimized parameters for measuring T₁ of brain tissue result in an underestimation of the T₁ of CSF by about a factor of 4 compared to a value of 4500 ms obtained with a multipoint inversion recovery technique.¹⁴ T₁ of CSF in this study was 1020±65 ms. The proposed technique, therefore, cannot accurately measure T₁ values for brain tissues and CSF with a single set of inversion times TI₁ and TI₂ because we do not obtain phase information of inverted spins. Therefore, to accurately measure T₁ of CSF with this approach, the second inversion time of the sequence needs to be adjusted for CSF and a separate dataset acquired. In contrast to brain tissue, T₁ measurements of CSF are accurate for TI₂ values of about 5 s. However, a TI₂ of 5 s is no longer optimal for gray, white, and most other brain tissue.

Because the proposed technique requires only two TI points with a reference EPI scan and no more than a few seconds to map T₁, this technique should be useful for any clinical study that requires an estimate of the T₁ of brain tissue. In addition, the proposed method is ideally suited for use in combination with EPI-based arterial spin labeling perfusion studies to quantitatively measure cerebral blood flow in brain. The arterial spin labeling perfusion images and a T₁ map can be obtained with the same spatial resolution and similar EPI-related image distortions. Another possibility to derive T_1m from S_e and S_IR2 datasets is to calculate the log transform of the images and compute T_1m according to T_1m =TI₂/ln[(1−k)S_e/(S_e − S_IR2)]. However, this method is very sensitive to the selection of the inversion time.

In conclusion, the proposed T₁ measurement based on two IR images utilizes the full dynamic signal range and requires only a few seconds for acquisition, yet yields results similar to those of a conventional method. Therefore, this new method may be useful for obtaining T₁ values of brain tissue in clinical studies, where short scan times and simplicity of data processing are imperative.