Power Computations in Time Series Analyses for Traffic Safety Interventions

Abstract

The evaluation of traffic safety interventions or other policies that can affect road safety often requires the collection of administrative time series data, such as monthly motor vehicle collision data that may be difficult and/or expensive to collect. Furthermore, since policy decisions may be based on the results found from the intervention analysis of the policy, it is important to ensure that the statistical tests have enough power, that is, that we have collected enough time series data both before and after the intervention so that a meaningful change in the series will likely be detected. In this short paper we present a simple methodology for doing this. It is expected that the methodology presented will be useful for sample size determination in a wide variety of traffic safety intervention analysis applications. Our method is illustrated with a proposed traffic safety study that was funded by NIH.

1. Introduction

Intervention analysis (Box and Tiao, 1976; Cook and Campbell, 1979, Ch. 6; Hipel and McLeod, 1994, Ch.19) provides a statistical method for quantifying the effect on known interventions on a time series. It has been one of the most commonly used statistical procedures to evaluate traffic safety interventions or other policies that can affect road safety (e.g. Abdel-Aty and Abdelwahab, 2004; Blose and Holder, 1987; Elder et al., 2004; Elder et al., 2002; Gruenewald and Ponicki, 1995; Hagge and Romanowicz, 1996; Hingson et al., 2000; Holder and Wagenaar, 1994; Holder et al., 2000; Langley et al., 1996; Mayhew et al., 2001; Murray et al., 1993; Nathens et al., 2000; Vernon et al., 2004; Voas et al., 1997). Indeed, various applied researchers have written specifically on the value of using time series analyses in intervention or evaluation research (Biglan et al., 2000; Gruenewald, 1997; Rehm and Gmel, 2001)

Often applied researchers are under pressure to evaluate the impact of a traffic safety intervention soon after its implementation. In these time series analyses, sample size may be limited. For example, Vingilis and Salutin (1980) evaluated the impact of a spot-check enforcement program called R.I.D.E. (Reduce Impaired Driving in Etobicoke). This program was a one-year pilot project and sponsors of the program wanted an evaluation of the impact at the end of one year. The evaluation used a mixed-methods, multi-measures evaluation methodology. Among their measures was the time series analysis of collisions for two years prior to the R.I.D.E. program and for the one-year intervention, for a total of 36 data points -- 24 month pre-intervention and 12 months post-intervention. The results of the time series analyses found a near significant downward trend at p ≈ 10% for alcohol-related collisions for the intervention area. The study concluded: “The ultimate change in alcohol-related accidents might not be in evidence because of contaminations mentioned previously or because of the need for a longer time period” (Vingilis and Salutin,1980, p.274). This study is an example of how difficult it is to interpret a near significant finding as one cannot discern whether the program had little impact or whether statistical power was at issue. Thus, it is important to know whether a proposed time series analysis has a chance of detecting a meaningful change in the system.

Power is the statistical term used for the probability that a test will reject the null hypothesis of no change at level α for a prescribed change. As the statistical literature contained no power computation methods for use with time series analyses, a method was developed for computing the power function for the general case of intervention analysis (McLeod and Vingilis, 2005). When planning a future study only limited information is usually available and so the approach described in the next section is often useful for determining approximate sample sizes, that is, of the lengths of the pre-intervention and post-intervention series needed to ensure that the analysis can detect meaningful change caused by the intervention.

It is important to understand that it is only statistically meaningful if the power computations are carried out before the data are analyzed (Lenth, 2001; Verrill and Durst, 2005). The article of Verill and Durst (2005) demonstrates that as the sample size increases, the power rapidly approaches one. This result underlines the importance of power computations in planning the collection of data.

Van Belle (2005, Ch.2) gives advice and rules of thumb for sample size computations for non-time series statistical tests and Lenth (2006) provides an online power calculator for many sorts of statistical tests. Our online calculator (McLeod, 2007) implements the method described in this note.

2. Methodology

2.1 Introduction

Let y_t denote the time series of interest such as monthly accident fatalities. The null hypothesis is that the effect of some change introduced at time T is zero and the alternative hypothesis is simply the negation of the null hypothesis. There are many sorts of changes that could occur but one the most common types is a simple step change. This means at time T there is a permanent increase in the mean level. The size of the increment is denoted by ω and the hypothesis testing problem can be written H₀: ω = 0 vs H_a: ω ≠ 0. More complex types of interventions can sometimes occur and this problem is addressed in our earlier paper (McLeod and Vingilis, 2005). Note that sometimes one-sided formulations of the alternative hypothesis are used but as pointed out by van Belle (2005, §1.8) we agree that this practice should be discouraged.

The next step is the collection and assembly of the required data. In some cases this may be laborious and expensive. The purpose of this paper is to provide a simple method for estimating how much data to collect before and after the intervention so that the subsequent analysis has a good chance of detecting a meaningful change. For convenience we may set the time series origin to t = 1, the series length to n and the intervention time to t = T. So the pre-intervention series corresponds to y_t, t = 1,…,T−1 and is of lengthT. Similarly, the post-intervention series y_t, t = T,…,n is of length n−T. For adequate power both T and n−T need to be chosen large enough. The purpose of this note is to show how to provide a method of selecting suitable T and n−T which is useful in many applications.

2.2 Model formulation

The intervention analysis model may be written,

$$y_t=\xi +\omega S_t^{(T)}+e_t$$ (1)

where t = 1,2,…,n indicates the observation number, y_t is the dependent variable, $S_t^{(T)}$ is a step intervention which occurs at time t,

$$S_t^{(T)}=\{\begin{array}{l}0t<T\hfill \\ 1t\ge T\hfill \end{array}$$ (2)

and e_t is the autocorrelated error with mean zero. In this model the means of the pre/post intervention series are respectively ξ and ξ+ω. The autocorrelated error, e, is assumed to be generated by an AR(1) process, e_t = φe_t−1+a_t, where a_t is a sequence of independent normal random variables with mean zero and standard deviation σ_a. The parameter φ in this model equals the lag-one autocorrelation and it may be estimated by the sample lag-one autocorrelation in the pre-intervention series. Alternatively, sometimes an approximate value of this lag-one autocorrelation coefficient is known from previous studies and this value may be used.

In summary, it is assumed that there are n observed time series values in total with T occurring before the intervention and n−T occurring after the intervention. The intervention component ω $S_t^{(T)}$ is illustrated in Figure 1. The effect of this intervention is to shift the mean of the series by an amount ω. When φ = 0 this model reduces to the two-sample test for equality of means (Moore, 2007, Ch. 19).

Figure 1.

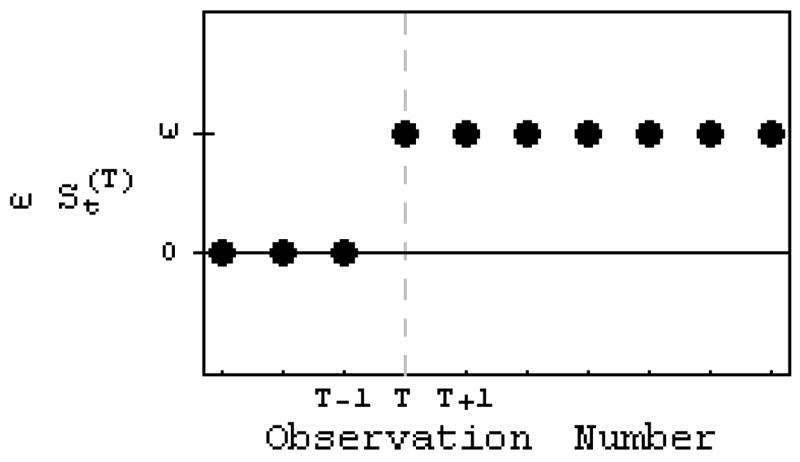
The simple step intervention model. This model is the time series analogue of the widely used two-sample t-test.

2.3 The power computation

The variance of ω̂ may be written (McLeod and Vingilis, 2005),

$${\sigma }_{\widehat{\omega }}^2={\sigma }_a^2{I}_{1,1}/(I_{1,1}{I}_{2,2}-I_{1,2}^2),$$ (3)

where I_1,1 = n(1−φ)², I_2,2 = (n−T )(1− φ)²+1 and I_1,2 = I_2,2− φ. If n, T, φ and σ_a are known, the power function for the test of the statistical significance of the intervention, H₀ : ω = 0 vs. H_a : ω ≠ 0, can be computed. Usually for planning purposes it is more convenient to work with the scaled intervention parameter δ = ω/σ_e, where σ_e is the standard deviation of the pre-intervention time series or equivalently the standard deviation of e_t. Basically we are measuring the size of the intervention effect we wish to detect in units corresponding to standard deviations of the pre-intervention series. In this case the power function for δ depends only on the parameters n, T and φ. The power function for a two-sided test H₀ : δ = 0 vs. H_a: δ ≠ 0 at level α may now be written

$$\mathrm{\Pi }(\delta )=1+\mathrm{\Phi }(-Z_{1-\alpha /2}-\tau \delta )-\mathrm{\Phi }(Z_{1-\alpha /2}-\tau \delta ),$$ (4)

where $\tau =\sqrt{(I_{1,1}{I}_{2,2}-I_{1,2}^2)/(I_{1,1}(1-{\phi }^2))},$ Z_1−α/2 is the upper 1−α/2 quantile of the standard normal distribution and Φ(z) denotes the cumulative distribution of the standard normal distribution. This power function is easily evaluated using a programmable calculator or a suitable quantitative programming environment. An online Javascript is also available for computing the power function (McLeod, 2007).

2.4 Numerical Illustration

Suppose that a researcher has collected 20 data values before and after an intervention has occurred. If it is assumed that values before and after are statistically independent then the two-sample t-test may be used to test the null hypothesis H₀: no effect. If, in fact, an effect had occurred equal to one standard-deviation, the probability of detecting this change using a pooled two-sample t-test can be determined using the online power calculator of Lenth (2006). For a two-sided 5% level pooled t-test we obtained that the probability of detecting a change of one standard deviation was 87%. Using our online software (McLeod, 2007) with parameter n, T, ø = 40, 20, 0, indicates this probability is 88%. This slight difference of 1% is due to the fact that in the present case our intervention analysis model simplifies to the standard Z-test rather than the t-test assumed in Lenth (2006).

If these data were collected as a time series then the independence assumption is not likely to hold and consequently the t-test power could be seriously inflated. The first-order autoregressive model provides a more realistic model than independence and a simple step intervention model provides a much improved method for statistical analysis. Based either on experience with previous data or on the pre-intervention series, an estimate can be made of the lag-one autocorrelation. For moderate autocorrelation, such as in many past traffic safety time series studies, φ = 0.5 is a conservative estimate, that is, we usually have 0<φ<0.5. Using inputs n, T, ø = 40, 20, 0.5, for our online program we find that the probability of detecting a one standard deviation change is now only 51%. Increasing the lengths of the pre-intervention and post-intervention series to 50 so we have n, T, ø = 100, 50, 0.5, results in a substantial increase in power. The probability of detecting a one standard deviation change is now 85%.

In summary, this example shows that the effect of positive autocorrelation is to increase the amount of data needed to have a high probability of detecting a change. By experimenting with different choices for n and T, the researcher can select how much data is needed to obtain adequate power.

2.5 Model estimation and diagnostic checking

After the data is collected, the intervention model may be fit and the test of the hypothesis H₀: ω = 0 vs H_a: ω ≠ 0 may be carried out. In practice, a confidence interval for the parameter ω should also be considered since it is more informative about the magnitude as well as the statistical significance of the change. Many software packages such as SPSS can be used to fit the model given in eqn. (1). More complex types of intervention models as discussed by Box and Tiao (1979) and Hipel and McLeod (1994, Chapter 19) may also be fit using a variety of software packages such as SAS or the MHTS package (McLeod and Hipel, 2005).

2.6 The effect of model mis-specification

We have assumed a simple step intervention model with first-order autoregressive errors. Both of these assumptions are just working approximations. The most common type of intervention, likely to be of scientific interest to traffic safety researchers is likely to be a step intervention which corresponds to a permanent change. Testing for pulse and other dynamic effects is most likely of secondary interest.

The other assumption is that the error term is assumed to follow a first-order autoregression. This simple form of Markovian dependence arises in a wide variety of stationary time series observed in practice but occasionally other forms of dependence may arise in which case more complicated ARMA or other time series models may be needed. Monthly time series frequently occur in traffic safety studies. Less frequently these monthly time series may exhibit significant seasonal variation. In this case, the monthly means of the pre-intervention time series may be used to deseasonalize this series and φ can be estimated as the lag-one autocorrelation for the deseasonalized pre-intervention series. If pre-intervention series exhibits other pronounced effects not consistent with a first order autoregression, such as slowly decaying autocorrelations or non-regular cyclic behaviour, then the more general method discussed in McLeod and Vingilis (2005) should be used.

2.7 Illustrative example of the effect of mis-specification

Suppose that we inadvertently make the wrong assumption and that the true autocorrelation model is not a first order autoregression but rather a more complex ARMA(1,1). As in §2.4 we will assume the lag-one autocorrelation is 0.5. In the ARMA(1,1) case, the model equation for the error term may be written, et = φe_t−1+a_t−θa_t−1, where a_t ~ NID(0, σ²), |φ|<1 and |θ|<1. The lag-one autocorrelation coefficient is given by

$${\rho }_1=\frac{(\phi -\theta )(\phi \theta -1)}{1-{\theta }^2-2\phi \theta }$$

Setting ρ₁ = 0.5 we can solve for the parameters φ and θ. It is found that valid and unique solutions for θ exist for each 0<φ<1. Figure 2 shows the value of the θ parameter corresponding to each φ. When φ = 0.5, θ = 0 and the ARMA(1,1) reduces to the first-order autoregressive case. However when 0<φ<0.5, the ARMA(1,1) has weaker autocorrelations which are even smaller than the first-order autoregression. For 0.5<φ<1, the autocorrelations are stronger at higher lags. When φ = 0.9, the autocorrelations are slowly decaying and the series exhibits wandering near-nonstationary behavior similar to financial time series such as stock market prices. Taking n = 100 and T = 50, the more general algorithms given in McLeod and Vingilis (2005) were used to compute the probability of detecting a one-standard deviation change for each possible parameter combination of φ and θ satisfying the condition ρ₁ = 0.5. This power as a function of φ is shown in Figure 3. It is seen that when 0<φ<0.7, the first-order autoregressive approximation provides a reasonable estimate of power. But in the case of slowly decaying autocorrelations, 0.7≤ φ<1, the power quickly declines. In this situation the more general method given in McLeod and Vingilis (2005) should be used.

Figure 2.

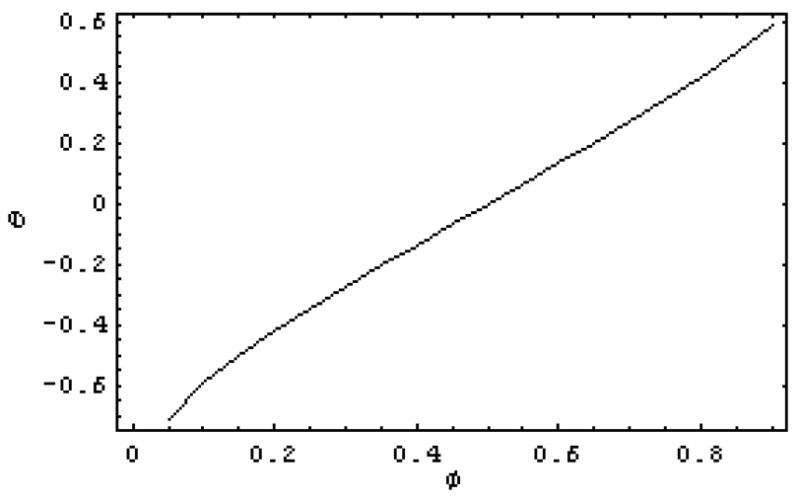
ARMA(1,1) parameter values which correspond to a lag-one autocorrelation equal to 0.5.

Figure 3.

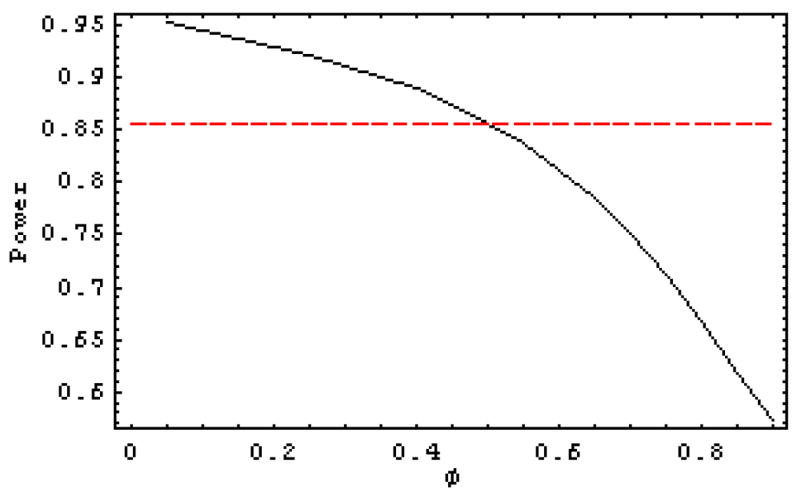
Probability of detecting a one standard deviation change when lag-one autocorrelation is assumed to be 0.5 but the underlying error time series is assumed to be ARMA(1,1). The length of each of the pre and post intervention series is assumed to be 50. The dashed line shows the power making the AR(1) assumption. It is seen that the power decreases significantly in the more highly autocorrelated cases when φ > 0.7

3. Illustrative Application to NIH Study of the Impact of Extended Drinking Hours

Drinking hours in Ontario were extended from 1 AM to 2 AM on May 1, 1996. This change provided an opportunity to assess the effect of extended drinking hours on monthly late-night automobile fatalities and serious trauma. Initially, it was planned to use monthly time series over the period from January 1994 to December 1998 which corresponds to n = 60 and T = 36. Data collection for this project was a major part of the expense and it was important to collect enough data to be reasonably certain of detecting if there was a meaningful change or shift in the fatalities. It was decided to compare the initial design with an enlarged study from January 1992 to December 1998 which corresponds to n = 80 andT = 48. If drinkers spread their drinking out over a longer period of time, it might be expected that the intervention might actually result in a decrease in automobile fatalities associated with drinking. On the other hand, if more alcohol was consumed, then an increase would be expected. So a two-sided test is needed. From previous work with motor vehicle collision time series (Vingilis et al., 1988) it is reasonable to assume the first-order autocorrelation is in the range 0≤ φ<0.5. Assuming n = 60, T = 36, φ = 0.5 and α = 0.05 the power function for a two-sided test may be obtained by evaluating eqn. (4), to obtain Π(δ) = 1 + Φ(−1.96−2.362δ)−Φ(1.96−2.362δ). The power function for a range of δ from 0 to 2 and for φ = 0, 0.25 and 0.5 is given in Table 1. It is seen that the power decreases as the autocorrelation, φ, increases but that even when φ = 0.5 the probability of detecting a change corresponding to δ = +1 on a two-sided 5% test is about 79% with the second plan (n = 80, T = 48 ) and only 65.6% with the original plan (n = 60, T = 36). Note that the power function for a two-sided test is symmetric, that is, Π(δ) = Π(−δ), so it is only necessary to show δ ≥ 0. Based on these power computations, the second plan with n = 80 and T = 48 was preferred.

Table 1.

Power function for two-sided tests for the two possible intervention analysis data sets. In this case, the power function is symmetric so only the power for δ ≥ 0 needs to be shown.

δ	T=36, n=60			n = 80 and T = 48
	φ = 0	φ = 0.25	φ = 0.5	φ = 0	φ = 0.25	φ = 0.5
0	0.050	0.050	0.050	0.050	0.050	0.050
0.25	0.159	0.117	0.091	0.206	0.144	0.106
0.5	0.480	0.324	0.219	0.624	0.430	0.281
0.75	0.817	0.616	0.425	0.927	0.762	0.543
1.	0.968	0.853	0.656	0.995	0.946	0.787
1.25	0.998	0.964	0.839	1.000	0.994	0.931
1.5	1.000	0.995	0.943	1.000	1.000	0.985
1.75	1.000	1.000	0.985	1.000	1.000	0.998
2.	1.000	1.000	0.997	1.000	1.000	1.000

4. Conclusion

The simple step intervention model is the time series generalization of the widely used t-test for the two-sample problem. The first order autoregression provides a realistic model for many traffic safety time series occurring in practice. These initial assumptions seem reasonable for a wide variety of applications and they allow the researcher to make simple power calculations to decide how long the pre and post intervention series should be in order to have a high probability of detecting a meaningful change. This power computation is implemented in an online calculator or it can be done with a hand-calculator using eqn. (4). The accuracy of this computation has been extensively tested by simulation and works well even for quite small samples (McLeod and Vingilis, 2005).

The method given in this note is not suitable for highly autocorrelated time series with slowly decaying autocorrelations or for more complex types of interventions such as ramp interventions or interventions with a dynamic response. McLeod and Vingilis (2005) provide a more general methodology applicable to such cases.