Shortening of Cardiac Action Potential Duration Near an Insulating Boundary

Abstract

It is known, from both experiments and simulations, that cardiac action potentials are shortened near a nonconducting boundary. In the present paper, this effect is studied in a simple, two-current ionic model, with propagation restricted to a one-dimensional fiber. An asymptotic approximation for the dependence of action potential duration on distance to the boundary is derived. This estimate agrees well with simulations.

1 Introduction

Cardiac cells are excitable in the sense that a brief electrical stimulus can cause the transmembrane voltage v to experience a prolonged elevation known as an action potential. Action potentials propagate through tissue because neighboring cells are connected electrically via intercellular channels (called gap junctions). These propagating electrical waves coordinate the contraction of cardiac muscle as needed for effective pumping of blood. Understanding the timing of these waves is a first step towards detecting and preventing potentially fatal arrhythmias.

As usual, let us define the action potential duration (APD) as the amount of time in which the voltage remains elevated above a specified threshold v_thr. In experiments, the threshold voltage is chosen anywhere from 70 to 90 percent¹ recovery from the peak voltage to the resting voltage.

In recent in vitro experiments [4], a small piece of frog heart tissue was stimulated using a unipolar pacing electrode and APD was measured on the surface of the tissue with voltage-sensitive fluorescent dyes. Figure 1 shows the APD’s measured along a representative radial line emerging from the stimulus site. The line terminates where the piece of tissue was cut from the whole heart. (Below we model this boundary with a Neumann condition.) As the figure shows, APD values near the electrode were 10% larger than values at the edge of the tissue. To prove that this effect was not simply the result of tissue inhomogeneity, the stimulating electrode was placed at several different sites around the tissue; always APD exhibited the same shortening with increasing distance from the electrode.

Figure 1.

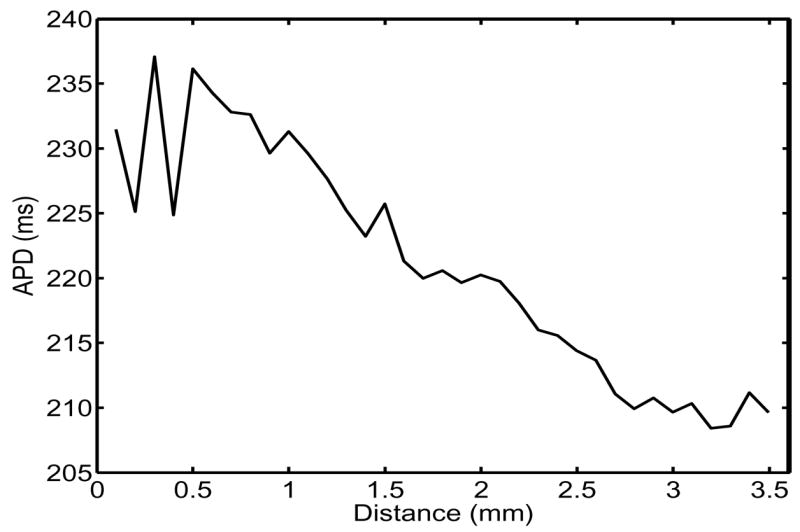
Experimentally measured spatial variation of APD. Stimuli were applied at x = 0, where x denotes distance from the pacing electrode.

Although it is not apparent from an experiment in such a small sample, we believe that this dependence of APD on distance from the stimulus site is a boundary effect. We support this claim with simulations using the two-current ionic model of [8, 10], which will be described in Section 2. In the simulations shown in Figure 2a, on a cable 1 cm long, APD decreases approximately linearly with distance from the stimulus site. By contrast, in those of Figure 2b, on a cable 4 cm long, APD is independent of position away from the ends of the cable, is elevated locally near the stimulus end, and is depressed locally near the distal end. On a longer cable, the central region is wider but the elevation and depression near the ends are virtually unchanged².

Figure 2.

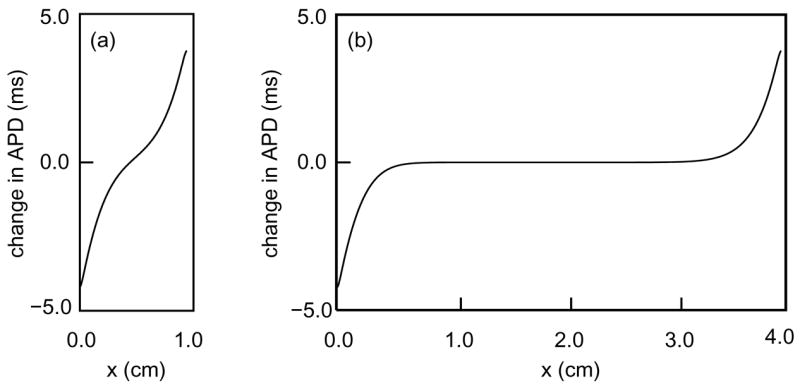
Spatial variation of APD in (a) a 1.0-cm cable and (b) a 4.0-cm cable as generated by numerical simulation of (4–5) with parameters from Table 1. Stimuli were applied at the right end of the fiber. The indicated variations are added to an unperturbed APD of 439.3 ms.

In this paper we study how the duration of a single action potential propagating along a long fiber³ is changed near the end of the fiber. In order to avoid modeling the details of stimulation, we restrict our attention to the distal end of the fiber. Specifically, for the two-current model, we derive an asymptotic approximation for δAPD(x), the change in APD expressed as a function of distance x along the fiber from a non-conducting boundary. This analytical result for a simplified model sheds light on phenomena in more realistic models or experiments.

Although this shortening is a relatively small fraction of the total APD, such boundary effects may play a role in generating arrhythmias. For example, under rapid periodic pacing, tissue may bifurcate into a period-2 orbit called alternans: i.e., the response to identically spaced stimuli alternates between short and long APD’s. In both simulations and experiments, as the pacing rate increases, alternans have been observed first and are strongest close to a boundary [7, 12].

The remainder of the paper is organized as follows. In Section 2, we recall the two-current ionic model [8, 10], including asymptotic estimates for APD in this model and the description of traveling waves in it. In Section 3, we derive our main result: an approximate formula for δAPD(x) near an insulating boundary. Finally, in Section 4 we show that our approximation agrees well with simulations, and we characterize how this phenomenon depends on the parameters in the model.

2 The two-current model

2.1 The equations

The two-current model [8, 10] for a patch⁴ of tissue consists of two ordinary differential equations (ODEs) for two variables: the transmembrane voltage v(t) and an inactivation gate variable h(t), both of which are dimensionless and scaled to vary between 0 and 1. The voltage equation takes the form

$$\frac{dv}{dt}=F(v,h)=J_{\text{in}}(v,h)+J_{\text{out}}(v),$$ (1)

where F(v, h) is a sum of inward and outward currents given by

$$J_{\text{in}}(v,h)=\frac{h}{{\tau }_{\text{in}}}{v}^2(1-v),J_{\text{out}}(v)=-\frac{v}{{\tau }_{\text{out}}}.$$ (2)

The parameters τ_in and τ_out are time constants that specify the strength of the inward and outward currents, respectively. The other variable, the gate that regulates inward current flow, obeys the ODE

$$\frac{dh}{dt}=G(v,h)=\{\begin{array}{ll}(1-h)/{\tau }_{\text{open}},\hfill & v<v_{\text{crit}}\hfill \\ -h/{\tau }_{\text{close}},\hfill & v>v_{\text{crit}}.\hfill \end{array}$$ (3)

Representative values for the time constants in (2,3) are given in Table 1.

Table 1.

Sample parameter values for the two-current model.

Parameter	Meaning	Units	Value
τin	time constant	ms	0.2
τout	time constant	ms	10
τopen	time constant	ms	130
τclose	time constant	ms	150
vcrit	critical voltage	dim’less	0.13
κ	diffusion constant	cm2/ms	0.001

Equations (1, 3) are easily modified to model the propagation of action potentials in a homogeneous one-dimensional cable—that is, an idealized fiber of cells electrically coupled via gap junctions. If x denotes distance along the fiber, the voltage v = v(x, t) obeys a partial differential equation (PDE)

$$\frac{dv}{dt}=\kappa \frac{{\partial }^{2}v}{\partial x^2}+F(v,h),$$ (4)

where κ is a diffusion constant; and the gate variable satisfies

$$\frac{\partial h}{\partial t}=G(v,h),$$ (5)

which by contrast contains no x-derivatives. In a finite-length or semi-infinite cable, Neumann boundary conditions on the voltage, corresponding to no axial current, are imposed at the ends of the cable.

When numerical simulations are required, we will use the parameter values listed in Table 1. Note that these time constants satisfy

$${\tau }_{\text{out}}\ll {\tau }_{\text{open}},{\tau }_{\text{close}}.$$ (6)

Below we shall always assume the time scales are well-separated in this way, and we shall make asymptotic approximations based on the small parameter

$$\epsilon =\frac{{\tau }_{\text{out}}}{{\tau }_{\text{close}}}.$$ (7)

2.2 Asymptotic estimates for APD in a patch

Observe that (v, h) = (0, 1) is a stable equilibrium of the ODEs (1,3). These equations exhibit excitability in that, if a stimulus raises the voltage slightly above this equilibrium value, then the voltage increases further and remains elevated for a long period before returning to equilibrium, as sketched in Figure 3. The structure of such an action potential may be characterized with asymptotics using the fact that, because of (6), the voltage evolves much more rapidly than the gate unless (v, h) lies close to the nullcline {dv/dt = 0}. By (1,2), on this nullcline either v = 0 or

Figure 3.

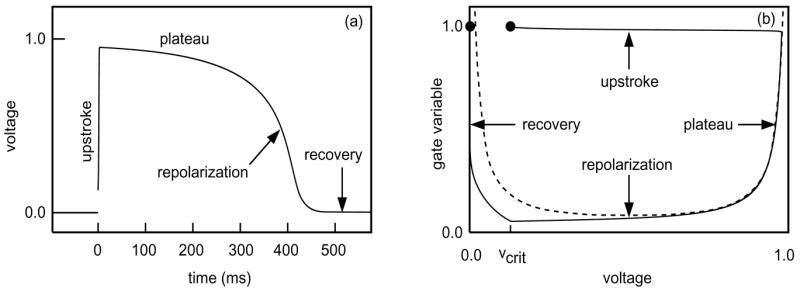
(a) Voltage trace illustrating the four phases of the action potential. (b) The corresponding phase plane trajectory. The dashed curve is the graph of the nullcline (8). Both trajectories were generated by numerical solution of (1–3) using the parameters in Table 1 and v(0) = 0.13, h(0) = 1.0.

$$h=\frac{{\tau }_{\text{in}}}{{\tau }_{\text{out}}}\frac{1}{v(1-v)}.$$ (8)

Alternatively, solving (8) for v, we obtain

$$v=v_{\pm }(h)=\frac{1}{2}\left(1\pm \sqrt{1-\frac{h_{min}}{h}}\right),$$ (9)

where

$$h_{min}=\frac{4{\tau }_{\text{in}}}{{\tau }_{\text{out}}}.$$ (10)

As illustrated in Figure 3, an action potential has four distinct phases. The dominant behavior in each phase may be described as follows and as summarized in Table 2. (See [10] for a more detailed discussion of the asymptotics.)

Table 2.

Summary of asymptotics during the four phases of an action potential

Phase	Name	Duration (order of mag.)	Simplification	Dominant equation
1	Upstroke	τin	h ≈ Const	(1)
2	Plateau	τclose	Jin + Jout ≈ 0	(3)
3	Repolarization	${\tau }_{\text{close}}^{1/3}{\tau }_{\text{out}}^{2/3}$	h ≈ Const	(1)
4	Recovery	τopen	v ≈ 0	(3)

1. Upstroke phase: Following a successful stimulus, the strong inward current J_in raises the voltage until it reaches V₊ = v₊(1) on the right branch of the nullcline (9). This occurs in a time on the order of $\mathcal{O}({\tau }_{\text{in}})$.

2. Plateau phase: As the gate closes according to (3)—i.e., h(t) = exp(−t/τ_close)—the voltage follows the nullcline (9), keeping the inward and outward currents balanced.

3. Repolarization phase: When the gating variable reaches h_min given by (10), the solution “falls off the nullcline”. I.e., at this point the inward current is no longer able to balance the outward current, and the voltage drops toward zero in a time that is short⁵ compared to τ_close.

4. Recovery phase, or diastole: The voltage stays small and the gate reopens with a time constant τ_open.

In Section 4.2 it will be useful to have estimates for the duration of such an action potential, which we denote by APD_max since this action potential is the largest possible APD that a cell can exhibit⁶. An APD consists of all of phase 2 plus parts of phases 1 and 3. According to (6), phases 1 and 3 are much shorter than phase 2. In fact, in leading-order asymptotics, APD_max equals the time in phase 2 during which, starting from 1, the gate decays exponentially to h_min. Thus,

$${\text{APD}}_{max}\sim {\tau }_{\text{close}}ln\left(\frac{1}{h_{min}}\right).$$ (11)

Strictly speaking, to compute APD we should introduce a threshold voltage v_thr and define APD as the length of time that v(t) > v_thr. However, because the voltage evolves rapidly in phases 1 and 3, the low-order estimates for APD_max do not depend on v_thr. Nevertheless, the choice of v_thr does affect (slightly) the boundary corrections to APD computed in Section 3.

At the next order of asymptotics, phase 3 does contribute to APD_max. At first glance, one might guess that the duration of phase 3 is $\mathcal{O}({\tau }_{\text{out}})$ since this parameter characterizes the strength of J_out, the dominant current in this phase; this would represent an $\mathcal{O}(\epsilon )$ correction to (11), where ε is given by (7). However, at the start of phase 3, pending further decay of h and hence of J_in, the two currents nearly cancel one another. As shown in [2], this effect slows the decrease of the voltage and thus lengthens the APD. (Cf. The analysis of Cartwright [3] and Dorodnicyn [5] concerning relaxation oscillations in the van der Pol equation.) Specifically, we find that (11) is augmented to

$${\text{APD}}_{max}\sim {\tau }_{\text{close}}\left\{ln\left(\frac{1}{h_{min}}\right)+z_1{\epsilon }^{2/3}\right\},$$ (12)

where z₁ = 2.33811 … is the first zero of the Airy function, Ai(−z). This formula predicts APD_max with surprisingly high accuracy. For example, using the parameters in Table 1, we estimate from formula (12) that APD_max = 436.5 ms, less than 1% below the true value (obtained numerically) of 439.3 ms. By comparison, the leading-order estimate (11) predicts that APD_max = 378.7 ms, a relative error of 14%.

2.3 Traveling-wave solutions in an infinite fiber

We seek a traveling-wave solution of equations (4, 5),

$$v(x,t)=V(t+x/c),h(x,t)=H(t+x/c),$$ (13)

where the speed c is to be determined. This yields a system of two ODEs for V and H with independent variable ξ = t + x/c. It is shown in [1] that, if τ_in/τ_out < 4/25, then for sufficiently small ε, this system indeed admits a traveling-wave solution⁷. For ξ < 0 the solution is quiescent (V ≡ 0, H ≡ 1); for ξ > 0 it is well-approximated by phases 2,3, and 4 of an action potential in a patch model; and these two outer regions are separated by an inner or wave-front layer in which voltage diffusion is crucial (see Figure 4).

Figure 4.

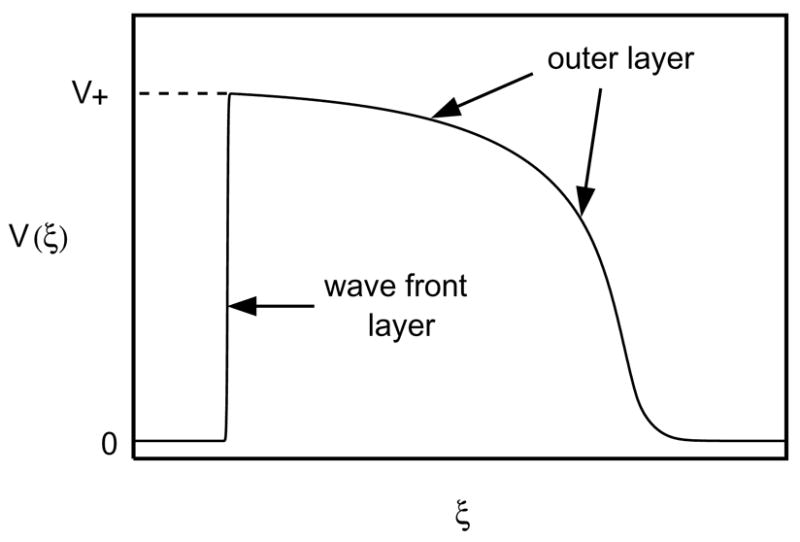
Voltage profile of a traveling pulse moving from right to left on an infinite cable.

In the inner layer, in a time that is $\mathcal{O}({\tau }_{\text{in}})$, the voltage climbs from 0 to V₊, where (cf. (9))

$$V_{\pm }=v_{\pm }(1)=\frac{1}{2}\left(1\pm \sqrt{1-h_{min}}\right).$$ (14)

We may approximate H ≡ 1 in the wave-front layer because, by equation (6), the time constants regulating H are much larger than τ_in. In terms of a scaled inner coordinate $\stackrel{\sim }{\xi }={\tau }_{\text{in}}^{-1}(t+x/c)$, to leading order the inner solution solves

$$V^{\prime }=\frac{1}{c^2}\frac{\kappa }{{\tau }_{\text{in}}}{V}^{″}+{\tau }_{\text{in}}F(V,1),$$ (15)

where prime indicates differentiation with respect to ξ̃. Equation (15) is subject to boundary conditions

$$\underset{\stackrel{\sim }{\xi }\to -\infty }{lim}V(\stackrel{\sim }{\xi })=0,\underset{\stackrel{\sim }{\xi }\to \infty }{lim}V(\stackrel{\sim }{\xi })=V_{+}.$$ (16)

Proposition 2.1. Problem (15,16) has a solution if

$$c=\left(\frac{1}{2}{V}_{+}-V_{-}\right)\sqrt{\frac{2\kappa }{{\tau }_{\text{in}}}}.$$ (17)

Proof

See Zeldovich et al. [15] or, for a more modern approach, Murray [11]. □

Incidentally, using the parameter values in Table 1, (17) predicts c = 46.9 cm/sec, while we find c = 46.7 cm/sec from numerical solution of (4,5). This good agreement provides a posteriori justification for the approximation that H is constant in the inner layer.

In the outer region ξ > 0, provided τ_in/τ_out < 4/25, the traveling-wave solution of (4,5) solves the ODE

$$\frac{dV}{d\xi }=F(V,H)\frac{dH}{d\xi }=G(V,H),$$

subject to initial conditions

$$V(0)=V_{+}H(0)=1.$$ (18)

This solution, which matches continuously onto the inner solution, corresponds to phases 2, 3, and 4 of an action potential in a patch.

While referring to [1] for proofs, let us offer a heuristic argument that this construction satisfies the PDE (4,5) to leading order. Consider for example values of ξ corresponding to phase 2 of an action potential. In this range of ξ

$$\frac{dV}{d\xi }\sim \frac{1}{{\tau }_{\text{close}}},\frac{d^{2}V}{d{\xi }^2}\sim \frac{1}{{\tau }_{\text{close}}^2}.$$

Thus, substituting into (13) and recalling (17), we see that

$$\kappa \frac{{\partial }^{2}v}{\partial x^2}\sim \frac{{\tau }_{\text{in}}}{{\tau }_{\text{close}}^2}\sim \frac{{\tau }_{\text{in}}}{{\tau }_{\text{close}}}\frac{\partial v}{\partial t}.$$

Hence, since τ_in/τ_close ≪ 1, the diffusion term, which distinguishes the PDE (4) from the ODE (1), is of higher order. Similarly for phases 3 and 4.

We summarize: If τ_in/τ_out < 4/25, then to leading order, the traveling wave differs from an action potential on a patch only in the wave-front layer. In this layer, the speed of the traveling wave is determined by the balance between diffusion and the strength of the inward current.

3 A formula for the boundary correction to APD

3.1 The governing equations on a half-line

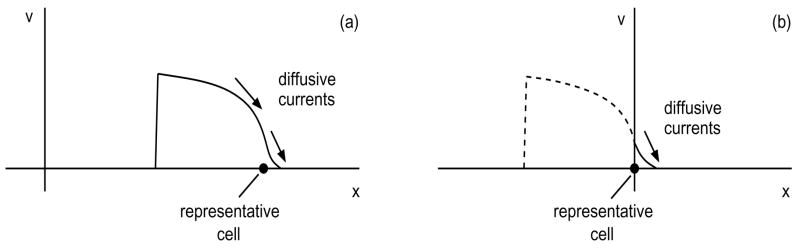
Consider a solitary action potential propagating along a long, homogeneous fiber toward an insulating boundary at x = 0. Intuitively, the shortening of APD as it approaches the boundary may be understood by comparing the diffusive currents near two representative cells, as shown in Figure 5, one far from the boundary and one at the boundary. For both cases, as the wave back passes through the cell, the diffusive current −κ∂v/∂x moves charge from this cell to its neighbors on the right, where the action potential has progressed further. Far from the boundary, as in Figure 5a, the loss of charge to neighbors on the right is approximately balanced by the gain of charge from neighbors on the left. By contrast, near the boundary, as in Figure 5b, neighbors on the left are missing. Thus, in the latter case the diffusive current lowers the voltage in the wave-back region and hence shortens the APD.

Figure 5.

Diffusive currents for a pulse (a) far from an insulating boundary and (b) after reaching the insulating boundary.

Mathematically, a propagating action potential can be modeled using (4, 5) on a half-space {0 < x < ∞, −∞ < t < ∞} subject to the boundary condition

$$\frac{\partial v}{\partial x}(0,t)=0(-\infty <t<\infty )$$ (19)

and the initial conditions

$$\underset{t\to -\infty }{lim}\underset{0\le x<\infty }{max}\mid v(x,t)-V(t+x/c)\mid =0$$ (20)

$$\underset{t\to -\infty }{lim}\underset{0\le x<\infty }{max}\mid h(x,t)-H(t+x/c)\mid =0.$$ (21)

In words, the initial conditions require that the difference between the exact solution and a pure traveling-wave solution is negligible when the pulse is far from the boundary.

We seek a solution of this problem of the form

$$v(x,t)=V(t+x/c)+w(x,t),h(x,t)=H(t+x/c),$$ (22)

where w is a correction to the voltage V in the traveling wave solution. (We neglect the correction to the gate variable, which is of higher order since the gate evolves more slowly than the voltage.) Since the maximum correction to APD at the boundary is hardly 1% (cf. Figure 2), one suspects w is a small correction. The computations summarized in Figure 6 verify this—the maximum value of w is approximately 0.045 while the voltage is of order unity⁸. Thus, substituting (22) into (4,19,20) and gathering the leading-order terms in w, we obtain the linearized problem

Figure 6.

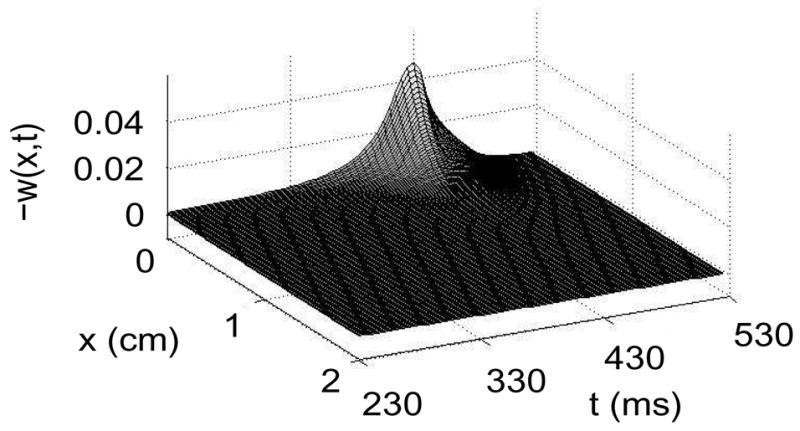
Plot of −w(x, t) versus x and t obtained by numerical solution of (4,5) using the parameters in Table 1. The maximum magnitude of w(x, t) is approximately 0.045, and is achieved at the insulating boundary x = 0 as the wave back approaches.

$$\frac{\partial w}{\partial t}=\kappa \frac{{\partial }^{2}w}{\partial x^2}+\gamma (x,t)w(x>0,-\infty <t<\infty )$$ (23)

$$\frac{\partial w}{\partial x}(0,t)=-\frac{1}{c}{V}^{\prime }(t)(-\infty <t<\infty )$$ (24)

$$\underset{t\to -\infty }{lim}w(·,t)=0,$$ (25)

where

$$\gamma (x,t)=\frac{H(t+x/c)}{{\tau }_{\text{in}}}[2V(t+x/c)-3V^2(t+x/c)]-\frac{1}{{\tau }_{\text{out}}}.$$ (26)

In order to obtain an explicit solution, we shall solve (23–25) making the approximation γ(x, t) ≈ γ(0, t): i.e.,

$$\gamma (x,t)\approx \gamma (t)=\frac{H(t)}{{\tau }_{\text{in}}}[2V(t)-3V^2(t)]-\frac{1}{{\tau }_{\text{out}}}.$$ (27)

This approximation will be discussed in Section 4.3.

3.2 Solution of the linearized problem

As a first step in attacking (23–25), we solve an analogous problem for the heat equation. Specifically, consider

$$\frac{\partial w}{\partial t}=\kappa \frac{{\partial }^{2}w}{\partial x^2}(x>0,-\infty <t<\infty )$$ (28)

$$\kappa \frac{\partial w}{\partial x}(0,t)=-j(t)(-\infty <t<\infty )$$ (29)

$$\underset{t\to -\infty }{lim}w(x,t)=0(x>0)$$ (30)

where in (29) we assume that j is bounded and integrable. The minus sign in (29) reflects the fact that a net influx of heat corresponds to a negative temperature gradient. The solution of (28–30) is given by

$$w(x,t)={\int }_0^{\infty }K(x,s)j(t-s)ds,$$ (31)

where

$$K(x,t)=\sqrt{\frac{1}{\pi \kappa t}}exp\left(-\frac{x^2}{4\kappa t}\right).$$ (32)

One may derive (31) by (i) defining w̃(x, t) = w(x, t) − xj(t), which satisfies a homogeneous Neumann boundary condition but an inhomogeneous equation [14], (ii) solving for w̃ by making an even extension to the whole line, and (iii) manipulating the resulting solution, including an integration by parts.

If the coefficient γ in (23) depends only on t, then we may reduce this equation to the heat equation by introducing an integrating factor. Specifically, let

$$\mathrm{\Gamma }(t)={\int }_0^t\gamma (s)ds.$$ (33)

Then (23) may be rewritten as

$$\frac{\partial }{\partial t}\left[e^{-\mathrm{\Gamma }(t)}w\right]=\kappa \frac{{\partial }^2}{\partial x^2}\left[e^{-\mathrm{\Gamma }(t)}w\right].$$

Applying (31), we find that the solution of (23–25) is given by

$$w(x,t)=\frac{\kappa }{c}{\int }_0^{\infty }K(x,s)e^{\mathrm{\Gamma }(t)-\mathrm{\Gamma }(t-s)}{V}^{\prime }(t-s)ds.$$ (34)

3.3 The boundary correction to APD

We apply formula (34) to extract the spatial variation in APD in the vicinity of the insulating boundary. Given x ≥ 0, we wish to estimate the amount of time in which the voltage v(x, t) remains elevated above the threshold voltage v_thr. To do so, we must determine the two times t for which

$$v(x,t)=V(t+\frac{x}{c})+w(x,t)=v_{\text{thr}}(x\ge 0\text{fixed});$$ (35)

i.e., the arrival times at x of the wave front and of the wave back.

In the asymptotic construction of the traveling wave in Section 2.3, the wave front of the unperturbed solitary pulse reaches the boundary {x = 0} at time t = 0; and the wave back at t = APD_max. In other words,

$$V(0)=V({\text{APD}}_{max})=v_{\text{thr}}.$$ (36)

Using (36) to generate a first estimate, we seek approximate times when (35) is satisfied by assuming

$$t+x/c={\delta }_1(x),\text{or}t+x/c={\text{APD}}_{max}+{\delta }_2(x),$$ (37)

where δ_i(x), representing the effect of the perturbing term w in (35), is small. Expanding V about 0 or APD_max, invoking (36), and neglecting δ_i(x) in the argument of w, we simplify (35) to

$$V^{\prime }(0){\delta }_1(x)+w(x,-x/c)=0,\text{or}{V}^{\prime }({\text{APD}}_{max}){\delta }_2(x)+w(x,{\text{APD}}_{max}-x/c)=0.$$

Solving these linear equations for δ_i(x), we compute that the change in APD due to pulse interaction with the boundary is given by

$$\delta \mathit{APD}(x)\equiv {\delta }_2(x)-{\delta }_1(x)\approx -\frac{w(x,{\text{APD}}_{max}-x/c)}{V^{\prime }({\text{APD}}_{max})}+\frac{w(x,-x/c)}{V^{\prime }(0)}.$$ (38)

Since $V^{\prime }(0)=\mathcal{O}({\tau }_{\text{in}}^{-1})$ represents the steep slope (see Figure 4) of the wavefront of the undisturbed traveling pulse, the second term in (38) makes only a higher-order contribution to δAPD. Retaining only the first term in (38) and recalling (34), we find our main estimate

$$\delta \mathit{APD}(x)\approx -\frac{\kappa }{c}{\int }_0^{\infty }K(x,s)e^{\mathrm{\Gamma }({\text{APD}}_{max}-x/c)-\mathrm{\Gamma }({\text{APD}}_{max}-x/c-s)}\frac{V^{\prime }({\text{APD}}_{max}-x/c-s)}{V^{\prime }({\text{APD}}_{max})}ds.$$ (39)

4 Discussion and conclusions

4.1 Numerical simulations

Computer simulations show that the shortening of APD predicted by (39) is in good quantitative agreement with results from numerical solutions of (4–5). Specifically, Figure 7 shows a comparison of the actual change in APD (solid curve) with the change predicted by (39) (dashed curve). The solid curve was generated by numerical simulation of (4–5) using the parameter values in Table 1, a threshold voltage v_thr = v_crit = 0.13, and a cable length of 4 cm. Initially, the cable was at rest (v = 0 and h = 1 for all cells). Then, voltage was suddenly raised to v = 0.8 for all cells with 3.95 ≤ x ≤ 4.0, eliciting an action potential propagating from right to left. The plot shows δAPD(x) in the region within 1 cm of the distal end of the cable. In generating the dashed curve using formula (39), Γ and V′ were computed by numerical simulation of the traveling wave.

Figure 7.

Comparison of δAPD(x) as predicted by (39) (dashed curve) and by numerical solution of the original PDEs (solid curve).

Incidentally, the small discrepancy between the two graphs in Figure 7 is due to the interaction of the wave front of the pulse with the boundary, which is neglected in (39): Near a boundary, the speed of an approaching pulse is accelerated because no diffusive current need be supplied to neighboring cells on the left, which slightly lengthens APD. This effect is similar to the interaction of the wave back with the boundary that shortens APD, but it is smaller and more localized.

4.2 The width of the boundary-correction layer

In this subsection we argue that the shortening of APD is concentrated in a layer of thickness

$$\mathrm{\Delta }x\sim {\epsilon }^{-1/6}\sqrt{\kappa {\tau }_{\text{out}}}$$ (40)

near the boundary. Note that $\sqrt{\kappa {\tau }_{\text{out}}}$ is the length constant of the tissue [9, 13].

The integrand in (39) may be decomposed into three factors,

$$K(x,s),e^{\mathrm{\Gamma }({\text{APD}}_{max}-x/c)-\mathrm{\Gamma }({\text{APD}}_{max}-x/c-s)},\text{and}\frac{V^{\prime }({\text{APD}}_{max}-x/c-s)}{V^{\prime }({\text{APD}}_{max})}.$$

The first factor, given by (32), is exponentially small if s ≪ x²/κ. In other words, no significant error is made if one restricts the integration variable s to values bounded away from zero, $s\ge \mathcal{O}(x^2/\kappa )$. In the third factor, the numerator V′(t) is largest for times in the repolarization phase (see Figure 8(a)). According to (12), this phase has width approximately

Figure 8.

(a) V′(t)/V′(APD_max) versus t. (b) The exponential factor in the integrand of (39), with x = 0. Both graphs are terminated at t = APD_max.

$$W={\tau }_{\text{close}}{z}_1{\epsilon }^{2/3},$$ (41)

which suggests making an approximation in (39) in which s is restricted to values such that

$$x/c+s<W.$$ (42)

This approximation cannot be justified on the basis of the third factor alone—as Figure 8 indicates, V′(t) has a long tail extending to times well before the wave back region. However, we now show that the second factor in (39) decays rapidly for s in this range (see Figure 8(b)), and this justifies restricting s as in (42).

According to (33), the exponent in the second factor equals

$${\int }_{{\text{APD}}_{max}-x/c-s}^{{\text{APD}}_{max}-x/c}\gamma (s^{\prime })d{s}^{\prime }$$

where γ is given by (27). Since H varies more slowly than V, let us consider, as a first step, an approximation of γ obtained by fixing the argument of H in (27) at a representative time t =t_*. We choose $t_{*}={\tau }_{\text{close}}ln{h}_{min}^{-1}$, the lowest order estimate for APD_max, because H(t_*) = h_min, which yields the simple approximation

$${\gamma }_{\text{approx}}=\frac{h_{min}}{{\tau }_{\text{in}}}[2V-3V^2]-\frac{1}{{\tau }_{\text{out}}}=\frac{1}{{\tau }_{\text{out}}}[8V-12V^2-1].$$ (43)

Figure 9 helps one understand the behavior of this approximation.

Figure 9.

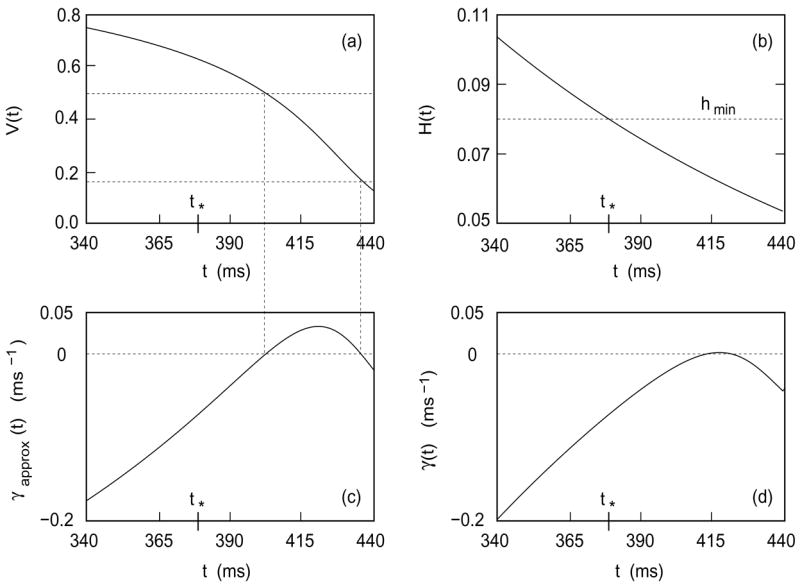
(a) V(t) versus t. Horizontal lines indicate V = 1/6 and V = 1/2. (b) H(t) versus t. Note that h(t_*) = h_min. (c) γ_approx versus t. Note that γ_approx vanishes when V passes through 1/2 and 1/6. (d) γ versus t.

• As shown in Figure 9(a,c), the quadratic expression on the right in (43) vanishes when V passes through 1/2 and through 1/6.

• As indicated in Figure 9(b), γ_approx(t_*) is negative. (This conclusion may also be extracted from the asymptotics of Section 2.2.)

• γ_approx becomes more and more negative as t decreases from t_*.

The exact γ, which is graphed in Figure 9(d), behaves similarly and is more negative than γ_approx. Although the magnitude of γ is not large, when it is integrated over times on the order of tens of milliseconds and exponentiated, the second factor in (39) becomes several orders of magnitude smaller than unity.

Combining the above ideas, we see that the effective range of integration in (39) may be regarded as the interval (x²/κ, W − x/c), where we have ignored dimensionless scale factors of the order unity. This interval shrinks to naught if

$$\frac{x^2}{\kappa }=W-\frac{x}{c}.$$ (44)

In other words, (44) identifies the edge of the zone where δAPD(x) differs significantly from zero.

Let us show that (44) is satisfied approximately when

$$x\sim {\epsilon }^{-1/6}\sqrt{\kappa {\tau }_{\text{out}}}.$$ (45)

First observe that from (41) that (45) comes from solving x²/κ = W: i.e., neglecting the term x/c on the RHS of (44). This term may be neglected compared to W because, for the value of x given by (45), we see, after some rearranging of powers of the time constants and recalling (17), that

$$\frac{x}{c}\sim {\epsilon }^{-1/6}\sqrt{{\tau }_{\text{in}}{\tau }_{\text{out}}}\sim {\epsilon }^{1/6}\sqrt{\frac{{\tau }_{\text{in}}}{{\tau }_{\text{out}}}}W\ll W.$$

Thus, (45) estimates to leading order the width of the boundary-correction layer. Figure 10 shows that the ε^−1/6 scaling for this width is quite accurate in the asymptotic range.

Figure 10.

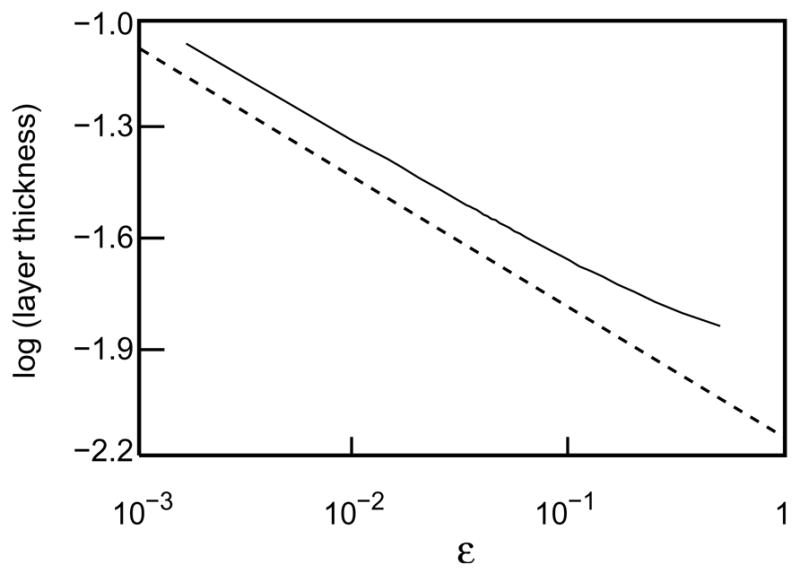
Log-log plot of layer thickness versus ε. Layer thickness was defined as the x value for which (APD_max − APD(x))/(APD_max − APD(0)) = 1/e. The dashed line has slope −1/6 and is included for reference.

4.3 The approximation (27)

The approximation γ(x, t) ≈ γ(0, t) is based on the fact that V (t + x/c), H(t + x/c), the traveling-wave solution, does not vary greatly over the range of x where w differs significantly from zero. This range of x was estimated in (40). During repolarization, the derivative dV/dξ is of the order at most $\mathcal{O}(1/{\tau }_{\text{out}})$ while dH/dξ is of the order $\mathcal{O}(1/{\tau }_{\text{close}})$ Thus, in the worst case

$$\mid V(t+x/c)-V(t)\mid \sim \frac{1}{{\tau }_{\text{out}}}\frac{{\epsilon }^{-1/6}\sqrt{\kappa {\tau }_{\text{out}}}}{c}\sim {\epsilon }^{-1/6}\sqrt{\frac{{\tau }_{\text{in}}}{{\tau }_{\text{out}}}}.$$ (46)

For the parameters in Table 1, the RHS of (46) is approximately 0.22, which is small but not extremely small. Thus, it is reassuring that, as illustrated in Figure 7, estimates based on the approximation (27) give highly accurate results.

4.4 Conclusions

In this paper we have studied how the duration of a propagating cardiac action potential is modified as it nears an insulating boundary. In order to obtain explicit analytical results, we described action potentials in a one-dimensional fiber using a simplified two-current model [8, 10]. Equation (39) estimates the shortening of APD at a site as a function of its distance from the boundary. As shown in Figure 7, this estimate agrees well with simulations. In (40) we determine how the width of the layer in which noticeable shortening occurs depends on the parameters in the model.