Abstract
The network analysis tools (NeAT) (http://rsat.ulb.ac.be/neat/) provide a user-friendly web access to a collection of modular tools for the analysis of networks (graphs) and clusters (e.g. microarray clusters, functional classes, etc.). A first set of tools supports basic operations on graphs (comparison between two graphs, neighborhood of a set of input nodes, path finding and graph randomization). Another set of programs makes the connection between networks and clusters (graph-based clustering, cliques discovery and mapping of clusters onto a network). The toolbox also includes programs for detecting significant intersections between clusters/classes (e.g. clusters of co-expression versus functional classes of genes). NeAT are designed to cope with large datasets and provide a flexible toolbox for analyzing biological networks stored in various databases (protein interactions, regulation and metabolism) or obtained from high-throughput experiments (two-hybrid, mass-spectrometry and microarrays). The web interface interconnects the programs in predefined analysis flows, enabling to address a series of questions about networks of interest. Each tool can also be used separately by entering custom data for a specific analysis. NeAT can also be used as web services (SOAP/WSDL interface), in order to design programmatic workflows and integrate them with other available resources.
INTRODUCTION
During the last decade, large-scale biological studies produced huge amounts of data that reveal various layers of molecular interaction networks: protein interactions, transcriptional regulation, metabolic reactions, signal transduction, etc.
Graphs (in the mathematical sense) have been used to represent, study and integrate such biological networks. By definition, a mathematical graph is a set of nodes (generally represented as dots) that are connected by edges (lines between dots). Edges may be enriched by several features, e.g. a direction (an edge from node A to node B is distinct from an edge from B to A), a color, a type and a weight (a value is associated to the edges).
Such edges and nodes provide convenient ways to represent biological features. For example, in a protein–protein interaction network, a node represents a polypeptide and an edge indicates the existence of a physical interaction between two polypeptides (1). A weight can optionally be put on edges to reflect the strength of interactions. In ‘compound-centric’ metabolic networks, nodes represent metabolites and the directed edges represent the enzymes used to convert a metabolite into another one (2). The metabolic networks may also be represented as bipartite graphs, i.e. a network with two distinct types of nodes (one for compounds and one for reactions), where edges must always link a node of one type to a node of the other type (3,4). Similarly, graphs can be used to represent regulatory relationships (5,6) and transduction pathways (7). Network biology is emerging as a very fertile field, as reflected by the rapidly increasing pace of relevant publications (8,9).
Despite the ever-increasing availability of data that may be represented as networks, large-scale analyses should be considered with caution, for several reasons. Firstly, high-throughput data are notoriously noisy (presence of false positives) and incomplete (10,11). In addition, some interaction networks have been characterized by several independent studies, which are providing complementary subsets of the data. Important efforts will thus be required to extract reliable information from the ever-increasing amount of data.
Specialized tools are required to extract and compare information obtained from multiple data sources, and apply various statistical parameters treatments to describe and understand networks properties. For this purpose, we developed the Network Analysis Tools (NeAT), a set of modular software tools supporting a large variety of operations on networks and clusters. The web interface provides a convenient and intuitive access to the tools and allows to thread user-provided data sets through typical analysis work flows, in order to interpret their networks. The NeAT programs may be grouped in three categories: tools for manipulating graphs (graph comparison, randomization, alteration, visualization, etc.), tools for analyzing clusters (or, equivalently, classes) (cluster comparison, etc.) and tools that establish the link between networks and clusters (graph clustering, graph–cluster mapping, etc.).
NeAT DESCRIPTION
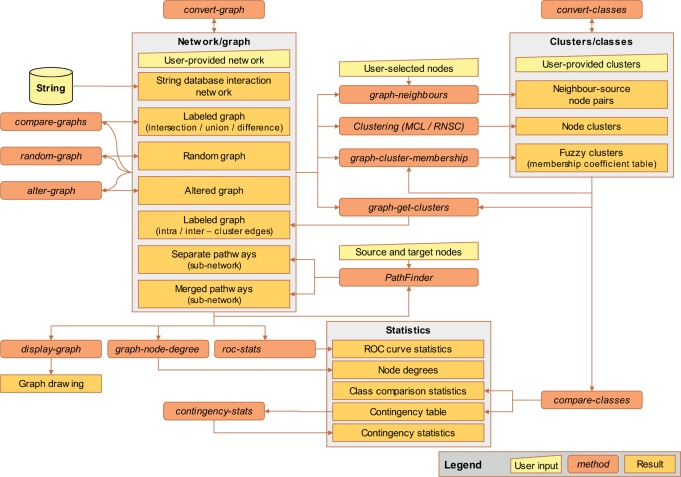
Figure 1 and Table 1 present the collection of tools available in NeAT as well as their input and output types. On the website, each tool is accessible via the menu on the left panel of the web page (Figure 3, inset).
Figure 1.
Flow chart of the tools and data types supported on NeAT. Trapezoidal boxes represent user-provided input, rounded boxes programs and rectangles results.
Table 1.
Description of the programs available in NeAT
| Program | Description | Input | Output |
|---|---|---|---|
| Network tools | |||
| convert-graph | Converts a graph from a format to another one, position the nodes and changes the edge colors and width according to its weight | A network in a given format | A network in the requested format |
| display-graph | Draws a network graphical representation | A network | A figure in the requested format |
| compare-graphs | Computes the intersection, the union or the difference of two networks | Two networks to be compared | A network (intersection, union, difference) |
| random-graph | Generates random graphs either from an existing graph or from scratch according to different randomization procedure. | A graph or a list of node names or nothing | A randomized network |
| graph-topology | Calculates the degree, betweenness and closeness of each node and specifies if this node is a source or a target node | A network, (list of nodes for which the degree has to be computed) | A table the requested centrality statistics of each requested node |
| alter-graph | Alters a graph either by adding or removing edges or nodes (targeted removal or not) | A network | An altered network |
| Pathfinder | Finds the k-shortest path between a set of source nodes and a set of target nodes | A network and the list of source and target nodes | A table of pathway or a network composed of the set of pathways |
| String dataset download | Downloads a subset of the network of the String database (40) | A list of nodes for which you want to know the neighbors in String | The neighbors of the nodes your entered in and the edges between them. |
| Network clusters tools | |||
| MCL (34,36) and RNSC (37) | Finds the densely connected subsets of the graph | A network | A list of clusters |
| graph-cligue | Extract al cliques from a graph | A network | A list of cliques |
| graph-neighbours | Extracts from a graph the neighborhood of a set of seed nodes | A network, (a list of seed nodes) | Clusters of neighbor-source node pairs |
| graph-cluster-membership | Maps a clustering result onto a graph and compute the membership degree between each node and each cluster, on the basis of edges linking this node to the cluster | A network, clustering results | A tab-delimited membership table, where each row represents a node and each column a cluster. Entries are the membership degree of the node. |
| graph-get-clusters | Compares a graphs with clusters. Extracts the intra-clusters edges or map the clusters on the network | A network | An edge-labeled network |
| Clusters tools | |||
| compare-classes | Compares two class files (the query file and the reference file). Each class of the query file is compared to each class of the reference file. | One or two cluster files | For each comparison, the number of common elements and comparison statistics or a contingency table |
| contingency-stats | Study of a contingency table | A contingency table | Statistics according to ref. (26) |
| Others tools | |||
| roc-stats | Calculates and draws ROC curve | Scored results associated with validation labels | For each score value, the derived statistics (Sn, PPV, FPR), which can be further used to draw a ROC curve. |
Input Parameters between brackets are optional.
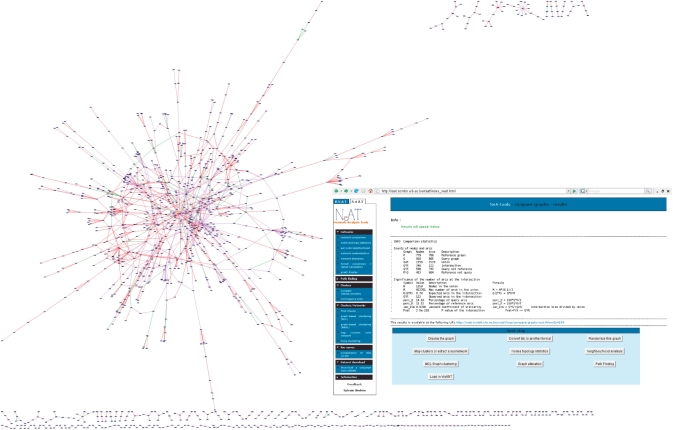
Figure 3.
The compare-graphs result. Main figure: result of the comparison between two large-scale yeast protein interaction networks obtained by the two-hybrid method (41,42). The networks were compared using compare-graphs and displayed with yED. Edge color code: green, edges present in both networks (intersection); red, edges present in Ito's; data set only; violet, edges present in Uetz’ dataset only. Inset: comparison statistics, including an estimation of the significance of the intersection between the network comparison, based on the hypergeometric distribution.
As shown in Table 1, NeAT tools can be broadly grouped in three categories: network tools perform various operations on one or several graphs, cluster tools are mainly dedicated to comparisons between clusters and network–clusters tools make the connection between networks and clusters.
We will briefly describe the function of each tool together and discuss some typical application. Further information and examples of utilization can be found in the cited literature.
NETWORK TOOLS
Network topology
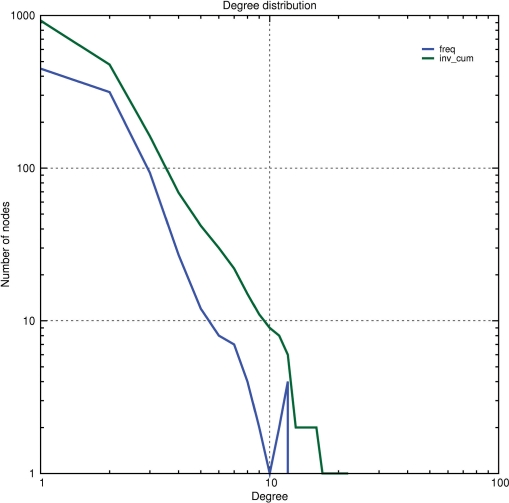
Several statistics have been defined to characterize global topological properties of a network. It has been shown that these topological properties distinguish biological networks from random networks. Noticeably, it is often stated that the distribution of degree (the number of edges connected per nodes) follows a power-law distribution (12). The program graph-topology computes the degree of each node of a graph, which can then be analyzed either as a full result table or visualized as a XY plot (Figure 2). Graph-topology also computes the betweenness (i.e. the proportion of shortest going through a node) and the closeness (i.e. the mean shortest distance of a node to all others) of each node in the network.
Figure 2.
Node degree distribution of a yeast protein interaction network obtained from two-hybrid data. The distribution was computed with the program graph-topology and plotted on log scales for both the abscissa and ordinates. The linear shape of the curve on the log–log graph suggests that this network follows a power-law distribution of degree. Color code : blue, absolute frequency; green, reverse cumulative frequency.
Node neighborhood
Starting from one or several nodes of interest, the program graph-neighbours collects neighbor nodes up to a user-specified distance. Neighborhood analysis can be for example applied to predict the function of an unknown polypeptide by collecting its neighbors with known function in a protein interaction network (‘guilty by association’) (13).
Network comparison
The program compare-graphs computes the intersection, the union and/or the difference between two input networks and estimates the statistical significance of the overlap (Figure 3, inset).
These basic operations between graphs can serve for many other tasks: the union can be used to integrate networks at different layers (e.g. metabolism, transduction signal and transcriptional regulation), the intersection to select interactions with evidences in two distinct experiments, the differences to select interactions detected by one method and missed by another one. A typical example of application is to estimate the relevance of a protein–protein interaction network obtained by some high-throughput experiment, by comparing it with a manually curated network [e.g. BioGrid or MIPS databases data (14,15)].
Evaluation of predicted networks using receiver operating characteristic (ROC) curves
The program roc-stats is typically used as a postanalysis program after a network comparison between predicted and annotated networks. It takes as input a set of scored results associated with validation status (positives or negatives) and computes, for each threshold on the score, the derived statistics: true positive rate (TPR, also called sensitivity), positive predictive value (PPV), false positive rate (FPR) and accuracy.
Those statistics are also further used to draw different graphical plots showing the performance as a function of the score threshold or allowing performance comparisons (precision recall and ROC curves).
ROC curves show the fraction of the true positives (TPR) versus the fraction of the (FPR) and are often used to compare the predictive performance of different programs (16).
Path finding in a network
Biochemical interactions form intricate networks, where a multitude of pathways can be used to join two nodes of interest. The search of optimal paths (minimizing the number of steps, or the distance, or some weight) has a long tradition in graph theory. Path finding algorithms have been applied to uncover signal transduction pathways from protein–protein interaction networks (17–19) or metabolic pathways in metabolic networks, respectively (20–22). Recently, we evaluated the performance of a k-shortest path finding algorithm for metabolic pathway inference and found that the correspondence between inferred and annotated pathways can be crucially improved by setting an appropriate weighting on the nodes of the metabolic network, in order to penalize highly connected compounds (4).
The NeAT interface includes a general k-shortest path finding algorithm, that supports searches from a set of (one or several) source nodes to a set of target nodes (23). Node weights can either be specified in the input graph or computed automatically according to node degree (4).
Network randomization and alteration
Random graphs are extremely useful to analyze statistical properties of graphs and to validate theoretical models (24–27). The significance of some properties observed in a biological network (e.g. node degree, clustering coefficient, network diameter, etc.) can be estimated by measuring the distribution of probability of the same property in a large set of random networks. Random networks can also be used to observe the behavior of a given algorithm (e.g. clustering) in absence of biological information.
The program random-graph supports different procedures to randomize a network, which can then be submitted to the same workflows in the same way as a real biological network. Random graphs can be generated from the scratch, according to an Erdös-Renyi model. Alternatively, random graphs can be generated by permuting the edges between the nodes of a given input graph. This randomization preserves the degree of each node. A third mode of randomization preserves the degree distribution of the input graph, without preserving the degree of individual nodes.
Another tool, alter-graph, performs a partial randomization of a given input graph, by combining two operations: random addition and/or deletion of nodes and/or edges. Altered graphs are particularly useful to study the robustness of procedures to the presence of noise (node/edge additions) or to missing information (node/edge deletions). This tool was used in our comparative assessment of four graph-based clustering algorithms (26).
Network display
NeAT includes a tool called display-graph, which generates static images of an input network. Such drawings are convenient for a quick inspection of the results from the web browser, especially when dealing with large graphs. However, the cost of this speed is that the layout is rather rudimentary and the resulting image is static.
For more sophisticated layouts and for a dynamical manipulation of the drawing, NeAT is also able to load a network directly into the VisANT graph editor via Java Web Start (28).
For more advanced visualization facilities, we recommend specialized graph editors like yED Graph Editor (http://www.yworks.com/en/products_yed_about.html) and Cytoscape [(29), http://www.cytoscape.org]. To this purpose, the tool convert-graph permits to export any network resulting from NeAT to the GML format (http://www.infosun.fim.uni-passau.de/Graphlet/GML/gml-tr.html) which is supported by both editors.
CLUSTER TOOLS
NeAT also presents a series of tools allowing to study clusters or classification (functional classes) (Table 1, clusters tools). For example, the program compare-classes can study if among the clusters of highly connected nodes extracted from a graph via some clustering algorithm, some overlap with biological relevant classes [e.g. gene ontology classes (30)] exists. This program also allows to create a contingency table that can be further analyzed via the contingency-stats application.
NETWORK–CLUSTER TOOLS
Network clustering
Various algorithms have been implemented to extract clusters (i.e. groups of densely connected nodes) from biological networks. Clustering algorithms are often used in biology in order to extract coherent groups of nodes from networks : detection of protein complexes (26,31–33), of protein families (24), extraction of co-expressed clusters from in co-expression networks (35), etc.
The graph-based clustering algorithms MCL (34,36) and RNSC (37) have been shown to obtain good performances for extracting protein complexes from protein interaction networks (26). These algorithms can deal with large graphs and are very efficient in time. For these reasons, we included them in the NeAT tool suite.
Moreover, NeAT also includes a tool that discovers cliques (fully connected set of nodes) in networks.
From partitions to fuzzy clusters
As many clustering algorithms, MCL or RNSC partition the graphs into nonoverlapping clusters: each node is assigned to one and only one cluster. However, in some types of biological data, a single assignment may fail to represent multiple relationships between a node and various types of neighbors (for example, a protein may be part of different complexes).
Some graph-based clustering algorithms support multiple assignment and nonassigned nodes (i.e. fuzzy clustering), but the tuning of their parameters is sometimes delicate and the results can sometimes be weaker than those of a partitioning algorithm.
To keep the best of both worlds, an approach is to first run a partitioning algorithm and to postprocess its result by measuring a posteriori the membership between each node and each cluster of the partition. The membership of a node to a cluster is the proportion of edges from this node that reach that cluster. If the graph is weighted, the membership can take edge weights into account.
This two-step approach has been used to perform a reticulate classification of phages and detect mosaic phages resulting from fusions between other phage genomes (38). The program graph-cluster-membership takes as input a graph and a clustering result, and returns a node/cluster table indicating the degree of membership of each node to each cluster.
On the NeAT site, clustering results can automatically be launched to the graph-cluster-membership form. graph-cluster-membership can easily be adapted to be combined with other graph-based clustering algorithms.
Mapping of classes onto network
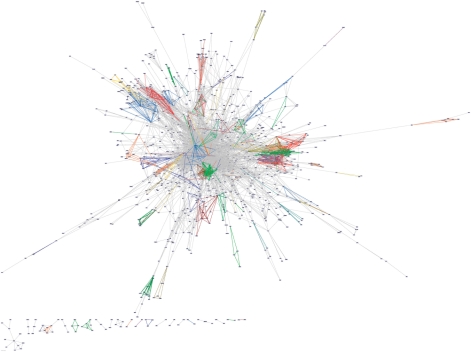
NeAT program graph-get-clusters then allows to extract or to map node clusters onto the network. A first function of such a mapping is to visualize the coherence of protein clusters or functional classes in the context of the network. Figure 4 displays a typical example of graph-get-clusters results, where known protein complexes (15) have been mapped onto a yeast protein interaction network obtained by high-throughput co-immunoprecipitation experiments (39). Edges between proteins belonging to annotated structural complexes have been colored according to their cluster (complex) membership. This helps the user to visualize the position of complexes in the interaction network.
Figure 4.
Comparison between a network and a set of classes. Mapping of the yeast protein complexes stored in MIPS database (15) on a large-scale interaction data set obtained by coimmunoprecipitation followed by mass spectrometry experiments (39). The mapping and coloring was performed with graph-get-clusters, and the image generated with the graphical editor yED. Intercluster edges (edges between nodes that do not belong to the same complex) are displayed in gray. Intracluster edges (edges between nodes belonging to the same complex) are colored with cluster-specific colors (one color for each protein complex).
DOCUMENTATION
NeAT programs are documented at various levels. Firstly, a manual is accessible from each query form, providing a systematic description of the parameters. Second, DEMO buttons automatically fill the query form with predefined examples (data sets + parameter values), in order to give the intuition of the result returned by the tools on a typical situation. Third, NeAT contains a tutorial, where users can learn using the tools on the basis of concrete biological data sets.
IMPLEMENTATION AND AVAILABILITY
Unless otherwise specified, all interaction data sets available in the NeAT demonstrations and the tutorials were downloaded from the BioGrid database (14) (http://www.thebiogrid.org/).
Moreover, NeAT includes a tool allowing to download and precisely filter subsets of the String database. This database contains protein interaction data obtained by integrating known and predicted interactions from a variety of sources (40).
Except for the path finding and the graph layout algorithms, all NeAT programs were developed in Perl and can be used as stand-alone applications on UNIX-based systems (tested on Linux + Mac OSX). The stand-alone version is freely available for academic users upon request (see Informations on the NeAT website).
The large majority of NeAT tools allows the treatment of graphs with several thousands of nodes and several tens of thousands of edges in a reasonable time. Typical published biological networks (a few thousands of nodes and tens of thousands of edges) are treated within seconds. However, some tools may be slower (cliques discovery (NP-hard), betweenness and closeness computation), but the execution time stays reasonable (minutes).
The web site (http://rsat.scmbb.ulb.ac.be/neat/) is free and open to all users and there is no login requirement.
NeAT programs are also accessible as web services (interface SOAP/WSDL), which allows to design programmatic workflows and integrate NeAT tools with various remote resources (databases and software tools). Actually, our website is itself a client for the web services, which guarantees a constant care for maintaining functional web services.
CONCLUSION
The Network Analysis Tools provide bioinformaticians and biologists with a set of web tools that can be combined to efficiently perform the main graph operations (comparison, node degree computation, clustering, etc.) used in today's; network biology. As all programs can be integrated in workflows, either on our website or via SOAP web services, users can easily use them to study the topology of a network of interest, discover densely connected groups of nodes, compare these groups to some reference classification and run negative control by submitting randomized graphs to the same analysis.
With the increasing number of studies involving biological networks, we are confident that the NeAT web server will be useful to biologists in general and to network bioinformaticians in particular.
ACKNOWLEDGEMENTS
Pathfinder is a Java wrapper around the REA algorithm written by Jimenez and Marzal in C. K.F. acknowledge these developers for putting their code in public. The NeAT java wrapper was inspired by a Python wrapper written by Pierre Schaus and Jean-Noël Monette at UCL (INGI), who are acknowledged for having helped K.F. K.F. would also like to thank the former aMAZE team for their support and help. The clustering algorithm MCL was developed by Stijn Van Dongen (Sanger Institute, UK). We are thankful to Stijn for making his code publicly available, for allowing us to integrate it in our web server, and for his extensive feed-back on the NeAT web interface. The clustering algorithm RNSC was developed by Andrew King (McGill Institute, Canada). We are thankful to Andrew King for making his code publicly available and for allowing us to integrate it in our web server. We thank Zhenjun Hu for helping us to integrate VisANT in NeAT and Morgane Thomas-Chollier (Université Libre de Bruxelles, Belgium) for her help in the website design and in the implementation of php scripts. We also acknowledge the following colleagues for having tested NeAT and for their constructive comments: Cei Abreu (Sanger Institute, UK), Bruno Contreras Moreira (University of Saragossa, Spain), Alexandre Irrthum (Université de Liège, Belgium), Philippe Gautier (MRC Edimburg, UK), Nicolas Simonis (Harvard Medical School, Boston, USA) and Shuye Pu (Hospital for Sick Children, Toronto, Canada). S.B. and R.J. are recipients of a PhD grant from the Fonds pour la Formation à la Recherche dans l'I;ndustrie et dans l'A;griculture (FRIA). K.F. is supported by The Actions de Recherches Concertées de la Communauté Française de Belgique (ARC grant number 04/09-307). G.L.M. is a fellow from the Fonds Xenophilia, ULB. The laboratory is a member of the BioSapiens Network of Excellence funded under the sixth Framework program of the European Communities (LSHG-CT-2003-503265). The BiGRe laboratory is supported by the Belgian Program on Interuniversity Attraction Poles, initiated by the Belgian Federal Science Policy Office, project P6/25 (BioMaGNet). Funding to pay the Open Access publication charges for this article was provided by the Région Wallonne de Belgique (TransMaze project 415925).
Conflict of interest statement. None declared.
REFERENCES
- 1.Jeong H, Mason SP, Barabàsi AL, Oltvai ZN. Lethality and centrality in protein networks. Nature. 2001;411:41–42. doi: 10.1038/35075138. [DOI] [PubMed] [Google Scholar]
- 2.Jeong H, Tombor B, Albert R, Oltvai ZN, Barabàsi AL. The large-scale organization of metabolic networks. Nature. 2000;407:651–654. doi: 10.1038/35036627. [DOI] [PubMed] [Google Scholar]
- 3.Gagneur J, Jackson DB, Casari G. Hierarchical analysis of dependency in metabolic networks. Bioinformatics. 2003;19:1027–1034. doi: 10.1093/bioinformatics/btg115. [DOI] [PubMed] [Google Scholar]
- 4.Croes D, Couche F, Wodak SJ, van Helden J. Inferring meaningful pathways in weighted metabolic networks. J. Mol. Biol. 2006;356:222–236. doi: 10.1016/j.jmb.2005.09.079. [DOI] [PubMed] [Google Scholar]
- 5.Luscombe NM, Babu MM, Yu H, Snyder M, Teichmann SA, Gerstein M. Genomic analysis of regulatory network dynamics reveals large topological changes. Nature. 2004;431:308–312. doi: 10.1038/nature02782. [DOI] [PubMed] [Google Scholar]
- 6.Babu MM, Luscombe NM, Aravind L, Gerstein M, Teichmann SA. Structure and evolution of transcriptional regulatory networks. Curr. Opin. Struct. Biol. 2004;14:283–291. doi: 10.1016/j.sbi.2004.05.004. [DOI] [PubMed] [Google Scholar]
- 7.Fukuda K, Takagi T. Knowledge representation of signal transduction pathways. Bioinformatics. 2001;17:829–837. doi: 10.1093/bioinformatics/17.9.829. [DOI] [PubMed] [Google Scholar]
- 8.Deville Y, Gilbert D, van Helden J, Wodak SJ. An overview of data models for the analysis of biochemical pathways. Brief Bioinform. 2003;4:246–259. doi: 10.1093/bib/4.3.246. [DOI] [PubMed] [Google Scholar]
- 9.Huber W, Carey VJ, Long L, Falcon S, Gentleman R. Graphs in molecular biology. BMC Bioinform. 2007;8(Suppl 6):S8. doi: 10.1186/1471-2105-8-S6-S8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.von Mering C, Krause R, Snel B, Cornell M, Oliver SG, Fields S, Bork P. Comparative assessment of large-scale data sets of protein-protein interactions. Nature. 2002;417:399–403. doi: 10.1038/nature750. [DOI] [PubMed] [Google Scholar]
- 11.Sprinzak E, Sattath S, Margalit H. How reliable are experimental protein-protein interaction data? J. Mol. Biol. 2003;327:919–923. doi: 10.1016/s0022-2836(03)00239-0. [DOI] [PubMed] [Google Scholar]
- 12.Yook S-H, Oltvai ZN, Barabasi A-L. Functional and topological characterization of protein interaction networks. Proteomics. 2004;4:928–942. doi: 10.1002/pmic.200300636. [DOI] [PubMed] [Google Scholar]
- 13.Letovsky S, Kasif S. Predicting protein function from protein/protein interaction data: a probabilistic approach. Bioinformatics. 2003;19(Suppl 1):i197–i204. doi: 10.1093/bioinformatics/btg1026. [DOI] [PubMed] [Google Scholar]
- 14.Breitkreutz B-J, Stark C, Reguly T, Boucher L, Breitkreutz A, Livstone M, Oughtred R, Lackner DH, Bähler J, Wood V, et al. The biogrid interaction database: 2008 update. Nucleic Acids Res. 2008;36(Database issue):D637–D640. doi: 10.1093/nar/gkm1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mewes HW, Amid C, Arnold R, Frishman D, Guldener U, Mannhaupt G, Munsterkotter M, Pagel P, Strack N, Stumpflen V, et al. MIPS: analysis and annotation of proteins from whole genomes. Nucleic Acids Res. 2004;32(Database issue):D41–D44. doi: 10.1093/nar/gkh092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Janky R, van Helden J. Evaluation of phylogenetic footprint discovery for predicting bacterial cis-regulatory elements and revealing their evolution. BMC Bioinform. 2008;9:37. doi: 10.1186/1471-2105-9-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Scott J, Ideker T, Karp RM, Sharan R. Efficient algorithms for detecting signaling pathways in protein interaction networks. J. Comput. Biol. 2006;13:133–144. doi: 10.1089/cmb.2006.13.133. [DOI] [PubMed] [Google Scholar]
- 18.Bebek G, Yang J. Pathfinder: mining signal transduction pathway segments from protein-protein interaction networks. BMC Bioinform. 2007;8:335. doi: 10.1186/1471-2105-8-335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rahman SA, Advani P, Schunk R, Schrader R, Schomburg D. Metabolic pathway analysis web service (pathway hunter tool at cubic) Bioinformatics. 2005;21:1189–1193. doi: 10.1093/bioinformatics/bti116. [DOI] [PubMed] [Google Scholar]
- 20.van Helden J, Gilbert D, Wernisch L, Schroeder M, Wodak S. Applications of regulatory sequence analysis and metabolic network analysis to the interpretation of gene expression data. In: Gascuel O, Sagot M-F, editors. Computational Biology : First International Conference on Biology, Informatics, and Mathematics, JOBIM 2000. LNCS Vol. 2066. Springer, Montpellier: 2001. pp. 155–172. [Google Scholar]
- 21.van Helden J, Wernisch L, Gilbert D, Wodak SJ. Graph-based analysis of metabolic networks. Ernst Schering Res. Found.Workshop. 2002;38:245–274. doi: 10.1007/978-3-662-04747-7_12. [DOI] [PubMed] [Google Scholar]
- 22.Croes D, Couche F, Wodak SJ, van Helden J. Metabolic pathfinding: inferring relevant pathways in biochemical networks. Nucleic Acids Res. 2005;33(Web Server issue):W326–W330. doi: 10.1093/nar/gki437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jimenez V, Marzal A. Computing the k shortest paths: a new algorithm and an experimental comparison. Proc. 3rd Int. Worksh. Algorithm Engineering (WAE 1999) 1999;1668:15–29. [Google Scholar]
- 24.Spirin V, Mirny LA. Protein complexes and functional modules in molecular networks. Proc. Natl Acad. Sci. USA. 2003;100:12123–12128. doi: 10.1073/pnas.2032324100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Han J-DJ, Dupuy D, Bertin N, Cusick ME, Vidal M. Effect of sampling on topology predictions of protein-protein interaction networks. Nat. Biotechnol. 2005;23:839–844. doi: 10.1038/nbt1116. [DOI] [PubMed] [Google Scholar]
- 26.Brohée S, van Helden J. Evaluation of clustering algorithms for protein-protein interaction networks. BMC Bioinform. 2006;7:488. doi: 10.1186/1471-2105-7-488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Milenkovic T, Lai J, Przulj N. Graphcrunch: a tool for large network analyses. BMC Bioinform. 2008;9:70. doi: 10.1186/1471-2105-9-70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hu Z, Ng DM, Yamada T, Chen C, Kawashima S, Mellor J, Linghu B, Kanehisa M, Stuart JM, DeLisi C. Visant 3.0: new modules for pathway visualization, editing, prediction and construction. Nucleic Acids Res. 2007;35(Web Server issue):W625–W632. doi: 10.1093/nar/gkm295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Shannon P, Markiel A, Ozier O, Baliga NS, Wang JT, Ramage D, Amin N, Schwikowski B, Ideker T. Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res. 2003;13:2498–2504. doi: 10.1101/gr.1239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gene Ontology Consortium. The Gene Ontology project in 2008. Nucleic Acids Res. 2008;36(Database issue):D440–D444. doi: 10.1093/nar/gkm883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sharan R, Ulitsky I, Shamir R. Network-based prediction of protein function. Mol. Syst. Biol. 2007;3:88. doi: 10.1038/msb4100129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Krogan NJ, Cagney G, Yu H, Zhong G, Guo X, Ignatchenko A, Li J, Pu S, Datta N, Tikuisis AP, et al. Global landscape of protein complexes in the yeast Saccharomyces cerevisiae. Nature. 2006;440:637–643. doi: 10.1038/nature04670. [DOI] [PubMed] [Google Scholar]
- 33.Pereira-Leal JB, Enright AJ, Ouzounis CA. Detection of functional modules from protein interaction networks. Proteins. 2004;54:49–57. doi: 10.1002/prot.10505. [DOI] [PubMed] [Google Scholar]
- 34.Enright AJ, Dongen SV, Ouzounis CA. An efficient algorithm for large-scale detection of protein families. Nucleic Acids Res. 2002;30:1575–1584. doi: 10.1093/nar/30.7.1575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lattimore BS, van Dongen S, Crabbe MJC. Genemcl in microarray analysis. Comput. Biol. Chem. 2005;29:354–359. doi: 10.1016/j.compbiolchem.2005.07.002. [DOI] [PubMed] [Google Scholar]
- 36.Van Dongen S. Ph.D. Thesis. Centers for Mathematics and Computer science (CWI), University of Utrecht; 2000. Graph clustering by flow simulation. [Google Scholar]
- 37.King AD, Przulj N, Jurisica I. Protein complex prediction via cost-based clustering. Bioinformatics. 2004;20:3013–3020. doi: 10.1093/bioinformatics/bth351. [DOI] [PubMed] [Google Scholar]
- 38.Lima-Mendez G, van Helden J, Toussaint A, Leplae R. Reticulate representation of evolutionary and functional relationships between phage genomes. Mol. Biol. Evol. 2008;25:762–777. doi: 10.1093/molbev/msn023. [DOI] [PubMed] [Google Scholar]
- 39.Gavin A-C, Aloy P, Grandi P, Krause R, Boesche M, Marzioch M, Rau C, Jensen LJ, Bastuck S, Dümpelfeld B, et al. Proteome survey reveals modularity of the yeast cell machinery. Nature. 2006;440:631–636. doi: 10.1038/nature04532. [DOI] [PubMed] [Google Scholar]
- 40.von Mering C, Jensen LJ, Kuhn M, Chaffron S, Doerks T, Krüger B, Snel B, Bork P. String 7-recent developments in the integration and prediction of protein interactions. Nucleic Acids Res. 2007;35(Database issue):D358–D362. doi: 10.1093/nar/gkl825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Uetz P, Giot L, Cagney G, Mansfield TA, Judson RS, Knight JR, Lockshon D, Narayan V, Srinivasan M, Pochart P, et al. A comprehensive analysis of protein-protein interactions in Saccharomyces cerevisiae. Nature. 2000;403:623–627. doi: 10.1038/35001009. [DOI] [PubMed] [Google Scholar]
- 42.Ito T, Chiba T, Ozawa R, Yoshida M, Hattori M, Sakaki Y. A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc. Natl Acad. Sci. USA. 2001;98:4569–4574. doi: 10.1073/pnas.061034498. [DOI] [PMC free article] [PubMed] [Google Scholar]