Bayesian Weibull tree models for survival analysis of clinico-genomic data

Abstract

An important goal of research involving gene expression data for outcome prediction is to establish the ability of genomic data to define clinically relevant risk factors. Recent studies have demonstrated that microarray data can successfully cluster patients into low- and high-risk categories. However, the need exists for models which examine how genomic predictors interact with existing clinical factors and provide personalized outcome predictions. We have developed clinico-genomic tree models for survival outcomes which use recursive partitioning to subdivide the current data set into homogeneous subgroups of patients, each with a specific Weibull survival distribution. These trees can provide personalized predictive distributions of the probability of survival for individuals of interest. Our strategy is to fit multiple models; within each model we adopt a prior on the Weibull scale parameter and update this prior via Empirical Bayes whenever the sample is split at a given node. The decision to split is based on a Bayes factor criterion. The resulting trees are weighted according to their relative likelihood values and predictions are made by averaging over models. In a pilot study of survival in advanced stage ovarian cancer we demonstrate that clinical and genomic data are complementary sources of information relevant to survival, and we use the exploratory nature of the trees to identify potential genomic biomarkers worthy of further study.

1. Introduction

Genomic information, in the form of microarray or gene expression signatures, has an established capacity to define clinically relevant risk factors in disease prognosis. Recent studies have generated such signatures related to disease recurrence and survival in ovarian cancer [62,2] as well as in numerous other disease contexts [72,58,48]. Analyses involving gene expression signatures have focused on clustering or classification to associate such signatures or patterns with ‘low-risk’ versus ‘high-risk’ survival prognoses. The clustering of tumors based on expression levels into multiple subgroups has been performed using various methods including support vector machines [72], k-NN models [62], PLS [45] and hierarchical clustering [47]. A more formal discussion and comparison of various tumor discrimination methods with gene expression data can be found in [19].

The application of gene expression signatures to the prediction of disease outcome is a research area distinct from clustering applications. Less attention has been focused on prediction to date, although single genes or gene signatures have been studied for the prediction of tumor classification related to ‘good’ versus ‘poor’ survival prognoses [70,21]. However, the ‘signature’ approaches to prediction of cancer outcome with microarrays have been shown to be highly unstable and strongly dependent on the selection of patients in the training sets [43]. This has been attributed to inadequate validation leading to overoptimistic results, but also reflects the heterogeneity of complex disease. From the perspective of the individual patient a sharper, more specialized approach to prediction is needed.

Bayesian regression tree models, described in Section 2, form the basis of one such approach. The conventional binary regression tree associated with CART [9] has been used successfully for prediction in various modeling contexts [5,63] as have the Bayesian versions of CART [12, 16], other Bayesian binary trees [49], and the relative risk trees of Ishwaran, Blackstone, Pothier, and Lauer [32]. A review of tree-based methods for survival can be found in [73]. Research has shown that the prediction accuracy of such models can be improved through Bayesian model averaging [25], bagging [5], boosting [60], and related methods [13]. This holds true for trees whether the model search is stochastic [67,7,35] or deterministic [10,44]. Our approach is a reflection of this finding and of the recent emphasis in the literature on ensemble methods for prediction [14,26,27]. A key aspect in our approach is the averaging of predictions over multiple candidate models, which we discuss in Section 3. Note that Bayesian model averaging not only improves predictive performance but the posterior parameter estimates and standard deviations directly incorporate model uncertainty [51].

In this article we discuss the development of Bayesian tree models that allow the use of clinical, histopathological, and genomic data in the prediction of disease-related survival outcomes. These regression tree models have ability to discover and evaluate interactions of multiple predictor variables, and define flexible, non-linear predictive tools [49]. Specifically, our method allows the direct evaluation of the relative importance of clinical and genomic predictors. Our approach is demonstrated in the context of prediction of survival after surgery for ovarian cancer patients. We stress the utility of such tree models in the exploration of genomic data, and the resulting identification of genes plausibly associated with clinical endpoints, as well as for prediction.

2. Regression trees

Our focus is the development of regression trees that recursively generate binary partitions of the covariate space, based upon specific clinical and genomic variables, and within each partition accurately model a continuous survival time response variable. One key advantage of such trees is their interpretability: the entire feature space can be explained by a single tree and the prediction for any given individual can be interpreted as a conjunction of simple logical expressions [17, 24]. Regression tree models serve as tools for prediction as well as for exploratory data analysis by discovering simple combinations of covariates that correlate with a particular outcome. In the case of genomic data these combinations can then serve as a basis for further biological study. Recent additions to the survival tree modeling literature, including [26,27] and [33], reflect the importance of survival trees as an analytic technique for data sets with complex structure.

In the remainder of this section we discuss model construction and model inference. We begin with a brief overview of recursive partitioning models (Section 2.1) and the use of the Exponential and Weibull distributions to model the conditional distribution of the response variable (Section 2.3). Then we discuss the splitting criterion based on Bayes factors and inference via Empirical Bayes methods (Section 2.2) and posterior distributions and predictive distributions (Section 2.4). The generation of predictive distributions by model averaging is discussed in Section 3. Although our models can be applied to censored data (under the assumption of non-informative censoring) [15,48], we confine our discussion to the fully observed case.

2.1. Recursive partitioning

We assume a continuous survival time response variable Y and a p-dimensional vector of covariates X. Each covariate X_j, j = 1, . . . , p, may be categorical or continuous. We assume that the distribution of Y|X can be expressed as Y|g(X) where g is a recursive binary partitioning or splitting of the covariate space into disjoint subspaces. Each binary split is defined by a rule which assigns an observation in the current partition to one of two partition subspaces based upon a predictor X_j and a threshold value τ. The choice of the pair (X_j, τ) is made by finding the pair which reorganizes the data in the current partition into two subgroups whose survival distributions are most different, as assessed by a splitting criterion (see Section 2.2.1). A split is performed if the value of this criterion exceeds a specified threshold of significance. This splitting process continues in a recursive fashion until the existing model cannot be improved. The result is a tree model M(Y, X) in which the terminal nodes or leaves represent a partition of the covariate space in which the distribution of Y is distinct.

For a given node and predictor it is possible that any of several threshold values would yield a significant split. The ability to generate multiple trees at a node may be advantageous. In problems with many predictors, this naturally leads to the generation of many trees, often with small changes from one to the next, and the consequent need to develop inference and prediction in the context of multiple trees generated this way. The use of ‘forests of trees’ and similar ensemble methods has been urged by Breiman [8] as well as others [26] and our perspective endorses this. The involvement of multiple trees in our analyses is supported by the viewpoint that the splitting of nodes is based on the selection of (predictor, threshold) pairs which we view as parameters of the overall tree model. Any single tree is formed by selecting specific values for these parameters and the uncertainty in these parameters is reflected in the variability among trees. The resulting models generate predictions via model averaging. This process is discussed in more detail in the following Section and in Section 3.

2.2. Tree generation

We employ a forward-selection process to generate tree models. If the data in a node of a single tree is a candidate for splitting, we find the (predictor,threshold) pair that maximizes the splitting criterion (see below) for a split at the given node. The node is split if the value of this criterion is sufficiently large. Given a current tree the splitting process continues until either the existing model cannot be improved, i.e., the splitting criterion is not sufficiently large for any choice of (predictor,threshold) at any node, or until all of the remaining candidate terminal nodes have very few observations (usually less than 5 observed survival times). Our strategy is unlike other tree-growing methods (including CART), which purposely overgrow a tree and then prune back, due primarily to our focus on prediction in settings of low signal to noise. We want to limit adaptivity and avoid overfitting, at the possible cost of missing an association of moderate significance.

2.2.1. Bayes factors

The choice of splitting criterion is based on the association between the outcome variable Y (survival time) and the covariates X in subsamples. Splitting variables and splitting thresholds are selected based on their ability to strengthen this association. With data y₁, . . . , y_n in a given node and a specified threshold τ on a given predictor X_j, our test of association is based on assessing whether the data are more consistent with a single exponential distribution (with exponential parameter μ_τ) or with two separate exponential distributions (with parameters μ₀,_τ and μ₁,_τ) defined by the specified partition.

In our Bayesian approach we adopt the standard conjugate Gamma prior model on the Exponential parameter [61]; the prior is Gamma(a, b) where b = a/m and m is the mean of the Gamma prior. We specify a fixed global prior mean but treat the scale parameter a as uncertain and node specific; a is estimated via Empirical Bayes (EB). In brief, suppose a node has r_z individuals with observed survival times and Y_z is the sum of all survival times (here z = 0, 1 identifies the node as one of two children nodes of a parent node). Assuming μ₀,_τ ≠ μ₁,_τ we take μ₀,_τ and μ₁,_τ to be independent with common prior Gamma(a_τ, b_τ) with mean a_τ/b_τ. Under the null hypothesis μ₀,_τ = μ₁,_τthe common value has the same Gamma prior. Let the parameters of the current prior Gamma(a_τ, b_τ) be expressed as a_τ = c_τ and b_τ = c_τ/m where m is the prior mean. The empirical Bayes approximation to μ_z,τ | (r_z, Y_z, μ_|1–|,τ) is Gamma $(c_{\tau }+r_z,(c_{\tau }∕{\widehat{\mu }}_{z,\tau })+{\mathit{Y}}_z)$ where ${\widehat{\mu }}_{z,\tau }$ is the marginal maximum likelihood estimate (found iteratively). The updated prior will serve as the prior on μ_z,τ and the EB estimate of a will be used in the splitting criterion. This has two key aspects: first, it permits ‘borrowing strength’ across the two subgroups or children nodes to estimate this key parameter; second, it allows for differing prior Gamma shape parameters at different nodes in each tree, thus it is flexible in responding to varying degrees of uncertainty as we move down the tree.

A candidate split of a given node will organize the data as follows: 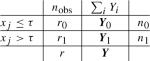where n_z is the total number of survival times in subgroup z (in the uncensored case r_z = n_z). The splitting criterion or test of association is based on assessing the Bayes factor B_τ [37] comparing the null hypothesis H₀ : μ₀,_τ = μ₁,_τ(with common value μ_τ) with the alternative H₁ : μ₀,_τ ≠ μ₁,_τ. The Bayes factor B_τ in favor of the alternative over the null hypothesis is simply

$$B_{\tau }=\frac{\Gamma (a_{\tau }+r_0)\Gamma (a_{\tau }+r_1)}{\Gamma \left(a_{\tau }\right)\Gamma (a_{\tau }+r)}\frac{b_{\tau }^{a_{\tau }}{(b_{\tau }+\mathbf{y})}^{a_{\tau }+r}}{{(b_{\tau }+{\mathbf{y}}_0)}^{a_{\tau }+r_0}{(b_{\tau }+{\mathbf{y}}_1)}^{a_{\tau }+r_1}}.$$

The Bayes factor is calibrated to the likelihood-ratio scale. However, it will provide more conservative estimates of significance than both likelihood-based approaches and more traditional significance tests [57]. The Bayes factor will naturally choose smaller models over more complex ones if the quality of fit is comparable and hence provide a control on the size of our trees [3].

In comparing predictors the Bayes factor can be evaluated for each predictor across a range of predictor-specific thresholds. For a given predictor this generates values of B_τ as a function of τ, which may suggest promising threshold values.

2.3. Weibull transformation

Suppose that a node of a given tree is to be split on a predictor x_j at the (threshold) value τ . Let y_zi and r_z be as defined in Section 2.2.1 where i denotes the ith individual in subgroup z, i = 1, . . . , n_z, and y_zi ∼ Exp(μ_z,τ). The data density is

$$p({\mathit{y}}_z\mid {\mu }_{z,\tau },r_z)={\mu }_{z,\tau }^{r_z}{\mathrm{e}}^{-{\mu }_{z,\tau }\sum _{i=1}^{n_z}{y}_{zi}}.$$

A careful examination of data from earlier studies of survival and cancer [2,15] revealed that the survival distribution could be more accurately represented by a Weibull distribution. The Weibull may be not only the most widely used parametric survival model but with its shape parameter it can be viewed as a generalization of the Exponential [30]. We subsequently denote the survival time as t_z where t_z has a Weibull distribution with parameters μ_z,τ and α. If t_zi is the survival time for individual i from subgroup z then

$$p(t_{zi}\mid {\mu }_{z,\tau },r_z,\alpha )=\alpha {\mu }_{z,\tau }{t}_{zi}^{\alpha -1}{\mathrm{e}}^{-{\mu }_{z,\tau }{t}_{zi}^{\alpha }}$$

for i = 1, . . . , n_z, z = 0, 1. Note that the Weibull distribution is a power transformation of the Exponential distribution ($y_{zi}=t_{zi}^{\alpha }$). For a specified, global Weibull shape parameter α, we can transform the data to Exponential, analyze the data and build trees with Exponential survival distributions, and then transform back to the original scale for predictions of new cases.

In our parameterization of the Weibull the scale parameter has been incorporated into the definition of μ_z,τ. As the value of μ_z,τ varies across different nodes of a tree so does the scale parameter. Since the splitting criterion for the trees is based on a significance test of the value of μ_z,τ, the scale parameter is implicitly, although not directly, incorporated into the splitting criterion and hence used for growing the tree. The current model could be reparameterized to address the scale parameter directly; however, this would require an entirely different Bayesian analysis as the interpretation of μ_z,τ is essential to the current conjugate analysis (see [61]).

2.4. Inference and prediction

Inference and prediction at a terminal node or leaf of a given tree involve the calculation of branch probabilities and the posterior predictive distributions which underlie the predictive probabilities for new cases. To calculate the branch probabilities for a leaf we must follow the path or sequence of nodes of the tree that connect the root node with the specified leaf.

We consider the kth node of the tree and suppose that it is split on the pair (x_jk, τ_jk), where the notation of Section 2.2 has been extended to include the node index. The data in node k can be divided into two groups based on the values of (x_j, τ_j), where the sums of all of the survival times in the X_j ≤ τ_j and X_j > τ_j groups are Y_0k and Y_1k, respectively. The implied conditional probabilities P(Y_zki > t | Z = z), i = 1, . . . , n_zk, for some time t are the branch probabilities defined by this split (the dependence of these probabilities on the tree and the data are suppressed for clarity). From Sections 2.2 and 2.3 we know that these probabilities are based on Exponential distributions for y_zki with parameter μ_z,τjk for z = 0, 1 and specified Gamma priors which we index by the parent node, i.e., Gamma(a_τjk, b_τjk). The use of EB to estimate a_τjk has been described in Section 2.2 and will not be discussed here. Assuming that node k is split, the resulting conditional posterior branch probability parameters would be independent with posterior Gamma distributions:

$${\mu }_{0,{\tau }_{jk}}\sim \text{Gamma}(a_{{\tau }_{jk}}+r_{0j},b_{{\tau }_{jk}}+{\mathit{y}}_{0j})\text{and}{\mu }_{1,{\tau }_{jk}}\sim \text{Gamma}(a_{{\tau }_{jk}}+r_{1j},b_{{\tau }_{jk}}+{\mathit{y}}_{1j}).$$

These distributions allow inference on the branch probabilities and play an essential role in predictive calculations, as we now describe.

Let x^★ be an observed vector of covariates for a new case and consider predicting the response P(y^★ > t | x^★) for a given time t. The current tree will define a single path for this observation from the root node to a terminal node or leaf. Prediction requires that we follow x^★ along its path down the tree to the implied leaf and construct the relevant posterior defined by the (x, τ) pairs at the splits that we encounter along the path. For example, suppose that our new case x^★ has an implied path through nodes 1 and 2 terminating at node 5 (a leaf), where each tree split defines exactly 2 children nodes (node numbers increase from left to right within levels starting with the root node as node 1). This path is based on (predictor, threshold) pairs (x₁, τ₁) and (x₂, τ₂) and is a result of predictor values ($x_1^{\star }\le {\tau }_1$) and ($x_2^{\star }>{\tau }_2$). After the root split the parameter of the Exponential distribution of the survival times in node 2 has a posterior Gamma distribution, i.e., μ₀,_τ1,1 ∼ Gamma($a_{\tau 1},1+r_{01},b_{\tau 1},1+{\mathit{y}}_{01}$).

The prior parameters $a_{\tau 1},1$ and $b_{\tau 1},1$ are updated via empirical Bayes using r₀₁ and y₀₁ resulting in $a_{\tau 2},2$ and $b_{\tau 2},2$. The split of node 2 would lead to a posterior Gamma distribution for the parameter of the Exponential distribution of the survival times in node 5, i.e., $\mu 1{,}_{\tau 2},2$ ∼ Gamma($a_{\tau 2}2+r_{12},b_{\tau 2},2+{\mathit{y}}_{12}$). For notational simplicity, let $\mu 1{,}_{\tau 2},2,a_{\tau 2},2+r_{12}$, and $b_{\tau 2},2+{\mathit{y}}_{12}$ be denoted by μ₅, a₅ and b₅, respectively. The prediction of the response P(y^★ > t | x^★) involves the posterior predictive distribution of future survival times for cases in node 5, i.e.,

$$P(y^{\star }>t\mid {\mathbf{x}}^{\star })=\frac{b_5^{a5}}{\Gamma \left(a_5\right)}{\int }_0^{\infty }{\mu }_5^{(a_5-1)}{\mathrm{e}}^{-{\mu }_5(t+b_5)}\mathrm{d}{\mu }_5=\frac{b_5^{a5}}{\Gamma \left(a_5\right)}\frac{\Gamma \left(a_5\right)}{{(b_5+t)}^{a_5}}={\left(\frac{b_5}{b_5+t}\right)}^{a_5}$$

which is a Gamma mixture of exponentials, or a Pareto distribution of the second kind (P(II)(0, b₅, a₅)) [34].

Prediction follows by estimating P(y^★ > t | x^★) based on the sequence of conditionally-independent posterior distributions for the branch probabilities that define it. Simply plugging in the posterior conditional means of each μ_z,τ,j will lead to a plug-in estimate of P(y^★ > t | x^★). Since each exponential mean follows a Gamma posterior, it is possible to draw Monte Carlo samples of the μ_z,τ,j and compute the corresponding values of P(y^★ > t | x^★) to generate a posterior sample for summarization. In this way we can examine the simulation-based posterior means and uncertainty intervals for P(y^★ > t | x^★) which represent predictions of the survival probabilities for the new case.

3. Generation and weighing of multiple trees

The use of forests of trees and similar ensemble methods has been urged by Breiman [8] as well as others [44,26] as previously noted. In our analyses the (predictor,threshold) pairs are viewed as parameters of the overall tree model. Statistical learning about relevant trees requires the examination of aspects of the posterior distributions of these parameters (and of the branch probabilities). Our Bayesian approach to survival tree modeling allows us to properly address model uncertainty, as has been done in similar contexts by others [10,16,12].

Trees are known as unstable classifiers [9]; however predictions may be improved by selecting a group of models instead of a single model and generating predictions by model averaging, as in [10,25]. Copies of the ‘current’ tree are made and the current node is split on a different significant (predictor,threshold) choice for each copy. Once a number of trees have been generated we can involve all or some of them in inference and prediction by weighting the contribution of each tree by its relative likelihood value. As a result of the current framework of forward generation of trees the likelihood values are easy to compute. For any single tree the overall marginal likelihood can be calculated by identifying the nodes which have been split and taking the product of the component marginal likelihoods defined by each split node. In other words (using the notation of Section 2.4) the marginal likelihood component defined by node k is

$$m_k={\int }_0^{\infty }\prod _{z=0,1}p({\mathit{y}}_{zk}\mid {\mu }_z,{\tau }_{jk},r_{zk},{\tau }_{jk})p({\mu }_z,{\tau }_{jk})\mathrm{d}{\mu }_z,{\tau }_{jk}$$

where ${\mu }_{z,{\tau }_{jk}}$ is the Gamma($a_{{\tau }_{jk}},b_{{\tau }_{jk}}$) prior for each z = 0, 1. We simplify this to

$$m_j=\prod _{z=0,1}\frac{b_{{\tau }_{jk}}^{a_{{\tau }_{jk}}}\Gamma (a_{{\tau }_{jk}}+r_{z}k)}{{(b_{{\tau }_{jk}}+{\mathit{y}}_{zk})}^{(a_{{\tau }_{jk}}+r_{zk})}\Gamma \left(a_{{\tau }_{jk}}\right)}.$$

The product of the component marginal likelihood values over all such split nodes k is the overall marginal likelihood value for the tree. This value is relative to the overall marginal likelihood values of all of the trees generated, which can be normalized to provide relative posterior probabilities for the trees based on an assumed uniform prior. These probabilities are valuable for both tree assessment and as relative weights in calculating average predictions for future observations. To represent predictions across many candidate trees, we use simulation: sample a tree model according to the posterior probabilities, i.e., the normalized relative likelihoods, then sample the implied unique Pareto distribution for a candidate future sample, based on the predictor profile of that case, in the chosen tree. Repeating this leads to a Monte Carlo sample from the predictive distribution that represents both within-tree uncertainties and, potentially critically, uncertainty across tree models. These samples can be summarized to produce point and interval estimates of survival probabilities at any chosen set of time points, and profiles of the full predicted survival distributions.

4. Sensitivity and performance on simulated data

Like any method for statistical inference our modeling approach and results will depend on various assumptions. These include the choice of prior and the data likelihood. In this section we consider the sensitivity of our method to the assumed value of the Weibull shape parameter α (see Section 2.3) in a predictive context using simulated data. To aid in determining whether our method behaves as expected, we employ two other modeling approaches for comparison. Our hope is that this assessment, although limited, will provide useful information concerning the strengths and weaknesses of our approach.

4.1. Setup

Our setup is similar to that of Hothorn et al. [28]. Five independent predictors X₁, X₂, . . ., X₅ were generated from a uniform distribution on [0,1]. Survival times were generated from a Exponential distribution with conditional survival function S(y|x) = exp(−yμ_x) under three models with logarithms of the hazards (A) log(μ_x) = 0, (B) $\log \left({\mu }_{\mathit{x}}\right)=3I(X_1\le 0.5\cap X_2>0.5)$, or (C) log(μ_x) = 3X₁ + X₂. These times were then transformed to follow a Weibull distribution with shape parameter α; values of were α [0.5, 0.8, 1.0, 1.2, 1.5].

The behavior of our models was compared to both a simple Kaplan–Meier curve and survival trees as implemented in the rpart package [66] in the R system for statistical computing [50]. Comparison to proportional hazards has been presented elsewhere [15]. The parameters for the rpart routine were set as in [28]. For our tree models the maximum number of trees allowed was 30, the minimum Bayes factor value required for a split was 2.5, and only nodes containing at least 3 observations were candidates for splitting. Numerous parameter combinations were tried with minimal impact on the results, if any. Trees with normalized likelihood values below 5% were removed from consideration. The mean integrated squared error was employed as a measure of the quality of the model predictions (computed by numerical integration). The learning sample contained 200 observations and the value of the predictions was evaluated on an independent sample of 100 observations.

4.2. Results

We have selected three representative runs to discuss: model A at α = 0.8, model B at α = 1.2, and model C at α = 1.5. Within each run the value of α assumed by the Weibull tree models (which we will refer to as α_fix) takes each value from the set [0.5, 0.8, 1.0, 1.2, 1.5]. The median MIE result and the 95% confidence interval for the median MIE calculated for 100 replications of the learning and evaluation sets for these runs are displayed in Figs. 1–3. For model A the Weibull tree performs best at values of α_fix near the true α. As expected, the error increases as α_fix moves away from α but the performance of the trees does not degrade notably until α_fix >> 1. Note that α = 1 is the transition point for the monotonicity of the hazard function (the hazard is decreasing for α < 1 and increasing for α >> 1). The Weibull method was able to capture the correct (null) model in all runs across α_fix values; however the number of trees selected increased as α_fix >> 1 (from an average of 1 tree selected to an average of 1.25 trees selected). For comparison the rpart method selected the correct (null) model in 91.8% of runs.

Fig. 1.

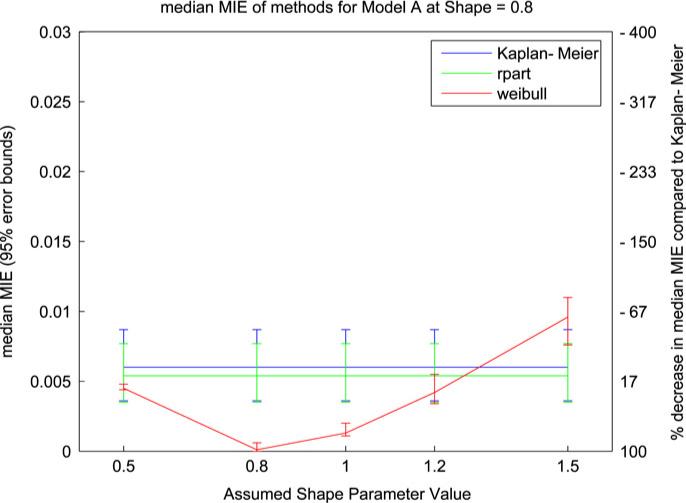
Median MIE values (with 95% error bars) from model A simulation with Weibull shape parameter = 0.8. The two y-axes indicate median MIE value (left) and percent improvement over Kaplan–Meier (right).

Fig. 3.

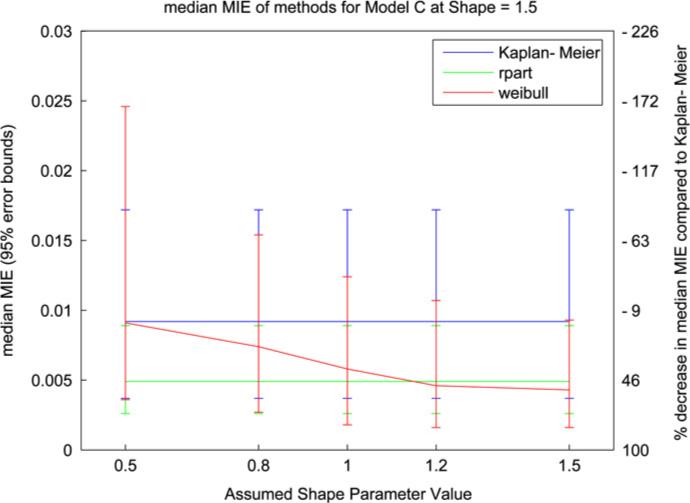
Median MIE values (with 95% error bars) from model C simulation with Weibull shape parameter = 1.5. The two y-axes indicate median MIE value (left) and percent improvement over Kaplan–Meier (right).

In Fig. 2 the Weibull model performs well for α_fix > 1 with α = 1.2. For small values of α_fix the error and variability of the results increase; this parallels an increase in the number of trees selected and a decrease from 97% to 71% in the number of runs where the correct model was selected (the rpart method selected the correct model in 86.6% of runs). Similarly to the results in Fig. 1 we see a loss of performance for values of α_fix < 1 where the monotonicity of the assumed hazard function is opposite to the monotonicity of the true hazard function. This pattern is also reflected in Fig. 3 but with relatively larger error bars. The increase in variability in Fig. 3 is the result of averaging over more trees (an average of 1.58 trees) in an attempt to capture the linear equation in the log hazard function. Overall the results demonstrate that the Weibull trees are sensitive to the monotonicity of the assumed hazard function, as reflected in the value of α_fix, and its correspondence to the monotonicity of the true hazard function.

Fig. 2.

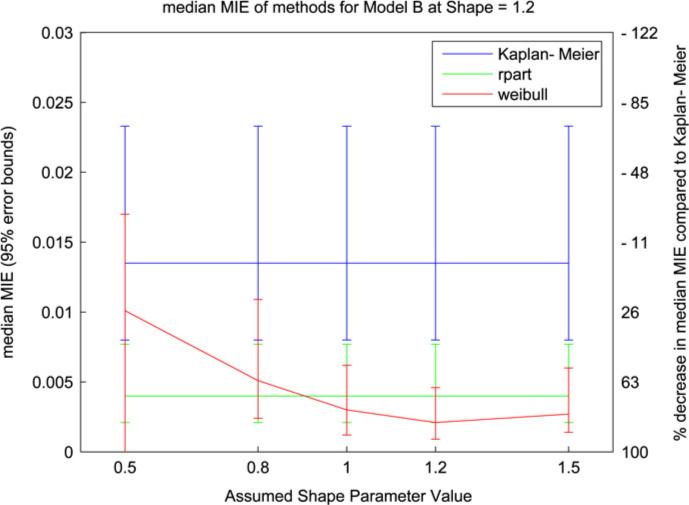
Median MIE values (with 95% error bars) from model B simulation with Weibull shape parameter = 1.2. The two y-axes indicate median MIE value (left) and percent improvement over Kaplan–Meier (right).

5. Analysis in ovarian cancer research

Ovarian cancer is the deadliest of the gynecologic cancers and the fifth leading cause of cancer deaths among women today [1]. When making ovarian cancer diagnoses and prognoses clinicians rely on subjective interpretations of both clinical and histopathological information, which can be incomplete or unreliable [62]. Recent studies in ovarian cancer have demonstrated the potential of genomic data to improve our ability to predict patient survival and treatment response [62,2].

We chose to utilize Weibull trees to explore pilot data collected from 119 advanced stage ovarian cancer patients treated at either Duke University Medical Center or H. Lee Moffitt Cancer Center & Research Institute. The primary purpose of this analysis was to determine whether genomic data could demonstrate ability to predict survival that was not reflected in available clinical data such as disease-free interval (time between primary chemotherapy/disease relapse and disease recurrence) and, if so, to explore which genes may demonstrate such ability and whether a larger study would be of interest. Tissue samples were collected at the time of initial cytoreductive surgery and all patients received primary chemotherapy with a platinum-based regimen (usually including taxane) subsequent to surgery. Detailed clinical records of traditional risk factors (age, stage, grade, debulking status) and measurement of disease-free interval were available for 55 of the 119 patients and have been summarized in Table 1. Gene expression data was generated for each patient at the institution of sample origin from RNA extracted from banked tissue derived from primary tumor biopsies. This RNA was hybridized to Affymetrix Human U133A GeneChips according to standard Affymetrix protocol. The results were expression levels from over 22,000 genes and expressed sequence tags (ESTs) for each individual. The pre-processing of the gene expression data (normalization and screening) and the use of dimension reduction techniques to build composite genomic predictors prior to analysis are discussed in Sections 5.1 and 5.2. The overall survival time (time from diagnosis to patient death) was selected as the response variable.

Table 1.

Ovarian cancer clinical data

	Duke			Moffitt
	N		%	N		%
Age
<45	2		5.7	2		10.0
45−55	8		22.9	5		25.0
55−65	11		31.4	7		35.0
65−75	11		31.4	4		20.0
>=75	3		8.6	2		10.0
Mean/Min/Max		60/33/79			59/33/76
Stage
III	31		88.6	14		70.0
IV	4		11.4	6		30.0
Grade
I	1		2.9	2		10.0
II	15		42.9	3		15.0
III	19		54.3	15		75.0
DFS interval (mo.)
<12	24		68.6	12		60.0
>=12	11		31.4	8		40.0
Mean/Min/Max		20.0/0.0/156.0			12.1/0.0/44.0
Surgical debulking
Suboptimal (>1 cm)	21		60.0	4		20.0
Optimal (<1 cm)	14		40.0	16		80.0
Platinum response
Yes	22		68.9	4		20.0
Partial	8		22.9	16		80.0
No/Stable disease	5		14.3	0		0.0
Survival time (mo.)
Observed	30		85.7	6		30.0
Censored	5		14.3	14		70.0
Mean/Min/Max		55.3/6.0/185.0			39.0/11.0/101.0

DFS = disease-free survival.

The clinical characteristics of the Duke and Moffitt samples were not comparable (see Table 1) and hence we could not use one for training the model and one for validation. We excluded the possibility of using leave-one-out cross-validation due to its instability in model selection [6] and decided instead to divide the combined data set of 55 samples into a training set (60% of samples) and a test set (40% of samples). Although this may introduce bias in internal validation [52], the primary interest in terms of a possible future study is in external validation. Training and test sets were balanced for age, array location (Duke or Moffitt), debulking status, and response to platinum therapy. In order to account for possible assignment bias due to unknown factors we performed 10 runs; in each run the samples were split into different training and test sets and all steps of the analysis, including expression data pre-processing, were repeated.

5.1. Pre-processing of expression data

The ovarian cancer data contained expression levels from over 22,000 genes and expressed sequence tags (ESTs) for each individual. We chose to use GeneChip RMA (GCRMA) as our measure of expression since it has been shown to balance accuracy and precision [31]. Our expression data were initially screened to exclude genes showing minimal variation across samples. We evaluated the remaining genes for consistency across both sets using integrative correlations as described in [46]. Across different runs an average of 6400 genes passed all screens (sd = 53.42 genes). Although individual genes could be used as predictors, we chose to create predictors from clusters of similar genes both to reduce dimension and to identify multiple underlying patterns of variation across samples.

5.2. Clustering and metagene selection

The evaluation and summarization of large-scale gene expression data in terms of lower dimensional factors of some form are being increasingly utilized both to reduce dimension and to characterize the diversity of expression patterns evidenced in the full sample [39,23]. The idea is to extract multiple patterns as candidate predictors while reducing dimension and multiplicities and smoothing out gene-specific noise. Discussion of various factor model approaches appears in [71]. Considering the number of genes in our data set and the heterogeneity of the sample patients we first applied k-means correlation-based clustering to the genes and selected the dominant principal component (or metagene [29]) to represent each cluster. These metagene predictors are input to the tree model analysis, along with the clinical predictors, as a re-expression of the genomic information contained in the original microarray data. Although k-means was chosen for its ease of use and wide availability our approach is amenable to other clustering techniques.

The k-means clustering algorithm was applied to the training data in each run, generating an average of 490 gene clusters (sd = 2.76 clusters). As the true number of clusters is unknown it was possible that some clusters did not represent subsets of related genes but were simply an artifact of the clustering algorithm. We identified such clusters by assessing the silhouette widths [38] of genes within clusters and removing clusters containing genes whose widths were not significant. This approach is similar to that of Dudoit and Fridlyand [18]. The significance of a width was determined by comparison to a permutation-based null distribution generated by randomly permuting the entries of each row of the observed gene expression matrix, clustering this permuted matrix using k-means as above, and calculating the silhouette values for the permuted genes. Only clusters whose genes had significant silhouette values (p < 0.05) were retained, leaving an average of 310 metagenes for analysis (sd = 20.87 clusters). The permutation null distribution and the gene silhouette values from the initial training/test run are displayed in Fig. 4. The silhouette values by cluster size are displayed in Fig. 5.

Fig. 4.

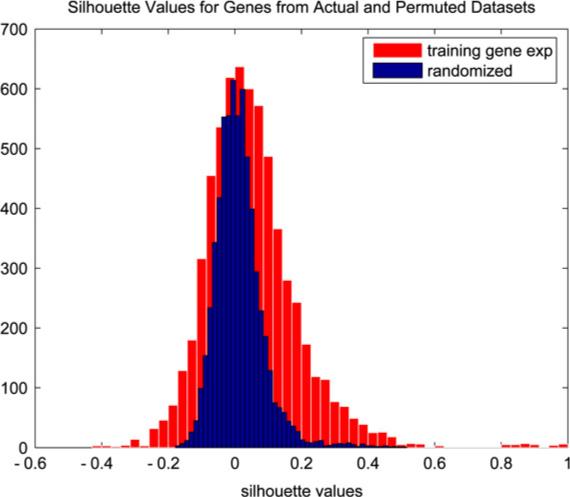
Permutation null distribution (blue) and distribution of gene silhouette values from run 1 (red). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 5.

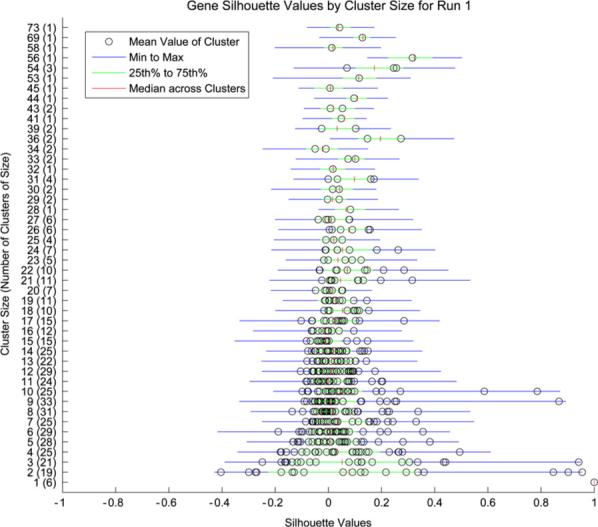
Gene silhouette values by cluster size from run 1.

5.3. Predictive results

Using the training data as a learning set we generated multiple trees under a variety of parameter settings using clinical predictors only, metagenes only, and both metagenes and clinical predictors. The parameter settings were as follows: Bayes factor thresholds of 2.0, 2.5, or 3 on the log base 2 scale, Weibull shape parameter values of 0.8, 1.0, or 1.2, Gamma prior parameters of α = 2 and β = 1/60 or 1/120, up to 20 splits (i.e., 20 new trees) at the root node and up to 3 at each second level node. The choice of Bayes factor threshold was based on frequentist properties: a Bayes factor of 3 is approximately equivalent to a p-value of 0.05. The Gamma prior parameters were chosen to roughly match the mean of the training data, i.e., αβ = μ. The Weibull shape parameter is unknown but values were selected based on the histogram of the training data. Any tree whose relative likelihood value exceeded 1% contributed to the generation of predictions via model averaging. The combination of parameter settings which produced the trees with the most accurate fitted values were retained and used to generate predictions for the validation set. A fitted value at time t for an individual was ‘accurate’ if the fitted probability of surviving for at least time t was greater than a specified cutoff if the recorded survival time for the individual is greater than time t, and vice versa. The specified cutoff was based on an ROC curve to balance specificity and sensitivity. The predictive accuracy of a fitted model was assessed by calculating the predicted auROC estimates at 3-, 4-, and 5-year survival endpoints [11].

As can be seen in Table 2 the predictive results varied across the runs with a validation auROC for the median predictions of the clinical only (C), genomic only (G), and clinico-genomic (CG) tree models of 78.96%, 81.27%, and 84.28% at 3-year survival; 79.94%, 81.19%, and 83.55% at 4-year survival; and 76.93%, 77.92%, and 81.11% at 5-year survival. For C models an average of 4 trees had appreciable relative likelihood and contributed to the predictions in any given run. For the G and CG models the average number of contributing trees was 35 and 36, respectively, although only an average of 4.2 and 2.4 trees, respectively, had relative likelihoods above 5%. Note that in several runs the genomic predictors did not improve upon the predictive ability of the clinical data, and in one run (run #8) none of the models demonstrated the ability to predict, but the additional predictive ability provided by the genomic variables is evident when looking across all runs.

Table 2.

Predictive auROC Values of Clinical only (C), Genomic only (G), and Clinico-Genomic (CG) Tree models at 3-, 4-, and 5-year survival endpoints

Validation accuracy in each of 10 training/test runs
3 years	1	2	3	4	5	6	7	8	9	10	Avg
C	52.2	89.0	98.8	65.5	82.2	87.5	78.9	54.4	81.1	100.0
	(45.6, 53.3)	(69.0, 94.0)	(93.4, 98.8)	(56.4, 68.2)	(82.2, 88.9)	(85.0, 92.5)	(74.4, 78.9)	(52.2, 54.4)	(78.9, 81.1)	(82.2, 100.0)	78.96
G	86.7	86.0	82.3	76.4	70.0	97.5	88.9	47.8	96.7	80.0
	(70.0, 86.7)	(77.0, 91.0)	(76.5, 82.3)	(67.3, 76.4)	(64.4, 70.0)	(86.3, 100.0)	(71.1, 88.9)	(41.1, 65.6)	(84.4, 96.7)	(60.0, 84.4)	81.27
CG	96.7	86.0	82.3	80.0	78.9	98.8	85.6	48.9	96.7	88.9
	(72.2, 96.7)	(81.0, 86.0)	(82.7, 85.2)	(66.4, 80.0)	(68.9, 82.2)	(86.3, 100.0)	(67.8, 85.6)	(36.7, 65.6)	(82.2, 96.7)	(66.7, 88.9)	84.28
4 years	1	2	3	4	5	6	7	8	9	10	Avg
C	53.8	86.9	98.8	68.8	87.0	91.4	78.9	55.0	78.8	100.0
	(48.8, 53.8)	(78.8, 89.9)	(93.8, 98.8)	(57.3, 70.8)	(85.1, 95.5)	(88.9, 93.8)	(74.4, 78.9)	(52.5, 55.0)	(76.3, 78.8)	(82.5, 100.0)	79.94
G	86.3	91.9	82.7	76.1	70.0	92.6	88.9	48.8	96.3	78.8
	(70.0, 86.3)	(77.8, 97.0)	(76.5, 82.7)	(64.6, 76.1)	(64.4, 70.0)	(84.0, 96.3)	(71.1, 88.9)	(45.0, 63.8)	(86.3, 96.3)	(60.0, 85.0)	81.19
CG	96.3	90.9	77.8	77.1	78.9	92.6	85.6	50.0	97.5	88.8
	(75.0, 96.3)	(81.8, 90.9)	(59.3, 77.8)	(62.5, 77.1)	(68.9, 82.2)	(81.5, 92.6)	(67.8, 85.6)	(40.0, 63.8)	(87.5, 97.5)	(66.3, 88.8)	83.55
5 years	1	2	3	4	5	6	7	8	9	10	Avg
	54.5	85.2	93.5	68.8	77.3	85.0	77.5	56.1	71.4	100.0
C	(50.7, 59.7)	(76.1, 88.6)	(85.7, 93.5)	(57.3, 70.8)	(77.3, 84.1)	(83.8, 85.0)	(72.5, 77.5)	(53.0, 56.0)	(66.2, 71.4)	(82.5, 100.0)	76.93
G	80.5	90.9	76.6	76.0	65.9	82.5	87.5	47.0	93.5	78.8
	(72.7, 80.5)	(75.0, 96.6)	(68.8, 80.5)	(64.6, 76.1)	(59.9, 65.9)	(73.8, 86.3)	(70.0, 87.5)	(37.9, 57.6)	(84.4, 93.5)	(60.0, 85.0)	77.92
CG	94.8	89.8	74.1	77.1	78.4	82.5	83.8	47.0	94.8	88.8
	(75.3, 94.8)	(79.6, 89.8)	(58.4, 74.0)	(62.5, 77.1)	(64.8, 78.4)	(71.3, 82.5)	(67.5, 83.8)	(31.8, 57.6)	(80.5, 94.8)	(66.3, 88.8)	81.11

auROC at average predictions and range of auROC over predictions are provided.

A high likelihood tree from run 1 is shown in Fig. 6; each node contains the (predictor, threshold) which created the node split, the number of sample individuals in the node, and the posterior predictive probability of 3-year survival for the node subpopulation. Several clinical variables, particularly disease-free interval but also age, grade, and debulking status, appear in top trees along with a group of metagene predictors. The specific metagene predictors vary with each run but by comparing the key metagenes across runs we do find genes which appear frequently and for which potentially very relevant biological connections can be made; see Section 5.4 for a discussion of several such connections. A summary of the predictors which appear in the top trees from run 4 is presented in a tree matrix plot in Fig. 7. For each predictor the sum of the probabilities of the trees in which the predictor appears is shown on the horizontal axis; this serves as a simple numeric assessment of the relative importance of these variables in the prediction of survival.

Fig. 6.

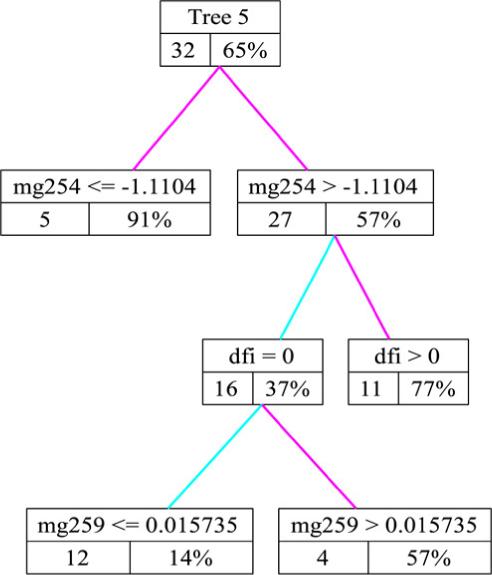
A high likelihood clinico-genomic survival tree; each node contains the (predictor,threshold) which created the node split, the number of sample individuals in the node, and the posterior predictive probability of 3-year survival for that subpopulation.

Fig. 7.

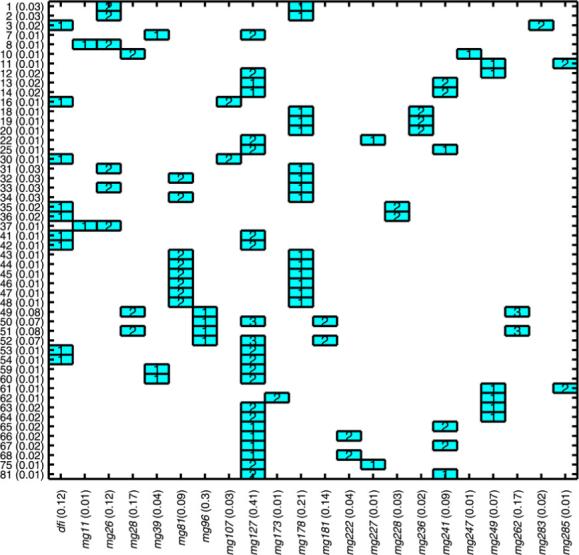
Summary of split variables and corresponding split levels for top trees in run 4. Vertical axis shows tree indices and tree weights; horizontal axis shows each split variable and sum of probabilities of trees in which variable occurs (importance weight).

Fig. 8 shows a snapshot of predictions of the probability of 3-year survival from run 6. In this example many of the uncertainty intervals are large which reflects the small sample size and heterogeneity of the sample population.

Fig. 8.

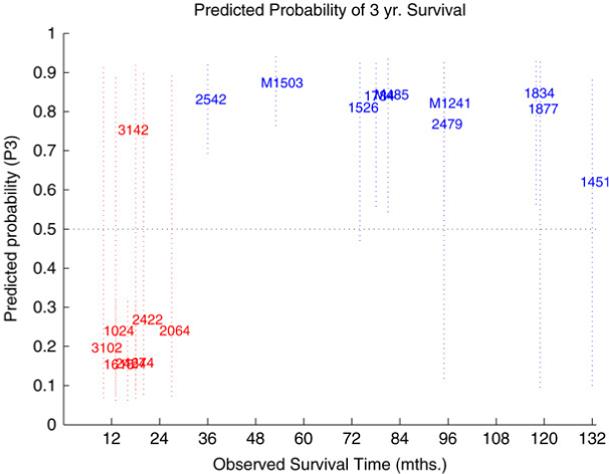
Predictions of 3-year survival for validation samples generated by averaging over trees.

A posterior sample of predictions for each individual can be generated via Monte Carlo sampling of the ${\mu }_{z,{\tau }_j}$ and computing the corresponding values of P(y^★ > t | x^★). This provides simulation-based posterior means and uncertainty intervals which are critical in determining the importance of a prediction in clinical decision making. To illustrate this, we selected three individuals from the data set and displayed their predicted survival curves from the CG models in the panels of Fig. 9. These curves extend over several years and include uncertainty intervals at certain time points. Cases 2424 and 1451 are examples where the confidence in prediction, either of short-term (#2424) or long-term survival (#1451), is quite high, as evidenced by the narrow uncertainty bars. Case #2424 was an older patient whose tumor was suboptimally debulked and whose disease remained stable after platinum chemotherapy; she had no disease-free interval and survived for 16 months. Case #1451 was also an older patient whose tumor was suboptimally debulked but whose disease responded to platinum chemotherapy; her disease-free interval was 28 months and her overall survival time was 132 months. In contrast, the predictive survival curves for other cases are highly uncertain. These are cases where the number of patients with similar characteristics is very small or there is conflict among the clinico-genomic predictors and hence disagreement among tree outcomes. Case #1774 was an older patient who was optimally debulked and whose disease responded to platinum therapy, which would classify her as clinically low risk. Her disease-free interval was more than 10 months and her overall survival time was 22 months. Upon closer examination it was revealed that she had values on key metagenes that conflicted with her low-risk clinical assessment. The short-term predictions for case #1774 were the result of her value for metagene 357; on further inspection we discovered that this metagene contained a probe for the gene TNK2 (alias ACK1) for which this patient had an extremely high value (see Section 5.4 for further discussion of this finding). It seems evident that the metagene predictors are capturing information in the genomic predictors which may or may not be reflected in the clinical predictors. In such cases it is important that the overall prediction summary recognizes and reflects this uncertainty and that models be open to investigation so that such results can be explored.

Fig. 9.

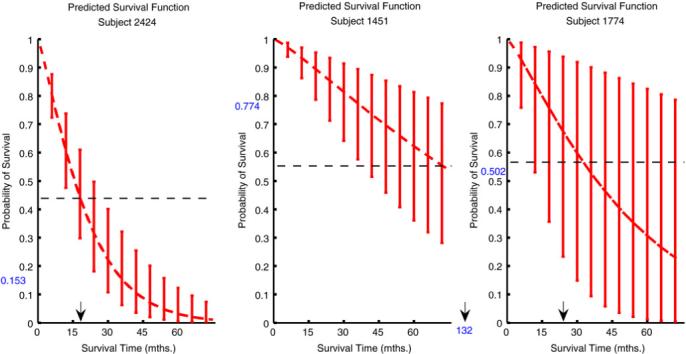
Predicted disease-free survival curves with uncertainty intervals at chosen time points for three individuals. The ROC cutoff (dashed line) for classification as short-term or long-term survivor and the prediction of survival at 3 years (blue number on the y-axis) are identified. The actual survival time is marked with an arrow on the x-axis. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.).

In some cases the results using clinical data alone are better than those using both clinical and genomic data (see, for example, Run 3 in Table 2). We suppose that this is due to heterogeneity in the patient subsamples, as no specific gene or metagene was found to be relevant to all samples. It is possible that the clinico-genomic trees could be improved further in these cases by altering the hyperparameter values, such as the Bayes factor threshold, but given the limited amount of data available we chose not to vary the parameter settings across different runs. Given more data the specific tuning of model parameters can be explored in more depth.

5.4. Biological relevance

As mentioned in Section 5.3 the metagene predictors vary with each run but we did identify genes which appear in the key metagenes of several runs and for which potentially very relevant biological connections can be made. This demonstrates the power of our approach for exploratory data analysis as well as prediction. We mention a few examples here; a more complete list of metagenes which appeared in predictive trees and their component genes are given in Table 3 [65].

Table 3.

Genes which appear in Weibull tree models in at least 3 of the 10 training runs

Key genes
Runs	Cluster	Affy probe ID	NCBI entrez gene	Gene ontology
1, 4, 5, 9	468, 185, 25, 422	213158_at	Unknown gene
1, 5, 8	468, 25, 473	205383_s_at	ZBTB20	Physiological process
1, 4, 10	378, 148, 295	207571_x_at	C1orf38
1, 4, 10	378, 148, 295	210785_s_at	C1orf38
1, 4, 10	195, 441, 135	201486_at	RCN2
1, 4, 10	195, 441, 135	209085_x_at	RFC1	DNA-dependent DNA replication/DNA metabolism
				Physiological process
4, 6, 10	441, 210, 241	213838_at	NOL7
3, 7, 10	448, 451, 241	200958_s_at	SDCBP	Substrate-bound cell migration/cell extension
				Physiological process
2, 4, 5, 7	161, 309, 475, 303	213705_at	MAT2A	Physiological process
2, 5, 9	161, 475, 213	219437_s_at	ANKRD11
2, 4, 7	161, 309, 303	202028_s_at	RPL38	Physiological process
2, 4, 7	161, 309, 303	208120_x_at	Unknown gene
2, 4, 7	161, 309, 303	210686_x_at	SLC25A16	Physiological process
2, 4, 7	161, 309, 303	211454_x_at	Unknown gene
2, 4, 7	161, 309, 303	212044_s_at	RPL27A	Protein biosynthesis/macromolecule biosynthesis
				Physiological process
2, 4, 7	161, 309, 303	213736_at	COX5B	Physiological process
2, 4, 7	161, 309, 303	214001_x_at	RPS10	Physiological process
2, 4, 7	161, 309, 303	214041_x_at	RPL37A	Protein biosynthesis/macromolecule biosynthesis
				Physiological process
2, 4, 7	161, 309, 303	221943_x_at	RPL38	Physiological process
2, 4, 7	161, 309, 303	218808_at	DALRD3	Protein biosynthesis/macromolecule biosynthesis arginyl-tRNA aminoacylation
				Physiological process
4, 7, 9	309, 487, 335	208141_s_at	HLRC1
4, 7, 9	309, 487, 335	216180_s_at	SYNJ2	Physiological process
5, 9, 10	404, 335, 313	208868_s_at	GABARAPL1
2, 4, 9	105, 185, 422	218962_s_at	FLJ13576
2, 4, 8	105, 185, 403	216713_at	KRIT1
2, 4, 8	105, 226, 403	34041_i_at	Unknown gene
2, 4, 8	105, 226, 403	221596_s_at	DKFZP564O0523
2, 3, 7	446, 23, 265	203277_at	DFFA	DNA fragmentation during apoptosis disassembly of cell structures during apoptosis
				Apoptotic nuclear changes
				DNA catabolism/DNA metabolism
				Physiological process
2, 3, 9	446, 23, 357	201155_s_at	MFN2
1, 2, 9	378, 446, 357	221269_s_at	SH3BGRL3
4, 5, 9	409, 25, 100	209120_at	NR2F2	Physiological process
4, 5, 9	409, 25, 100	209121_x_at	NR2F2	Physiological process
4, 5, 9	409, 25, 100	215073_s_at	NR2F2	Physiological process
4, 5, 7	409, 25, 449	212761_at	TCF7L2	Physiological process
1, 3, 10	373, 82, 285	202435_at	Unknown gene
1, 3, 10	373, 82, 285	202436_at	Unknown gene
1, 3, 10	373, 82, 285	202437_at	Unknown gene
1, 3, 10	282, 82, 282	209146_at	SC4MOL	Physiological process
4, 6, 10	226, 49, 473	202375_at	SEC24D	Physiological process
4, 6, 10	226, 99, 473	209501_at	CDR2
4, 6, 9	51, 466, 53	212205_at	H2AFV	DNA metabolism
				Physiological process
4, 6, 9	409, 466, 299	218127_at	NF-YB	Physiological process
4, 6, 7	312, 490, 434	213246_at	C14orf109
3, 5, 10	121, 55, 486	208070_s_at	REV3L	DNA-dependent DNA replication/DNA metabolism
				Physiological process
1, 5, 9	154, 97, 227	209170_s_at	GPM6B

First, the tree in Fig. 6 includes metagene (Mg) 254 as a split variable. This metagene includes multiple probes for gene CYP1B1; the enzyme encoded by this gene is involved in androgen metabolism and the metabolism of various procarcinogens. CYP1B1 has been associated with risk of endometrial cancer [55] and breast and ovarian cancer as a downstream target of BRCA1 expression during xenobiotic stress [36]. Second, the key variables which appear in the CG trees from run 4 appear in Fig. 7; we will focus on Mg 127 and Mg 178. Mg 127 contains Krit1 as a component gene; Krit1 has been shown to interact with a proposed tumor suppressor and may act as an antagonist of the oncogene Ras. The Krit1 cDNA has been mapped to a chromosomal location frequently deleted or amplified in multiple forms of cancer [59]. Mg 178 contains NR2F2 (COUP-TFII), a gene which encodes for a transcription factor shown to be critical for normal female reproduction in mice [64] and menstrual cycling in human ovaries [56]. This cluster also includes TCF7L2 (TCF-4) which plays a role in the beta catenin-Wnt signaling pathway, a pathway considered one of the key developmental and growth regulatory mechanisms of the cell [22]. In particular the regulation of Cyclin D1 by Rac1 is beta-catenin/TCF-dependent [20]; Cyclin D1 is a Wnt target gene which alters cell cycle progression and in which mutations, amplification and overexpression are observed frequently in a variety of tumors and may contribute to tumorigenesis. Finally, NF-YB is also found in this cluster; NFYB encodes a transcription factor necessary for the negative regulation of Chk2 expression by p53 [42]. This process is critical for the control of cell cycle progression in response to DNA damage. NF-YB also interacts with the oncogenes c-Myc, pRb, and p53 to control expression of the PDGF beta-receptor which is tightly regulated during a normal cell cycle [68].

The examination of subjects whose predictions improve significantly upon the inclusion of genomic data can also yield potentially informative genes. The ACK1 gene mentioned in Section 5.3 was discovered by this strategy. The amplification of the ACK1 gene in primary tumors has been shown to correlate with poor prognosis and the overexpression of ACK1 in cancer cell lines can increase the invasive phenotype of these cells both in vitro and in vivo [69]. In our data set the expression of ACK1 was found to be negatively correlated (not significantly) with survival; however, in the complete data set of 119 individuals this correlation was significant (see Fig. 10). These findings support the theory of Bernards and Weinberg [4] that genetic alterations acquired early in the process of tumor development may drive primary tumor growth and determine metastatic potential.

Fig. 10.

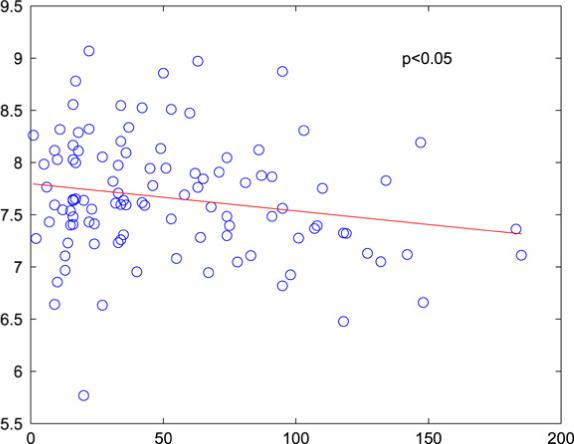
Relationship of ACK1 expression and survival; all 119 patients.

The identification of multiple genes with predictive ability and potential biological relevance to tumor development, reflective of the heterogeneity of the patient sample and the complexity of the underlying disease, is a key finding and suggestive of plausible directions for biological investigation.

6. Discussion

We have presented a Bayesian approach to tree analysis in the specific context of a survival time response and both clinical and genomic predictors. Survival times are assumed to follow a Weibull distribution and tree construction is based on forward selection where a split on a (predictor,threshold) pair is performed if the evidence for or against a difference in survival distributions between the resulting subgroups is significant, as assessed by the associated Bayes factor. By averaging predictions across trees with the relative likelihood values as weights we will tend to improve predictions by respecting, and properly accounting for, tree model uncertainty [25].

We note that although averaging predictions across trees does improve model performance, it also decreases the interpretability of the model. This is an important trade-off: predictive ability versus model interpretability. We advocate model averaging because of its improved predictions and because in high-dimensional data settings model uncertainty can be substantial. By building multiple tree models we can explore the covariate space and attempt to address model uncertainty.

We understand that in the interpretation of tree models (in terms of prediction accuracy as well as variable selection) it is important that the parameter estimates be unbiased. This has been stressed in the recent tree literature, e.g., [41,40,27]. Our models are not unbiased in the sense that variables with more splitting values are more likely to be selected in model building. To address this bias we have chosen a metric for model accuracy based on predictive accuracy. This metric will help us to identify and remove from consideration ‘fluke’ models which fit the data well but have poor predictive performance. We concede that this approach is not computationally efficient but it does allow for model exploration which is critical at this point of our analysis. Of course as more data is collected we suspect that computational expense will increase but model uncertainty will decrease, at which point we may focus on averaging over fewer models or employing an alternate method which places more emphasis on unbiasedness and model estimation.

We implemented our survival tree modeling in the analysis of pilot data from a study of advanced stage ovarian cancer. Multiple, related patterns of gene expression in combination with clinical data provided strong and predictively valid associations with survival. The models delivered predictive survival assessments together with measures of uncertainty about the predictions. As a result of tree spawning and model averaging these measures of uncertainty reflected within-tree variability as well as the variability resulting from the sensitivity of the Bayes factor to specific predictor choices and small changes in threshold values. An examination of genes which demonstrate predictive ability across various training and test sets revealed several genes with biologically plausible relevance to carcinogenesis, warranting further investigation.

We chose to use a conjugate Gamma prior in our analysis although a non-informative prior, such as a Jeffreys' prior, could have been employed. The Jeffreys' prior is a Gamma(a, b) where a = b = 0 [53]. This prior would put relatively more weight on extreme survival values; we felt it was more appropriate to choose values of a and b based on the observed survival times. However for large sample sizes there should be little difference in the results under the conjugate versus the Jeffreys' prior. Thus we expect little difference in the results from each prior at the root and upper level nodes. In small sample sizes, e.g., lower level nodes, we may see some differences in the models but the prior parameters are being updated by previous tree splits which will mitigate any differences. These suppositions were confirmed when we repeated a subset of the simulations from Section 4 using the Jeffreys' prior. The MIE values increased under the Jeffreys' prior relative to the results under the conjugate prior, and the ability to capture the correct model decreased, but qualitatively the results did not change.

In anticipation of future studies we intend to perform further comparisons with existing methods [27,33] and further simulations to examine the impact of tuning parameters and prior assumptions on model performance. Our current approach to missing values is to perform imputation prior to modeling; however, we are considering adjusting our method to deal with missing values as these are common in realistic data analysis contexts. In this study our models were built on 6400 genes and 310 metagenes; it is possible that information from normal tissue samples could be employed to perform further variable selection. Finally, although some progress has been made in developing stochastic simulation methods for Bayesian trees [54] the topic remains a very challenging research area, both conceptually and computationally, particularly in the context of more than a few predictors. We believe that in problems where the numbers of predictors is very large, properly addressing the issue of stochastic search will involve the development of a formal, conceptual foundation before making them practicable. The development of such ideas is a focus of our current research.