Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1999 Dec 7;96(25):14611–14616. doi: 10.1073/pnas.96.25.14611

Horizontal cells reveal cone type-specific adaptation in primate retina

Barry B Lee *, Dennis M Dacey †,‡, Vivianne C Smith §, Joel Pokorny §
PMCID: PMC24484  PMID: 10588753

Abstract

The human cone visual system maintains contrast sensitivity over a wide range of ambient illumination, a property known as light adaptation. The first stage in light adaptation is believed to take place at the first neural step in vision, within the long, middle, and short wavelength sensitive cone photoreceptors. To determine the properties of adaptation in primate outer retina, we measured cone signals in second-order interneurons, the horizontal cells, of the macaque monkey. Horizontal cells provide a unique site for studying early adaptational mechanisms; they are but one synapse away from the photoreceptors, and each horizontal cell receives excitatory inputs from many cones. Light adaptation occurred over the entire range of light levels evaluated, a luminance range of 15–1,850 trolands. Adaptation was demonstrated to be independent in each cone type and to be spatially restricted. Thus, in primates, a major source of sensitivity regulation occurs before summation of cone signals in the horizontal cell.

The human cone photoreceptor pathways are capable of maintaining contrast sensitivity to small changes in illumination over a 6-log-unit range, from absolute threshold [near 1 troland (td) for a foveal brief pulse] to a level at which most of the photopigment has been isomerized (6 million tds) (1). From absolute threshold to 10 tds, sensitivity regulation is minimal. From 10 to 5,000 tds, neural mechanisms maintain sensitivity regulation, whereas above 5,000 tds photopigment depletion resulting from bleaching becomes an important regulatory factor. Psychophysical measurements are consistent with some degree of sensitivity regulation in the cone photoreceptors (2, 3) and with the spatial extent of adaptation being restricted to the dimensions of a single cone (4). The human data thus suggest that there is a hierarchical distribution of light adaptation, with a significant portion occurring in the cones themselves before their signals are pooled by higher-order retinal neurons. Yet, recordings of both isolated primate cones (5) and the human electroretinogram (6) have found that cone sensitivity regulation appears only at light levels ≈100-fold higher than is observed psychophysically, suggesting that a major part of adaptation occurs after cone signals converge onto higher-order neurons. Here we reassess the degree, spatial extent, and type specificity of cone light adaptation in this critical illuminance range (10–5,000 tds) by recording cone signals in second-order interneurons, the horizontal cells, by using an in vitro preparation of the macaque monkey retina (7).

In macaque retina the long (L), middle (M), and short (S) wavelength sensitive cone signals are transmitted in parallel to two populations of horizontal cells (7). HI horizontal cells receive an excitatory input from L- and M-cones, but lack a significant input from S-cones. HII horizontal cells are excited by all three cone types, with the S-cones providing a particularly strong input. The HI and HII horizontal cell types each form an electrically coupled network with receptive field diameters much larger than the dendritic field size of a single horizontal cell, effectively summing input from hundreds of cones (8). The major horizontal cell output in nonmammalian retina is believed to be inhibitory synaptic feedback to the cones (9–11). Our strategy was to measure the degree of adaptation in cone signals and to test whether cone signals adapt independently before combining at the level of the horizontal cells. We reasoned that if significant light adaptation occurred via feedback or after the cone–horizontal cell synapse, then modulating the excitation level of one cone type would alter the sensitivity of all excited cones in the horizontal cell receptive field. Similarly, modulating the cone excitation in one part of the receptive field should affect the sensitivity of cones excited in other parts of the receptive field. Alternatively, if sensitivity regulation of the cone signals occurs at or before the synapse, as suggested by human psychophysical data, it would be cone type-specific and spatially restricted. We applied a stimulus paradigm in which a continuous test probe was superimposed on a modulated background. This permitted direct assay of adaptation and cone signal interaction in the horizontal cells. Our results show spatially restricted and cone type-specific adaptation over a broad illuminance range, in general agreement with the conclusions of psychophysical studies in human.

Materials and Methods

In Vitro Preparation and Histology.

Eyes from macaque (Macaca nemestrina or Macaca fascicularis) were enucleated immediately after euthanasia. The intact retina-pigment epithelium-choroid was dissected free of the eyecup in oxygenated Ames medium and mounted in a superfusion chamber on the stage of a light microscope. Temperature was maintained in the chamber at 36° ± 1°C and continuously superfused at ≈5 ml/min. 4′,6-Diamidino-2-phenylindole (DAPI) staining of HI and HII cell nuclei was achieved by incubating the eyecup before retinal dissection for ≈20 min in Ames medium, to which DAPI was added at a concentration of ≈10 mM. Intracellular penetrations were made under direct visual control with high-resistance micropipettes, and light responses were recorded in conventional bridge mode. The recorded cells were observed directly during recording by iontophoretically injecting the fluorescent dye pyranine. At the termination of recording, cells were preserved for later analysis by injection of Neurobiotin and subsequent horseradish peroxidase histochemistry (7, 12).

Light Stimulation.

The stimuli originated from light-emitting diodes (LEDs) with dominant wavelengths of 638, 559, and 462 nm and half-height band widths of 35, 40, and 60 nm, respectively. The LED outputs were under computer control (13) and were combined and projected through the camera port of the microscope to form a homogeneous field up to 10° in diameter on the vitreal surface of the retina. The LEDs were set to have equal luminance and modulated temporally in sinusoidal alternation. The irradiance and spectral composition of the light impinging on the retina was measured for each LED in the plane of the retina by means of a Gamma Scientific spectroradiometer (St. Louis). The mean quanta/sec per μm2 at the retinal surface for the LED outputs at the maximal average luminance were calculated to be 572,642 for the 638-nm LED, 42,415 for the 559-nm LED, and 185,935 for the 462-nm LED. For comparison with human observer data we converted our light levels to equivalent tds (14). The td equivalence for a human observer for this level of quantal stimulation at the flattened retinal surface of our preparation must be reduced to take into account the Stiles–Crawford effect (15). An upper estimate of the effective td equivalence is ≈500 tds for each LED.

In experiment 1 we investigated the effect of luminance variation on H1 horizontal cells’ responsivity. The 638- and 559-nm LEDs were modulated in-phase with matched Michelson contrast (LMAX − LMIN)/(LMAX + LMIN). The average illuminance was 1,000 tds and was of a chromaticity equivalent to 595-nm light. The stimulus was composed of two temporal sinusoids: a low-frequency (0.61 Hz), high-amplitude waveform, which modulated between 150 and 1,850 tds (the vehicle wave), and a high-frequency (19.52 Hz), low-amplitude (±150 tds) waveform (the test wave) (Fig. 1a). Thus, for the combined stimulus, the light level varied between 0 td when both were at their minima and 2,000 tds when both vehicle and test were at their maxima. The vehicle and test waves were 5° in diameter and spatially coextensive. The level of cone excitation was varied by the vehicle wave between 150 and 1,850 tds, and response amplitude was measured by the test wave. We chose 0.61 Hz for the vehicle wave because retinal ganglion cells show sensitivity regulation to variation in illuminance within a few tens of milliseconds (16). We chose 19.52 Hz for the test wave because horizontal cell temporal contrast sensitivity is similar at 0.61 and 19.52 Hz, indicating that sensitivity regulation can be assessed at this test wave frequency. Lower illuminances were obtained with neutral density filters, giving vehicle modulation ranges of 15–185 tds and 1.5–18.5 tds.

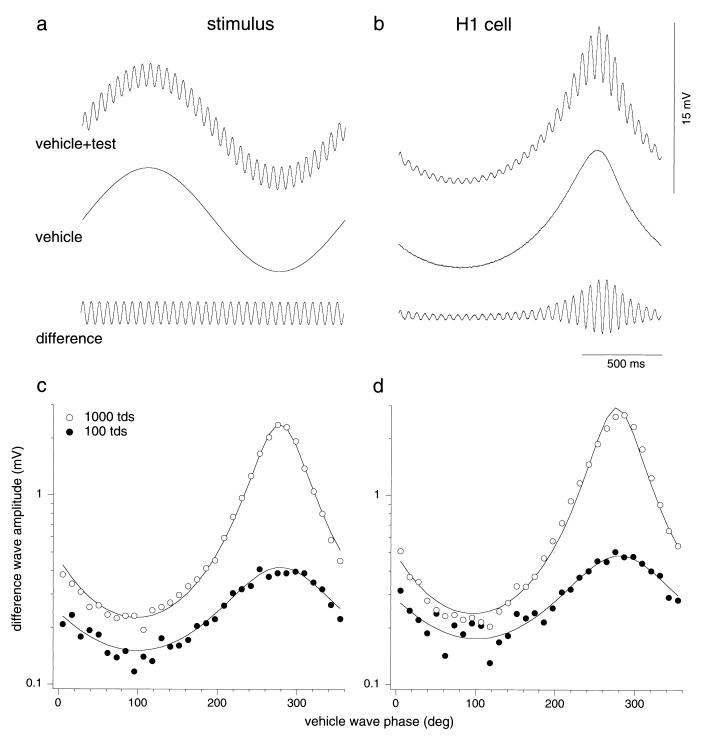
Figure 1.

Figure 1

Open in a new tab

(a) The light stimulus applied to the retina was a temporal waveform (Top) created by adding a high-frequency (19.52-Hz), low-amplitude test wave (Bottom) to a low-frequency (0.61-Hz), high-amplitude vehicle wave (Middle). Mean illuminance was 1,000 tds, and the contrast of the vehicle wave was 0.85. (b) HI horizontal cell response to luminance stimuli (5° field). (Top) Combined-wave response. (Middle) Response to vehicle wave alone. (Bottom) The difference wave obtained by subtraction. The test response varied with vehicle-wave phase. (c) First-harmonic amplitude of each cycle of the difference-wave response shown in b is plotted against vehicle-wave phase at 1,000 tds (○) and 100 tds (●). Solid lines show fit of the data by the inverse sine equation r = A/(BCsin(ΦM + Φlag) + 1), where ΦM is the vehicle-wave phase and C is vehicle-wave contrast. Free parameters are A, which is an overall scaling parameter, B, which scales the sine wave amplitude and is a measure of the degree of adaptation, and Φlag, representing an adaptation delay. (d) Equivalent data for a second H1 cell. At 1,000 tds the mean value of B was 0.77 (n = 32, SD = 0.14) and the mean Φlag corresponded to a delay of 41.4 msec (n = 32, SD = 0.14 msec). At 100 tds the mean value of B was 0.46 (n = 16, SD = 0.11) and the mean Φlag corresponded to a delay of 59.0 msec (n = 16, SD = 0.33 msec). In separate experiments, test amplitude was found to be linearly related to contrast over the range tested (not shown).

In experiment 2, we ran conditions designed to isolate the individual cone types (silent substitution) (17) in H1 and H2 horizontal cells. For H1 horizontal cells, the 638- and 559-nm LEDs were run in counterphase with their contrasts adjusted to excite only one cone type. The time-average stimulus was equivalent to the steady-state stimulus of experiment 1. The relative LED modulations required for the cone isolation conditions (17, 18) were calculated from the Smith–Pokorny cone fundamentals (7, 19), corrected for preretinal filtering by using tabulations in Wyszecki and Stiles (14). For selective L-cone modulation, contrast of the 559-nm LED was reduced to 0.167. The maximum Michelson contrast for the L-cone stimulus was 0.53. For selective M-cone modulation, the contrast of the 638-nm LED was reduced to 0.667. The maximum Michelson contrast for the M-cone stimulus was 0.74.

For study of H2 horizontal cells, all three LEDs were used; the average luminance increased to 1,370 tds (370 tds from 462-nm LED, 500 tds each from 559- and 638-nm LEDs). The time-average stimulus appeared pale blue (equivalent to 435 nm with colorimetric purity of 0.46). For selective S-cone modulation, the 462- and 638-nm LEDs were modulated in counterphase with the 559-nm LED; the 559-nm LED was modulated with a Michelson contrast of 1.00. The 462- and 638-nm LEDs were modulated with Michelson contrasts of 0.75 and 0.25, respectively. The maximum Michelson contrast for the S-cone stimulus was 0.85.

In experiment 3 we investigated the spatial spread of sensitivity control. A second channel with 638- and 559-nm LEDs was added to separate the spatial profiles of the vehicle (10° annulus) and test (1.5° spot) waves. The average illuminance was maintained at 1,000 tds.

Results

We first established the behavior of each cell on adaptation to changes in luminance. Responses when both vehicle wave and test wave were modulated in luminance (L- and M-cones excited in phase; mean luminance, 1,000 tds) are shown in Fig. 1. Fig. 1a shows the stimulus waveforms and Fig. 1b shows the response to both vehicle and test waves and to the vehicle wave alone. The response to the test wave showed a minimum (Fig. 1b, Top) close to the peak of the vehicle wave; note that light hyperpolarizes HI cells. This occurred in all cells tested (n = 32). The response to the vehicle wave alone (Fig. 1b, Middle) was subtracted from the combined response to give a difference wave (Fig. 1b, Bottom). The first-harmonic amplitude of each test cycle in the difference wave was plotted as a function of vehicle-wave phase in Fig. 1c, which also shows data obtained at an average luminance of 100 tds. The plot shows that, with luminance modulation, a clear effect on the sensitivity to the high frequency test wave is observed, with a small delay relative to the vehicle wave. The data have been fitted with an empirical function defined in the figure legend. Fig. 1d shows a comparable result from a second cell. Both cells show a large modulation in the difference wave at 1,000 tds. At 100 tds, there was still some modulation in the difference wave. At 10 tds, test response amplitudes were too small to yield reliable measurements. Although cells varied in absolute response amplitude, they showed similar behavior. Weber’s law was not achieved in the horizontal cell. As an estimate of the degree of adaptation, we took the average ratio of maximum to minimum test response. This was 6.67 (n = 32, SD = 2.27) when illuminance changed by a factor of 12.3 (from 150 to 1,850 tds) in the combined waveform. Weber’s law would have been obtained if these factors had been equal, but this was not the case.

We also performed control experiments by measuring test responses with a 9.7-Hz test wave and under steady-state conditions (equivalent to a very low vehicle-wave frequency). Test response amplitudes were similar to those obtained under the conditions in Fig. 1. We conclude that the results of Fig. 1 are robust and that use of the sine-wave vehicle provided a valid indication of sensitivity regulation.

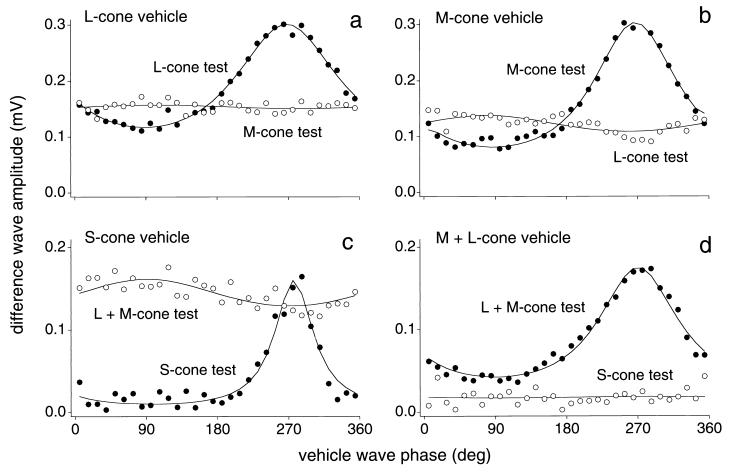
Our second goal was to perform the critical test for cone type-specific adaptation, when vehicle and test waves modulate different cone types. For an L-cone vehicle-wave, L-cone test-wave condition (Fig. 2a), the results were similar to those of Fig. 1b, though the response amplitudes were smaller because only one cone type was modulated. When the L-cone vehicle wave was paired with an M-cone test, however, the M-cone test response did not vary with L-cone modulation (Figs. 2b and 3a). First-harmonic amplitudes for the converse condition, M-cone modulation with M- and L-cone tests, gave a parallel result: the M-cone test response was dependent on the M-cone vehicle-wave phase whereas the L-cone test response was unaffected by M-cone modulation (Fig. 3b). The same result was found in all (n = 8) H1 horizontal cells tested. In an H2 horizontal cell, cone type-specific adaptation also was observed (Fig. 3c). There was, however, some indication of an inverse effect of the S-cone vehicle wave on the (L+M)-cone test response (Fig. 3c); there was an increase in the (L+M) response when S-cone excitation was high. A small, inverse effect also was found with two of the eight H1 cells studied with L- and M-cone-specific waves. One possible explanation for this effect in the cross-cone conditions is that there is some shunting in the parallel conductances within the cone pedicles for the different cones.

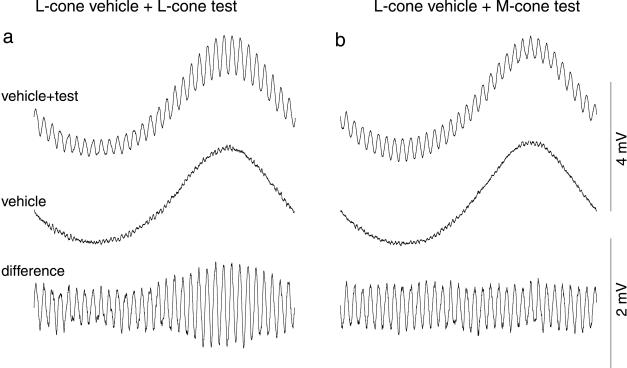
Figure 2.

Figure 2

Open in a new tab

Voltage responses of an HI horizontal cell to cone isolating stimuli (mean illuminance, 1,000 tds; 5° field as in Fig. 1). LED contrasts for cone-isolating conditions are given in Materials and Methods. (a) Same-cone condition: an L-cone-modulating vehicle wave was added to an L-cone-modulating test wave. Difference wave (bottom trace) shows that L-cone modulation affected response amplitude to L-cone test wave. (b) Cross-cone condition: an M-cone-isolating test wave was added to the L-cone-isolating vehicle wave. In this condition amplitude of the response to the M-cone test was not changed by the L-cone vehicle wave (see also Fig. 3a).

Figure 3.

Figure 3

Open in a new tab

HI and HII horizontal cell voltage response amplitudes to cone-isolating test waves plotted as a function of vehicle-wave phase (mean illuminance, 1,000 tds; 5° field). (a and b) Responses of an HI horizontal cell to cone-specific modulation. (a) L-cone vehicle-wave condition: L-cone test response amplitude varied with vehicle-wave phase (●) but M-cone test response did not (○). (b) M-cone vehicle-wave condition: M-cone test response amplitude varied with vehicle-wave phase (●) but L-cone test response did not (○). (c and d) Responses of an HII horizontal cell to cone-specific modulation. (c) S-cone vehicle-wave condition: S-cone test response amplitude varied with vehicle-wave phase (●) but (L+M)-cone test response did not (○). (d) (L+M)-cone vehicle-wave condition: (L+M)-cone test response amplitude varied with vehicle-wave phase (●) but S-cone test response did not (○). Solid lines are fits of equation given in the legend to Fig. 1.

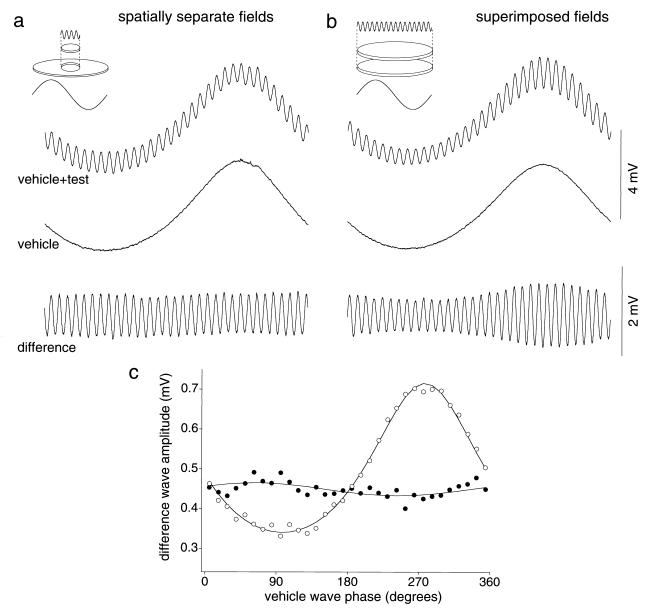
If there is no spread of adaptation from one cone type to another, one would predict a lack of spatial spread of adaptation. To study the spatial spread of cone signal adaptation, the test wave was delivered to a spot centered on the receptive field (300 μm, ≈1.5° visual angle) and the vehicle wave was delivered to a contiguous annulus around it (outer diameter = ≈2,000 μm, ≈10°). Receptive field sizes of horizontal cells at the eccentricity studied were ≈800 μm in diameter. When vehicle and test stimuli were spatially separated, the vehicle wave did not affect the test-wave response (Fig. 4a). As a control condition, we evaluated cell responses with superimposed fields after the contrast of the vehicle wave had been reduced to give a similar response amplitude as the annulus vehicle-wave response shown in Fig. 4a. There was a clear variation of test response amplitude (Fig. 4b), similar to that shown in Fig. 1b. The first harmonic test-wave amplitudes plotted as a function of vehicle-wave phase for the separate and superimposed conditions confirm the lack of spatial interaction across the HI horizontal cell receptive field (Fig. 4c); every cell studied (n = 7) showed this behavior.

Figure 4.

Figure 4

Open in a new tab

Test for spatial interaction between vehicle and test waves in the HI horizontal cell receptive field. (a) Spatially separate condition: when the test wave (100 td average, 1.00 contrast) was delivered to a central spot and the vehicle wave (900 td average, 0.90 contrast) was delivered to a contiguous, surrounding annulus (see Inset), the vehicle wave did not affect the test-wave response. (b) For the same cell, when vehicle and test waves are spatially superimposed, test response is modulated as in Fig. 1. Vehicle contrast was adjusted to give a similar response amplitude as in a (vehicle wave: 900 td average, 0.60 contrast). (c) First-harmonic test amplitudes for data of responses shown in a (●) and b (○). Solid lines are fits of the equation given in the legend to Fig. 1.

Discussion

We found adaptation in primate horizontal cells to be cone-specific and spatially local at 1,000 tds. This finding is in agreement with the psychophysical measurements discussed above, indicating that human light adaptation is spatially restricted to the dimensions of a single cone (4). In mammals other than the primate, physiological data on outer retinal adaptation are largely restricted to the experiments of Lankheet et al. (20, 21) in the intact cat eye. Although the basic properties of cat horizontal cells were similar to those we have measured in primates, adaptation was not found to be spatially local. The authors evaluated the spatial summation of adaptation by using both overlapping and nonoverlapping background and test light configurations. In the nonoverlapping configuration, background light falling outside the test light region modulated horizontal cell responses to the test light. This finding would suggest that multiplicative feedback may play a role in sensitivity regulation in this animal, although Lankheet et al. (21) did recognize that their results were in potential conflict with human psychophysical data. If optical artifacts in the intact cat eye can be ruled out, the only alternative explanation would be a difference between cat and primate cone light adaptation.

Cone type-specific and spatially local adaptation also has not been seen in horizontal cells of teleost fish and other nonmammals. Horizontal cells in these species provide a GABAergic inhibitory feedback to cones (9) that can spread through the coupled horizontal cell network so that one cone can influence its neighbors and create an inhibitory receptive field surround in the cones themselves (22). Inhibitory interactions across cone types can lead to spectral opponency in nonmammalian horizontal cells: they are hyperpolarized by light of some wavelengths and depolarized by light from other regions of the spectrum (23). Both multiplicative (24) and subtractive (25, 26) feedback have been proposed to mediate these interactions. Elsewhere, we have shown that primate horizontal cells do not show spectral opponency (8). Our results here constrain the role of feedback in primate outer retina, suggesting that a multiplicative cone–horizontal cell feedback is not operative.

In our data, sensitivity regulation is activated at 100 tds or less, in agreement with measurements of primate mass cone recordings (27). In addition, recent whole-cell photovoltage measurements made from cones in intact retinal pieces yield estimates of ≈640 tds for onset of cone adaptation (28), with considerable intercell variability. Sensitivity regulation in the most sensitive cells was close to the least sensitive H1 horizontal cells we measured. By contrast, photocurrent studies in isolated primate photoreceptors did not find evidence for sensitivity regulation below an estimated 2,000 tds (5). The preparations used for cone photocurrent and photovoltage measurements remain reduced from the in vivo state. The in vitro preparation used in the present study attempts to more closely mimic the in vivo condition: the retina is maintained in contact with the retinal pigment epithelium and choroid and is visually responsive at high photopic levels under continuous illumination for many hours. It thus is possible that the differences in the amount of primate cone adaptation measured physiologically may reflect the various preparations used.

In the illumination range tested, sensitivity regulation in outer retina was not complete, falling short of Weber’s Law. Weber’s law is observed at the retinal ganglion cell level in the magnocellular pathway (29, 30), implying adaptational mechanisms beyond the cone that may extend further the adaptational range. The concept of multiple stages of sensitivity regulation in postreceptoral pathways is well established in the psychophysical literature (1, 31–33). The in vitro preparation of the intact retina provides an ideal tool for studying sensitivity regulation at other points in the retinal circuitry. Specifically, it will be important to measure sensitivity regulation in bipolar cells, which provide a direct link between the photoreceptors and the ganglion cells.

Acknowledgments

We are especially grateful to Toni Haun and Keith Boro for technical assistance, Beth Peterson for editorial assistance and assistance preparing the figures, and Helen Sherk, Steve Shevell, and Brian Wandell for their comments. We thank the Regional Primate Center at the University of Washington for primate tissue. This work was supported by grants from The National Eye Institute (EY00901 and EY06678), the National Institutes of Health to the Regional Primate Center at the University of Washington, and the Deutsche Forschungsgemeinschaft (Le524/12-2).

Abbreviations

td

troland (104 cd·m−2)

L

long

M

middle

S

short

LED

light-emitting diode

Footnotes

This paper was submitted directly (Track II) to the PNAS office.

References

  • 1.Hood D C, Finkelstein M A. In: Handbook of Perception and Human Performance. Boff K R, Kaufamn L, Thomas J P, editors. Vol. 1. New York: Wiley; 1986. pp. 1–66. [Google Scholar]
  • 2.Stiles W S. Doc Ophthalmol. 1949;3:138–165. doi: 10.1007/BF00162601. [DOI] [PubMed] [Google Scholar]
  • 3.Stockman A, Mollon J. Perception. 1986;15:729–754. doi: 10.1068/p150729. [DOI] [PubMed] [Google Scholar]
  • 4.MacLeod D I A, Williams D R, Makous W. Vision Res. 1992;32:347–363. doi: 10.1016/0042-6989(92)90144-8. [DOI] [PubMed] [Google Scholar]
  • 5.Schnapf J L, Nunn B J, Meister M, Baylor D A. J Physiol (London) 1990;427:681–713. doi: 10.1113/jphysiol.1990.sp018193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Hood D C, Birch D G. Visual Neurosci. 1993;10:857–871. doi: 10.1017/s0952523800006076. [DOI] [PubMed] [Google Scholar]
  • 7.Dacey D M, Lee B B, Stafford D K, Pokorny J, Smith V C. Science. 1996;271:656–659. doi: 10.1126/science.271.5249.656. [DOI] [PubMed] [Google Scholar]
  • 8.Dacey D M, Lee B B. In: Color Vision: From Molecular Genetics to Perception. Gegenfurtner K, Sharpe L T, editors. Cambridge, U.K.: Cambridge Univ. Press; 1999. pp. 181–202. [Google Scholar]
  • 9.Wu S M. Curr Opin Neurobiol. 1992;2:462–468. doi: 10.1016/0959-4388(92)90181-j. [DOI] [PubMed] [Google Scholar]
  • 10.Burkhardt D A. Visual Neurosci. 1993;10:981–989. doi: 10.1017/s0952523800010087. [DOI] [PubMed] [Google Scholar]
  • 11.Vardi M A. Vision Res. 1998;38:1359–1369. doi: 10.1016/s0042-6989(98)00007-8. [DOI] [PubMed] [Google Scholar]
  • 12.Dacey D M, Lee B B. Nature (London) 1994;367:731–735. doi: 10.1038/367731a0. [DOI] [PubMed] [Google Scholar]
  • 13.Swanson W H, Ueno T, Smith V C, Pokorny J. J Opt Soc Am. 1987;4:1992–2005. doi: 10.1364/josaa.4.001992. [DOI] [PubMed] [Google Scholar]
  • 14.Wyszecki G, Stiles W S. Color Science: Concepts and Methods, Quantitative Data and Formulae. 2nd Ed. New York: Wiley; 1982. [Google Scholar]
  • 15.Wijngaard W, van Krusbergen J. In: Photoreceptor Optics. Snyder W, Menzel R, editors. Berlin: Springer; 1975. pp. 175–183. [Google Scholar]
  • 16.Yeh T, Lee B B, Kremers J. Vision Res. 1996;36:913–931. doi: 10.1016/0042-6989(95)00332-0. [DOI] [PubMed] [Google Scholar]
  • 17.Estévez O, Spekreijse H. Vision Res. 1982;22:681–691. doi: 10.1016/0042-6989(82)90104-3. [DOI] [PubMed] [Google Scholar]
  • 18.Smith V C, Pokorny J, Davis M, Yeh T. J Opt Soc Am. 1995;12:241–249. doi: 10.1364/josaa.12.000241. [DOI] [PubMed] [Google Scholar]
  • 19.Smith V C, Pokorny J. Vision Res. 1975;15:161–171. doi: 10.1016/0042-6989(75)90203-5. [DOI] [PubMed] [Google Scholar]
  • 20.Lankheet J M, van Wezel R J A, Prickaerts J H H J, van de Grind W A. Vision Res. 1993;33:1153–1171. doi: 10.1016/0042-6989(93)90205-b. [DOI] [PubMed] [Google Scholar]
  • 21.Lankheet J M, Przybyszewski A W, van de Grind W A. Vision Res. 1993;33:1173–1184. doi: 10.1016/0042-6989(93)90206-c. [DOI] [PubMed] [Google Scholar]
  • 22.Baylor D A, Fuortes M G F, O’Bryan P M. J Physiol (London) 1971;214:265–294. doi: 10.1113/jphysiol.1971.sp009432. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Kamermans M, Spekreijse H. Prog Retinal Eye Res. 1995;14:313–360. [Google Scholar]
  • 24.Kamermans M, Kraaij D A, Spekreijse H. Visual Neurosci. 1998;15:787–797. doi: 10.1017/s0952523898154172. [DOI] [PubMed] [Google Scholar]
  • 25.Burkhardt D A. Visual Neurosci. 1995;12:877–885. doi: 10.1017/s0952523800009433. [DOI] [PubMed] [Google Scholar]
  • 26.Shiells R, Falk G. Prog Retinal Eye Res. 1995;14:223–247. [Google Scholar]
  • 27.Valeton J M, van Norren D V. Vision Res. 1983;23:1539–1547. doi: 10.1016/0042-6989(83)90167-0. [DOI] [PubMed] [Google Scholar]
  • 28.Schneeweis D M, Schnapf J L. J Neurosci. 1999;19:1203–1216. doi: 10.1523/JNEUROSCI.19-04-01203.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Lee B B, Pokorny J, Smith V C, Martin P R, Valberg A. J Opt Soc Am A. 1990;7:2223–2236. doi: 10.1364/josaa.7.002223. [DOI] [PubMed] [Google Scholar]
  • 30.Yeh T, Lee B B, Kremers J. J Opt Soc Am A. 1995;12:456–464. doi: 10.1364/josaa.12.000456. [DOI] [PubMed] [Google Scholar]
  • 31.Hayhoe M, Benimoff N I, Hood D C. Vision Res. 1987;27:1981–1996. doi: 10.1016/0042-6989(87)90062-9. [DOI] [PubMed] [Google Scholar]
  • 32.Mollon J D, Polden P G. Philos Trans R Soc London B. 1977;278:207–240. doi: 10.1098/rstb.1977.0038. [DOI] [PubMed] [Google Scholar]
  • 33.Pugh E N J, Mollon J D. Vision Res. 1979;19:293–312. doi: 10.1016/0042-6989(79)90175-5. [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES