Probing concerted proton–electron transfer in phenol–imidazoles

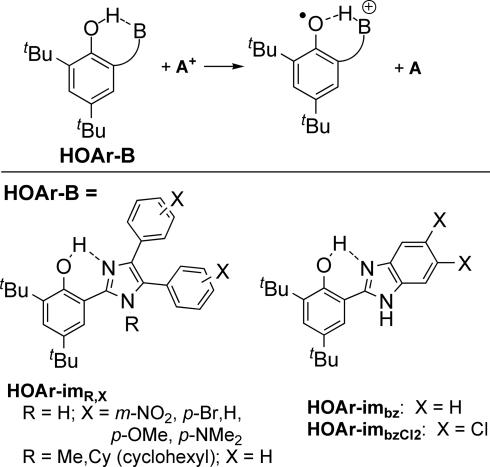
Abstract

A series of seven substituted 4,6-di-tert-butyl-2-(4,5-diarylimidazolyl)-phenols have been prepared and characterized, along with two related benzimidazole compounds. X-ray crystal structures of all of the compounds show that the phenol and imidazole rings are close to coplanar and are connected by an intramolecular ArOH⋯N hydrogen bond. One-electron oxidation of these compounds occurs with movement of the phenolic proton to the imidazole base by concerted proton–electron transfer (CPET) to yield fairly stable distonic radical cations. These phenol–base compounds are a valuable system in which to examine the key features of CPET. Kinetic measurements of bimolecular CPET oxidations, with E_rxn between +0.04 and −0.33 V, give rate constants from (6.3 ± 0.6) × 10² to (3.0 ± 0.6) × 10⁶ M⁻¹ s⁻¹. There is a good correlation of log(k) with ΔG°, with only one of the 15 rate constants falling more than a factor of 5.2 from the correlation line. Substituents on the imidazole affect the (O–H⋯N) hydrogen bond, as marked by variations in the ¹H NMR and calculated vibrational spectra and geometries. Crystallographic d_O⋯N values appear to be more strongly affected by crystal packing forces. However, there is almost no correlation of rate constants with any of these measured or computed parameters. Over this range of compounds from the same structural family, the dominant contributor to the differences in rate constant is the driving force ΔG°.

Reactive oxygen species (ROS) exhibit a wide range of reactivity, from the extraordinarily potent hydroxyl radical to much more inert aryloxyl and ascorbyl radicals. These species are sometimes categorized by their redox potentials at pH 7, but most reactions of ROS do not proceed by simple electron transfer (ET). Typically, ROS react by proton-coupled electron transfer (PCET), as in the disproportionation of hydrogen peroxide to dioxygen and water and the interconversions of tyrosyl radicals and tyrosine residues. Understanding the detailed mechanisms of these and other PCET processes is of significant current interest (1–3).

PCET in some contexts has come to include any overall process in which both electrons and protons are transferred. Such reactions can proceed by a series of simple ET and proton transfer (PT) steps (e.g., ET-PT or PT-ET). H⁺ and e⁻ can also transfer in a single kinetic step by concerted proton-electron transfer (CPET). When the e⁻ and H⁺ transfer together from a donor to an acceptor, the reaction is often called hydrogen atom transfer (2). Alternatively, the e⁻ and H⁺ could come from, or transfer to, different molecules, which we have termed separated CPET. This report examines separated-CPET reactions of phenol–imidazole compounds to give phenoxyl radicals (Scheme 1; A⁺ is a one-electron acceptor, B is a pendant base).

Scheme 1.

Concerted proton–electron transfer in phenol–base compounds (A⁺ = oxidant).

Understanding the fundamental properties of CPET provides insight to the chemistry of ROS and other biochemical processes. The interconversion of phenols and phenoxyls is of particular interest because of the wide importance of tyrosyl radicals (4) and the antioxidant ability of vitamin E (tocopherol) (5). The redox cycling of tyrosine Z (Tyr_ZOH/Tyr_ZO^•) in Photosystem II has received particular attention. Tyr_ZOH is oxidized by long-range electron transfer to a photoexcited chlorophyll (P₆₈₀⁺), with the proton likely transferred to the imidazole moiety of a nearby histidine (H₁₉₀) (6). Tyr_ZO^• is converted back to Tyr_ZOH by accepting H⁺ and e⁻, the latter from the oxidation of water to O₂ by the oxygen-evolving complex. These processes likely proceed by separated CPET, with the e⁻ and H⁺ transferring in a single kinetic step involving multiple sites (6).

Model studies of tyrosine oxidations in our lab and others have concluded that e⁻ and H⁺ movement occurs in a single kinetic step (separated CPET), whether the proton is transferred to bulk aqueous solution (7) or to a base in an aprotic solvent (8, 9). Our studies have focused on CPET in phenols with the H⁺ transferring to a pendant hydrogen-bonded base, HOAr-B (Scheme 1, HOAr = 2,4-di-tert-butylphenol-6-yl), which provides a well defined, intramolecular proton transfer coordinate (9). This work has included compounds in which B is a primary amine (–CPh₂NH₂), a 2′-pyridyl (py), or a 2′-imidazolyl moiety. In our systems, the CPET pathway is indicated because: (i) the potential phenol radical cation intermediate that would be involved in an ET-PT mechanism, and the zwitterionic intermediate in PT-ET, are too high in energy; (ii) the dependence of the energetic barrier on the driving force (ΔΔG^‡/ΔΔG°) is ≈0.5, as expected only for CPET; and (iii) primary k_OH/k_OD kinetic isotope effects of 1.6–2.8 are observed (9).

There is a great deal of ongoing theoretical work on the appropriate description of CPET (10–15). It is generally accepted that the proton must be treated quantum mechanically, which, in many if not all cases, tunnels through an energetic barrier as the system crosses from reactant to product surfaces. Because this tunneling is very sensitive to the distance the proton moves, CPET reactions have been a valuable probe of protein motions and their relationship to enzyme catalysis (16–18). A complete description of CPET is beyond the scope of this report—and at the moment beyond the ability of an experimental study to define. A more experimentally accessible first approximation, adapted from a recent review by Klinman (18), gives the rate constant as a product of an electronic coupling, a Frank–Condon term, and an exponential term (Eq. 1).

The exponential term resembles the exponential portion of the Marcus equation for ET, in which the potential energy surface is described as a quadratic function of the reaction driving force ΔG° and the intrinsic barrier λ. V^el is an effective electronic coupling, describing how strongly the electronic surfaces interact (sometimes given as H_RP²). The Frank–Condon term FC gives the probability of proton tunneling, integrated over the Boltzmann-weighted distribution of donor–acceptor distances. FC is quite sensitive to the proton vibrational frequency and the energy to modulate the donor–acceptor distance, and therefore the tunneling distance. More complete treatments include a sum over initial and final vibrational states, where ΔG°, λ, and the proton vibrational frequency all vary with the vibrational state (10–18).

The experiments described here use a series of phenol–imidazole compounds (Scheme 1) to probe the relative importance of the various parameters that affect CPET. These compounds can be considered approximate models for the Tyr_Z-His₁₉₀ cofactor in photosystem II. HOAr-im_H,H, HOAr-im_H,OMe, and HOAr-im_bz have been described by Benisvy et al. (19–21). We have reported the kinetics of oxidation of HOAr-im_H,OMe, together with related phenol–pyridine and phenol–amine compounds, HOAr-py and HOAr-CPh₂NH₂ (9). In the series of imidazole compounds described here, the different substituents modulate the intramolecular proton-transfer coordinate in ways that can be spectroscopically and structurally well defined. Although it is not possible in this (or any system) to measure all of the CPET parameters, we can vary the driving force ΔG° and, collectively, the set of parameters that define the Frank–Condon term FC. In essence, FC depends on the structure, the flexibility of the structure, and the nature of the hydrogen bond. In this report, the kinetics of CPET is correlated with changes in the thermodynamics and the chemical environment of the transferring proton. This study is part of a broad experimental survey of similar compounds that is providing insights into the relative importance of the parameters that affect CPET reactivity.

Results

Synthesis and Characterization of Phenol–Imidazoles (HOAr-im).

The 2,4-di-tert-butyl-phenol–imidazole compounds HOAr-im_R,X all have two aryl groups on the imidazole, with the subscript X indicating a substituent on these rings (Scheme 1). These were prepared by condensation between 3,5-di-tert-butyl-2-hydroxybenzaldehyde and the corresponding benzil by using formamide or ammonium acetate in acetic acid [see supporting information (SI) Appendix]. The N-cyclohexyl-imidazole derivative HOAr-im_Cy,H (Cy = cyclohexyl) was prepared analogously by using the N-cyclohexylimine of benzil (22), and the N-methyl compound was synthesized by alkylation of HOAr-im_H,H with CH₃I, employing KOH in acetonitrile. The benzimidazole compounds, HOAr-im_bz and HOAr-im_bzCl2 were prepared by condensation of the benzaldehyde with 1,2-diaminobenzenes and subsequent oxidation with 1,4-benzoquinone (23).

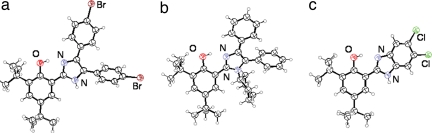
Crystal structures for all of the compounds have been determined by us or by Benisvy (20, 24); representative examples are shown in Fig. 1(see SI Appendix for other ORTEPs and all crystallographic details). The phenol-1H-imidazole moieties are all close to planar, with torsion angles between the phenol and imidazole rings of ≤16° except for HOAr-im_H,OMe (23°) (9). Each 1H-imidazole and benzimidazole compound has a solvent molecule hydrogen bonded to the imidazole NH, except for Benisvy's structure of HOAr-im_H,OMe (for which the crystals were grown from CH₂Cl₂/hexane) and one molecule in the unit cells of HOAr-im_bz·½H₂O (24). No solvent is present in the unit cell of the N-alkylated compounds. The phenolic protons were located in difference maps and refined isotropically.

Fig. 1.

ORTEP drawings of phenol molecules in the crystal structures of HOAr-im_H,Br·MeCN (a), HOAr-im_Cy,H (b), and HOAr-im_bzCl2·H₂O (c). Thermal ellipsoids are drawn at 50% probability.

All of the structures have an intramolecular O–H⋯N hydrogen bond involving the proton that transfers on oxidation (Scheme 1). These are strong hydrogen bonds based on the fairly short oxygen–nitrogen distances (d_O⋯N = 2.533 (2)–2.646 (2) Å; Table 1) (25). This key O⋯N distance varies by 0.11 Å over these structures, with little apparent pattern. The same d_O⋯N of 2.596 ± 0.007 Å is found for HOAr-im_H,X with X = H, Br, NMe₂, and NO₂, all of which have a solvent of crystallization. However, the two structures of HOAr-im_H,OMe have longer distances, 2.609(2) in Benisvy's unsolvated structure (24), and the much longer 2.646(2) Å in our structure with a methanol H-bonded to the imidazole NH. However, the same d_O⋯N values within error are found for acetone-bound HOAr-im_H,H and unsolvated HOAr-im_Me,H. When R is a much bulkier cyclohexyl group in HOAr-im_Cy,H the d_O⋯N [2.6065(16) and 2.6373(16) Å for the two molecules in the unit cell], is increased by 0.01–0.04 Å and the inter-ring torsion angle is increased from 26(2)° to 34(2)°. The shortest distances are observed in the structures of HOAr-im_bz, with d_O⋯N = 2.533(3)–2.6087(19) (average = 2.56 Å) for the total of four independent molecules in Benisvy's structure (24) and our own. Here, it is the unsolvated molecule of HOAr-im_bz·½H₂O (24), which has the longest distance. The 0.076(3) Å range of d_O⋯N between molecules of HOAr-im_bz illustrates that this distance is relatively pliable and can be affected by crystal packing forces. These data indicate that the crystallographic d_O⋯N values, although well determined, are not an accurate measure of the average O⋯N distance in solution where the reaction chemistry occurs. According to Krishtalik, rates of H tunneling decay with distance with a characteristic scale of ≈0.03 Å (k ≈ k₀e^{−Δd/0.03Å}) (15). This indicates one of the challenges of studying hydrogen transfer reactions: even with these structurally well characterized small molecules, the key distances are not easily measured.

Table 1.

Structural, spectroscopic, and thermochemical properties for HOAr-B

B	dO⋯N x-ray, Åa	dO⋯N calc, Åb	ν(OH)DFT,corr, cm−1c	δOH, ppmd	δNH, ppmd	E1/2, Ve	ΔEp, mVf
-imH,NO2	2.602(3)	2.637	3130	12.92	11.21	0.61	130
-imH,Br	2.597(4)	2.625	3073	13.11	10.97	0.55	99
-imH,H	2.596(2)g	2.621	3043	13.33	10.89	0.49	107
-imH,OMe	2.646(2)h,2.609(2)i	2.617	3022	13.42	10.77	0.42	112
-imH,NMe2	2.589(3)	2.612	2996	13.59	10.61	0.21,0.10	59,82
-imMe,H	2.597(3)	2.597	3010	12.72	NA	0.46	150
-imCy,H	2.6065,2.6373(16)	2.623	3071	11.61	NA	0.42	98
-imbz	2.533,2.547(2) 2.539,2.6087(19)i	2.603	2996	13.69	11.10	0.54	120
-imbzCl2	2.580(2)	2.611	3046	13.24	11.25	0.66	90

^aCrystallographic distance.

^bGeometry calculated at B3LYP/6-31G(d,p).

^cAccording to ref. 34, ν(OH)_DFT,corr = [ν(OH)_DFT − 159.5] · 0.9904.

^d1H NMR in dry CD₃CN.

^eReported vs. Cp₂Fe^+/0.

^fScan rate = 0.2 V·s⁻¹; see SI Appendix for cyclic voltammograms.

^gRef. 20.

^hRef. 9.

ⁱRef. 24.

Computed gas-phase structures, using density functional theory (DFT) B3LYP/6-31G(d,p) methodology (26), may be a better measure of the solution structures. These optimized O⋯N distances fall within range of the crystallographic values but show less variation (2.597–2.637Å; Table 1). There is little correlation between the crystallographic and DFT O⋯N distances (SI Fig. 4 in the SI Appendix), consistent with the importance of crystal packing in the solid-state structures. The DFT O⋯N distances for the five HOAr-im_H,X compounds do correlate with the Hammett σ parameters of the substituent X (SI Fig. 5 in the SI Appendix), with the more donating substituents leading to shorter d_O⋯N values as expected.

¹H NMR spectra of HOAr-im_R,X in dry, degassed CD₃CN show that the aromatic rings in the 4 and 5 positions of the imidazoles are inequivalent. Thus, imidazole rotation and proton transfer between imidazole nitrogens is slow on the NMR timescale, a result of the strong OH⋯N hydrogen bond. The OH resonances are sharp under these conditions; the NH resonances are slightly broader. The NH chemical shifts (Table 1) are more sensitive to trace amounts of water or polar solvents, because they engage in intermolecular hydrogen bonding (27). The δ_NH is more upfield with increasing electron density on the imidazole ring. The ¹H NMR spectra of the benzimidazole compounds follow the same pattern.

Substituent Effects on Hydrogen Bonding in Phenol–Imidazoles.

The chemical shift of the phenolic proton in these compounds (Table 1) is a measure of the proton chemical environment: the stronger the hydrogen bond, the more downfield the phenol OH chemical shift (28). Electron-donating substituents give larger δ(OH) values and thus, by this measure, strengthen the hydrogen bond. This is consistent with the general rule that AH⋯B hydrogen bonds are stronger when the acidity of A–H and B–H⁺ are similar. The pK_a values for free phenol and imidazolium in MeCN are 27 and 17 (29, 30), so electron-donating substituents make the imidazolium ion less acidic, closer to phenol, and therefore yield stronger H bonds. For the series HOAr-im_H,X a plot of δ(OH) vs. the Hammett parameter σ [a measure of substituent electronic effects (31)] is linear with ρ = 0.50 (R² = 0.97). The δ(OH) values also correlate well with the DFT-calculated d_O⋯N values. In contrast, N-alkylation of the imidazole shifts δ(OH) upfield, from 13.33 to 12.72 to 11.61 ppm for R = H, Me, Cy in HOAr-im_R,H, indicating weaker H bonds. This may reflect the larger inter-ring torsion angle for the alkylated derivatives or their lack of an N–H⋯solvent interaction (32). HOAr-im_bz has the most downfield δ(OH) in Table 1, despite the lower benzimidazolium pK_a of 14 (30), likely due to stabilization of the resonance-assisted hydrogen bond by the larger π system.

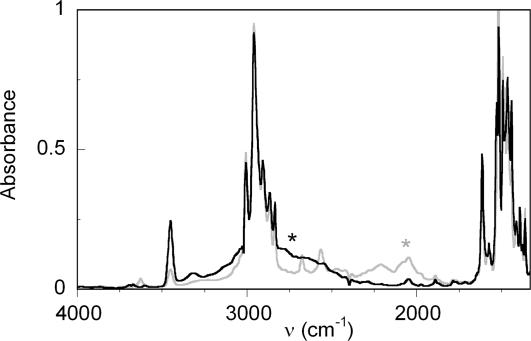
IR spectra of HOAr-im show strikingly broad, low-energy ν(OH) indicative of strong, resonance-assisted hydrogen bonds (25). The shape and structure of such bands have been extensively studied and are due to a complex interplay of anharmonic mixing with lower-energy modes (e.g., OH bending modes) and dynamical effects (33). In MeCN solution, ν(OH) for HOAr-im_bz has a maximum at ≈2,770 cm⁻¹ with a width (full width half-maximum) of ≈600 cm⁻¹ (SI Fig. 9 in the SI Appendix). In CHCl₃ solution, this band increases in intensity and the maximum is shifted into the CH stretching region at 2,800–3,025 cm⁻¹. For HOAr-im_R,X, limited solubilities preclude IR measurements in MeCN (the CPET reaction solvent). In CHCl₃, ν(OH) for HOAr-im_H,OMe is ≈2,900 cm⁻¹ (obscured by C–H stretches) with a width of ≈ 650 cm⁻¹, whereas the deutero analog has ν(OD) of ≈2,050 cm⁻¹ (Fig. 2). A much sharper band at 3,454 cm⁻¹ is assigned to ν_s(NH) [ν_s(ND) = 2,568 cm⁻¹]. Any shifts in ν(OH) as a function of substituent are unfortunately obscured by the extreme broadening of the band and its overlap with the C–H stretches.

Fig. 2.

Solution IR spectra of HOAr-im_H,OMe (black line) and DOAr-im_D,OMe (gray line) in CHCl₃. Asterisks indicate the approximate position of ν(OH/D).

The shifts in ν(OH) can perhaps be better analyzed computationally. Korth et al. have shown that for 26 2-substituted phenols with an intramolecular H bond, ν(OH) calculated at the B3LYP/6-31G(d,p) level of theory correlated well with experimental CCl₄ solution values (34). For HOAr-im_H,OMe, the calculated ν(OH)_DFT,corr of 3,022 cm⁻¹ is within the broad band observed in CHCl₃ (Fig. 2). Over the range of imidazole compounds from HOAr-im_H,NMe2 to HOAr-im_H,NO2, our corrected (34) B3LYP/6-31G(d,p) values of ν(OH) increase in energy by 134 cm⁻¹ (Table 1). N-Alkylation is predicted to have a smaller effect, 61 cm⁻¹ among HOAr-im_R,H, R = H, Me, Cy.

Thermodynamic Measurements on HOAr-im Compounds.

Electrochemical or chemical one-electron oxidation of these phenol–base compounds leads to the proton-transferred, distonic radical cations that have been characterized optically (9) and by EPR (35). Cyclic voltammograms of these compounds in anaerobic acetonitrile are chemically reversible with peak separations larger than the theoretical value of 59 mV (SI Fig. 10 in the SI Appendix), as have been observed with other hydrogen-bonded phenols (20, 36–39). Reduction potentials are taken as the average of cathodic and anodic peak potentials (E_1/2) and vary from 0.42 to 0.66 V (Table 1; all potentials in MeCN vs. Cp₂Fe^+/0). Electron-donating substituents decrease E_1/2, correlating well with Hammett σ values in the HOAr-im_H,X series (ρ = −0.18, R² = 0.92). N-Alkylation lowers the potential by 20 and 70 mV for R = Me or Cy. The benzimidazole compound HOAr-im_bz has a higher potential than HOAr-im_H,H, E_1/2 = 0.54 vs. 0.49 V, and HOAr-im_bzCl2 is higher still (E_1/2 = 0.66 V). The very electron-rich dimethylamino-substituted HOAr-im_H,NMe2 is unique in displaying two oxidation waves, at 0.21 and 0.10 V, consistent with titrations showing its reaction with two equivalents of the strong chemical oxidant [N(C₆H₄Br)₃]^+•.

Triflic acid protonates the imidazole compounds HOAr-im_H,H and HOAr-im_H,OMe in acetonitrile to give HOAr-im_H,HH⁺ and HOAr-im_H,OMeH⁺. Acid dissociation constants for these compounds were determined spectrophotometrically by addition of an indicator (bromothymol blue or methyl red, respectively) to MeCN solutions with large excesses of HOAr-im_H,X and HOAr-im_H,XH⁺ in different ratios. The derived pK_a values for HOAr-im_H,XH⁺, 10.1 ± 0.3 (X = H) and 10.3 ± 0.1 (X = OMe), show that the methoxy substituents have at most a small effect on the basicity of the imidazole. In free-energy terms, this ΔpK_a of 0.2 ± 0.3 is equivalent to ΔΔG° = 12 ± 18 mV, much smaller than the 90 ± 30 mV difference in redox potentials. This indicates that the lower E_1/2 values observed for imidazoles with electron-donating substituents cannot be attributed solely to increased basicity of the imidazole moiety.

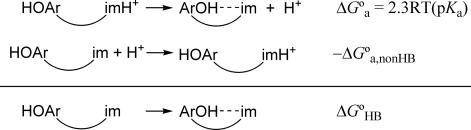
HOAr-im_H,HH⁺ and HOAr-im_H,OMeH⁺ are >6 pK_a units more acidic than the simple imidazolium ion. HOAr-im_H,XH⁺ are more acidic because deprotonation is favored by formation of the strong intramolecular O–H⋯N hydrogen bond. Scheme 2 shows that the observed energetics of deprotonation [ΔG_a° = 2.3RT(pK_a)] to yield the hydrogen-bonded phenol–base ArOH- - -im can be separated into the free energies of the O–H⋯N hydrogen bond (ΔG_HB°) and the free-energy change for deprotonation to yield the hypothetical phenol–base lacking the hydrogen bond (HOAr_im), ΔG_a,nonHB°. This analysis gives ΔG_HB° = ΔG_a° − ΔG_a,nonHB°. By using the acidity of imidazolium as an estimate of ΔG_a,nonHB°, Scheme 2 gives 9 kcal·mol⁻¹ for the strength of the hydrogen bond in HOAr-im_H,X. This is a lower limit because it is actually the difference between the strength of the O–H⋯N hydrogen bond and any Ar(H)O⋯H-im⁺ hydrogen bonding in HOAr-im_H,XH⁺. The value of ≥9 kcal·mol⁻¹ indicates a relatively strong hydrogen bond (28), consistent with resonance-assisted H-bonding and with the spectroscopic and structural data above (25).

Scheme 2.

Thermochemical cycle to estimate the free energy of ArOH⋯im hydrogen bonding, ΔG_HB°. ArOH- - -im is the predominant hydrogen-bonded form of a general phenol–imidazole (Scheme 1); HOAr_im is the hypothetical species lacking this hydrogen bond. ΔG_a° is the free-energy change for the experimentally observed protonation equilibrium.

Kinetic Studies of CPET Oxidations.

We have measured the kinetics of oxidations of these phenol–imidazoles with one-electron chemical oxidants: either triarylaminium salts, [N(Ar)₃]^+• or iron(III) tris-bipyridine or -phenanthroline complexes, [Fe(N–N)₃]³⁺ (Scheme 1). These studies were performed in acetonitrile under anaerobic conditions by using time-resolved visible spectroscopy with stopped-flow techniques. In reactions with [NAr₃]^+•, progress was monitored primarily by the disappearance of the intensely blue oxidants; with the iron(III) reagents, the reaction course was marked by appearance of the dark red iron(II). In some cases, an absorption for the phenoxyl radical product was also observed. The downhill reactions (E_rxn > 0, ΔG_rxn° < 0) are very rapid, with rate constants >10⁶ M⁻¹ s⁻¹, and are generally too fast for our stopped-flow instrument. Therefore, most reactions were studied in the uphill direction under approach-to-equilibrium conditions by using excess phenol. The time sequences of the optical spectra were analyzed globally by using SPECFIT (40) to yield second-order rate constants (Table 2). In each case, k was derived from ≈25 runs at five different concentrations of phenol. The potentials of [Fe(N–N)₃]³⁺ compounds vary with ionic strength (9), so reactions using these oxidants were performed in the presence of 0.1 M ⁿBu₄NPF₆ to match the electrochemical conditions. The reaction rate of HOAr-im_H,Br with [Fe(Me₄phen)₃]³⁺ was measured as a function of temperature from 281 to 318 K, yielding the Arrhenius parameters (k = Ae^−E_a/RT): log A = 10.9 ± 1.1 and E_a = 7.5 ± 1.4 kcal·mol⁻¹. Arrhenius analysis of our reported k vs. T data for HOAr-im_H,OMe + [N(C₆H₄OMe)₃]^•+ (9) gives log A = 9.7 ± 1.2 and E_a = 7.8 ± 1.6 kcal·mol⁻¹. The ΔG_rxn°for these two reactions are: +6.0 ± 0.7 and +1.4 ± 0.2 kcal·mol⁻¹, respectively.

Table 2.

Rate constants for phenol oxidations (T = 296 ± 2 K)

B	Oxidant	k, M−1 s−1	Erxn, V*
-imH,OMe	[N(p-C6H4OMe)3]•+	(1.1 ± 0.1) × 104	−0.26
-imH,H	[N(p-C6H4OMe)3]•+	(6.3 ± 0.6) × 102	−0.33
	[N(C6H4Br)2(C6H4OMe)]•+	(3.0 ± 0.6) × 106	−0.01
-imH,Br	[N(tol)3]•+	(4.1 ± 0.4) × 104	−0.17
	[Fe(5,5′-Me2bpy)3]3+	(2.0 ± 0.2) × 106	0.03
	[Fe(4,7-Me2phen)3]3+	(1.3 ± 0.5) × 106	−0.02
	[Fe(Me4phen)3]3+	(1.2 ± 0.3) × 105	−0.06†
-imH,NO2	[N(C6H4Br)2(C6H4OMe)]•+	(1.7 ± 0.2) × 105	−0.13
-imMe,H	[N(p-C6H4OMe)3]•+	(1.5 ± 0.2) × 103	−0.30
-imCy,H	[N(tol)3]•+	(1.3 ± 0.1) × 105	−0.04
	[N(C6H4Br)2(C6H4OMe)]•+	(3.0 ± 0.3) × 104	−0.10
-imbz	[N(C6H4Br)2(C6H4OMe)] •+	(1.6 ± 0.2) × 106	−0.06
	[Fe(5,5′-Me2bpy)3]3+	(3.6 ± 0.4) × 105	0.04
	[Fe(4,7-Me2phen)3]3+	(2 ± 1) × 106	−0.01
-imbzCl2	[N(C6H4Br)2(C6H4OMe)]•+	(1.6 ± 0.4) × 105	−0.18

*Estimated errors ± 0.03 V from cyclic voltammetry.

^†Estimated error ±0.01 V from equilibration experiments.

Discussion

The hydrogen-bonded phenol–imidazoles in Scheme 1 generally undergo chemically reversible oxidations, including cyclic voltammetry and equilibration with various oxidants. The stability of the phenoxyl radical product is due in part to the tert-butyl groups preventing dimerization of the phenoxyl radical. The reversibility of the oxidation depends on the availability of the proton on reduction of the radical cation. The reduction potentials for these phenols are quite low compared with those of phenols without a pendant base, for example, 0.49 V for HOAr-im_H,Br vs. E_p.a = 1.1 V for 2,4,6-tri-tert-butylphenol (41). Phenols become dramatically more acidic on oxidation: in 2,4,6-tri-tert-butylphenol, the pK_a drops from 27 to 0 on oxidation (29, 41, 42). From another perspective, this means that the not proton-transferred radical cation, [HOAr^•+-im], is a very-high-energy species, too high in energy to be an intermediate in these reactions. To avoid this high-energy intermediate, these reactions occur by concerted proton-electron transfer (CPET) rather than by a stepwise ET-PT pathway (9).

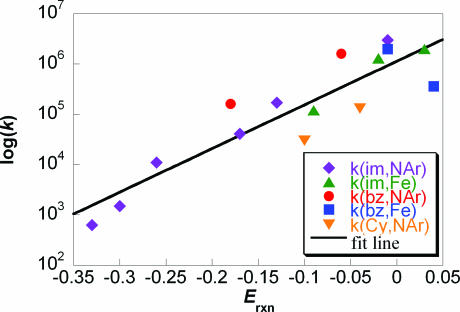
This is an attractive system to probe the factors that impact CPET reactivity because of the robustness of the compounds, the accessible potentials, and the availability of spectroscopic data. The rate constants in Table 2 vary from 6.3 × 10² M⁻¹ s⁻¹ to 3.0 × 10⁶ M⁻¹ s⁻¹. Fig. 3 shows that there is a close correlation of these rate constants with the energetics of the reaction, E_rxn (= −ΔG_rxn°/F). This figure includes multiple reactions of the same phenol with different oxidants, and multiple reactions of the same oxidant with different phenols. Over this range of almost a factor of 5,000 in rate constant, all but one of the experimental k's lie within a factor of 5.2 of the value predicted by the correlation line. The one exception is the reaction of HOAr-im_bz + [Fe(5,5-Me₂bpy)₃]³⁺ that is almost an order of magnitude slower than predicted. This does not appear to be a feature of the benzimidazole compound, because the closely related reaction with [Fe(4,7-Me₂phen)₃]³⁺ is a factor of 1.7 faster than predicted. A similar discrepancy between Fe-bpy and Fe-phen oxidants has been observed in reactions with related phenol–pyridine compounds (9). Overall, the good correlation indicates that the driving force for reaction, ΔG_rxn° = −FE_rxn, is the primary determinant of the differences among rate constants for this series of reactions.

Fig. 3.

Plot of log(k/M⁻¹s⁻¹) vs. E_rxn (V) for reactions of HOAr-im_R,X + [NAr₃^•+], HOAr-im_Cy,H + [NAr₃^•+], HOAr-im_R,X + [Fe(N–N)₃]³⁺, HOAr-im_bz + [NAr₃^•+], and HOAr-im_bz + [Fe(N–N)₃]³⁺. The fit line is k = (1.15 × 10⁶ M⁻¹ s⁻¹)e^(20.0*E_rxn).

The driving force is one of four contributors to the rate expression for CPET shown in Eq. 1, together with the electronic coupling V^el, the Frank–Condon term FC, and the intrinsic barrier λ (10–18). Some insight into the importance of these terms is provided by the dependences of k on temperature. For HOAr-im_H,Br + [Fe(Me₄phen)₃]³⁺ and for HOAr-im_H,OMe + [N(C₆H₄OMe)₃]^•+, the preexponential factors are: log (A/M⁻¹ s⁻¹) = 10.9 ± 1.1 and 9.7 ± 0.6 (9), respectively. These are not unusual values for bimolecular reactions. In the context of simplified CPET theory, as given in Eq. 1, this means that the product of the electronic coupling and the tunneling probabilities in the FC term cannot be very small. The parameters needed to rigorously evaluate the FC term are, unfortunately, not experimentally accessible despite the amount known about the phenol–imidazole molecules in this series. In particular, the FC term depends on the tunneling distance, the frequency of modulation of the O⋯N distance, and the stretching frequencies for the O–H in the reactant and the N–H in the product, both as a function of d_O⋯N and vibrational level. Still, the results described here—the solid-state structures, NMR chemical shifts of the phenolic hydrogens, IR spectra, and DFT calculations of ground-state HOAr-im—suggest that the various frequencies and distances vary significantly across the series of compounds. The donor–acceptor distance d_O⋯N in the solid-state structures varies by >0.11 Å, the computed distances by 0.04 Å, the proton chemical shifts by >2 ppm, and the computed OH-stretching frequencies vary by 119 cm⁻¹. The kinetic data show, however, that changes of this magnitude do not cause large deviations from the simple dependence of log(k) on ΔG° in Fig. 3. These results suggest that, to a first approximation, V^el × FC is fairly constant across this series of reactions.

The largest variations in V^el × FC—best observed as deviations from the correlation with ΔG°—are the reactions of HOAr-im_Cy,H. These are almost an order of magnitude slower than reactions of HOAr-im_H,X at a comparable driving force. The smaller rate constants coincide with an apparently longer d_O⋯N, a higher ν(OH)_DFT,corr, and a marked upfield shift in δ(OH), all of which should reduce the FC term and therefore k_CPET. However, reactions of HOAr-im_H,NO2 do not deviate from the ΔG° line even though this compound has calculated d_O⋯N and ν(OH) that are longer and higher than HOAr-im_Cy,H. Similarly, the phenol–benzimidazoles, with more downfield δ(OH) and somewhat shorter d_O⋯N, tend to react faster than HOAr-im_H,X compounds. Thus, the small deviations from the line in Fig. 3 do not simply correlate with any of the structural or spectroscopic parameters.

The rate constants for the HOAr-im_R,X + [NAr₃]^•+ reactions follow the Marcus-like dependence on ΔG° (E_rxn) that is predicted by Eq. 1 with the assumption of constant V^el × FC (SI Fig. 6 in the SI Appendix). This implies that the differences in rate constants, log(k₁/k₂), are mostly due to differences in apparent barriers (λ + ΔG°)²/4λ, or ΔG*_app. Recasting Fig. 3 in terms of relative ΔG*_app gives an equivalent fit line with a unitless slope, ΔΔG*_app/ΔΔG° = 0.55. Increasing the driving force by 1 kcal·mol⁻¹ lowers the apparent barrier by ≈0.55 kcal·mol⁻¹. This is in good agreement with the prediction of Marcus-type treatments, such as Eq. 1, that ΔΔG*/ΔΔG° (the Brønsted α) should be approximately ½ for reactions where 2λ ≫ |ΔG°|. Hammarström (43) and later studies of ours (9) and by Savéant and colleagues (13) have suggested that intrinsic barriers for CPET reactions are large enough to make 2λ ≫ |ΔG°| for this series. With the additional assumption that the V^el × FC term does not strongly depend on temperature, and by using the value of A derived from the variation of k with T for HOAr-im_H,OMe + [N(C₆H₄OMe)₃]^•+ the k vs. E_rxn data and Eq. 1 give λ ≅ 19 ± 4 kcal·mol⁻¹. No variation of ΔG° with temperature has been included because the variation (ΔTΔS°) is less than our experimental error (9). However, Savéant and colleagues have recently shown that even a small ΔS° leads to substantially lower values of λ from this kind of analysis (13). Although the value of λ is only a rough estimate, it is consistent with these reactions having 2λ ≫ ΔG°. From Table 2, all of the reactions have |ΔG°| < 8 kcal·mol⁻¹ and all but two have |ΔG°| < 4.2 kcal·mol⁻¹.

The ability to fairly well fit the rate constants in Table 2 to a line (Fig. 3) or to a Marcus-type parabola (SI Fig. 6 in the SI Appendix) also indicates that the intrinsic barriers do not vary substantially across this series of reactions. The changes in electronic structure and chemical environment of the phenol proton, over the range of compounds examined here, have at most a modest effect on λ_CPET. Hydrogen-bonding interactions between the imidazole (nontransferring) proton and solvent are also not a significant perturbation, because the kinetic data are similar for HOAr-im_H,H and HOAr-im_Me,H. A small variation in λ can be seen in the slower reactions of the [Fe(N–N)₃]³⁺ oxidants (green triangles in Fig. 3) vs. the [NAr₃^•+] reagents (purple diamonds). Slower reactions are expected for [Fe(N–N)₃]³⁺ because their self-exchange rates for outer-sphere ET are ≈10² slower than those for NAr₃^•+/0 [≈10⁷ M⁻¹ s⁻¹ (44) vs. 10⁹ M⁻¹ s⁻¹ (45)]. The Marcus cross-relation, with its square root, would therefore suggest a rate difference of a factor of 10 between these two oxidants in outer-sphere ET. The observed difference from Fig. 3 is significantly less than a factor of 10 but is at least in the correct direction. Deviations from the quantitative predictions of the cross-relation are not uncommon in ET (or HAT) processes (44, 46).

In general, the structural and electronic changes across this series of phenol–imidazole compounds have a much smaller effect on the rate of CPET than by the driving force. At the extreme of this series, the stronger hydrogen bond in HOAr-im_bz compared with HOAr-im_Cy,H—as evidenced by a shorter d_O⋯N [by 0.082(17) Å] and lower ν(OH) (by 75 cm⁻¹)—is coincident with a 10-fold increase in reaction rates. It should be noted that more substantial effects have been observed when there are larger differences in structure. The HOAr-im_H,X compounds all react >10 times faster (at comparable driving force) than the phenol-amine derivative, HOAr-CPh₂NH₂ (9). The imidazole and related pyridine derivatives have strong, resonance-assisted hydrogen bonds that facilitate CPET. When the resonance is broken, for instance, comparing HOAr-py with the nonconjugated HOAr-CH₂py, the hydrogen bond becomes much weaker—as indicated by the ≈280 cm⁻¹ higher ν(OH) and 3.7 ppm lower d_OH—and CPET becomes ≈10^1.5 slower (at the same driving force) (47). Together, these studies are beginning to define the key features that modulate CPET reactivity, a process of increasingly appreciated biological importance.

Conclusions

The generation and trapping of reactive oxygen species typically involve the transfer of proton(s) and electron(s), and often these processes occur by concerted proton–electron transfer (CPET). The studies described herein, on a series of substituted phenol–imidazoles, are helping to define the basic principles of CPET. These phenol–imidazoles have a strong ArOH⋯N(imidazole) hydrogen bonds, as indicated by short O⋯N distances and by a thermochemical cycle that yields ≥9 kcal·mol⁻¹ for the H-bond strength. Varying the substituents from electron donating to electron withdrawing has monotonic effects on the thermodynamics of CPET (from electrochemical measurements) and on the H bond, as evidenced in the NMR spectra and computational studies. However, the x-ray structures of these compounds indicate that packing effects are larger than those of the substituents. Despite the variations in the chemical environment of the proton within this set of similar compounds, the driving force E_rxn is the primary factor that determines the relative CPET rates. The dependence of the CPET rate constants on E_rxn follows a Marcus theory-type dependence, as suggested by current theories, and suggests that tunneling probabilities and the intrinsic barriers for CPET do not vary substantially over the range of phenol–imidazoles examined. Other studies have shown, however, that larger changes in chemical structure—for instance, comparing compounds with imidazole vs. amine bases—can have substantial effects on CPET reactions beyond the driving force (9, 47). Only by comparing reactions at similar driving force can one observe the more subtle effects of structure and substituent effects on other features of CPET such as tunneling probabilities and intrinsic barriers.