Casting polymer nets to optimize noisy molecular codes

Abstract

Life relies on the efficient performance of molecular codes, which relate symbols and meanings via error-prone molecular recognition. We describe how optimizing a code to withstand the impact of molecular recognition noise may be understood from the statistics of a two-dimensional network made of polymers. The noisy code is defined by partitioning the space of symbols into regions according to their meanings. The “polymers” are the boundaries between these regions, and their statistics define the cost and the quality of the noisy code. When the parameters that control the cost–quality balance are varied, the polymer network undergoes a transition, where the number of encoded meanings rises discontinuously. Effects of population dynamics on the evolution of molecular codes are discussed.

In the living cell, information is carried by molecules. The outside environment and the biochemical circuitry of the cell churn out fluxes of molecular information that are read, processed, and then stored in memory by other molecules. The cell's information-processing networks often need to translate a symbol written in one class of molecules into another symbol written in a different molecular language. This requires a code-table that translates between the two molecular languages. Perhaps the best-known example is the genetic code-table that translates 64 DNA base triplets into 20 amino acids (1, 2). One may think of such a code-table as a mapping—a probabilistic one because of the inherent noise—between the space of molecular symbols, e.g., the base triplets, and the space of molecular meanings, e.g., amino acids. The notion of mapping between two molecular spaces occurs also in biological codes of a much larger scale; for example, the transcriptional regulatory network that controls gene expression by DNA-binding proteins. This network may be seen as a mapping from the space of regulatory proteins to the space of their respective DNA binding sites. Evolution poses the organism with a semantic challenge: its code-tables must assign meanings to symbols in a manner that minimizes the impact of the molecular recognition errors while keeping down the cost of resources that the code-table necessitates. The present work describes a treatment of this biological optimization problem in terms of the statistical mechanics of polymer networks.

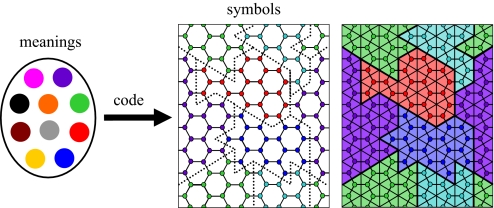
In the biophysical reality of the cell, actual polymer networks are essential for structural stability and motility (3, 4). However in the present context of coding, polymer networks are just mathematical entities that prove useful for describing the code-table and studying its optimization: Molecular recognition is inherently noisy because it involves energy scales that are not much larger than the typical thermal energy k_BT. To reflect these recognition errors, the space of symbols is depicted as a graph in which symbols are vertices and edges connect vertices that are likely to be confused by misreading (Fig. 1). A code-table is then constructed by assigning meanings to each vertex. This can be pictured as coloring the vertices according to their meaning (2), which partitions the graph into “islands of meanings.” The boundaries between these islands form a network, which can be likened to a self-assembling network of polymers or self-avoiding random walks (Fig. 1). Polymer networks are natural in this context because they are related to the notion of space partitioning that is central to coding theory (5). But the resemblance to a polymer network is not merely structural. Optimizing the fitness of the mapping is shown to be equivalent to minimizing the free energy of the polymer network. Such an optimal mapping must balance the three conflicting needs for maximal error tolerance, for maximal diversity, and for minimal cost. During evolution, the code-table adapts by altering the network in response to changes in the equipoise of these three evolutionary forces.

Fig. 1.

The code-table as an information channel and the relation to polymer networks. The code-table is an information channel or mapping that relates a space of meanings (Left), which are depicted as colors, to a symbol space (Center). The symbol space is a graph, hexagonal in this example, in which vertices are symbols and edges connect symbols that are likely to be confused by reading. The code-table induces a coloring pattern on the symbol space, which divides it into meaning islands (dotted lines). In the triangular dual graph (Right), the boundaries between meaning islands form a network of “polymers” (thick solid lines).

In the present work, we first discuss how the partition of the symbol space by the polymer networks determines the fitness of the code-table, where mathematical definitions of fitness and its determinants, error-load, diversity, and cost are given. Next, we discuss one purpose of the present work, which is to show that the fitness function of the code-table corresponds to the free energy of the polymer network. Thus, it suggests that the problem of optimizing the code-table is equivalent to calculating the equilibrium statistics of the polymer network. A second purpose is then to use this equivalence to examine the code optimization problem in parameter regimes that are hard to access otherwise. In particular, it is used to identify a first-order transition, in which the number of meaning islands changes abruptly in response to varying the error-tolerance–diversity–cost balance. Finally, to put the model within a context of population dynamics, we discuss possible aspects of metastability, mutations, and genetic drift that may affect the evolution of the code.

Model and Results

Fitness of Molecular Codes.

Information in the cell is recorded in molecules and then retrieved and translated into other molecules by a code-table. To discuss how the organism optimizes such a code-table, we represent the table as an information channel or a mapping that relates a meaning space, in which n_m meanings reside, to a symbol space, which contains n_s symbols (Fig. 1). The code-table maps (or encodes) meanings to symbols and thus partitions the space of symbols into meaning islands whose boundaries form a polymer network. In this section, we first calculate the fitness of a code-table as a function of the mapping as specified by the polymer network. The code fitness is composed of contributions due to the diversity of the code-table, its average error load, and the cost of constructing the molecular coding apparatus. There are two sources of noise in our simple description of the coding system, noise while reading and noise in the mapping itself. Recognition errors while reading a symbol are represented by the symbol graph whose edges connect symbols that misreading may confuse. The impact of this noise is included in the error-load component of the fitness. Noise in the mapping, which is implemented in error-prone molecular recognizers, is represented as a statistical average over an ensemble of polymer networks. This second recognition problem requires additional resources and is included in the cost (which together with the error load is defined below).

A code-table does not necessarily map all of the n_m available meanings to symbols but may possibly map only n_f ≤ n_m out of them. The larger is the number of encoded meanings n_f, the more diverse is the code. Diversity contributes to the fitness of the code because it increases the chance that when the organism needs to read, write, or process a certain meaning it can accurately encode it as one of the available symbols. However, diversity of meanings also increases the probability for misreading errors: To reconstruct the meaning encoded by a certain symbol, the organism has to read it. Because the molecular reading apparatus is not perfect, it may sometimes confuse this symbol with one of its neighbors in the graph (Fig. 1). If many meanings are encoded then, on average, the meaning islands defined by the network are smaller. In this finer network, the chance of confusing symbols of different meanings is larger, which costs the organism in a higher error load.

To find the error load, one needs to specify a partition into meaning islands and examine the average chance to cross by misreading the boundaries between the islands. We specify a partition (see Fig. 1) by assigning to each edge i–j a binary variable E_ij that indicates whether the edge is on the boundary between two meaning islands (E_ij = 1) or inside of an island (E_ij = 0). Misreading along the edge, which confuses i with j, occurs with a probability r_ij, while r_ii is the probability to correctly read i. There may be two possible outcomes of misreading: If both symbols are in the same island and are therefore synonymous, then misreading bears no load because the translated meaning does not change. If the symbols reside in two different islands and are therefore nonsynonymous, then the fitness of the organism decreases by one fitness unit. The contribution of an i–j misreading to the error load can be therefore quantified as r_ijE_ij and the total error load is a sum over all edges, Σ_i−j r_ijE_ij.

The need for diversity is an evolutionary force that counteracts the need to minimize error load. Our model assumes for simplicity that the contribution of diversity to the fitness is linear in n_f, the number of encoded meanings. The quality H_E, of a given network pattern E, is then a linear combination of the error load and the diversity,

where the parameter w_D measures the significance of diversity relative to error load. We use a sign convention in which an optimal code of high quality corresponds to low values of H_E. The quality depends on the coloring pattern of the code-table, which determines its error load and diversity. As illustrated in Fig. 1, each coloring pattern is determined by the network of boundaries between the islands, which is equivalent to a network of polymers. The quality is governed by the interplay between error load and diversity: If the reader were ideal r_ij = δ_ij, then it would have been advantageous to decode as many meanings as there are available symbols, n_f = n_s. However, because the molecular reader is not perfect, it is preferable to decode fewer meanings to minimize the effect of misreading errors. The quality H_E corresponds to a “microstate” specified by a deterministic network configuration E. The stochastic mapping of the molecular code is a “macrostate,” which is represented by an ensemble of such configurations and is calculated below. The code quality H_C is defined as the ensemble average of quality over all microstates, H_C = 〈H_E〉.

Besides the quality of the code, which combines its error load and diversity, the code fitness must also account for the cost of the molecular machinery that performs the mapping. Molecular codes are physically implemented by recognition interactions between the meanings, the symbols, and sometimes other intermediary molecules, such as the tRNA in the genetic code (1). High specificity of recognition improves the quality of the code because it enables more accurate mapping. However, highly specific binding requires a higher binding energy, which in general necessitates larger binding sites. It is plausible to assume that the cost of the code is proportional to the average size of the binding sites and therefore to the average binding energy (6). This is because the cost of synthesizing the molecules and maintaining their genes is proportional to their size. To estimate the cost, one notes that the binding probability scales like the Boltzmann exponent of the binding energy (in units of k_BT), P_b ∼ exp(E_b). It follows that the cost, which is equal to the average binding energy 〈E_b〉, can be approximated by the average 〈ln P_b〉, which is minus the entropy of the mapping of meanings to symbols, −S_C (see Methods). This entropy averages over the ensemble of all possible mappings, which is determined by all possible networks and the number of possible ways to color every such network.

Finally, the overall fitness of the code F_C is estimated by a weighted sum of the quality and the cost, F_C = H_C − w_C × S_C, where the parameter w_C measures the significance of the cost with respect to quality. F_C is like a free energy of all possible colorings of the code-table and may be derived from the partition function Z_C,

Within this analogy, the quality H_E plays the role of energy, and w_C is an effective temperature. The ensemble average in Z_C is due to the probabilistic nature of the molecular mapping. At high w_C, codes are fuzzy and smeared over many network configurations, whereas at low w_C, they are sharper because the mapping is almost deterministic. In principle, one can derive the code-table by performing the summation in Eq. 2 (6), but in practice this is a burdensome task that can be performed only numerically and even this only for codes of limited size. Tractable analytic results exist mostly at the limit of high w_C. In this regime, the code table undergoes a second-order phase transition from a noncoding state of no correlation between meanings and symbols to a coding state, in which such correlation has just emerged (2, 6–8).

The cost–quality balance of the code-table is analogous to the balance in an engineered noisy information channel between the average distortion in the channel H, which measures its quality, and the channel's rate I, which measures the cost of the channel by estimating how many bits are required to encode one meaning. Rate-distortion theory (9) focuses on the fundamental problem of optimizing a noisy information channel, which can be formalized as the following question: What is the minimal rate I required to assure that the distortion in the channel will be less than a certain desired value H? This optimal rate-distortion curve is calculated by minimizing a functional F = H + w_CI, where H, I, and F are analogues of H_C, −S_C, and F_C, respectively. The “temperature” w_C = −∂H/∂I, the slope of the optimal curve, measures the increase in quality due to an additional bit of information. In the biological context, w_C is expected to decrease with the complexity the organism and its environment: A complex organism transmits more information. It is therefore in the interest of this organism to pay a larger cost to improve the quality of its codes, and w_C = ∂H_C/∂S_C is lower. Similarly, a richer environment is also “colder.” At low w_C, the quality H_C dominates the free energy F_C and the code-table tends to one of the many minima of H_E. Derivation of the optimal code in this regime is difficult, even numerically, because of the rugged landscape of H_E. As we discuss below, the polymer network formalism offers insight into this regime and, specifically, suggests a first-order coding transition.

Statistics of Polymer Networks on the Dual Symbol Graph.

To formalize the analogy of molecular codes to polymer networks, we need to examine the dual of the symbol graph on which the network resides. To find the dual graph, one embeds the symbol graph in a surface (10). In the example of Fig. 1, the symbol graph is a hexagonal lattice that is embedded in a torus and the dual is a triangular lattice (see Methods). It is evident that the vertex-coloring pattern of the symbol graph corresponds to a connected “polymer” network whose monomers are a subset of the edges of the dual graph (Fig. 1).

By counting the number of edges and vertices in the polymer network one can derive the number of meaning islands n_f in the quality H_E (Eq. 1). For this purpose, we introduce another binary variable, V_i, that indicates whether a vertex i of the dual graph is part of the polymer network (V_i = 1) or not (V_i = 0). Then, the numbers of occupied edges n_e, occupied vertices n_v, and islands n_f are related through the definition of Euler's characteristic χ = n_v − n_e + n_f (10),

χ is determined by the topology of the surface in which the symbol graph is embedded; for example, χ = 0 for the torus in Fig. 1. By substitution of Eq. 3 into Eq. 1, we find that the code quality is H_E = Σ_i−j(r_ij − w_D)E_ij + w_DΣ_iV_i − w_Dχ, and the code's partition function is therefore Z_C = Σ_E,VN_EV exp(−H_E/w_C), where the summation is over all valid network configurations. The factor N_EV is the number of possible ways to color a given pattern specified by the fields E and V. As is common in biological codes, it is assumed henceforth that there are many more meanings than available symbols, n_m ≫ n_s ≥ n_f, so the combinatorial factor can be estimated as N_EV ≈ exp(n_f ln n_m). By substituting into Z_C the approximated N_EV with the island number n_f taken from Eq. 3, the partition function becomes

with the coefficients α = w_D + w_C ln n_m and β_ij = (r_ij − w_D) − w_C ln n_m.

The code partition function Z_C (Eq. 4) sums over all possible networks. The building blocks of these networks are self-avoiding polymers that fuse to each other at junctions. Within the analogy to physical networks, Eq. 4 may appear as a summation over two chemical “species”—one that resides on the edges with “excitation energies” (or chemical potentials) β_ij, and one on the vertices with the excitation energy α. However, these two species are not really independent and cannot be summed separately. A vertex is occupied if and only if its coordination number is at least two because “dangling ends” or isolated vertices are forbidden. Similarly, an edge is occupied if and only if it connects two occupied vertices. The relevant chemical species are the monomers, i.e., pairs of a vertex and a neighboring edge that carry energies of α + β_ij and the possible k-fold junctions (k > 2). The formation of a k-junction replaces k ends that contribute each an energy of α/2 by one vertex of energy α so that the overall energy change is (1 − k/2)α. Performing the summation over all possible networks proves to be tricky because the vertex and edge occupations are not independent. Below, we employ the n = 0 formalism to resolve this configuration counting problem.

Correspondence Between Code Optimization and Spin Networks.

The n = 0 formalism was devised by de Gennes to examine polymer solutions (11, 12). Recently, it was applied also to microemulsions, micellar solutions, and dipolar fluids (13–15). At the basis of this approach is a mathematical equivalence between a system of self-excluding polymers and a system of interacting n-component magnets, in the limit of vanishing number of components, n = 0. The n = 0 formalism is reviewed elsewhere (12, 13). Here, we only discuss concisely the basic idea and use this approach to show that the statistics of the code-table (Eqs. 2 and 4) can be mapped to that of the zero-component magnets.

To demonstrate the equivalence between the code-table problem and the spin system, let us consider the dual of the symbol graph on which the polymer network resides (Fig. 1) and assign to each of the edges i − j an n-component magnetic spin S_ij. The interaction is represented by a spin-Hamiltonian H_S and the spin partition function is Z_S = 〈exp(−H_S)〉, where 〈 … 〉 denotes the average over all possible spin orientations. A peculiar feature of this system in the limit of zero components (“the n = 0 property”) is that all averages over products of spins vanish except for the quadratic averages 〈S_ij²〉 = 1, where S_ij is any of the components of S_ij. This property enables mapping of the spin lattice to the network ensemble by tailoring a spin Hamiltonian H_S and a consequent spin partition-function Z_S, in which an 〈S_ij²〉 term appears if and only if the corresponding edge i–j is occupied in the network partition function Z_C. It is shown below that this correspondence is accomplished by the Hamiltonian H_S,

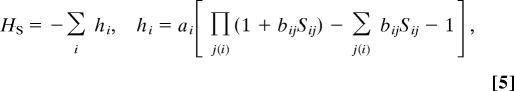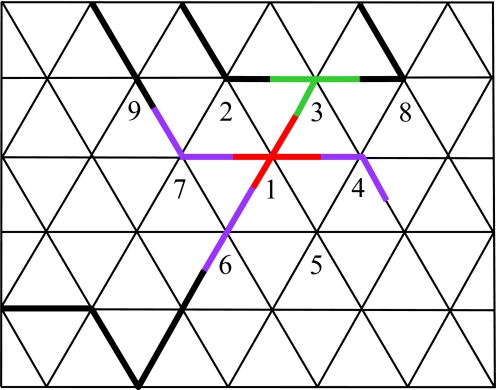
where j(i) are all of the neighbors of i, and the coefficients a_i and b_ij are related to the α and β_ij parameters (Eq. 4). The functions h_i are the contributions of each vertex i to H_S and consist of all possible products of two or more edges around i. Each of these products corresponds to a possible edge occupation state in a network (Fig. 2). The one- and zero-edge configurations are forbidden in the network and are therefore subtracted from h_i (the second and third terms).

Fig. 2.

Correspondence of the polymer networks to n = 0 spin systems. The solid lines denote boundaries between the meaning islands induced by the code on the dual graph (Fig. 1 Right). In the spin model, to each edge a spin S_ij is assigned. Each vertex i contributes to the spin Hamiltonian H_S a factor h_i, which accounts for all possible edge occupancies around this vertex. By the construction h_i (Eq. 5), if a vertex is occupied then at least two of the adjacent edges are occupied. In the present example, a four-junction at vertex 1 (red), which corresponds to a factor a₁b₁₃S₁₃b₁₄S₁₄b₁₆S₁₆b₁₇S₁₇, connects to three linear elements (magenta), e.g., a₇b₇₁S₇₁b₇₉S₇₉, and one three-junction (green), a₃b₃₁S₃₁b₃₂S₃₂b₃₈S₃₈. The corresponding contribution to the spin partition function Z_S is an average over all of the spin orientations. This contribution does not vanish because each spin appears exactly twice in the product because S_ij appears exactly once in both edge configurations of i and j. The weight of this contribution is the product of the b_ij-s and a_i-s for each edge and vertex in the product.

How this form of the Hamiltonian H_S ensures the equivalence is clear by expanding Z_S in a power series, Z_S = 〈exp(−H_S)〉 = 〈∏_i exp(h_i)〉 = 〈∏_i(1 + h_i + h_i²/2 + …)〉. Because of the n = 0 property, the infinite series can be exactly truncated at the second term and we obtain Z_S = 〈∏_i(1 + h_i)〉, which is a sum over averages of spin products. In this sum, the only nonvanishing terms are those in which each spin S_ij appears exactly twice. In those configurations, S_ij must appear in both contributions of h_i and h_j. As illustrated in Fig. 2, it is evident that such a spin configuration corresponds to a network configuration and the weight of this term in the partition function is a product of the b_ij-s and the a_i-s of the occupied edges and vertices. From all of this, we find that the spin partition function is

with the same occupation variables E_ij and V_i that are used to count network configurations in the code partition function Z_C (Eq. 4). Finally, to obtain the one-to-one correspondence one needs to identify the “fugacities” in Eqs. 4 and 6, b_ij² = exp(−β_ij/w_C) and a_i = exp(−α/w_C), which results in identical partition functions, Z_C = Z_S (up to an irrelevant factor), and free energies, F_C = F_S. In the following, this correspondence is used to gain insight into the noisy coding system from a mean-field solution of the spin system.

Mean-Field Solution of the n = 0 Spin System.

To solve for the optimum of a noisy molecular code, we employ a standard variational mean-field technique (13–15). We approximate the spin probability distribution by a product of independent single-spin distributions, ρ = ∏_ijρ_ij(S_ij), which is used to construct a variational least upper bound on the free energy of the system F_S (see Methods). By this mean-field procedure, it is straightforward to find that the average spin, s_ij = 〈S_ijρ_ij(S_ij)〉, is given by the relation

where g_ij are effective fields that involve the spins on neighboring edges, g_ij = a_ib_ij[∏_k(i)≠j(1 + b_iks_ik) + ∏_l(j)≠i(1 + b_jls_jl) − 2]. In a similar fashion, we obtain the mean-field free energy, F_S = −Σ_ih_i + Σ_i−j [g_ijs_ij − ln(1 + g_ij²/2)]. The first term in F_S is the average Hamiltonian, which is the quality of the average code, while the last term is entropic and accounts for the cost. The self-consistency relations (Eq. 7) are polynomial equations in the average spins, which link every spin s_ij only to the spins on the neighboring edges. Although in the general case a solution is obtained only numerically, it is much simpler to solve than the typical rate-distortion expression (e.g., ref. 6). More importantly, it provides insight into the “low-temperature” (low w_C) regime where the landscape of the code's free energy is rugged and therefore hard to calculate.

To make use of the equivalence between the spin system and the coding network, we need to express the average network occupancies, e_ij = 〈E_ij〉 and v_i = 〈V_i〉 as a function of the average spin s_ij. The average edge-occupancy is given by e_ij = (1/2)∂ ln Z_S/∂ ln b_ij = g_ijs_ij/2, a consequence of Eqs. 5–7. Likewise, the average vertex-occupancy is v_i = ∂ ln Z_S/∂ ln a_i = h_i (see Methods). Thus, one can calculate the average network configuration (that is the average code) for any value of the fugacities a_i and b_ij, or for the equivalent control parameters of the coding system, w_D, w_C, r_ij, and n_m. This is demonstrated below, where a first-order “coding transition” is deduced from the spin formalism.

Mean-field models similar to the one used here are standard in n = 0 treatments of self-assembling systems, such as polymer and micellar solutions (14, 15) and networks (13). The basic idea of the mean-field approach is to replace the spin–spin interactions by an interaction of a single spin with an effective field (the g_ij polynomials). This procedure vastly simplifies the problem and enables a relatively simple solution. However, this simplicity comes at the cost of disregarding the long-range spatial correlations between the spins and the corresponding correlations between the edges and the vertices. This implies, for example, that one can estimate the mean connectivity in the network but cannot tell how many loops it contains. In general, a mean-field treatment merely approximates qualitatively the behavior of thermodynamic functions. However, the accuracy of this approximation improves when each spin interacts with many neighbors. Therefore, when the symbol graph is highly connected—such as the graph of the genetic code, where each codon has nine neighbors—the mean-field approximation is expected to be relatively accurate and provides a basis to more elaborate models.

A First-Order Coding Transition.

The equivalence of the spin system and the code-table enables us to follow the evolution of the code-table in response to variation of the control parameters that govern its optimization: the cost weight w_C, the misreading matrix r_ij, the diversity weight w_D, and the number of meanings n_m. These parameters are not independent but related through the spin fugacities, a and b_ij, or the equivalent edge and vertex energies, α and β_ij. It proves convenient to represent these relations in terms of the normalized diversity, D = w_D/w_C + ln n_m = −ln a = α/w_C, and the normalized misreading probabilities, R_ij = r_ij/w_C = −ln(ab_ij²) = (α + β_ij)/w_C.

To examine the response of the code-table to variation of the four control parameters, we consider, for the sake of simplicity, regular symbol graphs, in which all of the vertices and edges are equivalent. Regular symbol graphs are useful in biological context. For example, a regular graph may approximate the symbol graph of the genetic code, where each of the 64 codons has 9 neighbors (2). Regular graphs may also describe large symbol spaces, for example the space of DNA binding sites of the transcription system, whose structure is not exactly known but whose average coordination number q is well determined. Regularity of the symbol graph implies uniform misreading r_ij = r and, as a result, homogenous average spin s_ij = s, and occupancies, e_ij = e and v_i = v. Because of symmetry, we need to solve a single self-consistence relation s = g(1 + g²/2)⁻¹ (Eq. 7) with g = 2ab((1 + bs)^q−1 − 1). The free energy per vertex of the dual graph is given by f = −h + (q/2)gs + (q/2)ln(1 + g²/2), where h = a((1 + bs)^q − qbs − 1) and q is the coordination number.

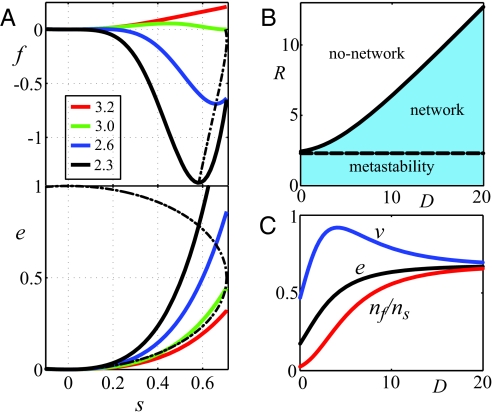
The resulting phase diagram of the regular symbol graph exhibits a line of first-order transitions, where the number of encoded meanings jumps discontinuously from n_f = 1, with a mapping that encodes a sole meaning, to a number n_f > 1 that scales extensively with the size of the symbol graph n_s (Fig. 3). The state n_f = 1 is termed noncoding, because the code-table in this state conveys no information because only one symbol is used. When a coding state, n_f > 1, emerges the coding system is capable of conveying information at a rate of log₂ n_f bits/symbol. Tracing the behavior of the free energy f as the scaled misreading R is varied (Fig. 3A), we find that at high R the system is at the noncoding, no-network state, as manifested in the profile of f by a global minimum at s = e = v = 0. This is because the system prefers to reduce the impact of misreading errors, which are too costly at a high R, at the expense of diversity. As R decreases, the system reaches the first-order transition, which occurs after a second, coding state minimum, s_C ≠ 0, emerges and exhibits f(s_C) = f(0) = 0.

Fig. 3.

The free energy and phase diagram of the code-table. (A) Free energy f (Upper) and the edge occupancy e (Lower) of the regular hexagonal symbol graph (Fig. 1) at scaled diversity D = 3.0 and scaled misreading R = 3.2, 3.0, 2.6, 2.3 (legend). All of the curves exhibit an extremum at the no-network state s = 0. At the coloring transition (green curve), the second minimum that corresponds to the network state s_C is at f(s_C) = f(0) = 0. At lower values of R, the network state becomes the global minimum. At R = (2q − 2) the no-network state is destabilized (black). The dashed curve traces the loci of the network state as R varies. These loci are found at the intersection of the edge density e = gs/2 and the ellipse 2s² + (2e − 1)² = 1 (Lower). (B) Phase diagram of the coding (network ↔ no network) transition (solid line) in the D–R plane. The dashed line bounds the region of metastability, beyond which the no-network state is destabilized. (C) Vertex occupancy v, edge occupancy e, and ratio meanings/symbol n_f/n_s along the transition line (see text).

In the D–R plane (Fig. 3B), the phase transition line approaches a straight line, R ≈ (1 − 2/q)D, which corresponds to a q-fold junction whose “energy” equals the thermal energy w_C, α + (q/2)β ≈ w_C. In other words, the system undergoes a phase transition when q-junctions become thermally excitable. Because q-junctions are the majority species, the emergent network is dense and highly connected. The transition line indicates various pathways that the system can take toward the formation of a network at a coding state: increasing the number of available meanings n_m, increasing the diversity parameter w_D, and decreasing the misreading r.

At the transition, the number of meaning islands n_f jumps abruptly and becomes proportional to the number of symbols (Fig. 3C). n_f is given by Euler's characteristic (Eq. 3) with the average edge occupancy e = gs/2 and vertex occupancy v = h. This implies that the number of meanings per symbol is n_f/n_s = χ/n_s + (p/2)e − (p/q)v, where p is the coordination number in the symbol graph and q in the dual graph. The curves of the vertex and edge occupancies approach a common high D limit, e, v → e₀ = a(bs)^q, where the resulting meanings/symbol ratio is n_f/n_s = p(1/2 − 1/q)e₀. For planar regular graphs, 1/p + 1/q = 1/2 and n_f/n_s = e₀. In Discussion, we examine possible effects of population dynamics on the evolution of the code.

Discussion

The mean-field solution allows us to draw an approximate fitness landscape where the evolution of the code takes place. In general, this code fitness landscape F_S(s_ij) (see Eq. 6) resides in a high-dimensional code space, whose coordinates are the average spins s_ij or their conjugates, the average edge occupancies e_ij. Each point in this space is a vector s = (s_ij …) of dimension equal to the number of edges, which represents a possible code. Symmetry may reduce this dimensionality, and for the regular symbol graph it becomes one-dimensional f(s) (Fig. 3). We imagine a population of “organisms,” simple information-processing systems, which compete according to the fitness of their codes. Each organism is depicted as a point in code space positioned at its code s, and the population is described by a probability density Ψ(s). The preceding discussion assumed implicitly that, as the control-parameters change, the evolution of the code more or less follows the track of the optimum in code space. In other words, the population density is a delta-distribution located at the optimal F_S. We conclude this work by considering several more realistic scenarios. First, we discuss the possibility that the coding system is stuck at metastable suboptimal states. Then, we consider mutations and genetic drift that may broaden the population toward codes of less optimal fitness.

Metastable Suboptimal Codes.

Even when the global optimum in the code fitness is at a network state, s_C ≠ 0, the no-network state, s = 0, may remain locally stable for some parameter range (Fig. 3B). To locate the metastable state, one examines the curvature of the free energy at its s = 0 extremum, which in the case of an isotropic symbol graph is f″ = ∂²f/∂s² ∼ 1 − 2(q − 1)e^R. A metastable state exists as long as this curvature is positive. We find that the curvature changes its sign at the line R = ln(2q − 2), which corresponds to a “monomer” (a vertex plus an edge) of energy α + β = w_C ln(2q − 2). This may be further clarified by considering the limit of the vertex/edge occupancy ratio near the no-network state, v/e → q/2. Because there are q/2 edges per vertex, this indicates that the dominant building block of the dilute network is the monomer. Thus, a coding system becomes unstable exactly when the monomers become “thermally excitable,” compared to the q-junctions that are excitable at the coding transition.

Effects of Mutations and Genetic Drift in the Codes Space.

So far, it was assumed that the population of organisms is sharply concentrated around a certain optimal or metastable, suboptimal code. This scenario applies to large populations at negligible mutation rates μ. Let us consider two possible effects of population dynamics that may smear the population over the code space, mutations and genetic drift. These effects were analyzed in detail within the framework of rate-distortion theory (6) and are discussed here only schematically, in the context of the present polymer network model.

We consider a population that is localized around a fitness optimum f₀ at an optimal code s₀, where the landscape is approximately f(s) ≈ f₀ + ½f″(s − s₀)² [a regular graph with a one-dimensional fitness f(s) is assumed for simplicity]. Mutations drive the organisms to diffuse into somewhat less optimal regions of the code space. This effect may be described in terms of reaction-diffusion dynamics of the probability distribution (6), ∂_tΨ = μ·∂_s²Ψ − f(s)Ψ, where the first term is due to mutations and the second represents reproduction at a rate −f(s). It is straightforward to find that this dynamics tends to a steady state, in which the population is broadened into a Gaussian, Ψ(s) ∼ exp[−(f″/2μ)^1/2(s − s₀)²] of width that scales like ∼(μ/f″)^1/4 (6). It implies that the width of a population at a metastable state (s = 0) will diverge near the metastability limit (f″ = 0) just before the Gaussian migrates to the coding state (s_C ≠ 0).

When the effective population size N is relatively small, fluctuations in the reproduction rate, termed genetic drift, become significant. In this regime, the dynamics is characterized by long periods when the population is localized around a fitness optimum, which are separated by fast diffusive migrations to new optima (6). The dynamics of the distribution is known to reach a Boltzmann partition, Ψ(s) ∼ exp(−Nf(s)), where the population size plays the role of an inverse temperature. Relatively small populations (which are “hot” in this sense) are expected to be partitioned by genetic drift between the available fitness optima. For example, the two minima of the free energy f(s) (Fig. 3) will be populated according to their fitness values.

In the previous sections, we have shown that each organism experiences “internal” noise due to stochastic molecular recognition in its coding system. The internal noise affects the fitness of the code through the error load and the cost (16). On top of this, mutations and genetic drift add “external” sources of noise, which may drive parts of the population away from the optimal code. The existence of metastable states may further delay the transition to a coding state. The present model and its conclusions suggest that the n = 0 polymer network formalism is a potential tool to study several other aspects of noisy coding systems.

Methods

Cost of a Code-Table.

The cost of a code-table is traditionally measured by the mutual information I between the symbols and the meanings that they encode, I = S_ME + S_SY − S_MS, where S_ME and S_SY are the entropies of the meaning space and symbol space, respectively, and S_MS is the joint entropy of these two spaces. The entropy of meanings S_ME is determined by their given distribution P_α, S_ME = −Σ_αP_α ln P_α, and similarly, S_SY = −Σ_iP_i ln P_i = ln(n_s). These are constant terms in the cost I that we can neglect, and consider only the joint entropy S_MS, which can be optimized by tuning the average partition pattern e_ij. S_MS is simply the entropy of all of the possible coloring patterns as determined by all possible networks and the number of possible ways to color every such pattern. It follows that the cost is therefore minus the coloring entropy I = −S_MS = −S_C.

Graph Embedding and the Dual Graph.

The embedded graph divides the surface into faces or cells, hexagons in our example (Fig. 1). Then, one finds the dual graph by the following correspondence (10): Every vertex in the symbol graph corresponds to a cell in the dual (a triangle in this example) whereas every cell in the symbol graph (a hexagon) corresponds to a vertex of the dual. The correspondence between the edges in the symbol graph and its dual is one-to-one; every edge corresponds to the edge that crosses it in the dual. The resulting dual graph is a triangular lattice. The hexagonal lattice is a regular graph in which all of the vertices have the same coordination number. However, the embedding procedure described here applies to any connected graph whether it is regular or not.

Mean-Field Approximation.

The spin probability distribution decouples into a product of independent single-spin distributions, ρ = ∏_ijρ_ij(S_ij). We use a variational inequality, which sets an upper limit on the spin free energy, F_S ≤ F_M = 〈ρH_S〉 + T〈ρ ln ρ〉, where ρ satisfies probability conservation, 〈ρ〉 = 1. We augment F_M with a Lagrange multiplier to account for probability conservation, L = F_M + η〈ρ〉, and take the derivative δL/δρ_ij = 0. The resulting distributions are ρ_ij(S_ij) = exp(g_ijS_ij)/〈exp(g_ijS_ij)〉, where the effective fields are g_ij = ∂H_S/∂S_ij = ∂(h_i + h_j)/∂S_ij = a_ib_ij[∏_k(i)≠j(1 + b_iks_ik) + ∏_k(j)≠i(1 + b_jks_jk) − 2] with s_ij = 〈ρS_ij〉 = 〈S_ijρ_ij(S_ij)〉. From the n = 0 property, it follows that 〈exp(g_ijS_ij)〉 = Σ_k g_ij^k〈S^k〉/k! = 1 + g_ij²/2 and 〈S_ijexp(g_ijS_ij)〉 = g_ij. This leads to the self-consistency relations, s_ij = 〈S_ijρ_ij(S_ij)〉 = 〈S_ij exp(g_ijS_ij)〉/〈exp(g_ijS_ij)〉 = g_ij(1 + g_ij²/2)⁻¹ (Eq. 7). In a similar fashion, we obtain the mean-field approximation for the free energy, F_S ≈ F_M = −Σ_ih_i + Σ_i−jg_ijs_ij − Σ_i−j ln(1 + g_ij²/2), and it is easy to verify that Eq. 7 defines the extremum ∂F_S/∂s_ij = 0. Eq. 7 is analogous to the self-consistency relation of an Ising magnet, s = sinh(gs)/cosh(gs); the different form is due to the truncation of the power-series expansion of the hyperbolic functions thanks to the n = 0 property. Solving Eq. 7 for g_ij as a function of s_ij, we find that the solution can be described graphically as the points where the function e_ij = g_ijs_ij/2 crosses the ellipse 2s_ij² + (2e_ij − 1)² = 1 (Fig. 3A).

Use of Euler's Characteristic.

When we apply Eq. 3, an underlying assumption is that the embedding is cellular (10); i.e., every meaning island is homeomorphic to an open disk. This is not necessarily true when the number of islands is less than the number of holes in the surface, that is the genus, γ = 1 − χ/2. In this case, some islands are expected to wrap between two holes and therefore are not homeomorphic to a disk. However, in the “thermodynamic limit” of many islands per hole, n_f ≫ |χ|, the embedding is mostly cellular and is well approximated by Eq. 3.