Protein model refinement using an optimized physics-based all-atom force field

Abstract

One of the greatest challenges in protein structure prediction is the refinement of low-resolution predicted models to high-resolution structures that are close to the native state. Although contemporary structure prediction methods can assemble the correct topology for a large fraction of protein domains, such approximate models are often not of the resolution required for many important applications, including studies of reaction mechanisms and virtual ligand screening. Thus, the development of a method that could bring those structures closer to the native state is of great importance. We recently optimized the relative weights of the components of the Amber ff03 potential on a large set of decoy structures to create a funnel-shaped energy landscape with the native structure at the global minimum. Such an energy function might be able to drive proteins toward their native structure. In this work, for a test set of 47 proteins, with 100 decoy structures per protein that have a range of structural similarities to the native state, we demonstrate that our optimized potential can drive protein models closer to their native structure. Comparing the lowest-energy structure from each trajectory with the starting decoy, structural improvement is seen for 70% of the models on average. The ability to do such systematic structural refinements by using a physics-based all-atom potential represents a promising approach to high-resolution structure prediction.

The past several years have witnessed significant progress in the field of protein structure prediction (1–10), with contemporary methods being able to assemble the correct topology for a large fraction of protein domains. Such approximately correct models typically vary in their structural similarity to the native state, with a rmsd (root mean square deviation) from native that ranges from 1 Å to ≈6 Å. Models with a rmsd to native of 1–2 Å are comparable to experimentally obtained structures and can be used in a broad range of applications, including studies of reaction mechanisms and virtual ligand screening (2). In contrast, the range of applicability of lower-resolution models (with a 3- to 6-Å rmsd from native) is smaller (2). Structure prediction methods often use a coarse-grained protein representation to enhance the conformational search efficiency. To further improve model quality, it is possible that additional structural details need to be included. A tempting approach is to use an all-atom detailed protein representation for the final stages of structure prediction, but despite considerable effort, all-atom refinement has seen little success (11–13). Over the years, there have been individual examples of successful refinement (11–16), with the best improvement of ≈2 Å (12, 16) and the largest refinement benchmarks consisting of a small set of proteins (12, 13, 17–19). Although isolated examples of refinement have been reported, the methods are far from routine; in reality, most models deteriorate instead of improve.

In protein structure prediction and refinement, the challenge is twofold: one needs an effective conformational search scheme and an energy function whose global minimum is in the protein's native state. Moreover, the energy surface should be funnel-like so that the potential can drive the structure toward lower energy, more native-like conformations. For this to occur, the energy function must have a correlation with native structure similarity (20). Previously (21), we explored the possibility of creating a funnel-like shape for the Amber ff03-based potential (22) by global optimization of the weights of the individual energy components. The optimized force field had a significant correlation with native similarity and, for decoy evaluation, could recognize the native conformation among decoy structures for a large fraction of proteins examined. Here, we test the refinement ability of the newly derived potential on a representative benchmark set of 47 proteins (among them, eight proteins were a part of the training set used in the optimization of the force field, and the remaining 39 proteins composed the testing set), each having a diverse set of compact all-atom decoy structures. In the following, we first describe the correlation of the energy with native-likeness of the decoys obtained in the refinement conformational search. Next, we discuss the improvement of decoy structures within each individual refinement trajectory. Finally, we present the results of structural refinement over the best initial models in the entire decoy ensemble and discuss the ability of the force field to select structures close to the native state from the entire decoy set.

Results and Discussion

Correlation of the Energy with Native Similarity as Measured by the Template Modeling Score (TM-Score).

The ability of a force field to refine a model and select the native or close to native structure by using energy as the selection criterion is related to the correlation of its energy with native structure similarity. The force field used in this study had an average correlation coefficient of energy with TM-score [a measure of structural similarity (23) whose range is (0, 1], with a TM-score of 0.3 for the best structural alignment of a pair of randomly related structures and 1.0 for identical structures] of 0.59 after global optimization as calculated on a large decoy set of 58 proteins (21). Moreover, for 47% of the tested proteins, the correlation coefficient was significant, above 0.60. However, the decoys were generated by using a different force field, the ff03 Amber potential (22). This high correlation coefficient of energy with native-likeness might be an artifact of optimization and could be lost during a thorough conformational search that is driven by the new potential. To explore this issue, we calculated the correlation coefficient (CC) between the energy and TM-score for the structures generated during conformational refinement by using the optimized force field for the 39 protein test set [see supporting information (SI) Table S1]. The resulting average value of CC was 0.59, with 46% of the proteins having the CC above 0.60; this corresponds well to previously obtained values after force field optimization and decoy ranking (21). Therefore, during the conformational search, the characteristics of our optimized energy landscape are preserved. Fig. S1 shows examples of the energy–TM-score clouds for the unoptimized original ff03 force field and decoys generated with the original ff03 potential (Fig. S1A), the optimized force field and decoys generated with the original ff03 potential (Fig. S1B), and the optimized force field and decoys generated with the optimized force field during the refinement runs (Fig. S1C).

For selection of the correct structure on the basis of energy, the most important quantity is the correlation of the minimum energy structure at a given TM-score with native structural similarity. This correlation of energy vs. TM-score for decoys obtained during the refinement search was 0.44, with 46% of proteins having a CC >0.6 and 51% having a CC >0.5. The corresponding correlation for the decoy set used in force field optimization and decoy ranking was 0.49, with 33% of proteins having a CC >0.6 and 53% having a CC >0.5.

Refinement of Protein Decoys.

Improvement within a trajectory.

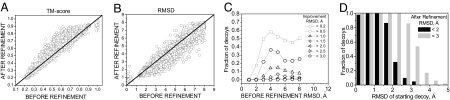
For each member of the 39-protein test set, the ability to refine 100 starting structures spanning a range of TM-scores was examined. During refinement, the TM-score and C^α rmsd improve for the majority of the decoys. In Fig. 1, the TM-score (A) and C^α rmsd (B) to the native structure of the lowest-energy decoy from each refinement trajectory are compared with the initial decoy TM-score and rmsd. For TM-score compared to rmsd, we observe a more pronounced improvement than decoy deterioration. This reflects the fact that the force field was optimized as a function of the TM-score, not the rmsd. Furthermore, the TM-score is generally more sensitive to native-like features. Sometimes improvements in TM-score may cause an increase of rmsd from the native structure, e.g., when the core of a protein is improved at the cost of moving a protein's termini farther from the native state. Below rmsd values of 1 Å (or TM-scores above 0.9), the force field cannot differentiate among structures. This insensitivity is evident in Fig. 1, where the native structures (TM-score close to 1) drift away from the crystal structures on average by ≈0.1 TM-score unit or by a rmsd of 1 Å. This drift defines the resolution of the force field, which corresponds to a C^α rmsd of ≈1 Å from the native state.

Fig. 1.

For all refinement trajectories, results of decoy structure refinement within each trajectory (100 decoys per protein, 39 proteins). (A and B) TM-score (A) and C^α rmsd (B) to the native structure of the lowest-energy decoy after refinement versus decoy's initial TM-score (A) or C^α rmsd (B). (C) Fraction of decoys that refined by more than a given C^α rmsd threshold (for 0.2-, 0.5-, 1.0-, 1.5-, and 2.0-Å rmsd thresholds) with respect to their initial native similarity. (D) Fraction of decoys that refined to (or remained within) the accuracy of 2-Å (black) and 3-Å (gray) C^α rmsd to the native state with respect to their initial native similarity. Fractions of decoys were calculated in 1-Å bins.

On average, with respect to the initial structure and over the whole range of native similarity, 70% of decoys improve their TM-score, 18% get worse, and 12% are unchanged (Fig. 1A). When rmsd (Fig. 1B) is used, 70% of decoys improve, 28% deteriorate, and 2% are unchanged. In Fig. 1C, we show the fraction of decoys that improved by more than a given rmsd value with respect to the decoy's initial rmsd. For 37% of decoys with initial rmsd of 3–4 Å, we observe improvement of >0.5 Å, and for 14%, the improvement was >1.0 Å. There are 28 cases of improvement compared to only 3 cases of deterioration larger than 2 Å (with the largest improvement being 3.63 Å and largest deterioration being 2.21 Å).

The ultimate goal, however, is to refine structures to near experimental accuracy, i.e., below 2- to 3-Å C^α rmsd to the native state. In our benchmark, as shown in Fig. 1B, a significant fraction of decoys improved to such accuracy; we refined 12%, 10%, and 4% of all of the decoys to an rmsd below 3, 2.5, and 2 Å, respectively, starting from structures with initial rmsd greater than the given threshold. Especially encouraging is that some of the refinements to near experimental accuracy occurred for the decoys that were 4–6 Å away from the native state; there are also improvements from above 3 Å to below 1.5 Å. The fractions of decoys that improved to an rmsd of 2 and 3 Å with respect to their initial rmsd to the native state are presented in Fig. 1D. We observed refinement below 2 Å rmsd for 34% of decoys with initial rmsd between 2 and 2.5 Å; an rmsd below 3 Å was obtained for 54% of decoys with an initial rmsd between 3 and 3.5 Å. Refinement below an rmsd of 2 Å is seen for decoys that were as far from the native state as 4 Å; improvement below 3 Å rmsd was seen even for decoys with initial rmsd 6 Å to the native structure. An improved sampling scheme may allow us to achieve larger improvement in structure and enable the refinement to experimental accuracy for decoys more structurally distant from the native state (above 4 Å).

More detailed analysis of the refinement results, demonstrating a domination of structural improvement over deterioration can be found in Fig. S2. Note that the native state is reasonably stable and deteriorates on average by only ≈0.05 TM-score unit, or 0.65 Å in rmsd.

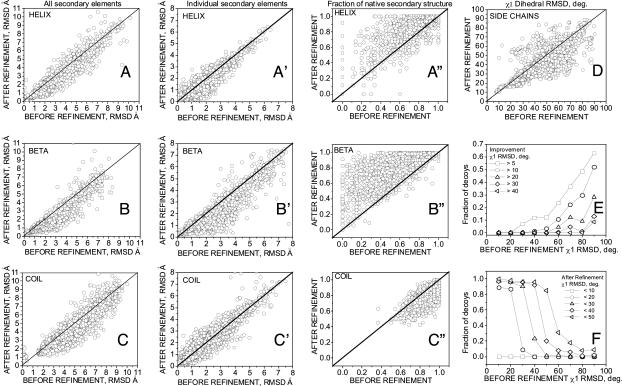
We also analyzed the improvement of different structural protein elements, i.e., helices, β-sheets, and loops. In Fig. 2 A–C and A′–C′, the C^α rmsd to the native structure for helices (Fig. 2 A and A′), β-sheets (Fig. 2 B and B′), and loops (Fig. 2 C and C′) for the lowest-energy decoy from each trajectory is shown with respect to its initial rmsd (see Materials and Methods for secondary structure definitions). In Fig. 2 A–C, we consider all of the secondary structure elements of a given type from the native structure superimposed together onto related elements in a decoy (e.g., all of the regions that are helical in the native structure were superimposed with the same regions in the decoy). This comparison, therefore, includes both the relative orientation and geometry of all secondary structure elements. In this analysis, we obtained improvement for 67%, 81%, and 66% of decoys over helical, β-sheet, and loop regions, respectively. The average improvement/deterioration was 0.41/0.27 Å for helices, 0.48/0.24 Å for β-sheets, and 0.58/0.39 Å for loop regions. The distribution of structural improvements with respect to the initial rmsd over secondary structure is shown in Fig. S3 A–C. For example, improvements larger than 1.0 Å are observed for ≈10% and 23% of decoys with initial rmsd between 3 and 4 Å over helical (Fig. S3A) and β-sheet (Fig. S3B) structures, respectively, and for ≈25% of decoys with initial rmsd between 4 and 5 Å over loop regions (Fig. S3C).

Fig. 2.

Results of decoy structure refinement within each trajectory (100 decoys per protein, 39 proteins) for different structural elements. (A–C and A′–C′) C^α rmsd to the native structure of the lowest-energy decoy after refinement versus the decoy's initial C^α rmsd, for helical (A), β-sheet (B), and loop (C) regions when all the native secondary structure elements of a given type are superimposed together onto the corresponding decoy regions, and for helices (A′), β-sheets (B′), and loops (C′) when individual secondary structure elements from the native are superimposed onto related decoy regions. (A″–C″) Comparison of fractions of the native secondary structure in the refined (lowest-energy decoy from each trajectory) and the initial decoy, for helical (A″), β-sheet (B″), and loop (C″) regions. (D–F) Refinement of packing of buried side chains. (D) χ1 rmsd (degrees) to the native structure of the lowest-energy decoy after refinement with respect to χ1 rmsd of the initial structure. (E and F) Fraction of the lowest-energy decoys that improved their χ1 rmsd by more than (E) or below (F) a given threshold with respect to χ1 rmsd of the initial structure. Fractions of decoys were calculated in 10° bins.

In Fig. 2 A′–C′, we considered each secondary structure element separately (e.g., each individual helix from the native structure was superimposed onto the related region in the decoy). In this analysis, only refinement of the secondary structure is considered, without the orientation component. We see improvement for 70%, 76%, and 50% of decoys for the helical, β-sheet, and coil regions, respectively. The distribution of structural improvements with respect to the initial rmsd over individual secondary structure elements is shown in Fig. S3 A′–C′. Improvements larger than 1.0 Å are observed for ≈3%, 21%, and 2% of decoys with initial rmsd between 3 and 4 Å over helical (Fig. S3A′), β-sheet (Fig. S3B′), and loop (Fig. S3C′) regions, respectively.

In Fig. 2 A″–C″, the assignment to secondary structure class between the native structure and decoys is compared. The fractions of the native helical (Fig. 2A″) and β-sheet (Fig. 2B″) content improve for the majority of the decoys. The fraction of native coil (Fig. 2C″) decreases; we observe some tendency of our force field to turn coil residues into helical conformation.

Refinement is seen on average for all secondary structure types, including loop regions, which are recognized as the most difficult to refine. Both the orientation and geometry of individual secondary structure elements improve. However, the refinement of loops is more pronounced in the correction of their relative orientation than in the improvement of the internal structure of individual loops.

Our force field was optimized only with respect to the correlation of the energy with the main-chain native similarity; the side-chain geometry has been neglected in the optimization process. Despite this neglect, we observe an average improvement in the χ1 dihedral angles of the side chains in the protein interior. Fig. 2D shows the χ1 rmsd of the buried side chains to the native structure for the lowest-energy decoy from each trajectory with respect to the initial decoy's χ1 rmsd (see Materials and Methods for explanation of the χ1 rmsd calculation and the definition of buried side chains). Side-chain packing improves for 68% and declines for 32% of the decoys, as judged by χ1 rmsd. The extent of improvement is large for larger initial distortions of χ1 (Fig. 2E); the largest improvements are >40°. In Fig. 2F, the fraction of decoys that improved their side-chain packing below a given threshold of χ1 rmsd is shown with respect to the initial χ1 rmsd. For 20% of the decoys with an initial χ1 rmsd between 40° and 50°, the χ1 rmsd decreases below 40°.

In Fig. S4, we show the fractions of decoys that improve/deteriorate for each protein in the entire 47-protein set. For most proteins, more than 50% of the decoys improve. Only 4 proteins, 1a19A, 1b9wA, 1c1yB, and 1dt4A, have less than a 50% improvement (with only 1b9wA and 1dt4A having more deteriorations than improvements). There are 9 proteins in the set that contain disulfide bonds (1a43, 1aazA, 1bunB, 1bvnT, 1cc7A, 1dtdB, 1f94A, 1b9wA, and 1cbp). Their refinement results are on average worse (61% improvement and 26% deterioration, as measured by the TM-score) than those for the remaining proteins. This observation indicates the need to include a disulfide bond potential in the force field; this inclusion is especially important for small proteins whose fold is mainly held together by S–S bridges.

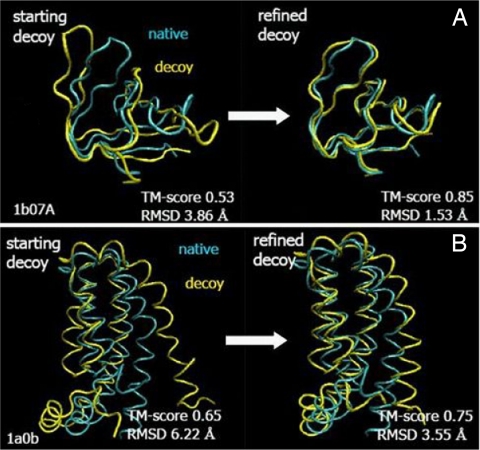
Some examples of refined structures are shown in Fig. 3. The largest observed improvement in TM-score was 0.32 (from 0.53 to 0.85 for 1b07A). Based on the above results, we conclude that our optimized force field enabled significant and systematic refinement of protein structures with respect to the set of initial decoy structures.

Fig. 3.

Examples of refinement for 1b07A (A) and 1a0b (B). Models (yellow) are superimposed onto the native structure (blue).

The focus of our method is the refinement of already folded and well packed models predicted by a coarse-grained method (e.g., TASSER). Therefore, our potential was optimized (21) for decoys within the rmsd range of 0–8 Å and TM-score range of 1–0.4 to the native state. For more distant structures, a correlation of energy with native similarity is not expected. Therefore, we did not test the ability to refine the decoys with an initial rmsd to the native structure >8 Å. However, most of the conformations sampled during our search that had a C^α rmsd >8 Å had high energies.

Structure refinement from an ensemble of structures below a given TM-score.

Previous analysis showed the refinement performance within each decoy trajectory; the lowest-energy structure was chosen from each decoy trajectory and separately compared with the starting decoy. In this section, we analyze the improvements over the best structure in the entire ensemble of the initial decoys whose TM-score was smaller and rmsd was larger than a given native structure similarity threshold. We considered TM-score thresholds of 0.8, 0.7, …, 0.4 and C^α rmsd ranges of 2.0, 3.0, …, 6.0 Å to the native state. For example, for a 0.7 TM-score threshold, for each protein we consider all of the refinement trajectories that started from structures with a TM-score ≤0.7. From each trajectory, the lowest-energy decoy is chosen; the decoys are then sorted by energy, and the best of the top five refined decoys is compared against the best initial structure within the given range; in this example, the best initial structure will have a TM-score ≤0.7, and we explore whether the top five lowest-energy refined structures have a TM-score ≥0.7.

A significant correlation of the bottom of the TM-score/rmsd-energy cloud is necessary to successfully choose the good structure on the basis of its energy. Therefore, in this analysis we focus only on the 20 proteins in the test set (marked in Table S2) that had an energy–TM-score correlation at the bottom of the energy–TM-score cloud >0.50. Such an analysis resembles a real prediction/refinement scenario, where a prediction method delivers many low-resolution models of unknown native similarity and the goal of refinement procedure is to improve structure over the best model.

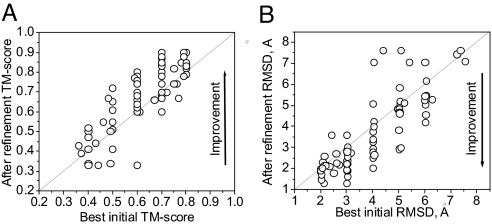
In Fig. 4 the TM-score (A) and C^α rmsd (B) to the native structure of the best of five lowest-energy decoys from all of the refinement trajectories starting from structures in a given TM-score range is compared with the best initial decoy TM-score or rmsd in this range. Overall, we see more improvement than deterioration with respect to the best initial structure in the specified TM-score range, with maximum of 81% of proteins having structural improvements in the range of TM-score <0.6 (Fig. S5A), and 78% of proteins having structures that improve in the range of rmsd >3 Å (Fig. S5). In conclusion, this stringent test of the refinement ability of our method gives promising results.

Fig. 4.

Results of the refinement of decoy structures over the entire ensemble of decoys above a given native similarity threshold (each circle represents one protein; the 20 testing proteins with energy–TM-score correlation coefficient larger than 0.5 for the bottom of the energy–TM-score cloud are used). (A and B) TM-score (A) and C^α rmsd (B) to the native structure of the best-of-five lowest-energy decoys after refinement with respect to the TM-score of the best initial structure within a given native similarity bin; e.g., for a threshold of 3 Å, for each protein we consider all the decoys with initial rmsd in the range 3–8 Å, and we compare the lowest initial rmsd in this range against the rmsd of the best-of-five lowest-energy decoy after refinement that had initial structure within this range. The analysis is repeated for each native similarity bin, i.e. 0.8–0.2, 0.7–0.2, …, 0.4–0.2 for TM-score, and 2–8, 3–8, …, 7–8 Å, for rmsd (this explains why there are more than 20 circles in the figure).

The previous analysis provided insight into the quality of decoy structures that are likely to be improved by this refinement procedure. Next, we explore our ability to select good protein structures out of the entire ensemble of structures that would be generated in a realistic prediction scenario. Thus for each protein, we analyze the TM-score and rmsd to the native state of the best of five lowest-energy decoys (highest TM-score or lowest rmsd) from the entire set of decoy structures sampled during the refinement search. In Fig. S6, we show the fraction of proteins for which the best of five lowest-energy refined structures had a TM-score larger (Fig. S6A) or rmsd lower (Fig. S6B) than the specified threshold value. Here, we consider all 39 test proteins that were not used for force field optimization (21). A stringent test of the force field that reflects real prediction conditions is to examine the quality of the lowest-energy structures when native decoys are excluded. Sixty-eight percent of the proteins have best-of-five lowest-energy structures with a TM-score to the native state above 0.70 (Fig. S6A, gray bars) and 77% have a C^α rmsd below 3.5 Å (Fig. S6B, gray bars). When the trajectory of the native structure is included, for 87% of proteins, the best-of-five lowest-energy structures has a TM-score to the native state above 0.7 and for 90% it has a C^α rmsd below 3.5 Å (Fig. S6, black bars). Structures coming from the native trajectory are usually better packed than decoys and therefore favored by energy. The discrepancy between results when the native trajectory is included/excluded points out the need for better conformational sampling.

We additionally consider the quality of the lowest-energy conformation (results not shown in Fig. S6). When native decoys are excluded, 59% of proteins have the lowest-energy structure with a TM-score above 0.70, and when native decoys are included, 79% have the lowest-energy structure with a TM-score above 0.70; 66% (native decoys excluded) and 82% (native decoys included) of proteins have the lowest-energy structure with an rmsd below 3.5 Å. Based on the above results, we conclude that the ability of the force field to find the native-like structures among decoys is quite good.

Analysis of Possible Reasons for the Observed Refinement.

We performed numerous analyses to establish the significance of our refinement results. One of the common problems in the training of potential functions is the decoy generation procedure (20). Some decoy sets contain certain characteristics that are easy to memorize during training, but are not transferable to other decoy sets. A classic example is the effect of “swollen” decoys, where the decoy set has a large correlation between native similarity and radius of gyration (CCRG) (21). With such a correlation, the recognition of the nearest-native structure is trivial: just pick the best-packed model. In contrast, the average CCRG for decoys in our set of 47 proteins is small (0.4). To ensure that the improvements are not dominated by those proteins with highest CCRG, for each protein we compared the correlation between native-similarity and the radius of gyration with the fraction of decoys that improved during the refinement. Although the fraction of improvements is on average a little higher for proteins with high CCRG, such a cross-correlation is only 0.4. There are proteins whose decoy set has a very low CCRG (e.g., 0.15) and yet >70% of their models improve during refinement. Improvement in structure quality dominates over deterioration also for decoys that are better packed than the native structure (smaller radius of gyration). Monitoring the extent of decoy improvement with respect to the contact order (24) of the decoys, instead of the radius of gyration, gives similar results. Although significant improvements are observed more often for decoys with lower contact order, the overall correlation between the rate of improvement and the initial contact order with respect to the native is low. Finally, we also found that structure improvement does not depend on the number of hydrogen bonds (normalized by the protein length). Decoys of β-type structures tend to refine slightly better than α-helix-containing protein structures, but a larger protein set is needed to confirm this tentative observation.

Conclusions.

In our previous work (21), we optimized a physics-based, all-atom energy function derived from the Amber ff03 potential to improve the correlation between native similarity (represented by the TM-score) and energy. Here, we tested the ability of such a funnel-shaped potential to refine decoys of 47 single-domain, nonhomologous proteins with different folds, 39 of which were not a part of the optimization protein set. When the lowest-energy structure from the particular refinement conformational search trajectory is compared with the starting decoy, we observe structural improvements for 70% of the models on average; 10% of decoys refined to near experimental accuracy, below 2.5 Å. Such systematic refinement results suggest a promising approach to high-resolution structure prediction. In a more stringent test, when the best (of five lowest-energy) refined structures selected by their energies are compared against the best available starting decoy within a given native similarity range, we see improvement for the majority of proteins that have a significant correlation of energy with TM-score.

As we discussed previously (21), the optimized force field used here does not include the electrostatic energy and generalized Born solvation (25) terms present in the original Amber ff03 force field (22). For the set of compact decoys used for force field optimization, these energy terms were uncorrelated with native-likeness and their relative weights were small. The lack of these terms might cause the appearance of some low-energy, unphysical structures during the conformational search, e.g., the burial of hydrophilic residues in the protein core. However, during the course of our refinement simulations, we did not observe such low-energy unphysical structures. Their absence can be attributed partially to the rather local conformational search during refinement that starts from already packed structures. For purposes of refinement, the exclusion of these energy components carries the advantage of faster energy evaluation and concomitantly more extensive conformational sampling for a given amount of simulation time.

We do not observe a significant correlation between the successful refinement and decoy radius of gyration, contact order, or number of hydrogen bonds per residue. Decoys of β-type structures tend to refine slightly better than those of α-type structures, probably because of the relatively large contribution of the hydrogen bond energy that is more sensitive to the misfolding of β-sheets, whereas the geometry of helices is rather insensitive to such effects. Finally, based on the results for small disulfide-bonded proteins, a better treatment of S–S bridges is required.

The direct comparison with the results of others is difficult because each group uses different procedures, refinement criteria, and different sets of proteins; however, none of the previously examined sets was large enough to be statistically significant. The status of previous work can be found in the SI Text.

Overall, we have demonstrated successful refinement for the majority of testing proteins over a range of lengths and with different secondary structure classes. The protein decoy structures systematically improve over all ranges of native similarity and for all major structural elements, i.e., helices, β-sheets, and loops; only for structures below the resolution of the potential, i.e., with a rmsd to native below 1 Å or a TM-score above 0.9, does this conclusion not hold. We also see improvement of side-chain packing in the interior of the protein. However, it is important to recognize that these results have been demonstrated for protein structures that satisfy the following: (i) the proteins are single-domain monomers, without cofactors; (ii) the decoys are compact, spanning the range of 0–8 Å C^α rmsd to the native structure; and (iii) the conformational search typically did not explore global changes in structures. It may be possible to apply our refinement protocol to low-resolution decoys directly generated by the TASSER coarse-grained force field (1) so that we can begin to address the end game of protein structure prediction: protein structure refinement that has been a long-sought goal of hierarchical approaches to protein structure prediction.

Materials and Methods

Conformational Search.

To search protein conformational space, we used the newly developed A-TASSER program, described previously (21). A-TASSER (for atomic-TASSER) represents the protein at atomic detail and employs the Replica Exchange Monte Carlo (REMC) (26, 27) search method with a Parallel Hyperbolic Sampling (PHS) acceptance criterion (28) to reduce higher energy barriers. A-TASSER uses three types of moves that change the torsional angles of the molecule: local “fixed end” moves (29), end moves, and the side-chain moves. During refinement, the bond lengths and valence angles were fixed at the values taken from the relaxed starting structures, after a gradient-based minimization with Amber ff03 force field (22). A detailed description of the A-TASSER search scheme can be found in the SI Text and in our previous work (21). We do note that enhancements in the move set are required.

Force Field.

The potential energy function used in this study to refine protein models is calculated according to Eq. 1:

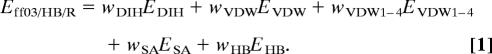In Eq. 1, the following abbreviations and symbols are used: E, total energy; w, weight of a given energy component; DIH, dihedral term; VDW, van der Waals component; VDW1–4, van der Waals energy for atom pairs separated by less than four bonds; SA, surface area-dependent term (the hydrophobic component of the solvation free energy); and HB, hydrogen bond term. The E_DIH, E_VDW, E_VDW1–4, and E_SA energy terms are identical with those used in the ff03 Amber force field. The E_HB hydrogen bond energy was implemented by following the DSSP approach (30) and was described previously (21). The weights of the energy terms, w (Table S3), were adjusted by using a global optimization method (31) for a large set of decoy structures of a representative 58-protein set (21). Optimization was aimed at maximizing the correlation of the energy with TM-score (23) and the energy gap between the native state and the decoys. The force field used in this study has an average correlation coefficient of energy with TM-score of 0.59 and ranks structures with TM-score >0.9 (native-like) as the lowest in energy for 72% of proteins, as calculated for the protein decoy set used in the optimization study (21).

Protein Set and Starting Decoy Structures.

We tested our method on 47 proteins, a subset of a previously prepared (23) comprehensive benchmark set, which covers the PDB library (32) with lengths from 41 to 200 residues at 35% sequence identity. The chosen proteins span lengths from 54 to 123 residues and represent different secondary structural classes. The list of proteins can be found in Table S1. Among them, eight (marked in Table S1 and in Fig. S4) were a part of the training set used in the optimization of the force field (21). These were excluded from most analyses to avoid any possible memorization effects. Only Fig. S4 shows results for all 47 proteins; all other results include only the 39 testing proteins. For each protein, we randomly chose 100 decoys from the force field optimization decoy set such that they span the range of C^α rmsd to the native structure from 0 to 8 Å. These 100 decoys per protein and the native structures in all-atom representation were starting models in our refinement benchmark.

Refinement Protocol.

For each decoy, we ran an A-TASSER search consisting of 1,000 swaps between replicas and 200 steps of Parallel Hyperbolic Sampling of each replica between swaps. From each decoy trajectory, the lowest or the best of the five lowest-energy structures were selected for analysis. No clustering was used in decoy selection.

Selection of Secondary Structure Elements.

The helices, β-strands, and loop regions of protein were defined by using the DSSP program (30) as applied to the native structure. Only continuous elements longer than three residues were considered.

Selection of Buried Side Chains.

The side chain was considered buried in the interior of a protein if its surface accessible area in the native structure was <50% of the surface accessible area of the free amino acid flanked by single glycine residues. The surface accessible area of each side chain was calculated by using DSSP (30).

rmsd over χ1 Dihedral Angles.

The rmsd over χ1 dihedral angles was calculated as the rmsd between the set of χ1 dihedral angles for buried side chains in the native structure and the χ1 dihedral angles of the same side chains in the decoy structure.