In vivo diffusion of lactoferrin in brain extracellular space is regulated by interactions with heparan sulfate

Abstract

The intercellular spaces between neurons and glia contain an amorphous, negatively charged extracellular matrix (ECM) with the potential to shape and regulate the distribution of many diffusing ions, proteins and drugs. However, little evidence exists for direct regulation of extracellular diffusion by the ECM in living tissue. Here, we demonstrate macromolecule sequestration by an ECM component in vivo, using quantitative diffusion measurements from integrative optical imaging. Diffusion measurements in free solution, supported by confocal imaging and binding assays with cultured cells, were used to characterize the properties of a fluorescently labeled protein, lactoferrin (Lf), and its association with heparin and heparan sulfate in vitro. In vivo diffusion measurements were then performed through an open cranial window over rat somatosensory cortex to measure effective diffusion coefficients (D*) under different conditions, revealing that D* for Lf was reduced ≈60% by binding to heparan sulfate proteoglycans, a prominent component of the ECM and cell surfaces in brain. Finally, we describe a method for quantifying heparan sulfate binding site density from data for Lf and the structurally similar protein transferrin, allowing us to predict a low micromolar concentration of these binding sites in neocortex, the first estimate in living tissue. Our results have significance for many tissues, because heparan sulfate is synthesized by almost every type of cell in the body. Quantifying ECM effects on diffusion will also aid in the modeling and design of drug delivery strategies for growth factors and viral vectors, some of which are likely to interact with heparan sulfate.

The spread of diffusible signals in brain extracellular space (ECS) is influenced by the local environment, with clearance mechanisms and the ECS volume fraction, tortuosity, and width among the best appreciated factors (1–3). The role that brain extracellular matrix (ECM) components play in modulating diffusion is less understood. Normal brain ECM is composed mostly of hyaluronic acid, a nonsulfated glycosaminoglycan, and proteoglycans carrying either chondroitin sulfate (CSPG) or heparan sulfate (HSPG) glycosaminoglycan side chains, along with the more recently identified reelin and tenascin glycoproteins (4, 5). Although aging (6–8), pathological insults (9, 10), or genetic modifications (11) resulting in altered brain ECM content are often associated with changes in ECS volume fraction, the ability of ECM components to specifically bind and slow the migration of diffusing substances in the ECS remains an open question. A direct ECM effect on extracellular diffusion (e.g., sequestration or slowing of a diffusing substance) has been postulated for proteins capable of binding HSPG (12, 13), but little evidence exists for this phenomenon in vivo.

HSPGs are thought to play essential roles in the physiology of all organ systems (14). They comprise a large group that are either cell-associated (e.g., the integral membrane syndecans and the glycosyl-phosphatidylinositol-anchored glypicans) or secreted (e.g., perlecan and agrin). Because secreted HSPG is often bound to cells indirectly by α-dystroglycan, integrins, or other receptors at the cell surface (15), both forms present essentially fixed sites of interaction for extracellular ligands. In vitro studies have shown many proteins are capable of binding to the HS chains of cell-associated and secreted HSPGs (16); these interactions are suspected to underlie many phenomena, e.g., shaping morphogen gradients during development (17, 18); trapping growth factors at the cell surface for subsequent receptor activation (19); and sequestering pathogenic proteins (20, 21), in part by attenuating extracellular diffusion (22–25). Most protein-HS interactions are inferred from binding studies, using the closely related anticoagulant heparin (H), a highly sulfated glycosaminoglycan commonly isolated from mast cells in the intestinal mucosa (25). Both H and HS are strongly anionic linear polymers of uronic acid and glucosamine disaccharide units, distinguished principally by higher degree of sulfation in H. Proteins that bind H typically bind HS, although the lower charge density of HS results in interactions of lower affinity (26). Many proteins possess putative heparin-binding regions (27), clusters of positively charged amino acids capable of forming ion pairs with negatively charged glycosaminoglycan groups in a specific manner (28). However, the capacity of a protein-HS interaction to attenuate diffusion has not been quantified in vivo.

Here, we used integrative optical imaging (IOI) (3, 29) to study two fluorescently labeled proteins, lactoferrin (Lf) and transferrin (Tf), to isolate the effect of a protein-HS interaction on diffusion in vivo. Human Lf and Tf are iron-binding proteins very similar in size (≈80,000 M_r), amino acid sequence homology (≈60%) and overall bilobal structure (30). However, the amino acid sequence of human Lf contains a region of basic amino acids near its N terminus that allows it to bind polyanions, such as H, HS, and DNA (31, 32); human Tf lacks such a region and does not bind H or other glycosaminoglycans under normal physiological conditions (33, 34). We first characterized the properties of Oregon green 514-labeled human Lf and Texas red-labeled human Tf, confirming their similar hydrodynamic sizes and the ability of Lf, but not Tf, to bind H and cell-associated HSPG. We next determined D* values for each protein after injection into the neocortex of anesthetized rats, showing that Lf diffused significantly more slowly compared with Tf or Lf coinjected with H, allowing us to quantify the effect of Lf–HS binding on the diffusion of Lf through brain ECS. Our results directly demonstrate sequestration of a diffusing molecule by proteoglycans in vivo.

Results

Free Diffusion Coefficients (D) for Fluorescent Protein Conjugates.

D values were determined by IOI (3, 29) at 37°C, allowing estimation of apparent hydrodynamic diameters (d_H) from the Stokes–Einstein equation [d_H = (kT)/(3πηD), where k is Boltzmann's constant, T is absolute temperature and η is the viscosity of water (6.9152 × 10⁻⁴ Pa·s at T = 310 K); see ref. 2.]. Fig. 1A shows representative IOI image sequences (background fluorescence subtracted) after pressure ejection of Lf or Tf solutions into dilute (0.3%) agarose, an essentially “free” medium. Fig. 1B shows the Gaussian-shaped fluorescence intensity distributions extracted from the images in Fig. 1A, superimposed with theoretical fits of the diffusion equation (3); the curves characteristically flatten and broaden with time as expected for diffusion from a point source. Fits to the data yielded the parameter γ_i²/4 at each time point, t_i; regression of γ_i²/4 upon t_i in turn yielded a straight line with a slope equal to D (Fig. 1C). Lf's mean D value was ≈30% lower with H (D = 5.0 ± 0.5 × 10⁻⁷ cm²·s⁻¹ with H (mean ± SD), n = 16 measurements; D = 7.1 ± 0.9 × 10⁻⁷ cm²·s⁻¹ without H, n = 14; P = 0.00011, ANOVA with Student-Newman-Keuls post test; Fig. 1D), confirming formation of an Lf–H complex with a significantly larger d_H than Lf without H (Table 1); no significant differences in D were observed for Tf with H (D = 7.6 ± 0.5 × 10⁻⁷ cm²·s⁻¹, n = 18) or without H (D = 7.5 ± 0.5 × 10⁻⁷ cm²·s⁻¹, n = 14) or between Lf and Tf alone. The results verified H binding to Lf, but not Tf, and the expected similarity in d_H for Lf and Tf in solution (Table 1).

Fig. 1.

Free diffusion measurements. (A) Representative images after ejection of Lf or Tf, with or without H, into dilute agarose. (Scale bars: 200 μm.) (B) Fluorescence intensity (I) profiles were extracted from each image (data in blue) and fit to the diffusion equation (fits in red) along a single axis (depicted in A at the far left). (C) Linear regression of data in A and B; γ_i² = 4D(t_i + t₀), so regression of γ_i²/4 on t_i returns a slope of D (data transformed to a zero y-intercept). Fitting yielded the following D values: Lf, 6.5 × 10⁻⁷ cm²·s⁻¹; Lf + H, 4.6 × 10⁻⁷ cm²·s⁻¹; Tf, 7.2 × 10⁻⁷ cm²·s⁻¹; and Tf + H, 7.9 × 10⁻⁷ cm²·s⁻¹. (D) Summary data (mean ± SD; *, P < 0.0002, ANOVA).

Table 1.

Stokes–Einstein diameters and in vivo tortuosity (λ) for fluorescently labeled lactoferrin and transferrin

Molecule	dH, nm	λexperimental = (D/D*)1/2	λpredicted†
			ECSpl	ECScyl
Lf	9.29 ± 0.32 (n = 14)	3.50 ± 0.19	2.27	2.29
Lf + H	13.1 ± 0.30 (n = 16)	2.54 ± 0.09	2.60	2.69
Tf	8.81 ± 0.17 (n = 14)	2.29 ± 0.11	2.24	2.24
Tf + H	8.68 ± 0.13 (n = 18)	2.28 ± 0.07	2.23	2.23

Experimental values (mean ± SEM) were determined at 37 ± 0.5°C.

^†λ predicted for inert substance of specified d_H from restricted diffusion models of planar (ECS_pl) or cylindrical (ECS_cyl) ECS pores (3).

Confocal Imaging of Lf and Tf Binding to Cultured Cells and the Effect of H.

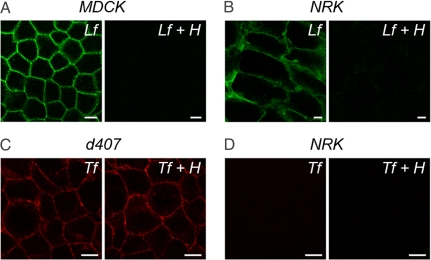
Before measuring diffusion in vivo, we studied the binding characteristics of each fluorescent Lf and Tf conjugate in vitro. Lf binding to cells is mediated mainly by high capacity, low affinity binding to cell surface HSPG, whereas uptake depends on low capacity, high affinity interactions with specific receptors such as the low density lipoprotein receptor-related protein (LRP) (35, 36). In contrast, Tf binding and internalization are mediated by low capacity, high affinity interactions with the Tf receptor (37, 38). We first evaluated binding of Oregon green 514-labeled human Lf to cultured Madin–Darby canine kidney (MDCK) type II cells, because cell surface HSPG content is particularly well characterized in this cell line (39). As expected, Lf binding to polarized MDCK cells was robust and nearly abolished in the presence of H at 4°C (Fig. 2A); Lf binding to normal rat kidney (NRK) fibroblasts was similarly robust and heparin-sensitive (Fig. 2B). Pharmacological inhibition of LRP in MDCK cells attenuated uptake but did not affect surface binding [supporting information (SI) Fig. S1], suggesting that initial binding was primarily due to cell surface HSPG and not LRP. In contrast, binding of Texas red-labeled human Tf to human d407 cells was heparin-insensitive (Fig. 2C), whereas no discernible binding was observed for Tf, with or without H, to NRK cells (Fig. 2D). The inability of Tf to bind NRK cells was not anticipated, because these cells display Tf receptors on their surface (40); Tf species differences or the presence of the fluorophore likely provide the explanation. The results indicate the fluorescent human Tf conjugate lacks affinity for the rat Tf receptor and, importantly, confirm heparin-sensitive binding of Lf, but not Tf, to cell surface HS sites.

Fig. 2.

Binding of fluorescently labeled Lf and Tf to cultured cells in the presence or absence of H. Representative confocal images of Lf binding to MDCK cells (A), Lf binding to NRK cells (B), Tf binding to d407 cells (C), and Tf binding to NRK cells (D) at 4°C. (Scale bars: 10 μm.)

In Vivo Diffusion Measurements in Brain.

D* values were measured at a depth of 200 μm in the somatosensory cortex of anesthetized rats by IOI (Fig. 3A), as described in ref. 3. Representative image sequences and extracted fluorescence intensity distributions after pressure ejection of Lf (Fig. 3 B and C), Lf + H (Fig. 3 D and E), and Tf (Fig. 3 F and G) showed hindered diffusion in brain relative to agarose. Direct comparison of matched fluorescence intensity distributions (Fig. 4A) and linear regressions to obtain D* (Fig. 4B) showed pronounced differences in the diffusion behavior of Lf, Lf + H, and Tf in brain. Lf diffusion in brain was remarkably slow, resulting in a mean D* value almost 60% lower than Tf (D* = 0.58 ± 0.1 × 10⁻⁷ cm²·s⁻¹ for Lf, N = 4 animals, n = 12; D* = 1.4 ± 0.3 × 10⁻⁷ cm²·s⁻¹ for Tf, N = 4, n = 8; P = 0.00013) (Fig. 4C), despite their similar sizes (d_H ≈ 9 nm). Lf also diffused significantly slower alone than when complexed with H (D* = 0.78 ± 0.1 × 10⁻⁷ cm²·s⁻¹ with H, N = 4, n = 10; P = 0.018; Fig. 4C), despite the complex's larger size (d_H ≈ 13 nm). Control experiments showed that H had no effect on D* for Tf (D* = 1.5 ± 0.2 × 10⁻⁷ cm²·s⁻¹ with H, N = 4, n = 9) or Texas red-labeled 3,000 M_r dextran (dex3), a relatively neutral, inert probe (D* = 4.7 ± 1.0 × 10⁻⁷ cm²·s⁻¹ with H, N = 3, n = 10; D* = 5.0 ± 1.0 × 10⁻⁷ cm²·s⁻¹ without H, N = 5, n = 6). Our in vivo results were, therefore, characterized by Lf's slow diffusion, its enhancement when complexed to H, and the absence of any effect of H on the diffusion of Tf or dex3.

Fig. 3.

Diffusion in brain versus free solution. (A) For brain measurements, Lf or Tf solutions were pressure ejected from a micropipette at a depth of 200 μm in normoxic neocortex. Left to Right: Low-power view of open cranial window; brightfield (BF) view of rectangle indicated in the leftmost image after insertion of micropipette; micropipette and background fluorescence (FL) before pressure injection (pre-inj); and fluorescent cloud of molecules just after injection (post-inj), showing the six axes used for diffusion analysis. (B) Representative images after Lf ejection into free solution (dilute agarose) or brain (cortex). (C) Profiles and theoretical fits along the 0° axis for images in B, yielding D = 7.0 × 10⁻⁷ cm²·s⁻¹ and D* = 6.1 × 10⁻⁸ cm²·s⁻¹. (D) Representative images after ejection of Lf + H solution. (E) Profiles and theoretical fits along the 0° axis for images in D, yielding D = 5.1 × 10⁻⁷ cm²·s⁻¹ and D* = 8.4 × 10⁻⁸ cm²·s⁻¹. (F) Representative images after ejection of Tf solution. (G) Profiles and theoretical fits along the 0° axis for images in F, yielding D = 8.0 × 10⁻⁷ cm²·s⁻¹ and D* = 1.5 × 10⁻⁷ cm²·s⁻¹. (Scale bars: 200 μm.)

Fig. 4.

Diffusion in brain: Comparison of profiles and summary data. (A) Representative profiles and theoretical fits for Lf, Lf + H, and Tf. (B) Linear regression of data in A; regression of γ_i²/4 on t_i returns a slope of D* (data transformed to a zero y-intercept). Fitting yielded the following D* values: Lf, 5.5 × 10⁻⁸ cm²·s⁻¹; Lf + H, 8.5 × 10⁻⁸ cm²·s⁻¹; and Tf, 1.6 × 10⁻⁷ cm²·s⁻¹. (C) Summary data (mean ± SD; *, P < 0.02; **, P < 0.0002, ANOVA).

Prediction of Heparan Sulfate (HS) Binding Site Density from Experimental Data.

Values of the experimental tortuosity [λ = (D/D*)^1/2] for Lf ± H and Tf ± H, determined from mean D and D*, are listed in Table 1. The dimensionless parameter λ is useful for characterizing hindrances to diffusion in complex media because the dependence of free diffusion on d_H is already accounted for by the inclusion of D in the definition of λ. The study in ref. 3 provided relationships that predict λ in vivo for inert substances of a specified size, based on a model for λ where normal neocortical ECS was envisioned as an isoporous environment of fluid-filled planar or cylindrical pores having a width, d_ECS, of 38 or 64 nm, respectively. This model separated λ into two components, referred to here as λ₁ and λ₂:

where D′ is an interstitial diffusion coefficient. The first component, λ₁, represents the hindrance expected for a vanishingly small inert molecule arising from obstructions (e.g., cells and the ECM) and possibly other factors (e.g., cell cavities or dead spaces), whereas the second component, λ₂, represents the increased hindrance expected from restricted diffusion due to steric hindrance and drag as d_H approaches d_ECS (see ref. 3). Experimental data and modeling suggest that λ₁ ≈ 1.6, whereas λ₂ may be estimated from analytical expressions that depend on d_H, d_ECS, and pore geometry (3). Table 1 lists predicted λ values from this two-component model, based on the measured values of d_H for Lf and Tf, with and without H. Experimental λ values for Tf ± H and the Lf + H complex agreed well with model predictions. However, Lf's experimental λ was significantly larger than predicted, suggesting the existence of a source of hindrance for Lf in addition to λ₁ and λ₂.

We hypothesized Lf binding to fixed HS sites could provide an explanation for Lf's high λ in neocortical ECS (Fig. S2). It is well appreciated that a chemical reaction, such as binding, can significantly affect the diffusion process (41). The simplest process would be where some portion of a diffusing substance becomes immobilized by reversibly binding to fixed elements (e.g., HS chains within brain ECS); if a linear equilibrium relationship exists between the immobilized and diffusing substance (i.e., c_A·B = c_A × R, where c_A·B and c_A are concentrations of the immobilized and free substance, respectively, and R is a constant) and the binding process is sufficiently rapid so as to be considered instantaneous, solutions to the diffusion equation take the following form (41):

If we further stipulate that the concentration of binding sites in the ECS, c_B, is constant and define an equilibrium dissociation constant for binding, K_D = (c_A·c_B)/c_A·B, Eq. 2 becomes the following (42):

Eq. 3 is identical to the solution for simple diffusion without binding, except that a modified diffusion coefficient, D″ = D/(c_B/K_D + 1), is used in place of D. Following this treatment, we can add to the previous model (Eq. 1) a third component, λ₃, to account for rapid, reversible binding to fixed sites within brain ECS:

where

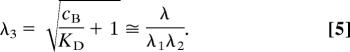Eq. 5 can be used to extract information about HS binding sites from the experimental λ for Lf, provided that (i) the binding process described by the treatment is justified; (ii) either c_B or K_D are known; and (iii) the product λ₁λ₂ can be estimated, either by using Lf's d_H (with the analytical expressions in ref. 3), experimental λ measurements with Lf where HS binding is prevented, or experimental λ measurements with a closely related surrogate that does not bind HS.

The validity of Eq. 5 necessitates that the binding events take place much faster than diffusion. Based on the rate constant for Lf diffusion in brain (i.e., D*/L², where L is on the order of a few hundred micrometers) and the binding kinetics estimated for a similar protein-HS interaction in vitro (22), Eq. 5 appears justified.

Neither c_B for HS binding sites nor K_D for Lf–HS binding in brain are available. Because our diffusion measurements used Oregon green 514-labeled human Lf in a rat tissue, we estimated K_D by quantifying binding of this fluorescent conjugate to NRK cells. A low affinity class of putative HSPG binding sites were characterized by a K_D of 2.6 μM (Fig. S3), in line with prior measurements using Lf and cell lines from other species (SI Results and Discussion).

Finally, λ/λ₁λ₂ (Eq. 5) for Lf was estimated by using either Lf's d_H with analytical expressions (3) or the experimental λ for Tf as a surrogate for nonbinding Lf, with λ₃ = 1.53 in both cases. Using this value for λ₃ and the experimental K_D for low affinity binding of Lf to NRK cells allowed us to estimate c_B = 3.5 μM [i.e., ≈0.7 μM based on total tissue volume, given an ECS volume fraction of 0.2 (7)]. Our in vivo diffusion measurements in rat somatosensory cortex are, therefore, consistent with the existence of HSPG at the site of injection, resulting in a density of fixed HS binding sites for Lf in the low μM range.

Discussion

Here, we report in vivo D* values for two biologically relevant proteins in the CNS. We have shown that Lf diffusion is dramatically hindered in the adult rat neocortex whereas Tf, a protein very similar to Lf in size and structure, diffuses as expected for an inert molecule. The different in vivo diffusion properties of Lf and Tf provide evidence that HSPGs can play an important role in modulating extracellular diffusion in vivo, because Lf's potential to bind HS is among the principal features distinguishing the two proteins. HS chains can extend remarkable lengths, e.g., 50 nm or more for a 30,000 M_r chain (43), so we hypothesize that both secreted and cell-associated forms of HSPG slowed diffusion of Lf by binding Lf as it migrated through brain ECS.

An important aspect of our study is the close agreement observed between predicted values of λ from a described theoretical model (3) and the experimental λ values for Tf ± H and the Lf–H complex. Indeed, we arrived at a prediction of neocortical HS binding site density in the ECS, c_B = 3.5 μM, by extending this previous model to account for the effect of rapid, reversible binding on the measured value of λ for Lf. Although a similar strategy has been applied to describe the diffusion and binding of a protein to HS in isolated corneal basement membranes (22), our study does so using in vivo measurements. Our estimate of c_B in the rat somatosensory cortex appears reasonable when compared against extrapolations from postmortem HS purification (SI Results and Discussion). We recognize that HSPG forms and concentrations may vary across different CNS areas; these variations will only become apparent after further study.

Suitability of Lf and Tf as in Vivo Diffusion Probes.

Lf and Tf have been particularly well characterized in terms of their structural similarities (30), stable monomeric solution properties (44, 45) and in vitro binding behavior (31–34). Our D values for each protein were consistent with those obtained by other methods [e.g., D values of 7.3–7.9 × 10⁻⁷ cm²·s⁻¹ and 8.1–8.3 × 10⁻⁷ cm²·s⁻¹ (37°C) are obtained for Lf and Tf, respectively, from small angle x-ray and neutron scattering data (46, 47)]. The reduction in D observed for Lf in the presence of H was, therefore, consistent with Lf–H complex formation and not Lf aggregation.

We used Lf as an HS-binding probe and Tf as a nonbinding surrogate for our diffusion measurements in brain. Normal brain does not contain H, so Lf binding in brain ECS was assumed predominantly because of cell- and ECM-associated HSPGs. Lf binding to other negatively charged ECM components in brain, e.g., CSPG or hyaluronic acid, although possible, was not considered important because these interactions are much weaker than those with HS (32, 48). Importantly, we expected to compete off Lf–HS binding in brain with H, which has both a higher charge density (H contains an average of 2.7 negative charges per disaccharide versus <2 for HS) and stronger affinity for Lf compared with HS (26, 32).

High affinity receptors for Lf (e.g., LRP) and Tf are present in brain (37, 49); however, their concentration and K_D are reportedly in the low nanomolar range (36, 37), multiple orders of magnitude below the likely tissue concentration profiles used to determine D* (both Lf and Tf were used at concentrations of ≈60 μM in the injecting micropipette) and beyond the expected limits of detection by our present system. Low capacity, high affinity binding, if present, would have been saturated over the entire course of our measurements, contributing negligibly to the imaged concentration profiles. Finally, experimental λ for Tf ± H and the Lf–H complex agreed well with the predicted λ for diffusing inert substances of equivalent size, suggesting that neither the Tf nor Lf–H measurements were appreciably affected by binding to HS or other sites.

Implications for Drug Delivery.

Our findings may be especially relevant for methods of drug delivery that involve the injection or infusion of drugs or gene therapy vectors directly into CNS tissue, e.g., convection enhanced delivery. Studies have shown that H can increase the gross distribution volume or effect size of certain protein growth factors (50) or the adeno-associated virus serotype 2 gene therapy vector (51) after administration into the mammalian CNS in vivo, but the mechanism of H enhancement was uncertain. Our findings with Lf provide a mechanistic explanation that can be extrapolated to other proteins possessing heparin-binding regions and may even be used to predict λ for such proteins, provided K_D is known. Finally, we note that although H complexation of Lf enhanced transport compared with Lf alone, the Lf–H D* did not increase to the level of Tf's D*, because the Lf–H complex was nearly 4 nm larger than Tf. Increased size will be accompanied by increased diffusional hindrance, becoming more pronounced as the size of the diffusing substance approaches the brain ECS width limit (3).

Materials and Methods

Fluorescent Conjugates.

Oregon green 514-labeled human Lf (OG514-Lf; iron-saturated; 2.9 mol of OG514/mol Lf; Molecular Probes) and Texas red-labeled human Tf (TR-Tf; iron-saturated; 2.0 mol of TR/mol Tf; Molecular Probes) were used at a concentration of 5 mg/ml in PBS (pH 7.2) unless indicated otherwise. TR-dex3 (0.26 mol of TR/mol dex3; Molecular Probes) was used at a concentration of 1 mM in a solution of 154 mM NaCl. Some solutions were made up with heparin sodium (50 mg/ml; Grade I-A from porcine intestinal mucosa, with H polymer chains mostly in the range 17,000–19,000 M_r; Sigma). All solutions were vortexed briefly and centrifuged at 12,000 × g before use.

Animal Preparation for Diffusion Measurements.

Experiments with female Sprague–Dawley rats (160–260 g) were carried out at the New York University School of Medicine in accordance with National Institutes of Health guidelines and local Institutional Animal Care and Use Committee regulations as described in ref. 3.

Diffusion Measurements.

We used the IOI method (2, 29), as described for in vivo measurements in ref. 3, with slight modifications. The diffusion equation (equation 4 in ref. 3) was fitted to the upper 90% of fluorescence intensity curves, using a nonlinear simplex algorithm, yielding estimates for a parameter, γ_i, at a succession of times, t_i. Linear regression of γ_i²/4 upon t_i yielded a slope of D* (or D). Curves were extracted from the data along each of six axes (Fig. 3A) and the final value of D* (or D) for each measurement was taken from the average of four axes, excluding the two axes giving highest and lowest values. Transforming to a zero y-intercept (subtracting D* × t₀ from γ_i²/4 and plotting versus t_i) was used to facilitate comparison. Typically, Lf and Tf diffusion were imaged over times ranging from 20 to 50 s for D and 200 to 300 s for D*.

In Vitro Lf Binding Measurements.

Madin–Darby canine kidney (MDCK) type II cells were cultured on Transwell filters (BD Biosciences) in DMEM plus 5% FBS for 4 days. Normal rat kidney (NRK) 49F cells and human retinal pigment epithelial cells (d407) (a gift of R. C. Hunt, University of South Carolina, Columbia) were each cultured on coverslips in DMEM plus 5% FBS or DMEM plus 3% FBS, respectively, for 48 h. All cells were incubated at 4°C for 20 min in recording medium (20 mM Hepes, 4.5 g/liter glucose, 1% nonessential amino acids, 1% FBS in HBSS) after which OG514-Lf (50 μg/ml) or TR-Tf (100 μg/ml) were added for 1 h in the presence or absence of H (100 μg/ml). Cells were then rinsed twice with cold recording medium and immediately fixed. Images were acquired with a Leica TCS-SP2 laser scanning confocal microscope and processed identically for all conditions. Additional experiments on Lf internalization and binding were conducted with MDCK and NRK cells (SI Experimental Procedures).