Abstract
Although gamma frequency oscillations are common in the brain, their functional contributions to neural computation are not understood. Here we report in vitro electrophysiological recordings to evaluate how noisy gamma frequency oscillatory input interacts with the overall activation level of a neuron to determine the precise timing of its action potentials. The experiments were designed to evaluate spike synchrony in a neural circuit architecture in which a population of neurons receives a common noisy gamma oscillatory synaptic drive while the firing rate of each individual neuron is determined by a slowly varying independent input. We demonstrate that similarity of firing rate is a major determinant of synchrony under common noisy oscillatory input: Near coincidence of spikes at similar rates gives way to substantial desynchronization at larger firing rate differences. Analysis of this rate-specific synchrony phenomenon reveals distinct spike timing “fingerprints” at different firing rates that emerge through a combination of phase shifting and abrupt changes in spike patterns. We further demonstrate that rate-specific synchrony permits robust detection of rate similarity in a population of neurons through synchronous activation of a postsynaptic neuron, supporting the biological plausibility of a Many Are Equal computation. Our results reveal that spatially coherent noisy oscillations, which are common throughout the brain, can generate previously unknown relationships among neural rate codes, noisy interspike intervals, and precise spike synchrony codes. All of these can coexist in a self-consistent manner because of rate-specific synchrony.
Keywords: gamma oscillations, neural code, neural computation
Gamma oscillations (30–100 Hz) are observed in field potential recordings from many brain areas (1–4). These oscillations are typically noisy, exhibiting fluctuations in amplitude and a broad frequency distribution. In vitro experiments using cortical brain slices (5) have demonstrated that gamma oscillations can be produced by sustained activation of networks of inhibitory neurons, which in turn produce highly correlated rhythmic membrane potential oscillations in the local population of pyramidal cells (6). This raises the general question of what role common noisy oscillatory synaptic inputs might play in producing synchronous action potentials across a population of neurons with differing mean firing rates. In the presence of correlated noisy gamma, neurons with the same mean firing rate would be expected to produce highly correlated spike trains (7). But what is the level of synchrony that will result when the mean firing rates are different? These correlations would be functionally important because relative spike timing on the millisecond time scale influences synaptic activation of postsynaptic targets (8, 9), timing-dependent short-term synaptic plasticity (10, 11), and pattern recognition (12).
Previous work has shown that weakly correlated noisy input to a pair of neurons produces an output correlation proportional to the geometric mean of their firing rates (13). In contrast, we are interested in the opposite regime of highly correlated common noisy input. This regime is more appropriate to the synaptic drive expected from gamma-producing inhibitory networks; it also is suggested from in vivo paired intracellular recordings (14).
To explore the relationship among common oscillatory drive, firing rate, and spike synchrony, we developed a network model (Fig. 1a) in which the average firing rate of each neuron is independently set by a constant input current, whereas spike timing is modulated by a common noisy oscillatory current. We studied this system experimentally by presenting a large sequence of stimulus epochs to an individual neuron in a cortical brain slice. The constant current levels used in the sequence of epochs were chosen to produce a broad range of mean firing rates, whereas the amplitude and time course of the noisy oscillatory current component was unchanged (frozen noise). We then analyzed spike synchrony for all epoch pairs by numerically simulating synaptic inputs to a postsynaptic coincidence detector read-out neuron with the timing of the inputs determined from the spike times from the two recorded spike trains. In separate analyses, epochs recorded with one neuron also were compared with those of another neuron recorded in a different session.
Fig. 1.
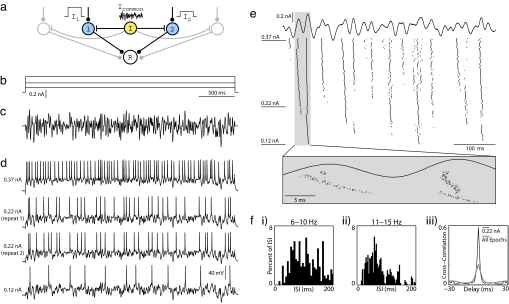
Protocol for studying synchrony induced by common noisy oscillations in vitro. (a) In our conceptual network model, a common noisy input (Icommon) modulates spike timing within a population of otherwise independently driven neurons (cells 1 and 2), and synchronous population activity is detected by a postsynaptic read-out neuron (R). (b and c) To reproduce this model experimentally, whole-cell patch recordings from layer 2/3 pyramidal neurons were stimulated in current clamp for 3 s with varying levels of constant current (b) combined with a common noisy oscillatory drive (c). The noisy waveform was generated to have a Gaussian Fourier spectrum, with a mean of 30 Hz and width of 30 Hz. Its rms amplitude was rescaled to 50% of the dynamic range of constant levels (Arms = 50%). (d) Four voltage traces from a set of 150 stimulus epochs on a single neuron are shown, including the minimum current (Lower) and the maximum current (Upper) injected, as well as two examples from an intermediate current. Step amplitudes are 0.12, 0.22, and 0.37 nA. (e) Fifty constant steps of uniform spacing were presented in random order, with each step repeated three times sequentially for a total of 150 noisy stimulus epochs. Step amplitudes were chosen to elicit firing between 0 and ≈30 Hz. Spike rasters are presented here for all 150 stimulus epochs during the first 500 ms of stimulation. Stimulus epochs are sorted by increasing stimulus amplitude from bottom to top. The expanded box illustrates changes in spike timing over fine time scales with increasing constant current. (f) (i–ii) Interspike interval distributions from a subset of stimulus epochs, pooled into successive 5-Hz ranges. Spike arrival times are irregular. (iii) Cross-correlograms obtained by comparing spike responses to 0.22-nA epochs only (black line) and all 150 epochs (gray line). Spikes were binned at 2 ms.
Our analyses reveal that the amount of synchrony between two neurons is strongly dependent on their relative mean firing rates, an effect we call rate-specific synchrony. The computational significance of rate-specific synchrony is that the common noisy gamma oscillation encrypts the different activation levels of a population of neurons into a set of distinct neural codes. Each subgroup of neurons with a similar level of activation has a unique fingerprint of action potential timing that can be detected and used for pattern recognition or synaptic plasticity.
Results
Whole-cell patch recordings from layer 2/3 pyramidal neurons in rat somatosensory cortex were stimulated in current clamp for 3-s epochs (Fig. 1). The constant current component was selected from a set of 50 uniformly spaced levels chosen to elicit action potential rates between 0 and ≈30 Hz. The noisy oscillation (Fig. 1c), which was identical for each stimulus epoch and added to the constant current component, was synthesized in software to have a Gaussian Fourier spectrum with a characteristic center frequency (Fc) and width (Fw). A run consisted of 150 epochs, with the 50 constant current levels of the stimulus used in random order and repeated three times. As shown in Fig. 1d, the rate of action potential firing increased with the level of constant current. Membrane voltage responses to identical constant current levels demonstrated reproducible spiking behavior (Fig. 1d Middle) as reported previously (7). We further observed that interspike interval distributions were noisy at each current level (Fig. 1f i and ii). Spike rasters from the entire run, ordered from bottom to top by increasing constant current level used in the stimulus epoch (Fig. 1e), show common firing patterns within local horizontal strips corresponding to nearby firing rates. When firing rates differ widely, however, the patterns appear to be qualitatively different, reflecting the combined effects of phase precession and discontinuous changes in spike timing (see Fig. 1e, shaded vertical box).
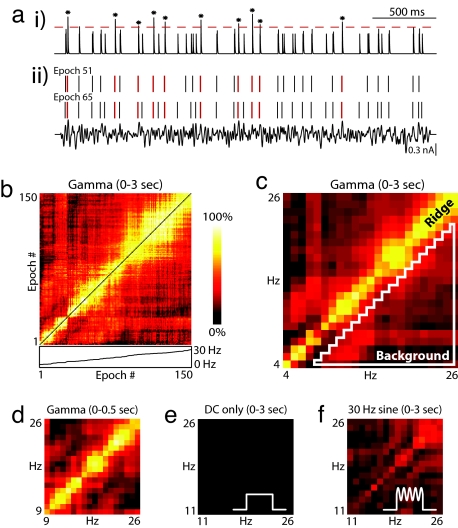
The qualitative differences in spike timing observed in raster plots like those in Fig. 1e suggest that the precise timing of action potentials might be a “fingerprint” that changes with firing rate. To quantitatively examine this idea, we evaluated pairwise synchrony for all possible combinations of rate. Through an analogy with biological coincidence detectors, the spike responses from two epochs were treated as distinct inputs to a simulated postsynaptic coincidence detector neuron. Each input activated a brief EPSP, and both synaptic inputs were summed and thresholded (see Methods) (Fig. 2a). The EPSP time constant (2 ms) and spike threshold (1.37) jointly defined a 2-ms window for synchrony detection; however, the same window duration was achievable by using longer EPSP time constants with higher thresholds. For the purposes of analysis, synchrony was quantified as the number of threshold-crossing events divided by the minimum number of spikes in either epoch. This measure of synchrony defines the probability of a synchronous event conditioned on the spikes of the lower firing rate epoch. In Fig. 2b, synchrony is plotted as a color-coded “synchrogram” for all nonidentical epoch pairs. Epoch number, indexed by increasing mean firing rate, runs from left to right and bottom to top along each axis. In general, epochs that are close in number have higher values of synchrony, producing a blocky yellow band along the diagonal. To directly examine the dependence of synchrony on rate, the data were re-binned by firing rate in Fig. 2c. The elevated ridge along the diagonal indicates that the neuron was synchronously active at identical rates, but desynchronized when either rate changed (in this example, by more than ≈3 Hz). We also evaluated synchrony restricted to a shorter time period by producing synchrograms using only the first 500 ms of spike data from each epoch. This time interval is consistent with the duration of epochs of elevated gamma power observed in LFPs in vivo (1, 15, 16). Despite the fact that rates are not as well sampled within this restricted window, the resulting synchrogram demonstrates that the ridge develops shortly after stimulus onset (Fig. 2d).
Fig. 2.
Noisy oscillations produce strong pairwise rate-specific synchrony. (a) Synchronous events between two stimulus epochs (ii) are identified by convolving each spike raster with an EPSP synaptic kernel, summing the resulting waveforms (i) and applying a threshold (indicated by the dotted line). Spike-conditional synchrony is then quantified by dividing the number of threshold crossings by the minimum number of spikes in either stimulus epoch. In this example, taken from the experiment shown in Fig. 1, synchronous spikes are in red, and threshold crossings in the synaptic trace are marked with an asterisk. There are 10 synchronous events and 30 reference spikes in stimulus epoch 51, corresponding to 33% synchrony. An EPSP kernel with a maximum value of 1 (arbitrary units) and a time constant of 2 ms is used here, along with a synchrony threshold of 1.37. The result is that two spikes must occur within 2 ms to be considered synchronous. (b) A synchrogram is used to visualize synchrony for all stimulus epoch pairs. The color of each (x,y) location in the plane corresponds to the degree of synchrony between each epoch pair at x,y along the horizontal and vertical axes. Shown here is a comparison of pairwise synchrony between all 150 stimulus epochs from Fig. 1. Stimulus epoch number, indexed by increasing mean firing rate, runs from left to right and bottom to top. In general, stimulus epoch pairs with similar firing rates exhibit higher synchrony than stimulus epochs with different firing rates, leading to a ridge of elevated synchrony along the diagonal. Below the x axis of the false color plot, the inset plots mean firing rate as function of epoch number. Note the presence of nonlinearities that contribute to the uneven quality of the ridge in the above plot. (c–f) Rate–rate synchrograms are created by averaging synchrony values for all epoch pairs that have the same combination of mean firing rates, rounded to the nearest integer Hz. Synchrograms are plotted as in b, but with firing rates on the axes. This analysis eliminates the nonlinearities observed in b. (c) Rate–rate synchrogram for all 150 trials evaluated over a 3-s window. The elevated ridge along the diagonal is characteristic of rate-specific synchrony, in which spike timing is reliable at similar rates, but desynchronization occurs at different rates. A quantitative measurement of rate-specific synchrony is obtained by dividing the mean on-diagonal (ridge) synchrony by the mean off-diagonal (background) synchrony. Ridge amplitude is calculated by averaging over all identical rate pairs. Background amplitude is calculated by averaging over all pairs with >3-Hz rate difference (area within white triangle). (d) Rate–rate synchrogram for the same data calculated by using spikes from the first 500 ms of each epoch. (e and f) Rate–rate synchrograms for control experiments on the cell shown previously. Constant current (DC) steps were presented without additive gamma (e) and with an additive 30-Hz sine wave (f).
To evaluate the importance of noisy gamma waveforms for the generation of rate-specific synchrony, we performed control experiments using constant current steps without any oscillatory input, as well as constant steps summed with a pure sinusoid for the common input. Fig. 2 e and f shows synchrograms from these control experiments conducted on the same neuron that produced rate-specific synchrony in response to noisy gamma in Fig. 2c. Rate-specific synchrony does not emerge in response to constant current steps (Fig. 2e) and only emerges weakly when a sinusoid is substituted for noisy gamma (Fig. 2f). More examples are provided in supporting information (SI) Fig. S1 f and g.
To quantify rate-specific synchrony, on-diagonal (ridge) synchrony was defined as the amplitude at zero rate difference, which is equivalent to calculating the mean of on-diagonal points in a synchrogram. Off-diagonal (background) synchrony was defined as the mean across firing rate differences of >3 Hz, which corresponds to the area inside the white triangle shown in Fig. 2c. Strong rate-specific synchrony was consistently observed (other examples found in Fig. S1a) for our most common stimulus paradigm of center frequency (Fc = 30 Hz, Fw = 30 Hz, and Arms = 50%), where Arms refers to the rms amplitude of the noisy gamma waveform relative to the range of the constant current steps. For these synchrograms (n = 23 runs), mean ridge amplitude was 0.62 ± 0.16 and mean ridge/background ratio was 3.06 ± 0.41. Similar results were obtained by using stimuli with other center frequency and bandwidth values (Fig. S1). For comparison, constant current control experiments (n = 12) (Fig. S1f) produced a mean ridge amplitude of 0.06 ± 0.01, and the mean ridge/background synchrony was 1.02 ± 0.16. For the pure sinusoid control experiments (n = 8) (Fig. S1g), the mean ridge amplitude was 0.33 ± 0.06 and the mean ridge/background synchrony was 1.52 ± 0.20. These quantifications demonstrate that rate-specific synchrony can be reliably produced and that the noisy gamma waveform plays an important role in its generation.
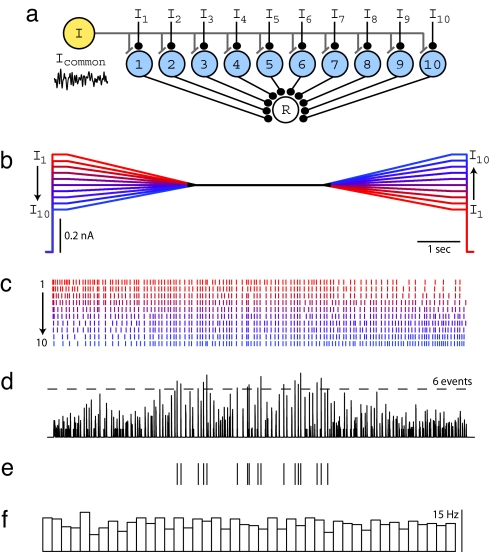
These results suggest that rate-specific synchrony could be useful as a computational mechanism in a network where each neuron receives independent time-varying inputs. Specifically, it might be used to determine whether and when many neurons in a network share a similar level of activation, thus implementing a form of pattern recognition known as Many Are Equal (MAE) (17). To explore this idea, we considered the network architecture shown in Fig. 3a, consisting of 10 neurons that share a common noisy gamma input, but also have slowly varying independent inputs (Fig. 3b). To study this experimentally, 10 different input current patterns were sequentially presented to an individual cortical neuron, and the elicited spike responses were later used to calculate the response in a postsynaptic detector cell produced by the summed synaptic responses of the 10 neurons. Each input current pattern started at a different level, converged to a common sustained level, and then diverged (Fig. 3b). As in earlier runs, the same noisy gamma waveform was added to each waveform to produce the 10 stimulus epochs of 10-s duration. Spike rasters obtained from a neuron using this protocol are shown in Fig. 3c. Elicited firing rates ranged between 5 and 30 Hz, and the mean firing rate, averaged over all stimulus epochs, remained relatively constant throughout the stimulus. Individual spike rasters (Fig. 3d) were used as input to a synchrony detector (see Methods) (Fig. 3a). When a simple threshold was applied to this waveform, all threshold-crossing events occurred during or near the central period when firing rates were similar (Fig. 3e) despite the fact that mean rate over all of the inputs was approximately constant across the entire stimulus epoch (Fig. 3f). Similar results were obtained for a biologically more realistic stimulus paradigm involving time-varying independent baseline currents (Fig. S2). This result directly demonstrates the feasibility of using rate-specific synchrony for MAE computation.
Fig. 3.
Rate-specific synchrony underlies MAE computation. (a) Model network used to test MAE computation in the presence of noisy oscillations. Each neuron in the population receives independent time-varying excitatory drive (I1–I10) and a common oscillatory input (Icommon). All 10 neurons provide synaptic input to a postsynaptic read-out neuron (R) that reports population synchrony by generating action potentials. (b) To reproduce this model experimentally, a single L2/3 cell was injected with 10 waveforms of 10-s duration. During the first 3.5 s, waveforms linearly converge from 10 distinct levels, remain fixed at a common value for 3 s, followed by another 3.5-s interval, during which they linearly diverge to 10 distinct levels. The time-averaged stimulus amplitude is identical for each epoch, as illustrated by waveform color coding: A high initial level is matched with a low final level, and vice versa, to guarantee identical time-averaged stimulus amplitudes across waveforms. During the experiment, a common noisy oscillatory stimulus with Fc = 30 Hz, Fw = 30 Hz, and Arms = 50% was added to each waveform in b to create stimuli for 10 stimulus epochs. (c) Spike rasters for all 10 stimulus epochs sorted by increasing initial constant current level and color-coded to match b. Stimulus epochs were presented in a random order during the experiment. (d) Spike rasters from each stimulus epoch were convolved with the EPSP kernel (τ = 2 ms) and summed to mimic synaptic input to a coincidence detector postsynaptic to 10 neurons. A threshold of six events was applied to detect population synchrony. (e) Ticks indicate threshold-crossing events in d. Population synchrony is greatly enhanced during the time period when all firing rates are approximately equal. (f) Average firing rate across all 10 epochs calculated by counting spikes in sequential bins of 220 ms. Average firing rate remains unchanged across time.
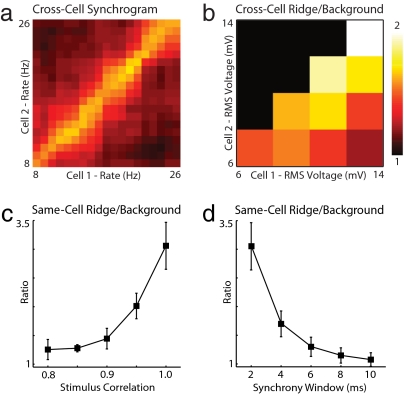
In the preceding analyses, the response of a single neuron was compared against itself on different epochs to examine whether synchrony was rate-specific and to demonstrate MAE computation. These approaches used the repeated stimulation of a single neuron as a proxy for stimulating a group of neurons of a similar type. Although this strategy was used for its technical simplicity, it was unable to account for the expected variability in physiological properties among a population of functionally similar neurons in an intact circuit. To examine whether rate-specific synchrony exists in the responses of different neurons, we compared epochs from all nonidentical neuron pairs that were stimulated by using our 3-s protocol (Fig. 1). As shown in Fig. 4a (also see Fig. S1e), rate-specific synchrony was found in some cross-neuron synchrograms. This result occurred despite differences in animal age, postdissection incubation time, and the precise anatomical location of the recorded cell. Some insight into what conditions might be necessary for rate-specific synchrony to be produced in vivo were obtained by grouping neurons based on the evoked rms fluctuations in the recorded voltage waveforms (Fig. 4b). This analysis reveals that pairs of neurons that responded with voltage fluctuations of similar amplitude showed stronger rate-specific synchrony than those with very different fluctuations. Additionally, neuron pairs with large absolute voltage fluctuation amplitudes showed strong rate-specific synchrony. These results suggest that the relative and absolute stimulus amplitudes are important determinants of population synchrony.
Fig. 4.
Robustness of pairwise rate-specific synchrony. (a) Cross-cell synchrograms were generated by comparing stimulus epochs from two different neurons. In this example, the horizontal and vertical axes now index-separate neurons presented with identical noisy gamma stimuli (Fc = 30 Hz, Fw = 30 Hz, and Arms = 50%). (b) Mean cross-cell ridge/background synchrony is plotted as a function of the rms amplitude of evoked membrane potential fluctuations in each cell (n > 5, all pairs). This ratio decays as the difference in stimulus amplitude increases. When stimulus amplitudes are equal, the ratio increases with increasing stimulus amplitude. (c) Summary of same-cell ridge/background synchrony versus input stimulus correlation for experiments with Fc = 30 Hz, Fw = 30 Hz, and Arms = 50% (n > 5 at all correlations) analyzed by using a 2-ms synchrony window. In each experiment, a common gamma waveform was corrupted by summation with an independently generated gamma waveform during each epoch to yield a desired mean pairwise stimulus correlation across epochs (see Methods). (d) Summary of same-cell ridge/background synchrony versus synchrony window duration for all 23 experiments with Fc = 30 Hz, Fw = 30 Hz, and Arms = 50%. In this analysis, EPSP time constants ranged from 2–10 ms with a fixed threshold of 1.37.
Although our experiments were motivated by evidence for highly correlated noisy oscillatory input (14), as in the gamma feedback produced by an activated network of oscillating inhibitory interneurons, it is unlikely that the input to any two neurons in a population will have perfect stimulus correlation. Therefore, we tested the robustness of pairwise rate-specific synchrony to reduced correlation of the common noisy gamma input. A stimulus ensemble was constructed in which the average pairwise correlation between the common gamma input during different epochs ranged between 0.8 and 1.0 (see Methods). As with the original 3-s paradigm, this stimulus ensemble was characterized by Fc = 30 Hz, Fw = 30 Hz, and Arms = 50%, and data were analyzed by using a 2-ms synchrony window. To control for heterogeneity in relative stimulus amplitude and cell properties, only same-cell comparisons were performed. The results (Fig. 4c) suggest that ridge/background ratio is robust to reduced stimulus correlation down to ≈0.9 (1.44 ± 0.18, n = 5). We verified that MAE computation remains feasible in this regime by modifying the stimulus paradigm from Fig. 3 to use 0.9 correlated gamma waveforms (Fig. S2).
Neurons can respond nonlinearly to coincident synaptic events at 2-ms temporal resolution (8, 9), but how the size of this detection window varies across brain regions remains unknown. To explore how rate-specific synchrony measurements change with increasing synchrony window duration, we reanalyzed the data from our 3-s protocol (Fig. 1) by using 2- to 10-ms windows (Fig. 4d). This analysis demonstrates that ridge/background synchrony decays with increasing window duration, approaching a ratio of 1.3 ± 0.17 (n = 23) at 6 ms. We conclude that neurons must be capable of detecting synchronous events at temporal resolutions of <6 ms for rate-specific synchrony to be used computationally in the brain.
Read-out of synchrony using a biologically inspired coincidence detector differs from other methods commonly used to study correlated activity in the brain. To address whether our results were dependent on the specific method we used, we also analyzed our 3-s stimulus data by using correlation coefficient (13) and spike cross-correlation as measures of synchrony. As shown in Fig. S3, synchrograms obtained by using these measures show a prominent diagonal ridge characteristic of rate-specific synchrony, and both techniques estimate higher ridge/background ratios than those obtained with our method at all temporal resolutions.
Discussion
Several previous conceptual models have addressed the relationship between gamma oscillations and neural synchrony (4, 18–20). Most have focused on phase codes during sinusoidal oscillation, in which the timing of an action potential changes systematically with neuron depolarization (21). Notably, however, phase models based on sinusoidal drive fail to account for Poisson-like interspike intervals commonly observed in single-unit recordings (22, 23). Rate-specific synchrony resolves this issue by demonstrating that noisy oscillations produce a fingerprint of irregular spike timings that changes with firing rate, rather than simple phase precession. Although this encoding is complex and constantly changing, the commonness of this code across a population of neurons would permit its use in neural information representation and computation. Fig. 3 demonstrates that rate-specific synchrony can be used to implement MAE computation, a powerful algorithm for scale-invariant pattern recognition (17).
When comparing our results to in vivo electrophysiological recordings, it is important to consider that rate-specific synchrony is likely to exist only while noisy gamma oscillations are present. This notion directly follows from our observation that no synchrony is produced in the absence of oscillatory input (Fig. 2e). Gamma oscillations in anesthetized (15), and behaving animals (1, 16) often show brief epochs of high power, typically with 100- to 300-ms duration. Because rate-specific synchrony emerges shortly after gamma onset (Fig. 2d) and degrades rapidly after gamma offset (Fig. S4), we would expect only brief periods of rate-specific synchrony to be associated with these brief gamma epochs in vivo.
The evaluation of rate-specific synchrony in vivo would be best performed by dual intracellular recording in awake animals, which, despite experimental advances (24, 25), remains technically challenging. However, a signature of rate-specific synchrony in extracellular recordings would be cross-correlation histograms that exhibit high peak amplitudes when rates are similar and gamma oscillations are present. By contrast, low cross-correlation peaks would be expected when long spike trains are compared without consideration of firing rate differences or LFP power in the gamma band, as is typically done with in vivo data. This expected reduction in peak amplitude can be demonstrated with our own in vitro experimental data (see Fig. 1f iii and Fig. S4f). A recent study showed that weak pairwise correlations also can occur because of low input stimulus correlation and demonstrated that spike correlations are determined by the geometric mean of firing rates in this regime (13). Here we show that spike correlation progressively moves to the regime of rate-specific synchrony as common noisy input correlation strengthens (see Fig. S5). This result would only be evident from in vivo recordings if the data were properly parsed by rate and the presence of gamma.
More work is required to understand how changing the parameters of the noisy oscillation, such as its center frequency, bandwidth, and phase relationships, changes rate-specific synchrony. In addition, modulation of currents that change the dynamic time scales of spike generation may modify or gate rate-specific synchrony (26). Preliminary numerical simulations using leaky integrate-and-fire and Hodgkin Huxley model neurons indicate that rate-specific synchrony can be reproduced in silico. Such studies were important in the design of our experiments and, together with analytical approaches (27), should provide a fertile testing ground for exploring this phenomenon.
Our present findings suggest that rate-specific synchrony is an emergent property of any neural system subject to common-mode noisy oscillations. Because MAE computation is trivially performed under such conditions, as shown in Fig. 3, we suggest a general role for this framework in brain areas where noisy oscillations, highly correlated synaptic input, and neuronal synchrony are observed.
Methods
Electrophysiology.
All experiments were performed in compliance with the Guide for the Care and Use of Laboratory Animals (www.nap.edu/readingroom/books/labrats). Specific protocols were approved by the Princeton University Institutional Animal Care and Use Committee. Sprague–Dawley rats (13–20 days postnatal; Charles River Laboratories) were anesthetized with isofluorane and decapitated, and the brain was removed under cold (<5°C) artificial cerebral spinal fluid (aCSF) (124 mM NaCl, 26 mM NaHCO3, 3 mM KCl, 1.25 mM NaH2PO4, 1.8 mM Dextrose, 1.8 mM MgSO4, and 1.6 mM CaCl2 continuously bubbled with 95% O2/5% CO2). Then 300-μm-thick semicoronal somatosensory cortical slices were prepared by using a VS 1000 vibratome (Leica) and incubated at room temperature (T = 20–22°C) in an interface chamber. After 1–5 h, individual slices were placed in a submerged slice recording chamber and maintained at 32–35°C, with aCSF perfused at 2–4 ml/min flowing over both surfaces.
Blind whole-cell patch recordings were acquired from layer 2/3 cortical neurons using 4–7 MΩ pipettes pulled with 1.2-mm OD/0.6-mm ID glass (FHC) on a P2000 puller (Sutter Instruments) and filled with intracellular solution [148 mM K-gluconate, 10 mM Hepes, 2 mM MgCl2, 3 mM ATPNa2, and 0.3 mM GTPNa2 (pH balanced to 7.3 with KOH)]. Intracellular current clamp recordings were made by using a BVC-700 amplifier (Dagan Instruments) with a 0.1 N gain headstage and digitized at 10 kHz (Digidata 1322A, Clampex software; Molecular Devices).
Stimulus Generation and Presentation.
Stimulus waveforms were created in Matlab (Mathworks) and imported as analog waveforms into Clampex (Molecular Devices). Experiments were performed in episodic stimulation mode, with a sequence of 150 3-s stimulus epochs applied to the external command of the BVC-700 operating in current clamp. The common oscillatory stimulus waveforms were created in Matlab by using the inverse Fourier Transform function operating on a 30,000-element conjugate symmetric Fourier Spectrum vector with a Gaussian amplitude profile and random independent phases. The Gaussian amplitude was characterized by two parameters: center frequency and width. The noisy oscillation was rescaled and added to 50 uniformly spaced constant steps, such that the rms amplitude of the oscillation was a specific fraction of the maximum constant step. The 50 constant steps were placed in random order, with each step repeated three times sequentially, for a total of 150 stimulus epochs in each run. Oscillation parameters used were Fc of 30 or 50 Hz, widths of 10–100 Hz, and Arms of 10–75%, relative to the maximum constant current step value. Parameter values were chosen for consistency with published EEG and LFP power spectra (28–30). Most commonly, experiments (n = 23) were done with 30 Hz Fc, 30 Hz Fw, and 50% Arms. Stimuli were offset and rescaled in amplitude for individual neurons in Clampex so as to induce firing between 0 and ≈30 Hz. A 5-s rest interval at 0 nA constant current was given between stimulus epochs. Thirty-eight runs of 150 stimuli were performed on 26 neurons in 13 preparations. Longer 10-s stimuli involving time-varying currents (Fig. 3 and Fig. S2) were created in a similar way. A 100,000-element Gaussian-profiled Fourier spectrum vector with random phases was used to create the common oscillatory drive. The common drive was then added to the 10 distinct current waveforms (Fig. 3b and Fig. S2b) after being scaled such that the Arms of the common drive was 25% or 50% of the dynamic range of currents presented. For decorrelation experiments, a frozen gamma waveform was chosen for a run, and on each epoch, a randomly generated and rescaled gamma waveform was added to the frozen gamma stimulus to produce the desired ensemble correlation value. Each decorrelated stimulus waveform was then rescaled to guarantee the desired Arms for that epoch. Twenty-two total runs of 150 stimuli were performed on 18 neurons in seven preparations by using this paradigm.
Synchrony Analysis.
Action potential onset times were detected in Matlab by thresholding high-pass-filtered (10-Hz cutoff) membrane voltage waveforms to create spike rasters. Pairwise synchrony between two stimulus epochs was calculated by convolving each raster with a synaptic kernel, S(t) = e−t/τ+ defined for t > 0 with τ+ = 2 ms and adding the outputs together. The maximum value at t = 0 was 1. A synchronous event was identified when the resulting waveform crossed a threshold of 1.37, chosen to yield a synchrony window duration of 2 ms. (Larger values of τ+ can yield the same window duration provided a suitable threshold is chosen.) Synchrony was then calculated as the number of synchronous events divided by the minimum spike count in either raster. This measure of synchrony defines the probability of a synchronous event conditioned on the spikes of the lower firing rate stimulus epoch. Synchrograms were created by plotting this pairwise measure as a color on a 2D grid with coordinates defined by stimulus epochs indexed along each axis. When synchrograms were plotted as a function of rate, mean firing rate was defined as the inverse mean interspike interval across the temporal window examined, rounded to the nearest integer Hz. When analyzing temporal windows smaller than the full 3 s, each stimulus epoch was truncated to span the desired window; otherwise, synchrograms were created using the same procedure. On-diagonal (ridge) synchrony, ridge width, and off-diagonal (background) synchrony were used to characterize synchrograms as defined in the text.
Supplementary Material
Acknowledgments.
We thank Clark Fisher, David Jangraw, and Xuemin Lu for help with pilot slice experiments. This work was supported by National Institutes of Health Training Grant T90 DA022770 (to F.C.) and Department of Energy Computational Science Graduate Fellowship Grant DE-FG02-97ER25308 (to D.A.M.).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0803183105/DCSupplemental.
References
- 1.Murthy VN, Fetz EE. Coherent 25- to 35-Hz oscillations in the sensorimotor cortex of awake behaving monkeys. Proc Natl Acad Sci USA. 1992;89:5670–5674. doi: 10.1073/pnas.89.12.5670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gray CM, Singer W. Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc Natl Acad Sci USA. 1989;86:1698–1702. doi: 10.1073/pnas.86.5.1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bragin A, et al. Gamma (40–100 Hz) oscillation in the hippocampus of the behaving rat. J Neurosci. 1995;15:47–60. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fries P, Nikolic D, Singer W. The gamma cycle. Trends Neurosci. 2007;30:309–316. doi: 10.1016/j.tins.2007.05.005. [DOI] [PubMed] [Google Scholar]
- 5.Whittington MA, Traub RD, Jefferys JG. Synchronized oscillations in interneuron networks driven by metabotropic glutamate receptor activation. Nature. 1995;373:612–615. doi: 10.1038/373612a0. [DOI] [PubMed] [Google Scholar]
- 6.Hasenstaub A, et al. Inhibitory postsynaptic potentials carry synchronized frequency information in active cortical networks. Neuron. 2005;47:423–435. doi: 10.1016/j.neuron.2005.06.016. [DOI] [PubMed] [Google Scholar]
- 7.Mainen ZF, Sejnowski TJ. Reliability of spike timing in neocortical neurons. Science. 1995;268:1503–1506. doi: 10.1126/science.7770778. [DOI] [PubMed] [Google Scholar]
- 8.Losonczy A, Magee JC. Integrative properties of radial oblique dendrites in hippocampal CA1 pyramidal neurons. Neuron. 2006;50:291–307. doi: 10.1016/j.neuron.2006.03.016. [DOI] [PubMed] [Google Scholar]
- 9.Pouille F, Scanziani M. Enforcement of temporal fidelity in pyramidal cells by somatic feed-forward inhibition. Science. 2001;293:1159–1163. doi: 10.1126/science.1060342. [DOI] [PubMed] [Google Scholar]
- 10.Dan Y, Poo MM. Spike timing-dependent plasticity of neural circuits. Neuron. 2004;44:23–30. doi: 10.1016/j.neuron.2004.09.007. [DOI] [PubMed] [Google Scholar]
- 11.Markram H, Lubke J, Frotscher M, Sakmann B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science. 1997;275:213–215. doi: 10.1126/science.275.5297.213. [DOI] [PubMed] [Google Scholar]
- 12.Brody CD, Hopfield JJ. Simple networks for spike-timing-based computation, with application to olfactory processing. Neuron. 2003;37:843–852. doi: 10.1016/s0896-6273(03)00120-x. [DOI] [PubMed] [Google Scholar]
- 13.de la Rocha J, Doiron B, Shea-Brown E, Josic K, Reyes A. Correlation between neural spike trains increases with firing rate. Nature. 2007;448:802–806. doi: 10.1038/nature06028. [DOI] [PubMed] [Google Scholar]
- 14.Lampl I, Reichova I, Ferster D. Synchronous membrane potential fluctuations in neurons of the cat visual cortex. Neuron. 1999;22:361–374. doi: 10.1016/s0896-6273(00)81096-x. [DOI] [PubMed] [Google Scholar]
- 15.Adrian ED. Olfactory reactions in the brain of the hedgehog. J Physiol (London) 1942;100:459–473. doi: 10.1113/jphysiol.1942.sp003955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
- 17.Hopfield JJ, Brody CD. What is a moment? Transient synchrony as a collective mechanism for spatiotemporal integration. Proc Natl Acad Sci USA. 2001;98:1282–1287. doi: 10.1073/pnas.031567098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lisman J. The theta/gamma discrete phase code occurring during the hippocampal phase precession may be a more general brain coding scheme. Hippocampus. 2005;15:913–922. doi: 10.1002/hipo.20121. [DOI] [PubMed] [Google Scholar]
- 19.von der Malsburg C, Buhmann J. Sensory segmentation with coupled neural oscillators. Biol Cybern. 1992;67:233–242. doi: 10.1007/BF00204396. [DOI] [PubMed] [Google Scholar]
- 20.Hopfield JJ, Herz AV. Rapid local synchronization of action potentials: toward computation with coupled integrate-and-fire neurons. Proc Natl Acad Sci USA. 1995;92:6655–6662. doi: 10.1073/pnas.92.15.6655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mehta MR, Lee AK, Wilson MA. Role of experience and oscillations in transforming a rate code into a temporal code. Nature. 2002;417:741–746. doi: 10.1038/nature00807. [DOI] [PubMed] [Google Scholar]
- 22.Bair W, Koch C, Newsome W, Britten K. Power spectrum analysis of bursting cells in area MT in the behaving monkey. J Neurosci. 1994;14:2870–2892. doi: 10.1523/JNEUROSCI.14-05-02870.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nowak LG, Sanchez-Vives MV, McCormick DA. Influence of low and high frequency inputs on spike timing in visual cortical neurons. Cereb Cortex. 1997;7:487–501. doi: 10.1093/cercor/7.6.487. [DOI] [PubMed] [Google Scholar]
- 24.Lee AK, Manns ID, Sakmann B, Brecht M. Whole-cell recordings in freely moving rats. Neuron. 2006;51:399–407. doi: 10.1016/j.neuron.2006.07.004. [DOI] [PubMed] [Google Scholar]
- 25.Crochet S, Petersen CC. Correlating whisker behavior with membrane potential in barrel cortex of awake mice. Nat Neurosci. 2006;9:608–610. doi: 10.1038/nn1690. [DOI] [PubMed] [Google Scholar]
- 26.Schreiber S, Fellous JM, Tiesinga P, Sejnowski TJ. Influence of ionic conductances on spike timing reliability of cortical neurons for suprathreshold rhythmic inputs. J Neurophysiol. 2004;91:194–205. doi: 10.1152/jn.00556.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jensen RV. Synchronization of randomly driven nonlinear oscillators. Phys Rev E. 1998;58:R6907–R6910. [Google Scholar]
- 28.Bressler SL, Freeman WJ. Frequency analysis of olfactory system EEG in cat, rabbit, and rat. Electroencephalogr Clin Neurophysiol. 1980;50:19–24. doi: 10.1016/0013-4694(80)90319-3. [DOI] [PubMed] [Google Scholar]
- 29.Wehr M, Laurent G. Odour encoding by temporal sequences of firing in oscillating neural assemblies. Nature. 1996;384:162–166. doi: 10.1038/384162a0. [DOI] [PubMed] [Google Scholar]
- 30.Buzsaki G, et al. Hippocampal network patterns of activity in the mouse. Neuroscience. 2003;116:201–211. doi: 10.1016/s0306-4522(02)00669-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.