Force-generation and dynamic instability of microtubule bundles

Abstract

Individual dynamic microtubules can generate pushing or pulling forces when their growing or shrinking ends are in contact with cellular objects such as the cortex or chromosomes. These microtubules can operate in parallel bundles, for example when interacting with mitotic chromosomes. Here, we investigate the force-generating capabilities of a bundle of growing microtubules and study the effect that force has on the cooperative dynamics of such a bundle. We used an optical tweezers setup to study microtubule bundles growing against a microfabricated rigid barrier in vitro. We show that multiple microtubules can generate a pushing force that increases linearly with the number of microtubules present. In addition, the bundle can cooperatively switch to a shrinking state, due to a force-induced coupling of the dynamic instability of single microtubules. In the presence of GMPCPP, bundle catastrophes no longer occur, and high bundle forces are reached more effectively. We reproduce the observed behavior with a simple simulation of microtubule bundle dynamics that takes into account previously measured force effects on single microtubules. Using this simulation, we also show that a constant compressive force on a growing bundle leads to oscillations in bundle length that are of potential relevance for chromosome oscillations observed in living cells.

Microtubules (MTs) are dynamic cytoskeletal polymers that constantly switch between growing and shrinking states in a process termed dynamic instability (1). They are able to generate pushing forces during their assembly process, and pulling forces during their disassembly process (2, 3). Pushing forces have been shown to contribute, for example, to nuclear positioning in fission yeast (4), while both MT pushing and pulling forces have been implicated in chromosome motion during mitosis (5). The force that a single growing MT can generate, and the effect that this force has on the assembly dynamics of the MT, has been studied in detail in in vitro experiments (6–10). It has been shown that the growth velocity decreases, and the catastrophe frequency (the rate at which MTs switch from growth to shrinkage) increases, as the compressive force on the MT end increases. This implies that growing MTs interacting with obstacles in cells, such as the cell cortex or chromosomes, are expected to enhance their probability of switching to a shrinking state because of compressive forces that are generated in these situations. In this way, force can provide a regulation mechanism to the cell to (locally) control MT dynamics (11).

Often, MTs do not operate alone but work together in bundles. In particular, in the case of mitosis, MTs that interact with the chromosomes grow in parallel bundles that could presumably generate collective forces on the chromosomes that greatly exceed the force generated by a single MT (12). A subset of these MTs associates with specialized attachment sites on the chromosomes called kinetochores (13). During anaphase, shrinking kinetochore MT bundles are believed to produce pulling forces on the chromosomes that cause poleward motion (14). During pro-metaphase and metaphase, poleward motion is alternated with anti-poleward motion, which is believed to be due to interactions of non-kinetochore MTs with motor proteins located on the chromosome arms (15) and/or pushing forces generated by the growth of MT bundles against kinetochores or chromosome arms (16). It is, however, not known what the collective force-generating capabilities of multiple growing MTs are and, thus, how importantly these forces might contribute to the anti-poleward motion of chromosomes observed during mitosis.

In this article, we ask how much force can be generated by multiple MTs that are growing in parallel from a common rigid base (without being otherwise cross-linked to each other). Do forces generated by single MTs add up in a linear fashion, and how are the dynamics of the single MTs and the bundle affected by the presence of a compressive force? To address these questions, we studied the dynamics of a MT bundle under force in an in vitro experiment where MTs growing from pure tubulin pushed against a microfabricated rigid barrier. We used an optical tweezers setup, as described in previous experiments on single MTs (9, 17). We show that multiple MTs that grow in parallel can reach much higher forces than single MTs, and that the increase in force is linear with the number of MTs present. Surprisingly, we also observe cooperative catastrophes, i.e., relatively abrupt switches to the shrinking state of the entire MT bundle, even though the probability for spontaneous near-simultaneous catastrophes of all MTs in the bundle is negligible under our conditions. When we grow the bundle in the presence of GMPCPP, a slowly hydrolysable analogue of GTP (18), bundle catastrophes no longer occur, and as a result the bundle reaches high forces more effectively. We can reproduce the observed behavior with a simple simulation of MT bundle dynamics that takes into account the force effects that have been measured for single MTs (6, 8). Apparently, the otherwise independent dynamics of individual MTs can be coupled to each other because of the presence of a compressive force. Interestingly, when in the simulation we exert a constant compressive force on the growing bundle, we observe length oscillations similar to chromosome oscillations measured in newt lung cells during pro-metaphase (19).

Results

Measurement of Bundle Forces and Dynamics.

To study the dynamics and force generation of a growing MT bundle in vitro, we used an optical tweezers technique that allowed us to grow multiple MTs from an axoneme, a naturally occurring rigid bundle of polarity-aligned stabilized MTs, against a rigid microfabricated wall (17, 20, 21) (Fig. 1A). The axoneme was aspecifically attached on one side to a bead. This construct was held in a keyhole trap, a time-shared optical trap that had a main trapping point to hold the bead and a weak line trap to align the axoneme (Fig. 1A). The construct was positioned halfway up a 7-μm-high sidewall of a microfabricated chamber (Fig. 1B) built into a flow system. When a solution containing tubulin and GTP was flown in, MT growth started. After growing MTs made contact with the wall, further length increases of the MTs led to a displacement of the bead in the trap and a linearly increasing force on the MTs. By determining the position of the bead in the trap and the trap stiffness, we could measure the forces generated by the bundle of MTs over time. To keep the MTs short (<1 μm) and thus prevent them from buckling, we started the experiment with the axoneme very close to or slightly pressed against the wall and chose a relatively high trap stiffness so that MTs would stall before they would grow too long (6).

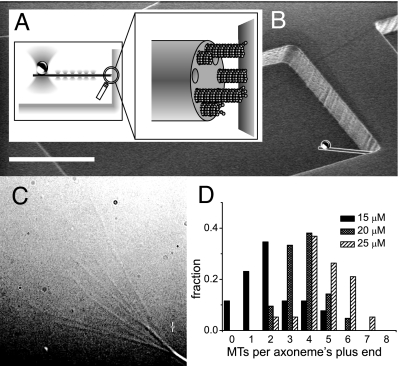
Fig. 1.

Experimental setup. (A) Schematic picture of a MT bundle nucleated by an axoneme growing against a barrier. A construct made of a bead attached to the axoneme is maintained in position by a “keyhole” trap: A single strong trap holds the bead while many shallow traps form a line trap constraining the axoneme's movement along a single direction. (B) Scanning electron micrograph of a microchamber, whose corner is used as a rigid barrier. A schematic construct (drawn to scale) is superimposed on the micrograph. (Scale bar: 20 μm.) (C) Video-enhanced differential interference contrast (VE-DIC) image of an axoneme from which several MTs are growing. (D) Histograms of the number of MTs observed per axoneme, for different tubulin concentrations at 27°C.

The axonemes we used had 9–11 nucleation sites for MTs (as determined from EM pictures; data not shown). The average number that was nucleated could be tuned by varying the tubulin concentration and the temperature. We first characterized the nucleation properties by sticking axonemes to the surface of a flow cell and by growing MTs at different temperatures and tubulin concentrations [see supporting information (SI) Methods]. We counted the number of MTs per axoneme in the first 5–10 min of the experiment, assuming that the end with the most MTs was the plus-end (Fig. 1C). MT plus-ends grow much faster than minus ends, so the corresponding end of an axoneme has more and longer MTs (22). To verify this, we occasionally introduced beads coated with kinesin molecules into our samples (23). When placed on an axoneme, these beads always moved to the side with the most MTs. In Fig. 1D, three histograms are shown with the number of MTs per axoneme at different tubulin concentrations at 27°C. At a tubulin concentration of 25 μM, the average number of MTs was 4.7 ± 1.2, with a maximum of 9 per axoneme. However, we expect this number to be an underestimate because we could not detect MTs shorter than ≈1 μm. When raising the concentration or temperature further, to get an average number close to the maximal number of nucleation sites, spontaneous nucleation of MTs occurred, which would have been a problem in the trap experiment. We decided to perform our trap experiments at 28°C with an initial tubulin concentration of 25 μM. We estimate that mixing in the flow cell diluted the tubulin down to ≈20 μM (corresponding to an average number of MTs of approximately four in Fig. 1D).

In Fig. 2A, four traces of plus-end MT bundle growth are shown. We could distinguish between plus- and minus-end growth because the plus-end grew faster and had catastrophes. Occasional measurements with much slower growth and no catastrophes, which we attribute to minus-ends, are not shown. When focusing on the first dataset in Fig. 2A (uppermost trace), it appears that indeed several MTs are growing together. First, a MT starts growing at t ∼ 25 sec until it reaches a force of 2.8 ± 0.7 pN, stalls, and has a catastrophe at t ∼ 105 sec. Given the conditions and previous results on single-MT force generation, we attribute this event to the growth of a single MT. At t ∼ 155 sec, a new MT starts to grow. In this case, no catastrophe is observed before t ∼ 295 sec, and forces up to 20 ± 5 pN are reached. This force is significantly higher than the force generated by a single MT, and we thus attribute this event to multiple MTs growing together in a bundle. If we assume that MTs can add up their forces linearly, there must be approximately seven MTs growing together in the bundle, close to the maximum number of nucleation sites on the axoneme. Interestingly, the MT bundle switches to an apparent shrinking state at t ∼ 295 sec, an event that is reminiscent of catastrophe events that are normally observed for single MTs. Measurements were stopped when all tubulin had flown through the experimental chamber. In some cases (lower trace in Fig. 2A), the measurement was stopped because the construct became stuck to the wall (because of a nonspecific interaction). We detected this by translating the wall away from the trap after the force had reached an apparent static plateau.

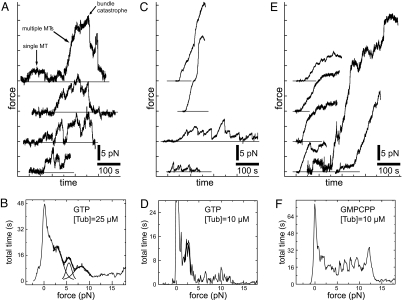
Fig. 2.

Force generation by growing MT bundles in the presence of GTP and GMPCPP. (A) Force traces as a function of time for a tubulin concentration of 25 μM in the presence of GTP. For clarity, the three upper curves were shifted upward by 10 pN, 20 pN, and 30 pN, respectively. Horizontal lines indicate the zero-force level in each case. Arrows in the uppermost trace indicate growth of a single MT, followed by the growth of a bundle consisting of multiple MTs. (B) Histogram of measured forces for nine traces obtained under similar conditions. The three lower curves from A were used, as well as six extra curves not shown here. A 0.1-pN force binning was used. In addition to the peak at zero-force, three almost equally spaced peaks are observed at higher forces. The center positions of these peaks were estimated by simultaneously fitting the sum of three Gaussian distributions to the histogram between 2 and 11 pN. The Gaussian distributions, and their sum, are superimposed onto the histogram. (C) Similar to A for a tubulin concentration of 10 μM. (D) Histogram of forces obtained from four traces shown in C. A Gaussian distribution was fitted to the histogram between 1.4 and 3.2 pN, to estimate the (single) peak position centered around 2.4 pN. (E) Similar to C in the presence of GMPCPP. (F) Histogram of forces obtained from 12 traces such as shown in E. No clear ≈3-pN-spaced peaks can be observed in this histogram (see Fig. S1B).

Fig. 2B shows a histogram of the data collected from nine force traces taken under as much as possible identical conditions, representing a total measurement time of ≈3,300 sec. This included three traces where the force reached up to ≈40 pN, which we attribute to the presence of probably two bundled axonemes, which together can nucleate >11 MTs. The histogram shows the total amount of time the bundles spent at a given force. As expected, the histogram has a first peak at zero force, which simply represents the nongrowing bundle undergoing thermal fluctuations around a zero-force average. In addition, the histogram shows three other peaks, whose center locations were determined by a simultaneous fit of three Gaussian distributions on a restricted force range (2–11 pN). The three peak positions, at 2.7, 5.5, and 8.1 pN, respectively, are approximate multiples of 2.7 pN. The 2.7 pN value can be compared with the maximum force developed during the single-MT event in the upper trace in Fig. 2A. Because the peak locations observed in the histogram in Fig. 2B correspond to multiples of the maximum force developed by a single MT, we attribute these peaks to the maximum force generated by a bundle made of one, two, or three MTs, respectively. One expects that close to its maximum reachable force, a bundle grows slower or stalls, thus increasing the amount of time it spends at that force. For forces >10 pN, no clear peaks are distinguishable anymore in the histogram. This is likely the result of the reduced statistics at higher forces (high forces are reached less frequently, because of bundle catastrophes; see also Fig. S1A), as well as the presence of experimental error, which broadens the force distribution. The main experimental error comes from the fact that the trap stiffness has to be determined for each individual experiment, introducing an error of up to ≈20% between forces measured in different experiments (due to variable bead sizes). One therefore expects that at high forces the absolute error becomes comparable with the spacing between peaks.

Even though the number of experiments we combined in a single force histogram was limited to nine, both the observed histogram peaks and the maximum forces reached in individual cases are clearly consistent with a linear addition of single-MT maximum forces: A bundle made of N MTs appears to generate a maximum force N times higher than the single-MT maximum force. As a consequence, when a MT bundle reaches its maximum force, each MT in contact with the wall feels a force that is equal to its own maximum (stall) force. The observation that a bundle can still experience an apparent catastrophe must mean that there is a finite chance that all MTs in the bundle switch within a small amount of time to a shrinking state. We propose that this is due to the fact that the catastrophe rate of individual MTs is highly force-dependent (8). When one of the MTs has a catastrophe, the force on the others increases, which means the probability to also experience a catastrophe is expected to increase. This leads to what could be considered a force-induced coupling of the dynamic instability of single MTs.

One would expect that the probability for the bundle to experience a catastrophe is affected not only by force, but also by the rate at which individual MTs experience a catastrophe in the absence of force. Because this rate is sensitive to the growth rate of MTs, and therefore the tubulin concentration (8), we repeated the bundle experiment in the presence of a lower concentration of tubulin (Fig. 2CD). We found that, in this case, catastrophes often occurred before high forces could be reached. Although in individual cases we still observed forces generated by multiple MTs (Fig. 2C), a histogram of the force data only revealed a clear peak corresponding to single-MT events (Fig. 2D). When, at the same low tubulin concentration, we inhibited catastrophes by adding GMPCPP instead of GTP (18), bundle catastrophe no longer occurred and forces corresponding to multiple MTs were again observed (Fig. 2EF). Note that in this case one would expect to observe maximum forces corresponding to the stall force of 9–11 MTs (the number of nucleation sites). In individual cases, we indeed observed large forces. However, we had to terminate most of our measurements before this situation was reached, again because the construct got stuck to the wall. Note also that in the GMPCPP case, clear peaks due to stalling of individual MTs can only be expected if nucleation of subsequent MTs is slow. Instead, we observe a rather continuous, slightly increasing distribution of forces, which is expected as a bundle of near-simultaneously nucleated MTs slows down at increasing force (see Fig. S1B). This absence of clear peaks unfortunately prevents us from addressing whether the stall force of single MTs is influenced by GTP-hydrolysis.

Simulations.

To test whether the mechanism described above provides a plausible scenario for bundle catastrophes, we performed simple computer simulations of bundle dynamics that included previously measured effects of force on the dynamics of individual MTs (6, 8) (Fig. 3A; see Materials and Methods). The nucleation of new MTs from axonemes and the catastrophes of individual growing MTs were modeled as stochastic processes with Poissonian distributions. The growth itself was treated as a deterministic and continuous process. We simulated the experimental conditions by applying a linearly increasing force to the growing bundle to represent the spring-like character of the trap. We assumed that the force only acted on the MTs that were in contact with the barrier; the force that was exerted upon each MT was taken as the total force divided by the number of force-sharing MTs in contact with the barrier (24).

Fig. 3.

Simulations of MT bundle dynamics under force. (A) Schematic picture showing the geometry and some of the parameters used in the simulations. MTs grow from nucleation sites provided by an axoneme. Before they reach the barrier, their zero-force growth velocity is v_g(0). When N MTs are in contact with the wall, each single MT is submitted to a force F/N, where F is the total force exerted on the MT bundle. F is proportional to the increase in bundle length L − L₀ and to the trap stiffness k_trap. After a MT undergoes a catastrophe, it shrinks with a velocity v_s. The bundle has a growth velocity v_bundle(F). (B) Force trace generated by the simulations. The thick line represents the force generated by the bundle, which is proportional to the length of the longest MTs in the bundle. The thin lines show the dynamics of individual MTs that are not (yet) in contact with the barrier. Oblique thin lines represent growing MTs whereas vertical lines represent shrinking MTs. (C) Selected event from a simulated force trace. Arrows represent events to be compared with experimental data in D (see text). (D) Experimental force trace (same data as the uppermost curve in Fig. 2A). Arrows represent events to be compared with the simulated growth event in C.

In the simulation, we tracked the length of the bundle as well as the individual MTs in the bundle (Fig. 3B), allowing us to study the effect of single MT behavior on the dynamics of the whole bundle. To compare the simulations and experiments, we plotted the force generated by the bundle, which is linearly proportional to the length of the longest MTs in the bundle. In Fig. 3B, the simulated dynamics of a MT bundle can be seen, whereas in Fig. 3C we zoom in on a specific event to visualize details in the growth curve that can be compared with experimental results (Fig. 3D). The MT bundle as a whole shows a force-dependent growth velocity that depends on the number of MTs that are in contact with the barrier. Newly nucleated MTs grow faster than the MTs under force and quickly reach the barrier. When a newly nucleated MT reaches the barrier, the bundle starts to grow faster (large black arrows in Fig. 3 C and D), whereas an individual MT catastrophe slows the bundle down (white arrows). The opposing force couples the dynamics of the MTs in the bundle. This cooperative behavior is most obvious just before the bundle as a whole undergoes a catastrophe. In Fig. 3C, the bundle has grown quite persistently until the first MT in the bundle has a catastrophe at ≈280 sec. As a result, the force on the other MTs increases, their velocity goes down (and even becomes negative), and their probability to also have a catastrophe increases. Every new catastrophe in the bundle increases this probability even further, and a single catastrophe in the bundle can thus induce a cascade of catastrophes, resulting in a catastrophe of the entire bundle. Qualitatively, this behavior is quite insensitive to the exact choice of parameters. For example, more MTs leads to higher forces and longer bundle catastrophe times. An increased individual catastrophe rate, or higher sensitivity of the catastrophe rate to force, leads to shorter bundle catastrophe times. However, high forces and catastrophes of the entire bundle are always observed. Note that apparent rescues of the bundle are also observed. This is, however, not due to rescues of individual MTs but the result of newly nucleated growing MTs catching up with a shrinking bundle at low force (small black arrows). Although in Fig. 3D we compare an experimental trace with a simulated trace (Fig. 3C) that was selected for its specific similarity to the experimental data, the simulated trace is quite representative of other simulated growth events, as can be seen by comparing Fig. 3 B and C. The similarity between the experimental and simulation results suggests that the experimentally observed dynamic instability of MT bundles can indeed be explained as a force-induced coupling of the dynamic instability behavior of single MTs.

Discussion

The combined results of our experiments and simulations show that the maximum forces MTs can generate linearly add up when growing in a parallel bundle. Sharing the force allows the MTs to show cooperative dynamic behavior in the form of bundle catastrophes. In practice, the maximum forces that are generated are a function not only of the number of MTs that can be nucleated but also of the probability that individual MTs undergo catastrophes. One might argue that it is not very surprising that multiple biopolymers that grow together in a parallel bundle can share a force. In fact, for multiple protofilaments growing in parallel within a single MT, something similar has been predicted and observed (7, 24). The difference, however, is that MTs in a bundle are only connected at their base and not cross-linked to each other in any other way. Therefore, they have no direct way of influencing each other's growth dynamics. A priori, it is therefore difficult to predict what level of cooperativity to expect. In the case of a parallel growing actin bundle, we have in fact found evidence that the generated force is limited to the force generated by a single filament (25). In that case, the force seems to be carried always by the single longest filament, whereas the identity of this filament constantly changes because of depolymerization events. The exact details of this apparently different behavior remain to be understood.

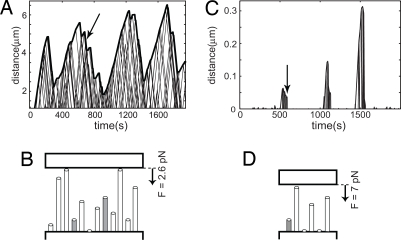
The measurements and simulations we presented so far were all on MT bundles growing against a spring-like force. However, the simulation also allowed us to study the dynamics of a MT bundle growing against a constant force. We found that if a constant small force was applied, the bundle as a whole experienced alternating collective catastrophes and apparent rescues resulting in oscillations around a constant length (Fig. 4A). Interestingly, during chromosome positioning in mitosis, chromosomes also exhibit oscillatory motions, as measured for example by Skibbens et al. (19). During mitosis, chromosomes first become mono-oriented (one of the two sister kinetochores associates with MT ends), then become bi-oriented (both sister kinetochores associate with MT ends), and eventually congress to the equator. In their article, Skibbens et al. show that chromosome oscillations observed during the mono- and bi-oriented phase are not sinusoidal but appear as a saw-tooth pattern consisting of abrupt switches between constant opposite velocities. We could reproduce bundle oscillations that were reminiscent of the specific mono-oriented oscillations described by Skibbens et al. by making only a few changes to our simulations (see Materials and Methods for details). We set both v_s and v_g(0) to the same value, because growth and shrinkage velocities are similar in magnitude in vivo. We increased the number of nucleation sites and the catastrophe rate, and assumed a constant small force applied on the bundle by the barrier. We found that the occurrence of oscillatory behavior is not very sensitive to the exact choice of the input parameters, as long as the force is small compared with the stall force of the MT bundle. For example, more MTs in the bundle lead to a longer average length around which the bundle oscillates, and at a low catastrophe rate, the bundle switches, on average, less frequently. The oscillations, however, remain. Only when either the number of MTs is too small and/or the force is too high, oscillations are no longer observed and short bursts of growth, similar to what we measure in our trap experiments, remain (Fig. 4 C and D).

Fig. 4.

MT bundle oscillations. (A) Simulations of bundle growth under a small constant force reveal length oscillations that are reminiscent of chromosome oscillations observed by Skibbens et al. (14). See text and SI Methods for a description of the simulation parameters used. The arrow indicates the time point corresponding to the sketch in B. (B) Situation sketch of the MT bundle shortly before an apparent rescue of a shrinking MT bundle. Gray tubes indicate growing MTs, and white tubes indicate shrinking MTs. (C) Similar to A for a larger force and lower number of MTs (see SI Methods). In this case, only short bursts of bundle growth are observed. (D) Situation sketch, similar to B, corresponding to the arrow in C.

In recent models describing chromosome oscillations, MT polymerization forces are considered to be negligible (26–30). Our findings suggest that the cooperative polymerization dynamics of MT bundles may instead be worth considering as a mechanism contributing to this phenomenon. Interestingly, Vandenbeldt et al. (31) studied kinetochore MT bundles and found that almost all bundles examined had a mixture of kinetochore MTs in the polymerizing and depolymerizing states. In our simulations, the individual MTs in the bundle are also very dynamic, although as a whole the bundle shows cooperative behavior (see Fig. 4 A and B). It is important to stress that the effects we describe may be relevant for both MTs in contact with the kinetochore and MTs pushing against the chromosome arms. It is also important to stress that, in reality, chromosome oscillations are undoubtedly the result of a more complex mechanism than is described here. For example, even mono-oriented kinetochores are often under tension (32), indicating that MTs generate pulling forces on the kinetochore at least some fraction of the time. Additionally, there is clear evidence that chromosome oscillations depend on the action of chromokinesins such as Kid (33). Neither effect is considered here.

In summary, we have shown, using a combination of experiments and simulations, that MT bundles in vitro can reach forces much higher than the stall force of individual MTs and can undergo force-induced catastrophes of the complete bundle. We propose that MT bundles can reach these high forces by sharing the force and that this sharing introduces coupling of their dynamic instability behavior. Additional results obtained by using our simulations suggest that this mechanism may contribute to chromosome oscillations observed in vivo. In the future, it would be very interesting to perform similar experiments under more physiological conditions; for example, in the presence of the MT cross-linker Xnf7 (34), which is believed to be involved in cross-linking kinetochore bundles during mitosis.

Materials and Methods

Materials.

Axonemes (a generous gift from Matt Footer, Stanford University School of Medicine, Stanford, CA) were purified from sea urchins according to ref. 20 and stored following a method from ref. 35, except that no glycerol was used. Their nucleating properties were characterized by using video-enhanced differential interference contrast (VE-DIC) microscopy (see SI Methods). Tubulin was purchased lyophilized from Cytoskeleton and resuspended in MRB80 (80 mM K-Pipes, 4 mM MgCl₂, 1 mM EGTA, pH 6.8).

Optical Tweezers.

The optical tweezers setup consisted of an infrared trapping laser (1,064 nm, Nd:YVO₄; Spectra-Physics), which was focused into the sample by a ×100/1.3 N.A. oil-immersion objective. The laser beam was time-shared by using acousto-optical deflectors (AODs) (IntraAction DTD-274HA6) to create a “key hole” trap consisting of a point trap and a line trap, as described in refs. 9 and 17. A low-power red laser (633 nm, HeNe, 1125P; Uniphase) was superimposed after the AODs on the IR beam. The red laser light was focused on a bead trapped in the point trap, and imaged onto a quadrant-photodiode for stiffness calibration. The stiffness of the point trap was determined by analysis of the power spectrum of the thermal fluctuations of the bead (36). Typically, trap stiffnesses in the range of 0.05–0.17 pN/nm were used.

Microfabricated Chambers.

Clean coverslips were spin-coated with SU-8 negative tone photoresist (Microchem) to produce a 7-μm-thick layer, which was then soft-baked. The coverslips were exposed to UV light and postexposure baked. The illuminated areas were developed (XP SU8-developer; Microchem) and hard-baked, leaving 7-μm-high chambers of 40 × 80 μm separated by 20-μm-wide walls (21).

Force Experiments.

A clean coverslip was built into a flow system, which consisted of a channel cut in parafilm squeezed between slide and coverslip. To block the surface of the chambers, first a 0.2% agarose solution at 70°C was flown in. The agarose was blow-dried by connecting a pump with the channel for a few minutes. Afterward, a 0.1% Triton X-100 (Sigma) solution was flown through to prevent bubble formation in the flow cell. A second blocking step was done by incubating the flow system for 15 min with a 50 mg/ml BSA solution in acetate buffer (21 mM acetic acid, 79 mM C₂H₃O₂Na, pH 5.2). The experiment started by flowing in axonemes and beads. First, a bead was trapped in the point trap. Then, an axoneme was caught in the line trap and aspecifically stuck to the bead (7). The tip of the axoneme was positioned very close or slightly pressed against a wall of the microfabricated chamber (Fig. 1B). At this moment, tubulin (with 5 mg/ml BSA and 1 mM GTP in MRB80) was added to trigger MT growth. The temperature of the experiment was kept at 28°C. Axonemes and beads were imaged by using VE-DIC. During the experiments, the image stream was digitized at 1 Hz and the position of the bead was tracked online by using a cross-correlation routine for live monitoring. Afterward, the recorded data from the DVD was digitized at a frame rate of 25 Hz. This image stream was used to track the bead offline. The bead tracking was automated by using home-written Interactive Data Language (IDL) software. The position of the bead was obtained with subpixel resolution down to 2–3 nm (17).

Simulations.

Using MATLAB, we simulated the dynamics of a parallel bundle of MTs nucleated by a surface with a fixed number of nucleation sites, growing against a barrier to which a load F was applied (Fig. 3A). Microtubule growth and shrinkage were treated as deterministic processes with well defined velocities, whereas nucleation and catastrophe events of individual MTs were treated as random processes. The parameters in the simulation were the nucleation rate of individual MTs, their average catastrophe time (T_c), and their growth (v_g) and shrinkage (v_s) velocities. The length L and growth velocity v_bundle of the bundle were defined as the length and velocity of the longest MT(s) in the bundle. The force exerted on the growing MT bundle was assumed to increase linearly with L − L₀ (L₀ being the bundle length upon first contact with the barrier) with a factor k_trap (the stiffness of the trap in our experiments), and assumed to be distributed evenly over all MTs in the bundle that are in contact with the barrier. For further details on parameter values, see SI Methods.