Compression, gain, and nonlinear distortion in an active cochlear model with subpartitions

Abstract

The propagation of inhomogeneous, weakly nonlinear waves is considered in a cochlear model having two degrees of freedom that represent the transverse motions of the tectorial and basilar membranes within the organ of Corti. It is assumed that nonlinearity arises from the saturation of outer hair cell active force generation. I use multiple scale asymptotics and treat nonlinearity as a correction to a linear hydroelastic wave. The resulting theory is used to explain experimentally observed features of the response of the cochlear partition to a pure tone, including: the amplification of the response in a healthy cochlea vs a dead one; the less than linear growth rate of the response to increasing sound pressure level; and the amount of distortion to be expected at high and low frequencies at basal and apical locations, respectively. I also show that the outer hair cell nonlinearity generates retrograde waves.

The mechanical response of the cochlea to sound is rich in nonlinear phenomena that are fundamental to the hearing process in mammals (1). One of the more important effects is called compression. This term is used to signify that the displacement of the cochlear partition (CP) at a fixed location along the cochlea does not increase in proportion to the input sound pressure level (SPL) of a pure tone at the stapes, as a linear system would, but at a smaller rate. The prevailing hypothesis concerning the source of compression is the saturation of the active process of outer hair cell (OHC) force production (2, 3). OHC active force production is also thought by some researchers to be the mechanism of producing gain of the putative cochlear amplifier (CA) (4). The term, CA gain, is utilized to describe the fact that to produce given displacements of the CP in response to a pure tone, a healthy, active cochlea requires a smaller SPL than does a damaged or dead cochlea. The effects of nonlinearity are not small, if assessed from the amount of compression or gain (5). One might expect a significant nonlinearity to modify various phases of a waveform differently, thus producing a significant harmonic distortion of a pure tone. However, this is not the case for measurements at the base at high frequency (5), although some distortion has been reported at the apex at low frequency (6, 7).

The primary aim of this study is to account for large compression, large gain, and small distortion in an active cochlear model when the source of the nonlinearity is the saturation of OHC force production. Thus, this work is an extension of our previous work that considered linear, active models having multiple transverse degrees of freedom, and which we studied by use of the multiple scale approximation in the frequency domain (8, 9). Here, I introduce from the outset that nonlinear distortion is small and can be calculated as a correction to linear theory. Quite surprisingly, large compression and gain follow as a natural consequence of this assumption. This approach differs significantly from previous computations in the frequency domain (10, 11), which were based on recursive numerical schemes that utilized an initially guessed waveform shape. First, the present work treats nonlinearity in the cochlea in a system with more than one transverse degree of freedom. To some extent, the role of the extra degree of freedom with regard to the nonlinear effects can be established. Second, the method developed here is computationally much simpler. Also, the methods presented allow analytical estimates for distortion and gain in terms of OHC force production and cochlear geometry.

Mathematical Formulation and Solution

The Model.

The linear model previously proposed and analyzed (8, 9) consists of a straightened duct with a rectangular cross section bounded by rigid walls. The organ of Corti (OC) separates two fluid-filled spaces. The coordinates (X, Y, Z), respectively, denote the radial, transverse (perpendicular to the partition), and axial (along the length of the duct) directions. Different parts of each OC cross section are free to oscillate with different amplitudes and phases. Such a representation is supported by recent experiments demonstrating significant relative motions within the OC (12, 13). An OHC transmits its force through its attachment at its two ends to a Deiter’s cell and to the reticular lamina (RL). The transverse component of motion of the RL must be followed by the tectorial membrane (TM) because we have shown that there is no squeezing motion between TM and RL (8). This prediction is consistent with experimental observations (12, 13). Thus, the CP model has to allow at least explicitly for independent transverse motions of the basilar membrane (BM) and the RL-TM complex. The simplest structural model of the OC is a lumped-parameter model with two degrees of freedom shown in Fig. 1. The observation of both transverse and radial displacements in the OC (12, 13) are treated as being kinematically coupled in the present model, and are not modeled as distinct degrees of freedom. Here it is assumed that OHC stereocilia sense motion at the TM-RL subpartition, and somatic motility of the OHC acts between the TM-RL complex and the BM (as occurs in vivo). Mechanical axial coupling is included through the fluid–structure interaction. Two fluid channels representing the scalae vestibuli and tympani, each filled with an incompressible liquid provide the fluid loading to the subpartitions. All properties such as mass, stiffness, and damping are allowed to vary slowly along the axial coordinate Z. Locally, the masses are assumed to perform piston-like oscillations, independent of X, displacing liquid transversely and axially in the adjacent channels. Elastic coupling of adjacent sections is neglected, but electrical axial coupling of OHCs is modeled through a wavelength-dependent active force mechanism (9).

Figure 1.

Structural elements in the transverse (X, Y) plane. Q⁽¹⁾ and Q⁽²⁾ denote the vertical displacements of the two masses TM and BM. The horizontal displacement Q^(s) denotes the shearing displacement of the TM, which is kinematically coupled to Q⁽¹⁾ in the present model, thus resulting in two independent degrees of freedom. The TM is constrained by a torsional spring and a rigid rod. Viscous components are not shown so as to keep figure simple.

Partition Equation.

The dynamic equations of motion of the partition can be written in matrix form

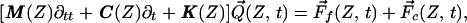1

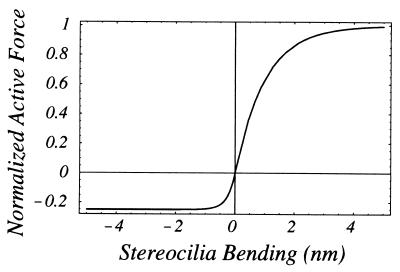
where the structural matrices for mass M, damping C, and stiffness K are detailed in the Appendix. Q⃗(Z, t) is a vector having components (Q⁽¹⁾, Q⁽²⁾) that represent the transverse displacements of the TM and BM (note that the TM radial motion Q^(S) is proportional to Q⁽¹⁾ in the model); F⃗_f(Z, t) = W(Z)P⃗(Z, t) is a fluid forcing vector having components W(Z) (−P⁽¹⁾, P⁽²⁾), where W(Z) is the local width of the partition, and P⁽¹⁾ and P⁽²⁾ are, respectively, the pressures, averaged over the transverse coordinate X and evaluated at the upper surface of the TM and lower surface of the BM. F⃗_c(Z, t) is the active control vector having the components (ψ(Q⁽¹⁾), −ψ(Q⁽¹⁾)), where ψ(Q⁽¹⁾) is a saturating function of the TM transverse displacement (Fig. 2), and the signs of the components reflect that an equal and opposite effect acts on the TM and BM.

Figure 2.

Saturation of OHC active force production. The curve is drawn with the hypebolic tangent functions: tanh(x) for x > 0; 1/4 tanh(4x) for x < 0 to represent data obtained for OHC receptor potential vs. stereocilia bending (16).

Multiple Scale Expansion.

To exploit the slenderness of the uncoiled cochlear geometry, the following scaled coordinates are introduced: z = Z/L; y = Y/W₀, where L is the length of the cochlea and W₀ is the width of the cochlear partition at the stapes end. The ratio ε = W₀/L ≪ 1 is the fundamental small parameter that forms the basis of the multiple scale expansions

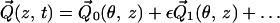2a

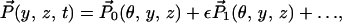2b

where θ = ωt − ε⁻¹ ∫₀^z k(ζ)dζ is the wave phase variable, with k(z) a dimensionless nonuniform wavenumber scaled by the characteristic width W₀. Substituting Eq. 2 into Eq. 1, and grouping terms together of O(ε⁰) yields, to the zeroth order, the coupled nonlinear homogeneous integro-differential equation system.

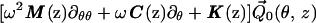3

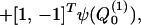where the Green’s function G(z, θ; ϕ) is derived in the Appendix,

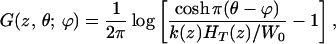4

where θ is the observation point, ϕ is the source point, and H_T is the scala height.

Subsidiary Small Distortion Expansion.

Rescale Eq. 3 by introducing the normalized displacement vector q⃗₀ = Q₀/Q*, where Q* is a characteristic value of the TM displacement at which the active force function ψ(Q⁽¹⁾) saturates. Also, rewrite ψ(Q⁽¹⁾) in the form ik⁻¹(z)F_aΨ(Q⁽¹⁾), where F_a is a the maximal active force per unit length of CP and Ψ is the normalized active force function shown in Fig. 2. The ik⁻¹(z) factor is introduced to show the dependence of the active force on the local wavenumber.‡ Also, divide each term of Eq. 3 by the inertia of the BM per unit length ω²M₂ = ρω²H_B(z)W(z) to obtain

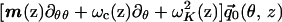5

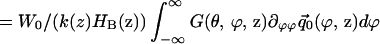The ratio δ = F_a/(ω²M₂) of maximal active control force to BM inertia is evidently small (see Discussion for estimates) and can serve as an auxiliary expansion parameter for the following small distortion expansions§:

6a

6b

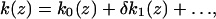6c

where (u₁, u₂) are the components of q⃗₀. Substitution of Eq. 6 into Eq. 5 and letting δ → 0 (no active force) yields, to zeroth order O(δ⁰), a coupled linear homogenous system for the passive amplitude vector A⃗ with components (A₁, A₂):

7

where [Z(z, ω)] is given by

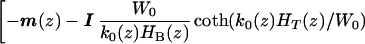8

A nontivial solution of Eq. 7 can exist only if the determinant of Z vanishes. We thus look for solutions k₀(z) of Det[Z(z, ω)] = 0. Notice that if k₀ is a solution of Det[Z(z, ω)] = 0, then so is −k₀, because [Z(z, ω)] is an even function of k₀. So for every forward wave there exists the possibility of a retrograde wave having the same wavenumber. This retrograde wave is not needed in the present study because the forward wave becomes sufficiently small at the helicotrema (z = 1) to satisfy the boundary condition of zero pressure difference across the CP. There is an infinite set of roots for the wavenumber. However, computations show only one root with a positive real part has a small negative imaginary part. This root determines the dominant forward propagating wave. All other roots represent evanescent waves that rapidly decay from the stapes (z = 0), and these roots are not used in the present study. Corresponding to each k₀, an amplitude ratio r = A₁/A₂ can be calculated. Calculation of the individual amplitudes is discussed in the section Determination of Partition Amplitudes.

Harmonic distortion of the partition and the correction of the wavenumber due to the active OHC force are determined from the O(δ) terms of Eq. 5. To this end introduce the Fourier series expansions:

9a,b

where the a_n and b_n are to be found. Also consider the Fourier series representation of the normalized nonlinear active force function Ψ:

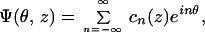10

where the coefficients are calculated from

11

Note that it is mathematically consistent to neglect the O(δ) correction term of Eq. 6a in the argument of the integrand of Eq. 11 because it would generate a higher order term of O(δ²) into the O(δ) partition equation. The O(δ) partition equation for the nth harmonic can be written as a forced linear system

12

where [Z_n(z, ω)] is given by

13

and f⃗_n is given by

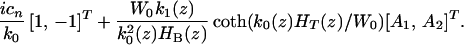14

The linear system defined by Eqs. 12–14 is straightforward to solve, except the case n = 1 which needs special attention. When n = 1, Z₁ = Z (compare Eqs. 8 and 13). Because Det[Z] = 0, Eq. 12 cannot be solved unless its right-hand side is orthogonal to the eigenvector of the adjoint of Z (14). Therefore f⃗_n must satisfy f_1,1Z₁₂ = f_1,2Z₁₁. This condition leads to the amplitude-dependent wavenumber correction

15

When n = 1, Eq. 12 has a particular solution and a homogeneous solution with an arbitrary multiplicative factor that we are free to specify. Choose the homogeneous solution such that a₁ = 0, then

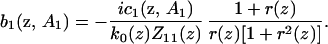16

The theory thus far indicates that the nonlinear characteristic shown in Fig. 2 produces a full set of harmonics that propagate apically (n = 1, 2, 3, …) and basally (n = −1, −2, −3, …), as well as producing a dc-shift (n = 0). The same can be said even for a purely antisymmetric characteristic with Ψ(A₁) = −Ψ(−A₁), except that a dc-shift is not produced. The n = 1 harmonic produced by the nonlinearity has a special importance in that it determines both the gain and compressive characteristics of the CA (see Discussion).

Determination of Partition Amplitudes.

Consideration of the O(ε) equations of the multiple scale expansion leads to an energy integral that determines the partition amplitudes (8). When the structural matrices are symmetric, as they are here, the energy integral states that the integral of the product of axial velocity and pressure over a cochlear cross section is an axial invariant. Hence

17

where

18

and a similar expression exists for P₂. Integration over the cross section yields

19

The integration constant can be evaluated at z = 0 in terms of the averaged stapes pressure P_S = 〈P₁(η, 0)〉.

Computational Results

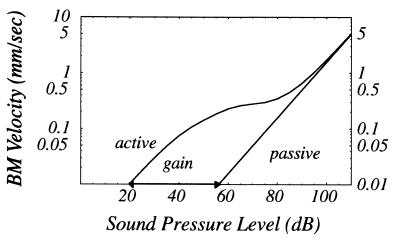
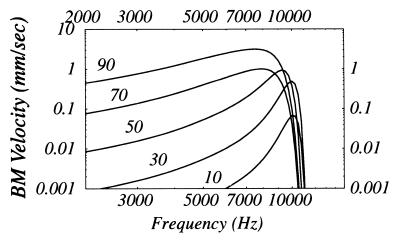
All computations are carried with parameter values given in the Appendix, which were selected with the chinchilla cochlea in mind. The input/output relation shown in Fig. 3 clearly shows the compression and gain effects recently measured in the chinchilla using laser velocimetry (ref. 5, cf. their figure 6). Linearity of the response at low SPL and its reemergence at high SPL as seen in our computation as well as others’ (10, 11), has been recently observed (5). Fig. 4 (Left) demonstrates negligible distortion in computed displacement waveforms of both the TM and BM at the base for a 10 kHz sinusoidal input signal in agreement with observations in ref. 5. Fig. 4 (Right) indicates observable distortion of a 1 kHz sinusoid at an apical location. Fig. 4 (Middle and Bottom) show the amplitudes of the harmonics relative to the fundamental. Tuning curves are computed at a basal location for various input sound pressure levels in Fig. 5. The phenomena of broadening and leftward-shifting of the peak with increasing SPL have been reported in the chinchilla (ref. 5, cf. their figure 8).

Figure 3.

Computed BM input/output function. Frequency: 10 kHz; normalized axial location: z = 0.18.

Figure 4.

Computed waveform distortions. (Left) Basal location, z = 0.18. (Right) Apical location, z = 0.9. (Top) Waveforms: solid lines, BM response; dashed lines, TM response. (Middle and Bottom) The amplitudes of harmonics n = 2, 3, … , 10 relative to the fundamental and expressed in dB. The dc offset from asymmetric saturation of OHC active force has been omitted.

Figure 5.

Computed BM tuning curves for various SPLs (dB). Normalized axial location: z = 0.18. Note at high SPL the system appears to respond linearly as in Fig. 3.

Discussion

Why Is Harmonic Distortion Observable at the Apex but Not at the Base of the Cochlea (cf. Fig.

4)? The relative magnitude of distortion is controlled by the parameter δ introduced in Eq. 5. This parameter is the ratio of the local OHC active control force to the inertial force of the BM at a saturating amplitude. Estimates of these forces per unit length of partition are: for the control force, (0.1 nN)/(mV-cell) (0.25 mV) (3 cells/row)/(15 μm/row), and for the inertial force, ρω²HWQ*, where ρ is the density of the BM (∼1 g/cm³), H is the effective BM thickness (∼50 μm), ω is the best frequency (rad/sec) at the observation location, W is the local partition width (∼0.15 mm at a basal location and ∼0.5 mm at an apical location), and Q* is the saturation amplitude (∼1 nm). The 0.1 nN/mV sensitivity was determined in isolated guinea-pig OHCs (15); the 0.25 mV receptor potential is estimated from data obtained from mouse organotypic cochlear culture (16). Thus, at a basal location at 10 kHz, δ ∼ 1/80 or −38 dB, which would be difficult to observe, while δ ∼ 1/4 or −12 dB at an apical location at 1 kHz, which would be observable. Note that the scaling method to obtain δ is not unique; it can also be interpreted as the ratio of the active force to the BM elastic restoring force at the local characteristic place, δ = F_a/(ω²M₂) = F_aK₂/(ω²M₂K₂) = F_aω₂²/(ω²K₂) ∼ F_a/K₂, because ω₂/ω = O(1). Because the stiffness is higher at the base than at the apex, the same arguments follow.

What Determines the Relative Phase Between the TM and BM in the Model (cf. Fig.

4)? The in-phase and anti-phase behavior at the apex and base, respectively, is determined by passive dynamics of the model. Active properties of the model affect only the higher harmonics. This seems to be consistent with experimental observations that phase is relatively unaffected by SPL (5) or efferent stimulation (17).

Why Is 6ω the Dominant Distortion Harmonic at the Apex (cf. Fig.

4)? The amplitude and harmonic number of the dominant distortion harmonic (n = 6) is in qualitative agreement with recent observations at the apex of the guinea-pig cochlea using laser heterodyne interferometry (S. M. Khanna, personal communication). Irrespective of the symmetry of the active force nonlinearity, a resonance effect in the model predicts that ±2ω, ±3ω, ±4ω, ±5ω, and ±6ω are the respective dominant distortion harmonics going from the base to the apex at the characteristic frequency of each location, with corresponding increases in magnitude. This effect should not be confused with the dominance of cubic distortion products when two tones are input.

How Can a Nonlinear Active Force Mechanism That Produces a Small Distortion at a Basal Location Produce a Large Gain at the Same Location (cf. Fig.

3)? The origin of the gain can be interpreted as a large “distortion” of the fundamental (n = 1) harmonic. In fact, for this case, the BM amplitude is augmented by the multiplicative factor exp[δ/ε ∫₀^z Im(k₁)dz], where k₁ is the correction term for the wavenumber given by Eq. 15. The analysis requires that the phase of the active force leads that of the TM displacement by π/2. The biophysical origin of this phase lead is as yet unclear; it may reside in more intricate micromechanics than contained in the present model, and/or it may be a result of electrotonic axial coupling of OHCs. Because the Im(k₁) integral is an O(1) quantity at the base, setting it equal to one gives a simple estimate of the gain in dB: 20(δ/ε)log₁₀e ∼ 9(δ/ε). Taking δ ∼ 1/80 at the base and ε ∼ 1/360 for the chinchilla cochlea, the basal gain is estimated to be ∼40 dB. The presence of the slenderness ratio ε in the gain estimate is interesting because it implies that the CA would depend on cochlear geometry and not just the local behavior of OHCs near the peak of the response. The model predicts there would a cumulative effect of active force generation, suppressing the response basal to the peak, while amplifying the response closer to the peak. The in-phase behavior of the TM and BM at the apex, and their amplitude ratio near unity contribute to distortion but not to the gain. At the apex, geometrical factors (e.g., the decreasing scala height and increasing tilt of the OHCs) conspire to reduce the magnitude of the Im(k₁) integral, and thereby prevent the gain from increasing in proportion to δ.

What Is the Mechanism for the Leftward Shift of the Tuning Curve Peak with Increasing SPL (cf. Fig.

5)? It has been suggested that this phenomena is evidence for softening of the BM by lengthening of OHCs (18). Here, it is demonstrated that the same effect can be produced without this softening mechanism. In the present model, the leftward shift is related to the compression shown in Fig. 3. Because compression cannot reduce the response at a given axial location with increasing SPL, but merely results in a less than linear increase, it is clear the peak of the spatial waveform at a given frequency must more toward the apex, which is equivalent to a shift towards lower frequencies in the tuning curve.

What Happens to the Gain Mechanism in the Present Model If It Is Constrained to Have One Transverse Degree of Freedom?

The gain is proportional to the k₁ integral as previously discussed, and because k₁ is proportional to the factor r(1 − r), where r is the TM/BM amplitude ratio (cf. Eq. 15), the gain will diminish as either r → 1 or r → 0. The former would occur if parallel supporting cells were made very stiff, while the latter would occur if the TM were made very stiff. This is not to say that an active model with one degree of freedom cannot produce a large enough gain. In fact a large gain has been demonstrated in such models (10, 11), but apparently at the expense of requiring a very large active force to be generated by OHCs.

Does a Nonlinear Active Force Mechanism Contribute to the Generation of Otoacoustic Emissions?

According to the present theory, the nonlinear active feedback force produces distortions to the dominant wave propagating from base to apex that have a negative harmonic index n. These harmonics correspond to retrograde waves, traveling backward toward the base. Whether or not these waves retain sufficient amplitude at the oval window to contribute to otoacoustic emissions still needs to be investigated. Another proposed mechanism for emissions is scattering from random inhomogeneities, which is thought to be the dominant mechanism at low SPL (19, 20).

ABBREVIATIONS

CP

cochlear partition

SPL

sound pressure level

OHC

outer hair cell

OC

organ of Corti

RL

reticular lamina

TM

tectorial membrane

BM

basilar membrane

Appendix

Structural Matrices.

The mass, damping, and stiffness matrices corresponding to the two degree of freedom system shown in Fig. 1 are

where the elements are slowly varying functions defined per unit length of the cochlear partition.

Parameter Values.

Computation were carried out with the following parameters, many of which have yet to be measured in the chinchilla but seem reasonable to the author. Geometrical quantities: uncoiled length L = 20 mm; scala height H_T = 0.44 mm; BM effective thickness H = 55 μm; TM effective thickness H = 40 μm; BM width function W(z) = 0.055(1 + 5z) mm. Elements of structural matrices are normalized by the BM mass/length and are expressed in terms of frequency (Hz): K₁ = 4,000; K₂(z) = 30,000 exp[−4z]; K₁₂ = 10,500; K_c = 3,000 exp[−0.25z]; C₁ = C₂ = C₁₂ = 200/(1 + 5z). Viscous damping has been neglected because this value of partition damping substantially exceeds viscous damping by three orders of magnitude even at 1 kHz. The maximal active force of an OHC is taken as 25 pN at a saturation value of TM displacement of 1 nm.

Green’s Function for Surface Pressure.

The fluid flow in the fluid-filled spaces above the TM and below the BM is assumed to be described by solution of the linearized Navier Stokes equations for an incompressible fluid having density ρ. The pressure fields then satisfy Laplace’s equation. Consider the space above the TM, and introduce the stretched vertical coordinate η = ky. The leading pressure term of the expansion Eq. 2b, P₀⁽¹⁾(θ, η, z) then satisfies Laplace’s equation (∂_ηη + ∂_θθ)P₀⁽¹⁾(θ, η, z) = 0 in an infinite strip with the boundary conditions: ∂_ηP₀⁽¹⁾ = −ρω² W₀k⁻¹(z)∂_θθQ₀⁽¹⁾ on the TM η = 0, and ∂_ηP₀⁽¹⁾ = 0 on the top η = k(z)H_T(z)/W₀ = α. To solve this boundary value problem introduce the Fourier transform pairs

The normal derivative of the transformed problem has the form

By the convolution theorem, the normal derivative can be written

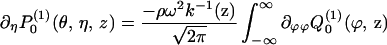where

Integration with respect to η gives the pressure field

Evaluating this expression on the surface η = 0 gives the Green’s function Eq. 4 in the text.

Note Added in Proof

The predicted dominance of the 2nd harmonic and its relative magnitude at the base (Fig. 4) has recently been experimentally confirmed (21).