The role of nanostructure in the wetting behavior of mixed-monolayer-protected metal nanoparticles

Abstract

Self-assembled monolayer-protected nanoparticles are promising candidates for applications, such as sensing and drug delivery, in which the molecular ligands' interactions with the surrounding environment play a crucial role. We recently showed that, when gold nanoparticles are coated with a binary mixture of immiscible ligands, ordered ribbon-like domains of alternating composition spontaneously form and that their width is comparable with the size of a single solvent molecule. It is usually assumed that nanoparticles' solubility depends solely on the core size and on the molecular composition of the ligand shell. Here, we show that this is not always the case. We find that the ligand shell morphology affects the solubility of these nanoparticles almost as much as the molecular composition. A possible explanation is offered through a molecular dynamics analysis of the surface energy of monolayers differing only in their domain structure. We find that the surface free energy of such model systems can vary significantly as a function of ordering, even at fixed composition. This combined experimental and theoretical study provides a unique insight into wetting phenomena at the nano- and subnanometer scale.

Self-assembled monolayer (SAM)-protected metal nanoparticles (NPs) are materials composed of a metallic core coated with a SAM of ligand molecules (1). The ligand shell serves as the link between the nanoparticle and its environment, providing these materials with important properties such as stability and solubility (2–4). The ligand shell also allows for NPs to behave and to be manipulated, to a first approximation, as organic molecules; for example, purification methods based on chromatography (5, 6), dialysis (7), or filtration (8) have recently been reported. One of the most attractive properties of these materials is the ease in which ligand shells composed of different molecules can be achieved. This allows each of the ligand shell molecule to provide a different property, thus enabling nanoparticles' use in fields as disparate as electronics (9) and biomedicine (10). It is known that most mixtures of thiolated molecules when coassembled on flat gold surfaces phase-separate into randomly sized and arranged domains (11, 12). Recently (13–19), using scanning tunneling microscopy (STM) and infrared spectroscopy, we found that when gold nanoparticles are coated with these same types of binary mixtures of molecules, phase separation occurs in a more ordered fashion, leading to the formation of ribbon-like domains of alternating composition with an unprecedented small average domain width of ∼5 Å (see cartoon in Fig. 1). In some cases, the nanoparticles' ligand shell is structured with an alternation of hydrophobic and hydrophilic regions so fine that it can be compared with the one present in the capsid of virus particles or to folded proteins. It is reasonable to expect that such a complex surface would interact in a peculiar way with macromolecules [we showed that it prevents efficiently protein nonspecific adsorption (13) and that it enables cell membrane penetration (20)] as well with small molecules, such as solvent molecules.

Fig. 1.

STM image of gold nanoparticles coated with a 2:1 ratio of OT/MPA showing ordered phase separation in their ligand shell. (Scale bar, 25 nm.) (Insets) Close up of nanoparticles showing the encircling, ribbon-like domains (Left) and a corresponding simplified schematic diagram in which the red pillars represent MPA, and the yellow represent OT (Right). (Scale bar, 5 nm.)

Although nanoparticles solubility has been thoroughly studied in polar solvents (19, 21–23) (typically water), where the main stabilization mechanism is the formation of an electrical double layer, less is known on the thermodynamic reasons that lead to the solubility of nanoparticles in organic solvents. It is commonly believed that the solvent is responsible for the entropy of mixing (24), whereas the ligand shell molecules play the key role in determining the enthalpy of mixing because of the ligand–solvent and the interparticle ligand–ligand interactions. In the case of particles coated with a mixture of ligands, where each same ligand–ligand interaction is stronger that any hetero ligand–ligand interaction, one would expect the enthalpy of mixing for mixed ligand nanoparticles to be an average of the enthalpy of mixing of the component homoligand nanoparticles weighted over the composition of the ligand shell. Here, we show that this is not the case when ribbon-like domains (referred to hereafter as ripples) arise in the ligand shell and that the enthalpy further depends on the domain spacing (which can be varied through the stoichiometric ratio of the ligands used in the synthesis) (13). Indeed, systematic studies on the solubility of nanoparticles as a function of composition show nonmonotonic behaviors indicative of physicochemical effects that go beyond those expected by a simple thermodynamic treatment (13).

Results

Mixed-ligand gold nanoparticles were synthesized by using a previously reported one-phase method (25). In the specific case of this study, this method has multiple advantages; first, it produces mixed-ligand nanoparticles with a ligand shell whose composition tends, on average, to be the same of the stoichiometric ratio used in the reaction. We recently proved this to be the case for the ligand mixtures used in this article by using IR spectroscopy (15). Second, the absence of a phase-transfer agent allows for easier purification approaches to achieve nanoparticles free of unbound molecules (2). Third, the presence of a reducing agent (sodium borohydrate) in the same phase of carboxylic acid-terminated ligands produces nanoparticles completely coated with the sodium carboxylate form of the molecule (15). Finally, although nanoparticles size distributions achieved with this approach are not ideal for many applications, we found that they are relatively insensitive to ligand shell composition and to day-to-day variations in synthetic procedures; hence, it is relatively simple to achieve multiple nanoparticles with approximately the same size distribution. Briefly, to an ethanol solution containing a gold salt and a mixture of thiolated ligand molecules of the desired ratio, an ethanol solution of sodium borohydride (10 mM) was added dropwise. The nanoparticles where then allowed to precipitate overnight in a refrigerator and were collected by filtration. After extensive purification, they were dried completely to avoid eventual solvent traces that might affect their solubility. All of the nanoparticles were characterized with IR spectroscopy to ensure uniformity of their ligand shell. All MPA molecules in the ligand shell were found to be carboxylates—probably complexed by sodium ions—(CO stretching ≈1,570 cm⁻¹) with no detectable presence of carboxylic groups (≈1,710 cm⁻¹) (26). Also, no unreacted thiol was found, given the absence of sulfer-hydrogen (S-H) characteristic vibrational modes (≈2,560 cm⁻¹ ≈800 cm⁻¹) (27). Transmission electron microscopy (TEM) was used to determine the nanoparticle size distribution. Supporting information (SI) Table S1 shows a list of all of the nanoparticles studied here together with their average diameter and polydispersity index. Care was taken to ensure that the NPs average sizes and distributions were approximately the same across NPs compositions to eliminate possible size effects on their solubility.

To study the solubility properties of these nanoparticles, we quantified the concentration of nanoparticles at saturation, i.e., the concentration in which nanoparticles in solution are in equilibrium with nanoparticles in the solid state. Our procedure consisted in dissolving 5 mg of NPs in 20 ml of the target solvent. The solutions were sonicated for 20 min, stirred for 3 h, and left for 1 week to decant. This allowed for the slow precipitation of most of the suspended nanoparticles, leaving only the dissolved nanoparticles in solution. The final nanoparticle concentration in solution was derived from optical density measurements at the plasmon peak. The extinction coefficients were calculated from the average NPs diameters by using the approach reported by Liu and coworkers (28). In all cases, the final concentration was lower than the initial one, confirming that the final concentration is equivalent to the saturation concentration. We estimate that the amount of NPs used in each experiment (≈5 mg), if all in solution, would have a concentration of the order of 10⁻⁵ M × l⁻¹, whereas the largest concentration measured after decanting the samples was of ≈10⁻⁷ M × l⁻¹. The choice of 1 week to measure the saturation concentration was determined by analyzing optical spectra at various time intervals. We observed a gradual decrease in optical density that after a few days became negligible (see Fig. S1). It should be stressed that once the saturation concentration is reached, the solutions are stable for months. To make sure that changes occurring in the first week were solely because of nanoparticles' decanting, we compared the nanoparticles' IR spectra taken before and after the experiments, and no noticeable change was observed (see Fig. S2). The only meaningful difference that we noticed is that in protic solvents, a fraction of the carboxylate was protonated (see Discussion below). We also analyzed the nanoparticles' size, extracting small amounts of solvents at various stages of the experiments (up to 1 month). No noticeable change in average diameter and size distribution was observed, ensuring that the nanoparticles are stable in solution in all of the solvents used. The invariance of the optical spectra with time indicated an absence of any form of aggregation in solution.

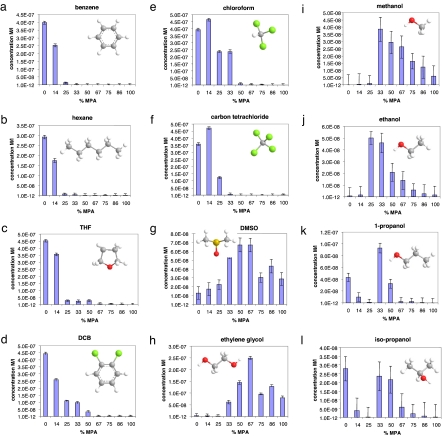
A series of nanoparticles coated with a mixture of octane-thiol (OT, CH₃-(CH₂)₇-SH) and mercaptopropionic acid (MPA, HOOC-(CH₂)₂-SH) ligands in various ratios were studied. These NPs are known for having phase-separated rippled domains in their ligand shell (Fig. 1) (13–15). Their saturation concentration was determined as a function of the percentage of MPA, or equivalently, as a function of domain presence and width in the ligand shell. One would predict that nanoparticles coated only with a hydrophobic ligand as OT would be mostly insoluble in a hydrophilic solvent (as ethanol) and would gain solubility monotonically the more hydrophilic MPA is present in the ligand shell. The inverse behavior should be observed when studying the solubility in a hydrophobic solvent such as benzene. Fig. 2 illustrates that, for many of the solvents studied, this is not the case and that often a nonmonotonic behavior is observed. Throughout the article, molar compositions are the stoichiometric ratios used during the nanoparticle synthesis, something we proved to be the case through IR studies (15).

Fig. 2.

Plot of the saturation concentrations (expressed in M × l⁻¹) for OT/MPA NPs as a function of the ligand shell composition, for NPs dissolved in various solvents: benzene (a), hexane (b), THF (c), DCB (d), chloroform (e), carbon tetrachloride (f), DMSO (g), ethylene glycol (h), methanol (i), ethanol (j), 1-propanol (k), and isopropanol (l). Error bars are the largest variation in concentration observed for different spectra on the same sample and/or on samples with the same composition prepared on different occasions (they account for instrumental, dilution, and sample-preparation uncertainties). The molecular structures of the solvents used have the following color code: carbon (gray), hydrogen (white), oxygen (red), sulfur (yellow), and chlorine (green).

To ensure that the data acquired were reflective of true thermodynamic interactions between the solvent molecules and the surface of the nanoparticles, we (i) proved that the concentrations measured where stable with time and (ii) repeated the measurements on the same sample or on different samples. We then (iii) picked a couple of immiscible solvents from the ones shown in Fig. 2 (specifically DMSO and hexane) and generated a partition function (shown in Fig. S3). The shape of this function also presents a clear nonmonotonic behavior. More importantly, we (iv) varied the nanoparticles in such a way that their surface hydrophobic-to-hydrophilic content and structure would not change relative to the OT/MPA nanoparticles: i.e., we synthesized a series of nanoparticles coated with various ratios of hexane thiol (HT, CH₃-(CH₂)₅-SH) and MPA.

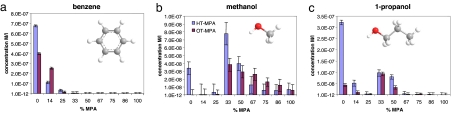
These latter nanoparticles have the same striated structure and spacing than the OT/MPA one but obviously have a different depth in the structure (being HT shorter than OT) (14). We verified that the composition of these NPs is very close to the ligand ratio used in the synthesis by means of FTIR (Fig. S4). As shown in Fig. 3, the trends shown in Fig. 2 stay unaltered; the only variation is in intensity (see also Fig. S5 for a more complete study). This experiment is a strong indication of the nature of the phenomenon under observation. To further strengthen this conclusion, we have performed this comparison also between nanoparticles coated with OT and mercaptoundecanoic acid (MUA) and HT and MUA, obtaining similar results, as shown in Fig. S6.

Fig. 3.

Plots of the saturation concentrations for HT/MPA NPs (blue bars) and OT-MPA NPs (purple bars) dissolved in various solvents: benzene (a), methanol (b), and 1-propanol (c). Error bars are the largest variation in concentration observed for different spectra on the same sample and/or on samples with the same composition prepared on different occasions (they account for instrumental, dilution, and sample-preparation uncertainties). The molecular structures of the solvents used have the following color code: carbon (gray), hydrogen (white), and oxygen (red).

Discussion

Fig. 2 shows clearly that the saturation concentration of nanoparticles with structured ligand shells does not follow a clear monotonic trend, as would be expected from a simple thermodynamic treatment. A strong nonmonotonic behavior is evident (Fig. 2 g–l) with results that would be, to an extent, counterintuitive, such as the nanoparticles containing only 33% of the hydrophilic MPA, and 67% of the hydrophobic OT being the most soluble in polar alcohols (e.g., methanol and isopropanol). We notice that these nanoparticles are the ones that we found to have the largest spacing^† in their ligand shell. At the same composition (and same phase spacing), the nanoparticles containing 33% of MPA and 67% of HT are the most soluble in methanol and isopropanol (Fig. 3). We believe that to rationalize this result, one has to invoke the appearance of an ordered phase separation at composition that ranges from ≈20% to ≈80% of MPA (13, 14). When this structuring happens, solvent molecules are forced to interact in a unique way with the nanoparticles surface; in a sense, the solvent wetting of the nanoparticles' ligand shell is constrained. Solubility (in the sense of saturation concentration) is an equilibrium between two states, a solvated state and a solid state in which nanoparticles are packed in a specific way. One might argue that the presence of striated domains affects both states, and hence, the results shown here are difficult to interpret. We do not believe this argument for two reasons. First, most of the solid-state free energy is due to the enthalpic gain in the interdigitation of the ligand molecules, but in the nanoparticles chosen, because of the charges present in the NPs ligand shell, we can assume that the amount of interdigitation is negligible. We confirmed this using differential scanning calorimetry according to methods in the literature (23, 29, 30). More importantly, the same nanoparticles (powders from the same batch) were used to perform the solvation studies in all of the solvents presented in Fig. 2. For all of these studies, the solid state is the same (at a given composition), and hence, the fact that one nanoparticle is the most soluble in a specific solvent indicates that, at that composition (and with that structure), the solvated state has a lower free energy. This reasoning can also be used to conclude that, in our systems, the effects of structure on interdigitation (18) are small when compared with the overall solvation energy. For example, the nanoparticles with 25% MPA and 75% OT are not very soluble in methanol and 1-propanol but are the most soluble in ethanol; the free energy of the solid state is identical in all cases, the only change being in the wetting free energy. The fact that these nanoparticles are more soluble than their “neighbors” with slightly less and slightly more MPA in the ligand shell in ethanol, whereas the phenomenon is reversed in methanol and 1-propanol, is hard to explain without invoking a certain role of the structure in the ligand shell.

We notice (see Fig. 2) that in most of the solvents where one of the two homoligand NPs (100% OT and 100% MPA) is strongly soluble in one solvent, and the other is insoluble, the solubility trend with composition is monotonic with one of the ligands, and the solubility properties depend mainly on the composition rather than their nanostructured phase separation. The solubility of OT/MPA NPs in chloroform and carbon tetrachloride show a similar trend with little deviations, probably because a small amount of MPA in the ligand shell spaces the OT molecules and renders them more available to positive solvation interactions. Strong nonmonotonic behavior is observed when the homoligand NPs have either little or no solubility in a given solvent. This is the case of methanol, ethanol, 1-propanol, isopropanol, ethylene glycol, and dimethyl-sulfoxide (DMSO). This behavior does not appear to be correlated with the solvents' dipole moment or polarity index (see Table S2). For instance, methanol, ethanol, 1-propanol, isopropanol, and THF have very similar values for the dipole moment, but the solubility trends for OT/MPA NPs in these solvents are quite different. The behaviors in nonpolar solvents such as benzene, carbon tetrachloride, hexane, and (in first approximation) ethylene glycol are also quite different. A larger dielectric constant helps the dissolution of MPA-rich NPs, but larger saturation concentrations occur for intermediate compositions. We noticed that the nonmonotonic behavior is observed for solvents that have the largest values of the Hildebrand parameter (31) between the ones studied. This suggests that what governs the solubility of this NPs are the amount of the overall interaction with the solvent and that these interactions are maximized in many solvents when the ripples are formed. We propose that it is likely that the ligand shell domains—whose spacing changes with composition (13)—favor the wetting of the different solvents when their sizes and chemical groups match the solvent molecules' size and chemical functionality thus contributing to the total NPs' solubility. For example, it is highly probable that the 25% MPA content nanoparticles have a ripple spacing that strongly favors wetting from ethanol, creating an interaction that provides the enthalpic contribution needed to efficiently dissolve the nanoparticles. Note that for the alcohols studied and for DMSO, the solubility reaches a maximum for the central compositions, where ripples are known to be present.

The presence of carboxylate groups on the NPs affects significantly the solubility properties of the NPs avoiding, for instance, the possibility of hydrogen bonding between different NPs or with the solvent molecules. It should be noted that the IR spectra of OT/MPA NPs that were in methanol solutions for 14 days, obtained after evaporating the solvent, show a meaningful difference with respect to the spectra obtained just after the synthesis. The peak of the C–O stretching characteristic of the carboxylic group is found in the spectra, whereas the corresponding peaks of the carboxylate group loose intensity if we compare them to the spectra obtained just after synthesis. Although this effect could affect the solubility of the nanoparticles, we note that the fraction of protonated carboxylic acids is not correlated to the saturation concentration (Fig. S7). To further test this, we dissolved the nanoparticles in a basic methanol solution (to prevent protonation) and found the same solubility trend.

To elucidate the role that a nanostructured surface has in solubility, we have explored a model system with extensive classical molecular dynamics simulations. The calculation of interfacial free energies usually requires advanced techniques, such as thermodynamics integration (32). However, in this case, we are specifically interested in exploring solubility as a function of ordering of mixed monolayers at a given composition. In a standard picture in which interfacial free energy is purely a function of composition, solubility would not change upon ordering. Although this is an appropriate assumption at the mesoscale, it remains to be seen what the ranges of its applicability are as the length scales characteristic of a given topography approach the dimension of the molecular solvent.

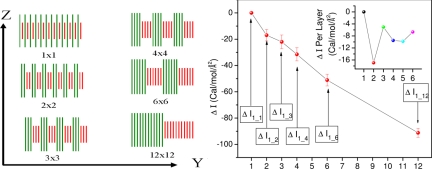
Our simulations are designed to compare the interfacial free energies between a solvent (ethanol, in this case) and a mixed-monolayer surface of fixed composition but with different ordering patterns. In particular, we studied surfaces composed of alternating rows of alkane and dicarboxylic acid chains, of varying periodicity, as illustrated in Fig. 4(we label the different structures with superlattice indices, so that a nxm structure is composed of n parallel rows of the alkane, followed by m rows of the acid, all periodically repeated in two dimensions. For example, a 1 × 1 system has 12 repeating units of one alkane and one acid chain, a 2 × 2 system has 6 repeating units of two alkane and two acid chains, a 3 × 3 system has 4 repeating units of three alkane and three acid chains, and so on (Fig. 4 Left). The model system does not include the nanoparticle itself (whose role is to induce different monolayer patterns on its surface) (13–15), and we clamp the central atom of each chain to avoid chain diffusion with solvent molecules present both above and below the surface.

Fig. 4.

Plot of the surface energy dependence on structure at the nanoscale. (Left) Surface morphologies studied in the present work; a superlattice convention is adopted, where a n × m surface has n rows of alkane intercalated by m rows of acid—a 1 × 1 system has 12 repeating units of one alkane and one acid chain, a 2 × 2 system has 6 repeating units of two alkane and two acid chains, a 3 × 3 system has 4 repeating units of three alkane and three acid chains, and so on. (Right) Change in interfacial free energy as a function of surface morphology. (Inset) Change in interfacial free energy per layer added to the alkane and acid part of the surface (point 2 corresponds to the change in interfacial free energy going from 1 × 1 to 2 × 2, point 3 corresponds to the change in interfacial free energy going from 2 × 2 to 3 × 3, point 4 corresponds to the change in interfacial free energy going from 3 × 3 to 4 × 4, point 5 corresponds to the change in interfacial free energy going from 4 × 4 to 6 × 6 divided by 2 (because 2 layers are added going from 4 × 4 to 6 × 6), and point 6 corresponds to the change in interfacial free energy going from 6 × 6 to 12 × 12 divided by 6 (see Table S3).

Now, a key assumption is that we estimate the relative changes in interfacial free energies as a function of the superlattice order parameter by measuring changes in the excluded volume for the solvent; i.e., by performing constant volume simulations in periodic boundary conditions and in a unit cell filled by a solvent, by the changes in pressure. So, we attribute a change in the interfacial free energy I to the creation of an additional hydrostatic pressure (positive or negative, depending on the sign of the free-energy change). We suggest that the energetic stability can be estimated from:

Here, ΔP is the change in equilibrium pressure, V_solv is the volume occupied by the solvent, ΔI is the change in the interfacial free energy, and A is the area of the surface. From this, we can obtain:

where we have defined as Z_eff the effective thickness that our equilibrated solvent would have in the bulk, if its transverse section were chosen to be A. Z_eff is obtained by adjusting the thickness (z dimension) of the 1 × 1 system (keeping the transverse section fixed) until the system achieves zero average pressure. This value of Z_eff is then used in all other simulations. Because Z_eff is the effective thickness that the solvent would have in the bulk, if its transverse section were chosen to be A, V_solv is easily calculated by performing a bulk simulation—from which we can calculate the bulk number density and hence the volume occupied by n solvent molecules in our simulations. We use in Eq. 1 the volume of the solvent instead of the total system volume so that the calculated interfacial free energies are independent of the size of the alkane and acid components that make up the surface.

We performed extensive molecular dynamics simulations using the DL_POLY code (33) in conjunction with the OPLS (34–36), United Atom (UA) force field with periodic boundary conditions. Our system was constructed by placing C₁₅H₃₂ and HOOC-CH₂-CH₂-CH₂-COOH on a hexagonal lattice with an interchain spacing of 4.5 Å. The central carbon of each chain was fixed, giving rise to a symmetric geometry exposing two identical surfaces on either side of the middle plane (see Fig. 4). The different morphologies studied are such that the overall composition is constant, the only difference being the superlattice ordering. Fig. 4 shows a schematic side view of different surface morphologies along with their nomenclature. The cell size used for all simulations had a cross-section of 58.6 Å × 98.6 Å, representing 12 chains in the x direction and 24 chains in the y direction.

All simulations were run in the canonical ensemble at a temperature of 295 K. Each system was equilibrated for 200 ps (300 ps for the 12 × 12) and averages were then taken over an additional 300 ps—these parameters provide well converged total average pressure and internal energy. The unit cell was filled with solvent (668 ethanol molecules), and the height of the cell (along z) was allowed to vary until an equilibrated average pressure of 0 kbar was found for the 1 × 1 ordering. We obtained a Z_eff of 11.24 Å, and all molecular dynamics (MD) simulations were then performed by using this cell size. The average pressure and the computed changes in the interfacial free energies going from 1 × 1 ordering up to 12 × 12 are shown in Fig. 4 and Table S3.

Several conclusions become apparent from the above data. First and foremost, there is a systematic and well defined change in the interfacial free energy that depends exclusively on the superlattice order parameter and not on composition. Second, these changes are of the same order of magnitude as the absolute interfacial free energies. Although computing accurate interfacial free energies is a challenging task (32), we can estimate them as a total energy difference between the equilibrated average for the bulk solvent, chains in vacuum, and chains plus solvent. For the 1 × 1 ordering, we obtain −163 cal/mol/Ų; this is to be compared with the −17 cal/mol/Ų change upon ordering into the 2 × 2 phase. These total energy estimates for the interfacial free energy are also comparable with those accurately calculated for a simpler solid–liquid interface using thermodynamic integration (32).

Conclusions

In conclusion, we have shown that the solubility of gold nanoparticles coated with phase-separated mixtures of ligands depends critically on the ligand shell morphology. The results presented show that wetting behaviors on surfaces with nanostructuring on a molecular-length scale are dominated by steric constraints and cannot be explained with mesoscopic theories. We believe that the data presented will stimulate research on wetting at the molecular scale.

Experimental Procedures

Materials.

The 1-octanethiol, 3-mercaptopropionic acid, 1-hexanethiol, 3-mercaptoundecanoic acid, sodium borohydride, and hydrogen tetrachloroaurate (III) hydrate, were purchased from Aldrich. Fully deuterated hexanethiol, D 98% [HT(d13)] was purchased from CDN Isotopes. Methanol, acetone, and chloroform were purchased from Mallinckrodt, ethanol from Pharmco, isopropanol, o-dicholorobenzene, and carbon tetrachloride from Sigma—Aldrich, dimethyl sulfoxide and benzene from EMD, hexane and tetrahydrofurane from Omnisolv, ethylene glycol from BDH, and 1-propanol from Baker. All chemicals were reagent grade; all chemicals were used as received.

Nanoparticle Synthesis.

Nanoparticles were synthesized with a one-phase method following a published report (25). In a 500-ml round-bottom flask, a mixture (in the proper desired ratio) of thiol molecules was added to an ethanol solution (200 ml, kept at 0°C) of HAuCl₄ (0.9 mmol), so that the total thiol concentration was 0.9 mmol. A large excess of NaBH₄ (10 mmol in 200 ml of ethanol) was added dropwise at the rate of 4 ml/min. After the addition of NaBH₄, the solution was stirred for 4 h. The solutions containing OT/MPA NPs was kept in a refrigerator for the next 36 h to allow the NPs to precipitate. HT/MPA and HT(d13)/MPA NPs solutions were stored in the freezer for 36 h to favor precipitation. Every NPs solution was filtered on a quantitative filter paper (VWR 28297-942) under vacuum and then washed abundantly with ethanol and acetone; a black powder (≈150 mg) was recovered from the filter.

Nanoparticle Characterization.

An Agilent 8453 diode array absorption spectrometer was used for recording the UV–visible spectra of nanoparticles dissolved in different solvents; spectra with 1 nm of resolution and 5 s of integration time were acquired. Solvent (20 ml) was added in a vial containing ≈5 mg of NPs. Particular care was used to grid the NPs in powders of approximately the same mesh. The NPs were sonicated for 20 min and then stirred for 3 h and decanted for 7 days. The vials were taped to a table to avoid shaking when opening and closing. The NPs dissolved in ethylene glycol were sonicated for 40 min and stirred for 4 h. All of the optical densities recorded were between 0 and 1; in some cases a dilution of the solution was necessary for the optical density to be in that range.

Nanoparticle average core diameters were determined by using TEM images. A JEOL 200CX was used at 200 KV, and ≈200 NPs were counted for every sample.

A Nicolet Nexus FTIR spectrometer was used for the IR spectra of the nanoparticles. Spectra were taken in KBr pellets sintered at a pressure of 10 ton cm⁻²·256 spectra taken with a 1-cm⁻¹ resolution were acquired for every sample.

A Thermal Advantage DSC Q10 was used to record the DSC measures at a rate of 10°C/min.