Measuring molecular rupture forces between single actin filaments and actin-binding proteins

Abstract

Actin-binding proteins (ABPs) regulate the assembly of actin filaments (F-actin) into networks and bundles that provide the structural integrity of the cell. Two of these ABPs, filamin and α-actinin, have been extensively used to model the mechanical properties of actin networks grown in vitro; however, there is a lack in the understanding of how the molecular interactions between ABPs and F-actin regulate the dynamic properties of the cytoskeleton. Here, we present a native-like assay geometry to test the rupture force of a complex formed by an ABP linking two quasiparallel actin filaments. We readily demonstrate the adaptability of this assay by testing it with two different ABPs: filamin and α-actinin. For filamin/actin and α-actinin/actin, we measured similar rupture forces of 40–80 pN for loading rates between 4 and 50 pN/s. Both ABP unfolding and conformational transition events were observed, demonstrating that both are important and may be a significant mechanism for the temporal regulation of the mechanical properties of the actin cytoskeleton. With this modular, single-molecule assay, a wide range of ABP/actin interactions can be studied to better understand cytoskeletal and cell dynamics.

External mechanical forces and forces generated within the cell through actomyosin interactions play a critical role in various cellular processes including migration, division, growth, and apoptosis (1). These forces are largely sustained by the cytoskeleton, which consists of an organized structure of protein filaments. One of the major components of the cytoskeleton is filamentous actin (F-actin), which in eukaryotic cells represents 1–10% of all protein content by weight (1). In vivo, the organization of F-actin into higher-order structures is regulated by a wide variety of actin-binding proteins (ABPs) (2–8). Several of these ABPs, including filamin, α-actinin, fimbrin, spectrin, and dystrophin, have a conserved actin-binding domain, but their overall structure and function are quite different (7, 9–14). For instance, cross-linking proteins, such as filamin, promote the formation of a cortical load-bearing isotropic F-actin network at low concentrations near the plasma membrane (10, 15–17). Conversely, bundling proteins, including α-actinin, form thick F-actin cables that help both in maintaining the cell under a prestressed state (1, 18) and generating protrusions at the leading edge of a migrating cell (11, 19). In addition, many of these ABPs are also located at focal adhesion sites, anchoring the cytoskeleton to the extracellular matrix (11, 19, 20). Because all of these ABP/actin structures are located along force-transmission pathways, it is important to understand how forces affect the molecular interactions and the role that ABPs play in sustaining and regulating the mechanical behavior of the cell.

To understand the complex mechanical properties exhibited by the cell (21–24), the primary focus has been directed toward studies of reconstituted actin networks grown in vitro in the presence or absence of ABPs (8, 16, 17, 25–31). For example, in one study, actin networks cross-linked by filamin were shown to exhibit dramatically different mechanical properties from networks formed by α-actinin (17). Because filamin and α-actinin share a similar actin-binding domain, this result suggests that the regulation of the actin cytoskeleton by the ABPs may be governed not only by binding kinetics but also by the actual mechanical structure of the ABP. Moreover, rheological measurements have shown that above some critical load, the network displays substantial softening, suggesting a major disruption of the actin network, possibly because of filament rupture, filament buckling, unfolding of APBs, or unbinding of ABPs (16, 30). Although these in vitro network studies provide valuable information about the general behavior of the actin cytoskeleton, a more detailed description at a molecular level is required to better understand how the cell regulates the cytoskeletal machinery.

Currently, some suggest that the dynamic properties of the cytoskeleton are regulated by unfolding of ABPs bound to F-actin (20, 32, 33), whereas others argue that these properties arise from unbinding of ABPs from F-actin (29, 31). The first model implies that the forces required to unfold at least one of the folded domains of the bound ABP have to be lower than the strength of the bonds between the ABP and F-actin. Previous atomic-force microscopy (AFM) demonstrated that Ig-like subdomains of filamin unfold with forces ≈100 pN (20). The same group predicted with Monte Carlo simulations that unfolding will occur before unbinding (33). Nonetheless, to our knowledge, there are no force-induced unbinding experiments between filamin and F-actin to directly support this prediction. Therefore, a single-molecule experimental approach to study the strength of the interactions between F-actin and ABPs can prove useful in characterizing the origins of the mechanical properties of the cytoskeleton.

In vitro single-molecule studies using optical tweezers force spectroscopy (OTFS) provide the advantage of exploring a system of interest in an isolated environment to characterize the forces implicated in molecular interactions. Pioneering work at the single actin-filament level used OTFS to characterize the unbinding force between F-actin and α-actinin (34), and F-actin and myosin (35–37). For example, Miyata et al. (34), measured unbinding forces between a single actin filament and α-actinin in a range of 1.4–44 pN by immobilizing α-actinin on a nitrocellulose-coated glass. In this report, we expand on Miyata's work by probing the interaction of a single actin-binding protein, either α-actinin or filamin, linking two actin filaments.

In this report, we introduce a more native-like assay to examine the force required to break the interaction of two actin filaments linked together by either filamin or α-actinin using OTFS. We immobilized actin filaments on the surface of a flow channel, introduced either filamin or α-actinin, and formed tethers with actin filaments bound to beads. We performed force-induced unbinding experiments at different loading rates to better characterize the dynamic behavior of these interactions. We then modeled our results with theoretical descriptions (38) to obtain estimates for the parameters describing the molecular interactions including the intrinsic dissociation rate (k_off), the transition distance between the free energy minimum and the energy barrier (x^‡), and the height of this energy barrier to rupture (ΔG^‡). We present experimental evidence supporting the hypothesis that both unbinding and unfolding are significant mechanisms regulating the dynamic behavior of the cytoskeleton.

Results

Experimental Assay.

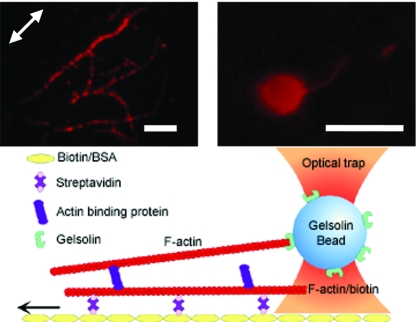
The assay developed consists of an ABP linking two actin filaments: one filament immobilized on a coverslip surface and the other one tethered to a polystyrene bead that serves as a handle to apply a load with an optical trap (Fig. 1). Biotinylated F-actin in 1% (wt/vol) dextran was immobilized on a streptavidin-coated surface of a flow channel (see Materials and Methods for details). The use of dextran greatly enhanced the binding efficiency of the filaments to the surface because of a depletion interaction that confines the F-actin into a thin layer just above the surface (39). ABP, either filamin or α-actinin, was then introduced to the flow cell, followed by the addition of preformed single F-actin bound to gelsolin-coated beads (40) (Fig. 1). The tethers formed were ≈5 μm long. Because we reduced the density of ABPs to nanomolar concentrations and verified that after each rupture event the force level dropped to zero, we are confident that one cleanly isolated single molecular interaction was probed per rupture event.

Fig. 1.

Schematic representation of the experimental assay. A tethered bead is captured with the optical trap, and the sample is moved relative to the trap until rupture occurs between the actin filaments and the ABP (filamin or α-actinin). The bottom filament is biotinylated and is immobilized on a streptavidin-coated surface, whereas the top filament is tethered on its barbed end to a gelsolin-coated bead. The arrow indicates the direction of the movement of the piezo-stage relative to the trap. The micrographs above the diagram show actin filaments on the coverglass surface generally aligned with the direction of flow (Left) and a single actin filament bound to a gelsolin-coated bead (Right). Actin was fluorescently labeled with Alexa Fluor 555 phalloidin, and the bead was labeled with BSA conjugated with Alexa Fluor 555. (Scale bars: 5 μm.)

The assay was interchangeable between filamin and α-actinin without need of adjustments. This assay consistently produced ≈30 tethers per field of view (110 μm × 110 μm), whereas control samples produced only ≈2–4 tethers per field of view. Control samples were tested by systematic removal of streptavidin, biotinylated F-actin, or ABP to ensure that we were probing the desired interaction. The few tethers found in control samples were weak (rupture forces <1 pN) and could not sustain loads because they ruptured almost instantaneously after force application. To test the strength of the filament–bead and the filament–surface interaction, we attached biotinylated F-actin to the gelsolin-coated beads and immobilized the bead-bound filaments on a surface coated with streptavidin. We found that these interactions could not be broken with the maximum force exerted by the trap (≈150 pN); thus demonstrating that during experiments, rupture most likely occurred at one of the two filament–ABP bonds.

Force-Induced Unbinding.

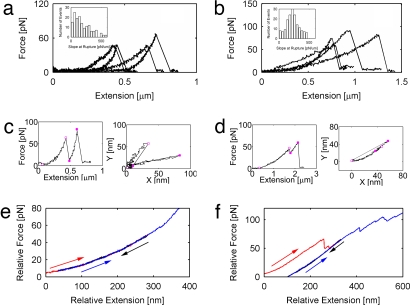
We used OTFS to probe the interaction between F-actin and filamin or α-actinin. Briefly, 1-μm beads tethered to F-actin were located to the position-detection zone by using an automated 3D centering routine, captured with a stationary optical trap (41) and then loaded by moving the sample relative to the trap at a constant velocity with a piezo-electric stage along the direction of immobilized filaments on the surface. To explore the effects of dynamic loading, the pulling rate at the point of rupture/unfolding was varied from ≈4 pN/s to ≈50 pN/s by adjusting the trap stiffness and the velocity of the stage. Typical force-induced rupture/unfolding traces are shown in Fig. 2 a and b for α-actinin and filamin, respectively. The loading rate was experimentally obtained for each event from the slope of a linear fit to the force-vs.-time trace just before the break. The slope of the force–extension curve at rupture/unfolding was also determined (Insets in Fig. 2 a and b). For ≈60% of the pulling traces, we observed multiple abrupt drops in force, ranging from two to six per pull, indicative of either reattachment of the unbound filament or multiple binding locations along the filament. For these multiple unbinding traces, the characteristic distance between events is ≈2 μm. In most of these transitions, representing 63% and 72% of all observed transitions for filamin and α-actinin, respectively, the bead snapped back cleanly to its baseline location (zero force) after each break, confirming again that only one single-molecule interaction was loaded at each pull. Additional transitions that did not go to baseline were observed, and these potentially correspond to one or more of several events: loading two ABPs simultaneously, rapid rebinding, conformational changes, or unfolding. To further identify potential unfolding or conformational change transitions, we monitored the pulling rotational angle of the trapped bead in the x–y plane, which may indicate a potential application of torque to the bond. Transitions not going to baseline exhibiting a different angle before and after the transition represented 18% and 23% for filamin and α-actinin, respectively (Fig. 2c). Rupture-like transitions that did not go to baseline (zero force) having the same angle before and after the transition representing 19% and 5% in filamin and α-actinin, respectively, were counted as potential unfolding, conformational changes, or rebinding events (Fig. 2d). The pulling trajectory angle was calculated for all clean rupture events, and most of rupture trajectories were within 45° of the stage direction and showed a flat dependence of rupture force vs. angle [see supporting information (SI) Fig. S1]. Events >45° from the stage axis showed a reduction in rupture force vs. angle and were discarded from the analysis, 25 and 28 events for α-actinin and filamin, respectively.

Fig. 2.

Molecular response to force of actin–ABP interactions. (a and b) Force vs. extension curves showing typical rupture events for α-actinin/actin bonds (a) and filamin bonds (b). (Insets) The slope of the force–extension relationships just before rupture for all events relaxing to baseline, zero force. (c) Events are for filamin, showing an example of transition where the force does not relax to baseline, and in the corresponding x–y plot, different pulling trajectories are easily identified. (d) Events are for filamin, showing an example of transition where the force does not relax to baseline, and in the corresponding x–y plots, the transitions are along the same pulling trajectory. Additional examples are found in Fig. S5. (e) Smooth traces tended to follow the same trajectory during loading (red), relaxation (black), and reloading (blue). (f) Traces with abrupt, partial transitions typically showed relaxation along a new trajectory and did not recover the original loading trajectory after reloading.

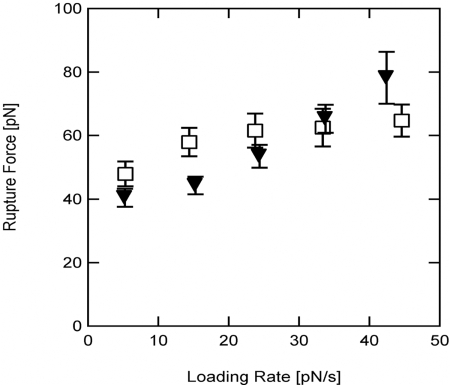
Results for the clean-rupture group show that for both α-actinin (n = 170) and filamin (n = 154), the rupture force increased with loading rate (Fig. 3), a trend predicted by theoretical models (38, 42) and observed in other molecular interactions (37, 43). For loading rates <30 pN/s, the α-actinin/actin and filamin/actin interactions ruptured at similar forces, with filamin showing a slightly stronger interaction (mean ± standard deviation): 40.4 ± 23.5 pN (n = 67) and 47.9 ± 30.3 pN (n = 61) at ≈5 pN/s pulling rate; 44.2 ± 19.9 pN (n = 52) and 58.0 ± 30.8 pN (n = 48) at ≈15 pN/s pulling rate; and 53.4 ± 19.7 pN (n = 30) and 61.5 ± 22.2 pN (n = 17) at ≈25 pN/s pulling rate. At higher pulling rates, the most probable rupture force for the α-actinin/actin interaction and filamin/actin interaction converged: 65.2 ± 16.0 pN (n = 13) and 62.4 ± 20.6 pN (n = 12) at ≈35 pN/s pulling rate; and 78.2 ± 18.3 pN (n = 5) and 64.7 ± 13.4 pN (n = 7) at ≈45 pN/s pulling rate. We note that the number of events in this range of higher loading rates diminishes rapidly. In general, the rupture forces measured here are in the same range as those recently reported for the myosin/actin interactions at similar loading rates (37).

Fig. 3.

Most probable force to rupture the α-actinin/actin (▾) and the filamin/actin interactions (□). Error bars indicate standard error on the mean of rupture force for the same data in Fig. 4.

The extensions shown in Fig. 2 exceed the folded protein contour length of both α-actinin (30 nm) and filamin (160 nm). Because our system consists of several linking elements, large extensions could be attributed to: (i) possible bending of actin filaments at surface and bead attachment points, similar to that observed by Dupuis et al. (44); (ii) rotation of molecular linkages that align with the applied force; and (iii) entropic stretching of the molecular elements along the force-transmission pathway. However, the contribution of these to the total deformation is difficult to assess.

To compare our results with a different protein immobilization strategy, we placed α-actinin nonspecifically on a glass coverslip and measured a mean rupture force between α-actinin and actin of 6.99 ± 4.40 pN for a loading rate of ≈5 pN/s (Fig. S2). Clearly, α-actinin is either weakly bound to the surface or the interaction with the surface is affecting its native binding with F-actin. This finding confirms that selecting the proper immobilization scheme is an important factor in the design of single-molecule experiments.

Furuike et al. (20) reported forces of ≈100 pN to unfold the Ig subdomains of filamin at a loading rate of ≈2,000 pN/s. From their data, we estimated that unfolding forces would extrapolate to ≈50 pN at our loading rates, assuming that force scales with the natural logarithm of loading rate (42). However, in our experiments, even at relatively higher forces (≈100 pN), most of the force-extension plots showed only one clean break, instead of the typical sawtooth footprint of unfolding events, despite having adequate spatial resolution (≈1 nm) to resolve individual subdomain unfolding of ≈30 nm (20). It is possible that during loading, the ABP could go through small conformational changes that were not detected in our study. For example, laser trap experiments on titin exhibit a stretch-transition region at forces <20 pN, characterized by an abrupt change in slope and hysteresis in force–extension curves (45) instead of a sawtooth pattern. This has been attributed to the multiple identical subunits and increased compliance of the trap and molecular linkage (46). However, we did not observe any such abrupt changes in slope in our experiments because rupture events show a single distribution in force-vs.-extension slope at rupture (Insets in Fig. 2 a and b). In addition, we performed loading-unloading experiments to explore molecular relaxation pathways and hysteresis. Smooth traces tended to follow the same trajectory during loading, unloading, and reloading, indicating a lack of hysteresis and unbinding (Fig. 2e). Traces with abrupt, partial transitions typically showed relaxation along a new trajectory and did not recover the original loading trajectory after reloading (Fig. 2f).

We performed a small number of pulls at higher loading rates, ≈270 pN/s, where we observed a greater tendency for unfolding-like transitions and some exhibited a sawtooth-like pattern (Fig. S3a). We also pulled directly on filamin and observed multiple transitions resembling those in the actin–filamin–actin system, consistent with unfolding one or more domains (Fig. S3b).

Rupture-Force Distributions and Modeling.

The rupture-force distributions were modeled as a single energy-barrier system as described by the theoretical approach developed by Hummer and Szabo (38) and referred to here as HS. This model provides estimates for the intrinsic dissociation rate, k_off, the transition distance from the free-energy minimum to the rupture barrier, x^‡, and the free energy of rupture, ΔG^‡ and an additional parameter describing a molecular spring constant, k_BTκ_m (38, 42) (see SI Text for details on the models). This spring constant is used to approximate the free-energy profile of a molecular interaction [note that the spring constant has units of force per unit length; therefore κ_m has units of inverse length squared, consistent with the notation in Hummer and Szabo (38)].

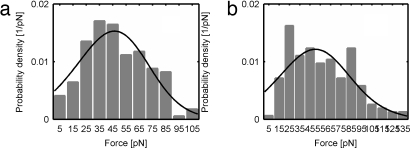
We fit the overall rupture distribution for a given ABP/actin interaction to obtain average fit parameters for each model. The results are graphically represented in Fig. 4. Fits from the HS model provide reasonable fits to the rupture-force distributions, with goodness of fits, R², of 0.84 and 0.67 for α-actinin and filamin, respectively. The intrinsic dissociation rate k_off estimated with the HS model are 0.066 ± 0.028 s⁻¹ for α-actinin and 0.087 ± 0.073 s⁻¹ for filamin. Previously, the lifetime of the α-actinin/actin interaction was found to be ≈20 s, as measured by rupture under constant load (34), corresponding to k_off ≈0.05 s⁻¹, slightly lower than the one found here. In contrast, bulk measurements with no load estimated a value of k_off for α-actinin and filamin of ≈0.4 s⁻¹ and ≈0.6 s⁻¹, respectively (47), corresponding to a bond lifetime of ≈2.5 s. This bond lifetime is almost an order of magnitude shorter than that recorded at the single-molecule level. This discrepancy could be attributed to the restricted unbinding reaction coordinate imposed by directional loads in single-molecule experiments; whereas with no load, the interaction is free to explore different unbinding trajectories.

Fig. 4.

Rupture-force probability distributions for α-actinin/actin (a) and filamin/actin (b) interactions. Average loading rates are 16.7 pN/s and 18.9 pN/s for α-actinin and filamin, respectively. The widths of the bin were 10 pN, and the histograms were fit to the HS model (solid) (38).

HS fits show a transition distance x^‡ of 2.75 ± 0.79 Å for α-actinin and 1.94 ± 1.49 Å for filamin. These transition distances are approximately half of those obtained for other protein interactions reported earlier (38, 48); however, we note that because we are lumping several loading rates, and the interactions probed may include multiple unbinding coordinates, our apparent rupture-force distributions are artificially broadened, potentially causing the apparent transition distances to be artificially lowered.

From the HS model, the characteristic spring constant, k_BTκ_m describing the molecular interactions was also obtained. The data suggest that the α-actinin/actin interaction is slightly more flexible (k_BTκ_m = 455 ± 215 pN/nm) than the filamin/actin interaction (k_BTκ_m = 820 ± 551 pN/nm); these values are in the range of previously reported stiffnesses for other molecular interactions (38). From the molecular spring constant, the free-energy profile along the pulling reaction coordinate, ΔG(x), is given by ΔG(x) = ½κ_mx², where x represents the pulling coordinate, and ΔG(x) has units of k_BT. The height of the free-energy barrier of rupture, ΔG^‡, is obtained by evaluating ΔG(x) at x = x^‡. For the α-actinin/actin interaction ΔG^‡ ≈4.3 k_BT and for the filamin/actin interaction ΔG^‡ ≈3.6 k_BT, indicating that slightly more energy is required for the dissociation of the α-actinin/actin interaction. However, in general, the results obtained for both ABPs' interaction with actin are fairly similar, exhibiting fit parameters within a factor of two, consistent with the observation that filamin and α-actinin possess similar actin-binding domains.

Discussion

ABP/actin interactions are largely determined by the molecular structure of the ABP and its actin-binding site. The filamin dimer is a long, flexible molecule formed by the binding of its subunits at their C-terminal domains, leaving two actin-binding domains at their N-terminals exposed (10). α-Actinin, also a dimer, is formed by the antiparallel arrangement of its subunits, leaving one actin-binding site exposed at each end, and a rigid central domain (7, 12). These exposed domains of both filamin and α-actinin have calponin-homology (CH) actin-binding sequences, which are also common among other ABPs such as spectrin, dystrophin, and fimbrin (7, 9–14). In essence, if the binding with actin is regulated only by this conserved sequence, these ABPs should have similar binding kinetics as shown in bulk experiments (47). Our results show that, in general, filamin and α-actinin/actin interactions have comparable binding strengths, consistent with the conserved actin-binding sequence.

It has been argued that the frequency-dependent mechanical properties of the actin cytoskeleton are influenced by either ABP unfolding (20, 32, 33) or ABP unbinding (29, 49). Here, we directly measured the forces required to rupture the interaction of F-actin with two structurally different ABPs. Although potential unfolding or conformational changes were observed, our results present important single-molecule experimental evidence supporting the work that suggests that ABP unbinding is important in the temporal regulation of the cytoskeleton. From previous data at much higher loading rates (20, 33), we extrapolated their unfolding forces to our loading rates and estimated ≈50 pN for the Ig subdomains of filamin. Previous measurements have exhibited two different types of behavior attributable to protein unfolding. In one, generally observed with AFM measurements, a sequence of abrupt drops in force (sawtooth pattern) is seen, each drop corresponding to unfolding of a single domain (20, 50). These events tend to occur at regular intervals and typically cause only partial relaxation of the applied force. In the other scenario, observed with more compliant optical traps, a plateau is observed in the force–extension curve (45, 51). Our experiments show neither of these behaviors. Instead, we observe either a single, gradually steepening force–extension curve, with a single force drop to zero, or a curve punctuated by a relatively small number (typically one) of partial drops, terminated by a definitive drop to zero force. This pattern appears consistent with our view that unfolding events are seen, but unbinding events are more likely at these low loading rates. We note that mechanisms such as rupture and rebinding during bead snapback remain a possible explanation for transitions that do not go to baseline and remain along the same angle. Further experiments to explore the unbinding vs. unfolding properties of the ABP/actin complex at higher loading rates than those reported here, where rupture forces would increase and could increase the likelihood of unfolding, are needed and will help to explain this discrepancy. For example, mechanisms that strengthen or stabilize an ABP–actin-binding interaction may lead to increased likelihood of unfolding. Thus, by positioning unbinding and unfolding energy barriers near each other, the cytoskeletal machinery has a greater range of regulation.

Although we did not fit the rupture-force distributions to subsets of loading rates, more than one energetic barrier may exist and dominate at different regimes of loading rates as evidenced by changes in slope of the rupture force vs. loading rate plot and as suggested by Miyata et al. (34). Because both interactions show this phenomenon, this behavior might be a general characteristic of the actin-binding sequence shared by several ABPs. A similar phenomenon has also been observed with the actin/myosin interaction (37) and other molecular complexes (52, 53). We note that a more detailed study of this phenomenon with greater numbers of events over a wider range of loading rates can further elucidate the frequency-dependent behavior of the actin cytoskeleton. In addition, expansion of the molecular theoretical models to incorporate several energy barriers at different loading rates can prove useful in the analysis of experimental data obtained from complex molecular interactions.

One factor that can also influence the unbinding properties for molecular interactions is the direction of the applied load (54, 55). The immobilized filaments on the surface are generally aligned in the direction of the flow, and we applied the load in the same direction and always from the barbed end of the tethered filament (Fig. 1). Here, we measured the unbinding properties along a distribution of, on average, parallel reaction coordinates; however, other preferred reaction coordinates are possible because filamin forms 90° cross-links between filaments (10), whereas α-actinin arranges them in parallel fashion (7). In addition, our assay includes possibilities of both surface and bead-tethered actin filaments oriented with the barbed ends toward the same or opposite directions, which, combined with lumping the loading rates into a single distribution, may result in broadening of the rupture-force probability distributions, leading to a small transition distance. Nonetheless, similar transition distances for protein–protein interactions have been shown (38, 48), thus the broad distribution of our results may still be feasible. Our assay, combined with fluorescence labeling of filaments and proteins to identify pulling directions and rupture location, provides a unique platform for exploration of directional unbinding.

Previous experiments with reconstituted F-actin networks cross-linked with filamin showed that these networks will rupture after a critical applied stress, σ_max, of ≈1–60 Pa (16). Tharmann et al. (29) attributed myosin cross-linked actin network reorganization at a maximum stress to unbinding and showed that an estimate for the maximum force for a single cross-link, 8pN, was in good agreement with rupture forces for myosin-actin interactions, 9 pN. Using the scaling approximations from Tharmann et al. (see SI Text) and our single-molecule most probable rupture forces of 20–70 pN, we estimate σ_max ≈12–42 Pa, corresponding roughly with the values reported earlier in bulk rheology. This finding provides evidence in support of the importance of ABP unbinding in the regulation of the properties of the cytoskeleton.

The broad applicability of this assay was demonstrated by probing the interaction of two structurally different ABPs with F-actin. With slight modifications, we envision that this assay can be readily implemented to study other important F-actin interactions such as those regulating cell migration, division, and focal-adhesion formation. These studies can expand the knowledge base on the regulation and control of the cellular machinery starting from the molecular building blocks.

Materials and Methods

Protein Preparation.

Actin monomers (Cytoskeleton) from rabbit skeletal muscle were diluted in fresh G-buffer [5 mM Tris·HCl (pH 8.0), 0.2 mM CaCl₂, 0.5 DTT, 0.2 mM ATP, 0.01% (wt/vol) NaN₃] to 11 μM and incubated on ice for 1 hour. For biotinylated filaments, a solution of 220 μM nonlabeled actin was mixed with an equal volume of 22 μM biotinylated actin monomers (Cytoskeleton), diluted to 11 μM total actin concentration in G-buffer and incubated on ice for 1 hour. Actin polymerization, for both the nonlabeled filaments and the biotinylated filaments, was initiated by adding 1/10 of the final volume of 10× F-buffer [50 mM Tris·HCl (pH 7.5), 500 mM KCl, 2 mM MgCl₂, 2 mM CaCl₂, 2 mM DTT, 5 mM ATP, 0.01% (wt/vol) NaN₃]. To label the filaments, 4 μl of 66 μM Alexa Fluor 555 phalloidin (Invitrogen) (see Fig. S4).

Recombinant filamin-A was purified from Sf9 cell lysates (56), and recombinant human gelsolin was produced in Escherichia coli (57). Lyophilized rabbit skeletal muscle α-actinin was obtained from Cytoskeleton. All proteins were stored in G-buffer at −80°C before use.

Bead Preparation.

Carboxylated beads (1-μm; Polysciences) were coated with gelsolin per Suzuki et al. (40), with the amount of protein modified to 260 μg of BSA, 40 μg of BSA conjugated with Alexa Fluor 555, 50 μg of actin monomers, and 50 μg of gelsolin. The gelsolin-coated beads were stored in a rotator at 4°C. Before use, 100 μl of gelsolin-coated beads were diluted with 100 μl of storage buffer [25 mM imidazole-HCl (pH 7.4), 25 mM KCl, 4 mM MgCl₂, 0.1 mM CaCl₂, 0.1 mM ATP, 1 mM DTT, 0.04% (wt/vol) NaN₃] and washed four times by centrifugation at 6,000 rpm for 4 min in a table-top centrifuge (centrifuge 5415C, rotor F-45-18-11, Eppendorf). After the last wash, the beads were resuspended with 40 μl of 1× F-buffer and mixed with 2 μl of 10 μM F-actin (nonbiotinylated). The bead–F-actin solution was incubated overnight in a rotator at 4°C in the dark. Under these conditions, we ensured that only one filament was bound per bead (Fig. 1).

Sample Preparation.

The experimental flow chamber (25.8 mm × 8 mm × 0.1 mm) was built in-house from a microscope slide and a KOH-etched coverslip held together by double-sided tape. The experimental sample was prepared by sequential incubation of: (i) 2 mg/ml of BSA conjugated with biotin in PBT [100 mM phosphate buffer (pH 7.5), 0.1% (vol/vol) Tween 20]; (ii) 0.1 mg/ml streptavidin in PBT; (iii) 50 nM F-actin/biotin in 1× F-buffer supplemented with 2 mg/ml BSA and 1% dextran (400 kDa; Sigma); (iv) 20 nM filamin or α-actinin in 1× F-buffer with 2 mg/ml BSA; and (v) 100-fold dilution of gelsolin beads bound to F-actin in 1× F-buffer with 2 mg/ml BSA. Each incubation step was performed for ≈20 min in the dark in a humidity-preserving chamber. After step i, the flow chamber was washed with 100 μl of PBT and after steps ii–iv, it was washed with 100 μl of 1× F-buffer with 2 mg/ml BSA. After step v, the flow chamber was sealed with nail polish. Approximately 30 tethers per field of view were found throughout the ≈3 h of experimental time.

Instrumentation and Data Collection.

Unbinding experiments were performed at room temperature in an instrument that combines optical trapping and fluorescence microscopy, as described (41). A tethered bead was captured with the optical trap and centered in 3D with an automated routine. Note that, given the overall geometry, 1-μm bead size and typical length of an actin filament (5 μm), the vertical angle will be <≈10°. Then, a dynamic load was applied to the actin–ABP–actin linkage by moving a piezo-electric stage (Polytec PI) at a constant speed while keeping the trap location stationary. The direction of the load was parallel to the flow direction along the general orientation of the immobilized filaments on the surface. Back-focal plane position detection (58) was used to continuously track the position of the bead until rupture from the surface was detected. Bead and stage positions were recorded at either 20 Hz or 200 Hz. After rupture, each bead was position-calibrated, and the stiffness of the trap, k_trap, was determined by using the variance method (59). By using the Stokes calibration method (59), the optical trap was characterized to have a linear range of force (F = k_trapx_bead) for displacements up to ≈170 nm from the center of the trap waist. For consistency, any rupture that occurred at a displacement of the bead >170 nm was discarded because the rupture force became uncertain. Custom software (LabView; National Instruments) acquired all signals through a 16-bit A/D board (National Instruments), and data analysis was performed with Matlab (Mathworks). Rupture events that went to baseline were scored, and loading rates determined from the experimental loading rate at rupture were recorded for each event. The angle of bead displacement out of the trap relative to the pull direction was also determined. Large angles may represent a situation where excessive torque is exerted on the bond and may, therefore, rupture at lower force. Rupture events that did not go to baseline were also monitored for pulling direction. Potential unfolding or conformational change transitions were identified as a subset of events that showed the same angle before and after a transition. Rebinding to the same filament during bead snapback is another explanation for these transitions.