Dynamic effects on the periselectivity, rate, isotope effects, and mechanism of cycloadditions of ketenes with cyclopentadiene

Abstract

The cycloadditions of cyclopentadiene with diphenylketene and dichloroketene are studied by a combination of kinetic and product studies, kinetic isotope effects, standard theoretical calculations, and trajectory calculations. In contrast to recent reports, the reaction of cyclopentadiene with diphenylketene affords both [4 + 2] and [2 + 2] cycloadducts directly. This is surprising, since there is only one low-energy transition structure for adduct formation in mPW1K calculations, but quasiclassical trajectories started from this single transition structure afford both [4 + 2] and [2 + 2] products. The dichloroketene reaction is finely balanced between [4 + 2] and [2 + 2] cycloaddition modes in mPW1K calculations, as the minimum-energy path (MEP) leads to different products depending on the basis set. The MEP is misleading in predicting a single product, as trajectory studies for the dichloroketene reaction predict that both [4 + 2] and [2 + 2] products should be formed. The periselectivity does not reflect transition state orbital interactions. The ¹³C isotope effects for the dichloroketene reaction are well-predicted from the mPW1K/6−31+G** transition structure. However, the isotope effects for the diphenylketene reaction are not predictable from the cycloaddition transition structure and transition state theory. The isotope effects also appear inconsistent with kinetic observations, but the trajectory studies evince that non-statistical recrossing can reconcile the apparently contradictory observations. B3LYP calculations predict a shallow intermediate on the energy surface, but trajectory studies suggest that the differing B3LYP and mPW1K surfaces do not result in qualitatively differing mechanisms. Overall, an understanding of the products, rates, selectivities, isotope effects, and mechanism in these reactions requires the explicit consideration of dynamic trajectories.

Selectivity in cycloadditions may take many forms, e.g., endo/exo stereoselectivity, regioselectivity, facial stereoselectivity, and diene/dienophile role selectivity. When two distinct formally allowed processes are possible, as in the [4 + 2] versus [6 + 4] cycloadditions of cyclopentadiene with tropone,¹ their differentiation is referred to as periselectivity. The underlying framework within which chemists usually understand any of these forms of selectivity is transition state theory (TST). The preferred product would be that involving the lowest-energy transition state, and the degree of selectivity would be determined by the relative energies for separate transition states. Even when there is no enthalpic barrier, reactivity and selectivity can be discussed in terms of free-energy barriers.² Qualitative theories of selectivity such as FMO theory may be thought of as a simplified surrogate for TST, easing the task of predicting which cycloaddition barrier is lowest in energy.

This all seems so fundamental that the assumptions involved in understanding selectivity with TST may be obscured. One of these assumptions is that intramolecular vibrational energy redistribution (IVR) is fast on the time scale of reaction coordinate motion.³ This is not necessarily the case. One possible result of relatively slow IVR is “non-statistical” transition state recrossing, slowing reaction rates in a way that cannot be predicted by statistical theories such as microcanonical variational TST.⁴ Hase in particular has extensively studied this effect in gas-phase S_N2 reactions.^4,5 Another effect of relatively slow IVR is that the selection of trajectories passing through an initial transition state can influence selectivity among subsequent transition states. Due to such a “dynamic matching” effect, the selectivity among products requires consideration of dynamic trajectories.⁶ Carpenter has brought to light the importance of this phenomenon in a series of organic reactions.⁷ Related effects can impact reactions in which trajectories pass through a flat, typically diradicaloid, area of a potential energy surface.^8,9,10 Alternatively, trajectories can effectively bypass minima on the reaction coordinate.^11,12

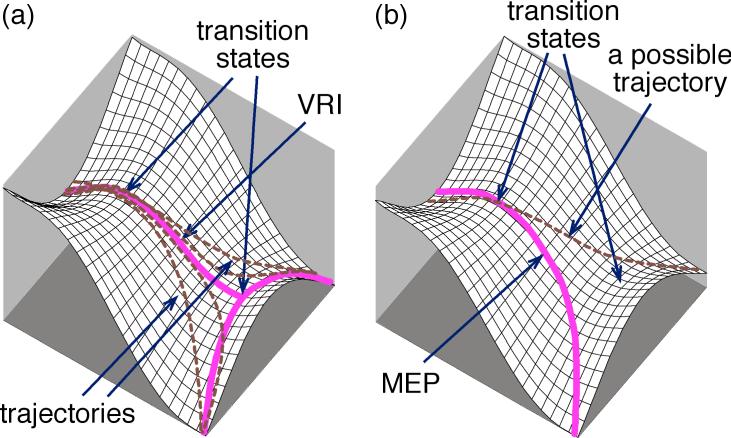
Another assumption in understanding selectivity, perhaps more subtle, is that the separate products arise from separate transition states. The intertwined idea that a transition state may only connect a reactant set with a single product set was once considered a rule, usable to exclude certain symmetries in transition states.¹³ However, this pervasive implicit assumption is not reliable.^14,15,16 On a bifurcating energy surface, such as those shown in Figure 1, the rate-limiting transition state is adjacent to a transition state interconverting products, and reactants that pass through the rate-limiting transition state can proceed to two product wells without barrier. If the surface is symmetrical, as in Figure 1a, the minimum-energy path (MEP) bifurcates to afford equally two equivalent products. Such bifurcating surfaces associated with symmetry breaking have been analyzed theoretically for many simple reactions.^16,17 Examples include the ring opening of cyclopropylidene to form allene,¹⁸ pseudorotations in SiH₄F– and PH₄F,¹⁹ 1,2-hydrogen migration in H₃CO•,²⁰ photodissociation of thioformaldehyde,²¹ bond shifting in cyclooctatetraene,²² dimerization of cyclopentadiene,²³ and deazetization leading to semibullvalene.²⁴ The selectivity in symmetry breaking is naturally 1:1, and the products are either indistinguishable or enantiomers, so that the selectivity has no synthetic consequence. Lluch has proposed that variational TST may sometimes be applied to predicting selectivity when the otherwise symmetrical surfaces are desymmetrized by isotopic substitution.²⁵

Figure 1.

Bifurcating surfaces in which dynamic effects would control selectivity. (a) The surface is symmetrical and the MEP bifurcates at a second transition state. Real trajectories would tend to diverge from the MEP in the area of the valley-ridge inflection (VRI). (b) The surface is unsymmetrical and the MEP does not bifurcate. However, some possible trajectories afford a product not on the MEP.

More chemically interesting, but far less understood, are reactions on unsymmetrical bifurcating surfaces,^{26,27,28,29,30,11b} as in Figure 1b. On such a surface, the MEP does not bifurcate but there may still be trajectories that lead to two, now distinguishable, products. In this case, the product mixture cannot currently be predicted from any form of TST.³¹ No qualitative theory presently exists for understanding selectivity in such reactions, and trajectory calculations are required for quantitative predictions. We recently found that singlet oxygen ene reactions appear to involve a surface of this type, and trajectory calculations were applied to understand the experimental formation of two regioisomeric products despite having only one of the products connected to the starting material by an MEP.^28,29

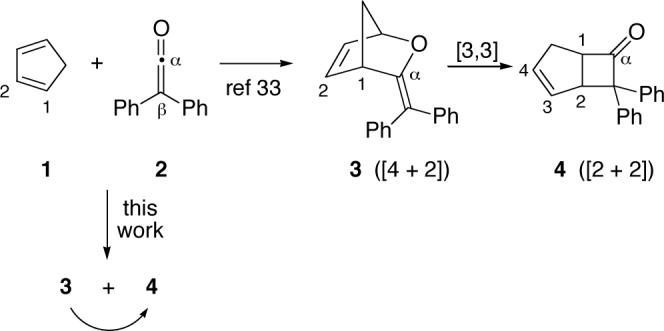
The reaction of interest here is the cycloaddition of ketenes with 1,3-dienes. Early workers were surprised to find that these reactions afforded cyclobutanones from a formal [2 + 2] cycloaddition instead of the expected [4 + 2] Diels-Alder products.³² The [2 + 2] cycloadditions of ketenes played a significant role in the elaboration of the Woodward-Hoffmann rules,³³ and their particularly facile reactions with 1,3-dienes have found substantial synthetic utility. It was therefore quite momentous when Machiguchi and Yamabe reported that [4 + 2] cycloadducts (e.g., 3) are the initial product in reactions of diphenylketene (2) with cyclic dienes such as cyclopentadiene (1).³⁴ The ultimate cyclobutanones (e.g., 4) were concluded to arise by a [3,3]-sigmatropic (Claisen) rearrangement of the initial product.

In the mechanism of Machiguchi and Yamabe, 4 is formed exclusively via 3. In fact, their theoretical calculations place the transition structure for the direct formation of 4 over 14 kcal/mol higher in energy than the transition structure for formation of 3, so that any formation of 4 without the intermediacy of 3 would be inconsistent. Despite this, we report here that some 4 is formed directly.

This seemingly minor difference in experimental observations gains significance from the inability of the standard³⁵ theoretical analysis via TST to explain the periselectivity observation. Additional experimental observations – kinetic isotope effects (KIEs) seemingly inconsistent with other kinetic observations – are equally perplexing within the standard framework. While our results cannot be understood within current TST, we find that a consistent and explanatory picture of the mechanism arises with the detailed consideration of dynamic trajectories. The results challenge some standard ideas used to understand the reactivity, selectivity, and mechanism of cycloadditions.

Results

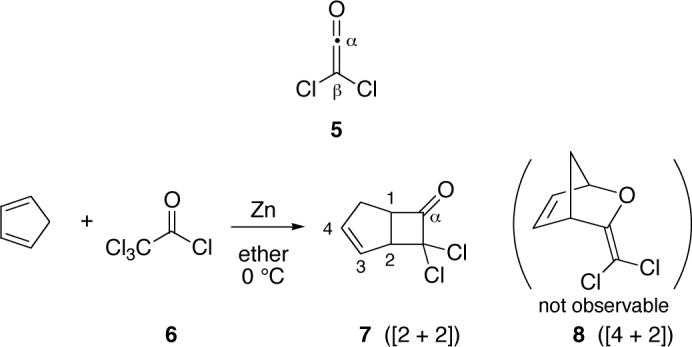
The two reactions studied here are the cycloadditions of cyclopentadiene with diphenylketene and with dichloroketene (5). Diphenylketene is isolable and is readily reacted with cyclopentadiene in quantitative yield under diverse conditions. However, dichloroketene is highly reactive and unisolable. This high reactivity increases its utility in cycloadditions,^36,37 and dichloroketene has seen common use in complex synthesis.³⁸ Dichloroketene is conveniently generated in situ by treatment of a solution of cyclopentadiene and trichloroacetyl chloride (6) with powdered zinc at 0 °C in ether. Under these conditions, cyclobutanone 7 is formed cleanly, except for a small amount of dicyclopentadiene.

Product Composition and Kinetics

Due to unusual isotope effect observations (vide infra), we began to suspect that the reaction of cyclopentadiene with diphenylketene was not as simple as had been reported. Machiguchi and Yamabe had previously examined this reaction at low temperatures by NMR, but we could not determine from their data whether 3 was the exclusive initial product in the reaction. We therefore reexamined this reaction. Figure 2 shows the composition of 3 and 4 versus time in a reaction in CD₂Cl₂ at −20 °C. At this temperature, the concentration of 3 reached a maximum at ≈2 h then fell off slowly due to the isomerization of 3 to 4. A key observation was that the concentration of 4 increased steadily, even within the first half hour while the concentration of 3 was relatively low. This was not consistent with 4 arising solely by isomerization of 3. A best-fit simulation of the reaction composition versus time at −20 °C had rate constants of 4.1 × 10⁻⁴ M⁻¹s⁻¹ for formation of 3, 0.9 × 10⁻⁴ M⁻¹s⁻¹ for formation of 4, and 2.9 × 10⁻⁵s⁻¹ for rearrangement of 3 to 4.

Figure 2.

Composition versus time for the diphenylketene reaction at −20 °C, based on NMR observations. Solid lines are predicted, based on a kinetic model in which both 3 and 4 are formed concurrently, with 3 rearranging directly to 4. The inset shows an expansion of the early points.

An alternative kinetic model in which the conversion of 3 to 4 occurs indirectly, via reversion to cyclopentadiene + diphenylketene, did not reasonably fit the composition data (See the Supporting Information). A mixed kinetic model, in which some conversion of 3 to 4 occurs directly and some via starting materials, was also explored. The fit of the mixed model with the experimental data became poor if less than 75% of the conversion of 3 to 4 was direct, but it was not possible to exclude that some portion of the conversion of 3 to 4 occurs via reversion to the starting materials. The predominantly

direct nature of the conversion of 3 to 4, important later, is supported by Machiguchi and Yamabe's observation of a maximum of 8% addends in the rearrangement of isolated 3 at −10 °C.

For the reaction of cyclopentadiene with dichloroketene, repeated attempts to observe an initial [4 + 2] adduct 8, as would be analogous to 3, were unsuccessful.

Kinetic Isotope Effects

Because of the complicating [1,5]-sigmatropic rearrangement in cyclopentadiene and the instability of ketenes, these reactions are not readily amenable to a standard study of their intermolecular KIEs. However, the ¹²C/¹³C isotopic composition at C1 versus C4 and C2 versus C3 of the product 4 should reflect an intramolecular isotope effect. Intramolecular isotope effects in general reflect the transition state for product-determining steps, but as long as a reaction's regiochemistry or stereochemistry is settled in the rate-limiting step, as would be expected here, the intramolecular isotope effect should reflect the rate-limiting step. If the mechanistic pathways affording 3 and 4 result from competing rate-limiting transition states, the isotope effects will reflect a weighted average of the pathways, but if the 3/4 kinetic selectivity is determined subsequent to a single rate-limiting step, the isotope effects will reflect the single initial transition state. The subsequent rearrangement of 3 to 4 is irrelevant as long as cycloreversion to starting materials is minimal.

The intramolecular ¹³C KIEs in the formation of 4 were determined at natural abundance by our previously reported NMR methodology.^39,28 Samples of 4 were analyzed by ¹³C NMR under the demanding requirements for accurate relative integrations within spectra. This includes high digital resolution, long delays, centering of the peaks of interest within the spectral window, and integration ranges that are a constant multiple of the peak width at half height. A complication in the numerical interpretation of these integrations is that C1 and C2 are subject to three ¹J ¹³C-¹³C couplings with satellites not included in the integration range, while C3 and C4 are only subject to two such satellite couplings. To allow for this, the integrations at C3 and C4 were adjusted by the 0.0107(8) natural abundance of ¹³C.⁴⁰ After this correction, the integration of the ¹³C peak for C4 of 4 was consistently less than for C1, and integration of the ¹³C peak for C3 of 4 was consistently greater than that of C2 (Figure 3a). The ratios of abundances represent the inverse of the relative isotope effects at C1 versus C4 and at C2 versus C3, and these intramolecular isotope effects are also shown in Figure 3a.

Figure 3.

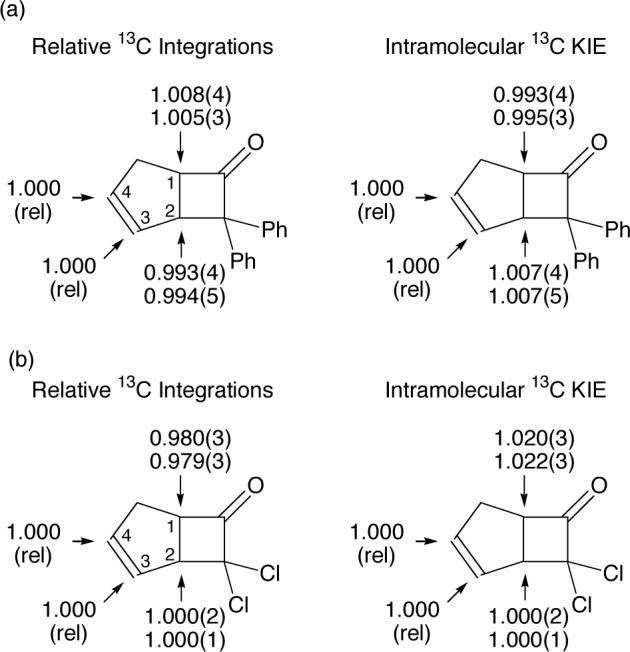
(a) Relative ¹³C integrations in samples of 4 and the derived intramolecular ¹³C KIEs (25 °C), defined as (k_12C/k_13C at C1)/(k_12C/k_13C at C4) or (k_12C/k_13C at C2)/(k_12C/k_13C at C3). (b) Relative ¹³C integrations in samples of 7 and the derived intramolecular ¹³C KIEs (0 °C), defined as above. The numbers in parentheses refer to 95% confidence limits on the last digit.

To interpret these results qualitatively, their relative nature must be kept in mind. If the σ bonding to a carbon is changing in the rate-limiting step (either making or breaking a σ bond), that carbon should exhibit a higher relative isotope effect than a corresponding center that is not undergoing a σ bonding change in that step. The low relative isotope effect at C1 of 4 thus qualitatively indicates that this carbon is not changing bonding in the rate-limiting step. Since both the major formation of 3 and the minor formation of 4 require C1-Cα bond formation, the C1-Cα bond must already be fully formed when the isotope effects are decided.⁴¹

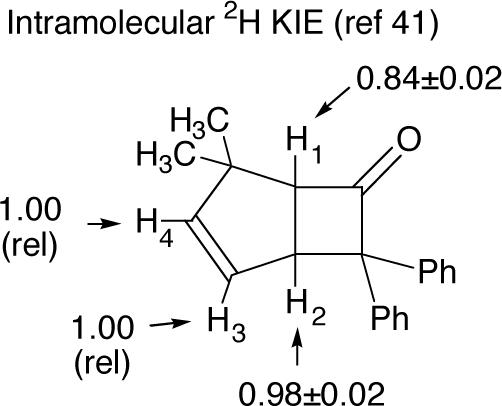
This conclusion fits well with intramolecular ²H isotope effects previously obtained by Holder and coworkers for the reaction of diphenylketene with 5,5-dimethylcyclopentadiene.⁴² The inverse H1/H4 isotope effect of 0.84 ± 0.02 observed in the Holder reaction is so large that it does not fit with rate-limiting C1-Cα bond formation. For comparison, isotope effects of ≈0.91 are seen in highly asynchronous Lewis-acid catalyzed Diels-Alder reactions.⁴³ Holder's KIE is quite consistent with a fully formed C1-Cα bond.

One possible explanation for the observed ¹³C and ²H KIEs would be a stepwise cycloaddition in which reversible bond formation at C1 is followed by rate-limiting bond formation at C4 to form 3 or C2 to form 4. However, it will be seen that this is inconsistent with the kinetic observations. An alternative explanation involving dynamic trajectories is presented below.

The intramolecular ¹³C KIEs in the formation of 7 were determined in an analogous fashion to those of 4 (Figure 3b). Unlike the formation of 4, the rate-limiting step for the formation of 7 appears to involve substantial σ bonding change at C1 but little or no bonding change at C2. Because the absolute KIE at C4 is unknown, the intramolecular KIE for C1 versus C4 cannot qualitatively distinguish an asynchronous [4 + 2] transition state from one in which there is solely bond formation at C1.

Standard Theoretical Results for the Diphenylketene Reaction

The reactions of diphenylketene and dichloroketene with cyclopentadiene were examined using mPW1K⁴⁴ and B3LYP⁴⁵ methods as the primary calculational models explored.⁴⁶ (See the Supporting Information for RHF/6−311+G** and BPW91/6−311+G** results, along with some MP2/6−311+G** single-point energies.) It will ultimately be concluded that one of these methods provides an inaccurate energy surface, but we discuss both because they predict differing mechanisms to consider versus experimental observations.

In RHF calculations employing a 3−21G basis set, Machiguchi and Yamabe had located two transition structures for the cycloaddition of cyclopentadiene with diphenylketene.^34b A “[4 + 2]” transition structure, appearing to lead to the [4 + 2] product 3, was 13.7 to 14.3 kcal/mol (MP2/6−31G*//RHF/3−21G including thermal and entropy corrections) below a “[2 + 2]” transition structure leading directly to the final product 4. These results supported the described initial formation of 3. They appear inconsistent with the direct formation of 4 found here, as 4 could only arise from 3 via a Claisen-rearrangement transition structure that was 0.6 to 1.0 kcal/mol below the [4 + 2] transition structure.

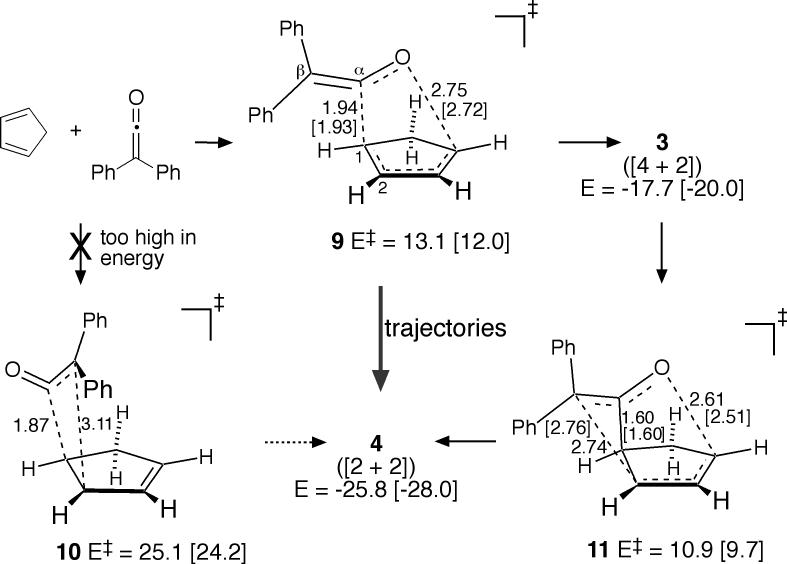
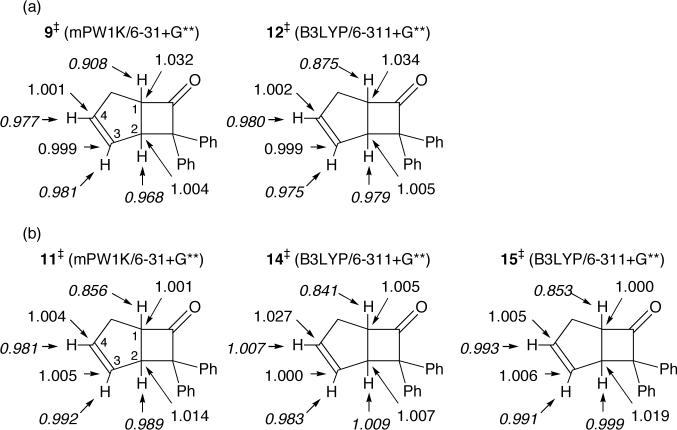
Superficially, our results in mPW1K/6−31+G** calculations are quite similar (Figure 4). The only locatable low-energy transition structure was 9. Structure 9 would be described as a [4 + 2] transition structure, based on its MEP connection with 3, though it will be seen that this description is simplistic. The alternative [2 + 2] transition structure 10 is predicted to be 12.0 kcal/mol⁴⁷ above 9. It is unlikely that the predicted energies of 9 versus 10 could err so greatly, so by a standard analysis, these results again appear inconsistent with the experimental direct formation of 4. Instead, it would be expected that 4 would be formed from 3 via the [3,3]-sigmatropic rearrangement transition structure 11.

Figure 4.

Diphenylketene cycloaddition pathway in mPW1K/6−31+G** [mPW1K/6−31G*] calculations. Energies (see ref 47) are in kcal/mol, relative to the separate starting materials.

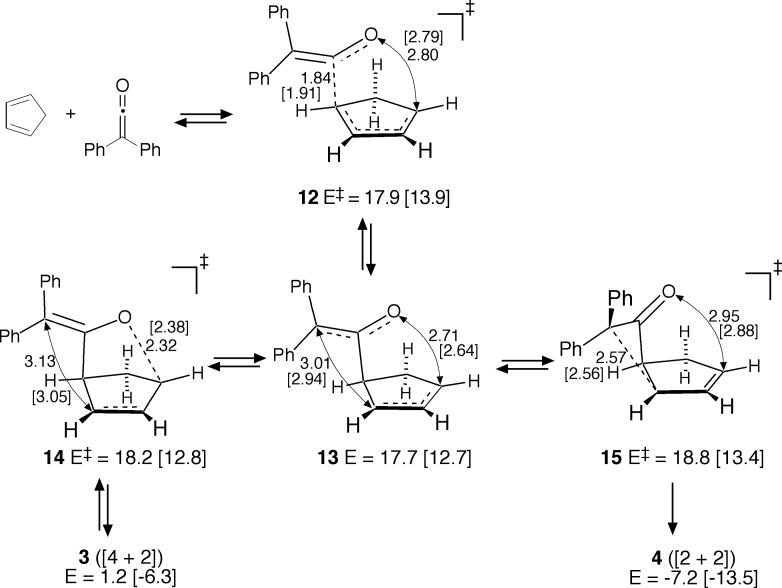
B3LYP calculations predict a quite different mechanism (Figure 5). On the B3LYP/6−311+G** surface, the MEP through initial transition structure 12 leads to intermediate 13. Structure 13 is diradicaloid in connectivity but, interestingly, its restricted wavefunction is stable. The potential energy well associated with intermediate 13 is very small, only 0.2 kcal/mol at B3LYP/6−311+G**. From 13, the transition structures 14 and 15 lead to 3 and 4, respectively. On this surface, then, the concurrent formation of both 3 and 4 can be viewed in a standard sense as resulting from the formation of an intermediate that may then react by two separate transition states to afford the two products. However, the B3LYP/6−311+G** surface is inconsistent with our experiments in a different way. Including zpe and thermal and entropy estimates at −20 °C from the harmonic frequencies, the free-energy barriers associated with 12, 14, and 15 are 30.9, 32.2, and 33.4 kcal/mol respectively. From this, 15 should be the rate-limiting transition structure and that the path from 3 to 4 would primarily be indirect, via 1 + 2, in contrast with experiment.

Figure 5.

Diphenylketene cycloaddition pathway in B3LYP/6−311+G** [B3LYP/6−31G*] calculations.

It would thus seem that neither the mPW1K nor the B3LYP surfaces are consistent with experimental observations. It will be seen later that this is incorrect.

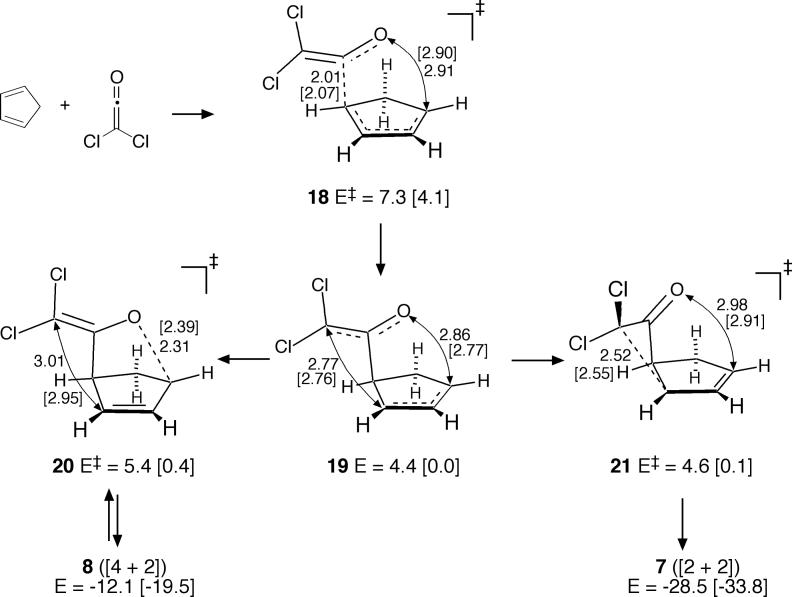
Standard Theoretical Results for the Dichloroketene Reaction

The high reactivity of dichloroketene is in part the result of the relative instability of having chlorine as a substituent on an sp² carbon. From this, the formation of 7 should be more exothermic than the formation of 4 and that the energetic preference for the [2 + 2] product 7 over [4 + 2] 8 should be greater than the energetic preference for [2 + 2] 4 over [4 + 2] 3. Predicted energies agree with these qualitative expectations; at the mPW1K/6−31+G** level, formation of 7 is exothermic by 45.7 kcal/mol and favored by 14.6 kcal/mol over formation of 8, while formation of 4 is exothermic by only 25.8 kcal/mol and favored over 3 by only 8.1 kcal/mol.⁴⁸ The overall energy surface for the dichloroketene reaction is affected by this relatively greater thermodynamic preference for the [2 + 2] product.

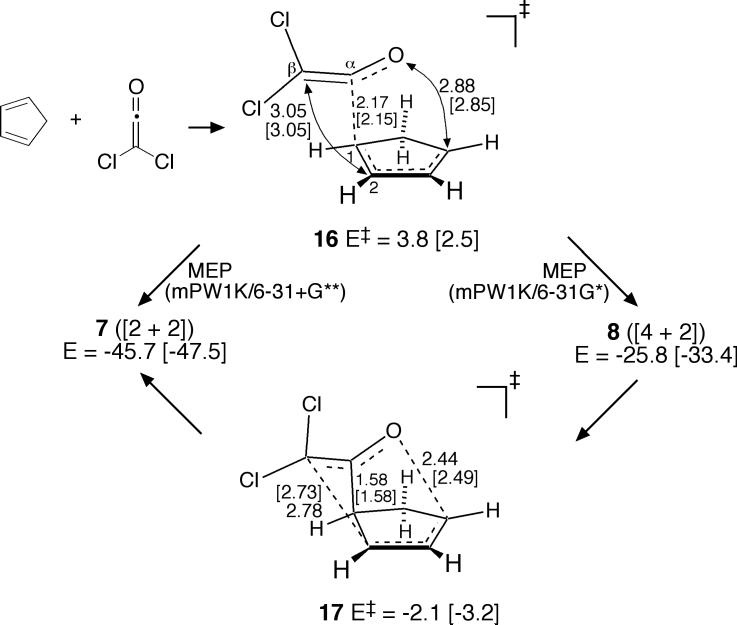
In mPW1K/6−31+G** calculations (Figure 6), the only locatable low-energy transition structure was 16. (A transition structure analogous to 10 was 12.7 kcal/mol higher in energy.) Two startling observations were associated with 16. Firstly, since 16 seems to closely resemble 9, it might be anticipated that 16 is a transition structure for the [4 + 2] cycloaddition. This is not correct. Rather, the MEP emanating from 16 leads to 7, not 8. Secondly, in the smaller 6−31G* basis set, 16 changes little, but the MEP emanating from 16 at mPW1K/6−31G* affords 8, not 7!

Figure 6.

Dichloroketene cycloaddition pathway in mPW1K/6−31+G** [mPW1K/6−31G*] calculations.

In both cases, the MEPs pass near another transition structure 17, which is the transition structure for the [3,3]-sigmatropic rearrangement converting 8 to 7. With the larger basis set, the MEP from 16 passes slightly to the “7-side” of 17, while with the smaller basis set, the MEP passes slightly to the “8-side” of 17. It is notable that a standard theoretical analysis of this reaction performed only with a 6−31G* basis set would have predicted that only 8 is formed, but not 7, while an analysis performed only with a 6−31+G** basis set would have predicted that only 7 is formed, but not 8. Obviously, this points to a substantial weakness in predicting the products of reactions from MEPs. It will be seen below that dynamic trajectories provide more realistic predictions.

As with the diphenylketene reaction, the B3LYP/6−311+G** energy surface for the reaction of cyclopentadiene with dichloroketene contains a very shallow dip for the diradicaloid/zwitterionic structure 19 (Figure 7).⁴⁹ From 19, the favored pathway would be formation of the [2 + 2] product 7 via transition structure 21, while transition structure 20 leading to 8 is only modestly higher in energy and would be expected to be competitive. The initial transition structure 18 is predicted to be rate limiting. (See the Supporting Information for similar BPW91/6−311+G** results.)

Figure 7.

Dichloroketene cycloaddition pathway in B3LYP/6−311+G** [B3LYP/6−31G*] calculations.

Overall, the mPW1K and B3LYP calculations predict mechanisms that are descriptively quite different. The experimental isotope effects will provide some measure of which method is more accurate for the current reaction. Trajectory studies will then show that the apparent difference in mechanisms on the mPW1K and B3LYP surfaces is largely fallacious.

Predicted Isotope Effects

Prediction of isotope effects for the dichloroketene reaction is relatively straightforward, as the B3LYP and mPW1K methods both predict that the initial attack via transition structures 16 or 18 is rate limiting. The ¹³C KIEs associated with these transition structures were predicted from the scaled theoretical vibrational frequencies⁵⁰ using TST by the method of Bigeleisen and Mayer.⁵¹ Tunneling corrections were applied using the one-dimensional infinite parabolic barrier model.⁵² Such KIE predictions have proven highly accurate in reactions not involving hydrogen transfer, so long as the calculation accurately depicts the mechanism and transition state geometry.⁵³

The results are summarized in Figure 8. Both 16 and 18 are predicted to afford a substantial ¹³C KIE at C1 and near unity KIEs at C2, C3, and C4, in qualitative agreement with experiment. However, the C1 KIE based on the mPW1K structure 16 is strikingly quantitatively accurate, while the C1 KIE predicted for the B3LYP structure 18 is less accurate. This favors the accuracy of the mPW1K/6−31+G** surface over the B3LYP/6−311+G** surface. The results also support the general interpretation of the isotope effects in terms of a rate-limiting transition state in which there is substantial bond formation to C1 and little or no bond formation to C2 or C4. Notably, the relatively tight delimitation of the transition state by the combination of isotope effects and calculations still does not confidently define whether the [4 + 2] or [2 +2] product should be major.

Figure 8.

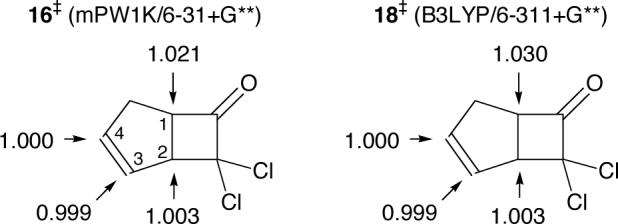
Predicted absolute ¹³C KIE at 0 °C for the dichloroketene reaction, based on the mPW1K/6−31+G** transition structure 16 and the B3LYP/6−311+G** transition structure 18.

For the transition structures 9 and 12 for initial attack of the diphenylketene on the cyclopentadiene, substantial ¹³C KIEs are predicted for C1 and small KIEs are predicted for C2, C3, and C4 (Figure 9a), in analogy with the predictions for 16 and 18 in Figure 8. These predictions are clearly inconsistent with the experimental observations in Figure 3a. In addition, the relative ²H KIEs predicted for H1 versus H4 are not as inverse as experimentally observed by Holder,⁴² in line with the qualitative argument presented earlier. This again weighs against rate-limiting C1-Cα bond formation.

Figure 9.

Predicted absolute ¹³C and ²H KIEs at 25 °C for the diphenylketene reaction, treating the various transition structures as rate-limiting. For comparison with the experimental KIEs, relative KIEs at competitive positions (C1/C4, C2/C3, H1/H4, H2/H3) should be considered.

The predicted isotope effects based on later transition structures in the diphenylketene mechanisms are enlightening (Figure 9b), ignoring for now apparent experimental inconsistencies. The KIEs for transition structure 11 are notably close to the experimental values – the relative KIEs at C1 and C2 would be 0.997 and 1.009, respectively. For 14, the relative isotope effect at C1 would be 0.978, much lower than the experimental value. Transition structure 15, rate limiting in the B3LYP/6−311+G** calculations, leads to relative KIEs at C1 and C2 of 0.995 and 1.012, respectively. While the latter is larger than the observed relative KIE of about 1.007, the pattern of inverse KIE at C1 and normal KIE at C2 resembles that of the experimental KIEs. All of the structures 11, 14, and 15 have relative ²H KIEs predicted for H1 versus H4 that are consistent with Holder's observations.⁴² Overall, the comparison of experimental and predicted KIEs suggests that the molecular geometry when the KIEs are decided has a fully formed C1-Cα bond and little bond formation to C2 or C4, roughly resembling 11.

Trajectory Studies of the Reaction of Cyclopentadiene with Ketenes

As will be discussed below, the kinetic observations and isotope effects for the diphenylketene reaction are inconsistent when viewed in a standard way, so that no orthodox mechanism can be reconciled with the experimental observations. From the apparent contradictions, it was suspected that the reaction's energy surface is of the type in Figure 1b. To explore this issue, we turned to trajectory studies.

Transition structures 9, 12, 16, and 18 (as their 6−31G* variants) were used as the starting point for quasiclassical direct dynamics trajectories^{4,5,8,9,11,12,54} on the mPW1K/6−31G* (for 9 and 16) and B3LYP/6−31G* (for 12 and 18) potential energy surfaces, using Gaussian 03⁴⁶ to calculate forces at each point and using previously described code²⁹ to initiate and propagate trajectories (see the Supporting Information for complete code and details). Limited sets of trajectories emanating from 9 and 16 (as their 6−31+G** variants) at the mPW1K/6−31+G** level were also studied. With all atomic motions freely variable, the trajectories were initialized^8b by giving each mode a random sign for its initial velocity, along with an initial energy based on a random Boltzmann sampling of vibrational levels appropriate for 273.15 K, including zero point energy. The mode associated with the imaginary frequency was treated as a translation and given a Boltzmann sampling of translational energy “forward” over the col. The starting atomic positions on the potential energy ridge in the area of the transition structures were randomized using a linear sampling of possible harmonic classical displacements for each normal mode, adjusting the kinetic energy for each mode accordingly. Employing a Verlet algorithm, 1-fs steps were taken until either the [4 + 2] or [2 + 2] products were formed or recrossing occurred to afford the starting materials (defined by a C1-Cα distance > 2.4 Å) up to a maximum of 500 fs. The results are shown in Table 1.

Table 1.

Results from quasiclassical trajectories starting from 9, 12, 16, and 18.

starting transition structure	total trajectories	[4 + 2] trajectories (3 or 8)	[2 + 2] trajectories (4 or 7)	recrossing trajectories	trajectories exceeding time limit
diphenylketene
9 (mPW1K/6−31G*)	130	67	4	56	3
9 (mPW1K/6−31+G**)	24	8	1	15	0
12 (B3LYP/6−31G*)	81	18	3	54	6
dichloroketene
16 (mPW1K/6−31G*)	130	70	47	13	0
16 (mPW1K/6−31+G**)	37	8	24	5	0
18 (B3LYP/6−31G*)	121	15	75	20	11

Among several striking observations, the most conspicuous is that trajectories passing through transition structures 9 and 16 afford both the [4 + 2] and [2 + 2] products. The MEPs passing through either lead to a single product, as must be true in the absence of symmetry, but the trajectories show that these transition structures may lead to two products.

The MEPs do retain value here in predicting the major product from trajectories. Despite quite similar geometries for 16 predicted with 6−31G* versus 6−31+G** basis sets, a modest majority of the 6−31G* trajectories afford the [4 + 2] product 8 while three quarters of the productive 6−31+G** trajectories afforded the [2 + 2] product 7. (The majority product is in each case statistically significant at 95% confidence.) This fits with the surprising MEP results described in a previous section.

On the B3LYP surface, transition structures 12 and 18 lead to intermediates that can in a standard manner partition to the two products, so it is perhaps not surprising that trajectories afford both [4 + 2] and [2 + 2] products in these cases. However, an examination of the trajectories suggests that the intermediates 13 and 19 have little impact. The standard view is that the mechanism passes through 13 on its way to 3 and 4, but in fact 9 out of the 18 trajectories affording 3 exhibited a monotonic decrease of the incipient C4—O bond distance with time. Such trajectories bypass 13, and in such cases the standard “stepwise” mechanism seems best understood as a concerted [4 + 2] cycloaddition. Similar results were seen for the formation of 8 from 18 – 9 out of 15 trajectories showed a monotonic decrease in the incipient C4—O distance, effectively bypassing 19. Intriguingly, the [2 + 2] process acts more in accord with the involvement of an intermediate – 71 out of 75 trajectories forming 7 from 18 involve a significant oscillation of the incipient C2-Cβ bond distance before forming 7, and these trajectories take longer than forming 8 (median of 342 fs versus 178 fs for forming 7). Still, few trajectories are caught in the area of the intermediate to the time limit of 500 fs.

A final remarkable observation is the large number of trajectories recrossing to afford the reactants on both the mPW1K and B3LYP surfaces, particularly for the diphenylketene reaction. These trajectories typically form the C1-Cα bond completely, passing through the area of 11 or 13, then run into a potential energy “wall” associated with a short C1-Cα internuclear distance and bounce back to starting materials. The recrossing may be understood in statistical terms on the B3LYP surface, viewing 13 as an intermediate that may partition in three ways, including going back to starting materials. However, the extensive recrossing from the area of 11 on the mPW1K surfaces is problematical to rationalize statistically. Of 23 trajectories started statistically in the area of 11 on the mPW1K/6−31G* surface, 12 afforded 3, 10 afforded 4, and only one afforded cyclopentadiene plus diphenylketene. This supports the idea that the recrossing seen above in trajectories starting from 11 is non-statistical. The congruence of these results with experimental observations will be discussed below.

Should solvent collisions impact the non-statistical recrossing? The efficiency of the recrossing should depend on the rate at which energy is lost from a normal mode associated with the C1-Cα stretch, either due to IVR or solvent collisions. In 11, this mode has a frequency of 634 cm⁻¹. The loss of energy from such modes in solution should be dominated by IVR and occur at a time scale on the order of picoseconds.⁵⁵ The median time for recrossing trajectories at the mPW1K/6−31+G** level, from their start at 9 to a C1-Cα separation > 2.4 Å, was 112 fs, and the time available for energy loss is so short that the recrossing in gas-phase trajectories should be negligibly affected in solution.

Discussion

The discussion here starts by considering the difficulty of reconciling the experimental results with any standard mechanistic scheme, largely ignoring the theoretical results. It then considers which of the calculational methods is more coherent with experiment, and discusses how a consistent mechanism can be described once dynamic trajectories are taken into account. Finally, we discuss how these results complicate the understanding of the selectivity, rate, isotope effects, and mechanism of cycloadditions.

Possible Mechanisms and an Experimental Paradox

Figure 10 shows a series of possible kinetic mechanisms for the cycloaddition of cyclopentadiene with diphenylketene. In Figure 10a, 3 and 4 are formed concurrently and irreversibly (or effectively so) via separate transition states, and 3 is converted to 4 directly without reverting to the starting materials. This is the simplest mechanism that is consistent with the kinetic observations from the low-temperature NMR reaction. However, this mechanism is not consistent with the intramolecular KIEs of Figure 3a, as a substantial relative KIE at C1 would be expected (as actually observed in the dichloroketene reaction in Figure 3b). The same problem would apply to any more complicated variation of this mechanism in which initial attack of the ketene on the diene is rate limiting. This mechanism also receives no theoretical support.

Figure 10.

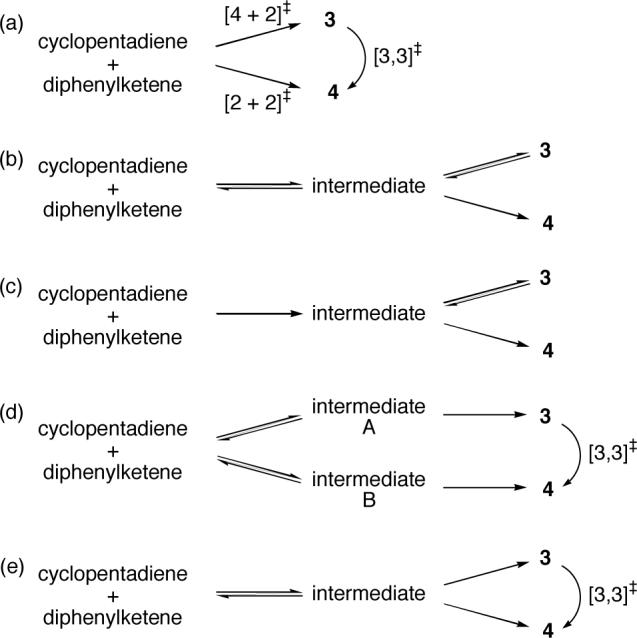
Limiting kinetic mechanisms for the reaction of cyclopentadiene with diphenylketene. Single arrows imply that a step is effectively irreversible under the reaction conditions, while paired arrows imply reversibility.

Figures 10b and 10c depict limiting mechanisms in which an intermediate is formed followed by partitioning to the two products and the rearrangement of 3 to 4 passes through the intermediate. In 10b, formation of both 3 and 4 from the intermediate would be slow and the intermediate would predominantly fragment to starting materials. In 10c, intermediate formation from starting material is irreversible. A mechanism in between 10b and 10c, involving competitively rate-limiting steps, could also be envisioned. The pathway in 10b is essentially that predicted by B3LYP calculations, when viewed in a standard way ignoring trajectories. Our NMR kinetic observations, showing that rearrangement of 3 to 4 occurs principally or exclusively by a direct process, rule out a majority contribution from mechanism 10b. The mechanism in 10c is consistent with the NMR results, as the rearrangement of 3 to 4 would occur without involving reversion to starting materials. However, if 10c were the majority mechanism, the intramolecular KIEs for 4 would reflect the C1-Cα bond forming step and should not so drastically differ from those for 7.

Many more complicated kinetic mechanisms can be considered – Figures 10d and 10e show two examples. To account for the experimental results, these mechanisms have the key feature that the rearrangement of 3 to 4 occurs without crossing the path of the intermediates involved in the cycloaddition. In 10d, two transition states lead to two distinct intermediates, with each intermediate forming a single product, either 3 or 4. In 10e, reversible formation of a single intermediate is followed by irreversible formation of 3 and 4. We cannot exclude kinetic mechanisms like these - they are clearly consistent with experiment. However, a difficulty arises when filling in the details of such mechanisms, as they invariably must involve three geometrically similar but distinguishable transition states; one for the formation of 3, the second for formation of 4, and the third for the [3,3] sigmatropic rearrangement. We have been unable to concretely envision such mechanisms involving three similar but distinct transition states, and calculations provide no support for such a possibility. For example, in the B3LYP calculations the rearrangement passes through the same intermediate as formed initially in the cycloaddition process, and we were unable to locate an alternative rearrangement mechanism.

Overall, the experimental results present a paradox, irresolvable by a standard view of the reaction mechanism. The paradox will be resolvable once trajectories are taken into account.

Evaluation of the Calculational Methods

The B3LYP and mPW1K methods make descriptively distinct predictions for the cycloadditions of cyclopentadiene with ketenes. Which is more accurate? A variety of experimental observations aid this evaluation.

The KIEs observed in the reaction of dichloroketene with cyclopentadiene support the mPW1K calculations over the B3LYP, as the former lead to much more accurate predictions of the experimental KIEs. The mPW1K calculations predict a lower barrier to the cycloaddition and an earlier transition structure (cf. 16 versus 18), resulting in a lower ¹³C KIE at C1 that is more consistent with the observed value. The barrier for the dichloroketene reaction is not known, so it is unclear which method is more accurately predicting the barrier in this case, but in the diphenylketene reaction the rate constant of ≈5 × 10⁻⁴ M⁻¹s⁻¹ at 253 K corresponds to a ΔH^‡ barrier of ≈8.4 kcal/mol, assuming a ΔS^‡ of ≈-40 e.u.⁵⁶ The mPW1K/6−31+G** barrier is closer than the B3LYP/6−311+G** barrier by 4.8 kcal/mol, though it still overestimates the phenomenological enthalpy barrier.

For the overall thermodynamics of the reaction, the B3LYP calculations perform very poorly. After allowance for an entropy estimate (25 °C, unscaled harmonic frequencies), the B3LYP/6−311+G** calculations place the [2 + 2] product 4 at 4.1 kcal/mol above cyclopentadiene + diphenylketene at standard state. This conflicts with the manifest experimental observation that 4 is formed and is stable. This error is in line with recent observations.⁴⁸ The mPW1K/6−31+G** calculations predict that the formation of 4 is exergonic by 8.3 kcal/mol.

One critical issue to consider is the mechanism of the [3,3]-sigmatropic (Claisen) rearrangement of 3 to 4 or 8 to 7. The B3LYP calculations predict that this rearrangement proceeds by a loose stepwise mechanism, while the mPW1K calculations predict a tighter concerted process. In this regard, it should be noted that for the parent Claisen rearrangement of allyl vinyl ether, B3LYP calculations predict a transition structure that is too loose versus KIEs or higher-level calculations.^53b The mPW1K/6−31+G** transition structure for the parent Claisen (see Supporting Information) closely resembles the KIE-supported MP2, MP4, and QCISD transition structures.

Overall, from these considerations, it would be expected that the mPW1K energy surfaces more accurately represent the experimental reactions. The critical question then is whether the mPW1K surfaces can account for three key observations here: the KIEs, the direct formation of 4, and the direct rearrangement of 3 to 4.

A Consistent Picture of the Mechanism from Trajectories

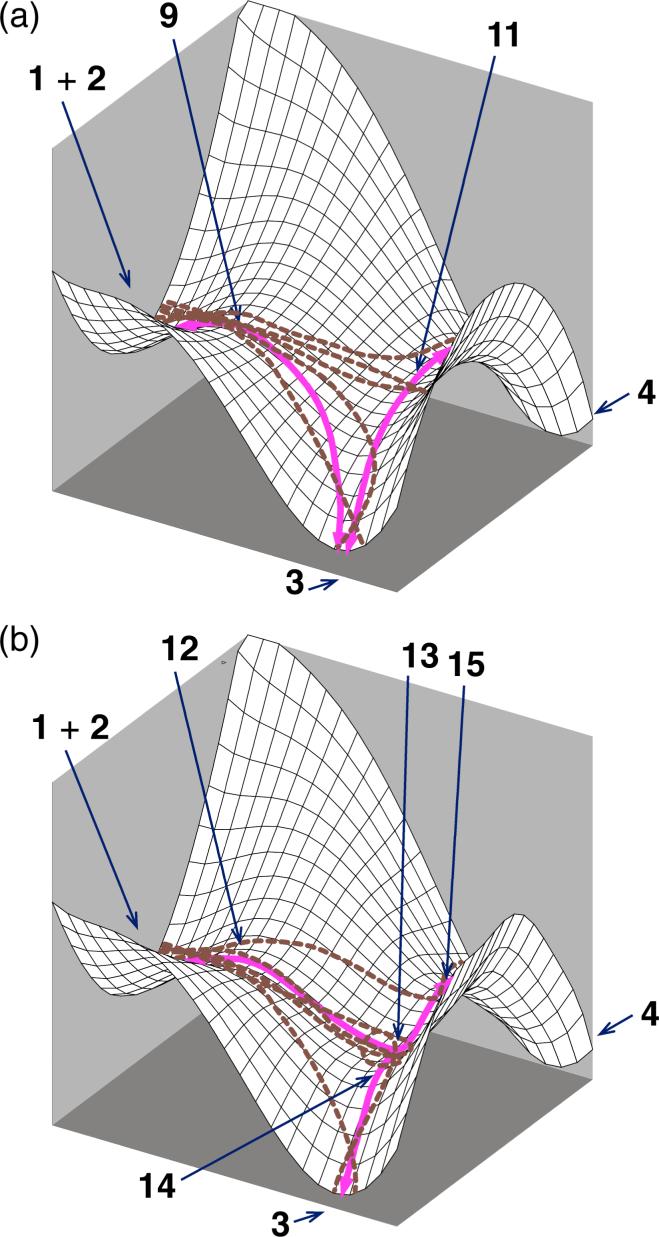
The observed formation of 4 without the intermediacy of 3 appeared inconsistent with the mPW1K surfaces, on which the only low-energy transition structure (9) leads by an MEP to 3. However, the trajectory studies show that both 3 and 4 can be formed from 9. Thus, the trajectories resolve the contradiction between experiment and theory.

The formation of 4 from 9 can be understood by consideration of the qualitative potential energy surface in Figure 11a. The MEP emanating from 9 passes near 11, and trajectories occasionally end up on the “[2 + 2] side” of saddle point 11. Both 3 and 4 are downhill from 9, so it should not be surprising that trajectories can afford either. The proportion of trajectories through 9 forming 4 is low (4:3 is 4:67 at 6−31G*, 1:8 at 6−31+G**) versus experiment (4:3 is approximately 1:4.5) but from the necessarily limited trajectories, the statistical uncertainty in the predicted product ratio is high. The critical observation is that some trajectories afford 4.

Figure 11.

Qualitative potential energy surfaces for reaction of cyclopentadiene with diphenylketene (1 + 2). Solid lines are the MEP and dashed lines are possible trajectories. (a) On the mPW1K surface, there is no intermediate and no transition state leading directly from starting materials to 4. However, 4 can be formed from trajectories passing through 9. (b) On the B3LYP surface, the MEP passes into shallow intermediate 13. Trajectories may bypass this intermediate to afford 3 directly.

The mPW1K/6−31G* and mPW1K/6−31+G** surfaces predict that the barrier for rearrangement of 3 to 4 via 11 is lower than the barrier for cycloreversion to starting materials via 9, so the mPW1K calculations appear to naturally account for the experimental direct conversion of 3 to 4. However, the picture is complicated by entropy, from a thermodynamic perspective, or by the possible trajectories, from a dynamical perspective. After taking into account an entropy estimate at 253 K (based on the harmonic frequencies), the direct rearrangement is favored by only 0.2 − 0.5 kcal/mol (60−74% direct rearrangement at 253 K). The observation that a trajectory started statistically in the area of 11 can occasionally eschew downhill product formation in favor of cycloreversion suggests that the exit channel to starting materials is dynamically broad. From either perspective, then, the expectation is that some minor portion of 3 would revert to starting material before forming 4. The experimental observations are consistent with this, though most of the conversion of 3 to 4 is direct.

The intramolecular ¹³C and ²H KIEs for the diphenylketene reaction seem impossible to reconcile in a standard way with the mPW1K absence of an intermediate, but the trajectory studies suggest a solution to this riddle. A starting point is the differing amounts of recrossing with diphenylketene versus dichloroketene. With dichloroketene, only 10 − 14% of the trajectories started forward from the area of 16 revert to starting materials. From this, it would be expected that the trajectories should have little to no impact on the KIEs for the formation of 7. This is apparently observed, as there is a good correlation between the experimental and predicted KIEs for the formation of 7.

With diphenylketene, however, a large portion of the trajectories started forward from 9 recross to starting materials (44% at 6−31G*, 63% at 6−31+G**). In this case, the experimental KIEs should not match with those predicted from transition structure 9, as observed. No rules let us predict the KIEs in these circumstances – TST cannot be applied as there are no transition states that serve as barriers passing from 9 to products. However, the trajectories suggest that the “decision” to form product versus revert to starting material is made in the area around transition structure 11. The experimental KIEs, allowing for their relative nature, are quite close to those predicted KIEs for 11, supporting the idea that reactive versus non-reactive trajectories are decided in this area.

An alternative mechanism deserves mention. In this section we have rationalized observations by invoking dynamic effects in the initial cycloaddition process, treating the rearrangement of 3 to 4 as a standard reaction. An alternative would be to have the cycloaddition process occur stepwise through an intermediate in a standard way, then invoke a dynamic effect to explain the predominantly direct rearrangement of 3 to 4. That is, the mechanism of Figure 10b could perhaps act like that of Figure 10e due to Carpenter-like dynamic matching⁶ in the rearrangement process. This would be reasonably consistent with experimental observations, though it is not supported by the mPW1K calculations.

Implications Regarding the Understanding of Periselectivity

FMO theory provides predictions for the rates and selectivity of cycloadditions based on HOMO-LUMO interactions. Many specific reactions provide exceptions to the predictions of FMO theory,⁵⁷ as might be expected for any model using starting-material orbitals to explain transition state energies. The complication added here is that even transition state orbital interactions do not necessarily define the product of a cycloaddition.

Within FMO theory, the regiochemistry and periselectivity of a cycloaddition are decided by the interaction of the largest coefficient of the HOMO of one addend with the largest coefficient of the LUMO of the other addend.⁵⁸ Transition states derived from the reaction of unsymmetrical addends tend to be asynchronous, with leading bond formation between the centers that had the largest HOMO or LUMO coefficients and a weaker bonding interaction at the opposite end of the transition state. This disparity in interactions in an asynchronous cycloaddition extends to atomic motions - the predominant motions in the transition vector for an asynchronous cycloaddition involves the centers leading in the bond formation, with often very little approaching motion for the centers at the other end.⁵⁹ On the end of an asynchronous cycloaddition for which bonding is less advanced, the centers involved are not necessarily dynamically committed to bond formation.

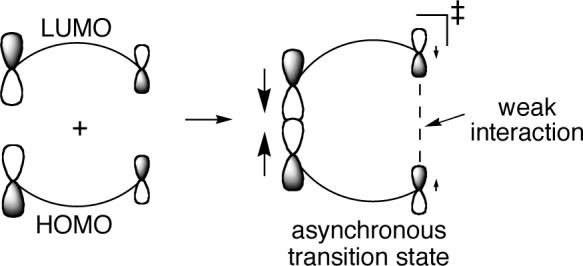
This idea allows a complication to arise in the periselectivity of cycloadditions. When an asynchronous transition state has available an alternative bonding interaction, two product structures may be downhill from the cycloaddition transition state. If there is no barrier to cross in the formation of either product, the periselectivity may be determined by the vagaries of dynamical motion. A steepest-descent path is likely to lead to the major product, but there is no simple way to predict the product ratio or relate it to the transition state orbital interactions.

These concepts provide insight into the cycloaddition of ketenes with cyclopentadiene. The low-energy π*_C=O of the ketene has its largest coefficient at Cα, and the asynchronous cycloaddition transition state may be viewed as resulting from the interaction of Cα with the HOMO of the diene at its large C1 coefficient. At the transition state, the interaction between the carbonyl oxygen and C4 of the diene is weak, and an alternative interaction can lead to the [2 + 2] product. If the “strength” of these interactions is judged by the dynamical outcome, then in the dichloroketene case the interactions are closely balanced, and either product may be formed. In the diphenylketene reaction, the C4-O interaction appears “stronger”, as the [4 + 2] product is major.

However, neither the dynamical outcome nor the MEP is a direct measure of transition state orbital interactions. This is highlighted by an atoms-in-molecules analysis⁶⁰ of 9 and 16 (as their 6−31+G** variants). In each case, there was no bond path between Cβ and C2, and, most interestingly, a C4-O bond path was found for 16 but not 9. It should be recalled that the MEP and a majority of trajectories from 16 with this basis set affords [2 + 2] product 7, effectively ignoring the C4-O bond. On the other hand, within the atoms-in-molecules formalism there is no C4-O bonding in 9, but the experimental product ratio reflects a significant dynamical preference for formation of this bond. Both observations

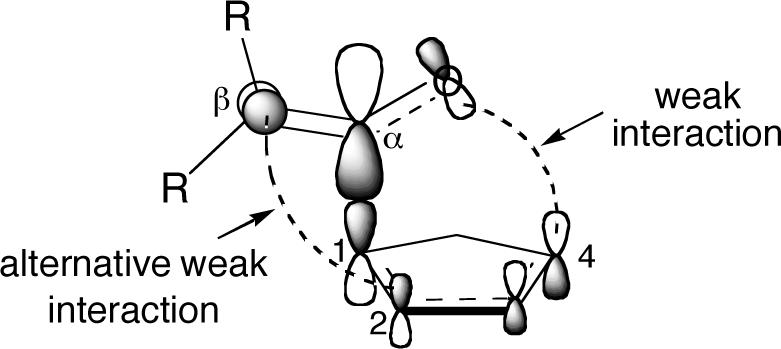
support the idea that the periselectivity does not necessarily reflect transition state orbital interactions.

Non-statistical Recrossing and Isotope Effects. No Transition State!

With the exception of hydrogen transfer reactions, the combination of conventional TST and a one-dimensional tunneling correction affords excellent predictions of heavy-atom KIEs (provided that the underlying theoretical mechanism is accurate).^53,61,62,43 When a reaction is enthalpically barrierless or involves a potential-energy saddle point in a nearly flat region of the energy surface, the effect of recrossing is often substantial and conventional TST is inadequate. In such cases, variational TST, which effectively allows for statistical recrossing, has provided good predictions of heavy-atom KIEs.⁶³

The results here suggest that non-statistical recrossing can also have a substantial effect on experimental observations. When recrossing is low, as in the dichloroketene trajectories, the observed KIEs reflect the conventional transition state. In the diphenylketene reaction, many of the mPW1K trajectories recross, and the experimental KIEs differ greatly from those predicted from conventional TST for 9. In perspective, the effect of non-statistical recrossing on the absolute rate of the reaction is small – even if 90% of trajectories recrossed, the rate effect is small compared to the exponential effect of barrier energy – so no readily recognizable effect of recrossing would be seen in the experimental rate. However, the recrossing is potentially much more easily recognized from the KIEs, or conversely, it appears that non-statistical recrossing must sometimes be taken into account to interpret KIEs. In this regard, it is perhaps notable that the prediction of KIEs for simple S_N2 reactions has proven surprisingly difficult,⁶⁴ since Hase has found that S_N2 reactions are subject to non-statistical recrossing.^4,5

The most fundamental idea in TST is that there exists a hypersurface, the transition state, dividing starting materials from products for defining reactive trajectories. In generalized TST, the hypersurface can be placed anywhere along the reaction coordinate, but a transition state is only useful for understanding rates or KIEs or selectivity if the transmission coefficient does not depart too drastically from unity. Useful transition states may be pursued in various ways – in variational TST, the position of a coordinate-space hypersurface transverse to the MEP is adjusted to minimize crossing, while microcanonical variational TST makes use of an energy-dependent continuum of hypersurfaces - but the ability to delineate a useful dividing hypersurface is a critical component of TST.

Because trajectories entering the area of 11 from starting materials tend to revert to starting materials, while statistical trajectories in the area of 11 tend to form 3 or 4, we cannot envision how a useful and tractable dividing hypersurface can be delineated in coordinate space for the reaction of cyclopentadiene with diphenylketene. It is perhaps possible that allowing for the momenta of atoms, a dividing surface could be manageably defined in phase space, but this is not within the realm of current versions of TST. Within current theory, there is no experimentally- or dynamically-consistent transition state for the cycloaddition of cyclopentadiene with diphenylketene.

Structurally, the presence of a bifurcating surface as in Figure 11a would not seem to be required for non-statistical recrossing. Rather, the key feature seems to be that the reaction involves two bond-forming processes, one of which is not “set up” at the transition state. In such circumstances, a reaction may fail to dynamically consummate an asynchronous pericyclic process after successfully completing the first bonding change. This could make non-statistical recrossing more common in complex reactions than in the simple reactions typically studied dynamically.

Bypassing Intermediates and the Mechanism of Cycloadditions

Although the B3LYP surface appears to be inaccurate in these reactions, the intriguing observation that many trajectories on this surface bypass the intermediates 13 and 19 requires some further comment. The outcome of these trajectories may be understood with reference to the qualitative potential energy diagram in Figure 11b. The intermediate 13 is a shallow dip in the potential energy surface, forward from the transition structure 12 on the MEP. However, the product 3 is also downhill from 12, so a portion of the trajectories proceed directly from 12 to 3. The great majority (about 72 out of 81) of the trajectories do indeed pass through the area of 13, but most end up recrossing 12 to starting materials. The formation of 3 on this surface depends substantially on trajectories being able to occasionally bypass 13.

We have recently reported that for an ene reaction, trajectories emanating from a formally “concerted” transition structure (a transition structure in which the MEP leads directly to the final product) often lead to the intermediate for a stepwise mechanism.³⁰ In the ene-reaction case, a stepwise mechanism can occur even though an arbitrarily accurate standard analysis would conclude it to be concerted. The opposite is observed here for the B3LYP trajectories, that is, a standard theoretical analysis would describe the mechanism as stepwise, but around half of the reactive trajectories act concerted.⁶⁵ The lesson from these observations, as well as other studies,^{6,7,8,12,28,66,67} is that the classical division of multibond reactions into stepwise versus concerted mechanisms is often an oversimplification. A majority of cycloadditions and related reactions are likely to be mechanistically simple, but for reactions approaching a stepwise/concerted boundary – just those cases where the question of concert is most interesting – the consideration of trajectories will often be essential to understanding the mechanism.

Conclusions

Mechanistic understanding starts with qualitatively accounting for the products. It is easy to understand the [4 +2] products 3 and 8 from the cycloaddition of ketenes with cyclopentadiene. The C=O π* is the lowest energy LUMO, the C=O is unhindered, and [4 + 2] cycloadditions are of course allowed pericyclic reactions with thousands of examples. It is much more difficult to understand the direct formation of the [2 + 2] cycloadduct 4 – the C=C of the ketene is not electron poor, and it is sterically hindered. A standard calculational analysis provides no help in understanding the formation of 4, as there is no low energy transition structure that leads by an MEP to 4. Nonetheless, it has been shown here that 4 is formed directly, at a rate that is amazingly competitive with the formation of 3.

How? One might try to explain this with a stepwise mechanism, but contradictions arise when one tries to propose a standard mechanism that also reconciles the direct conversion of 3 to 4 and the KIEs. The formation of 4 becomes understandable only once it is recognized that a single transition state can afford dynamically both [4 + 2] and [2 + 2] products. The most dramatic result here is that the mPW1K trajectories can account for a product in an ordinary cycloaddition that would otherwise be inexplicable.

A second mystery is presented by the KIEs. The rate-limiting step for the dichloroketene reaction involves C1-Cα bond formation, and TST performs well in accounting for the ¹³C KIEs. However, the ¹³C KIEs for the diphenylketene reaction are quite different. Supported by Holder's ²H KIEs,⁴² they appear to require a rate-limiting step that follows reversible formation of an intermediate. Yet the conversion of 3 to 4 must somehow eschew this intermediate, or else pass through starting materials. We can define no standard mechanism that fits both sets of results, and standard calculational analyses provide no helpful suggestions.

Once again, however, trajectories account for the observations. The predicted extensive recrossing to starting materials would effectively delay the cycloaddition's isotopic discrimination toward an area of the surface where the C1-Cα bond is fully formed, accounting for the KIEs. Because the recrossing is non-statistical, it can be independent of the rearrangement, even though the two involve similar areas of the energy surface. The trajectory-predicted failure of transition state theory regarding the rate of the reaction is too small to be experimentally gauged, but the observable impact on KIEs is potentially of great importance to their interpretation.

The role of trajectories in deciding the products, selectivities, rates, isotope effects, and mechanism of these reactions is all perhaps intellectually unsatisfying. The simple model of transition state theory has tremendous predictive value and provides insight. Chemists tend to equate the rates and selectivities and isotope effects for reactions with the properties of transition states, and implicitly assume that the product formed is fully defined by the transition state geometry and its orbital interactions. When instead, product selectivity depends on the details of trajectories on a dimensionally broad energy surface, the complexity of chemistry seems daunting. For example, it is disconcerting that after both experimentally and calculationally characterizing the transition state for the dichloroketene reaction, we still do not know the major initial reaction product. However, fully understanding the role of trajectories in complex reactions should prove an intriguing intellectual challenge for the future.

Experimental Section

NMR Study of the Cycloaddition of 1 with 2

A 0.038 M solution of 2 in CD₂Cl₂ was prepared, and 0.7887 g of this solution was placed in the 5 mm NMR tube to fill it to 4.5 cm. The tube was placed in a 400 MHz NMR and the probe was brought to −20° C, then tuned and shimmed. The system was left for 1 h at −20° C, and the instrument was reshimmed. The reaction was started by a series of operations involving rapidly ejecting the NMR tube, adding 100 μl of cyclopentadiene (pre-cooled at −78 °C), shaking the tube, reinserting the tube in the NMR, and immediately acquiring a spectrum, taking a total time of 90 s. After the initial spectrum and periodically throughout the experiment the NMR was shimmed. Additional spectra were acquired after 8, 10, 15, 20, 27, 30, 45, 60, 75, 90, 105, 120, 165, 720, 965, 1200, and 1440 min. The observed compositions were fit to possible kinetic schemes as described in the Supporting Information.

NMR Measurements

The preparation of samples of the known compounds 4 and 7 for NMR analysis is described in Supporting Information. NMR samples were prepared using 223.5 mg of 4 or 300 mg of 7 in a 5-mm NMR tube filled to a 5-cm sample height with CDCl₃. The ¹³C spectra of 4 were recorded at 125.7 MHz using inverse gated decoupling, 60 s delays between calibrated π/2 pulses, and a 6.4 s acquisition time to collect 512,000 points. Spectra of 7 were recorded at 100.577 MHz using 200 s delays and a 5 s acquisition time to collect 290,000 points. Integrations were determined numerically using a constant equal integration region for peaks compared. A zeroth-order baseline correction is generally applied, but in no case was a first-order (tilt) correction applied. Six spectra were obtained for each of two independent samples of 4, and six and 12 spectra were obtained for two independent samples of 7. The results in Figure 3 were obtained from the ratios of compared peaks in each spectrum, with the 95% confidence limits calculated in a standard way.