The Phase Shift Index for Marking Functional Asynchrony in Alzheimer’s Patients by fMRI

Abstract

Our previous study suggested that the functional MRI (fMRI) COSLOF Index could be used as a quantitative biomarker for Alzheimer’s Disease (AD). The fMRI COSLOF Index in the AD group was the lowest (0.13±0.10), followed by the mild cognitive impairment (MCI) group (0.20±0.05) and then, the control group (0.34±0.09). The current study continues an investigation into which of the following two factors has a dominant role in determining the COSLOF Index: the ratio of signal to noise or the phase shift of the spontaneous low-frequency components (SLFs). By using a theoretical model for the SLFs, it is demonstrated that the normalized COSLOF Index does not depend on the SNR of the SLFs. Further analysis shows that by taking the ratio of the cross-correlation coefficient to the maximum-shifted cross-correlation coefficient, the SNR factor can be canceled. Therefore, the determination of the Phase Shift Index (PSI) method is independent of the SNR and the PSI provides an accurate measure of the phase shift between the SLFs. By applying this PSI method to the normal control, MCI, and AD groups of the subjects, experimental results demonstrated that the PSI in the AD group was the highest (72.6°±11.3°), followed by the MCI group, (58.6°±5.7°), and, finally, the control group (40.6°±8.4°). These results suggest that the larger the PSI value, the more the asynchrony exists between SLFs.

INTRODUCTION

Alzheimer’s Disease (AD), a progressive neurodegenerative disorder characterized by neuritic plaques and neurofibrillary tangles in the human brain, occurs decades before clinical symptoms manifest. Mild cognitive impairment (MCI) is considered the prestage onset of AD, and those with MCI are at greater risk to develop Alzheimer’s Disease [1]. Current research has emphasized the need to determine early biomarkers, thereby facilitating the detection and/or monitoring of early brain changes suggestive of AD and MCI. Also, it promotes early intervention studies to hinder or slow disease progression [2]. Recent developments in functional MRI (fMRI) technology with high spatial and temporal resolution have made it possible to study early AD by noninvasively detecting the spontaneous low-frequency (SLF) oscillations (< 0.1 Hz) in the hippocampus of the human brain [3]. The hippocampus region is considered to be one of initial loci for AD. Neuropathological changes are thought to begin in the hippocampal formation and become severe with disease progression [4,5].

The characteristics of AD progression in the hippocampus region, together with the detection of SLF patterns, provide the foundation for the introduction of fMRI Indices as a preclinical biomarker for the disease. The previous fMRI Index, abbreviated as the COSLOF Index, was introduced to quantify the change in functional synchrony between pairs of voxel time courses. The COSLOF Index was defined as the mean of the cross-correlation COefficients of Spontaneous LOw Frequency between possible pairs of voxel time courses in the hippocampus of the human brain. We have demonstrated that the subjects with AD had a significantly lower COSLOF Index value than age-matched cognitively healthy elderly subjects.

The current study is a continuation of our previous work to quantitatively characterize and neurophysiologically understand the COSLOF Index. There are two factors that may affect the cross-correlation between two voxel time courses: the signal to noise ratio of the SLFs and the phase shift between the two voxel time courses. We will examine how these factors affect the cross-correlation coefficient and the COSLOF Index. When we evaluated the phase shift between the voxel time courses of the SLFs in the hippocampal region, we revealed that the Phase Shift Index (PSI) was a more sensitive marker of AD than the COSLOF Index.

THEORY

In a previous study, we utilized the COSLOF Index (CI) in the hippocampus region as a noninvasive biomarker to evaluate the preclinical stage of AD [3]. The CI is calculated from a matrix of the pairwise cross-correlation coefficients of all of the voxels within a region of interest (ROI). To focus on the SLFs, voxel time courses are convolved with a 9-point Hamming filter that has a passband of 0.015~0.1 Hz [3]. According to previous studies [6–8], the SLF has characteristics of a BOLDlike signal in physiological noise. In a given voxel, the signal at time t is expressed as:

$$s(t)=s_L(t)+n_0(t)$$ (1)

where the underlying SLF is s_L(t) and measurement noise is n₀(t). The cross-correlation coefficient cc_ij between the i^th and j^th voxels (i, j = 1, 2, …, K, i ≠ j, K is the number of voxels in the ROI) is calculated between voxel time courses s_i(t) and s_j(t) as:

$${\mathit{\text{cc}}}_{ij}=\frac{{\displaystyle {\sum }_{t=1}^N\left(s_i(t)·s_j(t)\right)}}{\sqrt{{\displaystyle {\sum }_{t=1}^N{\left(s_i(t)\right)}^2}}·\sqrt{{\displaystyle {\sum }_{t=1}^N{\left(s_j(t)\right)}^2}}}=\frac{{\displaystyle {\sum }_{t=1}^N\left(s_i(t)·s_j(t)\right)}}{{\widehat{\sigma }}_i·{\widehat{\sigma }}_j}$$ (2)

with t = 1, …, N. In Eq. (2), it is generically assumed that the voxel time courses have a mean of zero and are demeaned following filtering. The previously published CI that has been established as a preclinical biomarker for AD is defined as:

$$\mathit{\text{CI}}=\frac{2}{K(K-1)}{\displaystyle \sum _{i,j=1,i>j}^K{\mathit{\text{cc}}}_{ij}.}$$ (3)

Two factors may affect the cross-correlation between two voxel time courses: the signal to noise ratio of SLFs and the phase shift between the two voxel time courses. First, we examine the variation in the ratio of the SLFs to thermal noise and determine how a change in them might produce modifications in the cross-correlations and hence, COSLOF Indices. In the model presented in Eq. (1), the mean and variance of s_L(t) are assumed to be zero and ${\sigma }_L^2$, the mean and variance of n₀(t) to be zero and ${\sigma }_0^2$. The two components s_L and n₀ are independent so that cov(s_L,n₀)=0. The cross-correlation in Eq. (2) turns out to be:

$${\mathit{\text{cc}}}_{ij}=\frac{{\widehat{\sigma }}_{ij}}{\sqrt{\left({\widehat{\sigma }}_{Li}^2+{\widehat{\sigma }}_{0i}^2\right)\left({\widehat{\sigma }}_{Lj}^2+{\widehat{\sigma }}_{0j}^2\right)}}$$ (4)

where ${\widehat{\sigma }}_{ij}$ is the sample covariance between voxels i and j, while ${\widehat{\sigma }}_i^2={\widehat{\sigma }}_{Li}^2+{\widehat{\sigma }}_{0i}^2\text{and}{\widehat{\sigma }}_j^2={\widehat{\sigma }}_{Lj}^2+{\widehat{\sigma }}_{0j}^2$ are the sample variances in voxels i and j with constituents ${\widehat{\sigma }}_L^2\text{and}{\widehat{\sigma }}_0^2$ due to SLFs and thermal noise. It is immediately apparent that the thermal noise variance ${\widehat{\sigma }}_0^2$ that is estimated in each voxel and stochastically equivalent will affect the cross-correlation coefficient. According to Eq. (4), a higher signal to noise ratio (SNR), $\widehat{\eta }={\widehat{\sigma }}_L/{\widehat{\sigma }}_0$, may lead to higher cross-correlation coefficients, and higher COSLOF Indices. Since the SNR is a subject/scan specific factor, it may affect a comparison of the COSLOF Indices between subjects or between groups of subjects.

Based on this characteristic of the SLFs in the SNR, a cross-correlation coefficient without the impact of SNR variation can be obtained by normalizing the cc_ij to noise ${\widehat{\sigma }}_0^2$ in Eq. (4). The normalized cross-correlation coefficient ncc_ij is defined as:

$${\mathit{\text{ncc}}}_{ij}={\mathit{\text{cc}}}_{ij}·\frac{\sqrt{{{\widehat{\eta }}_i}^2+}1·\sqrt{{{\widehat{\eta }}_j}^2+1}}{{\widehat{\eta }}_i·{\widehat{\eta }}_j}$$ (5)

and the normalized COSLOF Index can be estimated as:

$$\mathit{\text{nCI}}=\frac{2}{K(K-1)}·{\displaystyle \sum _{i,j=1,i>j}^K\left({\mathit{\text{cc}}}_{ij}·\frac{\sqrt{{{\widehat{\eta }}_i}^2+1}·\sqrt{{{\widehat{\eta }}_j}^2+}1}{{\widehat{\eta }}_i·{\widehat{\eta }}_j}\right)}$$ (6)

To reduce the complexity of the computation, we assume the SNR η_m is identical in all voxel time courses within an ROI and is obtained as a sample mean signal to noise ratio over the ROI as:

$${\widehat{\eta }}_m=\frac{1}{K}{\displaystyle \sum _{i=1}^K{\widehat{\eta }}_i,}$$ (7)

Then, the normalized COSLOF in Eq. (6) is approximately simplified as:

$$\mathit{\text{nCI}}\approx \frac{{{\widehat{\eta }}_m}^2+1}{{{\widehat{\eta }}_m}^2}·\frac{2}{K(K-1)}·{\displaystyle \sum _{i,j=1,i>j}^K{\mathit{\text{cc}}}_{ij}.}$$ (8)

The validation of these approximations is provided by Monte Carlo simulations in the Appendix B.

Another factor that may affect the cross-correlation between two voxel time courses is the phase shift. To estimate the phase shift, we first model the SLFs by assuming two voxel time courses contain an identical frequency component f_c. The i^th voxel time course in Eq.(1) becomes:

$$s_i(t)={\eta }_i\sqrt{2}{\sigma }_0\text{sin}(2\pi f_c·t+{\theta }_i)+n_i(t).$$ (9)

where η_i is the SNR, θ_i is the phase of the frequency f_c, and σ₀ is the standard deviation of thermal noise. Then, the phase shift between the SLF signals in two voxel time courses can affect the value of the cross-correlation. With this simplification, Eq. (4) can be rewritten as:

$${\mathit{\text{cc}}}_{ij}=\frac{{\eta }_i{\eta }_j·\text{cos}({\theta }_{ij})}{\sqrt{{{\eta }_i}^2+}1·\sqrt{{{\eta }_j}^2+1}}$$ (10)

where θ_ij is the phase shift between SLF signals and is equal to |θ_i−θ_j|. Full synchrony between two signals, i.e. the zero phase shift between SLFs, can be reached by shifting one voxel time course by τ^m. Here, τ^m is the number of time points shifted to obtain a maximum cross-correlation between voxel time courses i and j, as shown below:

$${\tau }^m=\text{arg}\left(\underset{0<\tau <T}{\text{max}}\frac{{\displaystyle {\sum }_{t=1}^N\left(s_i(t)·s_j(t+\tau )\right)}}{\sqrt{{{\eta }_i}^2+1}·\sqrt{{{\eta }_j}^2+1}}\right),0<\tau <\frac{1}{f_L}$$ (11)

where f_L = 0.015 Hz, which is the lower limit of the passband of the filter, and T is 1/f_L/TR (TR is the repetition time of acquisition). Then, the maximum-shifted cross-correlation coefficient (mcc) becomes:

$${\mathit{\text{cc}}}_{ij}^m=\frac{{\displaystyle {\sum }_{t=1}^N\left(s_i(t)·s_j\left(t+{\tau }^m\right)\right)}}{\sqrt{{{\eta }_i}^2+1}·\sqrt{{{\eta }_j}^2+1}}=\frac{{\eta }_i{\eta }_j}{\sqrt{{{\eta }_i}^2+1}·\sqrt{{{\eta }_j}^2+1}}.$$ (12)

where we still assume the SLF signal is a single sinusoid function. Combining Eq. (10) and Eq. (12), the phase shift can be recovered immediately as:

$${\widehat{\theta }}_{ij}={\text{cos}}^{-1}\left(\frac{{\mathit{\text{cc}}}_{ij}}{{\mathit{\text{cc}}}_{ij}^m}\right).$$ (13)

For ROI evaluation, the phase shift can be estimated as:

$${\widehat{\theta }}_G=\overline{{\theta }_{ij}}=\frac{2}{K(K-1)}{\displaystyle \sum _{i,j=1,i\ne j}^K{\text{cos}}^{-1}\left(\frac{{\mathit{\text{cc}}}_{ij}}{{\mathit{\text{cc}}}_{ij}^m}\right)}.$$ (14)

To minimize the effect of nonuniformity of SNR in real data, it is suggested that the ROI Phase Shift be calculated as follows:

$$\begin{array}{cc}{\widehat{\theta }}_G\approx \hfill & {\text{cos}}^{-1}\left(\frac{\mathit{\text{CI}}}{{\mathit{\text{CI}}}^m}\right)\hfill \\ \hfill & {\mathit{\text{CI}}}^m=\frac{2}{K(K-1)}{\displaystyle \sum _{i,j=1,i>j}^K{\mathit{\text{cc}}}_{ij}^m}\hfill \end{array}$$ (15)

where CI^m is defined as the maximum-shifted COSLOF. The validation of this approximation between Eq. (14) and Eq. (15) is provided by theoretical derivation and Monte Carlo simulations in the Appendix B.

The ROI estimate in Eq. (14) is named the Phase Shift Index (PSI) to quantify the regional phase shift. Clearly, a larger phase shift leads to lower cross-correlation coefficients; and for an ROI, a larger PSI leads to a lower COSLOF Index value. It is also noteworthy that the PSI is a normalized index and not sensitive to noise factors, because the ratio of CI to CI^m canceled the noise factor in Eq. (10) and Eq. (12).

The above derivations are made based on the assumption that the SLFs in two voxel time courses contain an identical frequency component with different phases In reality, the SLF signal could contain more than one frequency component. Then, the i^th voxel time course in Eq. (1) can be decomposed as:

$$s_i(t)={\displaystyle \sum _{f\in F}{\eta }_f\sqrt{2}{\sigma }_0\text{sin}(2\pi f·t+{\theta }_i(f))+n_i(t)}$$ (16)

where f is the frequency bin, F is the set of available frequencies for SLF signal, η_f  is the uniform SNR of the SLF component for frequency f, θ_i(f) is the phase of f, and σ₀ is the standard deviation of thermal noise. Thus, Eq. (10) becomes:

$${\mathit{\text{cc}}}_{ij}=\frac{{\displaystyle \sum _{f\in F}{{\eta }_f}^2\text{cos}}\left({\theta }_{ij}(f)\right)}{{\displaystyle \sum _{f\in F}{{\eta }_f}^2+1}}.$$ (17)

where θ_ij(f) is the phase shift for frequency f, i.e. |θ_i(f)−θ_j(f)|, between two voxel time courses.

If the |θ_i(f)−θ_j(f)| is zero for all frequency components by shifting one voxel time course at τ^m, the maximum-shifted cross-correlation coefficient in Eq. (12) turns out to be:

$${\mathit{\text{cc}}}_{ij}^m=\frac{{\displaystyle \sum _{f\in F}{{\eta }_f}^2}}{{\displaystyle \sum _{f\in F}{{\eta }_f}^2+1}}.$$ (18)

Combining Eq. (17) and Eq. (18), the phase shift estimated in Eq. (13) becomes:

$${\widehat{\theta }}_{ij}={\text{cos}}^{-1}\left(\frac{{\mathit{\text{cc}}}_{ij}}{{\mathit{\text{cc}}}_{ij}^m}\right)={\text{cos}}^{-1}\left(\frac{{\displaystyle \sum _{f\in F}{{\eta }_f}^2\text{cos}\left({\theta }_{ij}(f)\right)}}{{\displaystyle \sum _{f\in F}{{\eta }_f}^2}}\right).$$ (19)

In practice, due to the limited length of the voxel time courses, the ${\mathit{\text{cc}}}_{ij}^m$ is obtained by experimentally shifting one voxel time course at τ^m and the obtained ${\widehat{\theta }}_{ij}$ is considered an equivalent phase shift.

For the ROI evaluation, the estimation of the phase shift in the presence of many frequency components in SLFs can be estimated according to Eq. (14) and Eq. (15). In this study, the parameters of the COSLOF Index, normalized COSLOF Index, and PSI are all estimated and employed to distinguish the differences among AD, MCI and normal control groups.

MATERIALS AND METHODS

Human Subjects

Fourteen AD patients (age: 72±6 yrs), eight subjects with MCI (age: 69±3), and 13 cognitively healthy controls (age: 68±4 yrs) were recruited from the Memory Disorders Clinic at the Medical College of Wisconsin. Informed consents were obtained from all subjects for this IRB-approved study. The detailed inclusion and exclusion criteria for the three groups of subjects (AD, MCI, and control), and the diagnoses of probable/possible AD and MCI subjects were described previously [3]. All cognitively healthy subjects underwent a set of cognitive examinations; none reported subjective symptoms of cognitive impairment, their Mini Mental Status Examination (MMSE) scores were 27/30 or higher, and their modified Hachinski scores were 4 or less. Functional MR imaging was performed within a maximum of two months of cognitive testing.

fMRI

All fMRI data acquisition was conducted on a GE Signa 1.5 Tesla scanner (GE Medical Systems, Milwaukee, WI) using a local gradient coil and an end-capped birdcage RF coil. Foam padding was used to limit head motion within the head coil. A single-shot, gradient-echo EPI sequence in the sagittal plane wasused with the imaging parameters: TR = 2 s, TE = 40 ms, FOV = 24 cm, slice thickness = 7 mm, and matrix = 64 × 64. A total of 15 sagittal slices and 180 images per slice were obtained in 6 min. In all MR imaging sessions, the corresponding 256 × 256 T₁-weighted 3D SPGR anatomic images were also acquired. During scanning, all subjects were in resting state (performing no tasks with eyes closed).

Data Analysis

All functional datasets were preprocessed to detect motion and remove linear trends. Four AD patients and four controls were excluded from further data processing due to excessive motion (> 1 mm). The detailed procedures used to locate the hippocampus region and select the hippocampus voxels from EPI dataset have been previously described in detail [3,9]. Specifically, the left and right hippocampus were manually identified on the T1-weighted 3D SPGR images, according to Duvernoy [10]. The most anterior boundary of the hippocampus adjoins the ventral of the amygdala and the dorsal border is formed by the dorsal cerebrospinal fluid of the temporal (inferior) horn of the lateral ventricle and alveus. Its ventral border is formed by the white matter of the parahippocampal gyrus. The posterior cerebrospinal fluid and choroids plexus of the trigone of the lateral ventricle form the dorsal and posterior border of the hippocampus. Tracing was performed on all relevant sagittal slices with a mouse-controlled cursor, with boundaries displayed in real time on the MRI slices. Also, they were displayed in the remaining orthogonal slices. Then, these masks were transformed to the Talairach space. Since the spoiled GRE images had 1.1-mm spatial resolution and the functional MR images had 3.75-mm spatial resolution, the voxels included in the hippocampus region in the functional MR images were determined according to the masked volume in the 3D SPGR images by using a de-resolution program. (Note, functional MR images were also transformed into the Talairach space.) Only those voxels in functional MR images that contained more than 50% of the masked 3D SPGR voxels were included for the voxel time course analysis.

To extract the SLF components, the original time courses were filtered with a 9-point Hamming band-pass filter with a passband of 0.015 – 0.1 Hz. To compare SNRs in different brain regions, five regions in fMRI datasets were selected: the left and right hippocampus, white matter from the splenium of the corpus callosum, gray matter from the thalamus, CSF (lateral ventricle) and a pure noise region outside the brain region, as shown in Figure 1. Within the same slice containing the hippocampus region, three voxels in different (CSF) regions were selected as the regression vectors in order to remove CSF motion and potential aliased cardiac pulsations [11]. The voxel time courses in the left and the right hippocampus regions were employed to calculate the COSLOF Index, normalized COSLOF Index, and PSI for each of the control, MCI, and AD groups.

Figure 1.

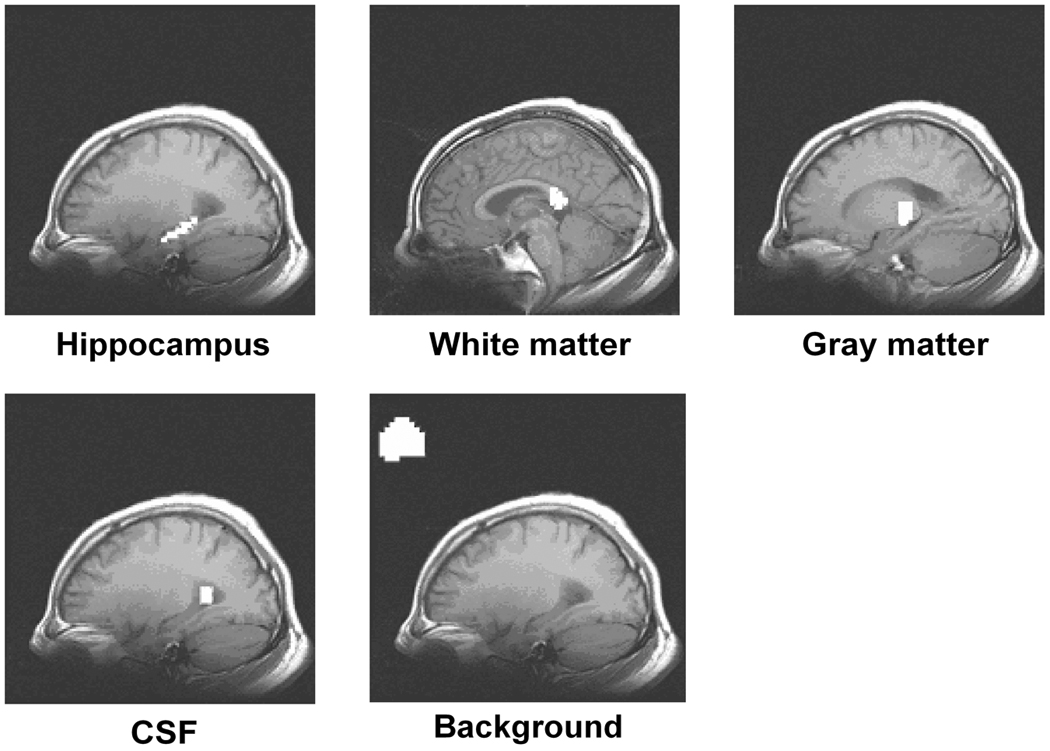
The representative regions (in white) selected for analysis: the hippocampus, white matter, gray matter, CSF, and the outside brain region from a subject. The selected regions are mapped onto T₁-weighted anatomical images.

After exclusion due to motion, the remaining subjects in the study were nine control subjects (three men, 70 ± 3 years old, and six women, 70 ± 7 years old), 10 AD patients (five men, 73 ± 5 years old and five women, 71 ± 10 years old), and eight MCI subjects (six men, 74 ± 3 years old and two women, 66 ± 2 years old).

Determination of Thermal Noise

It is known that the thermal noise in magnitude MR images is Rician distributed. Further, the Rician distribution is reduced to Rayleigh distribution when the signal is zero (e.g., outside the brain region in MR images). When the signal level is very large (e.g., inside brain regions in the MR images), the Rician distribution can be approximated as Gaussian distributed. However, for fMRI scans, the variations of the voxel time courses in the brain regions contain not only thermal noise but also other temporal variations such as physiologic noise. This makes it very difficult to estimate the standard deviation of thermal noise ${\widehat{\sigma }}_0$. Therefore, in the present study, we estimate the thermal noise standard deviation ${\widehat{\sigma }}_0$ in two steps. In the first step, voxel time courses outside the brain region at the upper left corner in the image are manually selected to estimate the Rayleigh-distributed noise standard deviation ${\widehat{\sigma }}_R$. The standard deviation of noise ${\widehat{\sigma }}_R$ is then converted to the Gaussian-distributed thermal noise standard deviation ${\widehat{\sigma }}_{M-\mathit{\text{noise}}}$ with a correction factor, according to Gudbjartsson and Patz [12]. In the second step, the estimated Gaussian noise standard deviation ${\widehat{\sigma }}_M$ is then scaled by the norm of the Hamming filter to adjust for the smoothing:

$${\widehat{\sigma }}_0={\widehat{\sigma }}_{M-\mathit{\text{noise}}}·{\left({\displaystyle \sum _t{h}^2(t)}\right)}^{1/2}$$ (20)

where h(t) represents the time domain 9-point Hamming filter coefficients. Then, the standard deviation of the SLF in the hippocampus region can be calculated as:

$${\widehat{\sigma }}_L=\sqrt{{{\widehat{\sigma }}_{M-\mathit{\text{hipp}}}}^2-}{{\widehat{\sigma }}_0}^2$$ (21)

where the ${\widehat{\sigma }}_{M-\mathit{\text{hipp}}}$ is the mean of the estimated temporal standard deviation of the voxel time courses in the hippocampus. Based on Eq. (20) and Eq. (21), the SNR can be estimated as $\widehat{\eta }={\widehat{\sigma }}_L/{\widehat{\sigma }}_0$.

Coherence and Phase Delay

In addition to the COSLOF Index and proposed PSI, coherence and phase delay were implemented and applied to our datasets to evaluate temporal correlation between voxel time courses. The coherence ρ between two voxel time courses [13–15] was estimated as follows:

$${\widehat{\rho }}_{ij}={\displaystyle \sum _{f=f_L}^{f_H}{\widehat{\rho }}_{ij}(f)}={\displaystyle \sum _{f=f_L}^{f_H}\frac{\left|S_{ij}(f)\right|}{\sqrt{S_{ii}(f)S_{jj}(f)}}}$$ (22)

where S_ii(f) and S_jj(f) are the spectral power on frequency component f of ith and jth voxel time courses, S_ij(f) is the cross-spectral power, f_L is the lower frequency bound of SLF, which is set as 0.015Hz, and f_H is the upper frequency bound set as 0.1Hz. The ROI coherence is simply the average of the coherences between each pair of voxel time courses. The phase delay τ can be estimated as [15]:

$${\widehat{\tau }}_{ij}=\left|\frac{{\displaystyle \sum _{f=f_L}^{f_H}{\phi }_{ij}(f)}}{2\pi {\displaystyle \sum _{f=f_L}^{f_H}f}}\right|,\text{where}{\phi }_{ij}(f)={\text{tan}}^{-1}\left(\frac{\text{Im}\left(S_{ij}(f)\right)}{\text{Re}\left(S_{ij}(f)\right)}\right),$$ (23)

On par with the ROI coherence, the ROI phase delay is simply the average of the phase delays between each pair of voxel time courses.

RESULTS

The SNRs in the hippocampus region for the three groups of subjects are presented in Table 1. The SNRs in the hippocampus regions for AD, MCI, and control groups are 2.75±0.61, 2.60±1.23 and 2.00±0.45, respectively. The one-way unbalanced ANOVA analysis data show no significant differences in the SNRs in the hippocampus regions among the groups (F(2,23)=1.861, p=0.1783). The obtained hippocampus volumes (sum of both sides) for the three subject groups are: 5.68±1.24 cm³ for the control group, 5.60±0.31 cm³ for the MCI group, and 4.62±1.17 cm³ for the AD group. The one-way unbalanced ANOVA analysis data show no significant differences in the volumes among the groups (F(2,23)=2.855, P=0.1122).

Table 1.

The SNR in four selected regions of three subject groups

A. SNR (signal to noise ratio) (Mean±SD)
SNR	AD		MCI		Control
Hippocampus	2.75 ± 0.61		2.60 ± 1.23		2.00 ± 0.45
White matter	1.24 ± 0.40		1.00 ± 0.28		0.71 ± 0.18
Gray matter	1.45 ± 0.70		1.57 ± 0.79		1.04 ± 0.25
CSF	4.29 ± 0.85		3.16 ± 0.33		3.78 ± 0.45
B. One-way unbalanced ANOVA for the SNR in the hippocampus region of three subject groups
		F (2,23)		p-value
SNR In Hippocampus		1.861		0.1783

Table 2 lists the original and normalized COSLOF Indices and their statistical differences in the five regions for the control, MCI, and AD groups, as based on Eq. (3) and Eq. (6). Table 2A shows the original COSLOF Indices and Table 2B shows the normalized COSLOF Indices in the five brain regions of the AD, MCI, and control groups. The one-way unbalanced ANOVA test indicates that both the original (F(2,23)=14.563, P <0.0001) and normalized COSLOF (F(2,23)=24.316, P <0.00001) Indices are significantly different in the three groups. The COSLOF Index is the largest in the normal control group, medium for the MCI group, and lowest for AD patients. Except in the case of AD vs. MCI, the CSF voxel regression does not significantly alter the statistical results, either in ANOVA analysis or in the one-tail t-tests. Table 2D shows that the pairwise t-test results for both original and normalized COSLOF Indices have significant statistical power to separate groups of AD vs control and MCI vs control. However, the ability for the COSLOF Index to distinguish between MCI and AD groups was moderate and became insignificant when CSF regression was employed. Further Z-statistical analysis revealed that the Z-score for the original COSLOF Index that separated MCI from the control groups is 3.215, and the score to separate AD from the control groups was 3.676. The Z-score for the normalized COSLOF Index that separated MCI from control groups was 3.571. The Z-score used to separate the AD from control groups was 4.286. The discriminating power of the normalized COSLOF Index is stronger than that of the original COSLOF Index.

Table 2.

Statistical comparison between original and normalized COSLOF Indices in five brain regions of three subject groups

A. Original COSLOF Indices (CI) (Mean±SD)
Region	AD		MCI		Control
Hippocampus nr	0.127 ± 0.095		0.196 ± 0.051		0.341 ± 0.085
Hippocampus rg	0.142 ± 0.090		0.171 ± 0.055		0.304 ± 0.065
White matter	0.088 ± 0.059		0.138 ± 0.092		0.108 ± 0.123
Gray matter	0.175 ± 0.062		0.134 ± 0.077		0.176 ± 0.112
CSF	0.069 ± 0.052		0.094 ± 0.071		0.079 ± 0.033
Pure noise region	0.004 ± 0.006		0.003 ± 0.003		0.005 ± 0.006
B. Normalized COSLOF Indices (nCI) (Mean±SD)
Region	AD		MCI		Control
Hippocampus nr	0.147 ± 0.106		0.277 ± 0.052		0.437 ± 0.079
Hippocampus rg	0.164 ± 0.099		0.236 ± 0.065		0.395 ± 0.084
White matter	0.172 ± 0.080		0.271 ± 0.154		0.287 ± 0.212
Gray matter	0.382 ± 0.233		0.233 ± 0.117		0.346 ± 0.175
CSF	0.072 ± 0.054		0.103 ± 0.078		0.085 ± 0.036
C. One-way unbalanced ANOVA for CI and nCI in the hippocampus of three subject groups
Measurement	Fnr(2,23)	p-valuenr		Frg(2,23)	p-valuerg
CI	14.563	<0.0001		11.055	0.0004
nCI	24.316	<0.0001		15.453	<0.0001
D. Pairwise T-test between three subject groups
One-tail t-test for COSLOF Index nr			One-tail t-test for normalized COSLOF Index nr
AD vs. MCI	p = 0.0513		AD vs. MCI *		p = 0.0494
MCI vs. CONTROL **	p = 0.0006		MCI vs. CONTROL ***		p = 0.0001
AD vs. CONTROL ***	p = 0.0001		AD vs. CONTROL ***		p < 0.0001
One-tail t-test for COSLOF Index rg			One-tail t-test for normalized COSLOF Index rg
AD vs. MCI	p = 0.2365		AD vs. MCI		p = 0.0566
MCI vs. CONTROL **	p = 0.0003		MCI vs. CONTROL **		p = 0.0004
AD vs. CONTROL ***	p = 0.0005		AD vs. CONTROL ***		p < 0.0001
E. Kruskal-Wallis Nonparametric Tests for CI and nCI of three subject groups
Measurement	Hnr	p-valuenr		Hrg	P-valuerg
CI	14.508	0.0007		11.164	0.0038
nCI	17.616	0.0001		14.829	0.0006

nr – no CSF voxels regression, rg – with CSF voxels regression, COSLOF Indices presented in this article in all other regions have been calculated without CSF voxel regression.

^*indicates p < 0.05

^**indicates p< 0.01

^***indicates p < 0.001

Because the distribution of the original or normalized COSLOF Indices is not assured to be Gaussian, the nonparametric Kruskal-Wallis Tests are conducted as a general statistical evaluation. As listed in Table 2E, the original and normalized COSLOF Indices can significantly detect the differences among the three groups (H = 14.508, P = 0.0007 for original COSLOF Indices, H = 17.616, P = 0.0001 for normalized COSLOF Indices).

Based on Eq. (10), Eq. (12) and Eq. (15), Table 3 lists the maximum-shifted COSLOF Index CI^m and the PSI θ_G, as well as the results of statistical comparisons for the PSI in the hippocampus region between the control, MCI, and AD groups. Table 3A illustrates that the CI^ms are comparably similar in each of the five regions between the three groups, while the Phase Shift Indices in the hippocampus region in the three subject groups are significantly different, as listed in Table 3B. The PSI without CSF voxel regression is the largest (72.6°±11.3°) for the AD group. It is the smallest (40.6°±8.4°) for the control group and the value is in between (58.6°±5.7°) for the MCI group. The larger the PSI, the less synchrony between the voxel time courses in the hippocampus region. In Table 3C, the one-way unbalanced ANOVA analysis shows a statistically significant difference in the PSI among the three groups of hippocampus regions (F(2,23)=25.789, P <0.0001). Table 3D shows the pairwise t-test results among the three groups. Although CSF regression has reduced the P values, the differences between control vs MCI, and control vs AD groups are still significant. The Z-statistical differences are significant between MCI and control groups (Z = 3.672) and between AD and control groups (Z = 4.365).

Table 3.

Statistical comparisons between maximum-shifted COSLOF Indices and PSI in five brain regions of three subject groups

A. Maximum-shifted COSLOF Indices CIm (Mean±SD)
CIm	AD		MCI		Control
Hippocampus nr	0.412 ± 0.075		0.390 ± 0.072		0.438 ± 0.054
Hippocampus rg	0.398 ± 0.061		0.362 ± 0.054		0.424 ± 0.037
White matter	0.304 ± 0.049		0.305 ± 0.056		0.280 ± 0.067
Gray matter	0.336 ± 0.063		0.331 ± 0.083		0.325 ± 0.055
CSF	0.307 ± 0.051		0.337 ± 0.069		0.282 ± 0.025
Pure noise region	0.233 ± 0.003		0.234 ± 0.006		0.232 ± 0.002
B. PSI θG (Mean±SD)
θG	AD		MCI		Control
Hippocampus nr	72.6 ± 11.3		58.6 ± 5.7		40.6 ± 8.4
Hippocampus rg	68.0 ± 14.1		58.9 ± 7.0		43.5 ± 10.1
White matter	74.1 ± 9.2		64.4 ± 14.7		77.9 ± 4.5
Gray Matter	60.5 ± 9.8		67.1 ± 11.5		70.7 ± 9.7
CSF	78.1 ± 7.9		73.8 ± 6.2		74.0 ± 12.3
Pure noise region	88.9 ± 1.6		88.2 ± 0.9		88.5 ± 1.5
C. One-way unbalanced ANOVA for CIm and θG of three subject groups
Measurement	Fnr(2,23)	p-valuenr		Frg(2,23)	p-valuerg
CIm	0.941	0.4049		2.661	0.0913
θG	25.789	<0.0001		10.462	0.0006
D. Pairwise T-test between three subject groups
One-tail t-test for PSI nr			One-tail t-test for PSIrg
AD vs. MCI **	p = 0.0047		AD vs. MCI		p = 0.1487
MCI vs. CONTROL **	p = 0.0001		MCI vs. CONTROL **		p = 0.0006
AD vs. CONTROL ***	p < 0.0001		AD vs. CONTROL ***		p = 0.0006
E. Kruskal-Wallis Nonparametric Tests for CIm and θG of three subject groups
Measurement	Hnr	p-valuenr		Hrg	p-valuerg
CIm	2.459	0.2924		4.073	0.1305
θG	17.939	0.0001		11.478	0.0032

nr – no CSF voxels regression, rg – with CSF voxels regression, COSLOF Indices presented in this article in all other regions have been calculated without CSF voxel regression.

^*indicates p < 0.05

^**indicates p < 0.01

^***indicates p < 0.001

Again, since the distribution of the maximum-shifted COSLOF Index CI^m and the PSI θ_G cannot be assured to be Gaussian, the nonparametric Kruskal-Wallis Tests are conducted. Significant differences in the PSI among the three groups are detected (H=17.939, P=0.0001), while maximum-shifted COSLOF Indices CI^m are not significantly different among the three subject groups (H=2.459, P=0.2924).

DISCUSSION

The present study consists of two parts: one provides a model of SLFs to investigate how SNR distributions could affect the calculations of the cross-correlation coefficients and the COSLOF Index, and the other applies this model in analyzing the functional synchrony in the hippocampus region of the normal, MCI, and AD subjects. In regard to the first part, our simulation study showed that SNR variations significantly affect the COSLOF Index calculation. The lower the SNR, the higher the error for the COSLOF Index. By normalizing the SNR factor, this error can be significantly reduced and the normalized COSLOF Index is no longer affected by the SNR factor. Therefore, the normalized COSLOF Index has a stronger discriminating power than the original COSLOF Index. However, the accurate SNR estimation is susceptible to background artifacts and temporal changes in the brain region. As a result, the method of normalizing the SNR factor is not ideal in providing an optimal measurement of the COSLOF Index. To overcome this problem, we further developed the PSI method.

Ideally, if there is no thermal noise present, the cross-correlation coefficient between two signals reflects the phase shift (the angle between two vectors). However, when the thermal noise is present, the variable SNR can affect the cross-correlation coefficient and make it less reliable to detect the phase shift, in turn, affecting the COSLOF Index calculation. Our simulation study demonstrated that the inaccuracy of the SNR estimation can be avoided through the cancellation of the SNR factor, by taking the ratio of the cross-correlation coefficient to the maximum-shifted cross-correlation coefficient, as shown in Eq. (10), Eq. (12), and Eq. (13). Therefore, no matter what the SNR is, the PSI method provided an accurate measure of the phase shift between the SLFs. As a result, the PSI measurement provides a stronger discriminatory power than the original and normalized COSLOF methods.

For the second part of study, we applied the model of the original COSLOF Index, the normalized COSLOF Index, and the PSI methods to investigate the functional synchrony in the hippocampus of the normal, MCI, and AD subjects. We have demonstrated that the normalized COSLOF Index and the PSI, quantified by θ_G, have higher statistical discriminatory power between these groups of subjects than that of the original COSLOF Index based on their Z-score comparisons. A large PSI value in the hippocampus region of the AD and MCI subjects reveals a significant large phase shift among voxel time courses, indicating asynchrony.

Unlike the thermal noise, which is not correlated and can be canceled when calculated with the PSI, the aliased cardiac signal cannot be canceled, because it can be cross-correlated as “signal.” With the TR of 2s, the cardiac component can be aliased into the frequency range of the SLF signal (0.015~0.1 Hz) and may affect the calculation of the PSI. Since we did not simultaneously record the cardiac pulse during the fMRI scanning and could not employ the retrospective correction technology [16,17], we employed the CSF signal as a regressor to test if the cardiac signal played a significant role. The CSF signal usually contains the aliased cardiac signal due to the steady-state free precession mechanism [18]. As demonstrated in Table 3C, the significances in the PSI measurement estimated with ANOVA were not altered with or without CSF regression. In addition, the significances in the PSI between the groups of MCI vs Control or AD vs Control were not altered with or without CSF regression (Table 3D). Therefore, this potential confounding factor did not play an important role in estimating the PSI. However, the CSF regression did affect the significance between the MCI and AD groups. The reason is not known. One possibility is that the CSF voxel time courses may contain other unknown signal sources, which might introduce uncertainty to the PSI estimations. We do not recommend the CSF regression method. Rather, the retrospective correction technology should be employed [16,17].

Respiratory signals may also be present in the fMRI VTCs. Its frequency usually lies within the range 0.1~0.3Hz [19,20]. With TR of 2 s, this respiratory frequency could fold over into the frequency range of 0.1~0.25Hz, which is outside of the Hamming filter passband. Therefore, the respiratory frequency generally does not contribute as a confounding factor.

Respiratory variation in volume, i.e. variation of the arterial CO₂ level, which acts as a vasodilator, could also induce BOLD signal variation. The spectral density of this temporal variation of the BOLD signal appears at about 0~ 0.05 Hz [18,19], which resides in the frequency range of SLF signals, hence, imposing a potential confounding factor for PSI calculations. The respiratory variations in volume were region-specific and the most affected regions were the posterior cingulate and precunues, while the hippocampus region seemed immune to this variation [19]. Further, a recent study on functional synchrony analysis of the parahippocampal region also showed that different cognitive tasks lead to different PSI values [21], which implies that it is unlikely that respiratory variation plays significant roles in both cases. Nevertheless, it will be necessary to record and regress this respiratory variation out in future studies.

It is interesting to note that the maximum-shifted COSLOF Index, CI^m, in the pure noise region shown in Table 3A is about 0.23 and is similar in the three study groups. Intuitively, the cross-correlation coefficient between noise time courses should be close to zero. The noticeably shifted cross-correlation coefficient of 0.23 for noise is explained below. As described in the Appendix A in detail, and shown in Figure 2, the relationship between the number of time points M and cc^m(η), theoretical calculation and simulation showed that the value of cc^m(η) depends on the number of time points, M, in a voxel time course. The larger M is, the smaller cc^m(η) is. As shown in Table 4, after truncation and band-pass filtering, the simulated cc^m(η) for noise is about 0.23 when M is 180. The simulated data are consistent with experimental results.

Figure 2.

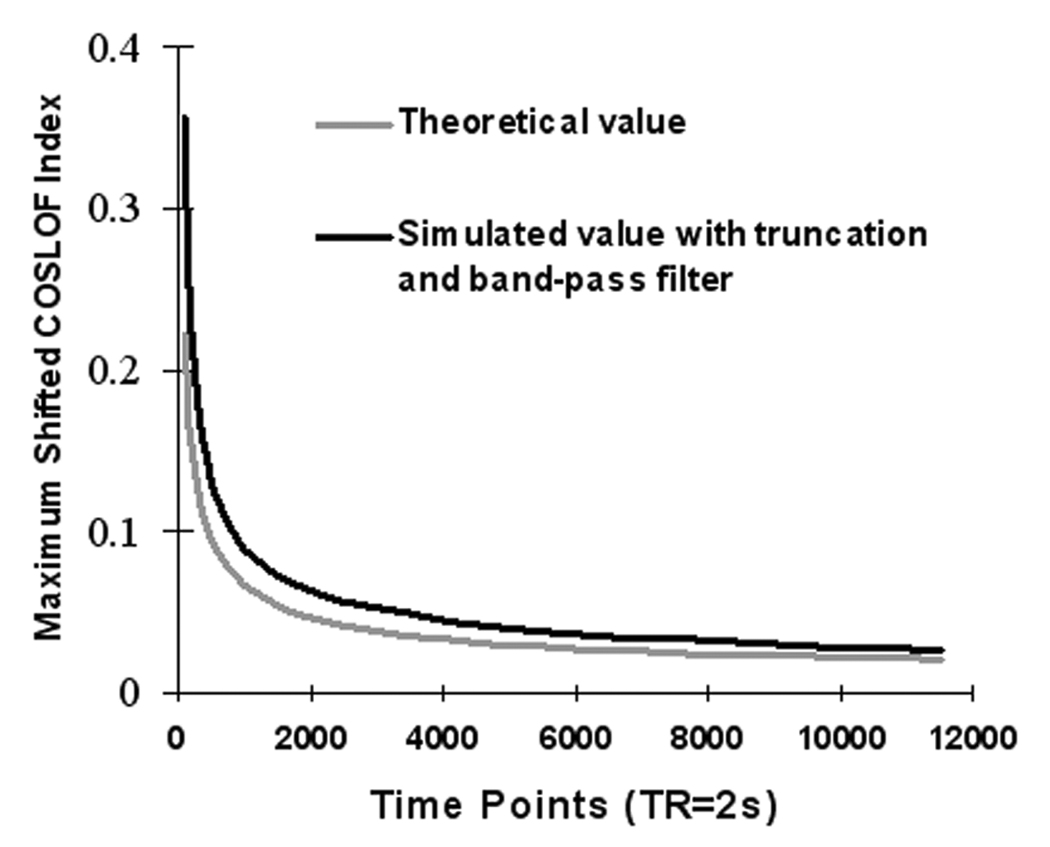
The relationship between the number of time points and the maximum-shifted cross-correlation coefficient, cc^m(0) between two noise time courses with standard normal distribution. The lighter gray line is the theoretical value and the dark line is the simulated value.

Table 4.

The relationships between the number of time points and the maximum-shifted cross-correlation of white normal noise cc^m(0) under different conditions

Time points (scanning time)	Theoretical ccm(0)	Simulated ccm(0)	Simulated ccm(0) with truncation	Simulated ccm(0) with band-pass filter	Simulated ccm(0) with truncation and band-pass filter
90 (3 min)	0.2221	0.2150	0.2740	0.2981	0.3554
180 (6 min)	0.157	0.1562	0.1663	0.2110	0.2307
360 (12min)	0.111	0.1114	0.1207	0.1453	0.1563
720 (24 min))	0.0785	0.0792	0.0786	0.1044	0.1077
1440 (48 min)	0.0555	0.0553	0.0564	0.0730	0.0745
2880 (96 min)	0.0392	0.0389	0.0391	0.0522	0.0529
5760 (192 min)	0.0277	0.0279	0.0280	0.0367	0.0363
11520 (384 min)	0.0204	0.0192	0.0198	0.0252	0.0256

As we have demonstrated, the PSI, with its cancelled noise factor, has much stronger statistical power than the COSLOF Index. Nevertheless, a certain level of SNR is necessary to reliably calculate the PSI. As shown in the Appendix A, it was estimated that the minimum SNR for reliable calculation of the Phase Shift Index is approximately 1. For a 3 T scanner, it is conceivable that the SNR will certainly be higher than at a 1.5 T scanner, resulting in a more reliable estimation of PSI.

Also, there are other methods that can be used to study the association between time series, such as the coherence analysis (frequency domain correlation) [13,14]. The phase delay, according to its conventional meaning, has also been developed without using a band-pass filter [15]. However, these methods are vulnerable to the lower SNR and complex spectrum. The SNR for SLFs is relatively low, as listed in Table 1. We have applied both coherence and phase delay methods to our experimental data. The estimated coherences for control, MCI, and AD groups are 0.43±0.08, 0.37±0.05 and 0.34±0.11, respectively; and the phase delay for control, MCI, and AD groups are 0.95±0.10, 0.94±0.08 and 1.03±0.13 seconds, respectively. There is no significant difference between each pair. This is also true of the ANOVA statistics. Therefore, we prefer the PSI over the coherence or phase delay method in this study.

We have examined how the signal to noise ratio of SLFs and the phase shift between the two voxel time courses affect the cross-correlation coefficient and the COSLOF Index. It is reasonable to ask how the spectral density of the SLFs would affect the correlation analysis. However, the spectral densities of the SLFs are rather complex because not all frequency components in SLFs contribute to the calculation of the cross-correlation coefficients between VTCs. In addition, those frequency components contribute to the cross-correlation coefficients that are different from different pairs of VTCs. Therefore, the concept of spectral density influencing the calculation of the cross-correlation coefficient is ill defined. Rather, we will focus on testing if there are intrinsic frequency components in SLFs that are relevant to the determination of the COSLOF Index.

APPENDIX A

In this section, we will derive a theoretical relationship between the number of time points M and the maximum-shifted cross-correlation coefficient, cc^m(0) of two time courses n₁(t) and n₂(t) of white noise with 0 as the expectation and 1 as the standard deviation. The zero in cc^m(0) represents no SLF in the time course.

Assuming the two courses n₁(t) and n₂(t) have M time points and maximum time shift points T, the maximum-shifted cross-correlation is calculated as:

$${\mathit{\text{cc}}}^m(0)=\underset{0<\tau <T}{\text{max}}\frac{1}{M}{\displaystyle \sum _{t=1}^M\left(n_1(t)·n_2(t+\tau )\right)}.$$ (A1)

Define the Γ(τ) as a cross-correlation function between n₁(t) and n₂(t) as follows:

$$\mathrm{\Gamma }(\tau )=\frac{1}{M}{\displaystyle \sum _{t=1}^M\left(n_1(t)·n_2(t+\tau )\right)}.$$ (A2)

Because it is white noise, n(t) is statistically independent of n(t+1). Thus, ∑n₁(t)·n₂(t) is independent of ∑n₁(t)·n₂(t+τ), (τ≠0, because ∑n₁(t)·n₂(t) is independent of ∑n₁(t+1)·n₂(t+τ+1), while the latter is equal to ∑n₁(t)·n₂(t+τ)). Thus, the probability function of the maximum-shifted cross-correlation coefficient is:

$$F\left(x|{\mathit{\text{cc}}}^m(0)<x\right)=F\left(x|\underset{0<\tau <T}{\text{max}}\mathrm{\Gamma }(\tau )<x\right)={\displaystyle \prod _{\tau =0}^{T}F\left(x|\mathrm{\Gamma }(\tau )<x\right)=}{\left(F\left(x|\mathrm{\Gamma }<x\right)\right)}^{T+1}.$$ (A3)

According to the Central Limit Theorem, the distribution of Γ approximates to a normal distribution with sample expectation and sample variance of 0 and 1/M, respectively. The probability function of Γ is:

$$F\left(x|\mathrm{\Gamma }<x\right)={\displaystyle {\int }_{-\infty }^x\frac{1}{\sqrt{2\pi }\widehat{\sigma }}}\text{exp}\left(-\frac{s^2}{2{\widehat{\sigma }}^2}\right)ds$$ (A4)

where $\widehat{\sigma }=1/\sqrt{M}$. By substituting Eq. (A3) with Eq. (A4) and taking the derivative, the probability density function of cc^m(0) is:

$$p_{{\mathit{\text{cc}}}^m(0)}(x)=\frac{T+1}{{\left(\sqrt{2\pi }\widehat{\sigma }\right)}^{T+1}}{\left({\displaystyle {\int }_{-\infty }^x\text{exp}\left(-\frac{s^2}{2{\widehat{\sigma }}^2}\right)ds}\right)}^T·\text{exp}\left(-\frac{x^2}{2{\widehat{\sigma }}^2}\right).$$ (A5)

Under the present experimental condition, T is 34, and σ̂ is $1/\sqrt{180}$. The expectation of cc^m(0) from Eq. (A5) is 0.157 and the standard deviation is 0.0362. For different time points M, there are different variance and expectation values of cc^m(0); the larger M is, the smaller the variance and expectation values. In practice, the time courses were bandpass-filtered and data were truncated due to the shift (there will be only M − τ time points matched for cross-correlation calculation for each shift attempt), which resulted in changes, as shown in Figure 2 (dark line). Table 4 further lists the detailed results to demonstrate the relationships between the number of time points and the expectations of cc^m(0), i.e. under different conditions. The expectation value of 0.23 for the simulated, truncated, and filtered datasets (as shown in Table 4, row 3, Column 6) are consistent with experimental results of 0.23, as shown in Table 3A, for pure noise region. All these results strongly support our theoretical model derived above.

In the following section, we will determine the minimum SNR in the voxel time courses required, which reliably obtains cc^m(∞), which resulted from SLFs instead of from noise. With the signal-noise model of Eq. (1), the maximum-shifted cross-correlation between two measured voxel time courses can be written as:

$$\begin{array}{c}{\mathit{\text{cc}}}^m\left({\widehat{\sigma }}_s\right)=\frac{1}{{{\widehat{\sigma }}_s}^2+1}\underset{\tau }{\text{max}}\left(\frac{1}{M}{\displaystyle \sum _t((s(t)+n_1(t))}·(s(t+\tau )+n_2(t+\tau )))\right)\hfill \\ =\frac{1}{M\left({{\widehat{\sigma }}_s}^2+1\right)}\underset{\tau }{\text{max}}\left({\displaystyle \sum _{t}s(t)s(t+\tau )+{\displaystyle \sum _{t}s(t)n_2(t+\tau )+{\displaystyle \sum _{t}s(t+\tau )n_1(t)+{\displaystyle \sum _t{n}_1(t)}{n}_2(t+\tau )}}}\right).\hfill \end{array}$$ (A6)

Assuming the SLFs in both voxel time course are the same stationary s(t), the sample standard deviation of s(t) is ${\widehat{\sigma }}_s$, the expectation is 0, and the noise n₁(t) and n₂(t) are both white noise with standard deviation of 1. When the length of the time course is infinite, M → ∞, only the first item will remain and other terms will approach zero. Assuming the SLFs are stationary, the correlation function, R_ss(τ), can be written:

$$R_{ss}(0)\ge R_{ss}(\tau )=\frac{1}{M}{\displaystyle \sum _{t}s(t)s(t+\tau )}.$$ (A7)

However, when M is finite and the SNR is small, there is the possibility that experimentally obtained R_ss(0) may not reflect the synchrony between SLFs, which means shifting the time course may not reach the maximum synchrony among the signals. To avoid such a confounding factor, the R_ss(τ) must be dominant in Eq. (A7), that is:

$$R_{ss}(0)\ge R_{ss}(\tau )\ge A=\left(\underset{\tau }{\text{max}}\left(\frac{1}{M}{\displaystyle \sum _{t}s(t)n_2(t+\tau )+\frac{1}{M}{\displaystyle \sum _{t}s(t+\tau )n_1(t)}+\frac{1}{M}{\displaystyle \sum _t{n}_1(t)}{n}_2(t+\tau )}\right)\right).$$ (A8)

Considering that the maximum summation of the three terms in Eq. (A7) is usually equal or smaller to the summation of their individual maximums, we make a more restrictive requirement by letting R_ss(0) satisfy Eq. (A7):

$$R_{ss}(0)\ge B=\underset{\tau }{\text{max}}\left(\frac{1}{M}{\displaystyle \sum _{t}s(t)n_2(t+\tau )}\right)+\underset{\tau }{\text{max}}\left(\frac{1}{M}{\displaystyle \sum _{t}s(t+\tau )n_1(t)}\right)+\underset{\tau }{\text{max}}\left(\frac{1}{M}{\displaystyle \sum _t{n}_1(t)n_2(t+\tau )}\right)\ge A.$$ (A9)

Assuming the distribution of B with an upper limit of $E(B)+3\sqrt{\mathit{\text{Var}}(B)}$, an approximation of Eq. (A9) is:

$$R_{ss}(0)>E(B)+3\sqrt{\mathit{\text{Var}}(B)}.$$ (A10)

Based on the premise of independence between signal and noise, s(t)n₁(t) will be independent with s(t)n₂(t). The distribution of $\underset{\tau }{\text{max}}\left(\frac{1}{M}{\displaystyle \sum _{t}s(t)n_2(t+\tau )}\right)$ is similar to $\underset{\tau }{\text{max}}\left(\frac{1}{M}{\displaystyle \sum _t{n}_1(t)n_2(t+\tau )}\right)$. Two terms on the right side of Eq. (A10) can be expressed respectively as:

$$\begin{array}{c}E(B)=2E\left(\underset{\tau }{\text{max}}\left(\frac{1}{M}{\displaystyle \sum _{t}s(t)n_2(t+\tau )}\right)\right)+E\left(\underset{\tau }{\text{max}}\left(\frac{1}{M}{\displaystyle \sum _t{n}_1(t)n_2(t+\tau )}\right)\right)\hfill \\ \mathit{\text{Var}}(B)=2\mathit{\text{Var}}\left(\underset{\tau }{\text{max}}\left(\frac{1}{M}{\displaystyle \sum _{t}s(t)n_2(t+\tau )}\right)\right)+\mathit{\text{Var}}\left(\underset{\tau }{\text{max}}\left(\frac{1}{M}{\displaystyle \sum _t{n}_1(t)}{n}_2(t+\tau )\right)\right).\hfill \end{array}$$ (A11)

By using the experimental parameters of 34 for T and 180 for M in Eq. (A5), we obtain sample estimation of E(Q) and Var(Q):

$$\widehat{E}(B)=0.314{\widehat{\sigma }}_s+0.157\text{and}\widehat{\mathit{\text{Var}}}(B)=0.00262{{\widehat{\sigma }}_s}^2+0.00131.$$ (A12)

Substituting Eq. (A10) with Eq. (A12), we obtain:

$${{\widehat{\sigma }}_s}^2>0.314{\widehat{\sigma }}_s+0.157+0.1086\sqrt{2{{\widehat{\sigma }}_s}^2+1}.$$ (A13)

By solving the above inequality with a simulation, the threshold of the SNR is 0.74. Considering the effects of the truncation and the Hamming filter, Eq. (A13) becomes:

$${{\widehat{\sigma }}_s}^2>0.46{\sigma }_s+0.23+0.2064\sqrt{2{{\widehat{\sigma }}_s}^2+1}.$$ (A14)

The solution of Eq. (A14) is:

$$\eta ={\widehat{\sigma }}_s>1.036.$$ (A15)

Again, the noise variance is 1. Equation (A15) suggests that with the SNR larger than 1.036, the maximum-shifted cross-correlation coefficient resulted from the synchrony of SLFs rather than noise. Based on the analytical solution in Eq. (A14), minimum required SNR of 1.036 would produce about 10% error, as simulated in Figure 3. The simulation was made with the assumption that both SLFs are the same sine waves with a frequency of 0.0575 Hz (center of the low-frequency band, 0.015~0.1 Hz) and with different levels of SNR. Clearly, if the SLF contains multiple frequency components, the required SNR for the same error level will be higher.

Figure 3.

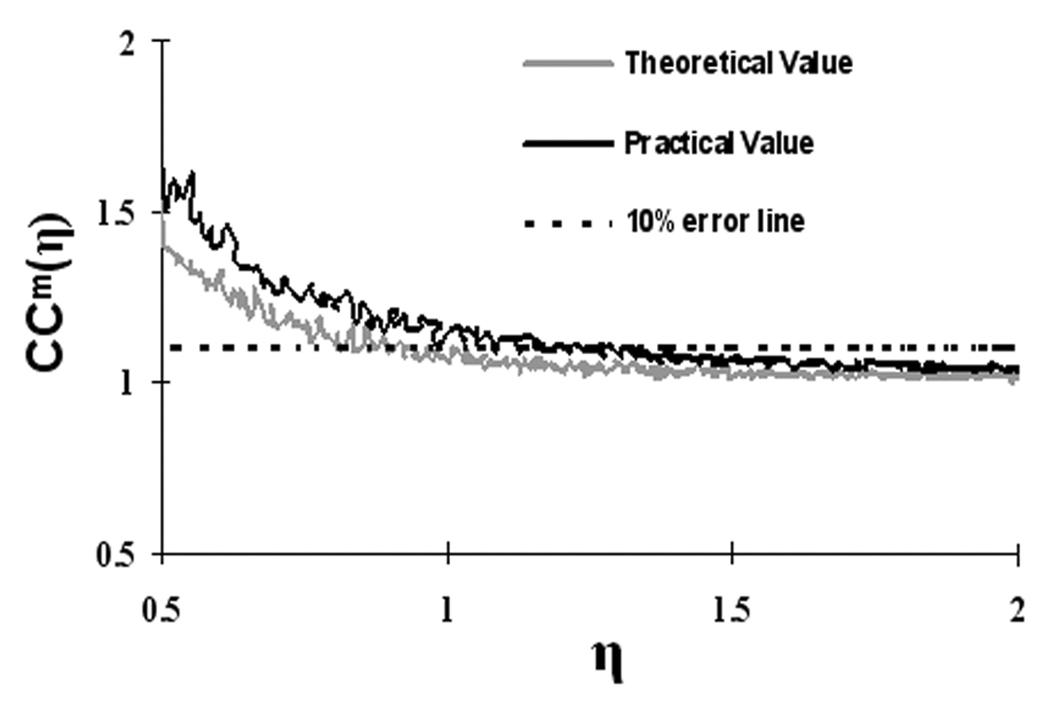
Normalized maximum-shifted cross-correlation coefficient, cc^m(η) vs. η. The lighter gray line is for theoretical values according to Eq. (A15) and the dark line is for practical values after truncation and filtering. The dashed line represents a threshold of 10% error in cc^m(η) at η = 1.036. The smaller η is, the bigger the error in cc^m(η), and vice versa.

APPENDIX B

To validate the approximation in Eq. (6) and Eq. (8), where the SNR η̂ is assumed to be identical in all voxel time courses within an ROI, and to compare the normalized COSLOF Index calculated from Eq. (6) and Eq. (8) to the original COSLOF index calculated from Eq. (3), the simulations are constructed as follows. The voxel time course from the ith voxel is expressed as in Eq. (9). For benchmark comparison, we have also constructed a hypothetical noise-free ROI with the voxel time course as:

$$u_i(t)=\sqrt{2}\text{sin}(2\pi f_{c}t+{\theta }_i)$$ (B1)

Three sets of simulations are implemented to examine the impact of SNRs on 1) the original COSLOF Index (oCI) based on Eq. (3), 2) normalized COSLOF index (nCI) based on Eq.(6) and 3) approximately normalized COSLOF Index (anCI) based on Eq.(8). Three sets of normal SNR distributions are defined as: N₁(1.75,0.25²), N₂(2.5,0.5²) and N₃(4,1²) based on the a reasonable representation of the substantial SNR variations that are observed across the hippocampus. In addition, the means and standard deviations of the SNR distributions are set to satisfy a minimum SNR of mean ± 3SD≥1, as described in Appendix A. θ_i is the phase which also obeys a normal distribution and is set to be N(0,(π / 4)²), according to a previous study [21]; f_c is a predefined frequency 0.0575Hz, which is the middle frequency of SLFs between 0.015~0.1 Hz; n_i(t) is the normal distributed thermal noise; η_i, θ_i and n_i(t) are independent of each other. The time length is 6 min, and the sampling frequency is 0.5Hz which corresponds to TR of 2 seconds.

In each set of the SNR distribution, we perform the Monte Carlo simulation by altering the SNRs and the number of voxels in an ROI from 10 to 150 with 10 as the increment. At a given voxel number, each voxelwised SNR level was randomly generated within a given SNR distribution. This procedure was independently repeated for 100 times. Then, the 100 estimations obtained of the COLSOF Index were averaged to yield a final simulated estimation. To evaluate the simulation performance, we employed the mean absolute errors (MAE), as calculated below:

$$\mathit{\text{MAE}}=\frac{1}{L}{\displaystyle \sum _{l=1}^L\left|V_1-V_0\right|}$$ (B2)

Where the V_l represents the COSLOF Index in each case of calculations (oCI, nCI, or anCI) obtained from Eq. (3), Eq. (6), or Eq. (8), respectively, at a given voxel number and SNR distribution, L equals to 100 as a trial repetition, V₀ represents the COSLOF Index calculated from Eq. (B1) without noise.

Fig. 4 shows the simulated results between the different levels of SNR distribution and the estimated COSLOF Index at the different number of voxels. Fig. 4A demonstrates that without noise, the oCI is 0.538±0.003. With the SNR distributions of N₁(1.75,0.25²), N₂(2.5,0.5²) and N₃(4,1²), the oCIs are 0.399±0.004, 0.456±0.008, and 0.501±0.007, respectively. Clearly, the SNR significantly affects the COSLOF Index estimation. When the SNR distribution is normalized, the accuracy of the COSLOF Index estimation is significantly improved, as shown in Figs. 4b–4d. Specifically, Fig. 4B shows that with SNR distribution of N₁(1.75,0.25²), the mean absolute error (MAE) for oCI is 0.135±0.002, for nCI is 0.005±0.002, and for anCI is 0.007±0.002. Clearly, the MAE is largest for the original COSLOF Indices calculation, based on Eq. (3) in contrast to the normalized COSLOF Index estimated by Eq. (6) and Eq. (8). Further, Fig. 4b shows that the assumption made from Eq. (6) to Eq. (8) is statistically valid since the difference is only 0.002. The MAE of 0.002, compared to the no noise case of the COSLOF Index of 0.538±0.003, only represents 0.4%. Similarly, with SNR distribution of N₂(2.5,0.5²) as shown in Fig. 4C, the corresponding MAEs are 0.082±0.002 for oCI, 0.003±0.001 for nCI, 0.009±0.001 for anCI; with SNR distribution of N₃(4,1²), as shown in Fig. 4D, the corresponding MAEs are 0.038±0.001 for oCI, 0.002±0.001 for nCI, 0.007±0.001 for anCI. These data not only demonstrate how the different SNR affect the original COSLOF Index estimation, but also prove that the normalization of the COSLOF Index is an optimal estimation. In addition, these data also validate our approximation from Eq (6) to Eq. (8) with a mean signal to noise ratio over an ROI. This assumption not only significantly reduced the computational cost, but also provided an accurate estimation on the normalized COSLOF Index.

Figure 4.

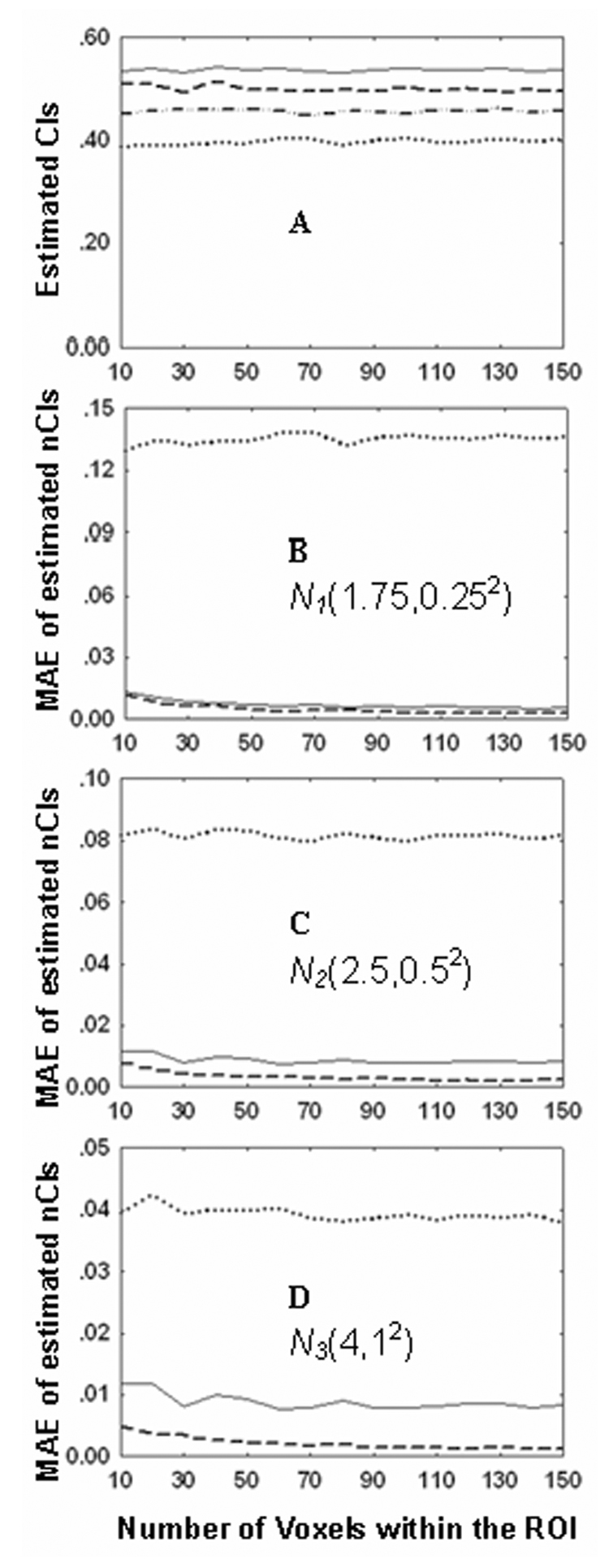
Simulation of independence of the normalized COSLOF Index on different SNRs. In Fig. 4A, four sets of simulations are implemented to examine the impact of different SNRs on the original COSLOF Index (oCI) based on Eq. (3). The solid line, the dashed line, the dash-dotted line, and the dotted line represent the oCI in cases of different noise distributions at noise-free, N₁(1.75,0.25²), N₂(2.5,0.5²), and N₃(4,1²), respectively. Figs. 4B–4D show the MAEs of oCI (dotted line), normalized COSLOF Index (nCI) (dashed line) based on Eq.(6) and approximately normalized COSLOF Index (anCI) (solid line) based on Eq.(8) at three different SNR distributions.

To validate the independence of the PSI on the SNRs and the approximation in Eq. (14) and Eq. (15), the same datasets of the simulation and procedures described above were employed. These were contained in three different SNR distributions, N₁(1.75,0.25²), N₂(2.5,0.5²), and N₃(4,1²) and a phase distribution $N\left(0,{\sigma }_{\theta }^2\right)$, where σ_θ is set to (π/4). Similarly, the MAE was employed to quantify the error between the given phase distribution and the calculated PSI with Eq. (14) and Eq. (15). As shown in Figure 5A, when using the noise-free SLF signal based on Eq.(B1), both PSI measurements with Eq. (14) and Eq. (15) provided accurate detection of the input phase σ_θ, which is set to π/4 (45 degree). When the SNR distribution is set to N₁(1.75,0.25²) and ROI is 10, the MAE of PSI from Eq. (14) is 2.09 degree and from Eq. (15) it is 1.6 degree (Fig. 5B). The PSI estimation based on Eq.(15) is more accurate than the approach based on Eq.(14). As shown in Figs. 5B–5D, the larger an ROI is, the more accurate the PSI estimation. For example, when voxels in an ROI are larger than 100, the MAE is about 0.5 degree for both estimations. These simulations validate our assumption between Eq (14) and Eq (15).

Figure 5.

Simulation of independence of the PSI estimation on the SNRs. In Fig 5A three sets of simulations are implemented to examine the impact of the approximation between Eq. (14) and Eq. (15) in case of the noise-free condition. The solid line, the dashed line, and the dotted line represent the given σ_θ and estimated ${\widehat{\sigma }}_{\theta }$ from Eq. (15) and Eq. (14), respectively. Figs. 5B–5D showed the MAEs of estimated ${\widehat{\sigma }}_{\theta }$ based on Eq. (14) (dotted line) and Eq. (15) (dashed line) at three different SNR distributions. The vertical units for Figs. 5A–5D are all in degrees.

It should be pointed out that the calculated ${\widehat{\theta }}_G$ from Eq. (14) is not directly equal to the σ_θ and they have a relationship of

$${\widehat{\theta }}_G=\frac{2}{\sqrt{\pi }}{\sigma }_{\theta }.$$ (B3)

To derive this relationship, we restate the phase distribution in the voxel time courses as N(θ₀,σ_θ²) and assume the phase of each voxel within the ROI are (θ₁,θ₂,…,θ_K). Based on Eq.(14),

$${\widehat{\theta }}_{G(\mathit{\text{Eq.}}14)}=\frac{2}{K(K-1)}{\displaystyle \sum _{i,j=1,i\ne j}^K\left|{\theta }_{ij}^d\right|=\frac{2}{K(K-1)}{\displaystyle \sum _{i,j=1,i\ne j}^K\left|{\theta }_i-{\theta }_j\right|}}$$ (B4)

where ${\theta }_{ij}^d={\theta }_i-{\theta }_j\sim N\left(0,2{{\sigma }_{\theta }}^2\right)$, and the SNR item is cancelled due to the ratio between the cross-correlation coefficient and maximum shifted cross-correlation coefficient. Therefore, the PSI within the region turns out to be:

$$\begin{array}{cc}{\widehat{\theta }}_{G(\mathit{\text{Eq.}}14)}=<\left|{\theta }_{ij}^d\right|& >\approx {\displaystyle {\int }_{-\infty }^{\infty }\left|t\right|·\frac{1}{2{\sigma }_{\theta }\sqrt{2\pi }}·e^{-\frac{t^2}{4{{\sigma }_{\theta }}^2}}dt}\\ & =\frac{1}{\sqrt{2\pi }{\sigma }_{\theta }}{\displaystyle {\int }_0^{\infty }t·e^{-\frac{t^2}{4{{\sigma }_{\theta }}^2}}}dt=\frac{2}{\sqrt{\pi }}{\sigma }_{\theta }\end{array}$$ (B5)

as shown in Eq. (B3) above. Similarly, the ${\widehat{\theta }}_G$ calculated from Eq. (15) and the σ_θ have the following relationship and can be derived as below:

$$\begin{array}{cc}\text{cos}\left({\theta }_{G(\mathit{\text{Eq.}}15)}\right)=\frac{\mathit{\text{CI}}}{{\mathit{\text{CI}}}^m}\hfill & =\frac{\frac{2}{K(K-1)}{\displaystyle \sum _{1\le i<j\le K}\left(\frac{{\eta }_i}{\sqrt{{{\eta }_i}^2+1}}·\frac{{\eta }_j}{\sqrt{{{\eta }_j}^2+1}}·\text{cos}({\theta }_i-{\theta }_j)\right)}}{\frac{2}{K(K-1)}{\displaystyle \sum _{1\le i<j\le K}\left(\frac{{\eta }_i}{\sqrt{{{\eta }_i}^2+1}}·\frac{{\eta }_j}{\sqrt{{{\eta }_j}^2+1}}\right)}}\hfill \\ \hfill & =\frac{\frac{2}{K(K-1)}{\displaystyle \sum _{1\le i<j\le K}\left({\tilde{\eta }}_i·{\tilde{\eta }}_j·\text{cos}({\theta }_i-{\theta }_j)\right)}}{\frac{2}{K(K-1)}{\displaystyle \sum _{1\le i<j\le K}\left({\tilde{\eta }}_i·{\tilde{\eta }}_j\right)}}\approx \frac{\overline{{\tilde{\eta }}_i·{\tilde{\eta }}_j·\text{cos}\left({\theta }_i-{\theta }_j\right)}}{\overline{{\tilde{\eta }}_i·{\tilde{\eta }}_j}}\hfill \end{array}$$ (B6)

where ${\tilde{\eta }}_i=\frac{{\eta }_i}{\sqrt{{{\eta }_i}^2+1}}$.

The last step of approximation in Eq. (B6) stands when the number of voxels within the ROI K is very large. As the initial assumption, η_i is independent of θ_i and so is ${\tilde{\eta }}_i$, and its mean is not zero, as predefined. Therefore, Eq. (B6) can be simplified as:

$$\text{cos}\left({\theta }_{G(\mathit{\text{Eq.}}15)}\right)\approx \overline{\text{cos}\left({\theta }_i-{\theta }_j\right)},1\le i<j\le K$$ (B7)

Use Taylor Series to expand the cosine item:

$$\begin{array}{cc}\text{cos}\left({\theta }_{G(\mathit{\text{Eq.}}15)}\right)\approx \hfill & \overline{{\displaystyle \sum _{n=1}^{\infty }\frac{{(-1)}^n}{(2n)!}{\left({\theta }_i-{\theta }_j\right)}^{2n}}}\hfill \\ \hfill & \approx \overline{1-\frac{1}{2}{\left({\theta }_i-{\theta }_j\right)}^2+\frac{1}{24}{\left({\theta }_i-{\theta }_j\right)}^4-\frac{1}{720}{\left({\theta }_i-{\theta }_j\right)}^6+\frac{1}{40320}{\left({\theta }_i-{\theta }_j\right)}^8}\hfill \\ \hfill & =1-{{\sigma }_{\theta }}^2+\frac{1}{2}{{\sigma }_{\theta }}^4-\frac{1}{6}{{\sigma }_{\theta }}^6+\frac{1}{384}{{\sigma }_{\theta }}^8\hfill \end{array}$$ (B8)

The above derivation utilizes the facts that θ_i is independent of θ_j when i ≠ j. The high even order moments of θ_i, such as E(θ_i⁴)=3σ_θ⁴, E(θ_i⁶)=15σ_θ⁶ and E(θ_i⁸)=105σ_θ⁸, are obtained from the generating function of the preassumed Gaussian distribution N(θ₀, σ_θ²), and the high odd order moments are zero. To improve the precision of recovering σ_θ further, higher order item in the Taylor series can be added. In practice, Eq. (B8) is sufficient and can be solved with Aitken method.

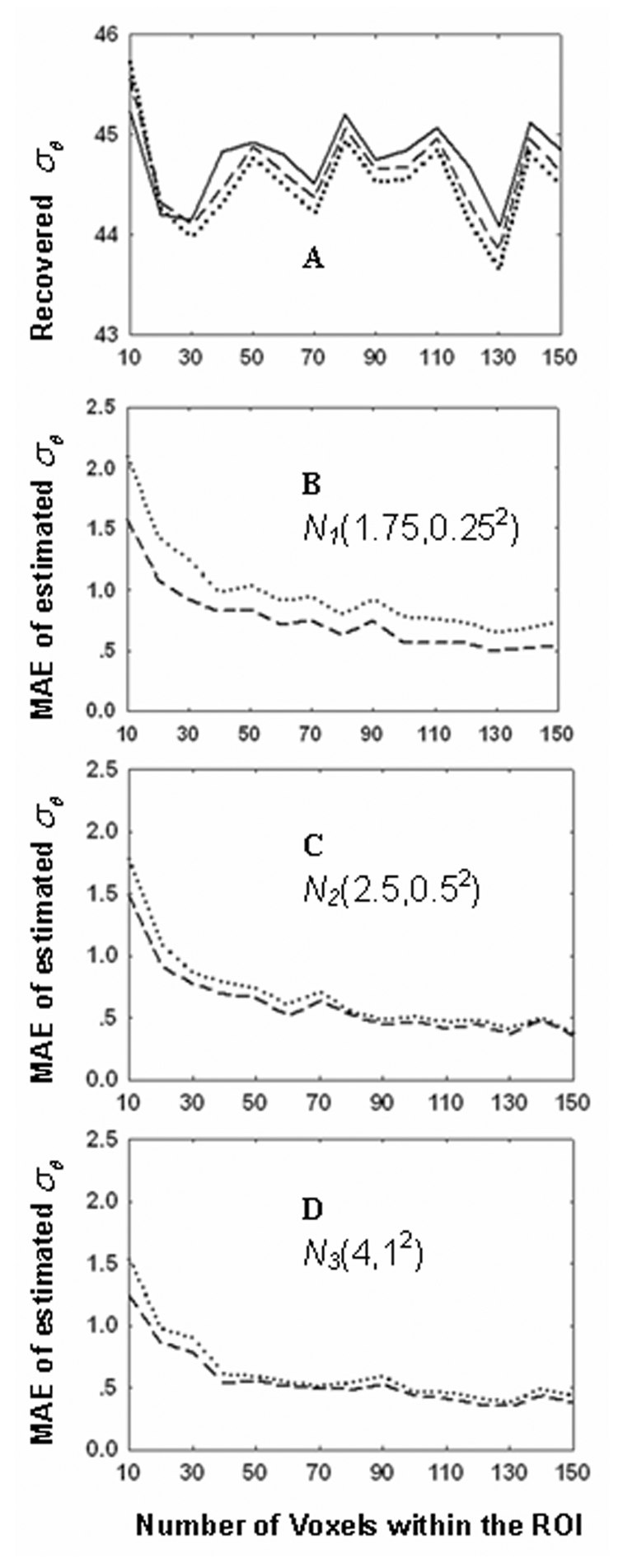
By applying Eq. (B8) to datasets obtained from the human hippocampus in Table 3, the σ_θ can be obtained from ${\widehat{\theta }}_G$. The results are listed in Table 5 and the statistical significances are the same as in Table 3.

Table 5.

Statistical significance of σ_θ calculated from Eq. (B8) based on ${\widehat{\theta }}_G$ calculated from Eq. (15) in the hippocampus region of three subject groups.

A. Recovered σθ (Mean±SD)
σθ(degree)	AD		MCI		Control
Hippocampus nr	59.07 ± 10.48		46.03 ± 5.36		30.30 ± 6.81
Hippocampus rg	54.99 ± 12.99		49.00 ± 7.33		32.78 ± 8.61
B. One-way unbalanced ANOVA for σθ of three subject groups
Measurement	Fnr(2,23)	p-valuenr		Frg(2,23)	p-valuerg
σθ	26.209	<0.0001		10.392	0.0006
C. Pairwise T-test between three subject groups
One-tail t-test for σθnr			One-tail t-test for σθrg
AD vs. MCI **	p = 0.0042		AD vs. MCI		p = 0.2594
MCI vs. CONTROL **	p = 0.0008		MCI vs. CONTROL **		p = 0.0047
AD vs. CONTROL ***	p < 0.0001		AD vs. CONTROL ***		p = 0.0002
D. Kruskal-Wallis Nonparametric Tests for σθ of three subject groups
Measurement	Hnr	p-valuenr		Hrg	p-valuerg
σθ	17.939	0.0001		11.478	0.0032

nr – no CSF voxels regression, rg – with CSF voxels regression.

^*indicates p < 0.05

^**indicates p < 0.01

^***indicates p < 0.001.