Is there a Population II analogy to the F star lithium dip?

Abstract

Observers have found a small number of lithium-depleted halo stars in the temperature range of the Spite plateau. The current status of the mass-loss hypothesis for producing the observed lithium dip in Population (Pop) I stars is briefly discussed and extended to Pop II stars as a possible explanation for these halo objects. Based on detections of F-type main-sequence variables, mass loss is assumed to occur in a narrow temperature region corresponding to this “instability strip.” As Pop II main-sequence stars evolve to the blue, they enter this narrow temperature region, then move back through the lower temperature area of the Spite plateau. If 0.05 M_⊙ (solar mass) or more have been lost, they will show lithium depletion. This hypothesis affects the lithium-to- beryllium abundance, the ratio of high- to low-lithium stars, and the luminosity function. Constraints on the mass-loss hypothesis due to these effects are discussed. Finally, mass loss in this temperature range would operate in stars near the turnoff of metal-poor globular clusters, resulting in apparent ages 2 to 3 Gyr (gigayears) older than they actually are.

The age and density of the universe remain outstanding issues in observational cosmology. As a sensitive indicator of baryonic density during Big Bang nucleosynthesis, the primordial lithium (⁷Li) abundance is of extreme interest (1–3). Estimating this value from observed stellar features depends on understanding the production and destruction mechanisms causing the abundance to evolve in individual stars and between stellar populations.

Complicating the determination of the original lithium abundance is a narrow temperature region in which lithium depletion is observed in Population (Pop) I stars (4, 5). Within 1 gigayear (Gyr) of the zero age main-sequence, F-type stars in the temperature range 6,600 ± 200 K show a substantial lithium depletion. The possible interaction of this “lithium dip” with the mechanism causing a general decrease of the lithium abundance in later-type stars must be understood in the metal-poor stars of the Spite plateau (6) from which the primordial value is determined.

The discovery of a lithium-deficient main-sequence turnoff star, G186-26 (7), demonstrated that a nonuniform depletion mechanism existed in the halo population. Evidence for this existence was strengthened by Thorburn (8) who has found two additional low-lithium stars in the temperature range 5,600 to 6,200 K. These objects are either pathologically low in lithium for some unknown reason or represent subgiants that have evolved from the “F-star dip.” For a halo age of 9 Gyr, or older, a few post-turnoff, subgiant stars are expected to be visible in this temperature region.

Hypotheses to understand the lithium dip in F-type stars include radiative diffusion (9, 10), rotational mixing (11, 12), and localized mass loss on the main sequence (13). Both radiative diffusion and rotational mixing have difficulty producing the shape of the lithium dip without some additional hypothesis like mass loss (11). There is evidence suggesting that something like rotation is operational in the G-star region. A study by Deliyannis, Pinsonneault, and Duncan (14) demonstrated that the spread in equivalent width of lithium lines among the lithium-depleted G stars was larger than expected from statistical fluctuation, although the spread appears small in comparison to the overall lithium depletion. If this G-star lithium depletion is due to rotation instead of convective depletion (15), it requires a very tight relation between the rotational mixing rate and the initial mass. If convective regions are responsible for the G-star lithium abundances, the spread in equivalent widths restricts rotation to be a modest contributor to the observed depletion. Additionally, observations of Pop II binaries (16) find that tidally locked systems show the same lithium abundances as field stars, suggesting a minimal role for rotation (for possible Pop I counter example, see Deliyannis et al. ref. 17). At the moment, each of these hypotheses is viable, and development is continuing. Here we will examine the consequences of the mass-loss hypothesis in Pop II stars to provide observational tests.

The mass-loss explanation was motivated by the coincidence of the observed lithium dip in F stars with an extrapolation of the instability strip down to the main sequence (18). The existence of Delta Scuti stars (early F-type variables about a magnitude above the main sequence) supported this extrapolation to the required temperature range. Delta Scuti stars themselves are thought to be subgiants that have evolved from slightly higher mass main-sequence objects (19) and would spend too little time in the instability strip to lose their lithium. On the main sequence itself, the detection of variability in a number of F stars (20) marks the high-temperature wing of the proposed instability (and mass-losing) strip.

In a preliminary study, Dearborn et al. (21) applied the mass-loss hypothesis to Pop II models and showed that subgiant stars with low lithium abundances would be expected to be seen in some stars. While the mass-loss rates necessary to produce the lithium dip are far too small for a direct observational signature, there is some hope to detect related phenomena. Mass loss in the presence of even a small magnetic field produces rotational breaking. If a careful comparison of the rotation rates in F-type stars showed a systematic lowering of rotation in those stars with a pronounced lithium deficiency, it would strongly suggest the occurrence of mass loss. Balachandran (22) saw some evidence that the rotation rates in lower-temperature, lithium-deficient stars were preferentially lower, but additional investigation (23) has found little correlation between rotation rate and lithium abundance. Such investigations might be extended to higher temperatures.

In an attempt to test the generalized mass-loss hypothesis, Swenson and Faulkner (24) examined the luminosity function of open cluster stars. They show that the luminosity function provides a powerful tool for testing the existence of mass loss. While available data can be used to exclude mass loss as the origin of the gradual decline observed in later G-type stars, the sparsity of open clusters inhibits testing the small amount of mass loss necessary for lithium depletion observed in F-type stars.

Globular clusters are much richer objects, and the development of charge-coupled device photometry has permitted the extension of luminosity functions down onto the main sequence. Low-metalicity (low-opacity) models are hotter, and so the most metal-poor, oldest globular clusters are the most likely to be affected by the mass loss discussed here. Pop I stars with a temperature of 6,500 K lie deep in the red wing of the lithium dip. The blue and visible color bands corresponding to this temperature are in the range 0.37 to 0.48, depending on the metalicity. The color of the turnoff in metal-poor ([Fe/H] = −2) clusters like M92 (25) is near 0.38, corresponding to a temperature where lithium depletion occurs in Pop I stars. [Recent work by Drake et al. (26) suggests that globulars may be even hotter than their blue and visible colors indicate, which would further support the possibility of the turnoff intersecting the varible strip.] Old clusters, like this, are the most critical for constraining the age of the universe, as discussed in Shi et al. (27). With this, the work of Swenson and Faulkner (24) suggests that globular cluster observations could provide a definitive test of the mass-loss hypothesis.

Here we begin a more specific study examining the effect of mass loss localized in a narrow temperature range (as motivated by the Pop I lithium dip) on the isochrones and luminosity function of Pop II models. An immediate consequence of this hypothesis is that stars evolving into the mass-losing region turn at an earlier stage of evolution. The resulting isochrones have a lower luminosity turnoff, causing clusters to appear “older.” Because the temperature range of the lithium dip is narrow, the mechanism that produces it will affect bluer, low-metalicity globular clusters more than those with higher metalicity.

As a result of this attempt to understand the features in lithium abundances, a mechanism results that affects the ages assigned to globular clusters (see also Wilson et al. ref. 18). These ages are an important constraint on cosmological models, and any plausibly supported mechanism that impacts them must be tested. By causing stars to turn earlier in their evolution, an excess of subgiant-like objects will occur in clusters whose turnoff is near the mass-loss region. While such an excess has been observed in the globular cluster M30 (28), it is small. Following Swenson and Faulkner (24), the luminosity function may be used to suggest mass loss in the F-star region and to limit its magnitude.

Mass-Loss Assumptions and Constraints

As a star approaches the main sequence, lithium, a fragile nucleus, is destroyed throughout the interior. For a 0.8 M_⊙ (solar mass) Pop II model, this results in a lithium-abundance profile in which the abundance drops rapidly, at a depth of about 0.05 M_⊙ below the original surface. Because the lithium profile is established early in the main-sequence lifetime, the lithium depletion is nearly independent of the time history of the mass loss and is primarily dependent on how much mass is lost.

The timescale of lithium depletion is affected by the presence of the small convection zone that exists in an F-type star. Once mass loss has driven the base of the convection zone into a lithium-deficient region, that material is mixed with the lithium-rich material present in the convection zone. The surface begins immediately to show a small lithium depletion. As Swenson and Faulkner (24) showed, the lithium abundance drops exponentially on a mass scale of the convection zone. A well developed lithium dip requires an amount of mass loss equal to about five times the mass in the convection zones, resulting in a gradual development of a lithium dip.

Boron and beryllium are hardier nuclei requiring slightly higher temperatures to destroy. In this temperature range, the lithium and beryllium regions in Pop I stars are well enough separated that lithium must be almost completely destroyed before a detectable beryllium depletion occurs. Indeed, observations of the Hyades by Boesgaard and Budge (29) show a well developed lithium dip with no beryllium depletion. A more recent paper by Deliyannis and Pinsonneault (30), however, identifies a Pop I star in which beryllium is depleted by a factor of 5-10 while lithium is still present at the percent level. If this star is representative of most lithium dip objects, and not a special case such as a binary, it presents a dilemma for the mass-loss hypothesis. The relative depletion of beryllium and lithium by mass loss is metal dependent. Structure differences in the outer layers of metal-poor stars result in a lingering of lithium past the point where beryllium depletion commences. In our metal-poor models, when lithium has decreased to 20% of its original value, the beryllium abundance has only begun to show some effect, and when the lithium abundance has decreased to 3%, the beryllium abundance has dropped to 60%. This will be discussed further in Results. Complete depletion of the beryllium requires nearly 0.1 M_⊙ of mass to be lost. As we discuss below, this much mass loss would strongly affect the luminosity function of a cluster of stars. Boron is hardier still.

The lifetime of Pop II stars with temperatures near 6,600 K is of order 10 Gyr, so that a steady rate of only 5 × 10⁻¹² M_⊙/yr will have a significant impact on the lithium abundance. As the F-star dip defines a narrow temperature range, evolving stars move through it and spend only part of their lifetimes losing mass. As a result, peak mass loss rates of order 10⁻¹¹ M_⊙/yr are required. Even this peak rate is below the limits placed on the mass-loss rate from the cooler, F5, Pop I star, Procyon (31). Because of their shorter lives, the peak rate required in Pop I stars is a few times higher than for Pop II stars and is slightly above the limit set for Procyon. The location of the instability strip (and any associated mass loss) is highly temperature sensitive, and the observed Pop I variables appear to be located at a slightly higher temperature.

The halo appears to be too old to have many stars defining the high-temperature wing of the lithium dip (>10 Gyr). Of the halo subgiants observed by Pilachowski et al. (32) few have temperatures above 6,000 K. A 2-Gyr difference in age results in an order of magnitude difference in the lithium abundance of subgiants. Most of the observed subgiants must originate from stars that never reach a temperature necessary for pulsation and possible mass loss. There almost certainly is some spread in ages for the halo, and as a result, it is hardly surprising that only a few of the observed subgiants show the lithium depletions discussed here. They could originate only from stars that were the last low-metal stars to form.

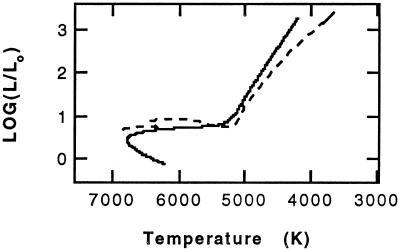
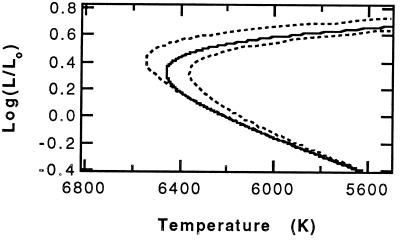
Because the lithium dip is not defined for Pop II stars, we must use the lithium distribution observed in the Pop I stars to define a temperature dependence for the mass-loss rate and apply this to Pop II models. The shape of the lithium dip in Pop I and Pop II stars will differ, even if the same temperature dependence is assumed for the mass loss. Fig. 1 shows the evolutionary track of a Pop I (M = 1.50 M_⊙, X = 0.70, Z = 0.02) model, and a Pop II model (M = 0.85 M_⊙, X = 0.76, Z = 0.0002), while on the main sequence, the temperature of the Pop I model decreases. The relatively small change in the temperature of these objects while on the early main sequence results in a lithium dip that is closely related to the mass-loss dependence assumed, though the region of lithium depletion will be shifted to slightly lower temperatures. The temperatures of Pop II models increase considerably over the main-sequence lifetime, resulting in a lithium dip that extends to higher temperatures than those observed in Pop I stars.

Figure 1.

Evolutionary tracks are shown for models that cross the temperature region of the lithium dip. While on the main sequence, Pop I models (1.50 M_⊙ X = 0.70, z = 0.02) decrease in temperature. The Pop II (0.8 M_⊙ X = 0.76, Z = 0.0002) model increases significantly in temperature and luminosity over its main-sequence lifetime, then decreases as a subgiant.

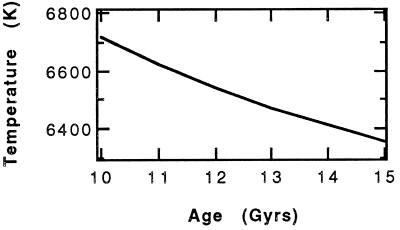
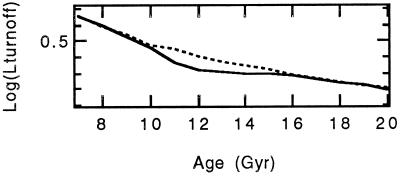
For the purpose of this paper, we will assume the mass loss has a gaussian dependence on temperature, with a peak loss rate of 10⁻¹¹ M_⊙/yr. Because Pop I stars evolve to lower temperatures, a central temperature below 6,500 K is unlikely to fit the observed location of the lithium dip, and we will consider temperatures of 6,500 K and 6,600 K. As discussed in the introduction, evolutionary tracks of stars that turn to the red in the mass-losing region will do so at a slightly lower luminosity and appear older. The age range affected is very dependent on the temperature of the mass-loss region. In Fig. 2, the turnoff temperature for a set of unperturbed models is plotted versus age. A peak mass loss centered near 6,600 K will affect the apparent age of clusters near 11 Gyr old. Reducing the central temperature of the mass loss to 6,500 K results in clusters between 12 and 13 Gyr looking 2 to 3 Gyr older.

Figure 2.

The temperature of the turnoff is plotted versus age for the non-mass-losing Pop II models (X = 0.76, Z = 0.0002). Mass loss in a narrow temperature range will affect the apparent age of clusters whose turnoff is near that age, making them look older.

The Models

Models were calculated at least every 0.05 M_⊙ between 0.6 and 1.0 solar masses, and when necessary every 0.02 M_⊙. The initial hydrogen mass fraction was set to 0.76, consistent with the most recent determinations of the primordial helium value (33, 34), and the metalicity set to 0.01 solar, representative of metal-poor globular clusters. The new opacities computed from the OPAL computer code (35, 36) were used at temperatures above 6,000 K, and Los Alamos opacities, including the contribution of molecules, were used for lower temperature regions (37).

All models were begun as pre-main-sequence objects on the Hayashi track and evolved to helium flash, and a mixing length was selected to fit the color magnitude data for M30 (28). The code that we used is derived from that of Eggleton (38, 39) and is described in Dearborn, Greist, and Raffelt (40). As a benchmark, the code produces a solar model with 7.9 solar neutrino units and matches the p-mode spectrum comparably to the calculations of Bachall and Ulrich (41).

The nucleosynthesis network used in this calculation included the reactions to track deuterium, ³He, ⁴He, ⁶Li, ⁷Li, ⁹Be, and all stable CNO isotopes. In the mass range that we examined here, pre-main-sequence deuterium was fully converted to ³He. At masses below 0.65 M_⊙, pre-main-sequence burning completely destroyed the fragile ⁶Li and reduced the surface abundance of ⁷Li, though not as much as in Pop I models (42). The ⁹Be showed no pre-main-sequence evolution. This pre-main-sequence depletion is probably substantially responsible for the lithium decrease seen at temperatures below the Spite plateau.

Results

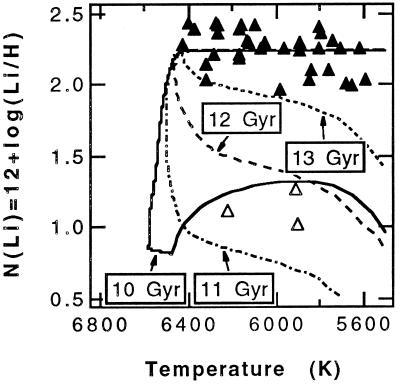
We begin by considering an individual case where the mass loss has a peak rate of 10⁻¹¹ M_⊙/yr centered at 6,500 K. The full width at half maximum of the gaussian was 200 K. This resulted in a lithium dip that matched the low-temperature wing of the Pop I dip, though, for reasons explained above, the high-temperature wing was broader. The resulting lithium abundances for ages between 10 and 13 Gyr are plotted against temperature in Fig. 3. The limits for the lithium-depleted objects observed by Hobbs et al. (7) and Thorburn (8) are shown as open triangles. Main-sequence stars lie along the top of the plot with their original lithium abundances shown as filled triangles (43). For the assumed values of mass loss, stars in the age range 10 Gyr to 12 Gyr have turnoffs in the lithium dip region, and subgiants show lithium depletion.

Figure 3.

The predicted lithium abundance for various ages is plotted against temperature for a mass-loss rate of 10⁻¹¹ M_⊙/yr centered at 6,500 K. Between 10 and 12 Gyr, the subgiants originate from lithium-depleted stars. Subgiants on the 10-Gyr isochrone originate in the warm wing of the lithium dip and do not show as much depletion of stars at the bottom of the dip. Subgiants of the 12- and 13-Gyr isochrones show progressively less lithium depletion as they arise from the red wing. Observed lithium abundances (7, 8, 43) are included for comparison.

For ages less than 10 Gyr, the subgiant stars originate on the high-temperature side of the lithium dip. Their passage through the mass-loss region is too quick to produce a significant lithium depletion. Increasing the mass-loss rate broadens the age range some, but as we will discuss later, rapidly leads to unacceptable modifications of the luminosity function. Between 10 Gyr and 12 Gyr, stars from the base of the lithium dip are subgiants and show the maximum amount of lithium depletion for the mass loss that occurs. After 12 Gyr, the low-temperature wing of the lithium dip begins to evolve, and again the lithium depletion is negligible.

The stars observed by Thorburn (8) have temperatures lower than those defined by the Pop I lithium dip. Regardless of mechanism, if the low lithium stars are related to the F-star dip seen in Pop I stars (either by mass loss or by diffusion), they must be subgiants. As the evolution rate increases considerably for subgiants, relatively few of the stars observed at any particular temperature are expected to be in this phase. It is simple to calculate the expected ratio of subdwarf to subgiant stars. In the temperature range 5,600 K to 6,300 K, the mass range contributing to this ratio is small (0.65 M_⊙ to 0.90 M_⊙ or less, depending on the age), so the result is insensitive to the assumed initial mass function. However, predicting this ratio for the halo is complicated by the possible age and metalicity range. For a population with a range of ages and compositions, the subgiant population can evolve from stars both above and below the F-star dip, although, as discussed above, most subgiants probably originate from stars that never reached the F-star region. Observations of halo subgiants by Pilachowski et al. (32) show many of them to have unperturbed lithium.

As the presence of a mass-losing region near the turnoff affects the evolutionary track of a star, the ratio of subdwarfs, main-sequence stars to subgiant stars is affected. For mass-loss rates centered at 6,500 K and 6,600 K, the ratio ranges from 60 to 80 subdwarf stars for every subgiant at an age of 8 Gyr. By 10 Gyr, the ratio drops to between 25 and 30, and by 15 Gyr the ratio is 10 to 13. An extensive survey by Thorburn (43) finds four lithium-depleted stars in a sample of 70 stars. While this ratio is consistent with the mass-loss hypothesis and an old halo, it neglects the fact that subgiants are 1 to 2 magnitudes brighter than dwarfs (depending on temperature) and, in a magnitude-limited survey are observed in a greater volume. This correction requires younger ages for the halo, near 10 Gyr. If mass loss in the temperature region of Pop I, F stars is causing the lithium depletions observed by Thorburn, the ratio of normal to depleted stars will be a sensitive indicator of the age range in the halo, once the volume correction is made.

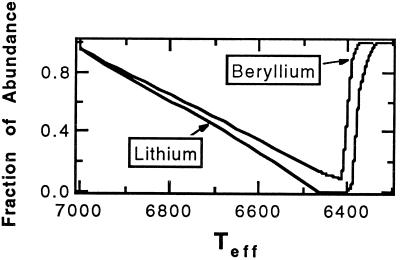
As discussed above, sufficiently high mass-loss rates in Pop II stars can cause detectable beryllium depletion while some lithium continues to exist. In Fig. 4, the beryllium and lithium depletions are shown for our current example at an age of 9 Gyrs. For this mass-loss rate, several percent of the original lithium still remains by the time that beryllium is depleted by a factor of 5.

Figure 4.

In low-metal objects, the beryllium depletion can begin before lithium is exhausted. This shows the lithium and beryllium reductions versus temperature for our standard mass-loss case at 8 Gyr.

Before turning to an examination of the effect that mass loss has an apparent cluster ages and luminosity functions, we wish to consider the sensitivity of our results to the assumed central temperature of the mass loss region. The observed lithium distribution in Pop I stars constrains the temperature of the peak mass-loss rate to a narrow range around 6,500 K or 6,600 K. Because more massive stars have a shorter lifetime, increasing the central temperature to 6,600° requires an approximately 20% increase in the peak mass-loss rate to provide the same levels of lithium depletion, and, in this case, the maximum lithium depletion occurs between 9 and 11 Gyr. Reducing the central temperature to 6,400 K requires reducing the peak mass-loss rate to obtain the lithium depletion without losing too much mass and concentrating all of the stars in the mass-losing region at the low-temperature edge. For this temperature, the peak lithium depletion occurs for stars with ages between 12 and 15 Gyr.

The ages determined for globular clusters are fundamentally dependent on the ability to identify the luminosity of the turnoff in an Hertzsprung–Russell diagram. Charge-coupled device photometry has improved the definition of this luminosity and reduced the associated uncertainty in globular cluster ages. In Fig. 5, the luminosity of the turnoff is plotted against age for a cluster without mass loss and one with the standard mass-loss assumptions described above. At 12 Gyr, subgiants originate from stars that have lost 0.05 M_⊙ and show lithium depletions exceeding an order of magnitude. The turnoff luminosity of the 12 Gyr isochrone is that of a 15-Gyr cluster without mass loss. This is shown more conventionally in the isochrone plots in Fig. 6. The 12-Gyr mass-losing isochrone is slightly bluer than the 15-Gyr standard isochrone because it is younger, and stars with masses below 0.75 M_⊙ have not been affected by the mass loss. A small reduction in the assumed mixing length will make these curves coincident.

Figure 5.

Mass loss in a narrow-temperature region lowers the luminosity of a clusters turnoff, making it look older. The effect of a mass loss rate of 10⁻¹¹ M_⊙/yr centered at 6,500 K is compared to non-mass-losing models. The 12-Gyr isochrone of a mass-losing model has the same luminosity as a 15-Gyr standard model.

Figure 6.

Twelve- and 15-Gyr isochrones (dotted lines) of models without mass loss are shown around the 12-Gyr isochrone (solid line) formed from models with a mass-loss rate of 10⁻¹¹ M_⊙/yr centered at 6,500 K. The mass-loss isochrone has the same luminosity as the 15-Gyr isochrone, but is bluer. A small reduction in the assumed mixing length would make these isochrones nearly identical.

If the order of magnitude-lithium depletions observed by Thorburn results from mass loss, they require approximately 0.05 M_⊙ of mass be lost over the main-sequence lifetime, and result in a cluster that appears as much as 25% older. A mass-loss rate that removes only 0.03 M_⊙, reduces the surface lithium by a factor of 3 instead of 10 and results in a cluster that appears approximately 17% older. We also evolved a set of models in which some stars lost 0.1 M_⊙. Stars from the base of the lithium dip retained virtually no lithium and appeared 50% older than they actually were. This much mass loss caused all of the stars in the mass-losing region to concentrate at the low-temperature edge of the region and significantly impacted the luminosity function. For the models calculated here, age changes of over 3 Gyr appeared to impact the luminosity function dramatically. A comparison to actual data will be made in a later paper to set firm limits on the possible age difference.

The same charge-coupled device photometry that is improving the color-magnitude diagrams for globular clusters is permitting the luminosity function to be determined down onto the main sequence. Standard, mass-conserving calculations of stellar evolution fit the general characteristics of the observed curves (28, 44), but there are some differences. First, a small, but significant, excess is seen at luminosities above the turnoff. Second, the drop to the giant branch is not as large in the observed clusters as it is in the calculations.

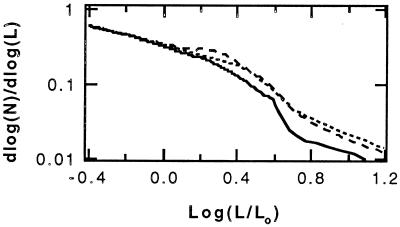
In Fig. 7, we assume a Salpeter mass function to plot the luminosity function [dlog(N)/dlog(L) vs. log(L)] of our models. The luminosity of a 15-Gyr cluster with no mass loss is shown as a solid line. Luminosity functions for clusters losing 0.03 (dashed line) to 0.05 (dotted line) solar masses are given for comparison. The ages of the mass-losing clusters were selected so that the isochrones would have the same turnoff luminosity as the mass-conserving cluster. The mass-losing models are seen to have a small excursion from the unperturbed curve and an increase in the level of the giant branch. Mass loss of 0.1 M_⊙ (not shown) produces a large bump in the luminosity function as all of the stars between 0.8 and 0.9 M_⊙ congregate at the lower mass edge of the temperature range where mass loss is assumed to occur.

Figure 7.

The calculated luminosity function of a mass-conserving cluster at an age of 15 Gyr is shown as a solid line. Luminosity functions predicted for models losing 0.03 M_⊙ (dotted line) and 0.05 M_⊙ (dashed line) are shown for ages that have the same turnoff luminosity. Mass loss in a narrow-temperature region enhances the number of stars at the lower edge of that temperature range, resulting in a bump on the luminosity function.

Conclusions

The hypothesis that a small amount of mass loss is responsible for the lithium depletion seen in Pop I, F-type stars has been extended to calculations of metal-poor Pop II models of the same temperature. Such mass loss affects the isochrones of models that would cause a cluster to appear older than it genuinely was. Small amounts of mass loss should improve the fit of the calculated luminosity function with actual data, but large amounts of mass loss probably can be excluded. It will require additional work to compare our models to globular cluster data, but it is exciting that globular clusters of 12 Gyr can appear as old as 15 Gyr (if the mass-loss hypothesis is correct). Observations of the lithium abundances in the subgiants of the oldest globular clusters will provide a definitive test of whether or not mass loss has occured at a sufficient level to affect the age.

Three lithium-depleted stars are known in the temperature range 5,900 K to 6,200 K, (7, 8). Subgiant stars in this temperature range are 1.5 to 2 magnitudes brighter than their main-sequence counterparts, and, in an apparent magnitude-limited sample, they are detected to a distance 2.0 to 2.5 times further out (for an age of 12 Gyr). This must be considered in comparing the expected number of lithium-depleted dwarfs in a particular temperature range.

This also leads to a major concern for the hypothesis, requiring that the lithium-deficient stars observed by Thorburn are evolved. In this hypothesis, the low-temperature lithium-deficient stars all must be subgiant stars. Thorburn considered this problem, and, using a luminosity for subgiants that is consistent with our models, found that the proper motions of her lithium-deficient stars corresponded to velocities of 725 and 910 km/s. These are much higher than the observed radial velocities of halo stars and would require an extended dark halo to be bound. If astrometry or surface gravity indicators prove these stars to be dwarfs, it will be necessary to abandon the hypothesis that they are related to the Pop I, F-star dip. Another potential concern for the hypothesis is the representativeness of Be depletion in Pop I stars with detectable Li remaining. (This would not be a problem for Pop II.)

ABBREVIATIONS

Pop

population

Gyr

gigayears