Abstract
Graphs of second harmonic generation coefficients and electro-optic coefficients (measured by ellipsometry, attenuated total reflection, and two-slit interference modulation) as a function of chromophore number density (chromophore loading) are experimentally observed to exhibit maxima for polymers containing chromophores characterized by large dipole moments and polarizabilities. Modified London theory is used to demonstrated that this behavior can be attributed to the competition of chromophore-applied electric field and chromophore–chromophore electrostatic interactions. The comparison of theoretical and experimental data explains why the promise of exceptional macroscopic second-order optical nonlinearity predicted for organic materials has not been realized and suggests routes for circumventing current limitations to large optical nonlinearity. The results also suggest extensions of measurement and theoretical methods to achieve an improved understanding of intermolecular interactions in condensed phase materials including materials prepared by sequential synthesis and block copolymer methods.
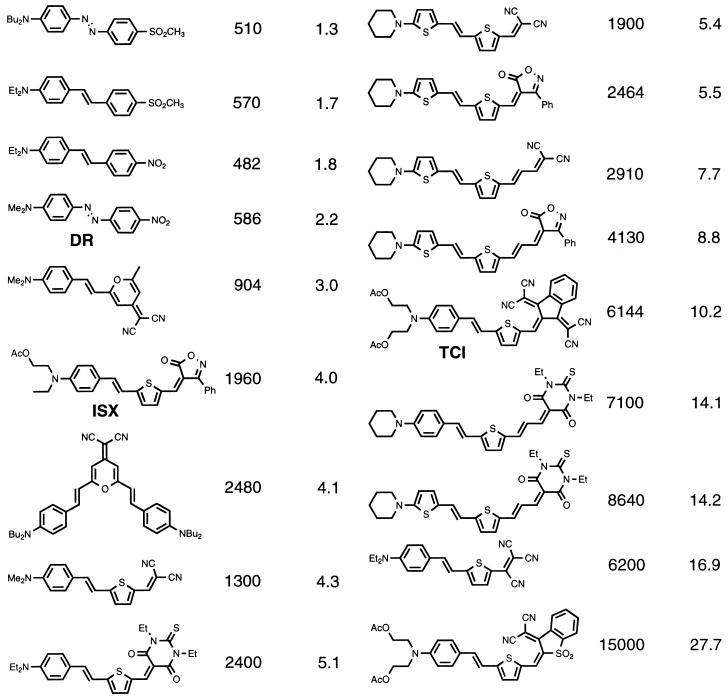
Nearly two decades ago, considerable excitement was generated by the theoretical prediction of large molecular hyperpolarizabilities for organic materials with extended π-electron systems (1–4). The past decade has witnessed refinement of theoretical calculations and translation of theoretical results to structure–function relationships that can be utilized by organic chemists to guide the synthesis of new chromophores (5–7). In Table 1, we summarize representative chromophores derivative from this activity (8–11). If these chromophores could be incorporated into perfectly ordered noncentrosymmetric lattices, electro-optic coefficients of many hundreds of picometers per volt could be anticipated. Materials exhibiting such large macroscopic optical nonlinearity would, in turn, have a dramatic effect on communication and electromagnetic field sensing technologies (11).
Table 1.
Representative high-μβ chromophores
| Chromophore | μB, 10−48 esu | μβ/MW | Chromophore | μβ, 10−48 esu | μβ/MW |
|---|---|---|---|---|---|
μβ/MW: μ, chromophore dipole moment; β, first molecular hyperpolarizability; and MW, chromophore molecular weight. DR, disperse red; ISX, isoxazolone; TCI, tetracyanoidane; esu, electrostatic units.
Such optical nonlinearities (hence, noncentrosymmetric order) have not yet been achieved. Efforts to obtain organic crystals exhibiting large electro-optic coefficients and which can be used to fabricate devices have largely proven unsuccessful (11). Very few crystal groups reflect noncentrosymmetric symmetry, and the small number that do are rarely assumed by organic chromophores. Moreover, when such organic crystals are realized (12), they are typically characterized by large growth anisotropy, making them unsuitable for device applications (11). Difficulty in obtaining suitable organic crystals has motivated attempts to fabricate noncentrosymmetric chromophore lattices by vapor phase deposition (or molecular beam epitaxy) methods (11, 13, 14), by Merrifield-type synthetic approaches (11, 13, 15, 16), by Langmuir–Blodgett film fabrication methods (13, 17), by block copolymer approaches (11), and by electric field and laser-assisted poling methods (11, 13). Of these methods, electric field poling is the protocol most easily applied to a wide range of chromophores and poling has been the most commonly used materials processing approach for fabrication of prototype devices utilizing organic nonlinear optical materials. To date, electric field poling has yielded materials with optical nonlinearities in the range of 20–55 pm/V (11, 18–20) which is substantially below the values expected if chromophore–chromophore electro-static interactions are neglected and electro-optic coefficients are predicted to scale as μβ/MW, where μ is the chromophore dipole moment, β is the first molecular hyperpolarizability, and MW is the chromophore molecular weight.
The neglect of chromophore–chromophore electrostatic interactions, although widely used in discussing putative scaling of microscopic to macroscopic optical nonlinearity (21–23), has not been justified. Indeed, it is more reasonable, in general, to assume that noncentrosymmetric order (and hence, electro-optic and second harmonic generation coefficients) will be determined by the competition of ordering and disordering electrostatic forces. Ordering forces include electric field poling forces and surface forces at phase boundaries. Disordering forces include chromophore–chromophore electrostatic interactions and thermal (entropic) effects.
The theories of London (24–27), Fowler (28), Piekara (29, 30), Debye (31), and Ehrenson (32) provide direction for the computation of order parameters, 〈cos3θ〉 (where θ is the angle relating the principal axis of the dipolar chromophores to the applied field direction), describing the acentric order that is defined by the competition of ordering and disordering forces. Explicitly,
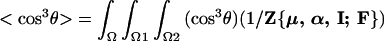 |
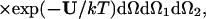 |
1 |
where the partition function is given by
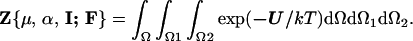 |
2 |
F is the effective electric field (including Onsager corrections for the dielectric constant of the medium); μ is the dipole moment, α is the polarizability, I is the ionization potential of the chromophore, respectively. T is the poling temperature and k is the Boltzmann constant. U is the total electrostatic energy U = UF + UDDα + Uiα. For an interacting chromophore pair, the chromophore-applied field interaction is UF = (μ1 + μ2)⋅F − (1/2)(α1 + α2)F′⋅F. The dipole–dipole and induced-dipole interactions are given by UDDα = EDD + Udα2,1 + Udα1,2. The dipole–dipole term, EDD, can be written, in general, in terms of the Eulerian rotation matrices interrelating the dipoles as
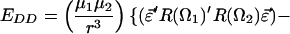 |
3 |
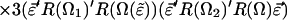 |
where
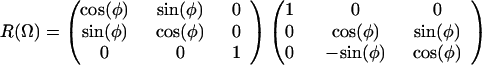 |
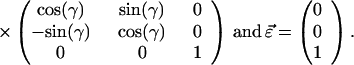 |
This can be simplified to
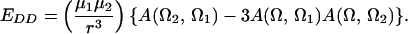 |
The induced dipole terms, Udα2,1 and Udα1,2, are of the form
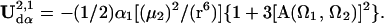 |
4 |
The total electrostatic energy is defined by rotation matrices relating the chromophores to the applied field [R(Ω1) and R(Ω2)] and to each other [R(Ω)]. The critical angular dependencies can be seen in the terms UF and UDDα; the dispersion term, UIα, add no new angular dependence. The order parameter is readily computed by evaluating Eq. 1 using numerical methods and such a treatment is necessary to explicitly consider the effects of chromophore shape.
To obtain an analytical result, we must follow London (24) and employ an “effective field” approach to computing the effect of one chromophore upon another. If we further assume spherically symmetrical chromophores and average over the relative orientation of one chromophore with respect to another, we obtain
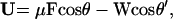 |
5 |
where θ is the angle between the chromophore principal axis and the poling field, θ′ is the angle between the chromophore principal axis and the intermolecular interaction direction. The chromophore–chromophore interaction energy now becomes
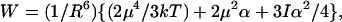 |
6 |
where R is the averaged distance between chromophores. If we also carry out a power series expansion in terms of (μF/kT), keeping only the first term, we obtain
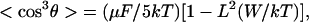 |
7 |
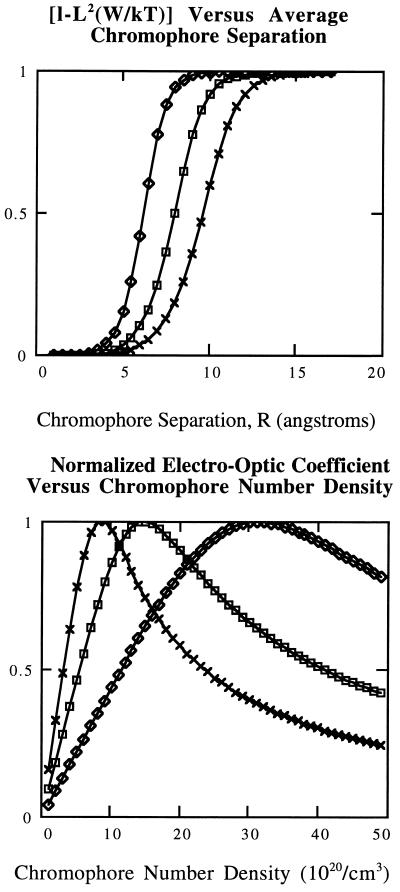
where L is the Langevin function. The term in brackets is an attenuation factor reflecting the reduction in acentric order associated with chromophore–chromophore electrostatic interactions. Graphs of this attenuation factor versus R are shown in Fig. 1 Upper for μ values of 5, 7.5, and 10 Debye and for values of polarizability (3.8 × 10−23 cm3) and ionization potential (8.3 × 10−19 J) appropriate for azobenzene or DR chromophores. These theoretical data suggest that there will be a problem of attenuation of noncentrosymmetric order at moderate to high chromophore loading even for azobenzene chromophores characterized by modest dipole moment and polarizability values and the problem will be even more severe for “high μβ chromophores.” To our knowledge, this communication represents the first correlated theoretical and experimental investigation of the limitation to optimization of macroscopic optical nonlinearities arising from chromophore–chromophore electrostatic interactions that become important at moderate to high chromophore loading.
Figure 1.
(Upper) Graphs of [1 − L2(W/kT)] versus R are shown as a function of varying chromophore dipole moment (5 Debye, solid line with diamonds; 7.5 Debye, solid line with squares; and 10 Debye, solid line with x’s). Other variables correspond to those for the DR chromophore (see text). (Lower) Graphs of normalized electro-optic coefficient versus chromophore number density N are shown. Symbols have the same meaning as in Upper.
EXPERIMENTAL METHODS
Materials.
Most of the chromophores listed in Table 1 have been prepared and examined in a variety of polymer matrices [polymethylmethacrylate, polycarbonate, and poly(p-phenylene)] utilizing both chemical and physical incorporation to prepare homopolymers and composite materials, respectively. However, due to problems associated with chemical and photochemical instability (under electric field poling conditions) of chromophores containing acceptor functionalities such as the tricyanovinyl, thiobarbirturic acid, etc., groups, we limit the current discussion to chromophores that exhibit good chemical stability under conditions of electric field poling. These include aminonitroazobenzene or DR chromophores and chromophores containing TCI, ISX, and pyrazolone acceptor groups. The synthesis of the TCI and ISX chromophores has been described (ref. 33; A.W.H., S. S. Sun, L.R.D., B.H.R., S. M. Garner, A. Chen, A. Yacoubian, and W.H. Steier, unpublished data). These chromophores have been investigated as composite materials dissolved in the host matrices poly(methylmethacrylate) (PMMA; Aldrich), poly(carbonate) (Aldrich), or derivatized poly(p-phenylene) (POLY-X; Maxdem, San Dimas, CA). Chromophores were covalently incorporated into PMMA-type lattices as described (refs. 33 and 35; A.W.H. et al., unpublished data). Samples are studied as thin films of approximately 1′ μm thickness prepared by spin casting (A.W.H. et al. unpublished data). Details of electric field poling are provided elsewhere (ref. 11; A.W.H. et al., unpublished data).
Measurements.
Second harmonic generation was used for in situ monitoring of poling efficiency (36). Electro-optic coefficients were measured by ellipsometry (37), attenuated total reflection (38), and two-slit interference modulation (39, 40). The cross comparison of results obtained by different methods establish that the deviation of measured electro-optic coefficients from those predicted by μβ/MW scaling is not due to measurement artifacts. Order parameters, reflecting both centro- and noncentrosymmetric ordering, were determined from birefringence measurements, and optical loss was measured by waveguide immersion in a high index liquid as described (ref. 41; A.W.H. et al., unpublished data).
Calculations.
Calculations, at various levels of sophistication, were executed on a variety of computer systems described elsewhere (42). Steric effects and chromophore shape effects were taken into account by treating chromophores as hard geometric objects—e.g., prolate ellipsoids or spheres. Electro-optic coefficients, reff, are related to noncentrosymmetric order parameters, 〈cos3θ〉, by
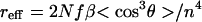 |
8 |
where N is the chromophore number density, f is a frequency dependent local field factor (a product of several terms), and n is the index of refraction. Chromophore number density, N, is related to chromophore weight fraction, w, by N = wN′ρ/MW, where N′ is Avogadro’s number and ρ is material density.
RESULTS AND DISCUSSION
Fig. 1 Lower shows plots of normalized electro-optic coefficients versus chromophore number density. Clearly, maxima are predicted for plots of reff versus N. Increasing dipole moment or polarizability results in shifting the maxima in the curves of reff versus N to lower chromophore number density. Also, the curves are observed to sharpen with increasing chromophore electrostatic interactions. These plots suggest the fundamental nature of the problem of attempting to optimize macroscopic electro-optic coefficient utilizing chromophores with increasing values of μβ (or μα). The linear increase of reff with N predicted and observed at low chromophore loading is rapidly offset by the L2(N2) dependence of 〈cos3θ〉 which dominates at higher loading.
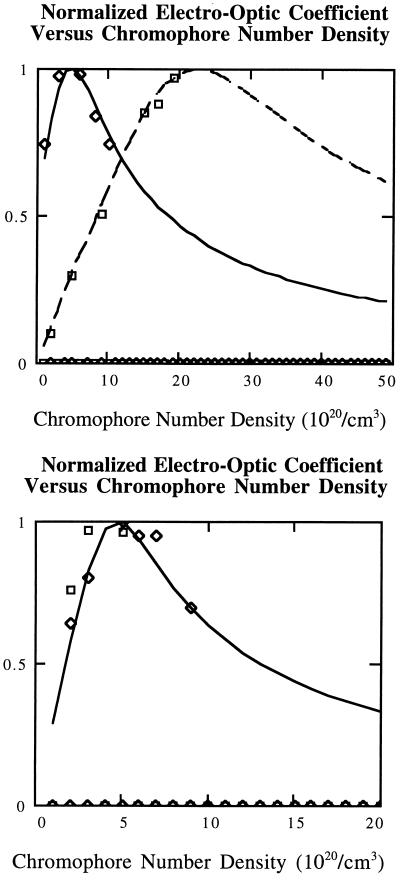
In Fig. 2 Upper, experimental data are shown for the DR chromophore of Table 1 covalently incorporated in PMMA. Also shown is the theoretical curve computed for the best available values of μ, α, I, and ɛ for the DR chromophore/PMMA polymer (A.W.H. et al., unpublished data) and the assumption of an isotropic chromophore. In this approximation and for the magnitude of parameters considered, reasonable agreement is obtained between the analytical result and numerical methods. Similar data and agreement between theory and experiment is observed for a modified DR chromophore dissolved in PMMA to form composite materials (A.W.H. et al., unpublished data). The agreement between theory and experiment is better than anticipated given the approximations involved in Eq. 7 and the nonspherical nature of the DR chromophore. The quality of the agreement may be enhanced by the fact that DR chromophores can undergo rapid trans-cis-trans isomerization in the liquid state that would result in more “isotropic” dynamical properties.
Figure 2.
(Upper) Experimental (squares) and theoretical (dashed line) values of normalized electro-optic coefficient versus chromophore number density are given for the DR chromophore of Table 1. The theoretical graph corresponds to the approximation of spherical chromophore shape and W = 1.14 × 106 Joule⋅(Å)6/R6, where R is given in angstroms. Experimental (diamonds) and theoretical (solid line) values of normalized electro-optic coefficient versus chromophore number density are given for the ISX chromophore of Table 1. Chromophore prolate ellipsoidal shape is explicitly taken into account. If a spherical chromophore shape is assumed then a value of W = 1.85 × 107 Joule⋅(Å)6/R6 is required for simulation of the data which is approximately a factor of two higher than that required for a prolate ellipsoidal chromophore shape. (Lower) Experimental (diamonds and squares) and theoretical (solid line) value of normalized electro-optic coefficient versus chromophore number density are given for the TCI chromophore of Table 1. Chromophore shape is taken into account. Although the dipole moment for the TCI chromophore is smaller than for the ISX chromophore, the polarizability is larger so that the overall electrostatic interaction energy is comparable for these two chromophores.
Experimental data for the ISX chromophore are also shown in Fig. 2 Upper while data for the TCI chromophore are shown in Fig. 2 Lower. The data shown are for composite materials but comparable data has been obtained for chromophores covalently attached to polymers such as PMMA (A.W.H. et al., unpublished data). As expected from theory, the experimental curves are both shifted to lower chromophore number density reflecting increased values of μ and α and the curves are narrower. Unfortunately, the theoretical fits shown are not unique but can be realized by variation of either electrostatic interactions or by variation of chromophore shape. The best fit curves shown do not correspond to experimentally determined values of μ, α, I, and ɛ for the ISX and TCI materials when the chromophores are treated as spheres (A.W.H. et al., unpublished data). This is not surprising given the pronounced prolate ellipsoidal shapes of the ISX and TCI chromophores and the fact that these shapes are not likely modulated by isomerization.
Note that chromophore crystallization (43) accompanying a decrease in second-order optical nonlinearity with increasing chromophore loading has been observed before but not analyzed in terms of London theory which permits consideration of “transient” chromophore–chromophore interaction as well as “nontransient” crystallization phenomena. Several experimental observations suggest centrosymmetric ordering phenomena for TCI-containing materials. The first is the observation of retention of birefringence but loss of second-order optical nonlinearity in “depoling” experiments where the temperature is raised and the electric poling field is turned off after induction of order by electric field poling. The second is the observation of induction of acentric order in pulsed poling experiments where no second-order nonlinear optical activity is observed at a fixed poling field strength until a pulsed electric field of increased strength is applied. The pulsed field apparently disrupts the “nontransient” aggregates sufficiently to permit equilibrium order (induced by the steady-state poling field) predicted by London theory to be achieved. The third is observation of increasing light scattering with increasing chromophore loading. Exceptionally stable aggregates of the TCI chromophore are not unexpected given the elongated prolate ellipsoidal shape of the chromophores and the strong dependence of chromophore interaction energy on R shown in Fig. 1 Upper. A final observation, which provides seemingly unequivocal proof of the role of chromophore–chromophore electrostatic interactions in attenuating optical nonlinearity at high loading, is the observation that derivatizing both ISX and TCI chromophores with bulky substituents (which inhibit close approach by steric interactions) leads to factors of two improvement in the maximum value of optical nonlinearity obtained—e.g., in the case of the TCI chromophore a maximum electro-optic coefficient of 21 pm/V (ref. 33; A. W. H. et al. unpublished data) is observed without derivatization while a value of 42 pm/V (A. W. H. et al., unpublished data) is observed with derivatization. In this simple experiment, derivatization to achieve an optimum shape for maximum optical nonlinearity was not achieved but the results provide strong support for the correctness of the theoretical approach employed here and suggests further experiments that should lead to the optimum optical nonlinearity which can be obtained with these chromophores. Note that the optimum realizable macroscopic optical nonlinearity for high μβ chromophores will never be that predicted by μβ/MW scaling.
For all chromophore/polymer materials studied, maxima are observed in plots of second-order optical nonlinearity versus chromophore number density if data are obtained for sufficiently high chromophore number densities. Care must be exercised in immediately assigning significance to the precise condition for which maxima are observed. Other factors such as conductivity and photoconductivity effects can also affect poling-induced noncentrosymmetric-order and second-order optical nonlinearity (A.W.H. et al., unpublished data). For example, significant photoconductivity (e.g., photocurrents on the order of microamperes for milliwatt optical exposure and ≈50% by weight chromophore loading) is observed for the ISX chromophore in derivatized poly(p-phenylene). Photoconductivity can be avoided by poling in the dark. When photoconductivity is associated with excitation across the highest occupied molecular orbital–lowest unoccupied molecular orbital (HOMO-LUMO) gap, it is not a problem for utilizing of the material for electro-optic modulator applications at the communications wavelengths of 1.3 and 1.5 microns. However, care must be taken to assure that two-photon excitations do not contribute significantly to photoconductivity.
Damage to the surface chromophore layer in corona and electrode poling is a potential problem and must be investigated for each material. Electro-optic measurements can only be made after the poling field is turned off so care must be exercised in establishing that relaxation of chromophore order by lattice dynamics has not artificially reduced optical nonlinearity. In situ second harmonic generation measurements are ideal for investigating the dynamics of poling-induced order.
Despite the fact that a large number of variables (A.W.H. et al., unpublished data) must be controlled to achieve meaningful measurement of the variation of second-order optical nonlinearity (second harmonic generation and electro-optic coefficients) as a function of chromophore number density and despite the acknowledged limitations of the London theory model used to analyze the competition of electric field poling and chromophore–chromophore electrostatic interactions, the experimental and theoretical data presented here strongly suggest that chromophore–chromophore interactions play the dominant role in limiting the translation of microscopic (molecular) optical nonlinearity to macroscopic optical nonlinearity. Explicitly, μβ/MW is not, as suggested by numerous publications, a good scaling parameter or nonlinear optical chromophore figure of merit. On the positive side, the realization of the importance of chromophore–chromophore interactions suggests means of overcoming the limitations of current chromophores by changing the shape of chromophores (e.g., making the chromophores more spherical and of a size to inhibit unacceptably small closest approach distances) and by exploiting chromophore–polymer attachment which inhibits chromophore–chromophore close approach. This approach has already been used to achieve factor of two improvements in macroscopic optical nonlinearity in agreement with the predictions of theory.
Observations, by researchers such as Marks and coworkers (44), of the dependence of the relative orientation of chromophores in lattices assembled by sequential synthesis methods on chromophore loading also likely reflect the role of electrostatic forces; and indeed, electrostatic interactions involving counter ions have already been systematically examined by these workers. Extensions of the simple models utilized here should provide useful insight to improved utilization of sequential synthesis and block copolymer self-assembly schemes for achieving noncentrosymmetric order. It is quite reasonable that computational models can be improved to point of providing useful quantitative prediction of the ordering of high μβ chromophores. The combination of measurements techniques uniquely sensitive to noncentrosymmetric order and the dominant role of chromophore–chromophore (as compared with chromophore–polymer) electrostatic interactions in influencing the dependence of order on chromophore loading makes the type of investigation demonstrated here of potential interest for gaining an improved understanding of condensed phase matter and the theoretical methods used to analyze condensed phase matter.
Another example of the utility of London theory for the consideration of condensed matter processes is our recent observation that thermosetting lattice hardening reactions can depend upon chromophore–chromophore electrostatic interactions (A.W.H. et al., unpublished data). This is not surprising in that reactive functionalities in thermosetting reactions are typically attached at the ends of chromophores (34, 45) and the oligomer distribution existing at any time in the thermosetting process will depend upon the relative orientational distribution of chromophores. The problem is particularly problematic for inhomogeneous thermosetting reactions (e.g., where a crosslinking reagent is used); for such reactions, chromophore association can lead to optical loss due to light scattering. We have shown that derivatization to sterically inhibit centric ordering can lead to a significant improvement in the thermal stability of poling-induced optical nonlinearity reflecting a more complete thermosetting reaction (A.W.H. et al., unpublished data).
Acknowledgments
We wish to acknowledge the assistance of Prof. W. H. Steier and his students with the numerous optical and nonlinear optical measurements alluded to in this communication (A. W. H. et al., unpublished data) and for many helpful discussions. This work was supported by the National Science Foundation and the Air Force Office of Scientific Research.
ABBREVIATIONS
- DR
disperse red
- TCI
tetracyanoindane
- ISX
isoxazolone
- PMMA
poly(methylmethacrylate)
References
- 1.Agrawal G P, Flytzanis C. Chem Phys Lett. 1976;44:366–370. [Google Scholar]
- 2.Williams D J, editor. Nonlinear Optical Properties of Organic Polymeric Materials, ACS Symposium Series. Vol. 233. Washington, DC: Am. Chem. Soc.; 1993. [Google Scholar]
- 3.Prasad P N, Williams D J. Introduction to Nonlinear Optical Effects in Molecules and Polymers. New York: Wiley; 1991. [Google Scholar]
- 4.Garito A F, Wong K Y, Cai Y M, Man H T, Zamani-Khamiri O. Proc SPIE. 1986;682:2–11. [Google Scholar]
- 5.Perry J W, Marder S R, Meyers F, Lu D, Chen G, Goddard W A, III, Bredas J L, Pierce B M. Polymers for Second-Order Nonlinear Optics, ACS Symposium Series. Vol. 601. Washington, DC: Am. Chem. Soc.; 1995. pp. 45–56. [Google Scholar]
- 6.Albert I D L, di Bella S, Kanis D R, Marks T J, Ratner M A. Polymers for Second-Order Nonlinear Optics, ACS Symposium Series. Vol. 601. Washington, DC: Am. Chem. Soc.; 1995. pp. 57–62. [Google Scholar]
- 7.Kanis D R, Ratner M A, Marks T J. Chem Rev. 1994;94:195–242. [Google Scholar]
- 8.Gilmour S, Montgomery R A, Marder S R, Cheng L T, Jen A K Y, Cai Y M, Perry J W, Dalton L R. Chem Mater. 1994;6:1603–1604. [Google Scholar]
- 9.Jen A K Y, Rao V P, Drost K J, Cai Y M, Mininni R M, Kenney J T, Binkley E S, Dalton L R, Marder S R. Proc SPIE. 1994;2143:321–340. [Google Scholar]
- 10.Jen A K Y, Chen T A, Rao V P, Cai Y M, Liu Y J, Drost K J, Mininni R M, Dalton L R, Bedworth P, Marder S R. Mater Res Soc Symp Proc. 1995;392:33–41. ,. [Google Scholar]
- 11.Dalton L R, Harper A W, Ghosn R, Steier W H, Ziari W, Fetterman H, Shi Y, Mustacich R V. Chem Mater. 1995;7:1060–1081. [Google Scholar]
- 12.Perry J W, Marder S R, Perry K J, Sleva E T. Proc SPIE. 1991;1560:302–309. [Google Scholar]
- 13.Dalton L R, Sapochak L S, Chen M, Yu L P. In: Molecular Electronics and Molecular Electronic Devices. Sienicki K, editor. Boca Raton, FL: CRC; 1993. pp. 125–208. [Google Scholar]
- 14.Burrows P E, Forrest S R, Burma T, Sapochak L S, Schwartz J, Ban V S, Forrest J L. Opt Soc Am Technol Dig Ser. 1995;21:420–423. [Google Scholar]
- 15.Lin W, Marks T J, Yitzchaik S, Lin W, Wong G K. Mater Res Soc Symp Proc. 1995;392:95–101. [Google Scholar]
- 16.Katz H E, Schilling M L, Ungashe S, Putrinski T M, Scheller G, Chidsey C E D, Wilson W L. Proc SPIE. 1991;1560:370–376. [Google Scholar]
- 17.Penner T L, Armstrong N J, Willand C S, Schildkraut J S, Robello D R. Proc SPIE. 1991;1560:377–386. [Google Scholar]
- 18.Boldt, P., Bourhill, G., Brauchle, C., Jim, Y., Kammler, R., Muller, C., Rase, J. & Wichern, J. (1996) J. Chem. Soc. Chem. Commun. 793–795.
- 19.Ahlheim M, Barzoukas M, Bedworth P V, Blanchard-Desce M, Fort A, Hu Z-Y, Marder S R, Perry J W, Runser C, Staehelin M, Zysset B. Science. 1996;271:335–337. [Google Scholar]
- 20.Jen A K-Y, Rao V P, Chen T-A, Cai Y, Drost K J, Liu Y-J, Kenney J T, Mininni R M, Bedworth P V, Marder S R, Dalton L R. Opt Soc Am Technol Dig Ser. 1995;21:251–254. [Google Scholar]
- 21.Moylan C R, Miller R D, Twieg R J, Ermer S, Lovejoy S M, Leung D S. Proc SPIE. 1995;2527:150–162. [Google Scholar]
- 22.Moylan C R, McComb I H, Miller R D, Lee V Y, Twieg R J, Ermer S, Lovejoy S M, Leung D S. Mol Cryst Liq Cryst. 1996;283:115–118. [Google Scholar]
- 23.Flipse M C, Van der Vorst J M, Hofstraat J W, Woudenberg R H, Van Gassel R A P, Lamers J C, Van der Linden G M, Veenis W J, Diemeer M B J, Donckers M C J M. In: Photoactive Organic Materials: Science and Application. Kajzar F, Agranovich V M, Lee C Y C, editors. Dordrecht, The Netherlands: Kluwer; 1996. pp. 237–246. [Google Scholar]
- 24.London F. Trans Faraday Soc. 1937;33:8–26. [Google Scholar]
- 25.London F. Z Phys. 1930;63:245–279. [Google Scholar]
- 26.Isrealachvili J N. Intermolecular and Surface Forces. London: Academic; 1985. [Google Scholar]
- 27.Hansen J P, McDonald I R. Theory of Simple Liquids. London: Academic; 1976. [Google Scholar]
- 28.Fowler R H. Proc R Soc London A. 1935;149:1–28. [Google Scholar]
- 29.Piekara A. Z Phys. 1938;108:395–400. [Google Scholar]
- 30.Piekara A. Proc R Soc London A. 1939;172:360–381. [Google Scholar]
- 31.Debye P. Phys Z. 1935;35:100–101. [Google Scholar]
- 32.Ehrenson S. J Comp Chem. 1989;10:77–93. [Google Scholar]
- 33.Sun S S, Zhang C, Dalton L R, Garner S M, Chen A, Steier W H. Chem Mater. 1996;8:2539–2541. [Google Scholar]
- 34.Chen M, Dalton L R, Yu L P, Shi Y Q, Steier W H. Macromolecules. 1992;25:4032–4035. [Google Scholar]
- 35.Xu C, Wu B, Todorowa O, Dalton L R, Shi Y, Ranon P M, Steier W H. Macromolecules. 1993;26:5303–5309. [Google Scholar]
- 36.Becker M W, Sapochak L S, Ghosn R, Xu C, Dalton L R, Shi Y, Steier W H, Jen A K Y. Chem Mater. 1994;6:104–106. [Google Scholar]
- 37.Teng C C, Man H T. Appl Phys Lett. 1990;56:1734–1736. [Google Scholar]
- 38.Dentan V, Levy Y, Dumont M, Robin P, Chastaing E. Opt Commun. 1989;69:379–383. [Google Scholar]
- 39.Ziari M, Kalluri S, Garner S, Steier W H, Liang Z, Dalton L R, Shi Y. Proc SPIE. 1995;2527:218–227. [Google Scholar]
- 40.Kalluri S, Garner S, Ziari M, Steier W H, Shi Y, Dalton L R. Appl Phys Lett. 1996;69:275–277. [Google Scholar]
- 41.Steier W H, Kalluri S, Chen A, Garner S, Chuyanov V, Ziari M, Shi Y, Fetterman H, Jalali B, Wang W, Chen D, Dalton L R. Mater Res Soc Symp Proc. 1996;413:147–157. [Google Scholar]
- 42.Dalton L R, Sapochak L S, Yu L P. J Phys Chem. 1993;97:2871–2883. [Google Scholar]
- 43.Watanabe T, Miyata S. Proc SPIE. 1989;1147:101–107. [Google Scholar]
- 44.Roscoe S B, Yitzchaik S, Kakkar A K, Marks T J, Lin W, Wong G K. Langmuir. 1994;10:1337–1339. [Google Scholar]
- 45.Oviatt H W, Shea K J, Kalluri S, Shi Y, Steier W H, Dalton L R. Chem Mater. 1995;7:493–498. [Google Scholar]