DETERMINATION OF INSTANTANEOUS STABILITY AGAINST BACKWARD BALANCE LOSS: TWO COMPUTATIONAL APPROACHES

Abstract

The purposes of this study were (1) to develop two computation methods and (2) to compare their performance (i.e. the accuracy and the time demand) in determining instantaneous stability, i.e., the shortest distance from an instantaneous center of mass (COM) state to all interpolated points on the stability boundary in the COM position-velocity state space. The intuitive numerical method interpolated the stability boundary against backward balance loss based on four sets of discrete boundary values with a spline function and a preset step size (Δx). Then a brute-force search approach was used to determine this shortest distance. The analytical method uses quadratic polynomial functions to represent the boundaries. The stability was then determined by using the Lagrange multiplier method to find the optimum for the analytical expression of the distance from this given COM state to the boundary. Because reducing Δx can supposedly improve the accuracy of spline fitting, we used this approach to establish the benchmark employed to determine the accuracy level of all other computations. Based on the results from a database of 67 sit-to-stand-slip trials and 687 gait-slip trials, we would recommend the numerical method with Δx =0.1 to reach an adequate accuracy level of 10⁻². By changing one order of Δx from 0.1 to 0.01, however, the accuracy level improved drastically from 10⁻² to 10⁻⁴. To achieve the same higher accuracy at a faster computing speed, however, we would recommend the analytical method, which costs 80% less time than the numerical approach at the level of 10⁻⁴.

INTRODUCTION

Slips can severely destabilize even healthy individuals, leading to backward losses of balance (BLOB) and falls (Kannus et al., 1999). Emerging evidence indicates that repeated slip exposure can facilitate rapid adaptive improvement in one’s stability (Bhatt et al., 2006a) with possibly long motor memory retention (Bhatt et al., 2006b). Measuring changes in stability throughout one’s locomotion could be a valuable tool to quantify such adaptive training.

We have recently extended definition of the stability region from static (Borelli, 1680) to dynamic conditions (Pai and Patton, 1997). This requires considering the instantaneous center of mass (COM) motion state (i.e. the horizontal position and velocity of COM relative to the base of support (BOS)). Discrete boundary values of the boundary against BLOB have been determined by mathematical simulation (Table 1) with the aid of 2-link (Pai and Iqbal, 1999; Pai and Patton, 1997) and 7-link (Yang et al., 2007; Yang et al., 2008) human model for bipedal symmetrical stance and asymmetrical movement, respectively. The instantaneous stability is defined as the shortest distance from the given COM state to the corresponding boundary (Pai et al., 2003). A COM state further below the boundary (i.e. the stability is more negative) is more unstable and will be more likely to lead to a BLOB due to the insufficient COM velocity which cannot bring the COM over the BOS as the COM velocity diminishes. Conversely, when the COM state is further above the boundary (i.e. the stability is more positive), the given COM velocity is ample to bring the COM over the BOS; and consequently BLOB should be less likely to occur. Based on the available discrete boundary values (Table 1), however, a method is needed to determine this shortest distance from a COM state to the boundary.

Table 1.

The initial center of mass (COM) horizontal velocities necessary to prevent backward balance loss derived by the 2- and the 7-link models under non-slip and slip conditions at all simulated initial COM positions.

	Boundary		Position (x)
			−1.25	−1.00	−0.75	−0.50	−0.25	0.0
Velocity	2-link	Non-slip*	0.232	0.186	0.140	0.094	0.047	0.0
(ẋ)	model	Slip+	0.517	0.462	0.383	0.281	0.143	0.0
	7-link	Non-slip#	0.290	0.259	0.213	0.150	0.075	0.0
	model	Slip§	0.521	0.460	0.386	0.292	0.175	0.0

The COM position and forward velocity relative to the base of support (BOS) are dimensionless variables expressed as a fraction of l_BOS and $\sqrt{\mathrm{g}\times \mathrm{b}\mathrm{h}}$, respectively, where l_BOS represents the length of the foot, g is the gravity constant, and bh the body height. For the COM position, negative and positive values respectively indicate that the COM is posterior and anterior to the posterior border of the BOS. Zero value implies that the COM is directly above the posterior border of the BOS.

^*data from Pai and Patton, 1997;

⁺data from Pai and Iqbal, 1999;

^#data from Yang et al., 2007;

^§data from Yang et al., 2008.

The purposes of this study were therefore (1) to develop two computation methods and (2) to compare their performance (i.e. the accuracy and the time demand) in determining the instantaneous stability. While one (“numerical”) method uses brute-force to search the shortest distance from the instantaneous COM state to the boundary, the other employs “analytical” approximations to reduce computational demand. The latter approach was included to offer an alternative appropriate for the stability-based online control that 1 requires minimal delay or for the optimization that relies on extensive iteration cycles.

METHODS

2.1. The numerical method

Based on discrete values of the boundary (Table 1), the entire boundary was represented regionally using cubic spline interpolation to generate N individual points at a constant increment, Δx, as computational step size along the COM position axis, x:

$${\left[\begin{array}{llllll}{x}_1\hfill & x_2\hfill & \cdots \hfill & x_i\hfill & \cdots \hfill & x_N\hfill \\ {\dot{x}}_1\hfill & {\dot{x}}_2\hfill & \cdots \hfill & {\dot{x}}_i\hfill & \cdots \hfill & {\dot{x}}_N\hfill \end{array}\right]}^T={\left[\begin{array}{llllll}{x}_1\hfill & x_1+\mathrm{\Delta }x\hfill & \cdots \hfill & x_1+i\mathrm{\Delta }x\hfill & \cdots \hfill & x_1+N\mathrm{\Delta }x\hfill \\ {\dot{x}}_1\hfill & \hfill {\dot{x}}_2\hfill & \cdots \hfill & \hfill {\dot{x}}_i\hfill & \cdots \hfill & \hfill {\dot{x}}_N\hfill \end{array}\right]}^T$$ (1)

where, N depended upon the selected Δx.

The brute-force search approach was used. All distances, d_i (i=1, 2,…, N), between a given COM state $\left(x_p,{\dot{x}}_p\right)$ and all points on the boundary $\left(x_i,{\dot{x}}_i\right)$ were calculated.

$$d_i=\sqrt{{(x_i-x_p)}^2+{\left({\dot{x}}_i-{\dot{x}}_p\right)}^2},i=1,2,\cdots ,N$$ (2)

Then, the magnitude of the stability at given instant was determined.

$$\mathit{d*}=\text{min}\left(d_i\right),i=1,2,\cdots ,N$$ (3)

The stability, s, was determined by the following judgment.

$$\{\begin{array}{cc}s=d^{*}& \left(x_p\ge x^{*}\right)\\ s=-d^{*}& \left(x_p<x^{*}\right)\end{array}$$ (4)

2.2 The analytical method

Based on Table 1, analytical expressions were sought for each boundary. The quadratic expression was adopted to approximate the discrete points (Table 2). The detailed process to identify the expression is provided in our online supplement.

$$\dot{x}=f(x)={\displaystyle \sum _{i=0}^2{a}_i{x}^i},x^{-}\le x\le x^{+}$$ (5)

Where x⁻ and x⁺ indicated the lower and upper bound, respectively, of the feasible range of x. High fitting accuracy could not be reached if a uniform equation is adopted to approximate the entire boundary (Table 1) because the shape of the boundary varies between low- and high-speed regions, especially for the boundary under slip condition. Hence, we divided each boundary into two sections: x ∈ [−0.5 0.0] and x ∈ [−1.25 −0.5]. The stability was calculated for each section, and the one with lesser magnetite of the two was the true stability of the given COM state.

Table 2.

The parameters for the analytical expression of the boundary, a_i, (i = 0, 1, 2), the correlation coefficients (R²) between the fitted analytical boundary and the baseline, and the root of mean square (RMS) of the residual error between the fitted analytical boundary and baseline for all boundaries. The baseline boundary is established by interpolating the computer derived points shown in Table 1 using cubic spline with 10⁻⁵ as the increment in x, the COM position.

Boundary		x	a2	a1	a0	R2	RMS
2-link model	non-slip	[−0.5 0]	2.3140 ×10−4	−1.8827 ×10−1	−8.5327 ×10−5	0.999	4×10−5
		[−1.25 −0.5]	2.4801 ×10−3	−1.8008 ×10−1	3.4997 ×10−3	0.999	2×10−4
	slip	[−0.5 0]	−3.2984 ×10−2	−5.9022 ×10−1	−2.5810 ×10−3	0.999	1×10−3
		[−1.25 −0.5]	−1.8213 ×10−1	−6.3270 ×10−1	1.1219 ×10−2	0.999	5×10−4
7-link model	non-slip	[−0.5 0]	2.1441 ×10−3	−3.0251 ×10−1	−7.8846 ×10−4	0.999	3×10−4
		[−1.25 −0.5]	−1.2952 ×10−1	−4.1240 ×10−1	−2.3666 ×10−2	0.999	3×10−4
	slip	[−0.5 0]	−4.7109 ×10−1	−8.0771 ×10−1	2.6057 ×10−3	0.999	1×10−3
		[−1.25 −0.5]	−1.3135 ×10−1	−5.3269 ×10−1	5.9536 ×10−2	0.999	7×10−4

The analytical boundary is expressed as ẋ = a₀ + a₁x + a₂x².

Analytically calculating stability became an optimization issue with one equality and two inequality constraints.

$$\text{Object function:}\text{min}d=\sqrt{{(x-x_p)}^2+{(\dot{x}-{\dot{x}}_p)}^2}$$ (6)

$$\begin{array}{ll}\text{Subject to:}\hfill & \dot{x}=f(x)\hfill \\ \hfill & x^{-}\le x\le x^{+}\hfill \end{array}$$

This optimization problem can be solved by the Lagrange multiplier method. The detailed derivation process for the analytical method and computer-program code for both methods are provided in online supplement.

2.3 Comparison of the methods

Existing experimental data were used to compare the calculation performance between these two methods. The slips were passively induced respectively in sit-to-stand (Pavol and Pai, 2002) and in gait (Bhatt et al., 2006a). Sixty-seven sit-to-stand-slip trials and 687 gait-slip trials were investigated.

To obtain a standard to evaluate the accuracy of two methods, we first used the numerical method to establish the benchmark by systematically reducing Δx, starting from 10⁻¹ with a decrement ratio of 10⁻¹. When such decrement in Δx stops to yield any difference, the baselines for comparison were decided. The computation resolution of the stability that can differentiate fall and recovery following slip perturbations (Pavol and Pai, 2007) and the reported trial-to-trial adaptive changes in the COM stability (Bhatt et al, 2006a) was in the order of 10⁻², and 10⁻² was therefore considered as the “adequate accuracy” level. The root of mean square (RMS), the relative RMS, the correlation coefficient (R²), the maximum value, and the relative maximum values of the difference between the calculated stability time history and its baseline were adopted to determine the corresponding accuracy level. Finally, the time consumed by the program to calculate the stability time history was determined for all trials. In addition, paired t-test was employed to compare the accuracy levels between two methods and between all Δx for the same sample trials. All computer programs were run on a personal computer with 3.0 GHz Intel CPU.

RESULTS

Detailed procedure and code for both methods, and their results were given in our online supplement for two typical trials, one sit-to-stand-slip trial (Fig. 1a–b) and one gait-slip trial (Fig. 1c–d). In these cases, stability-time history was computed from slip onset to the recovery step touchdown. The RMS (Fig. 2a), R² (Fig. 2b), maximum difference (Fig. 2c), relative maximum difference (Fig. 2e), and relative RMS (Fig. 2f) of the numerical method reduced drastically when Δx decreased from 10⁻¹ to 10⁻². The difference in the RMS of the stability time history became negligibly small (< 10⁻¹⁵) between Δx = 10⁻⁵ and 10⁻⁶. Therefore, the results calculated by using Δx = 10⁻⁵ were selected as the baselines for all other comparisons.

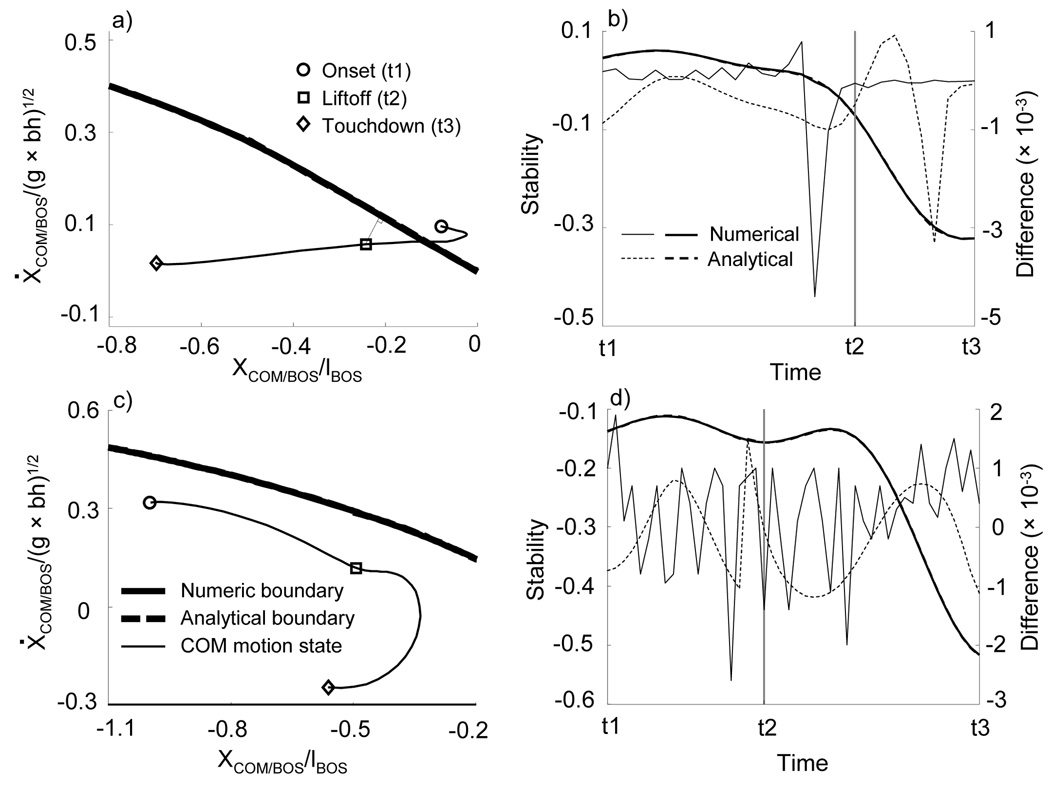
Fig. 1.

The typical center of mass (COM) motion state trajectories and the corresponding time histories of the COM dynamic stability in response to slip induced in sit-to-stand (a, b), and in gait (c, d). The thick solid lines, in (a) and (c) indicate the interpolated boundaries using cubic spline with 10⁻⁵ as the increment of COM position. The thick dash lines, in (a) and (c) represent the corresponding analytical boundaries. The thin solid lines in (a) and (c) describe the COM motion state trajectories. The thin straight solid line in (a) indicates the stability value at liftoff for the sit-to-stand-slip. The thick solid and dash lines in (b) and (d) indicate the time histories of the COM stability respectively shown in (a) and (c) calculated by numerical (step size is 10⁻²) and analytical methods, respectively. The thin solid and dash lines respectively reveal the discrepancies between the stabilities calculated by numerical and analytical methods and their baselines. Approximate slip onset (t1, circle in (a) and (c)) is seat-off and right touchdown for slips in sit-to-stand and gait, respectively. Liftoff (t2, square in (a) and (c)) and touchdown (t3, diamond in (a) and (c)) refer to the recovery step liftoff and its touchdown following slip onset. The posterior foot and the slipping foot are the base of support (BOS) for slips in sit-to-stand slip and gait, respectively. The positions of the COM are relative to the posterior border of the BOS and normalized to foot length, (l_BOS) with negative values indicating distance behind the BOS. The relative velocity of the COM to the BOS is normalized to$\sqrt{\mathrm{g}\times \mathrm{b}\mathrm{h}}$, where g is the gravity constant, and bh the body height. Stability is defined as the perpendicular distance from the boundary to the given instantaneous COM state. The COM state at liftoff during the sit-to-stand trial is the example used to demonstrate the proposed analytical and numerical approaches to calculate COM dynamic stability in our online supplement.

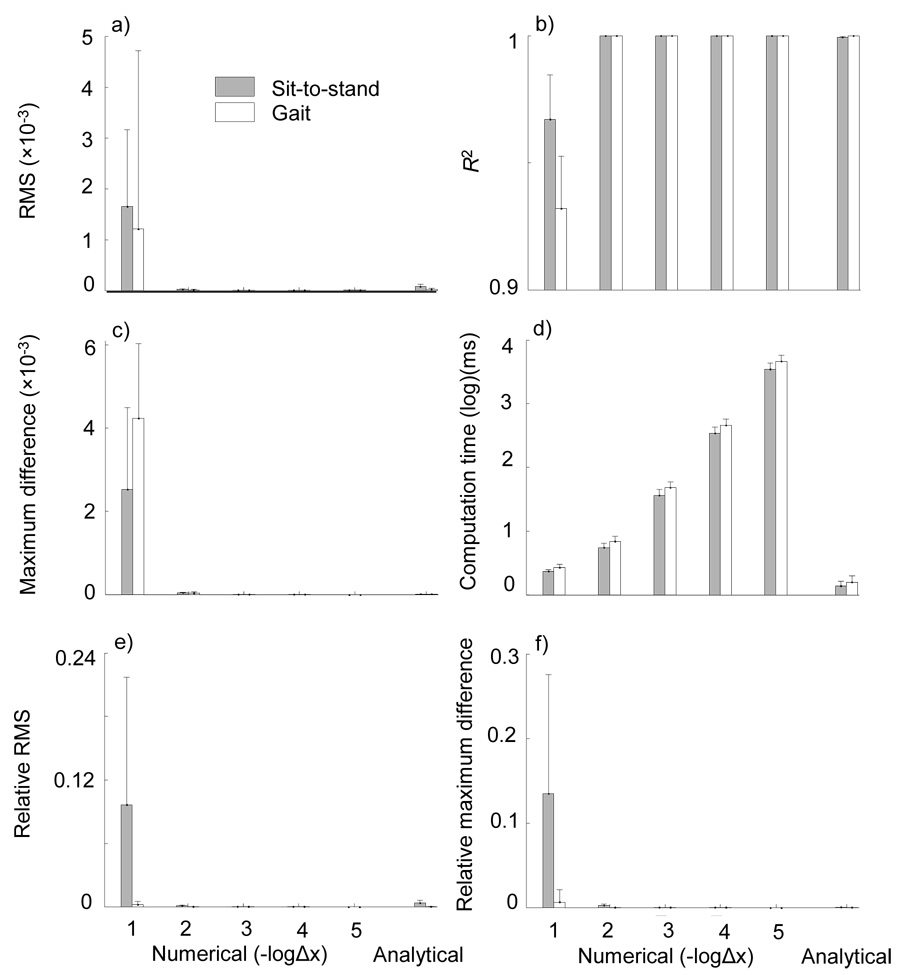
Fig. 2.

Group mean ± SD value of (a) the root-mean-square (RMS) of calculation error, (b) the correlation coefficient R², (c) the maximum difference between the calculated stability and the baseline, (d) the computation time, (e) the relative RMS, and (f) the relative maximum difference for the numerical method as a function of the calculation step size and the analytical method to calculate the time history of the center of mass (COM) stability in 67 sit-to-stand-slip (Pavol et al., 2002) and 687gait-slip trials (Bhatt et al., 2006a). The relative RMS and relative maximum difference are defined as the ratio of the RMS and maximum difference to the peak value of the corresponding baseline. A paired t-test illustrates the comparable calculation accuracy achieved by the analytical method and the numerical method with 10⁻² as the step size. The benchmarks were set by the numerical method with 10⁻⁵ as the calculation step size. The X axis shows the calculation step size in log to the base 10 of the opposite number for the numerical method. In (d), the Y axis shows the computation time in ms and in the log to the base 10. Because the results calculated numerically with 10⁻⁵ as the step size are the baseline, the RMS, the maximum difference, the relative RMS, and the relative maximum difference are all zero for the numerical method with 10⁻⁵ as step size. Hence, the R² for the numerical method with 10⁻⁵ as the step size is one.

With Δx = 10⁻², the numerical and analytical methods reached the same accuracy level of 10⁻⁴ from the benchmark (Fig. 2a–b). The computation times for the analytical method were only 20.1 ± 0.04% and 23.9 ± 0.05% of the time required by the numerical method at this accuracy level. The computation time of the numerical method continued to increase as Δx decreased (Fig. 2d).

DISCUSSION

Two methods to determine the instantaneous COM stability were compared based on the previously published discrete boundary values. The numerical method was relatively simple and straightforward to program, and therefore we would recommend this method to reach adequate accuracy level of 10⁻² by using Δx =0.1. It is noteworthy that by changing one order of Δx from 0.1 to 0.01, the accuracy level improved from 10⁻² to 10⁻⁴. To achieve higher accuracy at a faster computing speed, however, we would recommend the analytical method, which costs 80% less time than the numerical approach at the same accuracy level of 10⁻⁴.

The analytically derived results still have detectable error as compared to the baselines (Fig. 2a). The error may result from the inaccuracy of the boundary approximation (Table 2). To reduce this error, a higher-order polynomial is necessary to approximate the boundary. However, the higher-order polynomial would make the optimization problem analytically unsolvable. In fact, the calculation error of the current analytical approach is in the order of 10⁻⁴ (i.e. RMS < 10⁻⁴, R² > 0.999), which is perhaps far more than adequate. From this perspective, the quadratic function provides an excellent expression with high accuracy and efficiency (i.e. 4-time faster than the numerical method to achieve the same accuracy level with Δx =0.01 and 0.9-time faster than Δx =0.1).

Although such advantage from the analytical method in computation efficiency may not be important enough to make any real difference in offline data processing, it can still be desirable in online control mechanisms. For example, when online stability measure is required in functional neuromuscular stimulation that electrically stimulates muscle activation to change one’s dynamic stability, the difference between the two methods can be meaningful. In addition, stability online calculation is crucial to make the walking robots dynamically balanced and robust in locomotion (Geng et al., 2006). In this scenario, the analytical method can reduce this computation delay to merely 1 ms. In addition, if the analytical rather than the numerical method is coupled with Simulated Annealing algorithm in optimization that requires extensive iterative cycles (Yang et al., 2007), the computation demand can be reduced in the order of days.

In summary, to calculate instantaneous COM stability, we have developed an intuitive numerical approach, which is capable of achieving high accuracy level by reducing step size but at the expense of computation time. We also offered an analytical alternative, which is desirable when economical computation becomes important.