Tit-for-tat or Win-stay, Lose-shift?

Abstract

The repeated Prisoner’s Dilemma is usually known as a story of tit-for-tat. This remarkable strategy has won both of Robert Axelrod’s tournaments. Tit-for-tat does whatever the opponent has done in the previous round. It will cooperate if the opponent has cooperated, and it will defect if the opponent has defected. But tit-for-tat has two weaknesses: (i) it cannot correct mistakes (erroneous moves) and (ii) a population of tit-for-tat players is undermined by random drift when mutant strategies appear which play always-cooperate. Another equally simple strategy called ‘win-stay, lose-shift’ has neither of these two disadvantages. Win-stay, lose-shift repeats the previous move if the resulting payoff has met its aspiration level and changes otherwise. Here we use a novel approach of stochastic evolutionary game dynamics in finite populations to study mutation-selection dynamics in the presence of erroneous moves. We compare four strategies: always-defect, always-cooperate, tit-for-tat and win-stay, lose-shift. There are two possible outcomes: if the benefit of cooperation is below a critical value then always-defect is selected; if the benefit of cooperation is above this critical value then win-stay, lose-shift is selected. Tit-for-tat is never selected in this evolutionary process, but lowers the selection threshold for win-stay, lose-shift.

1. Introduction

A crucial question of evolutionary biology is how natural selection can lead to cooperative behavior. A cooperator is someone who pays a cost, c, for another individual to receive a benefit, b. Cost and benefit are measured in terms of reproductive success. Various mechanisms for the evolution of cooperation have been proposed including kin selection (Hamilton, 1964), group selection (Wilson, 1975; Wynne-Edwards, 1962), indirect reciprocity (Nowak and Sigmund, 1998, 2005) and spatial (or network) reciprocity (Nowak and May, 1992; Ohtsuki et al., 2006; Skyrms, 2004). Here we analyze direct reciprocity which was introduced by Trivers (1971). The hallmark of direct reciprocity is the repeated Prisoner’s Dilemma (Luce and Raiffa, 1957; Rapoport and Chammah, 1965).

In the Prisoner’s Dilemma (PD), two players have a choice to cooperate, C, or to defect, D. If both cooperate they receive a payoff R. If both defect, they receive a lower payoff P. But a defector versus a cooperator gains the highest payoff, T, while the cooperator is left with the lowest payoff S. The game is a Prisoner’s Dilemma if T > R > P > S. In a non-repeated PD, it is best to defect. Cooperation becomes an option if the game is repeated. For the repeated PD, we also ask that R > (T + S)/2. Otherwise alternating between cooperation and defection would lead to a higher payoff than mutual cooperation.

There are many conceivable strategies for the repeated PD, and in 1978, Robert Axelrod decided to conduct computer tournaments in order to find successful strategies (Axelrod, 1984; Axelrod and Hamilton, 1981). There were 14 entries to the first tournament and 63 to the second. In both tournaments, the simplest of all strategies won. It was tit-for-tat (TFT), submitted by Anatol Rapoport (see also Rapoport and Chammah (1965)). TFT cooperates in the first round and then does whatever the opponent has done in the previous round. It will play C for C and D for D. Hence, TFT embodies the simple principle ‘an eye for an eye and a tooth for a tooth’. It was remarkable that TFT won both tournaments, because participants of the second tournament knew the outcome of the first and tried to design (more sophisticated) strategies that were superior to TFT. The success of TFT inspired much subsequent research (Dugatkin, 1988; Milinski, 1987; Wilkinson, 1984).

TFT, however, has a weakness which did not become apparent in the error-free environment of Axelrod’s tournaments. If two TFT players interact with each other and one defects by mistake, then the other one will retaliate, which in turn leads to a sequence of alternating moves of cooperation and defection. In the presence of noise, in an infinitely repeated game, the expected payoff per round for TFT versus TFT is only (R+S+T+P)/4. TFT’s unrelenting punishment never forgives even a single deviation, but forgiveness is needed to restore cooperation after occasional errors (Fudenberg and Maskin, 1990; Molander, 1985; Nowak and Sigmund, 1992).

Another drawback of TFT is the following. Imagine a mixed population of players using TFT and players using the strategy ‘always-cooperate’ (ALLC). In the absence of noise, both strategies have the same average payoff. The frequency (=relative abundance) of ALLC can increase by random drift. This means TFT is not evolutionarily stable (Boyd and Lorberbaum, 1987; Selten and Hammerstein, 1984). Once the abundance of ALLC has fluctuated above a certain threshold, players using ‘always-defect’ (ALLD) can invade the population.

Win-stay, lose-shift (WSLS) is a very simple strategy which has neither of these two weaknesses (Nowak and Sigmund, 1993). WSLS works as follows. If WSLS receives payoff T or R it will repeat the same move next round; this is ‘win-stay’. If WSLS receives only payoff P or S, it will switch to the opposite move; this is ‘lose-shift’. Thus, the choice of the next action is based on some aspiration level which lies between P and R. The problem of adapting the aspiration level has been considered e.g. in Posch et al. (1999). Another name for WSLS is ”perfect tit-for-tat;” this name reflects the fact that for typical payoffs the rule is a symmetric subgame-perfect equilibrium, while TFT is typically not. WSLS is also known as Pavlov (Kraines and Kraines, 1989, 1995). Milinski and Wedekind (1998) provide empirical evidence for WSLS. For longer memory versions of WSLS see Neill (2001) and Wakano and Yamamura (2001).

As illustrated in Fig. 1, WSLS allows (i) to correct mistakes and (ii) to exploit ALLC. Hence, a WSLS population receives a high average payoff even in the presence of errors and is stable against random drift to ALLC. However, WSLS is exploited by ALLD in every second round whereas TFT is not. Evolutionary analysis and computer simulations of heterogeneous populations using a set of probabilistic strategies indicate that WSLS outcompetes TFT in most cases (Nowak and Sigmund, 1993; Nowak et al., 1995). Fudenberg and Maskin (1990) considered a concept of evolutionary stability for repeated games with errors and showed that WSLS is, in this sense, evolutionarily stable in the set of strategies of finite complexity, while TFT is not.

Fig. 1.

WSLS cooperates against itself most of the time: A mistake by one of two players that use WSLS triggers a single round of punishment and then both return to cooperation. Moreover, WSLS can exploit unconditional cooperators, so that WSLS is proof against random drift to ALLC.

2. Mutation-selection dynamics in the presence of erroneous moves

Here we present an exact calculation that allows us to study the evolutionary dynamics of WSLS and TFT under mutation, selection and random drift in finite populations and in the presence of noise. We consider a population of N individuals. Each individual derives a payoff by interacting with (a representative ensemble of) all other individuals. The fitness of an individual is given by a constant, representing the baseline fitness, plus the payoff from the game. Weak selection means that the baseline fitness is large compared to the payoff. See Traulsen et al. (2006) for a discussion of the influence of the intensity of selection on evolutionary stability. In each time step, a random individual is chosen for reproduction proportional to fitness. The offspring replaces another randomly chosen individual. These dynamics describe a frequency dependent Moran process (Nowak, 2006; Nowak et al., 2004), but we expect that similar processes, for example those based on pair-wise comparison and updating would lead to qualitatively similar conclusions (Imhof and Nowak, 2006; Traulsen et al., 2005, 2007). Reproduction can be genetic or cultural.

Mutation means that the offspring of one individual need not always adopt the parent’s strategy, but with a small probability, u, a different, randomly chosen strategy is adopted (Kandori et al., 1993; Young, 1993); see Chapter 5 in Fudenberg and Levine (1998) for a survey of adjustment models with mutations. The resulting mutation-selection process leads to a stationary distribution, where each strategy is represented by a certain fraction of the population. We characterize this mutation-selection equilibrium in the limit of small mutation rate (u → 0) and large population size (N → ∞). Our approach is similar to that of Imhof et al. (2005), but here we consider the infinitely repeated PD with noise.

At first, we study a simplified version of the PD which is characterized only by two parameters, the cost, c, and the benefit, b, of cooperation. The payoff matrix is given by

$$\begin{array}{ccc}\hfill & \hfill \text{C}\hfill & \hfill \text{D}\hfill \\ \begin{array}{c}\text{C}\\ \text{D}\end{array}\hfill & \hfill (\begin{array}{c}b-c\\ b\end{array}\hfill & \hfill \begin{array}{c}-c\\ 0\end{array}).\hfill \end{array}$$ (1)

This game is a PD if b > c. Note that the matrix in (1) describes a subset of possible PD games. The general case and all relevant proofs are discussed in the Appendix.

We begin by studying only two strategies, ALLD and TFT. Both strategies are best replies to themselves, but TFT has the larger basin of attraction. The equilibrium distribution of our mutation-selection process is entirely centered on TFT (Fig. 2a).

Fig. 2.

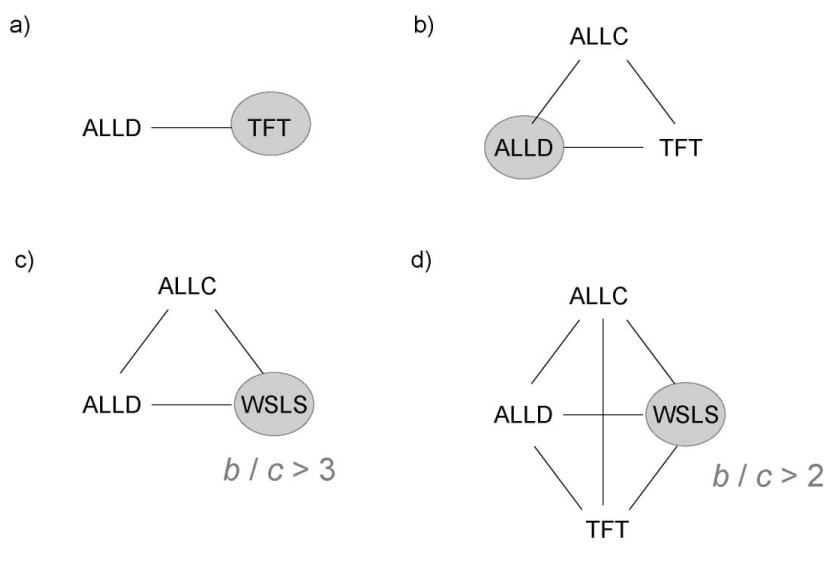
Selected strategies in large populations when mutation rates are small. a) ALLD against TFT is a coordination game, where TFT is always selected as long as the benefit, b, is larger than the cost, c. b) If unconditional cooperators are added, they can invade and take over a TFT population by random drift, but an ALLC population is quickly taken over by ALLD players. ALLD is the selected strategy. c) If instead of TFT, WSLS competes with ALLC and ALLD, then WSLS is selected, provided the benefit-to-cost ratio, b/c, is sufficiently large. The critical value is 3 in the limit of weak selection. d) Similar behavior as in c) is observed if TFT is added, but the critical value is now lowered to 2 for any intensity of selection.

Let us now add ALLC and analyze the competition of three strategies: ALLD, TFT and ALLC. In this system, the equilibrium distribution is entirely centered on ALLD. Therefore, adding ALLC undermines the evolutionary success of TFT (Fig. 2b).

Next we consider ALLD and WSLS. The remarkably simple criterion

$$b/c>3$$ (2)

is a necessary condition for the selection of WSLS. If b/c < 3 then ALLD is selected. If b/c > 3 then WSLS is selected provided the intensity of selection is sufficiently weak. Adding ALLC does not change this outcome. In the three strategy system, ALLD, WSLS and ALLC, it is also the case that b/c > 3 allows the selection of WSLS for weak selection (Fig. 2c). For stronger selection, the critical threshold for b/c is somewhat larger than 3 (Fig. 3).

Fig. 3.

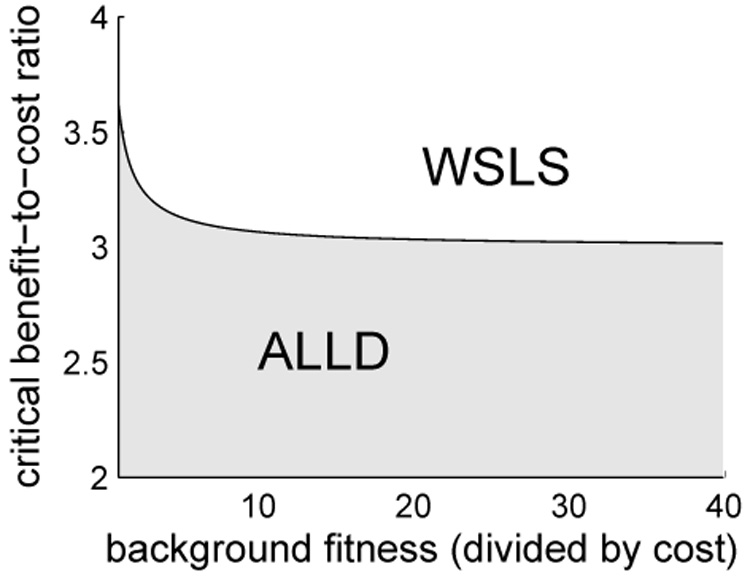
In the system with strategies ALLD and WSLS, there is a critical threshold for the benefit-to-cost ratio, b/c, that determines whether ALLD or WSLS is selected in large populations. WSLS is selected if and only if b/c exceeds the threshold. The figure shows how the critical value depends on the intensity of selection. The value is about 3.6 for strong selection, decreases with increasing background fitness, and approaches 3 in the limit of weak selection. In particular, if b/c > 3, then WSLS is selected if the intensity of selection is sufficiently weak.

Now comes another surprise. Let us add TFT and therefore consider the four strategy system, ALLD, ALLC, WSLS and TFT. If

$$b/c>2$$ (3)

then WSLS is selected for any intensity of selection (Fig. 2d). If b/c < 2 then ALLD is selected. Remarkably, TFT is never selected, but the presence of TFT lowers the threshold for the evolution of cooperation. As noted previously (Nowak and Sigmund, 1992), TFT is a catalyst for the emergence of cooperation, but is not the target of evolution.

There is a nice intuitive justification for the critical thresholds in (2) and (3). In the absence of noise, the payoff matrix for WSLS versus ALLD is given by

$$\begin{array}{lll}\hfill & \text{WSLS}\hfill & \text{ALLD}\hfill \\ \begin{array}{c}\text{WSLS}\\ \text{ALLD}\end{array}\hfill & \hfill (\begin{array}{c}b-c\\ b/2\end{array}\hfill & \hfill \begin{array}{c}-c/2\\ 0\end{array}).\hfill \end{array}$$

The entries represent the average payoffs per round. Adding small amounts of noise introduces only small perturbations of the payoff values. Remember that WSLS cooperates against ALLD every other round. If we only compare WSLS and ALLD, then all that matters is which strategy is risk dominant (Fudenberg and Levine, 1998, p. 138; Nowak et al., 2004). WSLS is risk dominant if b/c > 3. If we add TFT, then an ALLD population is rapidly invaded by TFT (Imhof et al., 2005; Nowak et al., 2004) and the decisive criterion is that WSLS versus ALLD is a coordination game. This is the case if b/c > 2. If on the other hand b/c < 2, then WSLS is dominated by ALLD. This intuitive justification also explains the more complicated criteria for the general PD game, which are discussed in the Appendix.

We have focused on the four strategies, ALLC, ALLD, TFT and WSLS, because they represent important basic types of behavior in a repeated PD. It would be interesting to add further strategies, e.g. generous TFT (GTFT). GTFT cooperates if the opponent cooperated in the previous round and cooperates with a fixed probability q > 0 if the opponent defected. Thus GTFT can also correct mistakes although not as effciently as WSLS. Unfortunately, adding GTFT makes it difficult to prove mathematical results for our stochastic model. The numerical results in Table 1 suggest that ALLD and GTFT may persist for a certain range of benefit-cost ratios but WSLS is again selected if that ratio is sufficiently large. Our findings hold for the simultaneous PD, but not for the alternating PD (Frean, 1994; Nowak and Sigmund, 1994), where WSLS is not error correcting. For the alternating PD one may consider strategies with longer memory that use ideas of WSLS and are able to correct mistakes (Neill, 2001). Further challenges for future research include finite population dynamics for the continuous PD (Killingback et al., 1999; Roberts and Sherratt, 1998; Wahl and Nowak, 1999a, 1999b), for general repeated games (Aumann and Shapley, 1976; Fudenberg and Maskin, 1986) and finally for repeated games with imperfectly observed actions (Fudenberg et al., 1994; Fudenberg and Levine, 1994).

Table 1.

Limit distributions of the stochastic system for the four strategies ALLC, ALLD, TFT and WSLS and of the augmented system which contains also GTFT. Here GTFT cooperates with probability q = 1/10, q = 1/3 or q = 1/2, respectively, if the opponent defected in the previous round. The population size is N = 10000, the cost of cooperation is c = 1 and the background fitness is K = 10.

	b	ALLC	ALLD	TFT	WSLS
	1.5	0.0005	0.9741	0.0179	0.0075
	2.0	0.0010	0.9201	0.0176	0.0613
	2.5	0.0001	0.0343	0.0006	0.9650
	3.0	0.0000	0.0000	0.0000	1.0000
b	ALLC	ALLD	TFT	WSLS	GTFT
					q = 1/10
1.5	0.0001	0.3592	0.0036	0.0043	0.6328
2.0	0.0003	0.3028	0.0031	0.0201	0.6736
2.5	0.0001	0.0343	0.0003	0.9445	0.0207
3.0	0.0000	0.0000	0.0000	1.0000	0.0000
b	ALLC	ALLD	TFT	WSLS	GTFT
					q = 1/3
1.5	0.0003	0.9482	0.0092	0.0049	0.0375
2.0	0.0003	0.4570	0.0046	0.0503	0.4879
2.5	0.0000	0.0201	0.0002	0.9290	0.0506
3.0	0.0000	0.0000	0.0000	1.0000	0.0000
b	ALLC	ALLD	TFT	WSLS	GTFT
					q = 1/2
1.5	0.0003	0.9779	0.0095	0.0043	0.0080
2.0	0.0005	0.8912	0.0089	0.0385	0.0609
2.5	0.0000	0.0209	0.0002	0.9569	0.0220
3	0.0000	0.0000	0.0000	1.0000	0.0000

In summary, we have studied stochastic game dynamics in populations of finite size under the influence of both mutation and selection. We consider the infinitely repeated PD with noise. Players make mistakes when implementing their strategies. In a population consisting of the three strategies, ALLC, ALLD and TFT, we find that the equilibrium distribution of our evolutionary process is entirely centered on ALLD. In contrast, a population consisting of ALLC, ALLD and WSLS settles predominantly on WSLS provided the benefit-to-cost ratio exceeds three, b/c > 3. Otherwise the system chooses ALLD. Finally, we have studied a population consisting of four strategies, ALLC, ALLD, TFT and WSLS. If b/c > 2 then WSLS is selected, otherwise ALLD is selected. Note that TFT lowers the selection threshold for WSLS, but is never chosen itself. Tit-for-tat is the catalyst for the emergence of cooperation, but win-stay, lose-shift is its target.

Appendix

Appendix A: Evolutionary dynamics in finite populations

We consider a discrete-time frequency dependent Moran process with mutations for a 2-player game with n strategies and payoff matrix A = (a_ij). The possible states of a population of size N are given by the vectors x = (x₁, … , x_n) $\in {\mathbb{N}}_0^n$ with x₁ + ⋯ + x_n = N. Here x_i denotes the number of individuals using strategy i. If the baseline fitness is K and the current state of the population is x, then the fitness of every individual that plays i, is given by

$$f_i(x)=K+\frac{{\displaystyle {\sum }_{j=1}^n{a}_{ij}{x}_j-a_{ii}}}{N-1},$$

where we assume that individuals do not interact with themselves. At every time step, one individual is chosen for reproduction and the probability of being chosen is proportional to fitness. That is, the probability that an individual using strategy i reproduces is equal to x_if_i(x)/∑_j x_jf_j(x). With probability 1 − u, the offspring uses the same strategy i. Otherwise, he mutates to one of the other n − 1 strategies with each of them being equally likely. The offspring replaces a randomly chosen member of the current population. For positive u, this procedure give rise to an irreducible Markov chain with a unique invariant distribution, denoted by π = π(x; u, K, N).

Letting the mutation probability u go to zero, we obtain a limit distribution, which concentrates on the homogeneous states, where all individuals play the same strategy. Let ${\pi }_1^{*}(K,N),\dots ,{\pi }_n^{*}(K,N)$ denote the limits corresponding to strategies 1, … , n, respectively. In the case of 2 × 2 games, the frequency-dependent Moran process is a simple birth-death process, and using an explicit representation of the invariant distribution (Ewens, 2004), one may show that

$$\frac{{\pi }_1^{*}(K,N)}{{\pi }_2^{*}(K,N)}={\displaystyle \prod _{i=1}^{N-1}\frac{f_1(i,N-i)}{f_2(i,N-i)}.}$$ (A.1)

For n × n games with n ≥ 3, the limit distribution can be determined using the results of Fudenberg and Imhof (2006). This approach requires the computation of every fixation probability ρ_ij, which is the probability that in the absence of mutations, a single individual using strategy j takes over a population where otherwise only strategy i is used. In particular, one needs to consider only the no-mutation process along the edges, where just two different strategies are present. This stems from the fact, that for small mutation rates u, the Moran process spends almost all its time at the homogeneous states, an amount of time of order O(u) on the edges and only o(u) at all other states.

We say that strategy i is selected, if ${\text{lim}}_{N\to \infty }{\pi }_i^{*}(K,N)=1.$

Appendix B: The repeated Prisoner’s Dilemma with errors

Consider the PD with payoffs T > R > P > S > 0 and suppose that R > (T + S)/2. We now derive the payoffs for the strategies ALLC, ALLD, TFT and WSLS in the infinitely repeated PD when in each round each player makes an error with probability ε > 0. The successive actions chosen by players using such strategies can be modeled by a Markov chain, see Nowak and Sigmund (1990). The presence of noise guarantees that the chain is ergodic. In particular, the initial action does not influence the average payoff per round, when infinitely many rounds are played. Computing the ergodic distribution of the realized actions for each pair of strategies, we obtain the payoff matrix in (B.1), where all terms of order O(ε²) have been ignored.

$$\left(\begin{array}{llll}\begin{array}{c}R\\ -\epsilon (2R-S-T)\end{array}\hfill & \begin{array}{c}S\\ +\epsilon (R+P-2S)\end{array}\hfill & \begin{array}{c}R\\ -\epsilon (3R-T-2S)\end{array}\hfill & \begin{array}{c}\frac{R+S}{2}\\ +\frac{\epsilon }{2}(T+P-R-S)\end{array}\hfill \\ \begin{array}{c}T\\ -\epsilon (2T-R-P)\end{array}\hfill & \begin{array}{c}P\\ +\epsilon (S+T-2P)\end{array}\hfill & \begin{array}{c}P\\ +\epsilon (S+2T-3P)\end{array}\hfill & \begin{array}{c}\frac{P+T}{2}\\ +\frac{\epsilon }{2}(R+S-T-P)\end{array}\hfill \\ \begin{array}{c}R\\ +\epsilon (2T+S-3R)\end{array}\hfill & \begin{array}{c}P\\ +\epsilon (T+2S-3P)\end{array}\hfill & \frac{T+R+P+S}{4}\hfill & \frac{T+R+P+S}{4}\hfill \\ \begin{array}{c}\frac{R+T}{2}\\ +\frac{\epsilon }{2}(S+P-R-T)\end{array}\hfill & \begin{array}{c}\frac{P+S}{2}\\ +\frac{\epsilon }{2}(R+T-S-P)\end{array}\hfill & \frac{T+R+P+S}{4}\hfill & \begin{array}{c}R\\ +\epsilon (T+2P+S-4R)\end{array}\hfill \end{array}\right)$$ (B.1)

Appendix C: Selection results

1. Competition of ALLD and TFT

If P > (T + R + P + S)/4, then ALLD strictly dominates TFT. Here and throughout we assume that ε is sufficiently small. It follows from (A.1) that ALLD is selected in large populations. Suppose that P < (T + R + P + S)/4. Then ALLD against TFT is a coordination game. Approximating the logarithm of the right-hand side of (A.1) by Riemann sums, one may show that TFT is selected if and only if

$${\displaystyle {\int }_0^1\mathrm{\text{log}}\frac{P+K+O(\epsilon )}{[P+O(\epsilon )]x+(T+R+P+S)(1-x)/4+K}\mathit{\text{dx}}}<0.$$

But for ε small enough, the integral is obviously negative. In the simplified version of the PD which is characterized by benefit b and cost c, we have T + R + P + S = 2(b − c) > 0 and P = 0, so that TFT is always selected.

2. Competition of ALLC, ALLD and TFT

It is shown in Example 2 of Fudenberg and Imhof (2006) that the limit distribution is given by π* = [γ₁ + γ₂ + γ₃]⁻¹ (γ₁, γ₂, γ₃), where

$$\begin{array}{l}{\gamma }_1={\rho }_{21}{\rho }_{31}+{\rho }_{21}{\rho }_{32}+{\rho }_{31}{\rho }_{23},\hfill \\ {\gamma }_2={\rho }_{31}{\rho }_{12}+{\rho }_{12}{\rho }_{32}+{\rho }_{32}{\rho }_{13},\hfill \\ {\gamma }_3={\rho }_{21}{\rho }_{13}+{\rho }_{12}{\rho }_{23}+{\rho }_{13}{\rho }_{23}.\hfill \end{array}$$

Using a well-known explicit expression for the absorption probabilities (Karlin and Taylor, 1975) and an approximation based on Riemann sums one may show that

$$\begin{array}{ll}{\rho }_{21}(N)=O(e^{-\beta N}),\hfill & {\rho }_{23}(N)=O(e^{-\beta N})\hfill \end{array}$$

for some β > 0. On the other hand,

$$\begin{array}{llll}\begin{array}{c}\mathrm{\text{inf}}\\ N\ge 2\end{array}\hfill & {\rho }_{12}(N)>0,\hfill & \begin{array}{c}\mathrm{\text{inf}}\\ N\ge 2\end{array}\hfill & {\rho }_{31}(N)>0.\hfill \end{array}$$

It is now obvious that ${\pi }_2^{*}(N)\to 1$, so that ALLD is selected.

3. Competition of ALLD and WSLS

If (P + T)/2 > R, then ALLD strictly dominates WSLS, and so, in view of (A.1), ALLD is selected. Suppose next that (P + T)/2 < R. Then ALLD against WSLS is a coordination game and which equilibrium is selected depends on the sign of

$$\gamma (K)={\displaystyle {\int }_0^1\mathrm{\text{log}}\frac{(P+T)x+2P(1-x)+2K}{2Rx+(P+S)(1-x)+2K}\mathit{\text{dx}}.}$$

If γ(K) > 0, then ALLD is selected; if γ(K) < 0, WSLS is selected.

If the payoffs in the PD are given in terms of benefit b and cost c, and b/c < 2, then ALLD is strictly dominant, so that ALLD is selected. Suppose that b/c > 2. We have

$$\gamma (K)={\displaystyle {\int }_0^1\mathrm{\text{log}}}\frac{bx+2K}{(2b-c)x-c+2K}\mathit{\text{dx}},$$

and it can be shown that

$$\gamma (K)<0\text{for all}K\text{sufficiently large}\iff \frac{b}{c}>3..$$

More precisely, if b/c > 3, there is a critical value K*(b/c) such that if K < K*, then γ(K) > 0, so that ALLD is selected, and if K > K*, then γ(K) < 0, so that WSLS is selected. Fig. 3 shows the relation between K* and the benefit-cost ratio. Notice that K* → ∞ when b/c approaches 3 from above. If b/c < 3, then γ(K) > 0 for all K, so that ALLD is selected independently of the intensity of selection.

4. Competition of ALLC, ALLD and WSLS

ALLD strictly dominates ALLC and WSLS strictly dominates ALLC. If (P + T)/2 > R, ALLD strictly dominates WSLS and ALLD is selected. Suppose next that R > (P + T)/2, so that ALLD against WSLS is a coordination game. Let

$$\begin{array}{l}{\beta }_{21}={\displaystyle {\int }_0^1\mathrm{\text{log}}}\frac{Tx+P(1-x)+K}{Rx+S(1-x)+K}\mathit{\text{dx}},\hfill \\ {\beta }_{41}={\displaystyle {\int }_0^1\mathrm{\text{log}}\frac{(R+T)x+2R(1-x)+2K}{2Rx+(R+S)(1-x)+2K}\mathit{\text{dx}},}\hfill \\ {\beta }_{24}={\displaystyle {\int }_0^{z_{24}}\mathrm{\text{log}}\frac{(P+T)x+2P(1-x)+2K}{2Rx+(P+S)(1-x)+2K}\mathit{\text{dx}},}\hfill \\ {\beta }_{42}={\displaystyle {\int }_0^{z_{42}}\mathrm{\text{log}}}\frac{(P+S)x+2R(1-x)+2K}{2Px+(P+T)(1-x)+2K}\mathit{\text{dx}},\hfill \end{array}$$

where

$$\begin{array}{ll}{z}_{24}=\frac{P-S}{2R-S-T},\hfill & z_{42}=\frac{2R-P-T}{2R-S-T}.\hfill \end{array}$$

If min{β₄₂, β₄₁} < min{β₂₄, β₂₁}, then ALLD is selected. If min {β₄₂, β₄₁} > min {β₂₄, β₂₁}, then WSLS is selected. Examining the integral conditions for K → ∞, one may show that in the simplified version of the PD, WSLS is selected for K sufficiently large if and only if b/c > 3.

5. Competition of ALLC, ALLD, TFT and WSLS

If R < (P + T)/2, then ALLD is selected. Suppose R > (P + T)/2 and P < (T + R + P + S)/4. Then ALLD and WSLS form a coordination game and so do ALLD and TFT. In this case, WSLS is selected. Suppose next that 2R > P + T and P > (T + R + P + S)/4, so that again ALLD and WSLS form a coordination game, but ALLD strictly dominates TFT. In this case, either ALLD or WSLS is selected, and which one is selected can be determined by comparing certain integrals similar to those in the analysis for the competition between ALLC, ALLD and WSLS. This last case cannot occur in the simplified version of the PD characterized by benefit b and cost c, and it follows that ALLD is selected if b/c < 2, and WSLS is selected if b/c > 2.