The emergence of form by replication

Abstract

It is shown with a simple mathematical model that if a system exhibits a given form (a spatial structure) and is put in contact with another system of the same type but in a state of spatial disorder, then under certain conditions their mutual interaction as they evolve in time allows replication of form in the disordered system with a controllable degree of faithfulness.

In evolution, from prebiotic to higher levels, replication of form and function are basic processes (1–10). Take, for instance, a protein that is already a highly sophisticated form. Crick (2, 3) notes that “at first sight it would seem a very difficult task to make an exact copy of the intact three-dimensional structure of a protein in its well organized native fold. One could conceive making a molecular cast of the surface, as one might for a piece of sculpture, but how would one copy the inside of the molecule? We need to carry the considerable amount of information as instructions to form the complexity that characterizes life, and unless this information is copied with reasonable accuracy the mechanism will decay under accumulated weight of errors. Perfect accuracy is not a requirement.”

Here we show how during their time evolution, the (mutual) interaction between two subsystems, one organized in a given form, a steady pattern, and the other spatially disordered, leads to replication of the form in the initially disordered system; the disordered system provides the raw materials. A given form and its replica may be replicated as many times as we wish provided we have nearby enough raw material ready for interaction. Replication produces entities that can themselves be copied by the replication process. This replication process is not merely that of a printing press.

We show with a simple two-dimensional model of reaction-diffusion equations the possibility of replication of form with a controllable degree of faithfulness. There are previous reports on replication of form and self-replication of patterns in reaction-diffusion systems (8–16). However, we depart from those approaches in that we address the question of replication of a form, a pattern at once, by using nearby available appropriate raw materials, which are spatially disordered.

We consider two interacting dynamical subsystems with dissipation, irreversibly evolving in time. In particular, we study the interaction of two identical, gradient lattice subsystems,

1

where u and v denote the evolving quantities (concentrations of chemical species), the dot indicates time derivative, and the cubic function f(w) is given by

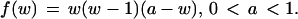The symbols h and κ denote coupling coefficients: h characterizes the strength of coupling between the two lattices, one describing the system with a pattern, the other the spatially disordered system; and κ characterizes the interaction among elements in each lattice, which are bistable units with two steady states. The pair (j, k) defines a space lattice point (j, k = 1, 2, … , N). Thus one subsystem has (2^N2) stationary states.

The fact that both systems, the patterned and disordered, are taken to be identical greatly simplifies our task. Yet, the huge space of accessible steady states of Eq. 1 makes the interaction and evolutionary problem nontrivial. The use of a gradient system, i.e., a system derivable from a potential, is a technical restriction to ensure the existence of steady states, hence time evolution leading to permanent forms. If nonvariational terms are involved in the dynamics, the system may not settle to any time-independent state or structure.

We impose on the two systems (Eq. 1) the condition of no mass transfer to the surroundings. If h = 0, the system (Eq. 1) represents two independent lattice systems. We denote by L₀ each of these subsystems, and, for the particular choice of f(w), they are a discrete version of the nonlinear Schlögl model with diffusion (17). It can be shown (18, 19) that for the parameters taken in the region

2

where u_min and u_max are the coordinates of the minimum and maximum of the function f(u), the system (Eq. 1) has (2^N2) steady states (attractors). This huge number of attractors can be coded by arbitrary N × N matrices consisting of two symbols (for instance, “0” and “1”) corresponding to the concentrations of the two steady states at each lattice site. Therefore, if the lattice “size” is large enough, then depending on initial conditions, this lattice displays attractors of an arbitrary spatial structure corresponding to a matrix of 0 and 1 given beforehand. Thus not only we have a huge number of accessible states but also a rich variety of patterns. On the other hand, it can also be shown that if

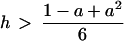3

is satisfied, for h ≠ 0, the mutual interaction of the subsystems in Eq. 1 is such that all the stationary states of the patterned subsystem slave the disordered subsystem, and hence may become replicated.

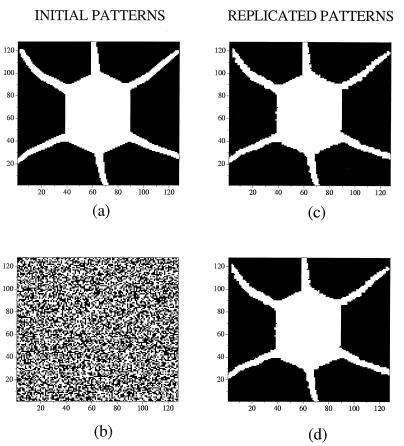
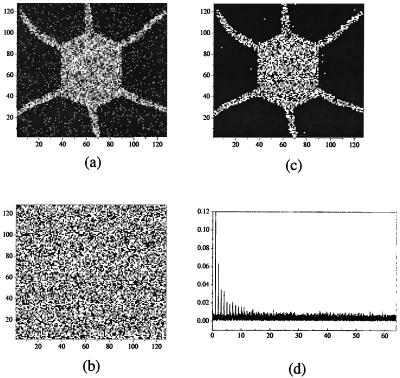
For illustration, initial conditions in each lattice of Eq. 1 were taken in the form of various patterns that had been produced by each single subsystem L₀ taken separately. Using a Runge-Kutta integration routine we observed that for the strength of coupling h satisfying Eq. 3 after interaction the two lattices display identical forms. Fig. 1 depicts our first replication exercise. One subsystem initially possesses a given form (Fig. 1a) and the other is in a state of spatial disorder at the initial time (Fig. 1b). As time proceeds, the two systems evolve until they produce identical patterns (Fig. 1 c and d). Replication for a = 0.5 is quite faithful. We obtain an almost perfect duplication of the initial pattern.

Figure 1.

Replication of form through mutual interaction of a system in a state defined by a steady “regular” pattern and another in a state of spatial disorder, hence raw material. (a and b) Initial conditions. (c and d) Offspring of two identical patterns. Parameter values, a = 0.5, = 0.006, and h = 0.4.

The rationale behind this result is the following. The inequalities Eqs. 2 and 3 demand that the intralattice coupling be weak enough, while the interlattice coupling h is strong enough, hence h ≫ κ. Because each lattice element is bistable, the overall interaction can be considered as a competition between the two possible locally stable states. It can be said that the small, but nonnegligible, value of κ provides the initial condition for this competition. For instance, the elements taken from the pattern carrying a regular image may have predominance over those of the disordered pattern. Then as the system (Eq. 1) derives from a potential, for a = 0.5, both competing states are at the same potential; the initial conditions determine the winner, and among the initial conditions a disordered state is less preferable, hence the loser.

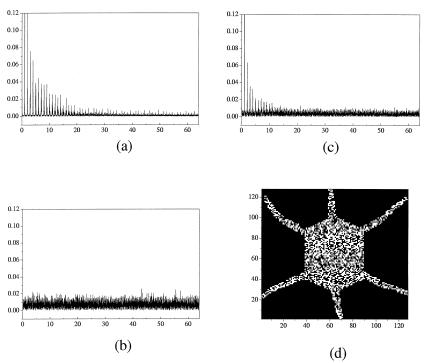
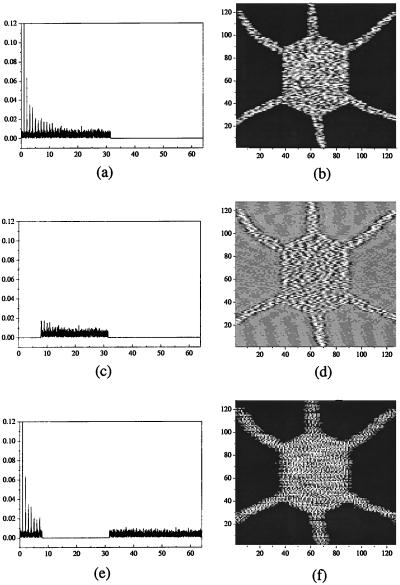
However, for a ≠ 0.5, say a = 0.6, we do not have potential equivalence of the two possible states, hence initial conditions and potential asymmetry act simultaneously in the competition. Thus we have no accurate duplication of either initial subsystem. Rather we have the appearance of two new patterns, identical to each other although inheriting key features of the original form we want to replicate. This can be appreciated, qualitatively, in real space and, quantitatively, in the spatial Fourier power spectra of the subsystems. Fig. 2 a and b are the initial spectra corresponding to Fig. 1 a and b, respectively. Fig. 2c is common to the two identical copies (Fig. 2d) obtained after the interaction, for a = 0.6, of the two L₀ subsystems in Eq. 1. Note that for vanishing κ only the nonlinearity (parameter a) defines the shape of the terminal patterns.

Figure 2.

(a and b) Spatial Fourier power spectra corresponding to the patterns of Fig. 1 a and b, respectively. (c) Spectrum corresponding to two identical offspring permanent patterns (d) obtained when a = 0.6 and that now exhibit noise in their core. Parameter values, a = 0.006, and h = 0.4.

We have checked our computations to assure that a steady state is attained. For this purpose the function

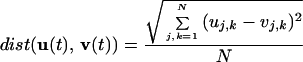4

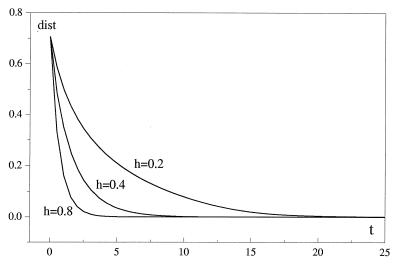
characterizes the distance between two patterns in the N² state space. The zero of this function corresponds to the terminal stage in the replication process of the pattern. Fig. 3 illustrates the evolution of the distance between the initial distributions shown in Fig. 1, for a = 0.5, and for different other values of the coupling strength h.

Figure 3.

Plot of distance, Eq. 4 vs time. At the initial time, a nonvanishing distance, dist ≠ 0, accounts for the difference between Fig. 1 a and b. In the course of evolution, the mutual interaction of the two subsystems L₀, Eq. 1, yields identical steady patterns (provided h satisfies condition 3, and time goes to infinity). The numerical calculation is illustrated for three values of h, the parameter characterizing mutual interaction, a = 0.5 and κ = 0.006. Similar behavior occurs for other values of a.

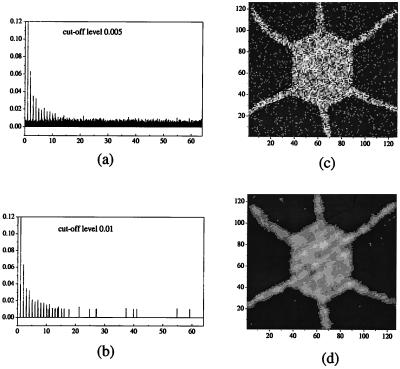
Fig. 4 illustrates up to what extent the replication process corresponds to copying key features of the original pattern although as, said earlier, replication is quite faithful for a = 0.5 (Fig. 1). The two power spectra (Fig. 4 a and b), when inverted, provide the patterns of Fig. 4 c and d, respectively. They have been obtained by eliminating trace elements, i.e., broad band noise or disorder at different amplitude levels (0.005 and 0.01, respectively). Fig. 5 shows the replication of a pattern, already replicated, in particular the form shown in Fig. 4c. From the initial states (Fig. 5 a and b) evolution with mutual interaction leads to two copies identical to that shown in Fig. 5c. Then, Fig. 5d is their corresponding, and common, spatial Fourier power spectrum. When comparing the first (Fig. 2d) and second (Fig. 5c) replicated forms with the original pattern (Fig. 1a) we see the rather faithful replication of the essential aspects of the original pattern (at least peaks in the power spectrum, and for a = 0.5 the complete spectrum).

Figure 4.

Details of replication features with reduced noise level. (a and b) Trace element/noise level reduced power spectrum (Fig. 2c) at two cut-off levels in height (0.005 and 0.01, respectively). (c and d) Corresponding patterns obtained upon inverting the Fourier transform of a and b, respectively.

Figure 5.

Replication of an already replicated form for a = 0.6, κ = 0.006, and h = 0.4. a is Fig. 4c. (b) An initial disordered state. The mutual interaction of the two L₀ subsystems (Eq. 1) yields two identical steady patterns (c) with identical power spectrum (d).

Our system does not possess a “natural” selection mechanism. Rather when two patterns compete, a mixed combination is produced in duplicate. It is only when one of the two systems is in a disordered state, hence like raw material, that a form tends to dominate, and eventually be replicated.

Fig. 6 shows various cuts in the spatial Fourier power spectrum (Fig. 2c) of Fig. 2d. Fig. 6 (a and b), (c and d), and (e and f) provide the reduced power spectra with corresponding forms in real space obtained by inverting the Fourier transform. To obtain function of a given pattern we may not be interested in the faithful replication of that pattern but rather in the accurate replication of some of its key features, significant for function, like correlations, correlation patterns, or appropriate parts of the spatial Fourier spectrum. Thus, the relationship of our findings to the study of pattern recognition becomes evident (20–22). Note that neither catalyst-like agents are needed nor any statistics are involved in our replication process, other than that associated to the choice, or spontaneous appearance, of initial conditions. Extending our results to a three-dimensional case may present mathematically technical difficulties, but not an intrinsic impossibility.

Figure 6.

(a, c, and e) Reduced power spectra of Fig. 1c when deletion of parts is applied, and corresponding patterns (b, d, and f) obtained by inversion of the Fourier transform.

We have shown the possibility of replication in vitro in relatively simple reaction-diffusion equations by the interaction of a structured subsystem on an equivalent, but spatially disordered, subsystem. The process may be of interest for in vivo systems. We believe that our results hold for systems without a potential, a condition more commonly met. Further we speculate that the results hold also for less restrictive conditions, such as long-lived metastable states rather than only stationary states.