Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1997 May 13;94(10):5045–5049. doi: 10.1073/pnas.94.10.5045

Cell membrane fluctuations are regulated by medium macroviscosity: Evidence for a metabolic driving force

Shmuel Tuvia *, Ada Almagor †, Arkady Bitler *, Shlomo Levin *, Rafi Korenstein *,‡, Saul Yedgar †
PMCID: PMC24628  PMID: 9144187

Abstract

Extracellular fluid macroviscosity (EFM), modified by macromolecular cosolvents as occurs in body fluids, has been shown to affect cell membrane protein activities but not isolated proteins. In search for the mechanism of this phenomenon, we examined the effect of EFM on mechanical fluctuations of the cell membrane of human erythrocytes. The macroviscosity of the external medium was varied by adding to it various macromolecules [dextrans (70, 500, and 2,000 kDa), polyethylene glycol (20 kDa), and carboxymethyl-cellulose (100 kDa)], which differ in size, chemical nature, and in their capacity to increase fluid viscosity. The parameters of cell membrane fluctuations (maximal amplitude and half-width of amplitude distribution) were diminished with the elevation of solvent macroviscosity, regardless of the cosolvent used to increase EFM. Because thermally driven membrane fluctuations cannot be damped by elevation of EFM, the existence of a metabolic driving force is suggested. This is supported by the finding that in ATP-depleted red blood cells elevation of EMF did not affect cell membrane fluctuations. This study demonstrates that (i) EFM is a regulator of membrane dynamics, providing a possible mechanism by which EFM affects cell membrane activities; and (ii) cell membrane fluctuations are driven by a metabolic driving force in addition to the thermal one.

The viscosity of body fluids is determined by the level of macromolecules consisting of proteins, lipoproteins, and polysacharides (1). Accordingly, elevated plasma viscosity has been observed in various diseases associated with increased levels of proteins and lipoproteins, such as diabetes, hyperlipidemia, macroglobulinemia, multiple myeloma, nephrosis, and others (1–5). Various studies have shown that solvent viscosity affects protein dynamics and reactions (6–10). However, in these studies the solvent viscosity was modified by the addition of high concentrations of small cosolvents such as glycerol and sucrose, producing relatively high viscosity levels. This is incompatible with physiological and pathological states, where fluid viscosity is altered by small concentrations of large macromolecules (1). Other studies, in which the viscosity was elevated by macromolecular cosolvents, have shown that extracellular fluid macroviscosity (EFM) is a regulator of cellular processes, such as secretion of renin (11) and lipoproteins (12), phospholipase A2 activity at the cell membrane (13, 14), and ganglioside metabolism (15). In search of the mechanism of this phenomenon, the effect of macroviscosity, as modified by macromolecules, on isolated proteins in aqueous solutions was examined (16, 17). It was found that the effect of solvent viscosity decreases with increasing molecular weight of the cosolvent and is practically diminished when the cosolvent molecular weight exceeds that of the protein. Because the activity of cell membrane enzymes is known to be sensitive to the physical properties of the membrane (18), we considered the possibility that the effect of macroviscosity on cell function is transduced through a direct effect of EFM on cell membrane dynamics. To examine this hypothesis, we investigated the effect of extracellular fluid viscosity on the cell membrane fluctuations (CMF).

CMF, first explored in red blood cells (erythrocytes; RBCs) (19), consist of submicron, out-of-plane displacements of the cell membrane in the frequency range of 0.3–30 Hz. CMF were recently observed in different types of nucleated cells (20–23), suggesting that CMF are a common characteristic of the living cell. RBC plasma membrane and its underlying skeleton are relatively well characterized, making it an optimal cellular model system to study CMF.

In the present study we examined the modulation of RBC membrane fluctuations by the macroviscosity of the external medium. The CMF were monitored by point dark field microscopy (20–24), where a very small area (0.25 μm2) at the cell edge was illuminated and the time-dependent intensity changes of the reflected and scattered light due to cell membrane movement in and out of the focused light spot were recorded.

MATERIALS AND METHODS

Preparation of RBCs and Nonresealed RBC Ghosts.

Fresh human RBCs were obtained immediately before each experiment from a healthy donor. A total of 50–100 μl of blood was diluted 50-fold in a PBS solution containing 130 mM NaCl, 20 mM K/Na phosphate buffer, 10 mM glucose, and 1 mg/ml BSA (pH 7.4). The employment of 1 mg/ml BSA in the PBS solutions was essential for preserving the normal shape of RBCs. RBCs were washed twice with PBS by centrifugation (200 × g, 2 min at 20°C), the buffy coat was removed and the amount of RBCs, in the final suspension, was ≈5 × 106 cells/ml. For long-term studies, penicillin/streptomycin (0.5 unit/ml) was added to the PBS solution. The RBCs were introduced into the experimental chamber at a low amount, so that the volume ratio of cells/solution in the chamber was 1:3000. The experimental chamber consisted of two cover glasses separated by a distance of 0.2 mm. Incubation in chamber for 20–30 min at 22–24°C allowed the RBCs to adhere firmly and irreversibly to the glass substratum. In some experiments we coated the cover glass by low concentration (5–40 μg/ml) of poly-l-lysine (54 kDa) and made sure, by phase contrast microscopic observation, that cell shape did not change (cover glass coated by high concentrations of poly-l-lysine of the order of 100 μg/ml may lead to shape deformation of the RBC). Preparation of nonresealed RBC ghosts was carried out by a similar procedure to the one described for the preparation of RBCs up to the step where RBCs were attached to the cover glass. Hemolysis of the RBCs was performed by perfusing the chamber with 50 μl of 0.0075% saponin in PBS for 30 s and then washing out the saponin by an additional 150 μl of “KCl solution” (130 mM KCl/20 mM K/Na phosphate buffer/10 mM glucose/1 mg/ml BSA, pH 7.8). These nonresealed RBC ghosts possessed dimensions similar to those of intact adhered RBCs, having a flat rather than a biconcave shape (24).

Preparation of ATP-Depleted RBCs.

Irreversible depletion of ATP in RBCs was carried out by incubating RBCs for 1 hr at 37°C in Tris⋅HCl buffered KCl solution, deficient of glucose and containing 10 mM inosine and 6 mM iodoacetamide (25). The addition of glycolytic substrates, in the presence of iodoacetamide, speeds up ATP depletion since the substrate consumes ATP, while glycolytic ATP production is blocked (25). To further accelerate ATP depletion glucose was replaced by the more efficient substrate, inosine. Thus, incubation of RBCs in the presence of 10 mM inosine and 5–6 mM iodoacetamide reduces the intracellular ATP from 1.2 mM ATP down to 1–5 μM in less than 1 hr of incubation at 37°C (26). The procedure of irreversible ATP depletion is known to also lead to a partial shape change in the RBC population, leading to the appearance of echinocytes and stomatocytes in addition to normal discocytes. However, under our conditions of irreversible ATP depletion, most of the RBCs kept their biconcave discocyte shape. To compare the effect of ATP depletion on CMF amplitudes, without having to take into consideration shape change of RBCs, the measurement of CMF was restricted to RBCs possessing a normal discoid shape.

Modulation of Extracellular Medium Macroviscosity.

The macroviscosity of external medium, in which RBCs or RBC ghosts were incubated, was varied by adding to the PBS solution various macromolecules that differ in size, chemical nature, and in their capacity to increase fluid viscosity. The macromolecules included dextran 70 (Dex-70; 70 kDa), dextran 500 (Dex-500; 500 kDa), and dextran 2000 (Dex-2000; 2,000 kDa), polyethylene-glycol (PEG; 20 kDa) and carboxymethyl-cellulose (100 kDa) (all purchased from Sigma). At first, a suspension of RBCs in PBS (1 centi Poise, cP) was introduced into the experimental chamber for 15–20 min until RBCs firmly adhered to the glass substratum. The nonadhered RBCs were washed out from the chamber. Then, a viscous cosolvent was introduced and the RBCs were incubated for 20 min at each viscosity before measuring the CMF. The medium viscosity was determined by measuring its flow time, relative to water, using an Ostwald capillary viscometer (12). All measurements were performed at 25°C. To examine whether the viscosity effect on CMF was reversible, after measuring the CMF in viscous medium the macromolecule containing medium was washed away with 150 μl PBS medium and CMF was measured in control PBS solution (1 cP). The exposure of nonresealed RBC ghosts to elevated medium viscosity was preformed by incubating the RBC ghosts in a KCl solution in the presence of different quantities of Dex-70 containing medium. RBC ghosts, attached to the cover glass, were perfused by 100 μl KCl solution at different viscosities in the range of 1–5 cP. Ghosts were incubated for 20 min at each viscosity before measurement, and CMF were monitored for 20–25 min. Again, the reversible effect of medium viscosity was carried out by measuring CMF following the washout of the viscous media by 150 μl KCl solution (1 cP).

Measurements of Membrane Fluctuations by Point Dark Field Microscopy.

The measurement of local mechanical fluctuations of the cell membrane was carried out on RBC and RBC ghosts by a novel optical method based on point dark field microscopy (20, 24). Using cells attached to a cover glass, we illuminate a very small area (0.25–1 μm2) at the cell edge and record cell membrane displacements by monitoring the time-dependent changes of light reflection and scattering, employing a home-made set-up of point dark field microscopy, similar to a previous report (20). The fluctuation of the light intensity depends on the changes of the membrane area moving in and out of the focused light spot near the cell’s edge. The time-dependent changes of the scattered light intensity (ΔI) are normalized by division by the time-independent component of the scattered light intensity (I). The analysis of the time-dependent scattered light intensity was carried out in terms of normalized maximal amplitude of the scattered light intensity (ΔImax/I). A linear relationship between the normal maximal intensity amplitude of scattered light from a single illuminated area along the cell periphery and the amplitude of the cell’s edge displacement was previously shown to exist over distances as long as 300 nm (ΔImax/I of ≈20%) (20). The accuracy of the experimental set-up was ≈1%. All measurements were carried out at 25–28°C. It was found that the change of CMF in this temperature range was negligible. The measurements of CMF amplitudes were taken over large times scale, up to 10 min, under steady-state conditions (constant maximum levels of fluctuation). Thus, the analysis should take into consideration the steady-state character of the measurements. In addition it was found that the strength of adherence to the glass substratum had no effect on CMF since, RBCs attached to a poly-l-lysine precoated cover glass (5–40 μg/ml of 54 kDa poly-l-lysine) exhibited the same CMF as RBCs attached to an uncoated cover glass.

Data Analysis.

A quantitative examination of CMF recordings was performed by the method of amplitude distribution analysis. The scattering from each surface area was recorded routinely for 55 or 110 s (sampling rate of 75 points/s). The data analysis process starts by dividing the whole data range into a number of bins of equal size where the number of data points within each bin was normalized to the total number of events. Derived probabilities have been tabulated. A graph of probabilities is plotted versus values of the grouped data points forming a frequency polygon, namely amplitude distribution. The “amplitude histogram” is used to graphically display the estimator of probability distribution. It is well known that a probability distribution can be described by the set of its moments (e.g., the first moment corresponds to the mean value, the second moment corresponds to the squared standard deviation). For the normally distributed variable (or Gaussian distribution) the first two moments (i.e., mean and squared standard deviation) are enough to describe the probability distribution. Thus, if the test of normalcy for the recorded traces of light intensity fluctuations is positive, the probability distribution is described completely by the estimations of the mean and the half-width. If one uses central moment estimations, only the second moment estimation will remain. Thus, when the assumption of normalcy is valid, the second moment (or standard deviation) estimation can be chosen as a single parameter to characterize fluctuations. The asymmetry and excess of the empirical probability distribution have been calculated and compared with the corresponding values from the statistical tables. In addition, all mentioned sets passed the χ2 test for normalcy.

Calculation of the Mean Energy of CMF.

The mean energy of CMF was calculated on the basis of the classical theory of thermally induced fluctuations. The elastic energy of fluctuation distortion of a unit membrane element was taken in a form first proposed by Helfrich (27). Because we measure light scattering from a very small area (≈0.25 μm2), the effect of spontaneous curvature on local fluctuations can be neglected. Using the thermodynamic theory of perturbation, the mean value of energy of the illuminated area is defined by the first two terms of expansion. The unperturbed state was chosen as the energy of the small fluctuation modes, with wavelengths that are larger than the linear size of the illuminated area. The energy of distortions of the real illuminated area was estimated to be small relative to the energy of the unperturbed state. Based on this approach we have derived the relationship between the mean fluctuation energy and mean squared apparent displacement (or local roughness). Employing the interrelationship between the apparent displacement and the mean squared fluctuation of scattered light intensity, one can obtain the following estimation of the mean elastic energy of fluctuations based on the light scattering data:

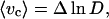graphic file with name M1.gif 1

where 〈vc〉 is the relative dimensionless mean elastic energy of the fluctuation induced distortion of the cell membrane (normalized by the bending modulus Kc); D = [〈I(t)2〉 − (〈I(t)〉)2]/(〈I(t)〉)2 is the relative mean squared deviation of the normalized scattered light intensity (variational coefficient); the multiplier Δ is a parameter independent of viscosity.

RESULTS AND DISCUSSION

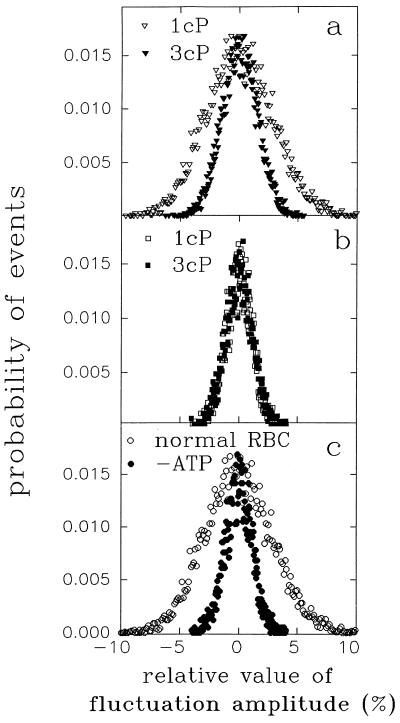
We examined the effect of medium viscosity on the amplitude distribution of CMF. The medium viscosity was changed by adding viscous macromolecules to the suspension medium. To ensure that the CMF were in a steady state, the RBCs were incubated in each specific viscosity for at least 20 min before measuring the time series of scattered light intensity. Analysis of CMF in terms of amplitude histograms yielded equal values of half-width at different time intervals, demonstrating that CMF were measured under steady-state conditions. Fig. 1a shows that while at 1 cP the half-width was 10.3 ± 0.3%, increasing the medium viscosity to 2.4 cP decreased the half-width down to a value of 8.2 ± 0.4%. Further increase of EFM to 3.0 cP (Fig. 1a) and 5.5 cP resulted in half-width of 7.2 ± 0.5% and 7.1 ± 0.5%, respectively. The decrease of CMF amplitudes was fully reversed upon replacing the high viscosity medium by a standard one (1 cP).

Figure 1.

Figure 1

Open in a new tab

The effect of medium viscosity on amplitude distribution of CMF in normal and ATP depleted human RBCs. (a) Amplitude distribution of CMF (see Materials and Methods) in RBCs perfused with medium having viscosity of 1 cP (▿) and 3 cP (▾). (b) Amplitude distribution of CMF in ATP depleted RBCs perfused with medium having viscosity of 1 cP (□) and 3 cP (▪). (c) Amplitude distribution of CMF in normal RBCs (○) and ATP depleted RBC (•) perfused with medium viscosity of 1 cP.

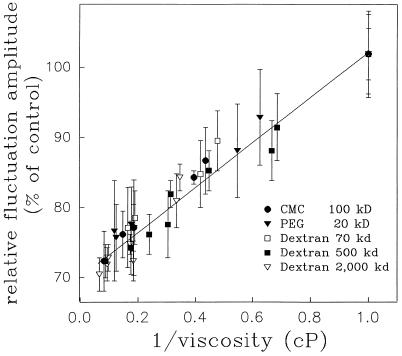
As described in Materials and Methods, to be able to differentiate the viscosity per se, as a hydrodynamic parameter, from other solution properties that might be altered by the addition of viscous macromolecules such as osmolarity or chemical interactions, CMF were determined in the presence of a variety of macromolecular cosolvents, which differ in their size, capacity to elevate fluid viscosity, and in their chemical nature. As shown in Fig. 2, the maximal CMF amplitudes (measured at 0.3 Hz) are attenuated with the increase of solvent macroviscosity, regardless of the cosolvent used to elevate EFM. The possibility that the observed effect is due to adsorption of the polymers to the cell surface would be supported provided the effect depend on the polymer’s size, concentration, or chemical nature. However, because no such correlation was found, the possibility of adsorption of the cosolvent to the RBC’s surface can be disregarded. This is further supported by the finding that the effect could be readily reversed by washing out the viscous medium and replacing it with the PBS control medium, as it is well known that a single washout would not wash away the adsorbed polymers (14). These findings and arguments suggest that the observed effect is due to the change in the EFM per se, and not to a possible cosolvent–membrane interaction or a change in the solution’s refractive index. Of special interest is the finding that this effect was obtained in the physiological fluid viscosity range of 1–4 cP, approaching an asymptotic value at viscosities higher than 5 cP, where the CMF amplitude was lower from control by 40%.

Figure 2.

Figure 2

Open in a new tab

The effect of medium viscosity on maximal amplitudes of CMF as modified by different macromolecular cosolvents. Each data point is a mean ± SD of at least 10 replications.

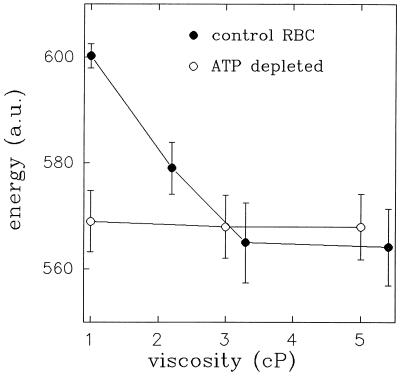
To understand the origin of the influence of medium macroviscosity on CMF, we considered the energy of CMF at different medium viscosities. To estimate this characteristic of erythrocyte membrane fluctuations we used Eq. 1. This last relationship was obtained on the basis of the classical model of thermally induced fluctuations of thin elastic sheet (27, 28). One should point out that the basic assumption of this theory is the validity of the equipartition theorem—i.e., that these fluctuations are driven solely by thermal energy. Therefore, the mean fluctuation energy of CMF should be independent of the external medium viscosity. However, calculating the mean elastic energy of fluctuations from the light scattering data, based on the model of thermally induced fluctuations, shows a pronounced dependence on viscosity in normal RBCs (Fig. 3).

Figure 3.

Figure 3

Open in a new tab

The effect of medium viscosity on the mean energy of CMF in normal and ATP-depleted RBCs. Filled and empty circles represent normal and ATP depleted RBCs, respectively. The results are expressed as mean ± SD. Each data point is an average of 20 time series.

The viscosity-induced change in the probability distribution of fluctuation amplitudes, or the observed change in the power spectrum upon raising the viscosity, cannot be attributed to the shift of CMF to a region of lower frequencies. The minimal mode (or maximal wavelength), and thus the slowest mode (the biggest relaxation time of the mode), exists due to the finite size of a cell. If R0 is the largest radius of the RBC, the maximal wavelength is equal to λmax = 2πR0 and the minimal transverse component of the wave vector is qm = (R0)−1. The respective maximal relaxation time τm, is given by (18): 4πηc/(Kcqm3) = 4πηcR03/Kc, where ηc is the viscosity of the cytoplasm and Kc is the curvature elastic modulus. The estimation of τm, by employing commonly used values for ηc = 6 cP, R0 = 4 μm = 4 × 10−4 cm, Kc = 2 × 10−12 (erg) yields a value of τm ≈5 s, corresponding to a minimal frequency of ≈0.2 Hz. Because the maximal size of the RBC is about 8 μm, the maximal wavelength (or the minimal mode) is approximately equal or smaller than this value. The corresponding frequency upper limit of this minimal mode yields a lowest boundary frequency of 0.2 Hz. This excludes the possibility that the decrease of CMF energy upon viscosity increase is due to a shift of the CMF to a lower frequency region inaccessible to our measurements.

According to the classical theory of thermally induced fluctuations of thin elastic sheets it is expected that CMF energy (as a thermodynamic parameter) should not depend on medium’s viscosity (a kinetic parameter). However, the observed dependence of CMF energy on medium viscosity contradicts this expectation and suggests the existence of a nonthermal driving force for CMF. Therefore, we have considered the possibility that the effect of medium’s viscosity on CMF is associated with a metabolic driving force.

To examine this hypothesis, we determined the effect of EFM on CMF in ATP-depleted RBCs (26), since MgATP has been shown to be a metabolic regulator of CMF (24). Fig. 1b clearly shows that, in ATP depleted cells, CMF are not affected by medium viscosity. In addition, Fig. 3 shows that increasing EFM reduces the mean fluctuation energy of normal RBCs to that of ATP-depleted cells. These findings suggest that the effect of medium viscosity is linked to a metabolic driving force. In addition, Fig. 3 also shows that the mean energy of fluctuations in ATP depleted RBCs is independent of the external medium viscosity. This implies that in ATP depleted RBCs CMF are indeed driven predominantly by a thermal driving force, since, as noted above, such independence is expected by the classical theory of thermally induced fluctuations.

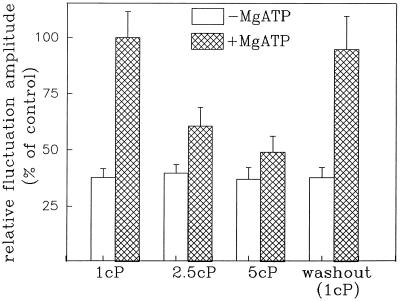
To rule out the possibility that the effect of EFM on CMF is related to the viscosity gradient between intra-extra cellular fluids, we measured CMF in nonresealed (open) RBC ghosts (where the internal and external viscosities are equal), in the absence and presence of MgATP, under varying medium macroviscosity. Fig. 4 shows that in the absence of MgATP, no effect of medium viscosity on maximal CMF amplitude was observed in RBC ghosts, as in ATP depleted RBCs. However, when the CMF were reconstituted to their maximal amplitude by the addition of MgATP to the ghosts, they were attenuated upon increasing medium viscosity (Fig. 4). The similar dependence of CMF on macroviscosity in intact RBCs and nonresealed RBC ghosts suggests that the effect of viscosity does not depend on the viscosity gradient across the cell membrane.

Figure 4.

Figure 4

Open in a new tab

The effect of medium viscosity on CMF maximal amplitudes of nonresealed RBC ghosts in the presence and absence of MgATP. The shaded and open columns depict the CMF of RBC ghosts in the presence of 1 mM MgATP or in the absence of MgATP, respectively. Each data point is a mean ± SD of at least 25 replications.

This study demonstrates that EFM is a regulator of membrane dynamics, in particular the metabolic-driven component of CMF. As noted above, enzyme activity at the cell membrane is sensitive to the membrane physical properties. Thus, this finding provides a mechanism by which EFM affects cell membrane enzyme activities. In view of previous findings that the effect of solvent viscosity on proteins decreases with increasing molecular weight of the viscous cosolvent (17), it may be proposed that the effect of solvent viscosity on a solute (proteins or cells) is determined by the size ratio of the viscous cosolvent to the solute; while for proteins the macromolecules are too big to affect their microenvironment, for cells they can be viewed as a microenvironment.

It has been previously shown that RBC filterability, a major determinant in microcirculation, is directly related to CMF (29, 30). Thus, in addition to altering vascular flow resistance, elevated plasma viscosity may influence the microcirculation by decreasing RBCs ability to pass through narrow pores.

The viscosity range studied here, using macromolecule concentrations similar to those in blood plasma, is in the range of viscosity changes that occur under physiological and pathological states (31). Elevated viscosity of blood and plasma is considered a risk factor for cardiovascular diseases and has been studied mainly in relation to microcirculation and hemodynamics. The results of the present study suggest that elevated plasma viscosity is pertinent to biochemical and cellular functions of blood cells.

Acknowledgments

This work was supported by grants from the Office of Naval Research (N00014-94-1-5 to S.L. and R.K; N00014-91-J-1880 to S.Y.) and the U.S.–Israel Binational Science Foundation (91-00209 to R.K. and S.L.; 91-00164 to S.Y.). This work was carried in partial fulfillment of the Ph.D. thesis requirements of S.T. and A.A.

ABBREVIATIONS

EFM

extracellular fluid macroviscosity

CMF

cell membrane fluctuations

RBC

red blood cell

cP

centi Poise

References

  • 1.Harkness J. In: Clinical Aspects of Blood Viscosity and Cell Deformability. Lowe G D O, Barbenel J C, Forbes C D, editors. Berlin: Springer; 1981. pp. 79–87. [Google Scholar]
  • 2.Dintenfass L, editor. Blood Viscosity. Boston: MTP Press; 1985. pp. 163–306. [Google Scholar]
  • 3.Leblond . In: Clinical Hemorheology. Chien S, Dormandy J, Ernst E, Matrai A, editors. Dordrecht, The Netherlands: Nijhoff; 1987. pp. 227–254. [Google Scholar]
  • 4.Barnes, A. & Willars, E. in Clinical Hemorheology, eds. Chien, S., Dormandy, J., Ernst E. & Matrai, A. (Nijhoff, Dordrecht, The Netherlands), pp. 275–310.
  • 5.Yedgar S, Eilam O, Shafrir E. Am J Physiol. 1985;248:E10–E14. doi: 10.1152/ajpendo.1985.248.1.E10. [DOI] [PubMed] [Google Scholar]
  • 6.Gavish B, Werber M M. Biochemistry. 1980;18:1269–1275. doi: 10.1021/bi00574a023. [DOI] [PubMed] [Google Scholar]
  • 7.Beece D, Eisenstein L, Frauenfelder H, Good D, Marden M C, Reinisch L, Reynolds A H, Sorensen L B, Yue K T. Biochemistry. 1980;19:5147–5157. doi: 10.1021/bi00564a001. [DOI] [PubMed] [Google Scholar]
  • 8.Rholam M, Scarlata S, Weber G. Biochemistry. 1984;23:6793–6796. [Google Scholar]
  • 9.Lavalette D, Tetreau C. Eur J Biochem. 1988;177:97–108. doi: 10.1111/j.1432-1033.1988.tb14349.x. [DOI] [PubMed] [Google Scholar]
  • 10.Almagor A, Yedgar S, Gavish B. Biophys J. 1992;61:480–486. doi: 10.1016/S0006-3495(92)81852-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Chien S, Kung-ming J, Simchon S. Biorheology. 1990;27:589–597. doi: 10.3233/bir-1990-273-437. [DOI] [PubMed] [Google Scholar]
  • 12.Yedgar S, Weinstein D, Patch W, Schonfeld G, Steinberg D J. Biol Chem. 1982;257:2188–2192. [PubMed] [Google Scholar]
  • 13.Hovav E, Halle D, Yedgar S. Biorheology. 1987;23:377–384. doi: 10.3233/bir-1987-24403. [DOI] [PubMed] [Google Scholar]
  • 14.Yedgar S, Reisfeld N, Halle D, Yuli I. Biochemistry. 1987;26:3395–3401. doi: 10.1021/bi00386a022. [DOI] [PubMed] [Google Scholar]
  • 15.Yedgar S, Reisfeld N, Sela B. Lipids. 1986;21:629–633. doi: 10.1007/BF02537211. [DOI] [PubMed] [Google Scholar]
  • 16.Almagor A, Yedgar S, Gavish B. Biorheology. 1990;27:605–610. doi: 10.3233/bir-1990-273-439. [DOI] [PubMed] [Google Scholar]
  • 17.Yedgar S, Tetreau C, Gavish B, Lavalette D. Biophys J. 1995;68:665–670. doi: 10.1016/S0006-3495(95)80227-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Mouristen O G, Biltonen R L. In: Protein-Lipid Interactions. Watts A, editor. Amsterdam: Elsevier; 1993. pp. 1–39. [Google Scholar]
  • 19.Brochard F, Lennon J F. J Phys (Paris) 1975;36:1035–1047. [Google Scholar]
  • 20.Krol A Ju, Grinfeldt M G, Levin S V, Smilgavichus A D. Eur Biophys J. 1990;19:93–99. doi: 10.1007/BF00185092. [DOI] [PubMed] [Google Scholar]
  • 21.Mittelman L, Levin S, Korenstein R. FEBS Lett. 1991;293:207–210. doi: 10.1016/0014-5793(91)81188-e. [DOI] [PubMed] [Google Scholar]
  • 22.Korenstein R, Tuvia S, Mittelman L, Levin S. In: Biomechanics of Active Movement and Division of Cells, NATO ASI Series H: Cell Biology. Akkas N, editor. Vol. 84. New York: Springer; 1994. pp. 415–423. [Google Scholar]
  • 23.Mittelman L, Levin S V, Korenstein R. Biochem Biophys Res Commun. 1994;203:899–904. doi: 10.1006/bbrc.1994.2267. [DOI] [PubMed] [Google Scholar]
  • 24.Levin S V, Korenstein R. Biophys J. 1991;60:733–737. doi: 10.1016/S0006-3495(91)82104-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Lew V L, Ferreira H G. Curr Top Membr Transp. 1978;10:217–221. [Google Scholar]
  • 26.Lew V L, Gracia-Sancho J. Methods Enzymol. 1989;173:100–112. doi: 10.1016/s0076-6879(89)73008-1. [DOI] [PubMed] [Google Scholar]
  • 27.Helfrich W Z. Z Naturforsch C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
  • 28.Milner S T, Safran S A. Phys Rev A. 1987;36:4371–4379. doi: 10.1103/physreva.36.4371. [DOI] [PubMed] [Google Scholar]
  • 29.Tuvia S, Levin S, Korenstein R. FEBS Lett. 1992;304:32–36. doi: 10.1016/0014-5793(92)80583-3. [DOI] [PubMed] [Google Scholar]
  • 30.Zamir N, Tuvia S, Riven-Kreitman R, Levin S, Korenstein R. Biochem Biophys Res Commun. 1992;188:1003–1009. doi: 10.1016/0006-291x(92)91331-j. [DOI] [PubMed] [Google Scholar]
  • 31.Chien S. In: Clinical Hemorheology. Chien S, Dormandy J, Ernst E, Matrai A, editors. Dordrecht, The Netherlands: Nijhoff; 1987. pp. 125–164. [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES