Spectral diffusion in a fluctuating charge model of water

Abstract

We apply the combined electronic structure/molecular dynamics approach of Corcelli, Lawrence, and Skinner [J. Chem. Phys. 120, 8107 (2004)] to the fluctuating charge (SPC-FQ) model of liquid water developed by Rick, Stuart, and Berne [J. Chem. Phys. 101, 6141 (1994)]. For HOD in H₂O the time scale for the long-time decay of the OD stretch frequency time-correlation function, which corresponds to the time scale for hydrogen-bond rearrangement in the liquid, is about 1.5 ps. This result is significantly longer than the 0.9 ps decay previously calculated for the nonpolarizable SPC/E water model. Our results for the SPC-FQ model are in better agreement with recent vibrational echo experiments.

Ultrafast time-resolved vibrational spectroscopy has been used extensively to investigate the dynamics of liquid water.^1–23 These techniques are especially powerful because the vibrations of a water molecule are sensitive to the different environments in the liquid (i.e., the vibrational frequencies of the molecule depend on the number and relative strengths of its hydrogen bonds). The time resolution of these experiments allows the dynamics of hydrogen-bond network rearrangement to be probed. Understanding the elementary mechanisms and time scales for making and breaking hydrogen bonds in water is an important step toward the development of improved water simulation models, and also of theories of chemical reactions occurring in aqueous solution, particularly for crucial electron and proton transfer processes relevant to biochemistry.

Recently we have developed a flexible computational strategy for relating the vibrational frequencies of a water molecule (or other solute) to its molecular environment. This approach combines electronic structure (ES) methods with molecular dynamics (MD) simulation, and was applied to the OH (OD) stretch of dilute HOD in liquid D₂O (H₂O).^6,7,24 The method is closely related to one recently developed and applied to N-methylacetamide in aqueous solution by Cho and co-workers.^25–27 Briefly, the combined ES/MD approach begins with a short MD simulation of the solute/solvent system, whose potential typically includes Coulomb interactions between point charges. From this initial simulation we extract clusters of the solute and its local solvent environment for analysis by ES. As an example, for HOD in D₂O we analyzed 100 small clusters consisting of the HOD molecule along with four to nine solvating D₂O molecules. The clusters form a representative sample of the kinds of solvation environments the HOD molecule experiences in the liquid. The OH vibrational frequency was then calculated for each cluster by determining the ab initio potential energy curve for stretching the OH bond. The resulting anharmonic vibrational frequencies (for the 0–1 transition) are then empirically related to the local environments by performing a linear fit to the electric field, due to the point charges (from the simulation model) of the solvent molecules, at the H atom in the direction of the OH bond. A second MD simulation is then performed, and a trajectory of the OH vibrational frequency is obtained by simply evaluating the relevant component of the electric field at each time step and employing the empirical frequency-field relationship. From the frequency trajectory a number of quantities can then be calculated that are related to experimental observables. Complete details of the ES/MD approach applied to HOD in H₂O and D₂O have been reported elsewhere.²⁴

An important quantity that can be obtained directly from ES/MD simulation and is measured by time-resolved infrared experiments, is the frequency time-correlation function (FTCF), C(t) = 〈δω(t) δω(0)〉, where δω(t) is the fluctuation of the instantaneous vibrational frequency from its equilibrium value: δω(t) = ω(t) − 〈ω〉. The time scales for the decay of the FTCF (that is, for spectral diffusion) describe how quickly the frequency loses memory of its initial value (i.e., how quickly the molecule loses memory of its initial solvation environment). MD studies have demonstrated that the long-time decay of the FTCF corresponds to the dynamics of forming and breaking hydrogen bonds in the liquid.^28–31 In Ref. 24 we employed the ES/MD methodology to calculate the OH FTCF of HOD in D₂O for two commonly used models of liquid water: SPC/E (Ref. ³²) and TIP4P.³³ For the SPC/E model the long-time decay of the FTCF was 0.9 ps, and for the TIP4P model it was 0.5 ps. These values are in agreement with those reported previously using different theoretical approaches for the same water models.^{29–31,34,35}

Experimental time scales for the long-time decay of the FTCF span the range from 0.4 to 15 ps!^{3–7,12,13,15,21–23} A critical discussion of the differences and limitations of the different techniques that have been used to obtain these FTCFs is presented in Ref. 7. The general conclusion is that vibrational echoes³⁶ (as opposed to pump-probe experiments) provide superior time resolution, and that frequency-resolved three-pulse echoes that discriminate between the 0–1 and 1–2 transitions are most useful for determining the FTCF for the 0–1 transition. Along these lines Asbury et al.,⁷ using two-dimensional echo correlation spectroscopy, found that for HOD/H₂O the long-time decay of the FTCF is 1.8 ps. More extensive experiments³⁷ on the same system find a more accurate value of 1.41 ps. Earlier two-pulse heterodyned echo experiments by Yeremenko, Pshenichnikov, and Wiersma found 0.9 ps for the HOD/D₂O system, ⁵ and three-pulse integrated echo peak shift measurements by Fecko et al. found 1.2 ps for the same system.⁴

Comparing our theoretical results to the time scales measured in these most recent experiments, it is apparent that the SPC/E and TIP4P water models predict a decay of the FTCF that is too fast. This implies that the kinetics of hydrogen-bond rearrangement are not properly represented within either of these commonly used water models. Xu, Stern, and Berne have suggested that these models underestimate the lifetime of a hydrogen bond in liquid water because they lack the effects of polarizability (i.e., because of their fixed charges, the water molecules in the SPC/E and TIP4P models do not respond to their changing environments).³⁸ In models that do include the effects of polarizability (e.g., the TIP4P-FQ and SPC-FQ fluctuating charge models of Rick, Stuart, and Berne³⁹) the interactions between a pair of water molecules depends not only on their relative orientations and positions, but also on their environments. This gives rise to many-body interactions and cooperativity in hydrogen-bond dynamics. Xu, Stern, and Berne investigated the differences between the hydrogen-bond lifetime for the TIP4P and TIP4P-FQ models, and found that the lifetime was about 50% longer for the latter.³⁸ MD simulations of the polarizable PSPC model⁴⁰ have also demonstrated that the effect of polarizability is to significantly lengthen orientational correlation times.⁴¹ This is particularly interesting when taken in the context of the recent suggestion by Gallot et al. that the lifetime of a hydrogen bond in liquid water is rotation limited (i.e., that there is significant coupling between rotational and OH···O motions).⁴² The evidence from all of these previous studies suggests that the decay time of the FTCF would also be longer for these polarizable models, and hence in closer agreement with experiment.

In the present work we applied the combined ES/MD approach of Ref. 24 to the SPC-FQ water model, details of which are described in Ref. 39. Our MD simulations of the SPC-FQ model contained 128 H₂O molecules. The size of the cubic simulation box was chosen to give the number density of water at 300 K (3.33×10²⁸ m⁻³),⁴³ and periodic boundary conditions were employed. The electrostatic forces were calculated using an approximation to the Ewald sum, ⁴⁴ and the equations of motion were integrated using the leapfrog algorithm.⁴⁵ The rotations were treated using quaternions.⁴⁶ Equilibration of the system temperature to 300 K was accomplished by periodically rescaling the velocities of the molecules. The temperature of the charge degrees of freedom³⁹ was maintained at 5 K by scaling the charge velocities every 1000 time steps. From a short simulation run we generated 100 clusters containing five to ten water molecules each. As described above we then established a linear relationship (with correlation coefficient 0.9) between the calculated ab initio vibrational frequencies and the electric field, which in this case was due to the actual instantaneous values of the atomic charges from the solvent molecules in the cluster (as extracted from the configuration of the liquid). Within our approach the normalized FTCF is simply the normalized time-correlation function of the electric field fluctuations, ²⁴ which can be obtained directly from simulation.

In our previous work we ran MD simulations specifically for HOD in H₂O (or D₂O).²⁴ However, since the FTCF is primarily sensitive to the dynamics of the solvent, in the present work we have calculated the FTCF for neat H₂O. This is accomplished by supposing, for the purposes of the calculation, that every OH bond in the neat liquid is treated as the OD vibration of interest. Thus, we calculate two OD vibrational frequencies for each molecule in the simulation. This approach is much more computationally efficient because there are 256 vibrations in the simulation rather than just one. To demonstrate that there is no loss of accuracy in this approach, in Fig. 1 we show the normalized OD stretch FTCF for the SPC/E model calculated using a 50 ns trajectory of HOD in H₂O. Also shown in Fig. 1 is the FTCF computed from a 0.5 ns trajectory of neat H₂O. The results are numerically identical, indicating that the small change in the dynamics of the single HOD molecule compared to a H₂O molecule are not manifested in the FTCF.

FIG. 1.

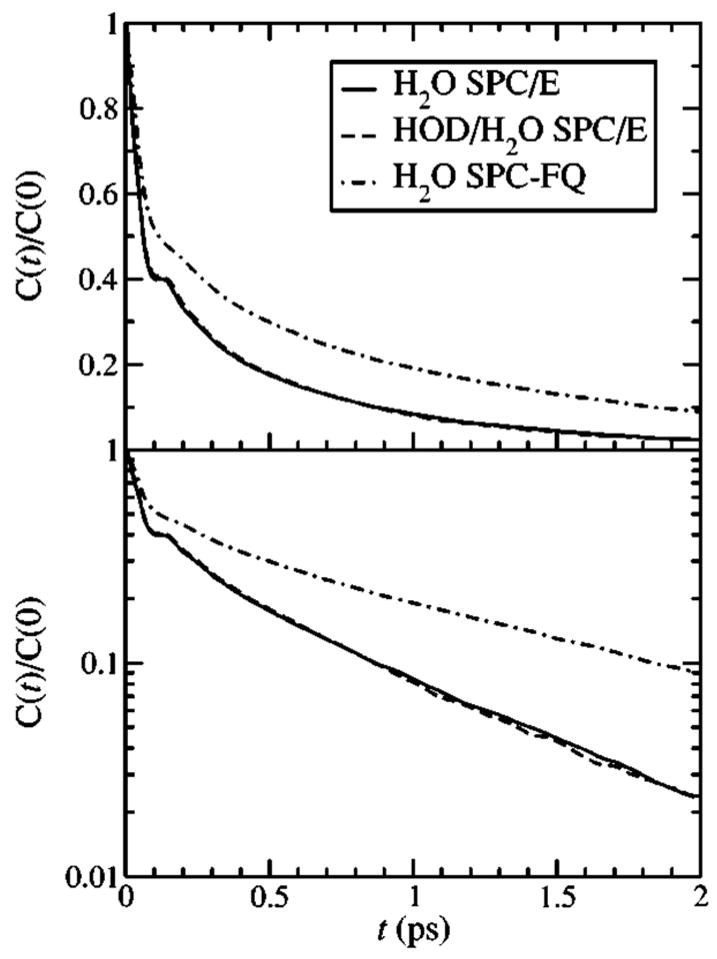
The normalized OD stretch FTCFs for the SPC/E and SPC-FQ water models. These functions were calculated with the combined ES/MD approach described in Ref. 24.

In Fig. 1 we also show the normalized OD stretch FTCF for the SPC-FQ model. The normalized FTCF is fit well by three exponentials with decay times of 48 fs, 352 fs, and 1.45 ps, and amplitudes of 0.44, 0.20, and 0.36, respectively. As anticipated from the work of Xu, Stern, and Berne³⁸ the long-time decay of 1.45 ps is about 50% longer for the SPC-FQ model than the 0.9 ps decay of the SPC/E model. The SPC-FQ FTCF does not contain the oscillation at about 150 fs present in the SPC/E (and TIP4P) FTCFs, which has been attributed to an intermolecular hydrogen bond stretching motion.^{4,28–31,47–49} We have also calculated FTCFs for (the OH stretch of HOD in) neat D₂O. These are not shown because for both the SPC/E and SPC-FQ models they are quite similar to those of H₂O. In particular, for the SPC-FQ model the triexponential fit gives decay times of 52 fs, 419 fs, and 1.52 ps, with amplitudes of 0.43, 0.23, and 0.34, respectively.

In Fig. 2 we show the FTCFs obtained from three recent vibrational echo experiments for HOD in D₂O (Refs. ⁴ and ⁵) and H₂O.³⁷ In the latter case the normalized FTCF was fit to a sum of three exponentials, with amplitudes of about 0.41, 0.15, and 0.43, and decay times of 45 fs, 400 fs, and 1.4 ps, respectively.³⁷ Because the fastest exponential is in the motionally-narrowed limit, ^2,50 it is difficult to determine its amplitude and decay time separately, and so the decay time was simply set to 45 fs. One sees that the three experimental results are qualitatively different: the result of Fecko et al.⁴ shows a substantial oscillation at about 150 fs, whereas the results of Yeremenko, Pshenichnikov, and Wiersma⁵ and Asbury et al.⁷ do not. Furthermore, the relative amplitudes of the short- and long-time features differ among these three results. Finally, the rate of the long-time decays of Fecko et al.⁴ and Asbury et al.⁷ are similar, while the decay of Yeremenko, Pshenichnikov, and Wiersma⁵ is somewhat faster. Also shown in the figure are our theoretical results for the TIP4P, SPC/E, and SPC-FQ models for H₂O. One sees that the TIP4P and SPC/E results are not in particularly good agreement with any of the experiments in that they decay too fast (as discussed above). On the other hand, the SPC-FQ model is more similar to the results of Asbury et al. and Yeremenko, Pshenichnikov, and Wiersma, and its long-time decay is more similar to those of all three echo experiments. It is interesting to note that although the amplitudes of the three exponentials differ somewhat between the fit of Asbury et al.³⁷ and the SPC-FQ model, the intermediate and slow decay times are very similar.

FIG. 2.

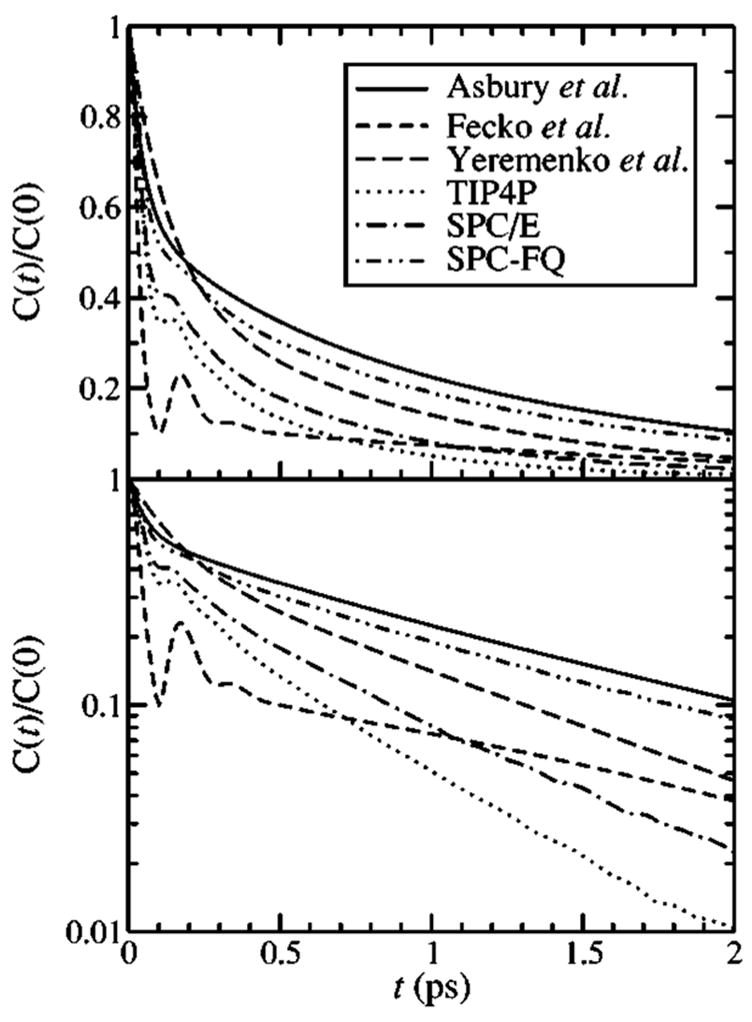
The normalized FTCFs for three different vibrational echo experiments and three different theoretical models of water: TIP4P, SPC/E, and SPC-FQ. The theoretical FTCFs are for neat H₂O, and were calculated with the combined ES/MD approach described in Ref. 24. Asbury et al. (Ref. ³⁷) studied HOD/H₂O, and Fecko et al. (Ref. ⁴) and Yeremenko et al. (Ref. ⁵) studied HOD/D₂O.

Given the level of disagreement among experiments on one system (HOD in D₂O, ^{3–5,12,13,15,22,23}), it remains unclear whether there is a significant difference between spectral diffusion in normal and heavy water. The experimental diffusion constant for heavy water is smaller than that for normal water by about 20%. Since spectral diffusion reflects a similar collective dynamical process, one would guess that spectral diffusion in heavy water would also be slower (relative to that for normal water). This trend was observed experimentally by the Bakker group—they find a spectral diffusion time of 400 fs for H₂O compared to 500 fs for D₂O.^13,21 However, the more recent experiments show the opposite trend: for D₂O 0.9 ps,⁵ 1 ps,²³ and 1.2 ps (Ref. ⁴) have been reported for the long-time decay, while for H₂O the corresponding values are 1.4 ps (Ref. ³⁷) and 2 ps.²³ Future experiments will hopefully quantify more accurately the difference between these two systems, but in the meantime we feel reasonably comfortable discussing the experiments without undue attention to this possible difference.

In summary, the results of our spectral diffusion calculations within the SPC-FQ model are consistent with the fact that polarizability slows down the dynamics of hydrogen-bond rearrangement in the liquid.^38,41 The FTCF for the polarizable SPC-FQ model is in better agreement (compared to the fixed-charge models) with the most recent vibrational echo experiments briefly described here.³⁷ There still remain substantial differences among the different experimental results, which hopefully will be resolved in the near future. It is possible that despite the considerable success that the fluctuating charge models have had with reproducing other dynamical properties such as the frequency-dependent dielectric constant, ³⁹ the SPC-FQ model will not quantitatively reproduce the experimental FTCFs. Indeed, this would not be entirely surprising, since in the absence of reliable dynamical experiments, this model (like its predecessors) was primarily parametrized from thermodynamic and structural data. In any case, these experiments will provide important benchmarks for testing the dynamics of present and future water models.