Efficient Ca²⁺ buffering in fast-spiking basket cells of rat hippocampus

Abstract

Fast-spiking parvalbumin-expressing basket cells (BCs) represent a major type of inhibitory interneuron in the hippocampus. These cells inhibit principal cells in a temporally precise manner and are involved in the generation of network oscillations. Although BCs show a unique expression profile of Ca²⁺-permeable receptors, Ca²⁺-binding proteins and Ca²⁺-dependent signalling molecules, physiological Ca²⁺ signalling in these interneurons has not been investigated. To study action potential (AP)-induced dendritic Ca²⁺ influx and buffering, we combined whole-cell patch-clamp recordings with ratiometric Ca²⁺ imaging from the proximal apical dendrites of rigorously identified BCs in acute slices, using the high-affinity Ca²⁺ indicator fura-2 or the low-affinity dye fura-FF. Single APs evoked dendritic Ca²⁺ transients with small amplitude. Bursts of APs evoked Ca²⁺ transients with amplitudes that increased linearly with AP number. Analysis of Ca²⁺ transients under steady-state conditions with different fura-2 concentrations and during loading with 200 μm fura-2 indicated that the endogenous Ca²⁺-binding ratio was ∼200 (κ_S= 202 ± 26 for the loading experiments). The peak amplitude of the Ca²⁺ transients measured directly with 100 μm fura-FF was 39 nm AP⁻¹. At ∼23°C, the decay time constant of the Ca²⁺ transients was 390 ms, corresponding to an extrusion rate of ∼600 s⁻¹. At 34°C, the decay time constant was 203 ms and the corresponding extrusion rate was ∼1100 s⁻¹. At both temperatures, continuous theta-burst activity with three to five APs per theta cycle, as occurs in vivo during exploration, led to a moderate increase in the global Ca²⁺ concentration that was proportional to AP number, whereas more intense stimulation was required to reach micromolar Ca²⁺ concentrations and to shift Ca²⁺ signalling into a non-linear regime. In conclusion, dentate gyrus BCs show a high endogenous Ca²⁺-binding ratio, a small AP-induced dendritic Ca²⁺ influx, and a relatively slow Ca²⁺ extrusion. These specific buffering properties of BCs will sharpen the time course of local Ca²⁺ signals, while prolonging the decay of global Ca²⁺ signals.

GABAergic interneurons are essential for information processing in cortical neuronal networks. Within this group of morphologically and functionally diverse cell types (Freund & Buzsáki, 1996; Somogyi & Klausberger, 2005), fast-spiking parvalbumin-expressing basket cells (BCs) are thought to have particularly important functions. These interneurons represent the most abundant interneuron subtype, corresponding to ∼20% of all GABAergic interneurons in the hippocampus (Freund & Buzsáki, 1996). BCs have an extensive axonal arborization, by which they innervate a large number of target neurons. BCs also generate large inhibitory postsynaptic conductances in their target cells (Kraushaar & Jonas, 2000). Furthermore, BCs mainly contact the perisomatic region of postsynaptic neurons, permitting efficient control of action potential (AP) initiation in the axon initial segment and proximal axon (Cobb et al. 1995). These specialized properties allow BCs to efficiently participate in feedforward and feedback inhibition (Pouille & Scanziani, 2004).

Previous studies revealed that BCs show fast electrical signalling at multiple levels (Jonas et al. 2004). BCs receive a fast excitatory synaptic input, which allows them to detect coincident excitation of pyramidal neurons (Miles, 1990; Geiger et al. 1997; Galarreta & Hestrin, 2001). BCs are able to generate high-frequency trains of APs during sustained current injection in vitro (Rudy & McBain, 2001) and during theta–gamma activity in vivo (Bragin et al. 1995; Penttonen et al. 1998; Csicsvari et al. 2003). Finally, BCs generate rapid inhibitory output signals in their target cells, especially if the postsynaptic neuron is another BC (Bartos et al. 2007). Rapid signalling in BCs appears to be essential for both the fast inhibition of principal neuron ensembles and the generation of network oscillations in the gamma frequency range (30–90 Hz; Jonas et al. 2004; Bartos et al. 2007).

Whereas a large amount of information is available on electrical signalling in BCs, Ca²⁺ signalling in these interneurons has remained largely uncharacterized. However, indirect evidence suggests that the properties of Ca²⁺ signalling in BCs may be distinct from those of principal cells or other interneuron subtypes. First, BCs selectively express Ca²⁺-permeable glutamate receptors of the l-α-amino-3-hydroxy-5-methyl-4-isoxazolepropionate (AMPA) subtype (Koh et al. 1995; Geiger et al. 1995; Toth et al. 2000; Lei & McBain, 2002; Goldberg et al. 2003b). Second, BCs selectively express the Ca²⁺-binding protein parvalbumin. However, the contribution of this Ca²⁺-binding protein to endogenous Ca²⁺ signalling is unknown, since parvalbumin binds Ca²⁺ slowly in the presence of physiological Mg²⁺ concentrations (Schwaller et al. 2002; Müller et al. 2007). Third, BCs differ from principal cells in the expression of Ca²⁺-dependent signalling molecules. For example, BCs lack the expression of the α subunit of calcium-calmodulin-dependent kinase II and calcineurin (Sík et al. 1998). Finally, BCs express distinct forms of Ca²⁺-dependent synaptic plasticity at their glutamatergic input synapses (Kullmann & Lamsa, 2007). However, a quantitative analysis of Ca²⁺ buffering in identified BCs has not been performed. Understanding the Ca²⁺ buffering in interneurons may be also important to understand the selective resistance or vulnerability of these neurons under pathophysiological conditions (Sloviter et al. 2003).

To determine the endogenous Ca²⁺ buffering in rigorously identified BCs, we combined whole-cell patch-clamp recordings with ratiometric Ca²⁺ imaging at proximal apical dendrites, using both the high-affinity indicator fura-2 and the low-affinity dye fura-FF. The goal was to determine the endogenous Ca²⁺-binding ratio (i.e. the ratio of buffer-bound Ca²⁺ changes over free Ca²⁺ changes; Neher & Augustine, 1992; Neher, 1998), the amplitude of the Ca²⁺ transient evoked by single APs in the absence of exogenous buffers, and the Ca²⁺ extrusion rate. Our results reveal that, in comparison to pyramidal neuron dendrites (Helmchen et al. 1996), BC dendrites show a high endogenous Ca²⁺-binding ratio. Although BCs are coincidence detectors at the level of synaptic currents and potentials (Geiger et al. 1997; Galarreta & Hestrin, 2001), they behave as integrators at the level of AP-induced Ca²⁺ signals. A preliminary account of the data was published in abstract form (Aponte et al. 2006a).

Methods

Patch-clamp recording from basket cells in hippocampal slices

Transverse 300-μm-thick slices were cut from the hippocampus of 18- to 21-day-old Wistar rats using a commercial (Dosaka, Kyoto, Japan) or a custom-built vibratome (Geiger et al. 2002). Animals were killed by rapid decapitation without anaesthesia in accordance with national and institutional guidelines. Experiments were approved by the Animal Care Committee Freiburg according to §15 of the Tierschutzgesetz (registry T-04/10). Slices were kept at 35°C for 30 min after slicing and then at room temperature in physiological extracellular saline containing (mm): 125 NaCl, 25 NaHCO₃, 2.5 KCl, 1.25 NaH₂PO₄, 2 CaCl₂, 1 MgCl₂ and 25 glucose, equilibrated with 95% O₂–5% CO₂. Dentate gyrus basket cells were tentatively identified by the size and the location of the soma at the granule cell layer–hilus border using infrared differential interference contrast (IR-DIC) videomicroscopy (Koh et al. 1995; Aponte et al. 2006b).

Patch pipettes were pulled from borosilicate glass tubing (2.0 mm outer diameter, 1.0 mm inner diameter; Hilgenberg, Malsfeld, Germany). A Multiclamp 700A amplifier (Molecular Devices, Palo Alto, CA, USA) was used for current-clamp recordings. Series resistance (5–15 MΩ) was compensated by the bridge-balance circuit of the amplifier. The resting membrane potential measured after obtaining a whole-cell recording was between −65 and −54 mV and was set to −70 mV (membrane potential values uncorrected for liquid junction potentials) by injecting a constant negative holding current (< 150 pA). Voltage signals were filtered at 4 kHz with a 4-pole low-pass Bessel filter and sampled at 10 kHz. Pulse generation and data acquisition was performed using FPulse (U. Fröbe, Physiological Institute) running under Igor Pro 5.01 (Wavemetrics, Lake Oswego, OR, USA) on a personal computer, which controlled a 1401plus interface (CED, Cambridge, UK).

To obtain somatic whole-cell recordings, we used patch pipettes (2–4 MΩ) filled with internal solution containing (mm): 125 potassium gluconate, 4 MgCl₂, 4 K₂ATP, 0.3 NaGTP, 10 Na₂-phosphocreatine and 10 Hepes, different concentrations of Ca²⁺ indicator dyes, and 0.2% biocytin (pH adjusted to 7.2 with KOH). Free ATP concentration in this solution was estimated as 0.63 mm. Action potential (AP) patterns were determined in the current-clamp configuration using 1 s depolarizing current pulses. Only fast-spiking neurons with an average AP frequency larger than 50 Hz were used for subsequent Ca²⁺ imaging experiments. Recordings were made at 22–24°C, unless specified differently.

Fluorescence measurements with fura-2 and fura-FF

For the measurement of the intracellular Ca²⁺ signals, different concentrations of fura-2 or fura-FF (Invitrogen, Eugene, OR, USA; Neher, 1995) were added to the pipette solution. The excitation light source (Polychrome I with 75 W xenon lamp, Till Photonics, Munich, Germany) was coupled to the epifluorescent port of the microscope (Axioskop FS2, Zeiss, Göttingen, Germany; 60× water immersion objective, Olympus, Tokio, Japan) via a light guide. Light intensity was adjusted to minimize bleaching of the fluorescent dyes, which was ∼0.2 ± 0.1% (n = 7) during a 5 s sweep, estimated as the decrease of fluorescence emission with excitation at the isosbestic wavelength of 356 nm (the Ca²⁺-insensitive wavelength under our experimental conditions). The filter combination for excitation and emission comprised a beam splitter (BSP400) and an emission filter (BP430-630; AHF Analysentechnik Tübingen, Germany).

Fluorescence was measured with a backilluminated frame-transfer charge-coupled device (CCD) camera (EBFT 512, Princeton Instruments, Trenton, NJ, USA). Images with full spatial resolution were taken with exposure times of 5 s. For high-speed Ca²⁺ measurements (100 Hz sample frequency), a rectangular region of interest (ROI) was defined over the proximal apical dendrite of a BC (typical size 5 μm × 20 μm) at a distance of 10–60 μm from the border of the soma. Fluorescence measurements were initiated ∼10 min after the whole-cell configuration was obtained, with the exception of loading curve experiments in which measurements were started immediately after breaking in (Fig. 5). Fluorescence traces had a duration of 5–30 s and were separated by intersweep intervals of 10–30 s. Signals were corrected for background, which was obtained from a second ROI with identical size but shifted 10–15 μm perpendicularly to the dendritic axis in comparison to the original ROI (Normann et al. 2000). The pixels included in the two ROIs were binned on-chip and digitized subsequently by the camera controller (Micromax, 1 MHz, Princeton Instruments). Image acquisition was controlled using custom-made programs written in Visual Basic running under WinView 32 (Princeton Instruments). For display purposes, a subset of traces with fura-FF was digitally filtered at a cutoff frequency of 15 Hz.

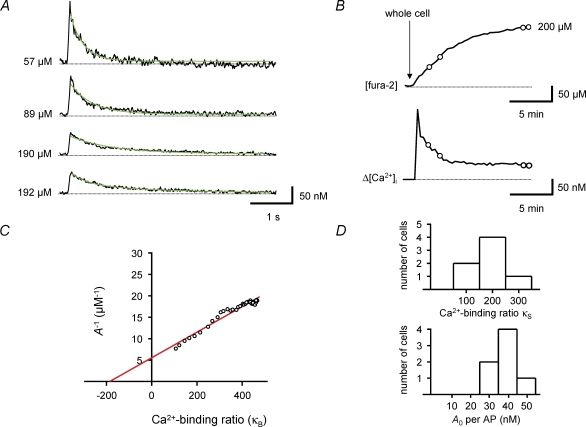
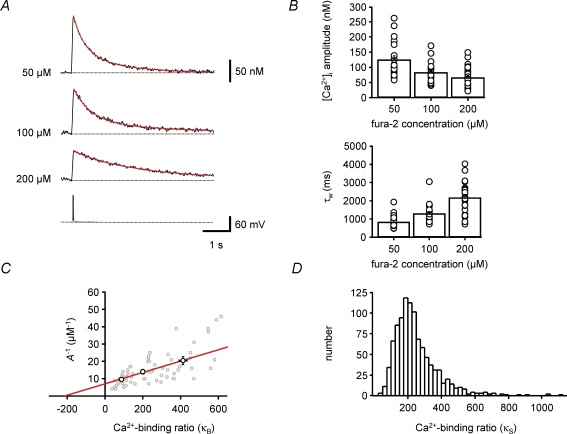
Figure 5. Estimation of endogenous Ca²⁺-binding ratio during loading with the high-affinity indicator fura-2.

A, single traces of Ca²⁺ transients recorded at different time points in a BC during loading with 200 μm fura-2, corresponding to different fura-2 concentrations in the dendrite (as indicated on the left of each trace). Green curves represent monoexponential fits to the decay phase of the Ca²⁺ transients. Note that the peak amplitude of the Ca²⁺ transients decreases, while the decay time constant increases during loading. B, plot of fura-2 concentration (upper trace) and simultaneously measured peak amplitude of Ca²⁺ transients (lower trace) before and after the whole-cell configuration was obtained. Circles indicate the data points corresponding to the traces shown in A. C, plot of the inverse of the peak amplitude of Ca²⁺ transients against exogenous Ca²⁺-binding ratio, i.e. the Ca²⁺-binding ratio of the indicator (κ_B). The continuous line represents the results of unweighted linear regression. The endogenous Ca²⁺-binding ratio (κ_S), estimated from the intercept of the fitted line with the horizontal axis, was 186 in this BC. Data in A–C were obtained from the same cell. D, histograms of endogenous Ca²⁺-binding ratio (κ_S, upper graph) and amplitude of dendritic Ca²⁺ transient per AP in the absence of fura-2 (A₀, lower graph) in 7 BCs. All experiments were performed with 100 Hz bursts of 5 APs.

Calibration of the Ca²⁺ measurements

To convert the fluorescence signals into Ca²⁺ concentrations, we used isosbestic ratioing (Neher & Augustine, 1992; Schiller et al. 1995; Normann et al. 2000). The AP-induced fluorescence change was recorded at an excitation wavelength of 380 nm. The isosbestic fluorescence was measured immediately before and after each sweep, using the Ca²⁺-insensitive excitation wavelength of 356 nm. The ratio of the background-corrected fluorescence signals R = F₃₅₆/F₃₈₀ was calculated, and converted into the Ca²⁺ concentration using the equation (Grynkiewicz et al. 1985):

(1)

with K_eff=K_d (R_max/R_min), where K_d is the dissociation constant, R_min the ratio in Ca²⁺-free solution and R_max the ratio when the Ca²⁺ indicator is completely saturated with Ca²⁺. These values were determined directly in BCs with internal solutions containing either 10 mm EGTA (Ca²⁺ free), 30 mm CaCl₂ (maximal Ca²⁺) or a mixture of 7.06 mm CaEGTA and 2.94 mm EGTA (Ca²⁺ calibration kit, Invitrogen), resulting in a free Ca²⁺ concentration of 400 nm. Using these solutions, the values for fura-2 were R_min= 0.72 ± 0.01 (n = 11), R_max= 4.83 ± 0.08 (n = 6), and R₄₀₀= 1.41 ± 0.03 (n = 9) resulting in a K_d of 297 nm. The corresponding values for fura-FF were R_min= 0.60 ± 0.01 (n = 16), R_max= 4.30 ± 0.06 (n = 7), and R₄₀₀= 0.65 ± 0.01 (n = 8), corresponding to a K_d of 4.18 μm.

‘Single compartment’ model of dendritic Ca²⁺ buffering

To analyse the dendritic Ca²⁺ buffering properties in BCs, a ‘single compartment’ approach was used, assuming that reactions between Ca²⁺ and buffers are instantaneous and buffers are non-saturable (Neher & Augustine, 1992; Helmchen et al. 1996, 1997; Neher, 1998). The fraction of Ca²⁺ which binds to endogenous Ca²⁺ buffers (S) during the Ca²⁺ influx evoked by a short AP can be quantified by the endogenous Ca²⁺-binding ratio, which is defined as

(2)

where ΔSCa represents the increase in buffer-bound Ca²⁺ and ΔCa²⁺ the increase in the free Ca²⁺ concentration (Neher & Augustine, 1992). Similarly the Ca²⁺-binding ratio of the exogenous buffer fura-2 (B) can be expressed as κ_B=Δ[BCa]/Δ[Ca²⁺]. Assuming that the intracellular Ca²⁺ concentration within a dendritic compartment, corresponding to a recorded ROI, is homogenously elevated during an AP from a resting level [Ca²⁺]₁ to a peak level [Ca²⁺]₂, the exogenous binding ratio can be calculated according to the law of mass action as

(3)

where B_t and K_d represent the total concentration and the Ca²⁺ dissociation constant of fura-2, respectively (Neher & Augustine, 1992). If we assume that a total amount of calcium Ca²⁺_t enters a dendritic compartment with volume V and instantaneously binds to the different buffers, it will increase the free Ca²⁺ concentration (Δ[Ca²⁺]_i), the Ca²⁺-bound fraction of fura-2 (Δ[BCa]), and the Ca²⁺-bound fraction of the endogenous Ca²⁺ buffers (Δ[SCa]) according to the relationship

(4)

Using the definition of the Ca²⁺ binding ratios, eqn (4) can be rewritten as

(5)

where Δ[Ca²⁺]_t= Ca²⁺_t/V. With A⁻¹= 1/Δ[Ca]_i, eqn (5) can be rearranged as

(6)

Thus, A⁻¹ plotted against κ_B should follow a straight line, which intercepts the horizontal axis at −(1 +κ_S). Using this relationship, it is therefore possible to estimate the endogenous Ca²⁺-binding ratio κ_S by measuring the amplitude of the Ca²⁺ transients with different concentrations of fura-2 (leading to different values for κ_B according to eqn (3)). Furthermore, the amplitude of Ca²⁺ transients in the absence of fura-2 can be obtained by extrapolation to κ_B= 0. Although the described approach is strictly valid only for rapidly binding buffers, the additional presence of a slow buffer will primarily interfere with the decay time course, but not with the peak amplitude. Therefore, we determined the endogenous binding ratio using peak amplitudes rather than decay time constants (Lee et al. 2000b).

The amplitude of the Ca²⁺ transient in the absence of exogenous buffers was also approximated by measurement of Ca²⁺ transients with 100 μm of the low-affinity Ca²⁺ indicator fura-FF. For [Ca²⁺] << K_d, the exogenous Ca²⁺ binding ratio can be estimated as κ_B=[fura-FF]/K_d= 100/4.18 = 24, an order of magnitude smaller than the endogenous binding ratio κ_S. Finally, the lumped Ca²⁺ extrusion rate (γ) comprising both Ca²⁺ extrusion across the plasma membrane and uptake into organelles was calculated from the decay time constant (τ_w) measured with fura-FF as

(7)

the factor (1 +κ_B+κ_S) arises because for constant extrusion rate, the decay time constant scales linearly with the amount of buffer-bound Ca²⁺ (Helmchen & Tank, 2005).

Post hoc visualization of morphology and immunocytochemistry

For morphological identification of BCs, neurons were filled with biocytin. After ∼20–30 min recording, slices were fixed overnight with 4% paraformaldehyde in phosphate-buffered solution (PBS; 0.1 m, pH 7.3). Following wash with PBS, slices were incubated with FITC-conjugated avidin-D (Vector Laboratories, Burlingame, CA, USA) in PBS and 0.3% triton X-100 overnight at 4°C. After wash, slices were embedded in Prolong Gold Antifade (Invitrogen). Labelled neurons were examined either by epifluorescence or with a confocal laser-scanning microscope (LSM 510, Zeiss). Only cells with an axonal arborization confined to the granule cell layer (> 90%) were included in this study.

Additionally, a subset of BCs was examined for the expression of the Ca²⁺-binding protein parvalbumin. Slices were incubated with 10% goat serum for 1 h and subsequently with a primary monoclonal antibody against PV (mouse, Swant, Bellinzona, Switzerland, 1 : 10000) in PBS containing 5% goat serum and 0.3% triton X-100 for 20–24 h at 22°C. The secondary antibody (goat anti-mouse, Alexa 568, 1 : 500, Invitrogen) was applied together with FITC-conjugated avidin-D in PBS and 0.3% triton X-100 at 4°C overnight. From a sample of 60 BCs examined by immunochemistry, 27 were immunopositive for parvalbumin, consistent with partial preservation of parvalbumin in the whole-cell recorded neurons.

Data analysis and statistics

Ca²⁺ transients were analysed with procedures running under Igor Pro. The peak amplitude of the AP-induced Ca²⁺ transient was measured as the difference between baseline and the absolute maximum during the trace; the maximum typically occurred shortly after the last AP in the train stimulation. The decay time course of the AP-induced Ca²⁺ transients were fitted with either a single exponential or the sum of two exponentials y(t) =A₁ exp(−t/τ₁) +A₂ exp(−t/τ₂), and the amplitude-weighted time constant was calculated as τ_w= (A₁τ₁+A₂τ₂)/(A₁+A₂). The A⁻¹versusκ_B relationship was analysed by unweighted linear regression according to eqn (6). Traces of Ca²⁺ transients in the figures represent averages of 5 to 10 consecutive sweeps, unless specified differently. Values indicate mean ±s.e.m. Error bars in figures also represent s.e.m. Statistical significance was tested by a non-parametric Mann–Whitney or Kruskal–Wallis test at the significance level (P) indicated, using Graphpad Prism 3.0 (Graphpad Inc., San Diego, CA, USA). Confidence intervals of estimates of κ_S from population data were obtained by bootstrap procedures implemented in Mathematica 4.1 (Wolfram Research, Champaign, IL, USA; see Efron & Tibshirani, 1998). 1000 artificial data sets were generated from the means and SEMs of the original data set using normally distributed random numbers, and analysed as the original.

Results

Ca²⁺ signalling in apical dendrites of BCs

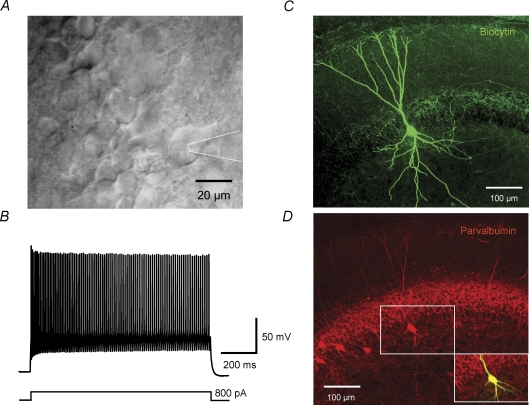
To analyse the endogenous Ca²⁺ buffering in BCs, we combined whole-cell patch-clamp recordings with ratiometric Ca²⁺ imaging in proximal apical dendrites. BCs were rigorously identified on the basis of their appearance in the IR-DIC image (Fig. 1A), the fast-spiking action potential (AP) phenotype (Fig. 1B), and the location of the axonal arborization, which was visualized by biocytin labelling in all recorded cells (Fig. 1C). Furthermore, the expression of the Ca²⁺-binding protein parvalbumin was examined in a subset of recorded neurons (Fig. 1D). Only neurons that generated > 50 APs per second during sustained current injection and showed an axon with > 90% of collaterals in the granule cell layer were used for subsequent analysis.

Figure 1. Identification of parvalbumin-expressing, fast-spiking basket cells in the dentate gyrus.

A, infrared differential interference contrast videomicroscopy image of a BC near the border between granule cell layer and hilus. Dotted lines indicate recording pipette. B, fast-spiking AP phenotype of the same BC recorded in the current-clamp configuration during a 800 pA, 1 s current pulse. The mean action potential frequency in this cell was 94 Hz. C, confocal stack projection of a BC filled with biocytin and stained with FITC-conjugated avidin. The axon is mainly located in the granule cell layer. D, immunohistochemistry of the same BC with an antibody against parvalbumin. Inset: overlay of biocytin signal and parvalbumin immunoreactivity, showing that the recorded cell is parvalbumin positive.

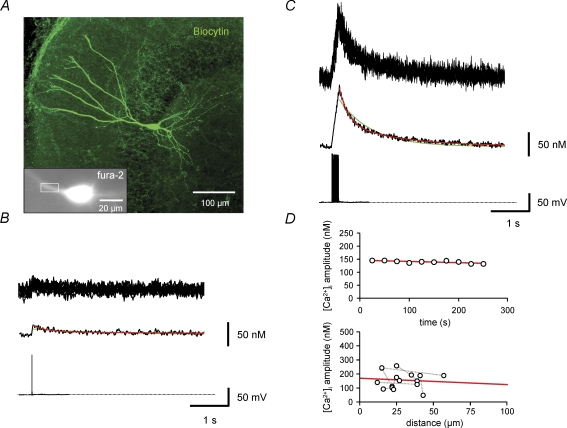
To characterize Ca²⁺ signalling in BCs, we first recorded Ca²⁺ transients in the proximal apical dendrites of BCs with the high-affinity indicator dye fura-2 (Fig. 2A). With 100 μm fura-2, the resting Ca²⁺ concentration was 71 ± 7 nm (n = 41). Single APs evoked Ca²⁺ transients with a peak amplitude of 22 ± 1 nm (n = 30; Fig. 2B). In contrast, 50 or 100 Hz trains of 10 APs evoked Ca²⁺ transients with larger peak amplitude of 208 ± 19 nm under identical conditions (Fig. 2C). We then fitted the decay time course of Ca²⁺ transients with mono- and biexponential functions (Collin et al. 2005). A biexponential fit was preferred if both fast and slow components had amplitude contributions of > 10%. Using this criterion, Ca²⁺ transients were considered biexponential in 25 of 30 BCs for single APs and 22 of 22 BCs for 10 APs. On average, the fast time constant (τ₁) was 300 ± 33 ms (49% amplitude contribution) and the slow time constant (τ₂) was 1926 ± 155 ms for single APs, resulting in an amplitude-weighted decay time constant (τ_w) of 980 ± 69 ms. For a train of 10 APs, the corresponding values were τ₁= 395 ± 32 ms (62% amplitude contribution), τ₂= 1915 ± 144 ms and τ_w= 991 ± 96 ms. The peak amplitude of the Ca²⁺ transients in the proximal apical dendrite was constant over time (Fig. 2D, upper panel) and was not significantly dependent on the distance in the range of ∼10–60 μm from the soma (P > 0.5; Fig. 2D, lower panel), indicating stationarity and spatial homogeneity.

Figure 2. Ca²⁺ transients in proximal apical dendrites of BCs evoked by single spikes and trains of APs.

A, fluorescence image of a BC filled with 100 μm fura-2 (excitation wavelength 380 nm), shown together with an overview of the morphology of the same cell filled with biocytin and stained with FITC-conjugated avidin (large image). Rectangle indicates the region of interest used for imaging of Ca²⁺ transients. B and C, Ca²⁺ transients in the proximal apical dendrite evoked by single APs (B) or trains of 10 APs at 50 Hz (C). Upper traces, single consecutive sweeps; middle traces, average of 10 sweeps; lower traces, corresponding APs evoked by brief current pulses. Green curves represent monoexponential fits, red curves biexponential fits to the decay phase of the Ca²⁺ transients. Data in A–C were obtained from the same BC. D, plot of peak amplitude of Ca²⁺ transient against recording time in the same cell shown in A–C (upper graph) and against distance (measured from the border of the soma to the centre of the region of interest) in a subset of BCs in which measurements were made at multiple distances. Data from the same cell are connected by gray dotted lines. Continuous red lines represent the results of linear regression.

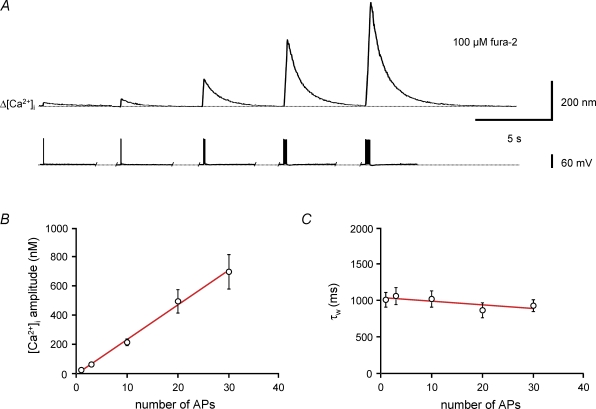
To examine whether Ca²⁺ transients evoked by single APs summated linearly, we compared peak amplitude and kinetics of Ca²⁺ transients evoked by bursts of different numbers of stimuli (Fig. 3). As the number of APs was increased from 1 to 30, the amplitude of the Ca²⁺ transients became markedly larger (Fig. 3A and B). Quantitative analysis revealed that the amplitude of the Ca²⁺ transient was proportional to the number of spikes (Fig. 3B). In contrast, the amplitude-weighted average decay time constants τ_w of the Ca²⁺ transients were not significantly dependent on the number of spikes (P > 0.1; Fig. 3C). In conclusion, the amplitude of the Ca²⁺ transients evoked by a burst of APs was proportional to the number of APs, whereas the decay of the Ca²⁺ transients was independent of AP number. These results were consistent with linear Ca²⁺ signalling in the proximal dendrites of BCs.

Figure 3. Linear summation of Ca²⁺ transients evoked by different numbers of action potentials.

A, Ca²⁺ transients in the apical dendrite of a BC filled with 100 μm fura-2 evoked by a single AP or 100 Hz bursts of 3, 10, 20 and 30 APs. Upper traces, averages of 20 sweeps; lower traces, corresponding APs and trains of APs evoked by brief current pulses. B, plot of peak amplitude of Ca²⁺ transients against the number of APs. Continuous curve represents the results of linear regression, yielding a steepness of 24 nm AP⁻¹. C, plot of amplitude-weighted decay time constant (τ_w) of the Ca²⁺ transients against the number of APs. Note that τ_w is almost independent of the number of spikes. Continuous curve represents the results of linear regression, yielding a steepness of −5 ms AP⁻¹. Data from 18 BCs loaded with 100 μm fura-2.

Endogenous Ca²⁺-binding ratio under steady-state conditions and during indicator loading

To quantify the endogenous buffer capacity of BCs, we took advantage of the competition between endogenous buffers and exogenous Ca²⁺ indicators. BCs were loaded with either 50, 100 or 200 μm fura-2, and Ca²⁺ transients evoked by a burst of five APs were measured under steady-state conditions 10–20 min after the whole-cell recording configuration was obtained (Fig. 4). Ca²⁺ transients recorded with different concentrations of fura-2 showed significantly different peak amplitudes and time courses (Fig. 4A). The peak amplitudes were 125 ± 13 nm, 83 ± 8 nm and 66 ± 7 nm with 50, 100 and 200 μm fura-2, respectively (P < 0.01; Fig. 4B, upper panel). Likewise, the corresponding amplitude-weighted average decay time constants τ_w were 833 ± 81 ms, 1291 ± 119 ms and 2171 ± 166 ms (P < 0.001; Fig. 4B, lower panel). Both the reduction in peak amplitude and the prolongation of the decay time course with increasing concentration of fura-2 indicate competition of the Ca²⁺ indicator dye with endogenous buffers.

Figure 4. Estimation of endogenous Ca²⁺-binding ratio by population analysis under steady-state conditions.

A, Ca²⁺ transients evoked by 100 Hz bursts of 5 APs. Three different BCs were loaded with fura-2, with dye concentrations indicated on the left. Each Ca²⁺ transient trace is an average of 20 single sweeps. The lower trace represents the corresponding AP train. Red curves represent biexponential fits to the decay phase of the Ca²⁺ transients. Note that peak amplitude of the Ca²⁺ transients decreases, whereas the decay time constant increases with increasing concentration of fura-2, indicating competition between fura-2 and endogenous Ca²⁺ buffers. B, summary bar graphs showing the peak amplitude (upper graph) and amplitude-weighted decay time constant (τ_w, lower graph) of Ca²⁺ transients evoked by 100 Hz bursts of 5 APs at different concentrations of fura-2. Bars represent mean ±s.e.m.; circles represent data from individual BCs. C, plot of the inverse of the peak amplitude of Ca²⁺ transients against the exogenous Ca²⁺-binding ratio, i.e. the Ca²⁺-binding ratio of fura-2 (κ_B). κ_B was calculated from the fura-2 concentration according to eqn (3). Gray circles, data from 66 individual BCs; black circles, plot of mean values for 50, 100 and 200 μm fura-2. Continuous line represents the results of unweighted linear regression to the mean data. The endogenous Ca²⁺-binding ratio (κ_S), estimated from the intercept of the fitted line with the horizontal axis, was 214. D, estimation of confidence intervals for κ_S. 1000 bootstrap replications of the original mean data were generated and corresponding κ_S values were determined by linear regression (see Methods). The histogram shows the distribution of estimated κ_S values. The 15.9–84.1% confidence interval was [138, 355]. Measurements were taken > 10 min after the whole-cell configuration was established.

To determine the endogenous Ca²⁺-binding ratio (Neher & Augustine, 1992), we plotted the inverse of the peak amplitude of the Ca²⁺ transients against the exogenous Ca²⁺-binding ratio (κ_B), which was calculated from the fura-2 concentration according to eqn (3). In the framework of a single-compartment model, the relation between A⁻¹ and κ_B is expected to fall on a straight line (eqn (6)). Therefore, data points from a population of 66 recorded BCs were fitted by linear regression and the endogenous Ca²⁺-binding ratio κ_S was obtained from the intercept of the fitted line with the horizontal axis. Analysis of mean values for the three fura-2 concentrations gave a κ_S value of 214. Because of the cell–cell variability of the data (Fig. 4C), the statistical reliability of the estimate of κ_S was addressed using a bootstrap method. This analysis revealed that the 15.9–84.1% confidence interval (corresponding to the standard deviation of a normally distributed variable) was [138, 355] (Fig. 4D). These values are markedly larger than the Ca²⁺-binding ratios in the apical dendrites of cortical pyramidal cells determined with the same methods (64–90; Helmchen et al. 1996).

As Ca²⁺ transients were measured under steady-state conditions 10–20 min after the whole-cell configuration had been obtained, mobile buffers are expected to be largely washed out by cell dialysis (Schmidt et al. 2003). Thus, the Ca²⁺-binding ratio obtained under these conditions would be primarily determined by fixed buffers. To quantify the Ca²⁺-binding ratio under conditions in which mobile buffers are better preserved, we performed Ca²⁺ indicator loading experiments (Fig. 5). Ca²⁺ transients were measured in the apical dendrites of BCs at different times after obtaining the whole-cell configuration with 200 μm fura-2 in the pipette solution. Ca²⁺ transients early in the loading procedure showed a large amplitude and a fast decay (Fig. 5A, upper trace). In contrast, Ca²⁺ transients recorded at later times showed a reduced amplitude and a prolonged decay (Fig. 5A, lower traces), again indicating competition between fura-2 and endogenous buffers.

For quantitative analysis, we determined the fura-2 concentration corresponding to different time points, assuming that the dye concentration in the proximal apical dendrite under steady-state conditions reached the concentration in the pipette (200 μm; Fig. 5B, upper graph). Next, we calculated the corresponding exogenous Ca²⁺-binding ratio (κ_B) from the fura-2 concentration. Finally, we plotted the inverse of the peak amplitude of the Ca²⁺ transient (Fig. 5B, lower graph) against κ_B. In the A⁻¹versusκ_B plot (Fig. 5C), data points on the left corresponded to early measurements, whereas data points on the right corresponded to late measurements in the loading experiment. Analysing the data by linear regression according to a single-compartment model revealed a mean endogenous Ca²⁺-binding ratio κ_S of 202 ± 26 (n = 7; Fig. 5D; Table 1), very similar to that obtained from the mean population data under steady-state conditions (Fig. 4). The similarity of the values of κ_S obtained from the two data sets suggests that the endogenous Ca²⁺-binding ratio in proximal apical dendrites of BCs is primarily determined by fixed buffers, whereas the contribution of mobile buffers is small. The value of κ_S in BCs obtained from loading experiments was larger than the values of κ_S estimated in cortical pyramidal cells with the same methods (126–168; Helmchen et al. 1996). In conclusion, analysis of population data under steady-state conditions and loading data under dynamic conditions indicate that the proximal apical dendrites of BCs show a large endogenous Ca²⁺-binding ratio mainly determined by fixed buffers.

Table 1.

Summary of Ca²⁺ signalling properties of BCs determined with high- and low-affinity Ca²⁺ indicators

Parameter	Fura-2 (22–24°C)	Fura-FF (22–24°C)	Fura-FF (34°C)
Resting [Ca2+]i	71 ± 7 nm (n = 41)	—	—
κS (population analysis, steady state)	214 [138, 355] (n = 66)1	—	—
κS (loading experiments)	202 ± 26 (n = 7)2	—	—
[Ca2+]i amplitude	43 ± 5 nm AP−1 (n = 7)3	39 nm AP−1 (n = 7)	22 nm AP−1 (n = 12)
Decay time constant τw	359 ± 38 ms (n = 7)4	390 ± 154 ms (n = 7)	203 ± 24 ms (n = 12)
[Ca2+]i amplitude during theta–gamma burst stimulation	—	50 nm AP−1 (n = 8)5	37 nm AP−1 (n = 7)5

¹Confidence interval was obtained by bootstrap analysis (Methods).

²Standard error of the mean was calculated from all κ_S values obtained by separate analysis of each cell.

³Value was obtained by extrapolation to κ_B= 0.

⁴Value was obtained from early time points in the loading experiments ([fura-2] < 50 μm).

⁵Values relate to the number of APs per burst.

Amplitude of the Ca²⁺ transient and Ca²⁺ extrusion rate with minimal exogenous buffering

We next attempted to measure the amplitude of the minimally perturbed Ca²⁺ transient and the Ca²⁺ extrusion rate in the proximal apical dendrites of BCs. To minimize the interference of exogenous Ca²⁺ indicators with the Ca²⁺ transients, experiments were performed using the low-affinity indicator dye fura-FF (Fig. 6). Ca²⁺ transients were evoked by bursts of 1–30 APs (Fig. 6A and B). As found for fura-2, the amplitude of the Ca²⁺ transients increased proportionally to the number of APs in the burst (Fig. 6C). The slope of the relation between the peak amplitude of the Ca²⁺ transients and the number of APs was A = 39 nm AP⁻¹. With an exogenous Ca²⁺ binding ratio κ_B of 24 (for 100 μm fura-FF) and an endogenous Ca²⁺-binding ratio κ_S of 202, this corresponds to a total Ca²⁺ load of A* (1 +κ_B+κ_S) = 8.9 μm AP⁻¹. These values directly measured with the low-affinity dye fura-FF were in close agreement with the estimates obtained by extrapolation towards an exogenous Ca²⁺-binding ratio of κ_B= 0 from the data measured with the high-affinity indicator fura-2 (43 ± 5 nm AP⁻¹; Fig. 5D; Table 1).

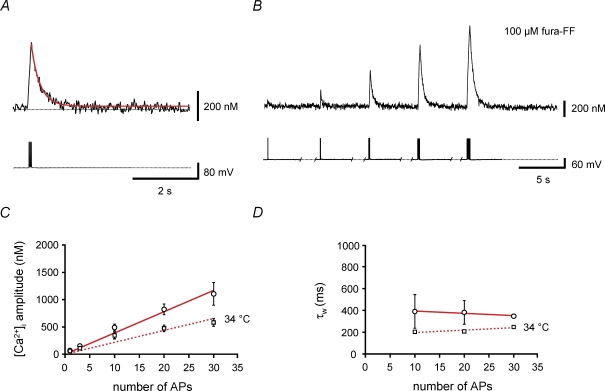
Figure 6. Direct measurement of the amplitude of Ca²⁺ transients and the Ca²⁺ extrusion rate with the low-affinity indicator fura-FF.

A and B, Ca²⁺ transients recorded in the proximal apical dendrite of a BC filled with 100 μm fura-FF. Upper traces, average Ca²⁺ transients (mean of 10 sweeps); lower traces, corresponding APs evoked by brief current pulses. A, Ca²⁺ transients evoked by a 100 Hz train of 10 APs; B, Ca²⁺ transients evoked by a single AP or 100 Hz trains of 3, 10, 20 and 30 APs. C, plot of peak amplitude of Ca²⁺ transients against the number of APs. ○, data obtained at 22–24°C; □, measurements taken at 34°C. Continuous and dashed lines represent the results of linear regression analysis of the two data sets, yielding steepness values of 39 nm AP⁻¹ and 22 nm AP⁻¹, respectively. D, plot of amplitude-weighted decay time constant (τ_w) of the Ca²⁺ transients against the number of APs. Data for 1 and 3 APs were omitted, because decay time constants could not be measured reliably. Note that τ_w is almost independent of the number of APs used as stimulus. ○, data obtained at 22–24°C; □, measurements taken at 34°C. Continuous and dashed lines represent the results of linear regression, yielding steepness values of −2.2 ms AP⁻¹ and 2.2 ms AP⁻¹, respectively. Data from 7 BCs (22–24°C) and 12 BCs (34°C) filled with 100 μm fura-FF.

To determine the Ca²⁺ extrusion rate, we plotted the amplitude-weighted average decay time constant τ_w against the number of APs (Fig. 6D). τ_w was not significantly dependent on AP number, with a mean value of 390 ± 154 ms (n = 7; P > 0.2). These decay time constant values directly measured with the low-affinity indicator dye fura-FF were in close agreement with those obtained with the high-affinity indicator fura-2 at early time points in the loading experiment (Fig. 5A; Table 1). From the value of the decay time constant of the Ca²⁺ transients, the exogenous Ca²⁺-binding ratio κ_B of 24 (for 100 μm fura-FF), and the endogenous Ca²⁺-binding ratio κ_S of 202, the lumped Ca²⁺ extrusion rate comprising Ca²⁺ extrusion across the plasma membrane and uptake into organelles can be calculated from eqn (7) as γ= 582 s⁻¹. Additional experiments at near-physiological temperature (34°C) gave a smaller amplitude, presumably caused by shortening of the action potential, and a faster decay of Ca²⁺ transients, probably caused by temperature dependence of extrusion (Fig. 6C and D). For 34°C, A = 22 nm AP⁻¹ and τ_w= 203 ± 24 ms were obtained (n = 12; Table 1). Assuming that both exogenous and endogenous Ca²⁺-binding ratio are independent of temperature, γ at 34°C can be calculated as 1118 s⁻¹. Thus, the extrusion rate in the proximal apical dendrites of BCs is slower than that in pyramidal cell dendrites (1500–2000 s⁻¹; Helmchen et al. 1996; their Table 1).

Ca²⁺ signalling in proximal apical dendrites of BCs with physiological activity patterns

When a rat explores the environment, BCs in vivo generate APs in a theta–gamma-modulated manner, with two to five APs per theta cycle (Bragin et al. 1995; Penttonen et al. 1998; Csicsvari et al. 2003). To examine Ca²⁺ signalling during such behaviourally relevant protocols, we applied repetitive theta–gamma-burst stimulation and measured the resulting Ca²⁺ transients (Fig. 7). To minimize interference with exogenous Ca²⁺ indicators, these experiments were performed with the low-affinity indicator dye fura-FF.

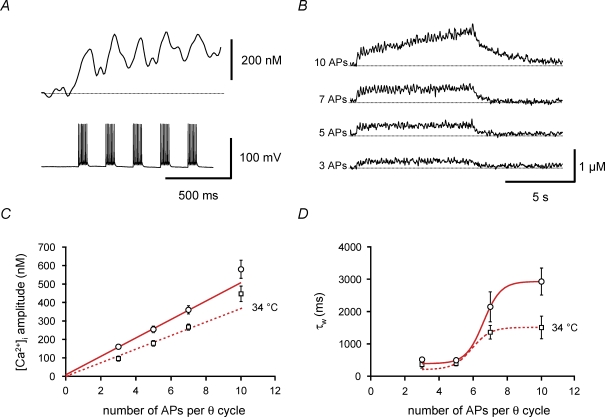
Figure 7. Switch from linear to supralinear Ca²⁺ signalling during repetitive theta-burst stimulation.

A and B, Ca²⁺ transients recorded in the proximal apical dendrite of a BC filled with 100 μm fura-FF. A, expanded view of Ca²⁺ transients evoked at the onset of repetitive 100 Hz burst stimulation. The number of APs per burst was 7, and the burst repetition frequency was 5 Hz. Upper trace, average Ca²⁺ transient; lower trace, corresponding APs evoked by brief current pulses. B, Ca²⁺ transients evoked by repetitive 100 Hz burst stimulation for 8 s with 3, 5, 7 or 10 APs per burst (as indicated on the left of each trace). The burst repetition frequency was 5 Hz. Traces of Ca²⁺ transients in A and B are averages of 5 individual sweeps. C, plot of mean amplitude of Ca²⁺ transients against the number of APs. Amplitudes were measured 2–5 s after stimulation onset. ○, data obtained at 22–24°C; □, measurements taken at 34°C. Continuous and dashed lines represent the results of linear regression of the data points for 3, 5 and 7 APs, yielding steepness values of 50 nm AP⁻¹ and 37 nm AP⁻¹, respectively. D, plot of amplitude-weighted average decay time constant (τ_w) of the Ca²⁺ transients after the end of stimulation against the number of APs per burst. Note that τ_w is similar for 3 and 5 APs, but increases markedly for a larger number of APs. ○, data obtained at 22–24°C; □, measurements taken at 34°C. Continuous and dashed curves represent non-linear fits with a Boltzmann function with a constant offset constrained to the mean τ_w for a single burst of 10 APs. Data from 8 BCs (22–24°C) and 7 BCs (34°C) filled with 100 μm fura-FF.

Sustained theta-burst stimulation resulted in a long-lasting elevation in intracellular Ca²⁺ concentration in proximal apical dendrites of BCs due to temporal summation of Ca²⁺ transients generated by individual bursts (Fig. 7A and B). For repetitive theta–gamma stimulation with three to five APs per theta cycle, the rise in steady-state Ca²⁺ concentration measured 2–5 s after stimulation onset was moderate, with a mean concentration that was linearly dependent on the number of APs per gamma cycle (slope 50 ± 2 nm AP⁻¹; Fig. 7C). Furthermore, the amplitude-weighted average decay time constant τ_w after termination of repetitive-burst stimulation was very similar to that of the Ca²⁺ transient evoked by a single burst (515 ± 58 ms and 493 ± 58 ms for 3 and 5 APs, respectively; Fig. 7D). In contrast, for repetitive theta–gamma stimulation with 7 or 10 APs per theta cycle, the rise in steady-state Ca²⁺ concentration was markedly higher, being supralinearly dependent on the number of APs. Likewise, τ_w after termination of repetitive burst stimulation was significantly prolonged (τ_w= 2928 ± 419 ms for 10 APs; n = 8; P < 0.01; Fig. 7D). This may indicate non-linearity of Ca²⁺ signalling, e.g. caused by saturation of Ca²⁺ uptake into intracellular stores during repetitive activity. Qualitatively similar results were obtained at near-physiological temperature (Fig. 7C and D). Thus, physiological theta-burst stimulation with three to five APs per theta cycle leads to a moderate rise in the global Ca²⁺ concentration in BC dendrites that is linearly dependent on AP number, whereas more intense stimulation is required to reach micromolar Ca²⁺ concentrations and to shift Ca²⁺ signalling into a non-linear regime.

Discussion

The main findings of the present paper are that the proximal apical dendrites of BCs show high endogenous buffer capacity, small AP-induced Ca²⁺ transients, and relatively slow Ca²⁺ extrusion. A large proportion of the endogenous buffers appears to be fixed, whereas the contribution of mobile buffers is minimal. Owing to the high Ca²⁺ buffer capacitance and the relatively slow extrusion, Ca²⁺ transients decay slowly and summate efficiently. Thus, although BCs are coincidence detectors at the level of synaptic currents and potentials (Geiger et al. 1997; Galarreta & Hestrin, 2001), they are integrators at the level of global Ca²⁺ signals.

Comparison of Ca²⁺ buffering in BCs with that in other cell types

In comparison to other cell types, BCs show a high endogenous Ca²⁺-binding ratio and a small amplitude of dendritic Ca²⁺ transients. Loading experiments reveal that the endogenous Ca²⁺-binding ratio in the proximal apical dendrites of BCs is ∼200, and measurements with fura-FF indicate that the amplitude of the unperturbed Ca²⁺ transients is ∼40 nm. In contrast, in the dendrites of principal cells the Ca²⁺-binding ratio is lower and the amplitude of the Ca²⁺ transients is higher, in both the neocortex (κ_S= 120 and A = 260 nm in layer 5 neocortical pyramidal neurons, Helmchen et al. 1996; κ_S= 110 and A = 190–240 nm in layer 2/3 pyramidal neurons; Koester & Sakmann, 2000) and the hippocampus (κ_S= 60–180 and A = 150–240 nm in hippocampal CA1 pyramidal neuron dendrites, Helmchen et al. 1996; κ_S= 27 in CA1 pyramidal neuron dendrites, Rozsa et al. 2004; κ_S= 20 and A = 1500–1700 nm in CA1 pyramidal neuron spines, Sabatini et al. 2002).

Ca²⁺ signalling in BCs also appears to be distinct from that of other interneuron subtypes examined previously. In hippocampal GABAergic interneurons in culture, the endogenous Ca²⁺-binding ratio (∼150) is similar to that in BCs, but the amplitude of the Ca²⁺ transients evoked by 3 ms pulses (presumably evoking a single action potential) is larger (> 100 nm; Lee et al. 2000a). Likewise, in bitufted interneurons in the neocortex, which presumably express the peptide somatostatin, the endogenous Ca²⁺-binding ratio is comparable (∼300) to that in BCs, but the amplitude of the Ca²⁺ transients is markedly larger (140 nm; Kaiser et al. 2001). Finally, in CA1 stratum radiatum interneurons a lower Ca²⁺-binding ratio of 71 was estimated (Rozsa et al. 2004). Thus, our results and the previous data support the view that interneurons show a higher Ca²⁺ buffer capacity than principal neurons, but also suggest differences between interneuron subtypes.

Shaping of local and global Ca²⁺ signalling by endogenous buffering properties

How does efficient Ca²⁺ buffering in BCs affect the local Ca²⁺ signals near transiently activated Ca²⁺-permeable AMPARs (Koh et al. 1995) or voltage-gated Ca²⁺ channels (Bucurenciu et al. 2008) and the global Ca²⁺ signals in dendrites or presynaptic terminals? For local Ca²⁺ transients examined near the source on the time scale of milliseconds, the early peak phase of the transient is expected to be only minimally affected by endogenous buffers, whereas the later sustained phase will be strongly attenuated according to the high Ca²⁺-binding ratio. Fixed buffers will have an even smaller effect on the peak amplitude than mobile buffers, because fixed buffers will be saturated near the source, whereas mobile buffers are rapidly replenished (Neher, 1998; Meinrenken et al. 2002, 2003). In contrast, for global Ca²⁺ transients examined further away from the source and at a slower time scale, Ca²⁺ buffers will reduce the amplitude and prolong the decay phase of the Ca²⁺ transient, because the buffers will slowly release previously bound Ca²⁺. Thus, the abundance of immobile buffers in BCs will sharpen the time course of local Ca²⁺ signals and at the same time prolong the decay of global Ca²⁺ signals. Concomitantly, the buffering properties will reduce the spatial extent of nanodomains around the Ca²⁺ source (Goldberg et al. 2003a). Thus, the abundance of fixed buffers will confer unique spatiotemporal properties on Ca²⁺ signalling in BC dendrites and presynaptic terminals.

Possible implications for synaptic transmission and plasticity

Shaping of Ca²⁺ signals in BCs by endogenous buffers may be important for the function of both input and output synapses of BCs. Accumulating evidence suggests that glutamatergic input synapses of BCs exhibit long-term potentiation (LTP; Alle et al. 2001; Perez et al. 2001; Kullmann & Lamsa, 2007). However, it is controversial which associative protocols are most efficient for LTP induction (Alle et al. 2001; Perez et al. 2001; Kullmann & Lamsa, 2007). Our results imply that the induction rules of synaptic plasticity at glutamatergic principal neuron–interneuron synapses may be complex. The associative nature and the Ca²⁺ dependence of LTP may suggest that both a local Ca²⁺ increase through Ca²⁺-permeable AMPARs and a global Ca²⁺ increase triggered by APs may be necessary for LTP induction. If pre- and postsynaptic activity were precisely coincident, synaptic efficacy may be unchanged, because Ca²⁺-permeable AMPARs are rapidly blocked by intracellular polyamines (Kullmann & Lamsa, 2007). In contrast, if the coincidence of pre- and postsynaptic activity is looser (Alle et al. 2001; Perez et al. 2001), AMPAR-mediated and AP-induced Ca²⁺ transients will summate efficiently (see Rozsa et al. 2004). Similarly, a prolonged train of large but subthreshold EPSPs may generate large intracellular Ca²⁺ signals. In both scenarios, the abundance of immobile buffers in BCs will prolong the decay of Ca²⁺ transients, widening the temporal window of LTP induction.

If the properties of Ca²⁺ buffering in BC terminals are the same as those in the apical dendrites, the high endogenous binding ratio will have implications for the efficiency and temporal precision of transmitter release at GABAergic BC output synapses (Bartos et al. 2007). In BC synaptic terminals, immobile buffers will have little effect on local Ca²⁺ transients at the peak, but reduce the Ca²⁺ concentration at later times. Thus, the buffering properties of BCs appear to be optimal to maximize the ratio of synchronous over asynchronous release. Together with the tight coupling of presynaptic Ca²⁺ channels and the Ca²⁺ sensors of exocytosis at this synapse (Bucurenciu et al. 2008), this would explain why fast-spiking, parvalbumin-expressing BCs release transmitter efficiently and with high temporal precision (Kraushaar & Jonas, 2000; Hefft & Jonas, 2005; Bucurenciu et al. 2007). Thus, Ca²⁺ buffering properties may contribute to the efficiency and temporal precision of BC-mediated inhibition in hippocampal microcircuits (Pouille & Scanziani, 2004).