Entropy-Driven Folding of an RNA Helical Junction: An Isothermal Titration Calorimetric Analysis of the Hammerhead Ribozyme

Abstract

Helical junctions are extremely common motifs in naturally occurring RNAs, but little is known about the thermodynamics that drive their folding. Studies of junction folding face several challenges: non-two-state folding behavior, superposition of secondary and tertiary structural energetics, and drastically opposing enthalpic and entropic contributions to folding. Here we describe a thermodynamic dissection of the folding of the hammerhead ribozyme, a three-way RNA helical junction, by using isothermal titration calorimetry of bimolecular RNA constructs. By using this method, we show that tertiary folding of the hammerhead core occurs with a highly unfavorable enthalpy change, and is therefore entropically driven. Furthermore, the enthalpies and heat capacities of core folding are the same whether supported by monovalent or divalent ions. These properties appear to be general to the core sequence of bimolecular hammerhead constructs. We present a model for the ion-induced folding of the hammerhead core that is similar to those advanced for the folding of much larger RNAs, involving ion-induced collapse to a structured, non-native state accompanied by rearrangement of core residues to produce the native fold. In agreement with previous enzymological and structural studies, our thermodynamic data suggest that the hammerhead structure is stabilized in vitro predominantly by diffusely bound ions. Our approach addresses several significant challenges that accompany the study of junction folding, and should prove useful in defining the thermodynamic determinants of stability in these important RNA motifs.

RNA helical junctions, single-stranded loops flanked by multiple double helices, are pervasive in known and predicted RNA structures. Helical junctions appear in a broad range of functional RNAs (1, 2), including small and large ribozymes, mRNA untranslated regions, riboregulatory RNAs, snRNAs, and rRNAs. Alone or in complex with proteins, junctions may serve as the major tertiary structural elements of small RNAs or as critical elements in organizing much larger architectures. Despite their prominence, little is known about the forces that drive the folding of RNA helical junctions. Pairwise coaxial stacking and ion-dependent folding have emerged as common themes in junction architecture, but the exact role of central, looped regions and the energetics of the folding process are still unclear. As a result, there are currently no general principles of helical junction folding dependable enough for use in predicting RNA tertiary structure, much less in predicting the impact of solution conditions or bound ligands on junction stabilities.

Significant challenges accompany the study of junction folding thermodynamics. Whereas RNA folding is quite hierarchical compared to protein folding, dissecting the components of helical junction folding is nevertheless problematic. For example, systematic nearest neighbor studies of bimolecular junction constructs have found that tertiary contacts between junction loop nucleotides and flanking helices confound nearest neighbor approaches to secondary structure prediction (3, 4). Furthermore, thermodynamic data derived from optical melting studies are most properly obtained from systems that undergo two-state folding. Because of largely offsetting contributions of enthalpy and entropy, ΔG values for non-two-state systems may be fairly well predicted by optical melting, but the corresponding ΔH and ΔG terms are less reliable. In a well-designed study mentioned above (3), bimolecular constructs exhibiting non-two-state behavior were analyzed by isothermal titration calorimetry (ITC)¹ to double-check the optical melting results. One strand of a construct was titrated into the other, and the resulting heats of folding were measured directly. Thus, although ITC in these cases was used for accurate measurements on non-two-state systems, the secondary and tertiary components of folding remained superposed.

Resolving the thermodynamics of junction core folding from those of flanking duplexes is desirable, as each component can respond differently to changes in the solution environment, particularly to changes in ionic conditions. The difficulty and importance of the problem is demonstrated by the controversial literature devoted to the role of metal ions in stabilizing RNA tertiary structure (5–13). A general consensus exists that cations are important for screening the Coulombic repulsion associated with close approximation of backbone phosphates in compact, folded structures. Beyond this point, agreement has been elusive. A popular image, reinforced by high-resolution crystallographic data on structured RNAs, is one of divalent cations acting as a sort of ionic “glue”, binding tightly to electronegative foci in folded RNAs (14). Certainly, such site-binding does sometimes occur, but do such favorable Coulombic attractions constitute the thermodynamic driving force for folding?

Nonlinear Poisson–Boltzmann (NLPB) calculations on RNAs of known tertiary structure have offered perhaps the most detailed description so far of the energetic linkage of particular RNA tertiary structures with associated ions (10, 15). In particular, NLPB calculations have brought quantitative insight to the distinct roles of diffusely bound and site-bound ions, and to the competition between monovalent and divalent species. However, NLPB approaches require high-resolution structural data, consider only electrostatic effects, and treat the structure of the RNA as if it were static, as opposed to the dynamic ensemble of conformations that is probably more typical for RNAs in solution. NLPB treatments are therefore most powerful as interpretive aids paired with data from other techniques, as demonstrated in recent studies employing fluorescently labeled helical junctions along with NLPB calculations to investigate junction folding and dynamics (13, 16).

In this study, we use ITC (17) to determine thermodynamic parameters for the folding of the hammerhead ribozyme (18), a three-way RNA helical junction. Recently, Lilley and co-workers reported ITC-measured values for Mg²⁺-binding and coupled folding of the hammerhead ribozyme and two folding mutants (19). The authors of the study titrated a concentrated solution of MgCl₂ into a preannealed, unimolecular hammerhead construct consisting of an RNA junction flanked by DNA helices. Our present work employs a fundamentally different strategy, involving all-RNA, bimolecular constructs of the hammerhead ribozyme that have been previously well-characterized.

We extend the bimolecular construct method of Diamond et al. (3) toward an energetic dissection of the components of junction folding. Our approach draws on previous work by Hertel et al. (20) that deconstructed hammerhead folding into “helix” and “core” components to demonstrate a free energy penalty for hammerhead core folding, ΔG^core = +3.3 kcal mol⁻¹. By using this deconstruction, we have obtained enthalpies and entropies of helix and core folding of the ribozyme. With the resulting dataset, we show that both helix and core folding in this helical junction occur with large-scale enthalpy/entropy compensation: whereas helix formation is enthalpy-driven (as expected), core folding is associated with a substantial, unfavorable enthalpy term and is entropically driven. The data show that this phenomenon is true whether folding is supported by millimolar concentrations of MgCl₂ or by molar concentrations of NaCl. From the temperature dependence of the measured enthalpies, we calculate distinct heat capacity changes for folding of the full ribozyme and for its helix and core components. Finally, we discuss the mechanism of hammerhead ribozyme folding in light of our observations.

MATERIALS AND METHODS

Sample Preparation

The RNAs used in the study were as follows (all are listed 5′ to 3′):

HH16 Long: GCGAUGACCUGAUGAGGCCGAAAG-GCCGAAACGUUCCC; A14G Long: GCGAUGACCUG-AUGAGGCCGAAAGGCCGAGACGUUCCC; HH16 Short (also A14G Short): GGGAACGUdCGUCGUCGC; HH16 StemlLong: GCGAUGAC;HH16Stem1 Short: GUCGUCGC; HH16 Stem 3 Long: CGUUCCC; HH16 Stem 3 Short: GGGAACG; HHαl Long: GGAAUCGAAACGCGAAA-GCGUdCUAGCG; HHαl Short: CGCUACUGAUGAGA-UUC; HHαl Stem 1 Long: UAGCG; HHαl Stem 1 Short: CGCUA; HH8 Long: GGCGACCCUGAUGAGGCCGAAA-GGCCGAAACAUU; HH8 Short: GGAAUGUCGGUCG. The “HH16 Short”, “HHα1 Long”, and “HH8 Short” RNAs each contained the site cleaved in active, all-RNA versions of these ribozymes. Therefore, a deoxy-C was included at the cleavage sites in these strands to prevent scission.

The 38-nucleotide HH16 and HH8 “long strands” and the 38-nucleotide A14G “long strand” were prepared in vitro by T7 transcription off synthetic DNA templates (21). The transcripts were purified by denaturing PAGE, eluted into 0.5 M ammonium acetate, ethanol precipitated, and resuspended in water. All other RNAs were chemically synthesized (Dharmacon, Inc.). Synthesized RNAs were deprotected according to the provided protocol. The 27-nucleotide HHα1 “long strand” was gel purified as described above. All other deprotected RNAs were resuspended in water and used after purity assessment by PAGE. Control ITC experiments showed no significant difference between gel-purified and non-gel-purified 17-nucleotide “short strands”. Concentrations of RNA stock solutions were determined by absorbance at 260 nm. ITC samples were prepared by dilution of concentrated RNA stock solutions into degassed buffer solutions containing all other sample components except MgCl₂. Samples were heat annealed for 2 min at 95 °C and allowed to cool ambiently. MgCl₂ was added when appropriate after cooling. Syringe and cell sample pairs were identical in composition except for the type and concentration of RNA.

Isothermal Titration Calorimetry

ITC was performed on a VP-ITC microcalorimeter (MicroCal, Inc.). Prior to data collection, the syringe and cell of the calorimeter were extensively decontaminated by (i) soaking at 65 °C in a 10% solution of Contrad-70 (Fisher Scientific), followed by flushing with 1 L of sterile ddH₂O, and (ii) soaking overnight in RNase Zap (Ambion), followed by flushing with 1 L of sterile ddH₂O. After decontamination, RNAs left in the syringe and cell for 4 h showed no evidence of degradation beyond that of a negative control, as assayed by denaturing PAGE. Titrations were carried out at 5, 20, and 35 °C (278, 293, and 308 K). All experiments involved bimolecular (two-strand) RNA constructs. All samples contained 50 mM HEPES pH 7.5 and one of the following three ionic conditions: 100 mM NaCl, 100 mM NaCl/10 mM MgCl₂, or 1 M NaCl. Titrations of wild-type and A14G HH16 with MgCl₂ were conducted against a 100 mM NaCl background. Each experiment typically consisted of 40 injections (at 7 μL per injection) of a 75 μM RNA sample (strand 1) into a cell containing 1.4 mL of a 5 μM RNA sample (strand 2). Stirring was performed at 310 rpm, and injection spacings of 2–5 min were used, depending on the construct assayed, the temperature, and the number of injections elapsed. In experiments involving full ribozyme constructs, the shorter strand was in the syringe (at 75 μM) and the longer strand was in the cell (at 5 μM). Control experiments inverting the direction of titration did not produce significantly different results. Additional titrations of the HH8 and HHα1 full constructs were conducted to verify that the ΔGs for ribozyme folding measured by ITC agreed with those previously measured by Hertel et al. (20) using cleavage kinetics. These additional titrations were conducted at 25 °C in the presence of 50 mM HEPES pH 7.5, 100 mM NaCl, and 10 mM MgCl₂.

Analysis of Raw ITC Data

Analysis was performed using ORIGIN software, version 7 (OriginLab Corporation, Northampton, MA). Raw injection data (in μcal/s vs time) were integrated to yield individual injection enthalpies, which were then normalized by the moles of added titrant. Normalized ΔH's were plotted against the molar ratio of titrant sample to cell sample. All experiments were designed to include many injections past saturation of the binding event, resulting in a long upper baseline. These baselines reflected the enthalpic contributions of dilution and mixing as they actually occurred in each experiment. Therefore, lines described by the terminal 10–15 injections of each experiment were extrapolated back to the first injection and subtracted from the full dataset. The resulting plots were directly fit to a one-site binding model to yield the reaction ΔH, K_A, and stoichiometry (n) of binding/folding. For a one-site model, the theoretical n = 1. Across the greater than 60 titrations of this study, n = 1.0 ± 0.1.

Titrations of full ribozyme constructs were fit as described to yield ΔH^full. Titrations of stem fragments were individually fit and then summed with a correction factor, ΔH^fuse, to yield ΔH^helix. As detailed in Results, ΔH^fuse corrects for the fact that ΔH^full incorporates two separate helix initiation events, whereas ΔH^full incorporates only one. ΔH^core was taken as the difference between ΔH^full and ΔH^helix.

Circular Dichroism Spectroscopy

CD spectra were collected on a Jasco J-715 spectropolarimeter. Samples were prepared by dilution of long strand and short strand from stock solutions into buffers containing all final components except MgCl₂. Samples were heat annealed 2 min at 95 °C, and allowed to cool ambiently. Where appropriate, MgCl₂ was added from a concentrated stock solution such that the sample was diluted by <0.5%. Each 250 μL sample contained 15 μM annealed wild-type or A14G HH16 ribozyme, 50 mM HEPES pH 7.5, and 100 mM NaCl. MgCl₂ titrations were conducted by splitting one preannealed ribozyme stock into two aliquots, to one of which MgCl₂ was added up to 10 mM. Ribozyme samples of intermediate MgCl₂ concentration were made by mixing varying proportions of the two aliquots. Spectra were collected in a 0.1-cm path length cell at 25 °C. Each final spectrum was averaged from 16 individual scans at 200 nm per min and 1 nm resolution. Spectra were baseline-corrected by subtraction of a buffer spectrum. Difference spectra reflecting the structural response of RNAs to added MgCl₂ were generated by subtraction of spectra taken of samples containing no MgCl₂ from corresponding spectra of samples containing 10 mM MgCl₂.

RESULTS

Bimolecular Constructs for ITC Dissection of Folding

Figure 1 depicts the hammerhead ribozyme constructs deconstructed in this study, HH16 and HHα1 (22, 23). Both ribozymes are three-way helical junctions containing asymmetric internal loops. Several of the bases within the loops participate in noncanonical interactions in the active form of the ribozyme (24, 25). By convention, the three helices—also called “stems”—are numbered 1 through 3, indicating their positions in the folded ribozyme, wherein stems 2 and 3 coaxially stack and stem 1 docks at an acute angle to stem 2.

FIGURE 1.

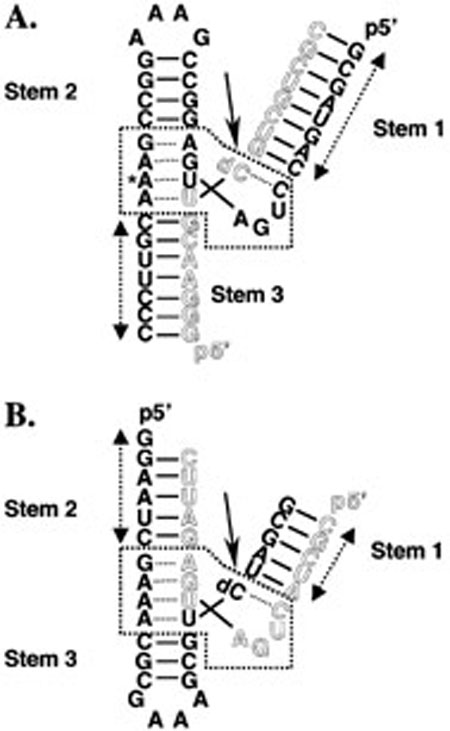
Schematic diagrams of the hammerhead ribozyme constructs used throughout all the studies. (A) Hammerhead ribozyme 16 (HH16). The long strand is shown in solid lettering, and the short strand is shown in outline. Solid lines between bases represent Watson–Crick base-pairing. Dotted lines between bases represent noncanonical interactions. The arrow indicates the normal site of ribozyme cleavage, but all of the experiments described were performed with a nonreactive substrate analogue containing a dC residue at position 17. The asterisk marks the position of mutation to G in the A14G folding mutant. The dotted box indicates the conserved core. Double-headed arrows delineate the extent of sequence included in stem fragment duplexes. (B) Hammerhead ribozyme α1 (HHα1). All conventions are the same as in panel A. Note the invariance of the core region.

Each construct consists of two oligonucleotides, a long strand and a short strand, delineated in Figure 1 by solid and outlined letters, respectively. The two strands anneal to form the complete, folded ribozyme. In each case, strand pairing leads to formation of two helices, corresponding to two of the three stems of the ribozyme. In HH16, pairing forms stems 1 and 3, whereas stems 1 and 2 are formed during annealing of HHα1. The remaining helix of each three-way junction exists as a preannealed stem-loop in the long strand, as confirmed by differential scanning calorimetry and optical melting (data not shown). In keeping with the formalism of Hertel et al. (20), the formation of two base-paired stems upon annealing represents the “helix” component of folding. Whereas the three stems flanking the central junction vary between ribozymes in length and sequence, the junction itself (boxed in Figure 1) is identical in HH16 and HHα1. This conserved junction is the catalytic core of the ribozyme. Active hammerhead ribozymes autocatalytically cleave themselves at the site within the core indicated by solid arrows in Figure 1. Therefore, the constructs employed a single dC at the cleavage site to prevent strand scission. The oligonucleotides comprising HH16 and HHαl have been previously shown not to assume alternate structures at high concentration (22, 23).

Ion-induced folding of the hammerhead ribozyme has been characterized by multiple methods. Comparative gel electrophoresis (26) and steady-state FRET (27) studies indicate two folding transitions as a function of added MgCl₂. In the absence of MgCl₂ and at low ionic strength, the stems are extended. At approximately 500 μM MgCl₂, the first transition occurs in which stems 2 and 3 coaxially stack. Millimolar concentrations of MgCl₂ induce the second transition, wherein stem 1 docks against stem 2. More recent, time-resolved FRET studies of hammerhead folding also show two folding events, but ascribes the stem 2 docking event to the first transition (13). The A14G point mutant of HH16 fails to undergo either of the two global folding events described above (28, 29). The asterisk in Figure 1A indicates the site of the adenosine to guanosine mutation used to generate the A14G folding mutant.

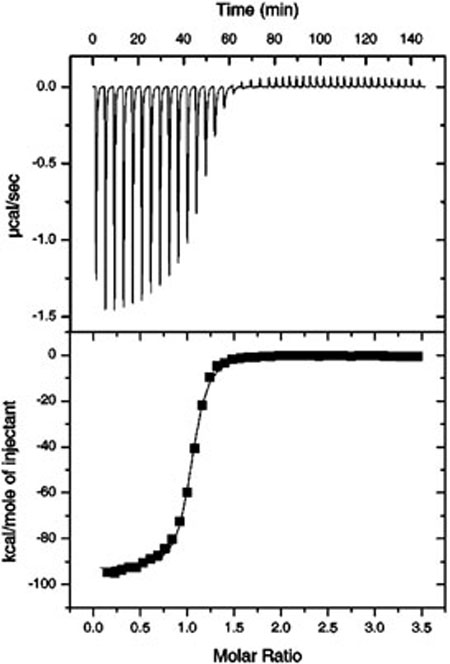
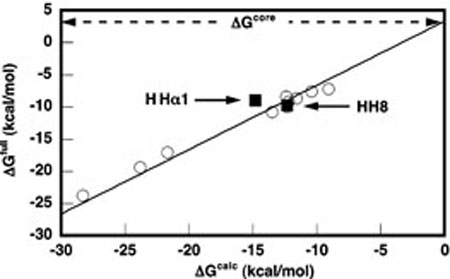
Enthalpies for total folding of the full ribozyme constructs (ΔH^full) were obtained from ITC experiments wherein hammerhead short strands were titrated into their long strand counterparts. Upon injection, the instrument measures the heat taken up or evolved due to binding and coupled folding, as well as heats of dilution and mixing. The heats are determined from the differential power required to maintain constant temperature between the injection cell and an identical reference cell. A representative example of the ITC data is shown in Figure 2, where the upper panel depicts the raw injection data, and the lower panel depicts the integrated injection enthalpy data after correction for the heats of mixing and dilution. The solid line in the lower panel is the nonlinear least-squares fit of the data to a one-site binding model (17). The fit yields experimental parameters for ΔH, K_A, and n, the reaction stoichiometry. All experiments were fit to a one-site binding model, for which the theoretical n-value is 1. Experimentally, n = 1.0 ± 0.1 across the entire dataset. Our analysis focused on the fitted ΔH. Many of the titrations resulted in significant base pairing, and therefore involved K_A values several orders of magnitude too large (i.e., » 10⁸) to be confidently fit by this method (17). However, to ensure that the enthalpies of folding we measured by ITC could be interpreted in light of the ΔG^core value previously determined by Hertel et al. (20), we performed titrations of two full ribozyme constructs under solution conditions used in the previous study (25 °C, 50 mM HEPES pH 7.5, 10 mM MgCl₂). We chose to conduct these titrations with the bimolecular hammerhead constructs HH8 and HHα1. HH8 shares both core sequence and strand topology with HH16, differing only in the length and exact sequence of helical stems 1 and 3 (see Materials and Methods). We chose these two constructs because—in contrast to HH16—the amount of base-pairing accompanying strand annealing would be small enough to allow a reasonable estimation of ΔG^full from direct fits to the ITC isotherms. (We attempted to determine ΔG^full for HH16 by using optical melting, but multistate thermal unfolding behavior precluded van't Hoff fitting of the data.) Figure 3 shows the results of our ITC determinations of ΔG^full overlaid with the dataset used by Hertel et al. to calculate ΔG^core, wherein observed ΔGs and those predicted from a nearest neighbor model (ΔG^full and ΔG^calc, respectively) correlated strongly across a range of 10 different hammerhead constructs, differing on average by a constant of +3.3 kcal mol⁻¹ at 25 °C. This constant reflected the difference between ΔG of folding for the full ribozyme and ΔG for helix formation, and was thus defined as ΔG^core. Our ITC results compare favorably with the previous data, especially for HH8, which was included in the set of 10 ribozyme constructs examined by Hertel et al. Even HHα1, which has a different strand topology than all the constructs used in the previous dataset, falls close to the previous correlation.

FIGURE 2.

ITC data for full HH16 construct in 0.1 M NaCl, 50 mM HEPES pH 7.5, 308 K. (Upper) Raw ITC data. The difference in power (μcal/s) required to maintain equal temperature between the sample cell and a reference cell is plotted as a function of time. Peaks correspond to individual injections. (Lower) Integrated data. Raw data are integrated to yield injection enthalpies (in kcal mol⁻¹) and normalized for the moles of titrant added. Normalized injection data are plotted (squares) as a function of molar ratio. These plots are directly fit (solid line) to a one-site binding model to yield ΔH = −92.4 ± 0.5 kcal mol⁻¹, K_A = 3.0 ± 0.2 × 10⁷, and n = 1.02 ± 0.003. Here, K_A is an apparent value determined from the binding of the last ~5% of strands in the sample cell, and cannot be reliably fit when the real association constant (K^real) exceeds ~10⁸ (17). In this case, $K^{\text{real}}\ge {10}^{14}\gg K_{\text{A}}.$

FIGURE 3.

ΔG^full for HHαl and HH8 (closed squares) as determined by ITC, plotted against ΔG^calc for the same constructs as predicted by the independent nearest neighbor-hydrogen bonding (INN-HB) model (30). The data are overlaid on a plot of the complete dataset (open circles) generated by Hertel et al. (20), correlating ΔG^full as determined largely from cleavage kinetics with ΔG^calc from the INN-HB model for a set of 10 bimolecular hammerhead ribozyme constructs. The previous dataset is fit to a line with a slope of 1 and an intercept of +3.3 kcal mol⁻¹, corresponding to ΔG^core. All data reflect measurements conducted at 25 °C in 50 mM HEPES pH 7.5, 10 mM MgCl₂.

The enthalpic contribution of secondary structure formation (ΔH^helix) to overall folding was assessed from titrations of stem fragment RNAs into their complements. The stem fragments analyzed by this method are indicated in Figure 1 by double-headed arrows, and correspond to the pairs of helices formed during annealing of full constructs. ΔH^helix was calculated from the sum of two individual stem enthalpies and a correction term, ΔH^fuse = −3.6 kcal mol⁻¹. Initiation of helical duplex formation requires bringing two strands together in a bimolecular event, and this initiation event carries with it an energetic penalty as determined by fitting of optical melting data to a nearest neighbor model for duplex formation (30). The ΔH^fuse term simply cancels out one initiation penalty, reflecting the fact that only one initiation event occurs in annealing of the full construct, whereas each stem fragment incurs its own initiation penalty. Since the initiation penalty has only to do with molecularity, it is sequence independent; ΔH^fuse is therefore also sequence independent. The enthalpy of core folding, ΔH^core, was taken as the difference between ΔH^full and ΔH^helix.

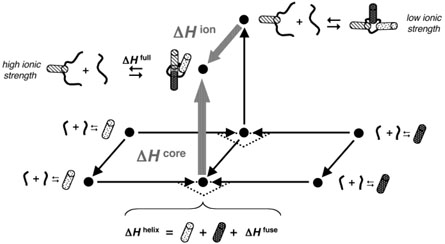
The experimental design can be summarized by a set of interconnected thermodynamic cycles, as shown in Figure 4. Each vertex point in the figure corresponds to the observed folding enthalpy for a given structure under a specific solution condition. Interconnecting vectors represent the enthalpies for moving between states. Movement along a given arrow may correspond to a physical process, such as the addition of ions, or to a virtual process, such as the fusion of stem fragments or the inclusion of a ribozyme core. The vector of greatest interest, ΔH^core, connects ΔH^helix to ΔH^full, and thus corresponds to the enthalpy required to move from a virtual state of purely secondary folding to the fully folded ribozyme. Hertel et al. (20) first used this thermodynamic deconstruction of two-strand hammerhead constructs to compare the free energies of hammerhead substrate strand binding (as derived from kinetic analysis) to those predicted from nearest neighbor analyses of stem sequences.

FIGURE 4.

Thermodynamic dissection of hammerhead folding into helix and core components. Individual ITC experiments are related by a set of interconnecting thermodynamic cycles. Vertex points correspond to experimental ΔH's for folding of full ribozyme (top) or stem fragments (bottom). Low ionic strength conditions (0.1 M NaCl, back) did not support tertiary folding, whereas higher ionic strength conditions (1 M NaCl or 0.1 M NaCl/10 mM MgCl₂, front) promoted tertiary folding. Vectors connecting the points represent the ΔH's associated with moving between states. The vectors ΔH^core and ΔH^ion are labeled in gray.

ITC of HH16 Folding

ITC experiments were conducted at multiple temperatures (278, 293, and 308 K) and under a variety of ionic conditions (100 mM NaCl, 1 M NaCl, and 100 mM NaCl/10 mM MgCl₂). Table 1 shows the ITC-measured enthalpies for the folding of HH16 and duplexes corresponding to stems 1 and 3, as well as the ΔH^helix and ΔH^core values calculated for each condition.

Table 1.

ΔH of Folding for HH16 and Associated Stem Fragments^a

construct assayed	salt condition	temp (K)	ΔH (kcal/mol)	ΔHhelix (kcal/mol)	ΔHcore (kcal/mol)
full	1 M NaCl	308	−73 ± 3	−117 ± 1	+44 ± 3
Stem 1	1 M NaCl	308	−57 ± 1
Stem 3	M NaCl	308	−56 ± 1
full	0.1 M NaCl, 0.01 M MgCl2	308	−78 ± 1	−119 ± 1	+41 ± 1
Stem 1	0.1 M NaCl, 0.01 M MgCl2	308	−56 ± 1
Stem 3	0.1 M NaCl, 0.01 M MgCl2	308	−59 ± 1
full	0.1 M NaCl	308	−92 ± 1	−111 ± 2	+19 ± 2
Stem 1	0.1 M NaCl	308	−53 ± 1
Stem 3	0.1 M NaCl	308	−54 ± 2
full	1 M NaCl	293	−54 ± 1	−94 ± 2	+40 ± 2
Stem 1	1 M NaCl	293	−41 ± 1
Stem 3	1 M NaCl	293	−49 ± 1
full	0.1 M NaCl, 0.01 M MgCl2	293	−61 ± 1	−101 ± 2	+40 ± 2
Stem 1	0.1 M NaCl, 0.01 M MgCl2	293	−46 ± 1
Stem 3	0.1 M NaCl, 0.01 M MgCl2	293	−51 ± 1
full	1 M NaCl	278	−47 ± 1	−76 ± 2	+29 ± 2
Stem 1	1 M NaCl	278	−28 ± 1
Stem 3	1 M NaCl	278	−44 ± 1
full	0.1 M NaCl, 0.01 M MgCl2	278	−50 ± 1	−78 ± 2	+28 ± 2
Stem 1	0.1 M NaCl, 0.01 M MgCl2	278	−33 ± 1
Stem 3	0.1 M NaCl, 0.01 M MgCl2	278	−41 ± 1

^aΔH values for full construct and stem fragment folding were derived from direct fitting to individual ITC isotherms. ΔH^helix was calculated by summing the fitted ΔH's for stem fragments 1 and 3 as well as ΔH^fuse, a −3.6 kcal mol⁻¹ correction factor (see Materials and Methods, Results). ΔH^core was calculated as the difference between ΔH^full and ΔH^helix.

As expected for short duplexes, formation enthalpies for stems 1 and 3 are large and negative across all ionic conditions tested. Typically, ΔH in the presence of 1 M NaCl or 10 mM MgCl₂ tends to be more favorable than in 0.1 M NaCl. In contrast to the stems, the enthalpy of full ribozyme folding (ΔH^full) grows significantly less favorable upon addition of NaCl or MgCl₂ at concentrations sufficient to promote tertiary folding. This observation is most markedly demonstrated in the calculated ΔH^core values, all of which are large and positive. Given the ΔG^core of +3.3 kcal mol⁻¹ determined by Hertel et al. (20), our results indicate that the core folding of the hammerhead three-way junction is entropically driven, proceeding with a ΔH^core +120 ± 10 cal mol⁻¹ K⁻¹ at 25 °C. Strikingly, ΔH^core is independent of whether folding is stimulated by 1 M NaCl or 10 mM MgCl₂.

ITC of HHα1 Folding

As stated previously, the three-helix junction of hammerhead ribozymes is conserved, whereas the stems may vary in length and sequence. Therefore, one would expect the thermodynamics of core folding to be similar across different hammerhead constructs. To support the generality of the HH16 core folding results, we subjected another well-characterized bimolecular hammerhead, HHαl (23), to ITC analysis. We chose HHαl (Figure 1B) because its stem length, stem sequence, and strand topology differ from HH16, but its core sequence is the same. We conducted ITC analysis of HHαl folding in a manner parallel to that used for HH16. The results are shown in Table 2. All experiments were conducted at 5 °C to promote full pairing of the short (5 bp) duplexes. HHαl stem 1 fragments were well-behaved in these experiments. Unfortunately, both strands of the HHα1 stem 2 fragment appeared to possess significant bimolecular self-structure across a wide range of concentration and temperature, as determined from numerous attempts to measure the thermodynamics of stem 2 duplex formation using both ITC and optical melting techniques. The major transition observed in optical melting experiments was in the vicinity of 0 °C, suggesting that the intended stem 2 duplex was in competition with other bimolecular structures and therefore destabilized. Therefore, the stem 2 fragment could not be directly analyzed by calorimetric or spectroscopic methods. We have estimated the enthalpy of stem 2 formation from nearest neighbor calculations (30) and from the per base-pair $\Delta C_{\text{P}}^{\text{helix}}$ observed in the HH16 stem fragments (see Figure 5, Table 2 footnotes). The estimate appears to be reasonable insofar as it predicts that stem 2 is just slightly less enthalpically favorable than stem 1, where both stems have the same number of base-pairs. We find that core folding in HHα1 is associated with significantly unfavorable enthalpy, close to that seen in HH16—probably, in fact, within the error of our stem 2 estimate. Thus, in two hammerhead constructs sharing only core sequence, junction folding is opposed by enthalpies of very similar magnitude.

Table 2.

ΔH of Folding for HHα1 and Associated Stem Fragments

construct assayed	salt condition	temp (K)	ΔH (kcal/mol)	ΔHhelix (kcal/mol)	ΔHcore (kcal/mol)
full	1 M NaCl	278	−29 ± 1	−52 ± 4	+23 ± 4
Stem 1	1 M NaCl	278	−25 ± 1
Stem 2	1 M NaCl	278	−23 ± 3a
full	0.1 M NaCl, 0.01 M MgCl2	278	−28 ± 1	−54 ± 4	+26 ± 4
Stem 1	0.1 M NaCl, 0.01 M MgCl2	278	−26 ± 1
Stem 2	0.1 M NaCl, 0.01 M MgCl2	278	−24 ± 3b
full	0.1 M NaCl	278	−44 ± 1	−48 ± 4	+4 ± 4
Stem 1	0.1 M NaCl	278	−23 ± 1
Stem 2	0.1 M NaCl	278	−21 ± 3c

^aThis value was estimated from a nearest neighbor calculation on the sequence that was corrected for heat capacity effects assuming $\Delta C_P^{\text{fold}}=$ −90 cal mol⁻¹ K ⁻¹ bp ⁻¹, applied to the five base-pairs of the stem across a −43 degree differential between the median T_M of the nearest neighbor dataset (321 K) and the temperature of the ITC experiment (278 K).

^bThis value was based on the estimate for the 1 M NaCl sample, applying a −1 kcal mol ⁻¹ correction for additional stability in 10 mM MgCl₂, as observed for stem 1.

^cThis value was based on the estimate for the 1 M NaCl sample, applying a +2 kcal mol ⁻¹ correction for reduced stability in 0.1 M NaCl, as observed for stem 1.

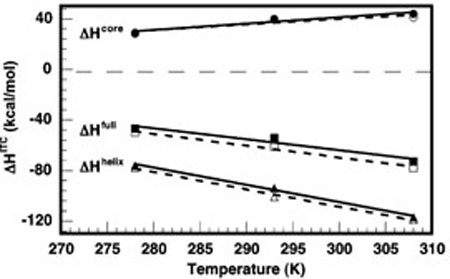
FIGURE 5.

Temperature dependence of ΔH^core (top), ΔH^full (middle), and ΔH^helix (bottom). Solid shapes and solid lines indicate data collected in 1 M NaCl and linear fits to those data. Open shapes and dotted lines indicate data collected in 10 mM MgCl₂ and linear fits to those data. The slopes of the fits represent the ΔC_P for each component, which did not significantly vary between 1 M NaCl and 10 mM MgCl₂ conditions: $\Delta C_P^{\text{core}}$ = +0.5 ± 0.1 kcal mol⁻¹K⁻¹, $\Delta C_P^{\text{full}}$ =−0.9 ± 0.1 kcal mol⁻¹ $\Delta C_P^{\text{helix}}$ = −1.4 ± 0.1 kcal mol⁻¹ K⁻¹.

The magnitudes of all the observed enthalpies vary considerably with temperature, revealing the presence of heat capacity changes (ΔC_P's) associated with the folding process, as shown in Figure 5. Again, the thermodynamic similarity between RNAs folded in NaCl and in MgCl₂ is remarkable. Both solution conditions exhibit full-ribozyme folding ΔC_p's of −0.9 ± 0.1 kcal mol⁻¹ K⁻¹. The heat capacities of helix formation are also similar at −1.4 ± 0.1 kcal mol⁻¹ K⁻¹. When normalized per base pair, $\Delta C_P^{\text{helix}}$ is approximately −90 cal mol⁻¹ K⁻¹ bp⁻¹. This value is in the consensus range of other heat capacities reported for helix formation (31–37). From $\Delta C_P^{\text{full}}$ and $\Delta C_P^{\text{helix}}$, we calculate a $\Delta C_P^{\text{core}}$ of +0.5 ± 0.1 kcal mor¹ K⁻¹.

Comparison of Ion-Induced Folding of HH16 and A14G

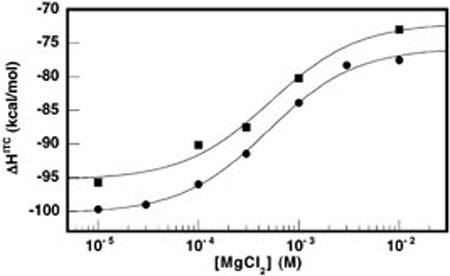
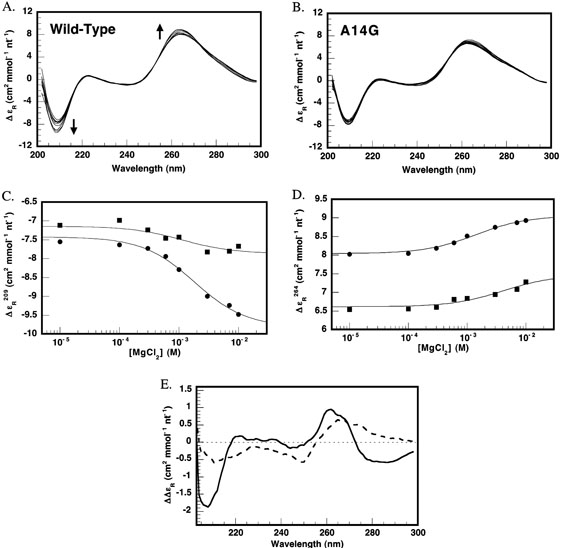
To further explore the phenomenon of entropy-driven core folding, we compared the ion-dependent folding enthalpies of wild-type HH16 and the A14G folding mutant. Titrations of full ribozyme constructs were performed at increasing concentrations of MgCl₂. The results are shown in Figure 6. Aside from a relatively constant offset of ~5 kcal mol⁻¹, the A14G variant exhibits the same MgCl₂-dependent enthalpic trend as wild-type HH16. In fact, noncooperative fits of ΔH^full as a function of MgCl₂ (solid lines in Figure 6) yield an apparent $K_{\text{D}}^{\text{Mg}}$ of 0.5 ± 0.1 mM and a transition amplitude of 24 ± 2 kcal mol⁻¹ for both HH16 and the A14G variant. Yet, circular dichroism (CD) spectra of the identical constructs clearly show that wild-type HH16 structurally responds to added MgCl₂ to a greater extent than does A14G. Figure 7A shows how wild-type HH16 CD spectra change as MgCl₂ is varied from 0 to 10 mM. Typically, MgCl₂-dependent changes in the CD spectra of globular RNAs correspond to tertiary structure formation (38). In the wild type construct, a significant ion-dependent increase in global structure is evident from the observed intensity changes at 209 and 264 nm. These spectral regions primarily report on global changes in chirality of the RNA backbone and bases, respectively (39). Close inspection of the wild-type spectra in Figure 7A also reveals an isodichroic point at 273 nm, suggesting that the spectra are reporting on the MgCl₂-dependent interconversion of unfolded and folded states. In contrast, the overall spectral change as a function of added MgCl₂ is diminished in the A14G mutant, and the isodichroic point is not evident at 273 nm (Figure 7B). MgCl₂-dependent changes in the CD intensities at 209 and 264 nm are plotted in Figure 7, panels C and D, respectively. Apparent $K_{\text{D}}^{\text{Mg}}$ values for wild-type and A14G at 209 nm were 1.5 ± 0.5 mM, in good agreement with values for MgCl₂-dependent folding of the hammerhead obtained by other methods (13, 26–29), and close to the values obtained from fits to the MgCl₂-dependent ITC data shown in Figure 6. Although wild-type and A14G possess similar intensities at 209 nm in the absence of added MgCl₂, the wild-type signal increases nearly 2.5-fold more than that of A14G. At 264 nm, the wild-type signal is more than 20% greater than that of A14G in the absence of added MgCl₂. As MgCl₂ is added, however, both RNAs exhibit similar increases in intensity. The extent of ion-dependent structure can be visualized by examining difference spectra, wherein a spectrum of the ribozyme in the absence of MgCl₂ is subtracted from the corresponding spectrum in the presence of 10 mM MgCl₂. Such difference spectra are shown in Figure 7E for both wild-type HH16 and the A14G mutant. The difference spectra recapitulate the traces at 209 and 264 nm, and also reveal that MgCl₂-dependent increases of CD intensity at 260–265 nm result from the growth of slightly different spectral components in the cases of wild-type and A14G. Thus, the CD data show that our bimolecular A14G construct is impaired in MgCl₂-dependent tertiary folding. This result is in agreement with previous studies by Lilley and co-workers that used comparative electrophoresis and steady-state FRET to demonstrate that A14G does not achieve the same compact, active tertiary fold as wild-type HH16, most likely due to the inability to engage in a key noncanonical core interaction between A14 and G8 (28, 29).

FIGURE 6.

Mg²⁺-dependent folding enthalpies for wild-type HH16 (circles) and A14G (squares) as determined by ITC. Titrations were conducted at 25 °C in a background of 50 mM HEPES pH 7.5 and 100 mM NaCl. Solid lines represent fits to a noncooperative binding isotherm. Both fits yield an apparent $K_{\text{D}}^{\text{Mg}}$ of 0.5 ± 0.1 mM.

FIGURE 7.

Circular dichroism (CD) spectra of wild-type and A14G HH16 RNAs as a function of added MgCl₂. Stacked spectra of (A) wild-type and (B) A14G HH16 at 0–10 mM MgCl₂. Arrows highlight the intensity changes at 209 and 264 nm as MgCl₂ is added, indicative of an increase in global structure concomitant with ion-dependent core folding. Note the isodichroic point at 273 nm in the wild-type spectra that is absent in the A14G spectra. (C) Changes in CD intensity at 209 nm as MgCl₂ is titrated into wild-type (circles) and A14G (squares) HH16. The solid lines represent fits of the data to an isothermal binding model, yielding an apparent $K_{\text{D}}^{\text{Mg}}$ of 1.5 ± 0.5 mM in each case. Note the much greater response of the wild-type to added MgCl₂ despite similar intensities of wild-type and A14G at low concentrations of MgCl₂. (D) Changes in CD intensity at 264 nm as MgCl₂ is titrated into wild-type (circles) and A14G (squares) HH16. Note the large difference in absolute intensity between the two samples. (E) Difference CD spectra showing the structural response of wild-type HH16 (solid line) and A14G (dotted line) to the addition of 10 mM MgCl₂. Spectra were collected for each RNA in the presence of 10 mM MgCl₂ and in its absence, and the Mg–no Mg difference is shown.

DISCUSSION

RNA helical junctions are nearly ubiquitous motifs in structured RNAs (1, 2), but very little is known about the thermodynamics of helical junction folding. This dearth of knowledge hinders our ability to predict RNA tertiary structures, to rationalize known structures, and to understand structural changes that regulate RNA function.

Some previous studies of RNA helical junctions have used optical melting techniques, and have had success in determining overall stabilities of junction constructs (3, 4). These studies used two-state fitting of thermal melting profiles to systematically determine free energy increments for use in a nearest neighbor model of RNA duplex formation. Thus, the energetics of junction folding were examined as a means to improve sequence-based secondary structure prediction. Additional techniques are required to study systems that deviate from two-state folding, to reliably dissect the energetics of secondary structure from higher order folding, and to obtain the most accurate picture of the contributions of ΔH, ΔS, and ΔC_P toward overall stability under non-standard solution conditions.

ITC (17) is a promising tool to address these needs. Indeed, it has already been used profitably to buttress optical melting studies on non-two-state RNA junctions (3). Here, we have employed ITC to study the folding of the hammerhead ribozyme, a three-way helical junction. We have combined ITC of bimolecular constructs with a deconstruction of the ribozyme into “helix” and “core” components to separate the ΔH and ΔC_P of duplex formation from the remainder of hammerhead folding. ITC experiments measured the folding enthalpies of full ribozymes and of duplexes corresponding to ribozyme helical stems. The resulting data yielded experimental values for ΔH^helix and ΔH^full from which we calculated ΔH^core. By using these strategies, we have shown that helix and core folding of the hammerhead ribozyme occur with opposing contributions of enthalpy and entropy: helix formation is enthalpically favored, whereas core folding is associated with very unfavorable enthalpy, and is entropy-driven. Moreover, the ΔH and ΔC_P of folding are essentially the same whether promoted by 1 M NaCl or 10 mM MgCl₂. This similarity is especially clear from ΔC_P's of HH16 folding derived from the temperature dependence of the measured enthalpies (Figure 5).

Hammerhead stem fragments investigated in this study behaved essentially as one would expect for RNA duplexes, in light of condensation theory (40). Enthalpies of duplex formation were relatively uniform across ionic conditions, with an overall trend toward slightly more favorable ΔH^helix values in the presence of MgCl₂ or high concentrations of monovalent salt. In addition, $\Delta C_P^{\text{helix}}$ fell well within the range of per base-pair ΔC_P's reported for nucleic acid duplexes elsewhere (34–37).

Ion-induced changes in ΔH^full suggested that hammerhead folding beyond the strand-annealing step proceeds with vastly different energetics than those of helix formation. Figure 6 demonstrates the progression toward less favorable enthalpy of total folding as one moves across the range of MgCl₂ concentrations known to promote proper folding. Interestingly, the same enthalpic trend is observed with the A14G point mutant of HH16. By using comparative gel electro-phoresis and steady-state FRET, Lilley and co-workers have previously shown that A14G does not achieve the same compact global fold as wild-type HH16 in response to added ions (28, 29), but appears to remain in a primarily “open” conformation. The authors showed similar folding behavior in a G8U mutant, suggesting that an A14-G8 interaction is necessary for complete folding. It is unclear whether the “open” conformation is rigidly open or represents the time-averaged structure of a globally dynamic fold. Our CD results demonstrate that our bimolecular A14G construct responds quite differently to added MgCl₂ than does its wild-type counterpart (Figure 7). Differences in the CD intensities of the RNAs at 209 nm indicate that the backbone structure of the wild-type changes much more than that of A14G as MgCl₂ is added. CD traces at 264 nm suggest that net changes in base stacking as a function of MgCl₂ appear to be similar between wild-type and A14G, although the absolute amount of chiral base structure is significantly greater in the wild-type. At the same time, wild-type and A14G have identical stem sequences, so the values of ΔH^core we have calculated for HH16 would be quite similar for A14G. Our observations are therefore consistent with a scenario in which (i) ΔH^core primarily reflects structural changes associated with rearrangements of core residues upon strand annealing and with initial folding to an “open” conformation of the ribozyme, and (ii) subsequent tertiary folding to the native, “closed” state is associated with a comparatively small change in enthalpy, possibly as a result of small net changes in base stacking.

Our results are difficult to compare with those of the previous ITC study by Hammann et al. (19), as the experimental strategies differed substantially. We have titrated the RNA strands of bimolecular hammerhead constructs into their counterparts, keeping buffer conditions constant between both samples. In the aforementioned study, a concentrated MgCl₂ solution was titrated into preannealed, unimolecular hammerheads consisting of an RNA core and mostly DNA stems. Consequently, observed enthalpies represented the superposition of nonspecific ion condensation with specific binding and folding events. The authors of the previous work did not observe any large-scale positive enthalpies concomitant with MgCl₂-induced folding, but reported small enthalpies (0.1−5.7 kcal mol⁻¹ in absolute magnitude) derived from fits to a sequential two-site binding model. Of course, in the study of Hammann et al., the energetics of core residue rearrangements upon strand annealing would not be observed, as the ribozymes were preannealed. ITC experiments in our laboratory employing the MgCl₂-titration strategy of Hammann et al. (19) with preannealed bimolecular HH16 have revealed enthalpically opposed folding behavior consistent with the results of our dissection approach (Figure S1, Supporting Information). We replicated experiments from the previous study, using the same solution conditions (50 mM Tris-HCl pH 8.0, 100 mM NaCl, 283 K), titration scheme, and background subtraction techniques as Hammann et al., but employing preannealed HH16 instead of a unimolecular, DNA/RNA chimera. Our results were quite different from those reported in the previous study, chiefly in that we observed large-scale, endothermic Mg²⁺-binding/folding (Figure S1A, Supporting Information). In addition, when we repeated the experiment using 50 mM HEPES pH 7.5 instead of Tris-HCl, we obtained a quantitatively different result (Figure S1B, Supporting Information); in particular, the ITC isotherm could be fit to a sequential two-site binding model, whereas the data collected in Tris-HCl required a sequential three-site binding model for adequate fitting. (The enthalpic contribution of Tris-Mg²⁺ interactions could potentially explain the discrepancy.) The total fitted enthalpy of all Mg²⁺-binding/folding transitions observed in the HEPES-containing sample was ΔH^total = +22.5 ± 0.8 kcal mol⁻¹ at 283 K and the total fitted entropy was ΔS^total = +110 ± 20 (see Table S1, Supporting Information). These values include contributions from nonspecific condensation of Mg²⁺ ions to the RNA. At the same time, they explicitly exclude the ion-dependent contributions of residual structure in single strands before annealing. Therefore, these ITC experiments represent different thermodynamic transitions, and should not be compared directly with the dissection values. We do note, however, that ΔS^total is within error of the ΔS^core calculated for HH16. We also observe that ΔH^core extrapolated to 283 K = +32 ± 4 kcal mol⁻¹ for HH16, where one would expect ΔH^core > ΔH^total due to the effects of residual structure on the former and ion condensation on the latter. In any case, our observations clearly reveal that the unimolecular DNA/RNA chimera used by Hammann et al. behaves differently than the bimolecular hammerheads used in both the present study and in prior kinetic studies (18, and references therein).

By using the helix/core deconstruction originally devised by Hertel et al. (20), we have dissected the previously determined ΔG^core penalty (+3.3 kcal mol⁻¹ at 25 °C) into largely compensating enthalpic and entropic components. What, then, can ΔH^core, ΔS^core, and $\Delta C_P^{\text{core}}$ tell us about the molecular nature of core formation? The observed ΔH^core and $\Delta C_P^{\text{core}}$ parameters would be consistent with a net loss of base stacking in the event that native core formation required the displacement of alternate structure in core residues. In this regard, it is important to note that any such alternate structures would apparently be present in both HH16 and HHα1, despite their differences in strand topology and sequence, and therefore exist within conserved core residues. Indeed, fluorescence and NMR data show evidence of Mg²⁺-dependent conformational dynamics in the hammerhead core (41, 42). The hammerhead core contains 11 formally unpaired nucleotides. At low ionic strength, these loop nucleotides very likely contain residual structure, including stacking and noncanonical hydrogen bonding interactions. However, the global conformation of the hammerhead is extended under these conditions (27, 29, 43, 44), so the core interactions are probably quite different from those in more compact states, as suggested by the fluorescence and NMR data mentioned above. Upon addition of NaCl or MgCl₂, the ribozyme can be expected to relax from a rigid, extended conformation to a dynamic ensemble of states as the added ions shield the charge of the polyanionic backbone. Ion-induced electrostatic collapse to non-native states has been observed previously for much larger RNAs, such as group I introns (45–49). This shielding effect would apply not only to functional ribozymes (such as HH16) but also to folding mutants (such as A14G), although the precise distribution of collapsed states might differ. It is reasonable to expect that some residual structure in core residues would be broken as the RNAs progressed from a rigidly open state to a dynamic ensemble of compact conformations. Such an interplay of electrostatic shielding and junction core rearrangement parallels a model proposed to explain folding behavior of the Tetrahymena group I intron (46), suggesting that similar forces may dictate the folding of both isolated RNA helical junctions and those occurring in the context of a much larger RNA.

Desolvation of polar surface area upon core folding could also contribute to the observed positive entropy and heat capacity changes we have observed in core folding. Polar moieties of unpaired nucleotides include phosphates, ribose oxygens and hydroxyls, as well as amine, imine, and carbonyl groups of bases. In a rigid, extended conformation of the ribozyme, unpaired nucleotides of the junction core likely expose many of these polar moieties to solvent, where they perturb intersolvent hydrogen bonding, as observed in molecular dynamics simulations (50, 51). Specifically, exposed polar surfaces, on average, increase the distortion of hydrogen-bond angles between solvating waters, decreasing the overall heat capacity of the system in a manner opposite to that observed for solvation of hydrophobic surface area. Upon ion-induced core folding, much of the exposed polar surface area may be buried as the core nucleotides engage in noncanonical interactions, releasing their solvating waters. Previous studies of protein folding have demonstrated that burial of polar surface area is accompanied by a positive ΔC_P (52–54). Thus, desolvation of polar moieties and the concomitant release of waters to bulk solvent could contribute to the increase in heat capacity and entropy our data reveal for the core folding process. Desolvation of site-bound ions could also play a role, but it is difficult to reconcile this notion with the very similar thermodynamics of folding observed in 1 M NaCl and 10 mM MgCl₂. Our data in this respect comport well with the previously demonstrated ability of high concentrations of monovalent ions to support hammerhead catalysis (55–57), and with the recent finding by Hampel and Burke that hammerheads folded in monovalent and divalent metal ions display identical patterns of solvent protection (58). Hammerhead folding in monovalent and divalent ions thus appears to be catalytically, structurally, and thermodynamically equivalent. This equivalence supports a predominant role for diffusely bound ions in the folding of the hammerhead three-way junction, as recently suggested by Rueda et al. (13). Thus, whereas desolvation of site-bound ions seems an unlikely contributor to the energetics of core folding we have observed, it is conceivable that, in aggregate, diffusely bound ions play a similar thermodynamic role. For example, as added ions localize around the RNA, their solvating waters may experience reduced electrostriction, yielding positive values for both ΔH and ΔS (59, 60).

Diffusely bound ion-driven folding of the hammerhead suggests another possible source of favorable entropy, as predicted by Ray-Manning theory (61) and recently described by Murthy and Rose (62). Briefly summarized, their theory states that ions condensed around isolated duplexes are restricted to the roughly cylindrical surface area of those duplexes. However, as helices pack, their electrostatic fields merge, creating additional volume for ionic diffusion and thus a favorable change in entropy. The effects of an increase in diffusional volume are distinct from counterion–correlation effects that have been predicted and observed in closely packed, highly charged polymers (63, 64). It is difficult to estimate the magnitude of entropy that would be associated with counterion-diffusional collapse in hammerhead folding, and we do not expect it to be the dominant driving force in folding. Nevertheless, such an effect is qualitatively consistent with our observations.

Taken together, our data seem most consistent with the following model for core folding of the bimolecular hammerhead construct. Strand-annealing causes rearrangement of conserved core residues, and these rearrangements are the primary source of the observed unfavorable enthalpies of folding. As ionic strength increases, the enthalpic cost of core folding increases because electrostatic shielding permits greater collapse of the RNA, leading to a greater net change in the structure of core residues, desolvation of polar moieties, and greater condensation of diffusely bound ions. Condensation of diffusely bound ions may further contribute to the observed enthalpy and entropy changes via reduced electrostriction of solvating waters or by increases in total ion diffusional volume. Furthermore, added ions may stabilize residual structure of core residues in the single-stranded state. This last aspect points to an important difference in the thermodynamics of folding observed by ITC as opposed to those measured via thermal scanning methods (e.g., optical melting, differential scanning calorimetry). Our method reports on net energetic changes between folded and unfolded states at a given temperature, where residual structure in the unfolded state may be present. Thermal scanning methods yield thermodynamic parameters that rigorously apply only at the T_M for a folding transition, which often occurs at temperatures too elevated to permit much residual structure in the unfolded state, and extrapolations to lower temperatures do not incorporate the effects of increased residual structure. Therefore, the two methods may report on different endstates. Whereas thermal scanning methods provide a convenient means to define a reference state (e.g., the T_M observed in 1 M NaCl), values obtained by ITC may better reflect energetics of folding under biologically relevant conditions.