Modelling of municipal mortality due to haematological neoplasias in Spain

Abstract

Objectives

To study the geographical pattern of mortality caused by haematological tumours in Spain at the municipal level using three Bayesian models and to compare their goodness of fit.

Methods

The fitted Bayesian hierarchical models were: (1) the Besag York and Molliè (BYM) model; (2) a model based on zero‐inflated Poisson (ZIP) distribution, which allowed a large number of event‐free areas; and (3) a mixture of distributions that enabled discontinuities (jumps in the pattern) to be modelled. The three models allow smoothed relative risk maps to be obtained for the all countries. The goodness of fit was evaluated using the deviance information criteria.

Results

The three models yielded similar results. The ZIP model plotted a pattern almost identical with the BYM model. The goodness‐of‐fit criteria indicate that the mixture model is the one that best fits our data. Haematological tumours display a geographical pattern that could be partly explained by environmental determinants, as many of the highest‐risk towns are located in heavily industrialised areas.

Conclusions

The choice of one or another model has scant practical consequences. The pattern of distribution supports the hypothesis that differences in lifestyles, air/industrial pollution and migratory phenomena may determine the pattern of urban mortality due to these tumours.

Spatial analysis of health events (spatial epidemiology) is a discipline that, despite still being in the developmental phase, can already claim its own domain in the field of health research.¹,² Its ability to suggest and detect possible sources of heterogeneity, which may account for spatial incidence and mortality patterns in different diseases, makes this tool of great interest in the sphere of epidemiology and public health.

Moreover, its potential is being reinforced by the ever‐increasing availability of geographically indexed population mortality and incidence data, as well as ongoing advances in computation techniques and geographic information systems. This is a situation that tends, in turn, to favour analysis of the geographical distribution of health data of ever‐finer resolution,² a category into which the so‐called “small‐area studies” fall.

The main advantages of small‐area studies are:

1. better interpretability than larger‐scale studies;

2. lower susceptibility to ecological biases; and

3. greater capacity to detect local effects linked to environmental problems, such as industrial pollution of the environment.³

The disadvantages, on the other hand, are well known and determine the complexity of the analytical techniques. These drawbacks are:

1. the data may be very disperse, with a large number of event‐free areas;

2. the data tend to evidence overdispersion;

3. as a general rule, there is interdependence among observations, associated with the phenomenon of correlation between adjoining areas not taken into account by classic Poisson regression models; and

4. the measurement of errors in both numerators and denominators.

The most widely used strategy for tackling the problems posed by small‐area analysis is to estimate the spatial distribution of risk by means of simulation based on Bayesian hierarchical models.⁴ This approach enables relative risk maps to be estimated for an entire country embracing a great number of areas, given that there are very few constraints over the model complexity and the number of terms included in the linear predictor. It does, however, add several problems to the four difficulties enumerated above. These are (1) computation times and (2) the use of homogeneous smoothing criteria for the whole country in cases where the components of spatial structure might vary between regions.

In view of the fact that there are several methodological alternatives for generating estimates with Bayesian hierarchical models, a comparison of the results yielded by such different approaches would probably help ascertain the true surface of risk. Apart from reporting the municipal pattern of distribution for mortality due to haematological tumours in Spain, this study sought to compare the goodness of fit of three different models, namely:

1. the Besag York and Molliè (BYM) model⁵;

2. a model based on zero‐inflated Poisson (ZIP) distribution, which allowed a large number of event‐free areas⁶; and

3. a mixture model that enables discontinuities (jumps in the pattern) to be modelled.⁷

Several authors have already tried to compare the performance of different spatial models⁷,⁸; in those cases, the BYM model has been compared with mixture models, but a ZIP model has not been evaluated.

The application of these models to the study of haematological tumours is justified, because the preliminary results of the umbrella project that encompasses this study (Atlas of Municipal Cancer Mortality in Spain) show that leukaemias, non‐Hodgkin's lymphomas (NHL) and multiple myeloma have a similar distribution pattern, with several areas of increased risk, suggesting the possible involvement of environmental factors in their aetiology.

This study seeks arguments to decide between the different methods of modelling,⁷,⁸ to determine geographical patterns in situations that include a large number of small areas (namely, a complete country), and, as one application of the methods, to determine the municipal mortality distribution of haematological tumours in Spain. Additionally, in this case, we have used an accessible software tool⁹,¹⁰ showing that these models can be easily applied in epidemiology and public health.

Materials and methods

Cases were sourced from individual entries recording deaths due to leukaemias, NHL and multiple myeloma (ICD‐9 codes 200, 202, 203 and 204–208), registered at a municipal nationwide level for the period 1989–98. These data were supplied by the National Statistics Institute (Instituto Nacional de Estadística) for the production of a municipal cancer mortality atlas, which includes some of these results. Figure 1 shows a political map of Spain.

Figure 1 Political map of Spain.

The municipal populations, broken down by age group (18 groups) and sex, were drawn from the 1991 census and the 1996 electoral roll. These years correspond to the mid‐point of the two quinquennia that comprise the study period (1989–93 and 1994–8). Person‐years for each such 5‐year period were then obtained by multiplying the above populations by 5.

Standard mortality ratios (SMRs) were calculated as the ratio between observed and expected deaths. To calculate expected cases, the overall Spanish mortality for the above two 5‐year periods were multiplied by each town's person‐years by age group, sex and quinquennium.

To plot the maps, smoothed municipal relative risks (RRs) were then calculated, using conditional autoregressive (CAR) models. These models were based on fitting spatial Poisson models with two random‐effects terms that took the following into account: (1) municipal contiguity (spatial term); and (2) municipal heterogeneity. Three different models were fitted.

The BYM model

This model was introduced by Clayton and Kaldor,¹¹ developed by Besag et al⁵ and subsequently applied in the field of ecological studies.¹² It is the most widely used model and is formulated as follows:

O_i ∼ P_O(E_iλ_i)

log(λ_i)  =  α + h_i + b_i

where λ_i is the relative risk in area i, O_i is the number of deaths in area i, E_i are the expected cases, h_i is the municipal heterogeneity term and b_i is the spatial term.

The Lawson mixtures model

The second model was proposed by Lawson and Clark.⁷ On the basis of the BYM model, Lawson specified a model that assumes the breakdown of RR into three components, one dealing with heterogeneity (h) and the other two forming a mixture that deals with the different behaviours of the spatial correlation (b and d), with b being the spatial correlation component and d the component that models the jumps in distribution. Finally, p_i is the proportion of random effect b_i for area i and (1−p_i ) the proportion of d_i. This mixture in the spatial term is included as treatment for any possible discontinuities displayed by distribution of the data.

O_i ∼ PO(E_iλ_i)

log(λ_i) = α + h_i + (p_i × b_i + (1−p_i)× d_i)

The ZIP model

Finally, we used the ZIP model.⁶,¹³ This model is constructed as a mixture of Poisson distributions, one of which has the parameter λ = 0 to include the high proportion of zeros possessed by these types of distribution. For study purposes, we used a ZIP model proposed by Durham et al,¹⁴ in which the Poisson distribution with λ>0 is taken directly from the BYM model.

O_i ∼ (p_i × PO(E_iλ_i) + (1−p_i) × PO(0))

log(λ_i)  = α + h_i + b_i

The models were fitted using Markov chain Monte Carlo simulation methods with non‐informative priors.⁴ Convergence of the simulations was verified using the Bayesian Output Analysis R program library.¹⁰ In view of the great number of parameters of the respective models, the convergence analysis was performed on a randomly selected sample of 10 towns and cities, taking strata defined by municipal size.

The Deviance Information Criterion (DIC)¹⁵ was used as the criterion for model selection. This criterion entails Bayesian generalisation of the Akaike Information Criterion and approximately describes the expected posterior loss when a particular model is adopted—that is, it is the description of the expected divergence of the model vis‐à‐vis the real data. The DIC is the parameter used in Bayesian models to assess the goodness of fit.

Posterior distributions of RR were obtained using WinBugs.⁹ The criterion of contiguity used was adjacency of municipal boundaries.¹⁶ Convergence of estimators was achieved before 100 000 iterations. For the maps shown, a burn‐in (iterations discarded to ensure convergence) of 300 000 iterations was performed and the posterior distribution was derived with 5000 iterations.

The results of the models were included in a Geographic Information System to plot municipal maps that depicted smoothed RR estimates and the distribution of the posterior probability that RR>1. In so far as this indicator is concerned, we applied Richardson's criterion,³ which recommends that probabilities in excess of 0.8 be deemed significant.

Results

A total of 55 430 deaths attributable to the haematological tumours covered by this analysis were registered from 1989 to 1998 in Spain. There are 8077 towns, in 3061 towns of which, no death due to this cause was registered. Using these data and conventional computers, we were able to compile and obtain the posterior distribution of RR on the basis of a single spatial model, including all towns of Spain and the 46 398 adjacencies existing between them, for the three strategies outlined above. Table 1 displays several descriptive statistics for the population and disease data. The total population was <40 million, and mortality due to leukaemia was two times higher than that due to multiple myeloma, and quite superior to mortality due to NHL. The mean number of cases per area for haematological tumours is 6.9, and the median is 1.

Table 1 Summaries of population and mortality due to haematological tumours in the 8077 Spanish towns.

	Total	Mean	Median	SD	Min	Max	Areas with zero counts, n (%)
Population	38 872 268	7812.7	600	44 081.1	5	3 010 492	0
Total observed	55 430	6.86	1	70.96	0	4774	3061 (37.8)
Total expected	55 744.65	6.9	1.3	65.17	0.0001	4514.3	0
Observed NHL*	18 363	2.27	0	25.02	0	1654	5008 (62)
Expected NHL*	18 471.6	2.28	0.42	21.67	0	1501.7	0
Observed myeloma	11 634	1.44	0	14.97	0	1039	5400 (66.8)
Expected myeloma	11 707.2	1.45	0.29	13.9	0	966.6	0
Observed leukaemia	25 433	3.15	0	31.13	0	2081	4215 (52.2)
Expected leukaemia	25 565.9	3.16	0.59	29.6	0	2045.9	0

*Haematological tumours include non‐Hodgkin's lymphomas (NHL), multiple myeloma and leukaemia. Total observed and expected deaths include mortality due to the three tumours studied.

Results of comparison of models

The DIC values listed in table 2 show that Lawson's model furnished the lowest values and was thus the one that best fitted our data.

Table 2 Deviance Information Criterion for the three models.

Model	E(D)	D(E)	pD	DIC
BYM	8114	7522	592	8706
Lawson	8058	7436	622	8680
ZIP	8206	7698	508	8714

BYM, Besag, York and Molliè; D(E), deviance evaluated with respect to expected values; DIC, Deviance Information Criterion; E(D), expected deviance; pD, number of effective model parameters = E(D) – D(E); ZIP, zero‐inflated Poisson.

DIC = goodness‐of‐fit (E(D)) + model complexity (pD). Model selection criteria.

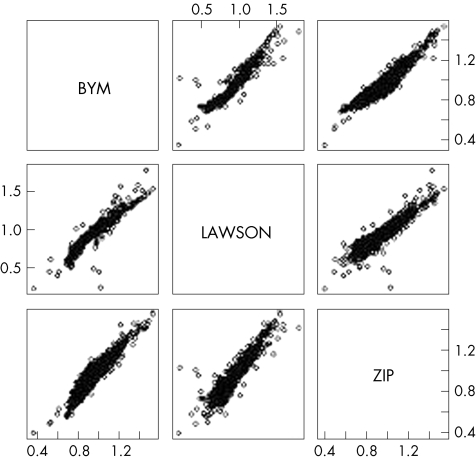
The correlation coefficients between the estimated RRs yielded by the three models were high, with the correlation between the BYM and Lawson models being slightly higher than that for the other two (BYM–Lawson r = 0.964; BYM–ZIP r = 0.938; Lawson–ZIP r = 0.932).

Figure 2 shows the combined representations of the cloud of points corresponding to the results for each pair of models. In all three cases, the data are aligned along the main diagonal, indicating equality of results yielded by the two models for any given town. As the correlation coefficients confirmed, the BYM and Lawson models yielded the most similar results, as the data are more closely superimposed along the diagonal than in the other two cases, in which the clouds of points are wider.

Figure 2 Clouds of points representing the estimated relative risk (RR) distributions of the respective models, taken in pairs. BYM, Besag York and Molliè; ZIP, zero‐inflated Poisson.

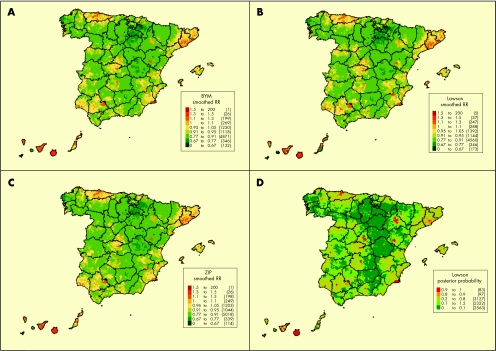
Figure 3(A–C) plots the smoothed RR maps for the three models. A comparison of the maps shows that the spatial distribution of RRs was practically identical in all three cases. When it came to detecting towns that registered high and medium risks, the behaviour of the three models was identical.

Figure 3 Municipal distribution of mortality due to haematological tumours in Spain. Distribution pattern of smoothed relative risk (RR), according to: (A) Besag, York and Molliè (BYM) model; (B) the Lawson model; (C) the ZIP model; and (D) the posterior probability of RR >1. Spain 1989–98.

The differences emerged when it came to allocating low RRs—that is, those <0.77. The ZIP model registered most towns with RRs of this type (804). By contrast, the traditional BYM model had the smallest number of towns with low RRs (316). The Lawson model registered the greatest number of towns with extreme RRs of both types—that is, very low, <0.67 (164) and very high, >1.5 (6).

Cases in which discordancies appeared between the results obtained for smoothed RR and those obtained for SMR were targeted for specific analysis. These discordancies can occur in two different directions: on the one hand, there is the case where the RR is high versus an SMR of <1—namely, when the RR has been overestimated—and, on the other hand, there is the case where the smoothed RR is <1 versus an SMR that is greater than unity—namely, when the RR has been underestimated. The appearance of such cases may be attributable to the influence of the spatial component on the smoothing process.

An examination of these two events in the results yielded by the three models showed that the best model in terms of appearance of cases with RR⩾1 and SMR<1 was the BYM model, with the lowest percentage of cases. By contrast, the Lawson and ZIP models registered a lower number of locations with RR<1 and SMR⩾1, with both displaying the same percentage.

The differences in the number of locations with opposite association between RR and SMR yielded by the three models were not sufficiently great to allow this criterion to be used for comparative purposes. For each model, percentages of small areas with RR⩾1 and significant SMR<1, α = 0.95, were around 3.7%, and those with RR<1 and significant SMR⩾1 around 5%.

Spatial distribution of mortality due to haematological tumours

From maps in fig 3(A–C), which depict the smoothed RRs estimated by the three models, it is clearly seen that the areas of highest risk were Barcelona Province and the Canary Islands (the islands of Gran Canaria, Tenerife and La Palma in particular), although Asturias also had several towns with high RRs.

In terms of the spatial location of the areas with opposite association, the results showed that most of the cases with RR⩾1 and SMR<1 were concentrated in the Canary Islands and Barcelona, whereas the areas with RR<1and SMR⩾1 were mostly in the Castile‐León Region.

The map in fig 3D depicts the distribution of posterior probability under Lawson's model, in as much as this was the model that furnished the lowest DIC. According to this model, there were 199 towns with a probability of >0.8 of their estimator of real risk being higher than unity. Their geographical distribution displayed two clearly differentiated patterns—namely, one with most towns in Barcelona Province (97 towns) and the Canary Islands (49 towns), and the remainder divided up among a series of provinces—for example, Madrid, Seville, Zaragoza, Salamanca, Toledo and Huelva; and the other with major cities such as Gijón, Vigo and Cartagena.

By combining the two patterns, the following emerges: on the one hand, there are the provinces in which the towns having the highest RRs are concentrated—namely, Barcelona and the two Canary Island Provinces; and on the other, there are important towns and cities that do not have such high RRs but, in contrast, do have an almost certain likelihood of such RRs being >1. Table 3 shows the towns—excluding those in the Canary Island Autonomous Region—that registered probabilities in excess of 0.9.

Table 3 Mortality due to haematological tumours in Spain.

Province	Town	Obs	Exp	SMR	RR (Lawson)	RR (BYM)	RR (ZIP)	p(RR>1) (Lawson)
Baleares	Palma de Mallorca	463	402.9	1.149	1.13	1.129	1.112	0.994
Barcelona	Badalona	314	253.9	1.237	1.21	1.219	1.213	0.999
	Barcelona	3186	2690.9	1.184	1.18	1.182	1.179	1
	Calella	25	17.8	1.408	1.267	1.249	1.294	0.95
	Llagosta (la)	18	11.7	1.533	1.202	1.201	1.192	0.913
	Manresa	128	110.2	1.162	1.112	1.124	1.127	0.94
	Mataro	151	130.7	1.155	1.136	1.143	1.144	0.96
	Molins de Rei	33	24.7	1.336	1.156	1.139	1.141	0.915
	Montcada I Reixac	33	32.6	1.012	1.093	1.074	1.117	0.902
	Piera	14	10.1	1.383	1.156	1.169	1.136	0.921
	Pineda de Mar	29	20.1	1.439	1.255	1.243	1.251	0.957
	Premia de Mar	44	26.9	1.632	1.374	1.331	1.254	0.994
	Rubi	65	55.8	1.164	1.128	1.133	1.139	0.924
	Sabadell	313	254	1.232	1.196	1.207	1.194	0.999
	S Adria de Besos	51	39.6	1.288	1.216	1.214	1.24	0.97
	Vilassar de Mar	22	16.8	1.31	1.189	1.184	1.208	0.924
	S Pere de Riudebitlles	8	3.5	2.269	1.278	1.195	1.264	0.919
	S Coloma de Gramenet	172	147.7	1.165	1.153	1.155	1.174	0.989
	Terrassa	255	220.9	1.154	1.133	1.143	1.134	0.992
	Vilafranca Del Penedes	64	39.6	1.614	1.374	1.342	1.353	0.995
	Vilanova I la Geltru	89	66	1.347	1.258	1.251	1.251	0.99
Cuidad Real	Ciudad Real	95	71.8	1.322	1.146	1.139	1.085	0.937
A Coruña	Coruña (A) (Corunna)	399	337.6	1.182	1.157	1.156	1.161	0.997
Granada	Granada	359	319.7	1.123	1.083	1.091	1.071	0.956
Guipúzcoa	San Sebastian	316	267.2	1.182	1.141	1.149	1.143	0.995
Huelva	Huelva	185	157.6	1.174	1.124	1.126	1.121	0.944
Madrid	Madrid	4774	4514.3	1.058	1.055	1.056	1.054	0.999
Murcia	Cartagena	240	210.7	1.139	1.107	1.112	1.112	0.947
	Union (LA)	23	14.9	1.534	1.333	1.242	1.333	0.924
Navarra	Alsasua	22	9.7	2.263	1.188	1.198	1.17	0.921
	Pamplona	330	256.8	1.285	1.179	1.204	1.171	0.999
Asturias	Corvera de Asturias	30	20.6	1.458	1.229	1.211	1.211	0.951
	Gijon	478	400.6	1.193	1.177	1.179	1.186	1
	Llanera	24	17.1	1.401	1.196	1.177	1.191	0.927
	Oviedo	340	296.6	1.146	1.125	1.132	1.13	0.991
Pontevedra	Vigo	393	347.8	1.130	1.101	1.103	1.105	0.972
Salamanca	Salamanca	275	240.3	1.144	1.1	1.101	1.088	0.951
Seville	S Juan de Aznalfarache	35	23.8	1.470	1.232	1.187	1.208	0.912
	Seville	936	850.7	1.1	1.09	1.094	1.088	0.995
Toledo	Toledo	117	82.9	1.41	1.266	1.228	1.158	0.993
Valencia	Canet D'en Berenguer	8	2.7	2.902	1.588	1.212	1.436	0.917
	Sagunto	106	82	1.292	1.150	1.156	1.112	0.925
Vizcaya	Barakaldo	173	145.2	1.191	1.104	1.125	1.107	0.920
Zaragoza	Zaragoza	953	868.4	1.097	1.065	1.081	1.062	0.972

Towns having a posterior probability superior to 0.9 of having a RR>1 (p(RR>1)). Towns listed in order of province (excluding those in the Canary Island Autonomous Region).

BYM, Besag, York and Molliè; Exp, expected deaths; Obs, observed deaths; SMR, standard mortality ratio; ZIP, zero‐inflated Poisson.

Discussion

The geographical patterns, performance and conclusions derived from the results of the three models discussed in this study are very similar, even though conclusions of previous studies suggests that the mixture models are more appropriate for modelling the RR pattern and do no over‐smooth maps.⁷,⁸

Haematological tumours register a geographical pattern that might be partially explained by environmental determinants, as many of the highest‐risk towns are located in heavily industrialised areas. The distribution pattern supports the hypothesis that differences in lifestyle and urban air pollution may determine the urban mortality pattern of these tumours,¹⁷ and this conclusion can be reached from any of the models.

Previous studies on provincial lymphohaematopoietic tumour mortality patterns have reported results with negligible geographical variability and without any defined pattern, save for the excess mortality observed for the Canary Islands.¹⁸ The use of towns as a level of study allows patterns that would otherwise remain hidden by virtue of provincial averaging to emerge; this advantage has been highlighted in previous studies of small areas in Spain regarding different causes of mortality that have not included haematological tumours.¹⁹

Provinces that display the highest number of towns with excess mortality are Las Palmas, Tenerife, Barcelona, Asturias and Girona. Equally important are municipal areas, many in the form of isolated areas, which correspond to major towns and cities, and the results for which are shown in table 3.

The case of the Canary Islands calls for special mention. This excess mortality was already visible in earlier studies, although the origin of this pattern remained unidentified. The pattern is repeated for both lymphomas and multiple myeloma, and to a lesser extent, for leukaemias, tumours that register a higher mortality in Las Palmas than in Tenerife.¹⁸ At various times, the effect of the proportion of the foreign population on mortality patterns in the Canary Islands (reliability of census data and case allocation) has been discussed. One of the problems detected is the difference between the population census figures and the municipal electoral roll, a larger difference than those found in other autonomous regions.²⁰ In our study, both sources were used as denominators. Were the problem to lie in the denominators, excess mortality, and probably excess incidence, would be observed in all the causes studied. Nevertheless, according to the information drawn from the Canary Island cancer registry, reported NHL incidence in both sexes is higher there than for the other registries in Spain, with no such excess being in evidence for the remaining tumour sites. It would therefore be of great interest if an in‐depth study were conducted on the determinants of these tumours in the Canary Island Autonomous Region, as this difference in mortality would not seem to be solely attributable to census‐related or demographic artefacts.

With respect to the results yielded by the different study models, the geographical pattern that emerges is similar. Models that seek to remedy the excess of zeros and display a pattern almost identical with the classic BYM model suggest that the ZIP model does not distinguish between areas with no cases and areas with cases. Although goodness‐of‐fit criteria indicate that the model proposed by Lawson best fits our data, the choice of one or another model probably has scant practical consequences. In regard to the use of the ZIP model, it may be unrealistic to think of null risk areas; however, this distribution has been used in small areas with rare diseases in previous studies.²¹,²²

In general, Bayesian models for plotting disease maps are conservative, in that they have a low sensitivity for detecting areas with moderate increases in risk, but, by contrast, have a pronounced specificity for detecting areas of high risk.³ That is to say, when the smoothing process yields high RR values, it is because the relevant SMR is high. Environmental risks are low, however, and as a result these methods have a limited power to detect them.³

The results that point to large cities could simply be attributable to the greater populations found there. In other words, statistically significant excesses are detected in places where the comparison has sufficient power. Yet, this does not happen with other tumours or groups of tumours. The municipal pattern for haematological tumours is thus specific and is different from that observed for other tumour sites.

What is already known

• Disease maps highlight geographic areas with high and low incidence of mortality rates of a specific disease.

• Bayesian hierarchical modelling has made it possible to obtain stable estimates of relative risk for small areas.

• There are several methodological alternatives for generating estimates with Bayesian hierarchical models.

• Small area studies allow patterns to emerge that would otherwise remain hidden in bigger areas analysis.

What this paper adds

• Information about the performance of different methods of modelling geographical patterns of health events in situations that include an important number of small areas show that these models (Bayesian hierarchical models) can be easily applied in epidemiology and public health

• The results of this study suggest that the geographical distribution of mortality caused by haematological tumours (leukaemias, non‐Hodgkin's lymphomas and multiple myeloma) supports the hypothesis that differences in lifestyle and urban air pollution may determine its mortality pattern in Spain

With the exception of ionising radiations and benzene in myeloid leukaemias, little is known about the aetiology of lymphohaematopoietic tumours. Nevertheless, suspicions surrounding the multiple risk factors present in the study—namely, ionising and non‐ionising radiations and exposure to different chemical substances (petroleum by‐products, hydrocarbons, pesticides, solvents),²³ —are shared vis‐à‐vis haematological tumours (leukaemias, NHL and myeloma). Some evidence suggests that leukaemias and lymphomas occur in neighbourhoods that include industrial sites.²⁴,²⁵ The pattern of municipal distribution linked to large cities suggests that factors associated with the process of urbanisation, such as air or industrial pollution, may be implicated in the aetiology of such processes.

The geographical pattern is determined by deaths in adults, who account for >85% of cases, as lethality among children is low. On examining municipal leukaemia mortality distribution in the <25‐year‐old age group in Spain, no geographical pattern is in evidence (data not shown). Although infectious aetiology may be present in haematological tumours, it seems highly unlikely that it would determine the pattern plotted for all age groups. With respect to the mechanisms implicated in the infectious aetiology of haematological tumours in childhood, the following three hypotheses have been advanced: exposure in the uterus or in the period immediately preceding birth; delayed exposure to common infections after the first year of life²⁶; and unusual population mixing.²⁷,²⁸ The population‐mixing hypothesis was initially formulated in terms of situations of immigration to isolated, sparsely populated areas.²⁹ The influence of migratory phenomena on mortality due to leukaemia has been studied, and it has been suggested that rural–urban migration may be implicated in mortality due to leukaemia in Italy and Greece.³⁰ In the period 1960–70, important migratory phenomena of this type took place in Spain, with Catalonia being a net recipient of immigration from many areas, thereby rendering the population‐mixing hypothesis plausible. Internal migratory flows were linked to the intensification of the industrialisation process and a decline in Spain's rural population.³¹ As a consequence, population mixing and exposure to environmental and industrial pollution are closely related phenomena in this country.

The different Bayesian models used in this study furnished some similar results. The high frequency of areas without cases would not seem to pose a serious difficulty to fitting these models, at least in this group of causes. It would be advisable to ascertain whether this conclusion can be generalised and, by extension, whether the above observations are therefore applicable to other tumour sites.

Abbreviations

BYM - Besag York and Molliè

CAR - conditional autoregressive

DIC - Deviance Information Criterion

NHL - non‐Hodgkin's lymphomas

SMR - standard mortality ratio

ZIP - zero‐inflated Poisson