Abstract
An efficient method is presented to calculate atomic charges of peptides and proteins derived from Mulliken electronic populations for terminally blocked amino acids (Ac–X–NHMe, X = any neutral or charged residue) calculated at the B3LYP/6-31G(d,p)//HF/6-31G(d,p) level of theory. This electronic population-derived atomic charges (EPAC) method is based on the geometry-dependent atomic charge (GDAC) method proposed by Cho et al., in which atomic charges are calculated by using the partial equalization of atomic electronegativities with electronegativity parameters and damping factors given by interatomic distances between covalently bonded atoms in a molecule. The overall mean absolute difference (mad) and root-mean-square deviation (rmsd) between dipole moments μEPAC and μB3LYP, obtained from EPAC charges and from B3LYP/6-31G(d,p) level calculations, respectively, for Ac–X–NHMe are estimated to be 0.38 and 0.59 D, respectively, for 26 representative conformations in the training set, and 0.54 and 0.79 D, respectively, for 172 representative conformations not used for parametrization. For Ac–(Ala)n–NHMe (n = 2−6), the EPAC method reasonably predicts the increase of the dipole moment with increase of the chain length, although the deviations from the μB3LYP values are somewhat larger. For Ac–Ala–NHMe and Ac– (Ala)3–NHMe, the EPAC charge for a specific type of atom does not depend on its position in the sequence or on the length of the sequence. In addition, charge neutrality holds for any Ala residue of these two peptides. Thus, these results suggest that the EPAC charges derived from B3LYP/6-31G(d,p) Mulliken populations can be used reliably for conformational analysis of peptides and proteins.
Introduction
Although atomic charges in a molecule cannot be measured experimentally, they have been used widely for conformational analysis and for interpreting molecular reactivity. For three decades, molecular force fields, such as ECEPP,1 CHARMM,2 AMBER,3 GROMOS,4 CVFF,5 OPLS,6 and others, have been used successfully for computing structures, and thermodynamic and kinetic properties of proteins, as well as their interactions. Electrostatic interactions, calculated from atomic charges, have been recognized as one of the essential factors for describing these properties of proteins.
Atomic charges in a molecule have been calculated by using quantum mechanical and empirical methods. The first quantum mechanical methods include orbital-based population analyses,7–9 a topological electron density analysis (the so-called “atoms in molecules” approach),10 a population analysis based on atomic polar tensors,11 and the electrostatic potential (ESP)-fitting methods,12 with their theoretical backgrounds and applicabilities discussed in detail.13,14 Electronic populations of organic molecules with various functional groups, computed by quantum mechanical methods with different basis sets, have been compared.13,14 A modified formalism has been proposed to obtain atomic charges from orbital-based population analyses by parametrizing bond dipoles to reproduce experimental dipole moments.15 Although these quantum mechanical methods were applied successfully to obtain atomic charges for small molecules, they cannot be adopted practically for larger molecules such as peptides and proteins.
Most of the empirical methods have been derived on the basis of the electronegativity equalization principle proposed by Sanderson,16 which states that when two or more atoms that initially differ in electronegativity combine to form a bond, they become adjusted to the same intermediate electronegativity within the compound. Several formalisms to implement this principle, such as the partial equalization of orbital electronegativity (PEOE),17 the full equalization of orbital electronegativity, 18 the electronegativity equalization method (EEM),19 the modified partial equalization of orbital electronegativity (MPEOE),20 the charge equilibrium approach (QEq),21 the atom-bond electronegativity equalization method (ABEEM),22 and the geometry-dependent atomic charge (GDAC) method,23 have been proposed. Recently, the parameters for EEM24 and ABEEM25 were reoptimized using Mulliken atomic charges calculated at the B3LYP/6-31G(d) level. New parameters have been proposed for PEOE26 and QEq27 by fitting to experimental solvation free energies of organic molecules using the Poisson–Boltzmann (PB) equation. A combined EEM and ESP-fitting method has been suggested to reduce the mathematical instability of the ESP-fitting methods.28
The atomic charges of the CHARMM,2 GROMOS,4 CVFF,5 and OPLS6 force fields are empirical, and have been parametrized to reproduce thermodynamic properties of organic liquids and/or crystal structures of organic compounds and peptides, whereas Mulliken charges and ESP-fitted charges were employed for the ECEPP1 and AMBER3 force fields, respectively. The AMBER force field with restrained ESP (RESP)-fitted charges and a scale factor of 1/1.2 for 1-4 electrostatic interactions satisfactorily reproduced observed relative conformational energies of small organic molecules, DNA base-pairing energies, and solvation free energies of methanol and N-methyacetamide. 29 However, the ESP-fitted charges have inherent problems, namely, they depend strongly on molecular conformation,30–32 on the fitting procedure,12g,14,33,34 and on sampling the grid points on the potential surface.12g,14,33,34 In particular, the conformational dependence of ESP-fitted charges can lead to problems of transferability of the force-field parameters and violation of charge neutrality of each neutral residue in peptides and proteins. For example, the ESP-fitted charges of the N and Cα atoms for extended conformations of Ac–Ala–NHMe and Ac–(Ala)3–NHMe, which were calculated by using the Merz–Singh–Kollman scheme12c,12f and by constraining charges to reproduce the dipole moment, are different depending on their positions in the sequence and on the length of the sequence, even though the backbone structures are identical (see Table S1 of the Supporting Information). In addition, charge neutrality for each residue does not hold except for the second Ala residue of Ac–(Ala)3–NHMe (Table S1 of the Supporting Information). To avoid this non-neutrality problem in the RESP-fitted charges for Ac–X–NHMe (X = any neutral residue) in the AMBER force field, additional constraints were applied to force each residue X and the two end groups to be neutral.35 Later, the effect of self-polarization was considered in the RESP charge-fitting procedure to improve the interaction energies for nucleic acid base pairs, the solvation free energies of methanol and N-methyl acetamide, and the chloroform/water partition coefficients of nucleic acid bases.36
Mulliken charges have been used widely, but they are known to have a strong dependence on the basis set.11,12b,12d,13,14 However, they have two good features, namely, transferability and neutrality. As seen here for Ac–Ala–NHMe and Ac–(Ala)3–NHMe in Table S1 of the Supporting Information, the Mulliken charge for a specific type of atom does not depend on its position in the sequence or on the length of the sequence. In particular, charge neutrality holds for any Ala residue of these two peptides. Thus, these results suggest that Mulliken charges can be used successfully for conformational analysis of peptides, if the proper level of theory and basis set is adopted.
In this article, we present an efficient method to calculate atomic charges of peptides and proteins derived from Mulliken electronic populations for terminally blocked amino acids calculated at the B3LYP/6-31G(d,p)//HF/6-31G(d,p) level of theory. This electronic population-derived atomic charges (EPAC) method is based on the geometry-dependent atomic charge (GDAC) method reported previously.23
Methods
The procedure adopted here consists of several steps. First, atomic charges and dipole moments are computed for Ac–XNHMe at the B3LYP/6-31G(d,p) level. To test the reliability of these B3LYP charges, the dipole moments, , computed from these B3LYP charges are compared to the dipole moments, μB3LYP, computed directly at the same B3LYP level. Then, because B3LYP/6-31G(d,p) calculations cannot be carried out practically for molecules much larger than Ac–X–NHMe, an empirical method based on the use of electronegativities is used to derive (transferable) charges for larger peptides and proteins. There are several definitions of electronegativity, and we chose electronegativities based on the MPEOE method20,23 that was found to reproduce experimental and theoretical (ab initio) dipole and/or quadrupole moments of small organic molecules. Hence, we derive a set of electronegativity parameters for each atom of Ac–X–NHMe to match the charges calculated at the B3LYP/6-31G(d,p) level and obtain empirical atomic charges from these electronegativity parameters.
Theoretical Background
According to the PEOE method,17 the atomic charge QA on an atom A can be calculated by an iterative procedure that converges when the charge transfer between all atoms in a molecule is zero. The degree of charge transfer, , from atom A to atom B at the nth iteration is described by17
| 1 |
where and are the electronegativities of atoms A and B at the (n − 1)th iteration, and χA+ is the electronegativity of the positive ion of atom A. fAB is a damping factor for the bond A−B, which is 0.5 in the PEOE method17 and a parameter determined during the optimization in the MPEOE method.20 In the GDAC method23 and in the procedure used here, fAB is expressed, however, as a function of a distance RAB between atoms A and B and is given by
| 2 |
where and are the van der Waals radii of atoms A and B, respectively, for which the values of Rowland and Taylor37 are used because they were obtained by analyzing more than 100 000 organic and organometallic compounds. Thus, the ratio of RAB to represents the orbital overlap between atoms A and B depending on the molecular conformation. For example, the values of fAB vary from 0.567 to 0.641 for the extended conformation of Ac–Ala–NHMe. As the iteration proceeds, i.e., as n increases, the value of (fAB)n decreases dramatically.
The atomic charge on atom A at the nth iteration, QA(n), is obtained by17,20,23
| 3 |
where , which was introduced by No et al. in the MPEOE method,20 represents the initial atomic charge before the iterative procedure starts. The index B sums over all the atoms covalently bonded to atom A, whereas the index n sums over the number of iterations until the convergence criterion < 10−6 e is satisfied, where e is the electronic charge. The quantity is obtained from eq 1.
In these calculations, the electronegativity of an atom i at the nth iteration is described as a linear function of the atomic charge as in the MPEOE20 and GDAC23 methods
| 4 |
where ai is the electronegativity of the neutral atom and bi is a coefficient describing the response of the electronegativity of the atom i to the changes in electron density. The quantity is obtained from eq 3. For given sets of parameters ai and bi for each atom type, the atomic charge QA on an atom A can be calculated by an iterative procedure using eqs 1–4.
In the MPEOE method,20 the damping factors and the sets of electronegativity parameters ai and bi were varied to reproduce experimental dipole moments and quadrupole moments of organic molecules with various functional groups. In the GDAC method,23 the sets of electronegativity parameters ai and bi were, however, derived only by fitting to the three components of the dipole moment and the total dipole moment computed at the B3LYP/6-31G(d,p) level of theory for 50 molecules representing the backbone and side chains of peptides and proteins. The dipole moments calculated at the B3LYP/6-31G(d,p) level were found to be in good agreement with experimental values, as shown in Table 1 of ref 23.
TABLE 1.
Comparison of Dipole Moments for Extended Conformations of Ac–X–NHMe in the Training Set Computed by the B3LYP, EPAC, and GDAC Methodsa
| X | confb | μB3LYPc | d | Δe | μEPACf | Δg | μGDACh | Δi |
|---|---|---|---|---|---|---|---|---|
| Ala | E | 2.92 | 2.97 | 0.05 | 2.95 | 0.03 | 2.41 | 0.51 |
| Val | Eg+g+ | 2.76 | 2.62 | 0.14 | 2.75 | 0.00 | 2.28 | 0.47 |
| Leu | Eg−t | 2.27 | 2.46 | 0.19 | 2.72 | 0.45 | 2.14 | 0.14 |
| Ile | Ett | 2.79 | 2.71 | 0.08 | 2.76 | 0.03 | 2.32 | 0.46 |
| Gly | E | 3.25 | 3.13 | 0.12 | 3.18 | 0.07 | 2.62 | 0.62 |
| Pro | tCdj | 2.65 | 3.06 | 0.41 | 2.80 | 0.14 | 2.78 | 0.13 |
| Cys | Etg+ | 1.72 | 2.52 | 0.80 | 2.55 | 0.83 | 1.32 | 0.39 |
| Met | Etg+ | 1.17 | 2.05 | 0.88 | 2.33 | 1.17 | 0.99 | 0.18 |
| His(δ)k | Etg+ | 2.74 | 2.39 | 0.35 | 2.24 | 0.50 | 2.25 | 0.48 |
| His(ε)k,l | Etg− | 4.55 | 3.83 | 0.72 | 3.55 | 1.00 | 3.29 | 1.25 |
| Phe | Etg+ | 2.71 | 2.75 | 0.03 | 2.68 | 0.03 | 2.21 | 0.50 |
| Tyr | Eg+g+ | 1.62 | 2.23 | 0.61 | 2.31 | 0.69 | 1.37 | 0.24 |
| Trp | Etg− | 4.24 | 2.69 | 1.55 | 2.60 | 1.64 | 3.98 | 0.25 |
| Asn | Etg− | 0.82 | 0.84 | 0.02 | 0.77 | 0.05 | 0.97 | 0.14 |
| Gln | Eg−g− | 2.88 | 2.87 | 0.01 | 2.51 | 0.37 | 2.39 | 0.49 |
| Ser | Etg+ | 1.68 | 1.36 | 0.33 | 1.48 | 0.20 | 1.32 | 0.37 |
| Thr | Etg+ | 1.69 | 1.44 | 0.25 | 1.30 | 0.39 | 1.27 | 0.43 |
| Lys | Eg+t | 3.99 | 3.98 | 0.01 | 3.97 | 0.02 | 3.61 | 0.38 |
| Arg | Etg+ | 5.85 | 4.59 | 1.27 | 4.52 | 1.33 | 4.82 | 1.04 |
| Asp | Etc | 2.60 | 2.25 | 0.36 | 2.56 | 0.04 | 2.05 | 0.55 |
| Glu | Eg−g− | 2.32 | 2.19 | 0.14 | 2.25 | 0.07 | 1.81 | 0.52 |
| Lys+l | Eg−g− | 11.08 | 10.90 | 0.18 | 11.12 | 0.04 | 16.52 | 5.44 |
| Arg+l | Eg−g− | 11.99 | 11.43 | 0.56 | 12.37 | 0.38 | 19.90 | 7.91 |
| His+l | Eg−g+ | 9.61 | 8.58 | 1.02 | 9.72 | 0.11 | 12.69 | 3.08 |
| Asp−l | Ett | 8.70 | 7.98 | 0.72 | 8.76 | 0.06 | 12.57 | 3.88 |
| Glu−l | Etg+ | 9.41 | 8.79 | 0.63 | 9.65 | 0.24 | 13.92 | 4.50 |
| 0.44m | 0.38m | 1.32m | ||||||
| 0.60n | 0.59n | 2.34n |
Units in Debyes. The 26 representative residues of the training set are listed in Table S4 of the Supporting Information.
Conformational letter codes. Each code represents the backbone expressed by a capital letter depending on its torsion angles Ф and ψ, and two side-chain torsion angles χ1 and χ2. See the text for definition of torsion angles.38,39
Dipole moments calculated directly at the B3LYP/6-31G(d,p)//HF/6-31G(d,p) level.
Dipole moments calculated from atomic charges obtained at the B3LYP/6-31G(d,p)//HF/6-31G(d,p) level.
Absolute differences between and μB3LYP values.
Dipole moments calculated by the EPAC method.
Absolute differences between μEPAC and μB3LYP values.
Dipole moments calculated by the GDAC method of Cho et al.23
Absolute differences between μGDAC and μB3LYP values.
Pro with the trans prolyl peptide bond and the down puckering.
His(δ) and His(ε) are isomers of the His residue depending on its protonation at Nδ and Nε, respectively.
Initial atomic charges were obtained by a trial-and-error procedure starting from the corresponding values in ref 23 to reproduce the B3LYP/6-31G(d,p) atomic charges for only these residues; see Figure S1 of the Supporting Information.
Mean values over all residues.
Rms deviations over all residues.
Training and Test Sets
Although the MPEOE20 and GDAC23 charges satisfactorily reproduced experimental dipole moments and quadrupole moments, and quantum-mechanically computed dipole moments of small organic molecules, respectively, it was found that these two methods occasionally produced unacceptable atomic charges and/or dipole moments for larger molecules such as terminally blocked amino acids (see Table 1 for comparison of dipole moments for Ac–X–NHMe, X = any neutral or charged residue, computed at the B3LYP/6-31G(d,p) level and by the GDAC method, and Table S2 of the Supporting Information for Ac–Ala–NHMe). In addition, whereas the Mulliken charges depend on the molecular conformation, the degree of dependence is relatively smaller than that found for ESP-fitted charges (see Table S3 of the Supporting Information). To avoid these two problems, we chose extended conformations of Ac–X–NHMe (X = any neutral or charged residue, except for Pro), shown in Table 1 and in boldface in Table S4 of the Supporting Information as a training set to derive the electronegativity parameters ai and bi. Because the Pro residue does not have an extended conformation, the tCd conformation was chosen as a representative one.1c
Several representative conformations were selected for each residue X of Ac–X–NHMe, not used for parametrization, and their dipole moments, computed with the EPAC charges, were compared with those calculated directly at the B3LYP/6-31G-(d,p) level in order to demonstrate the reliability of the EPAC method. In particular, the dipole moments of representative conformations of Ac–(Ala)n–NHMe (n = 2−6) computed with both the EPAC charges and also directly at the B3LYP/6-31G-(d,p) level are compared to examine the transferability of the present method for longer peptide chains (Table S5 of the Supporting Information).
The initial representative conformations for each residue were taken from the local minima for Ac–X–NHMe (X = any neutral residue)1c,38 optimized by the ECEPP21b and ECEPP31c force fields. All local minima for Ala, Gly, and Pro residues found by the ECEPP force fields were taken as initial conformations. For other neutral residues, however, local minima were chosen if they have C or E backbone conformations39 and different χ1 or χ2 side-chain conformations. Each conformation is represented by a letter code composed of a capital letter plus two side-chain codes depending on its backbone torsion angles ϕ and ψ, and side-chain torsion angles χ1 or χ1, according to the definition suggested by Zimmermann et al.39 All selected conformations of neutral His, Lys, Arg, Asp, and Glu residues were used as starting points for optimizations of charged His+, Lys+, Arg+, Asp−, and Glu− residues, respectively. For Ac–(Ala)2–NHMe and Ac–(Ala)3–NHMe, the initial representative conformations were generated by a combination of C, E, and A conformations for Ac–Ala–NHMe. Three representative conformations, for which every residue has the same A (or C or E) backbone conformation, were constructed for each peptide of Ac–(Ala)n–NHMe (n = 4−6). Then, these initial conformations were optimized using the ECEPP3 force field1c. In addition, mutants of extended Ac–Ala–NHMe with different N- and C-terminal groups were included in the training set only to derive the parameters for these terminal groups.
Quantum Mechanical Calculations
All representative conformations for Ac–X–NHMe, Ac–(Ala)n–NHMe (n = 2−6), and Ac–Ala–NHMe mutants with different N- and C-terminal groups obtained from the ECEPP3 force field were optimized at the HF/6-31G(d,p) level of theory using the Gaussian 9840 and 0341 packages. This level has previously been usedsuccessfullyforconformationalanalysesofAlaoligopeptides42–44 and in developing potential parameters of force fields.6b,45 B3LYP/6-31G(d,p) single-point calculations were carried out for all representative conformations optimized at the HF/6-31G-(d,p) level. The dipole moments for small molecules representing the backbone and side chains of peptides and proteins calculated at the B3LYP/6-31G(d,p) level were found to be in good agreement with experimental values.23 The Mulliken charges and dipole moments for these representative conformations computed at the B3LYP/6-31G(d,p)//HF/6-31G(d,p) level were used for deriving the electronegativity parameters ai and bi in eq 4 and in testing the quality of the method and its parameters. All representative conformations for Ac–X–NHMe and Ac–(Ala)n–NHMe (n = 2−6), optimized at the HF/6-31G(d,p) level, are listed in Tables S4 and S5, respectively, of the Supporting Information.
Parametrization Procedure
For given electronegativity parameters ai and bi for each type of atom in a molecule, the conformation-dependent atomic charges were calculated by using eqs 1–4. For most residues and end groups, the initial atomic charges Q(0) in eq 3 were chosen to be zero. However, for some residues such as His(Є) and charged residues (Lys+, Arg+, His+, Asp−, and Glu−) and for some N- and C-terminal groups, which are listed in Figure S1 of the Supporting Information, finite initial atomic charges were assigned. This was necessary in order to avoid large, sometimes oscillatory, changes in the electronegativity function, often preventing convergence of the procedure, as in the MPEOE20b and GDAC23 methods. The choice of these initial atomic charges was arbitrary, but their values (listed in Figure S1 of the Supporting Information) were obtained by a trial-and-error procedure, starting from the corresponding values in ref 23, to reproduce the B3LYP/6-31G(d,p) atomic charges during the optimization described below.
The parameters ai and bi for the training set were obtained by minimizing the following function S with the secant unconstrained minimization solver (SUMSL)46 with given sets of initial atomic charges
| 5 |
where the index k refers to a molecule in the training set, and i to an atom in molecule k; wik, , and are the statistical weight, EPAC charge, and B3LYP/6-31G(d,p) charge for atom i in molecule k, respectively. wik was taken as 1.000 during minimization. For those residues and end groups having nonzero initial atomic charges, the assignment of initial atomic charges and the optimization of parameters ai and bi were repeated until the difference between the computed charge and the corresponding B3LYP/6-31G(d,p) charge for each atom becomes less than 0.01 e.
The minimization of the function S, however, encounters the multiple-minima problem. It is not easy to find the best set of parameters if a large number of parameters are involved in the minimization procedure because the procedure is likely to be trapped in local minima. To overcome this problem and to obtain the best set of parameters depending on the chemical structure of each side chain, we first derived the parameters for aliphatic (Ala, Val, Leu, and Ile), Gly, and Pro residues, which correspond to the parameters for backbone and aliphatic groups of side chains. The sets of parameters for side chains of the other residues were optimized with the parameters from these six residues fixed. In this procedure, the residues not employed in the first optimization were classified into seven groups: (1) Asn, Gln, Ser, and Thr; (2) Cys and Met; (3) Asp and Glu; (4) Lys and Arg; (5) aromatic His(δ), His(Є), Phe, Tyr, and Trp; (6) positively charged Lys+, Arg+, and His+; (7) negatively charged Asp−, and Glu−. Then, all parameters ai and bi were reoptimized simultaneously to avoid accumulation of errors and to provide consistency in the parameters with initial atomic charges obtained in the previous optimization. The parameters ai and bi obtained from the GDAC method23 were used as initial values for optimization in the present EPAC method. In addition, the parameters for the N- and C-terminal groups were derived by a similar procedure by using the extended Ac–Ala–NHMe mutants with the parameters for the Ala residue fixed. Thus, we employed a total of 69 sets of atomic parameters ai and bi to reproduce 954 B3LYP/6-31G(d,p) atomic charges for Ac–X–NHMe (X = 21 neutral and 5 charged residues) and 10 mutants of Ac–Ala–NHMe with different end groups used in the training set.
Results and Discussion
Torsion angles for backbone and side chain, relative conformational energies, and dipole moments of representative conformations for Ac–X–NHMe and Ac–(Ala)n–NHMe (n = 2−6) calculated at the B3LYP/6-31G(d,p)//HF/6-31G(d,p) level, and their dipole moments computed by the EPAC method, are listed in Tables S4 and S5, respectively, of the Supporting Information.
B3LYP Charges and Dipole Moments
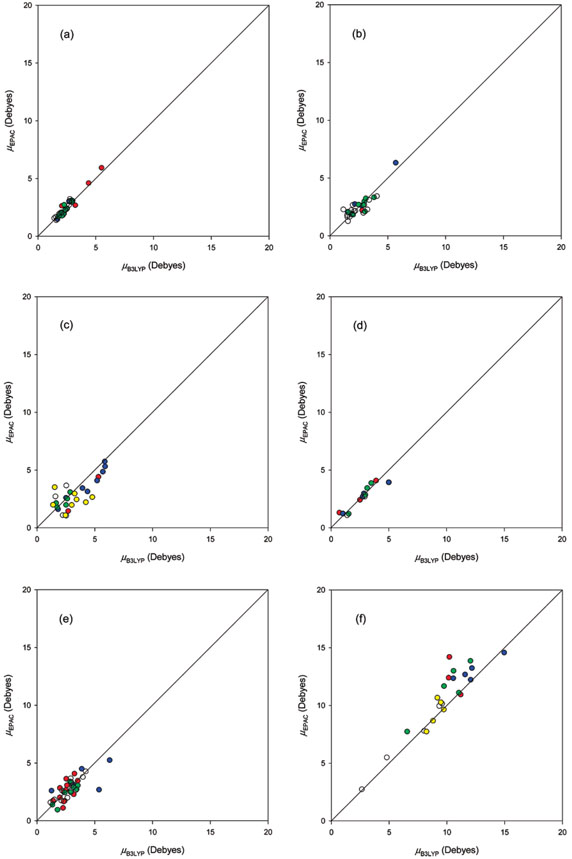
First, we compared the B3LYP/6-31G(d,p) directly computed dipole moments μB3LYP with the dipole moments computed by using B3LYP/6-31G(d,p) atomic charges for 21 neutral and 5 charged representative conformations of Ac–X–NHMe in the training set, which are shown in Table 1 and Figure 1a. The mean absolute difference (mad) between μB3LYP and values is 0.44 D and its rmsd is 0.60 D, although the absolute differences (ad's) for Trp, Arg, and His+ residues are larger than 1.00 D. These results suggest that the B3LYP/6-31G(d,p) Mulliken charges reproduce the dipole moment calculated at the B3LYP/6-31G(d,p) level well and can be used in deriving the EPAC parameters. Comparison of panels b and c in Figure 1 shows the improvement of the EPAC parameters over those of GDAC.
Figure 1.
Comparison of dipole moments μB3LYP computed directly at the B3LYP/6-31G(d,p) level with dipole moments , μEPAC, and μGDAC calculated with B3LYP/6-31G(d,p) Mulliken, EPAC, and GDAC charges, respectively, for representative conformations of Ac–X–NHMe (X = 21 neutral and 5 charged residues) in the training set: (a) vs μB3LYP; (b) μEPAC vs μB3LYP; (c) μGDAC vs μB3LYP. Units in Debyes. The same conformations shown in boldface in Table S4 of the Supporting Information were used in panels a–c.
Optimized Sets of Parameters
The sets of parameters ai and bi for the EPAC method, optimized for 26 representative conformations of Ac–X–NHMe in the training set, are listed in Table 2, in which the sets of parameters for N- and C-terminal groups are also listed. The dipole moments μEPAC calculated by using the EPAC charges for these representative conformations are compared with the B3LYP/6-31G(d,p) dipole moments μB3LYP in Table 1 and Figure 1b. The mad and rmsd between μEPAC and μB3LYP values are 0.38 and 0.59 D, respectively, although the ad's for Met, Trp, and Arg residues are larger than 1.00 D. This shows that the EPAC charges provide somewhat better dipole moments than the B3LYP/6-31G(d,p) charges, with the better results for the Val, Pro, Asp, Lys+, Arg+, His+, Asp−, and Glu− residues making the main contribution to the mad and rmsd. In addition, the dipole moments μGDAC, calculated using the atomic charges from the GDAC method23 for these 26 representative conformations, are compared with the B3LYP/6-31G(d,p) dipole moments μB3LYP in Table 1 and Figure 1c. The mad and rmsd between μGDAC and μB3LYP values are 1.32 and 2.34 D, respectively, to which the charged residues contribute the larger deviations.
TABLE 2.
Atomic Types and Optimized Parameters for Their Atomic Electronegativities
| atomic type |
description | aia | bia |
|---|---|---|---|
| H1 | aliphatic H | 2.1917 | 0.0489 |
| H2 | Hα of the peptide backbone | 2.5062 | −1.2773 |
| H3 | H of the Pro ring | 0.8253 | 12.7055 |
| H4 | aromatic H | 1.0280 | 13.4508 |
| H5 | amine H | 2.4868 | 1.7882 |
| H6 | amide H | 1.1118 | 5.7519 |
| H7 | H of OH | −0.5001 | 10.5861 |
| H8 | H of COOH | 2.8982 | 1.6472 |
| H9 | H of SH | 1.9730 | 0.4021 |
| H10 | H of H−N in His and Trp side chains | −2.1730 | 16.8150 |
| H11 | H attached to H2N+ | 1.7926 | 0.8722 |
| H12 | H of His+ side chain | 2.6350 | 0.7970 |
| H13 | H of the formyl amino end group | 3.1946 | −0.5623 |
| H14 | Hα when the N-terminal group is H2N+ | 2.2773 | −1.0843 |
| H15 | Hα when the C-terminal group is COO− | 1.6636 | 4.0451 |
| C1 | sp3 C of CH3 | 2.5925 | 1.2129 |
| C2 | sp3 C of CH2 | 2.4955 | 1.5058 |
| C3 | sp3 C of CH | 2.3457 | 1.3918 |
| C4 | sp3 Cα for non-Pro residues | 2.4504 | 0.6371 |
| C5 | sp3 C attached to C═O | 2.4158 | 0.7327 |
| C6 | sp3 C attached to amide N−H | 2.5234 | 1.4027 |
| C7 | sp3 C of the Pro ring | 2.6156 | 0.4805 |
| C8 | sp3 Cβ attached to the aromatic ring | 2.6586 | 1.6877 |
| C9 | sp3 C of CH2 attached to OH of Ser | 2.3773 | 0.5901 |
| C10 | sp3 C of CH attached to OH of Thr | 2.3507 | 0.5820 |
| C11 | sp3 C of CH2 or CH3 attached to S | 2.4492 | 0.2428 |
| C12 | sp3 C attached to C═O of the side chain in Asn, Gln, Asp, and Glu |
2.3983 | 0.7665 |
| C13 | sp2 C of C═O | −5.1345 | 14.1482 |
| C14 | aromatic C | 2.4449 | 0.4126 |
| C15 | fused aromatic C | 2.3480 | 0.1250 |
| C16 | aromatic C attached to sp3 C | 2.2973 | 0.6777 |
| C17 | aromatic C attached to OH of Tyr | 2.0084 | 1.9595 |
| C18 | Cδ of His and Cδ1 of Trp | 2.1780 | 4.8280 |
| C19 | Cε of His | 3.8312 | −3.1644 |
| C20 | Cε of Arg | 2.3846 | 1.5047 |
| C21 | Cζ of Arg | −3.4851 | 9.6585 |
| C22 | sp3 C attached to COO− | 2.7051 | 1.8741 |
| C23 | sp3 C attached to N+ | 3.5982 | 11.6359 |
| C24 | sp2 C of COO− | −1.7286 | 7.7191 |
| C25 | Cζ of Arg+ | 2.4697 | 1.0926 |
| C26 | Cζ of Arg+ | −14.8197 | 21.5072 |
| C27 | Cγ of His+ | 0.2430 | 8.0356 |
| C28 | Cδ and Cε of His+ | 2.7851 | 0.1440 |
| C29 | sp3 tertiary C of the t-Boc amino end group | 0.7942 | 5.5220 |
| C30 | sp3 C of CH2 or CH3 in OMe and OEt carboxylic end groups |
2.3756 | −0.0071 |
| C31 | sp2 C of C═O for the first residue when the N-terminal group is t-Boc |
−5.1838 | 8.9183 |
| C32 | sp2 C of C═O in OMe and OEt carboxylic end groups |
−5.0094 | 11.3808 |
| C33 | Cα when the N-terminal group is H2N+ | 2.2800 | 0.8454 |
| C34 | Cβ when the N-terminal group is H2N+ | 2.4330 | −1.5951 |
| C35 | C of C═O for the first residue when the N-terminal group is H2N+ |
−4.1541 | 11.3556 |
| C36 | Cα when the C-terminal group is COO− | 2.2838 | 5.2758 |
| N1 | sp3 amine N | 2.4955 | −8.9472 |
| N2 | sp2 amide N | 2.9703 | −0.1802 |
| N3 | sp2 amide N of the Pro ring | 3.0683 | -0.3431 |
| N4 | sp2 Nε and Nη2 of Arg | 2.8267 | −0.8363 |
| N5 | sp2 Nη1 of Arg | 2.5473 | 0.0262 |
| N6 | aromatic Nη of His and Trp | 3.2388 | 1.3470 |
| N7 | aromatic N of His and Trp | 4.4553 | 6.1260 |
| N8 | N+ of Lys+ | 3.4576 | 2.4448 |
| N9 | N+ of Arg+ | 7.4806 | 10.3003 |
| N10 | N+ of His+ | 9.4721 | 13.8330 |
| N11 | N of the NH amino end group | 2.6867 | −2.6812 |
| O1 | sp3 O of OH | 2.3877 | −2.5413 |
| O2 | sp3 O of COOH | 4.0066 | −1.5831 |
| O3 | sp3 O of the t-Boc amino end group | 3.3914 | −0.6520 |
| O4 | sp2 O of C═O | 4.2182 | −1.6118 |
| O5 | sp2 O of COO− | 2.7582 | 0.4253 |
| O6 | sp3 O of OMe and OEt carboxylic end groups | 2.9383 | 0.0708 |
| S1 | S in thiol, sulfide, and disulfide | 2.2551 | 2.4403 |
Tests for Other Conformations of Ac–X–NHMe Not Used for Parametrization
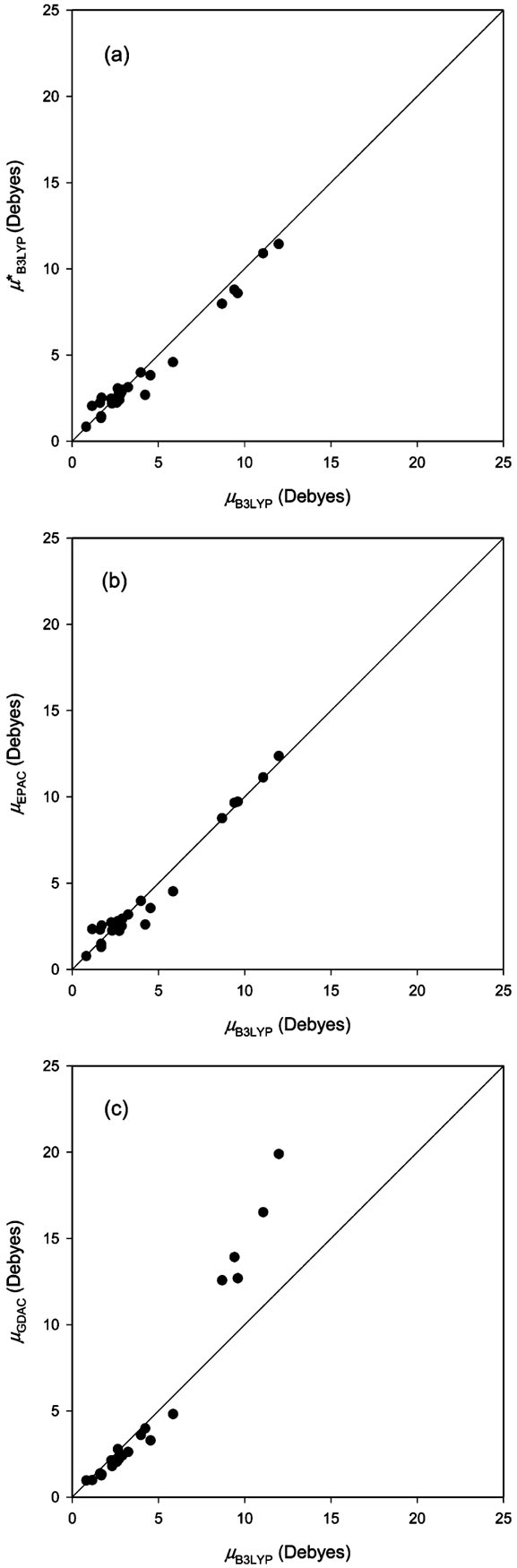
The optimized sets of parameters ai and bi for the EPAC method were tested for their applicability to other conformations of Ac–X–NHMe not used for parametrization. The mad's and rmsd's between the μEPAC and μB3LYP values for a total of 172 representative conformations of Ac–X–NHMe not used for parametrization are listed in Table 3, and their dipole moments are plotted in Figure 2. The overall mad and rmsd are calculated to be 0.54 and 0.79 D, respectively, which are similar in magnitude to those estimated for the training set. The calculated mad's and rmsd's for 38 aliphatic, 31 nonpolar, 27 aromatic, 13 polar, 40 charged-neutral, and 23 charged-ionized conformations are 0.19 and 0.25 D, 0.38 and 0.49 D, 0.87 and 1.05 D, 0.30 and 0.40 D, 0.55 and 0.72 D, and 1.03 and 1.41 D, respectively. Large deviations are found for aromatic and charged-ionized residues.
TABLE 3.
Mean Absolute Deviations (MADs) and Root-Mean-Square Deviations (RMSDs) of Dipole Moments for Ac–X–NHMe, Not Used for Parametrization, Calculated by the EPAC Method
| group | X | no.a | madb | rmsdc | |
|---|---|---|---|---|---|
| aliphatic | Ala | 5 | 0.41 | 0.44 | |
| Val | 4 | 0.17 | 0.20 | ||
| Leu | 15 | 0.14 | 0.20 | ||
| Ile | 14 | 0.18 | 0.22 | ||
| av.d | 0.19 | 0.25 | |||
| nonpolar | Gly | 2 | 0.58 | 0.58 | |
| Pro | 4 | 0.47 | 0.52 | ||
| Cys | 10 | 0.27 | 0.38 | ||
| Met | 15 | 0.41 | 0.54 | ||
| av.d | 0.38 | 0.49 | |||
| aromatic | His(δ)k | 2 | 1.07 | 1.09 | |
| His(ε)k | 8 | 0.58 | 0.71 | ||
| Phe | 5 | 0.27 | 0.34 | ||
| Tyr | 4 | 1.22 | 1.23 | ||
| Trp | 8 | 1.30 | 1.45 | ||
| av.d | 0.87 | 1.05 | |||
| polar | Asn | 3 | 0.28 | 0.36 | |
| Gln | 4 | 0.36 | 0.54 | ||
| Ser | 4 | 0.28 | 0.30 | ||
| Thr | 2 | 0.27 | 0.28 | ||
| av.d | 0.30 | 0.40 | |||
| charged-neutral | Lys | 15 | 0.53 | 0.64 | |
| Arg | 5 | 1.15 | 1.44 | ||
| Asp | 8 | 0.42 | 0.49 | ||
| Glu | 12 | 0.40 | 0.45 | ||
| av.d | 0.55 | 0.72 | |||
| charged-ionized | Lys+ | 3 | 2.16 | 2.64 | |
| Arg+ | 5 | 0.91 | 1.08 | ||
| His+ | 5 | 1.49 | 1.70 | ||
| Asp− | 5 | 0.45 | 0.50 | ||
| Glu− | 5 | 0.60 | 0.79 | ||
| av.d | 1.03 | 1.41 | |||
| overall av.e | 0.54 | 0.79 |
Number of conformations considered.
Mean absolute deviations from dipole moments calculated at the B3LYP/6-31G(d,p)//HF/6-31G(d,p) level.
Root-mean-square deviations from dipole moments calculated at the B3LYP/6-31G(d,p)//HF/6-31G(d,p) level.
Average values for each group.
Overall mean values for all 172 conformations.
Figure 2.
Comparison of dipole moments μEPAC, calculated with EPAC charges, with dipole moments μB3LYP computed directly at the B3LYP/6-31G(d,p) level for 172 representative conformations of Ac–X–NHMe not used for parametrization; units in Debyes: (a) aliphatic residues Ala (red), Val (blue), Leu (green), and Ile (open); (b) nonpolar residues Gly (red), Pro (blue), Cys (green), and Met (open); (c) aromatic residues His(δ) (red), His(ε) (blue), Phe (green), Tyr (open), and Trp (yellow); (d) polar residues Asn (red), Gln (blue), Ser (green), and Thr (open); (e) charged-neutral residues Lys (red), Arg (blue), Asp (green), and Glu (open); (f) charged-ionized residues Lys+ (red), Arg+ (blue), His+ (green), Asp− (open), and Glu− (yellow).
Tests for Longer Peptides
The dipole moments of representative conformations for Ac–(Ala)n–NHMe (n = 2−6), computed with the EPAC charges and at the B3LYP/6-31G-(d,p) level, are compared to assess the transferability of the present method for longer peptide chains. The mad's and rmsd's between μEPAC and μB3LYP values for these representative conformations are listed in Table 4 and their dipole moments are plotted in Figure 3. The overall mad and rmsd between μEPAC and μB3LYP values for these 23 representative conformations are estimated to be 0.95 and 1.40 D, respectively, to which the large deviations of Ac–(Ala)n–NHMe (n = 4–6) contribute dominantly. However, the mad's and rmsd's for Ac–(Ala)2–NHMe and Ac–(Ala)3–NHMe are only 0.19 and 0.20 D and 0.36 and 0.52 D, respectively. It should be noted that the EPAC method reasonably predicts the increase of dipole moment with the increase of chain length, although there are increasing errors with increasing n. In particular, the smaller deviations are found for extended conformations with the same E backbone conformation for every residue than for folded conformations with the same C or A backbone conformations for every residue for Ac–(Ala)n–NHMe (n = 4−6), which may imply that nonadditive effects, not considered here, would operate on folded structures of longer peptides.
TABLE 4.
Mean Absolute Deviations (MADs) and Root-Mean-Square Deviations (RMSDs) of Dipole Moments for Ac–(Ala)n–NHMe (n = 2−6) Not Used for Parametrization, Calculated by the EPAC Method
Figure 3.
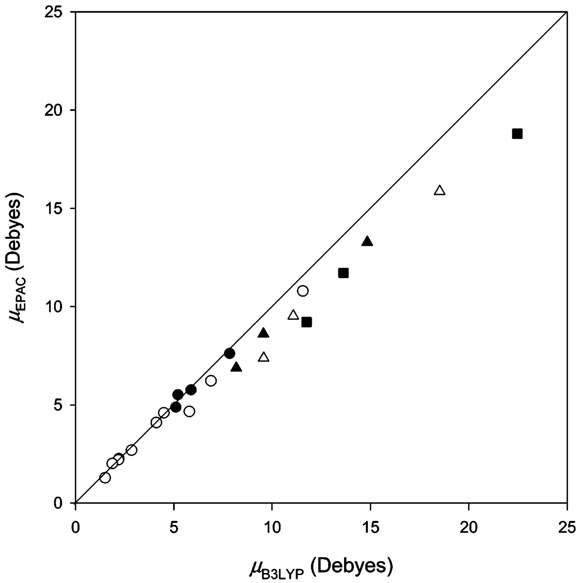
Comparison of dipole moments μEPAC calculated with EPAC charges with dipole moments μB3LYP computed directly at the B3LYP/6-31G(d,p) level for representative conformations of Ac–(Ala)n–NHMe (n = 2−6) not used for parametrization, units in Debyes: n = 2, ●; n = 3, ○; n = 4, ▲; n = 5, ∆; n = 6, ■.
Transferability and Neutrality of EPAC Charges
As seen for representative conformations of Ac–X–NHMe in the training set and for those not for used for parametrization, the EPAC charges reproduced the B3LYP/6-31G(d,p) dipole moments well, which suggests transferability of the charges obtained with the EPAC method. In particular, the EPAC charge for a specific type of atom does not depend on its position in the sequence or on the length of the sequence, as seen for Ac–Ala–NHMe and Ac–(Ala)3–NHMe in Table S1 of the Supporting Information. In addition, charge neutrality holds for any Ala residue of these two peptides. Thus, these results suggest that the EPAC charges derived from B3LYP/6-31G(d,p) Mulliken populations can be used reliably for conformational analysis of peptides and proteins.
For another test of transferability of the EPAC method to small molecules, we calculated the atomic charges and dipole moment of the water molecule optimized at the HF/6-31(d,p) level using the parameters of atom types H7 and O1 for the OH group (Table 2). The calculated EPAC charges are −0.7136 and +0.3568 e for O and H of water, respectively, and its dipole moment is computed to be 1.95 D. At the same B3LYP/6-31-(d,p)//HF/6-31(d,p) level, the corresponding ESP-fitted charges are computed to be −0.7340 and +0.3670 e, respectively, by using the Merz–Singh–Kollman scheme12c,12f and by constraining the charges to reproduce the dipole moment, and its dipole moment is computed to be 2.00 D. The EPAC charges of the water molecule are quite similar to the ESP-fitted charges, but the EPAC dipole moment is a little better than that from ESP-fitted charges because the experimental dipole moment is 1.84 D.
Conformational Variations of Atomic Charges
As seen for Ac–Ala–NHMe and Ac–(Ala)3–NHMe with the extended backbone conformation in Table S1 of the Supporting Information, the atomic charge for a specific type of atom does not depend on its position in the sequence or on the length of the sequence. Although atomic charges could vary from conformation to conformation, the deviations are quite small. For example, for local minima (C, E, D, C*, A*, and F*, shown in Table S4 of the Supporting Information) of Ac–Ala–NHMe, the mean atomic charges for O and C of the acetyl end group, N and H of the Ala residue, and N and H of the NHMe end group (refer to Table S2 of the Supporting Information for atomic definitions) are computed as −0.5265, +0.5671, −0.5110, +0.2757, −0.5263, and +0.2755 e, respectively. Although these atoms are involved in the formation of intramolecular hydrogen bonds for some conformations, their deviations are calculated to be ±0.008, ±0.005, ±0.004, ±0.0002, ±0.002, and ±0.0005 e, respectively. The EPAC dipole moments for these local minima C, E, D, C*, A*, and F* are calculated to be 1.96, 2.95, 4.60, 2.68, 5.93, and 2.63 D, respectively, shown in Table S4 of the Supporting Information. Thus, it can be said that the different dipole moments for the different conformations are caused by the configuration of atoms in a molecule and not by the different atomic charges depending on conformation.
Computation Time
The mean CPU time required for the calculation of the atomic charges and dipole moment by the EPAC method for a single conformation of Ac–(Ala)6–NHMe is less than 1 second on a PC with an Intel Core2Duo T7200 (2.0 GHz) processor.
Conclusions
An EPAC method is presented to calculate atomic charges of peptides and proteins derived from Mulliken electronic populations for terminally blocked amino acids (Ac–X–NHMe) calculated at the B3LYP/6-31G(d,p)//HF/6-31G(d,p) level of theory. The EPAC atomic charges are calculated by using the partial-equalization-of-atomic electronegativities method with electronegativity parameters and damping factors given by interatomic distances between covalently bonded atoms in a molecule.
For Ac–X–NHMe, the dipole moments μEPAC obtained with EPAC charges agree well with the dipole moments μB3LYP calculated directly at the B3LYP/6-31G(d,p) level for both the conformations in the training set and the conformations not used for parametrization. For Ac–(Ala)n–NHMe (n = 2−6), the EPAC method predicts the increase of dipole moment with the increase of chain length reasonably well, although the deviations from the μB3LYP values are somewhat larger.
For Ac–Ala–NHMe and Ac–(Ala)3–NHMe, it was found that the EPAC charge for a specific type of atom does not depend on its position in the sequence or on the length of the sequence, and that charge neutrality holds for any Ala residue of these two peptides. Thus, these results suggest that the EPAC charges derived from B3LYP/6-31G(d,p) Mulliken populations can be used reliably for conformational analysis of peptides and proteins.
Acknowledgment
The authors thank B. J. Byun for assistance in preparing the tables and figure of the Supporting Information. This research was supported by Grant No. MCB05-41633 from the National Science Foundation and No. GM-14312 from the National Institutes of Health.
Supporting Information Available: Atomic charges for Ac–Ala–NHMe and Ac–(Ala)3–NHMe calculated by the B3LYP/6-31G(d,p), EPAC, GDAC, and ESP methods; torsion angles, relative conformational energies, and dipole moments of representative conformations for Ac–Ala–NHMe and Ac–(Ala)n–NHMe (n = 2−6) calculated at the B3LYP/6-31G(d,p)//HF/6-31G(d,p) level and their dipole moments computed by the EPAC method; initial atomic charges for His(ε), charged residues, and some N- and C-terminal groups. This material is available free of charge via the Internet at http://pubs.acs.org.
References and Notes
- 1.Momany FA, McGuire RF, Burgess AW, Scheraga HA. J. Phys. Chem. 1975;79:2361. (a) [Google Scholar]; Némethy G, Pottle MS, Scheraga HA. J. Phys. Chem. 1983;87:1883. (b) [Google Scholar]; Némethy G, Gibson KD, Palmer KA, Yoon CN, Paterlini G, Zagari A, Rumsey S, Scheraga HA. J. Phys. Chem. 1992;96:6472. (c) [Google Scholar]
- 2.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J. Comput. Chem. 1983;4:187. (a) [Google Scholar]; MacKerell AD, Jr., Bashford D, Bellott M, Dunbrack RL, Jr., Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, III., Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiórkiewicz-Kuczera J, Yin D, Karplus M. J. Phys. Chem. B. 1998;102:3586. doi: 10.1021/jp973084f. (b) [DOI] [PubMed] [Google Scholar]
- 3.Weiner SJ, Kollman PA, Nguyen DT, Case DA. J. Comput. Chem. 1986;7:230. doi: 10.1002/jcc.540070216. (a) [DOI] [PubMed] [Google Scholar]; Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Jr., Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J. Am. Chem. Soc. 1995;117:5179. (b) [Google Scholar]
- 4.van Gunsteren WF, Berendsen HJC. Groningen molecular simulation (GROMOS) library manual. The Netherlands: 1987. (a), Biomos, Nijenborgh 16, 9747 AG Groningen. [Google Scholar]; Scott WRP, Hünenberger PH, Tironi IG, Mark AE, Billeter SR, Fennen J, Torda AE, Huber T, Krüger P, van Gunsteren WF. J. Phys. Chem. A. 1999;103:3596. (b) [Google Scholar]
- 5.Dauber-Osguthorpe P, Roberts VA, Osguthorpe DJ, Wolff J, Genest M, Hagler AT. Proteins. 1988;4:31. doi: 10.1002/prot.340040106. [DOI] [PubMed] [Google Scholar]
- 6.Jorgensen WL, Maxwell DS, Tirado-Rives J. J. Am. Chem. Soc. 1996;118:11225. (a) [Google Scholar]; Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL. J. Phys. Chem. B. 2001;105:6474. (b) [Google Scholar]
- 7.Mulliken RS. J. Chem. Phys. 1955;23:1833. [Google Scholar]
- 8.Löwdin P-O. Adv. Quantum Chem. 1970;5:185. [Google Scholar]
- 9.Reed AE, Weinstock RB, Weinhold F. J. Chem. Phys. 1985;83:735. [Google Scholar]
- 10.Bader RFW, Beddall PM, Cade PE. J. Am. Chem. Soc. 1971;93:3095. [Google Scholar]
- 11.Cioslowski J. J. Am. Chem. Soc. 1989;111:8333. [Google Scholar]
- 12.Momany FA. J. Phys. Chem. 1978;82:592. (a) [Google Scholar]; Cox SR, Williams DE. J. Comput. Chem. 1981;2:304. (b) [Google Scholar]; Singh UC, Kollman PA. J. Comput. Chem. 1984;5:129. (c) [Google Scholar]; Chirlian LE, Francl MM. J. Comput. Chem. 1987;8:894. (d) [Google Scholar]; Breneman CM, Wiberg KB. J. Comput. Chem. 1990;11:361. (e) [Google Scholar]; Besler BH, Merz KM, Jr., Kollman PA. J. Comput. Chem. 1990;11:431. (f) [Google Scholar]; Bayly CI, Cieplak P, Cornell WD, Kollman PA. J. Phys. Chem. 1993;97:10269. (g) [Google Scholar]
- 13.Wiberg KB, Rablen PR. J. Comput. Chem. 1993;14:1504. [Google Scholar]
- 14.Machrach SM. In: In Reviews in Computational Chemistry. Lipkowwitz KB, Boyd DB, editors. VCH Publishers, Inc.; New York: 1994. Chapter 3. [Google Scholar]
- 15.Storer JW, Giesen DJ, Cramer CJ, Truhlar DG. J. Comput.-Aided Mol. Design. 1995;9:87. doi: 10.1007/BF00117280. (a) [DOI] [PubMed] [Google Scholar]; Li J, Zhu T, Cramer CJ, Truhlar DG. J. Phys. Chem. A. 1998;102:1820. (b) [Google Scholar]
- 16.Sanderson RT. Science. 1951;114:670. doi: 10.1126/science.114.2973.670. [DOI] [PubMed] [Google Scholar]
- 17.Gasteiger J, Marsili M. Tetrahedron. 1980;36:3219. [Google Scholar]
- 18.Nalewajski RF. J. Am. Chem. Soc. 1984;106:944. [Google Scholar]
- 19.Mortier WJ, Ghosh SK, Shankar S. J. Am. Chem. Soc. 1986;108:4315. [Google Scholar]
- 20.No KT, Grant JA, Scheraga HA. J. Phys. Chem. 1990;94:4732. (a) [Google Scholar]; No KT, Grant JA, Jhon MS, Scheraga HA. J. Phys. Chem. 1990;94:4740. (b) [Google Scholar]
- 21.Rappé AK, Goddard WA., III. J. Phys. Chem. 1991;95:3358. [Google Scholar]
- 22.Yang Z-Z, Wang C-S. J. Phys. Chem. A. 1997;101:6315. [Google Scholar]
- 23.Cho K-H, Kang YK, No KT, Scheraga HA. J. Phys. Chem. B. 2001;105:3624. [Google Scholar]
- 24.Bultinck P, Langenaeker W, Lahorte P, De Proft F, Geerlings P, Waroquier M, Tollenaere JP. J. Phys. Chem. A. 2002;106:7887. [Google Scholar]
- 25.Yang Z-Z, Cui B-Q. J. Chem. Theory Comput. 2007;3:1561. doi: 10.1021/ct600379n. [DOI] [PubMed] [Google Scholar]
- 26.Czodrowski P, Dramburg I, Sotriffer CA, Klebe G. Proteins. 2006;65:424. doi: 10.1002/prot.21110. [DOI] [PubMed] [Google Scholar]
- 27.Yang Q, Sharp KA. J. Chem. Theory Comput. 2006;2:1152. doi: 10.1021/ct060009c. [DOI] [PubMed] [Google Scholar]
- 28.Berente I, Czinki E, Náray-Szabó G. J. Comput. Chem. 2007;28:1936. doi: 10.1002/jcc.20676. [DOI] [PubMed] [Google Scholar]
- 29.Cornell WD, Cieplak P, Bayly CI, Kollman PA. J. Am. Chem. Soc. 1993;115:9620. [Google Scholar]
- 30.Williams DE. Biopolymers. 1990;29:1367. [Google Scholar]
- 31.Stouch TR, Williams DE. J. Comput. Chem. 1992;13:622. [Google Scholar]
- 32.Urban JJ, Famini GR. J. Comput. Chem. 1993;14:353. [Google Scholar]
- 33.Stouch TR, Williams DE. J. Comput. Chem. 1993;14:858. [Google Scholar]
- 34.Sigfridsson E, Ryde U. J. Comput. Chem. 1998;19:377. doi: 10.1002/jcc.10024. [DOI] [PubMed] [Google Scholar]
- 35.Cieplak P, Cornell WD, Bayly C, Kollman PA. J. Comput. Chem. 1995;16:1357. [Google Scholar]
- 36.Cieplak P, Caldwell J, Kollman PA. J. Comput. Chem. 2001;22:1048. [Google Scholar]
- 37.Rowland RS, Taylor R. J. Phys. Chem. 1996;100:7384. [Google Scholar]
- 38.Vásquez M, Némethy G, Scheraga HA. Macromolecules. 1983;16:1043. [Google Scholar]
- 39.Zimmerman SS, Pottle MS, Némethy G, Scheraga HA. Macromolecules. 1977;10:1. doi: 10.1021/ma60055a001. Backbone conformations C (C*), A (A*), E, F, and D for each residue are equivalent to the γ-turn , α-helical αR (αL), β, polyproline-like (PII or PI), and β2 structures in the literature, respectively. Conformation F* is a mirror image of conformation F. The χ values for side chains in the range of 180 ± 30° are denoted as t, those in the range of 60 ± 30° as g+, and those in the range of −60 ± 30° as g−. [DOI] [PubMed] [Google Scholar]
- 40.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Zakrzewski VG, Montgomery JA, Jr., Stratmann RE, Burant JC, Dapprich S, Millam JM, Daniels AD, Kudin KN, Strain MC, Farkas O, Tomasi J, Barone V, Cossi M, Cammi R, Mennucci B, Pomelli C, Adamo C, Clifford S, Ochterski J, Petersson GA, Ayala PY, Cui Q, Morokuma K, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Cioslowski J, Ortiz JV, Baboul AG, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Gomperts R, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Gonzalez C, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Andres JL, Gonzalez C, Head-Gordon M, Replogle ES, Pople JA. Gaussian 98. Gaussian, Inc.; Pittsburgh, PA: 1998. revision A.7. [Google Scholar]
- 41.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Jr., Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian 03. Gaussian, Inc.; Wallingford, CT: 2004. revision C.02. [Google Scholar]
- 42.Gould IR, Kollman PA. J. Phys. Chem. 1992;96:9255. [Google Scholar]
- 43.Gould IR, Cornell WD, Hillier IH. J. Am. Chem. Soc. 1994;116:9250. [Google Scholar]
- 44.Beachy MD, Chasman D, Murphy RB, Halgren TA, Friesner RA. J. Am. Chem. Soc. 1997;119:5908. [Google Scholar]
- 45.Duan Y, Wu C, Chowdhury S, Lee MC, Xiong G, Zhang W, Yang R, Cieplak P, Luo R, Lee T, Caldwell J, Wang J, Kollman PA. J. Comput. Chem. 2003;24:1999. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 46.Gay DM. ACM Trans. Math. Software. 1983;9:503. [Google Scholar]
- 47.Mulliken RS. J. Chem. Phys. 1934;2:782. [Google Scholar]
- 48.Parr RG, Pearson RG. J. Am. Chem. Soc. 1983;105:7512. [Google Scholar]