Characteristic enrichment of DNA repeats in different genomes

Abstract

Using computer programs developed for this purpose, we searched for various repeated sequences including inverted, direct tandem, and homopurine–homopyrimidine mirror repeats in various prokaryotes, eukaryotes, and an archaebacterium. Comparison of observed frequencies with expectations revealed that in bacterial genomes and organelles the frequency of different repeats is either random or enriched for inverted and/or direct tandem repeats. By contrast, in all eukaryotic genomes studied, we observed an overrepresentation of all repeats, especially homopurine–homopyrimidine mirror repeats. Analysis of the genomic distribution of all abundant repeats showed that they are virtually excluded from coding sequences. Unexpectedly, the frequencies of abundant repeats normalized for their expectations were almost perfect exponential functions of their size, and for a given repeat this function was indistinguishable between different genomes.

The exponential growth of published genomic texts in recent years has fostered much information–content analysis. Very general approaches, including pattern matching (1), word-frequency counting (2), and basic linguistics techniques (3, 4), have been employed to show that genomic DNA is very nonrandom. This analysis, as well as numerous experimental approaches (5, 6), revealed that simple repeated sequences are remarkably abundant in some genomes. At the same time, many repeated sequences have the potential to adopt non-B DNA conformations, which are believed to be important for basic genetic processes (7). Therefore, we were interested in the genomic distribution and abundance of repeated elements, since these data might imply a role for the corresponding non-B DNA structures.

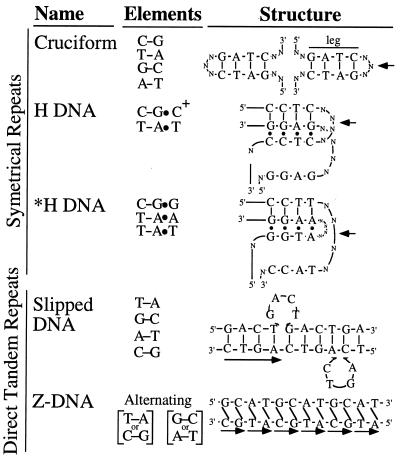
Three types of repeats that can form unusual structures are commonly considered (illustrated in Fig. 1): (i) long inverted repeats are capable of forming hairpins or cruciform structures (8), (ii) perfect or near perfect homopurine–homopyrimidine mirror repeats can adopt triple-helical H conformations (9), (iii) direct tandem repeats can adopt a variety of conformations, including slippage structures (7), left-handed Z-DNA (for alternating purine–pyrimidine repeats) (10), cruciforms (for repeated elements of perfect dyad symmetry and even length) (11), and H-DNA (for some homopurine–homopyrimidine sequences) (12).

Figure 1.

Non-B DNA structures adopted by different repeats. –, Watson–Crick base pairs; •, Hoogsteen base pairs; /, left-handed helix; arrow, center of symmetry.

Previous studies have shown that inverted repeats are statistically overrepresented in many genomes (6, 13–17), which implies a biological function. Z-forming purine–pyrimidine direct tandem repeats are primarily confined to eukaryotic genomes (18, 19). Other direct tandem repeats, for example trinucleotide repeats involved in numerous human neurological pathologies, have been proposed to adopt slipped-loop structures and hairpins (20–22) and have been shown to be statistically enriched in eukaryotes (23–25). Homopurine–homopyrimidine mirror repeats capable of adopting triple-helical H-DNA (26) were shown to be abundant in eukaryotic genomes, but occur infrequently in prokaryotic DNA (17, 27–30).

Though the above results were encouraging, many questions remained unanswered. First, the structure-forming ability of a repeat dramatically depends on its length (7, 31), yet the frequency of different repeats depending on their length was not studied. Second, the expected occurrence of different symmetrical sequences in a random sequence must depend on the local sequence degeneracy, which may vary considerably both in terms of GC-content of DNA (4) and dinucleotide biases (32). Therefore, it is important to adjust models of expectations for these repeats to the local sequence degeneracy. Third, while the general class of all mirror repeats has been previously analyzed, only homopurine–homopyrimidine sequences are capable of adopting H conformation. In addition, *H structures can be formed from CG•G, TA•A, and TA•T triads and thus can be formed by sequences with imperfect mirror repeats (9). Thus, it is of interest to compare the representation of different groups of mirror repeats. Finally, it is crucial to generalize these conclusions to as wide an array of organisms as possible.

To address these issues, we searched for various repeats in ≈12 Mb of published genomic sequences and compared them to their expected values. We analyzed only perfect repeats, since this allowed us to make simple mathematical models of repeat frequency expectations and compare them with observed frequencies. We are aware that this approach excluded the interesting biological phenomenon of interruptions within repeated sequences.

Our analysis shows that eukaryotes and bacteria have distinctly different patterns of repeat enrichment. The only archaebacterium studied and one eubacterium have no repeat enrichment, whereas other eubacteria and organelles are enriched in inverted and sometimes direct repeats. By contrast, eukaryotic genomes are enriched for all repeats studied, including H- and *H-motifs. The frequencies of overrepresented repeats normalized to expected occurrences were almost perfect exponential functions of their lengths, which were indistinguishable between enriched genomes for a given repeat. Because the structure forming ability of a repeat also depends exponentially on its length, we speculate that the abundance of long repeats may indicate an evolutionary advantage conferred by some DNA structures.

MATERIALS AND METHODS

Analyzed Sequences.

A 2.4-Mb Caenorhabditis elegans contig (35.4% GC) was obtained from ftp.sanger.ac.uk (The Sanger Center, Cambridge, U.K., pmn@Sanger.ac.uk). All other sequences were obtained from GenBank using the following accession numbers: Homo sapiens (3.7 Mb, 44.2% GC) from L03723L03723, L05367L05367, L11910L11910, L29074L29074, L36092L36092, L38501L38501, L40416L40416, L43581L43581, L44140L44140, L77570L77570, L78810L78810, M86525M86525, U07000U07000, U40455U40455, U47924U47924, U52111U52111, U52112U52112, U62317U62317, X87344X87344, Z72519Z72519, Z73986Z73986, Z74696Z74696, Z74739Z74739, Z75741Z75741 and Z75889Z75889; Saccharomyces cerevisiae (1.4 Mb, 38.6% GC) from D44605D44605, D50617D50617, S43845S43845, S49180S49180, S58084S58084, S93798S93798, U12980U12980, X59720X59720, X94335X94335, Z37996Z37996, Z37997Z37997, Z38059Z38059, Z38060Z38060, Z38061Z38061, Z38062Z38062, Z38113Z38113, Z38125Z38125, Z46728Z46728, Z46833Z46833, Z46861Z46861, Z46881Z46881, Z46902Z46902, Z46921Z46921, Z47047Z47047, and Z71255Z71255; Escherichia coli (1 Mb, 50.9% GC) from U28377U28377, M87049M87049, U00039U00039, and U18997U18997; the complete Haemophilus influenzae (1.8 Mb, 38.2% GC) and Methanococcus jannaschii (1.6 Mb, 31.4% GC) genomes from L42023L42023 and L77117L77117, respectively; the complete genome of Synechocystis sp. PCC6803 (155 kb, 46.9%) from D90917D90917; and chloroplast genomes (1.1 Mb, 33.8% GC) from D17510D17510, S54304S54304, S55425S55425, U38804U38804, X04465X04465, X15901X15901, X79898X79898, X86563X86563, Y00686Y00686, Z00044Z00044, Z11874Z11874, and Z67753Z67753. The total length of all sequences analyzed was 12 × 10⁶ nt. Sequences derived from several large but unrelated contigs (e.g., H. sapiens sequences) were assembled in random order for further analysis. Except for some complete organelle genomes, no sequence used was less than 50 kb.

Search Algorithms.

Various computer programs, written in think pascal (Symantec Corporation, Eugene, OR) or hypercard (Apple), were developed for the Macintosh OS 7.5 to analyze large genomic texts.

A symmetrical repeat of length n was said to exist at point x when, for some loop value L, every base x + 1 − i matches every base x + L + i for 1 ≤ i ≤ n. For this study, 2 ≤ L ≤ 6. Two bases, B₁ from one side of the repeat and B₂ from the other side of the repeat, are matched if element B₁,B₂ of a characteristic matrix, m, is 1 and unmatched otherwise. Different symmetrical structures have different characteristic matrices, according to the base pairing rules of that structure. The characteristic matrices used in this study are listed in Table 1. In some cases, symmetrical repeats were analyzed for being direct tandem repeats as well. For this purpose, the entire sequence from the most 5′ to the most 3′ was subjected to the assay described below.

Table 1.

Mathematical descriptions of different repeats studied

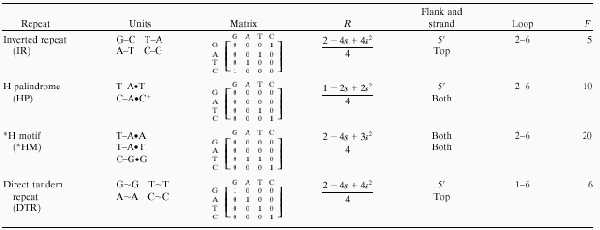
Units are the physical elements involved in the non-B DNA structures adopted by these repeats, either Watson–Crick base pairs, Hoogsteen triads, or unspecified interactions for inverted, mirror, and direct tandem repeats, respectively. IR, HP, *HM, and DTR are inverted repeats, H palindromes, *H motifs, and direct tandem repeats, respectively. The characteristic matrix summarizes the possible interactions such that 1 and 0 indicate that two bases can or cannot interact, repectively. R is the expected probability of a single pair of nucleotides matching (1 in the corresponding entry on the characteristic matrix) based on GC content. We searched for repeats on either the top or the top and bottom strands. In the case of *H motifs we also allowd both 5′ to 3′ and 3′ to 5′ orientations. Loops are assumed to be noninteracting bases in the case of symmetric repeats. For direct tandem repeats, the “loop” is the elementary repeat unit. F is a factor representing the number of cases examined at a single point (the range of loop sizes times the number of strands searched times the number of orientation examined).  

A direct tandem repeat of length n was considered to exist at point x when, for some core repeat length L, every base at position x + L + i − 1 matched position x + [(i − 1) modulo L] for 1 ≤ i ≤ n. For this study, 1 ≤ L ≤ 6 and L ≤ n. Note that this algorithm allows for partial repeats (e.g., GAGAG) and requires that the core element repeats at least once. The characteristic matrix for this match is a simple “identity” matrix listed in Table 1.

Depending on the asymmetry of the matching matrix, some repeats were searched for on both strands (H and *H motifs) or in both (5′ to 3′ and 3′ to 5′) orientations (*H motifs). Only the longest repeats for a given p and L were taken and n was constrained to be at least 8. Note that these algorithms find all possible repeats described by a given match matrix, including those that are identical except for the loop or core repeat size, L, or those that are near one another but which share flanking sequences. Because of the degenerate nature of the sequences studied, overlapping repeats are not independent events. To eliminate this problem, we counted clusters of overlapping repeats as single events. When repeats were considered in aggregate on blocks of contiguous DNA of length B, every repeat that overlapped with bases B(n − 1) + 1 and Bn (where n ∈ 1, 2, 3…) was counted as belonging to block n.

Probability Calculations.

The occurrence of a repeat depends strongly on the local GC content, s_i, of a genomic text,

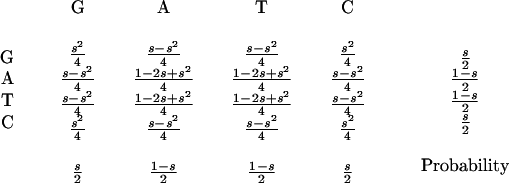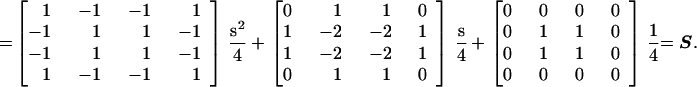such that the probability of all pair-wise combinations of two bases can be described as:

The probability of two randomly chosen bases being a correct match for a given repeat type is R = Σ_jk[S_jk × M_jk] for j,k ∈ {G, A, T, C}. Similarly, the probability of extending a symmetrical repeat by one step can be given in terms of dinucleotide probabilities. In this case, assume two previous bases, A and B, are matched (as defined by M). Then

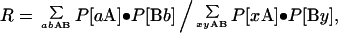where P[mn] is the dinucleotide frequency of pair mn, a and b are constrained to match by M, and x and y are arbitrary bases. If F (shown in Table 1) is the product of the number of orientations and strands searched (1, 2, or 4), then the expected number of repeats of length n at a point x is FRⁿ. Values of s (and hence R) at every point x were determined from a floating window of 21 bases (10 before and 10 after). In a block of text of size B, one expects BFRⁿ repeats and the probability of at least one occurrence is 1 − (1 − Rⁿ)^BF ≈ BFRⁿ for the range of n used in this study. Blocks in this study were taken to be consecutive, nonoverlapping genomic texts.

Overlap Analysis.

Repeats located as described above were compared for overlap with all RNA and peptide features described in published GenBank annotations. Statistics are from a one-sample proportion test (33).

RESULTS

Different repeated sequences that are able to form different non-B DNA conformations are presented in Fig. 1. Cruciforms are formed by inverted repeats using Watson–Crick GC and AT base pairs. H DNA is formed by homopurine–homopyrimidine mirror repeats (H palindromes) and is composed of CG*C⁺ and TA*T base triads. *H DNA can be built from intervening CG*G, TA*A, and TA*T triads, so that guanines should be mirror repeated, whereas adenines in one-half of the purine-rich strand could be reflected by either adenines or thymines in its other half. We term these sequences *H motifs. Slipped DNAs can be formed by direct tandem repeats where one or more of the repeats is looped out. Finally, Z DNA is formed by alternating purine–pyrimidine tandem repeats.

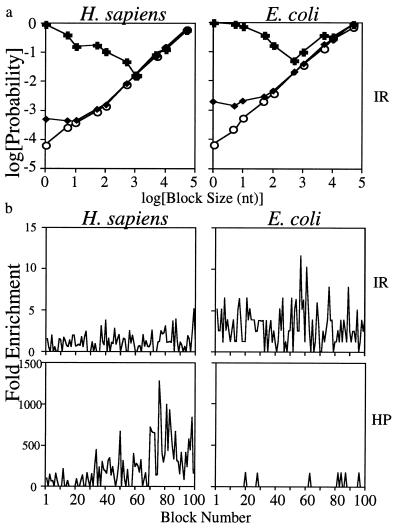
Preliminary investigations revealed that the presence of a cluster of repeats at one position indicated that others nearby were also likely, even when directly overlapping repeats were counted as single events. Many methods have been devised for eliminating this dependence, including r-scan analysis (34). It is important, therefore, to choose an adequate block size. We reasoned that for small consecutive blocks, the probability of having at least one cluster of repeats was dependent on the state of the block before. For sufficiently large blocks this probability would become independent. To find this point, we divided several genomes into consecutive, identical blocks differing in size from 1–100,000 nt and counted (i) the proportion of blocks that contained one or more repeats when the previous neighbor also had a repeat, (ii) the proportion of blocks with repeats when the previous neighbor had no repeat, and (iii) the proportion of blocks with repeats, irrespective of the previous block. At a block size that conferred independence these three probabilities must converge. Fig. 2a shows typical results for clusters of inverted repeats in the genomes of H. sapiens and E. coli. They show that 1,000 nt (H. sapiens) to 10,000 nt (E. coli) are required for cluster independence. This difference does not reflect the difference in the absolute number of inverted repeats among species (see Table 2 and discussion below). To provide a margin of safety, we chose 40 kb as our block size. To verify that this choice was appropriate, we calculated the ratio of the observed number of inverted repeats and H palindromes to their expected value (overrepresentation) on consecutive 40-kb intervals in human and E. coli. Fig. 2b shows a plot of these data where it can be seen that there is relatively small variation in the distribution of repeats. The remaining variation exists even at very large scales.

Figure 2.

Selection of block sizes with minimal clustering of repeats. (a) Conditional probabilities of blocks of different sizes having an inverted repeat based on the previous block having a repeat (+), not having a repeat (○), or regardless of the previous block (♦). Representative data are from inverted repeats of H. sapiens and E. coli. (b) Frequency of repeats in 40-kb blocks relative to expectations along the same length of genomic DNA. Inverted and H palindromes are shown for H. sapiens and E. coli. IR and HP are defined in Table 1.

Table 2.

Absolute frequencies of various putative structure-forming elements

	Obs  Err	Expected	P
H. sapiens
IR	0.48  ±  0.24	0.014	0.03	√
HP	0.74  ±  0.19	0.00001	<10−5	√
*HM	0.85  ±  0.13	0.0043	<10−16	√
DTR	1.00  ±  0.00	0.017	<10−16	√
S. cerevisiae
IR	0.29  ±  0.20	0.022	0.097	√
HP	0.31  ±  0.21	0.00001	0.075	√
*HM	0.58  ±  0.24	0.014	0.0096	√
DTR	1.00  ±  0.00	0.026	<10−16	√
Chloroplasts
IR	0.90  ±  0.090	0.039	<10−16	√
HP	0.033  ±  0.090	0.00002	0.15060
*HM	0.2903  ±  0.21	0.04175	0.11381
DTR	0.77  ±  0.17	0.047	0.00003	√
E. coli
IR	0.73  ±  0.20	0.012	1.4  ×  10−5	√
HP	0.00  ±  0.00	0.00001	1.0
*HM	0.00  ±  0.00	0.00131	1.0
DTR	0.12  ±  0.10	0.014	0.16
H. influenzae
IR	0.80  ±  0.16	0.023	<10−16	√
HP	0.00  ±  0.00	0.00001	1.0
*HM	0.00  ±  0.00	0.015	1.0
DTR	0.39  ±  0.24	0.027	0.064	√
Synechocystis
IR	0.00	0.024
HP	0.00	0.00006
*HM	0.00	0.002
DTR	0.25	0.014
M. jannaschii
IR	0.29  ±  0.20	0.055	0.13
HP	0.00  ±  0.00	0.00003	1.00
*HM	0.26  ±  0.19	0.073	0.16
DTR	0.19  ±  0.15	0.065	0.21

The frequencies of various repeats were calculated per 40,000 bp in different genomes. IR, HP, *HM, and DTR are as described in Table 1. The fraction of 40-kb blocks with at least one repeat is given (observed; Obs). Errors (Err) were calculated from sampling at least 25 blocks. The only exception is Synechocystis, the sequence of which consists of only four blocks. It is, however, the only eubacterium studied with no enrichment in inverted repeats. Expected frequencies were calculated as described in Materials and Methods. Significant differences (P < 0.10) are indicated by check marks. 

Adopting this block size, we counted the frequency of various repeats (nonoverlapping clusters) in 40-kb blocks in the genomes of organisms from all three divisions of life. Table 2 shows the result for all four types of repeats, each with at least 12 nt in one flank. We counted the proportion of blocks with at least one repeat, with errors calculated from a 7-block floating window from at least 25 trials (blocks). Expected frequencies were calculated based on the GC-content of the block. The P values are from standard χ² analysis of the difference between expected and observed proportions of blocks with at least one repeat. As can be seen in these data, all types of repeats are overrepresented in eukaryotes, but only inverted and direct repeats are significant in organelles and at least some bacteria. H palindromes are exclusively represented in eukaryotes.

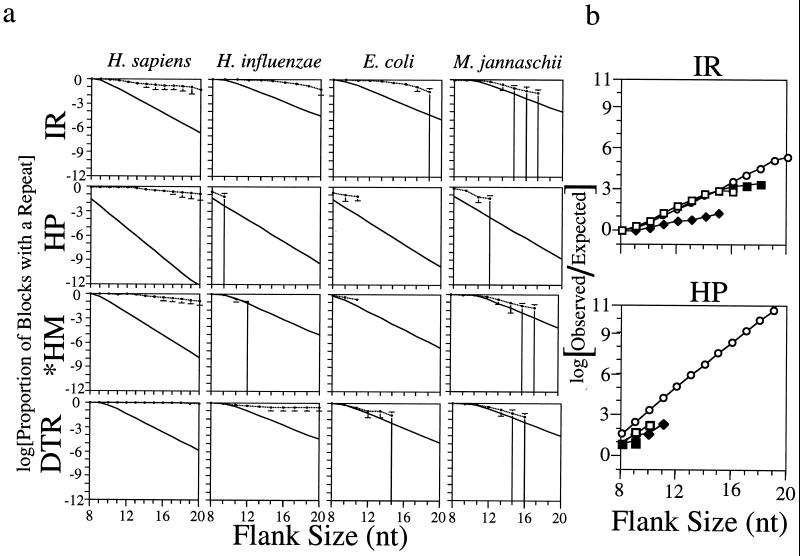
One of the canonical features of the structure-forming ability of many repeats is its length dependence. Since longer sequences are more likely to form structures (35), any selective advantage conferred by the structure-forming ability of a given repeat should be reflected in a similar length dependence of enrichment; longer repeats should become more common over time because they make more effective structures. On the other hand, it is well known that some repeated sequences are very unstable and are shortened in the process of replication, recombination, and repair (36). Thus, a long repeat that does not give evolutionary advantage is likely to be eliminated. To address this hypothesis, we compared each size category of repeats having from 8–20 nt in one flank. We counted the frequency of 40-kb blocks that contained at least one repeat of at least this size. Errors and expected frequencies were estimated as above.

Fig. 3a shows the results for a representative panel of species and repeat types. In general, repeats found to be enriched in Table 2 also show a length-dependent enrichment. It appears that the observed frequency-of-repeat occurrence only weakly depends on the size of the repeat, whereas expected frequencies drop exponentially to zero. By contrast, for the repeats that were not significantly enriched in Table 2, frequencies fall with length much like their expectations. Inverted repeats show strong length-dependent overrepresentation in eukaryotes, organelles, and many prokaryotes, but mirror repeats (including CA, AT, and GATC containing mirror repeats, data not shown) are a strictly eukaryotic function. Direct tandem repeats are common to eukaryotes but are absent in some bacteria.

Figure 3.

Length dependence of repeat frequencies. (a) Observed proportion of 40-kb blocks with at least one repeat compared with their calculated expectation. Lengths without data shown for a particular species have no repeat at that length. Error bars are 1 SD. Large error bars result from small samples. Upper lines are observed frequencies, whereas lower lines represent expected frequencies based on sequence heterogeneity. IR, HP, *HM, and DTR are defined in Table 1. (b) Ratio of observed to expected frequencies of inverted and mirror repeats for several genomes. (○), H. sapiens ratios, (□), E. coli ratios, (▪), H. influenzae ratios, (⋄), M. jannaschii ratios.

Because observed repeat frequencies are only weakly exponential, while expectations are strongly exponential, the ratio of observed to expected frequencies is an exponential function. Fig. 3b shows a plot of this ratio: it is identical in all organisms that show any enrichment. The strongest enrichment is seen for H palindromes, where it is several billion-fold for large repeats.

We modeled expected frequencies based on the GC content of the sequence and observed a very strong exponential drop in repeat expectations with increasing length. It could be argued that the use of other models for sequence degeneracy might lead to less dramatic dependence of expected repeat frequencies on their sizes. To address this possibility, we also employed another model for expectations based on observed dinucleotide biases of the sequence, as described in Materials and Methods. This model leads to virtually identical results as those based on the GC content model (data not shown). We do not believe, therefore, that overrepresentation of different repeats is merely a reflection of a dinucleotide bias.

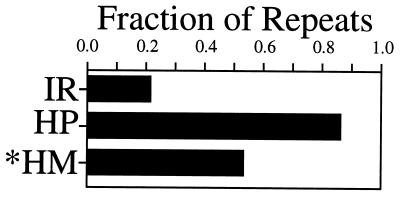
Whereas it has long been known that direct repeats are abundant in eukaryotes, the dramatic overrepresentation of such mirror repeats as H palindromes was a surprise. It should be noted, however, that a given sequence can often be considered as both a direct and a mirror repeat. Good examples are the frequent eukaryotic repeats d(G–A)_n•d(T–C)_n or d(G–T)_n•d(A–C)_n. This raises an important question: what fraction of our mirror repeats are also direct repeats?

To address this question, we analyzed the pool of different mirror repeats for being direct repeats according to the criteria described in the Materials and Methods. Fig. 4 shows the frequency of various symmetrical repeats that are also simple tandem direct repeats. Most mirror repeats in the human genome are also direct repeats. In the most extreme case, up to 85% of all H palindromes are direct repeats. For comparison, only 20% of inverted repeats are direct repeats as well. Similar proportions were observed in yeast DNA (data not shown). Note, however, that even the remaining 15% of H palindromes that are not also direct repeats represent a dramatic enrichment over the chance occurrence (P < 10⁻⁵ for length ≥ 12). Our calculations also show that this subset of mirror repeats retains exponential length dependence.

Figure 4.

Fraction of various repeats that are also perfect direct tandem repeats. IR, HP, and *HM are defined in Table 1.

We also noted that the overlap between mirror and direct repeats is most prominent for AT-rich sequences (data not shown). In contrast, the coincidence between being direct and mirror repeats is rare in prokaryotic DNA (data not shown). The high coincidence between symmetrical and tandem repeats in eukaryotes is not accidental: computer evaluation of all possible H palindromes with flanks of 8 nt or more revealed that only 20% were also direct repeats.

High overrepresentation of various repeats leads to an obvious question: what is their distribution in different genomes? It is particularly interesting for eukaryotic genomes, since we observed similar overrepresentation for all of them, while the fraction of the genome corresponding to coding sequences differs dramatically: from 67% in yeast DNA down to 4% in a representative human sequence.

To answer this question, we checked each structure for overlap with the coding features described by GenBank annotation as described above. By chance, overlap with coding sequences should equal the proportion of the genome covered by coding sequences. Comparisons shown in Table 3 are based on simple proportion tests. In eukaryotes, both inverted and mirror repeats are virtually excluded from coding sequences. The probability of this occurring by chance is extremely low. By contrast, only inverted but not mirror repeats are excluded from the coding sequences of E. coli DNA. The difference between eukaryotes and E. coli is not merely a function of the density of coding sequences, since yeast sequences have fairly similar coverage. Combining this with the frequency data, we believe that repeats that are represented above chance in a given DNA are efficiently excluded from coding sequences.

Table 3.

Overlap of inverted repeats and H palindromes with coding sequences

Species	IR		HP
	Overlap	P	Overlap	P
Human (4.2%)	9/426	0.01	0/627	≈10−9
Yeast (68%)	61/164	<10−9	31/102	<10−9
E. coli (87%)	125/254	<10−9	4/4	0.22

The overlap of published peptide and RNA sequences and different repeats was scored if any base in a coding sequence was also shared by at least one inverted repeat or H palindrome (IR and HP, respectively). Overlap lists the number of overlaps compared to the total number examined. P is the computed proportion test with the sample size in excess of 25 in all cases shown. 

DISCUSSION

Our data show that repeat enrichment varies between bacteria and eukaryotes. Though the differences in occurrence for repeats with a flank of at least 12 nt are statistically significant, they are not always large. Thus, we decided to expand this analysis to include the overrepresentation dependence on repeat length. To the best of our knowledge, this is the first analysis of this kind and it gives two principal results.

First, as seen in Fig. 3a, for every repeat showing overrepresentation in Table 2, length increase leads to a dramatic rise in frequency over chance expectations. For example, H palindromes are enormously (up to 10⁹-fold over chance) overrepresented in eukaryotes. This difference is highly significant and, thus, not accidental. At the same time, H palindromes occur at chance frequencies in prokaryotic and organelle genomes.

Second, if we normalize frequencies of occurrence of enriched repeats to their expected occurrence (Fig. 3b), we observe almost perfect exponential dependence of their length: O/E = e^−k1_N, where O is the observed and E is the calculated frequency, k₁ is a constant, and N is the sequence length. From elementary thermodynamics, we know that the probability, P, of the formation of a DNA structure also depends exponentially on the length of the sequence (35): P = e^−k2_N, where k₂ is a constant. Taken together, this implies that the overrepresentation of repeated sequences corresponds simply to the probability of a DNA structure formation: P^k1_/k2 = O/E. Consequently, it may not be that surprising that the most enriched repeats have the potential to form unusual DNA structures such as H DNA, Z DNA, cruciforms, and slipped structures.

The enrichment of different repeats raises the question of whether all sequences corresponding to a given repeat type are equally overrepresented. Our first observations lead to some interesting preliminary conclusions. First, symmetrical repeats in prokaryotes are almost never also direct repeats, whereas, in contrast, eukaryotic symmetrical repeats are very frequently directly repeated (Fig. 4). Second, the GC content of various prokaryotic repeats roughly reflects the average genomic sequence composition, whereas eukaryotic repeats are often quite unusual in sequence. Strikingly, most long eukaryotic inverted repeats are less than 10% GC rich, whereas long H palindromes show a bimodal distribution with one-half of these repeats having less that 10% GC and one-half having between 20 and 40% GC (data not shown).

Our data represent the first analysis of repeat frequency in archaebacteria. The finding that no repeat is enriched is particularly intriguing considering numerous speculations on the phylogenetic relations between archaea and eukarya. It indicates that, with respect to repeat distributions, M. jannaschii is much more similar to prokarya than eukarya. In the paper describing the M. jannaschii genome (37), the authors found several imperfect mirror repeats on the large extrachromosomal element, but our analysis shows that the frequency of these sequences is statistically close to chance.

Our finding that inverted repeats are common for both pro- and eukaryotes, while mirror repeats are only abundant in eukaryotes, is in agreement with the most complete previous study of Schroth and Ho (17). We disagree, however, with their conclusion that the enrichment of mirror repeats is different in different eukaryotes increases from yeast to human; we found that for a given mirror repeat enrichment is a very similar function of size in all eukaryotes studied. The difference between their study and ours is likely to be due to the fact that they calculated the chance occurrence for different repeats based on the assumption that DNA is homogeneously 50% GC, while we considered local GC content. Similarly, we observed identical enrichment of inverted repeats for eukaryotes and some eubacteria, whereas Schroth and Ho concluded that they are most frequent in E. coli.

The overrepresentation of mirror repeats raises the question of the mechanisms of their accumulation and maintenance. A key question is whether there exists a special mechanism leading to their propagation, or they are simply a byproduct of the propagation of direct repeats, widely acknowledged for eukaryotes (19, 29, 30, 38, 39). We found that up to 85% of all our mirror repeats can be considered to be direct repeats as well. Thus, the latter opportunity seems more likely. Note, at the same time, that even the remaining 15% of H palindromes represent an enormous enrichment over chance. This implies an evolutionary value for mirror repeat maintenance.